Validation of the EROSION-3D Model through Measured Bathymetric Sediments
Abstract
1. Introduction
- (a)
- To model and measure the sedimentation of a small reservoir in a small rural catchment;
- (b)
- To evaluate the role of an intensive rainfall event in the erosion process;
- (c)
- To validate the results from the physically-based EROSION-3D model through the bathymetric measurement of the mass of sediment in a small reservoir.
2. Materials and Methods
2.1. EROSION-3D Model
2.2. Long-Term Simulation in the EROSION-3D Model
- (1)
- The simulations are based on iterations where one or more events have recurred. How often single events or sequences of events are repeated is determined according to the iterative value.
- (2)
- A combination of individual single events is used to summarize the sequences of rainfall events. Based on this assumption, the model behaves like a continuous model and provides overall results.
- (3)
- A long-term simulation based on a continuous rainfall series consists of a chronological series of single rainstorms that occur within the period evaluated. Each rainfall event needs its own soil data set whose parameters account for the individual soil conditions and the stages of crop growth as of that date.
3. The Case Study
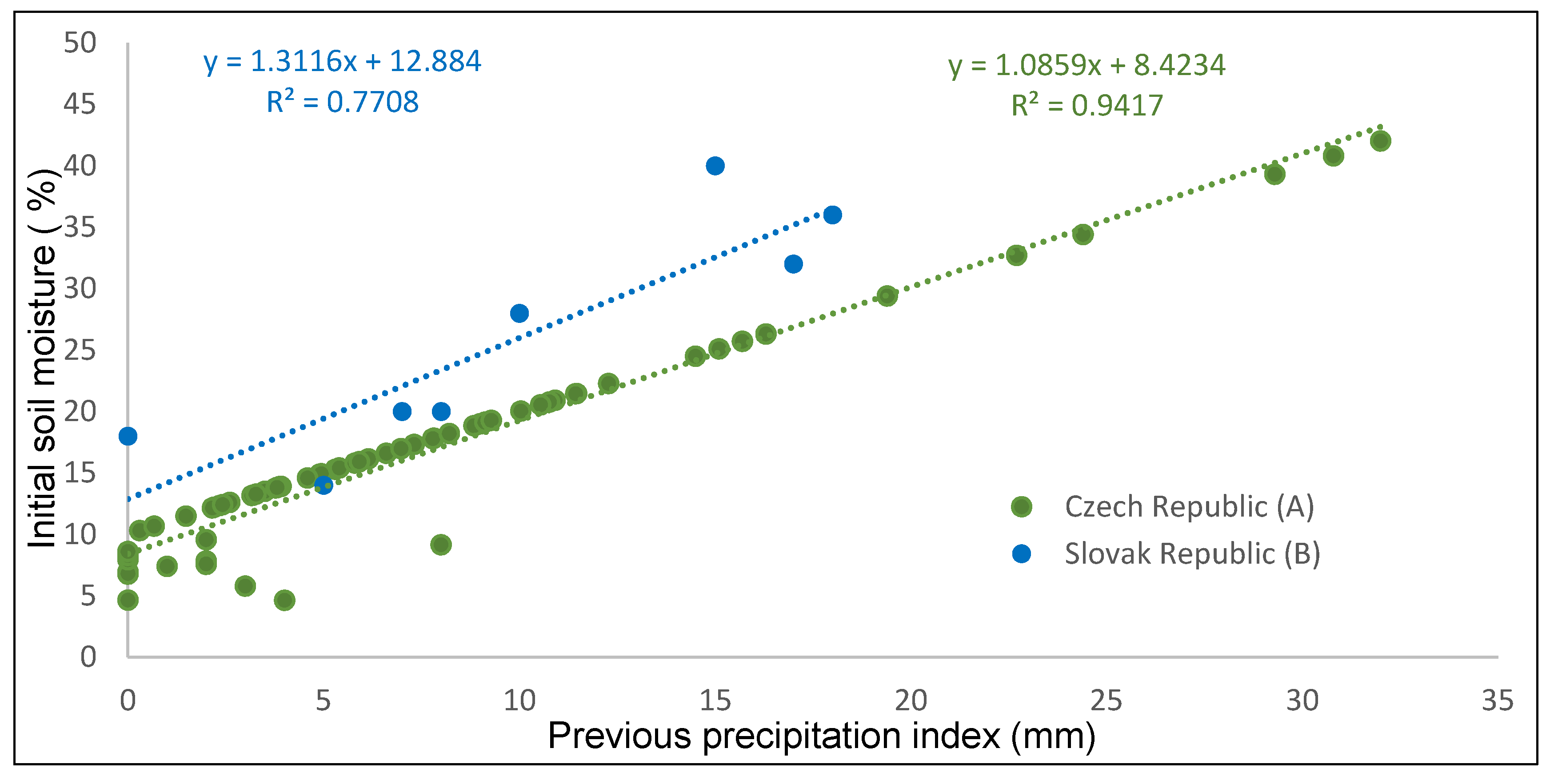
4. Data
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rawat, P.K.; Tiwari, P.C.; Pant, C.C.; Sharama, A.K.; Pant, P.D. Modelling of stream run-off and sediment output for erosion hazard assessment in Lesser Himalaya: Need for sustainable land use plan using remote sensing and GIS: A case study. Nat. Hazards 2011, 59, 1277–1297. [Google Scholar] [CrossRef]
- Markantonis, V.; Meyer, V.; Schwarze, R. Valuating the intangible effects of natural hazards—Review and analysis of the costing methods. Nat. Hazards Earth Syst. Sci. 2012, 12, 1633–1640. [Google Scholar] [CrossRef]
- Wainwright, J.; Parsons, A.J.; Michaelides, K.; Powell, D.M.; Brazier, R. Linking Short- and Long-Term Soil—Erosion Modelling. In Long Term Hillslope and Fluvial System Modelling, 1st ed.; Lang, A., Dikau, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 37–51. [Google Scholar]
- Hlavčová, K.; Kohnová, S.; Borga, M.; Horvát, O.; Šťastný, P.; Pekárová, P.; Majerčáková, O.; Danáčová, Z. Post-event analysis and flash flood hydrology in Slovakia. J. Hydr. Hydrom. 2016, 64, 304–315. [Google Scholar] [CrossRef]
- Renfro, W.G. Use of erosion equation and sediment delivery ratios for predicting sediment yield. In Present and Prospective Technology for Predicting Sediment Yields and Sources, 1st ed.; US Department of Agriculture Publication ARS-S-40: Washington, DC, USA, 2018; pp. 33–45. [Google Scholar]
- Kirkby, M.J.; Morgan, R.P.C. Soil Erosion, 1st ed.; John Wiley and Sons: Chichester, UK, 1980; p. 306. [Google Scholar] [CrossRef]
- Walling, D.E. The sediment delivery problem. J. Hydrol. 1983, 65, 209–237. [Google Scholar] [CrossRef]
- Richards, K. Sediment delivery and drainage network. In Channel Network Hydrology, 1st ed.; Beven, K., Ed.; Wiley: New York, NY, USA, 1993; Volume 1, pp. 221–254. [Google Scholar]
- Atkinson, E. Methods for assessing sediment delivery in river systems. Hydrol. Sci. J. 1995, 40, 273–280. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, H. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning, 1st ed.; U.S. Dep. of Agriculture: Washington, DC, USA, 1978; p. 85.
- Nearing, M.A.; Lane, L.J.; Lopes, V.L. Modeling Soil Erosion. In Soil Erosion Research Methods, 2nd ed.; Lal, R., Ed.; Routledge: New York, NY, USA, 1994; p. 127. [Google Scholar]
- Kandel, D.D.; Western, A.W.; Grayson, R.B.; Turral, H.N. Process parameterization and temporal scaling in surface runoff and erosion modelling. Hydrol. Process. 2004, 18, 1423–1446. [Google Scholar] [CrossRef]
- Merritt, W.S.; Letcher, R.A.; Jakeman, A.J. A review of erosion and sediment transport models. Environ. Mod. Soft. 2003, 18, 761–799. [Google Scholar] [CrossRef]
- Kwong, F.A.L. Quantifying Soil Erosion for the Shihmen Reservoir Watershed, Taiwan. Agric. Sys. 1994, 45, 105–116. [Google Scholar] [CrossRef]
- Pandey, A.; Himanshu, S.K.; Mishra, S.K.; Singh, V.P. Physically based soil erosion and sediment yield models revisited. Catena 2016, 147, 595–620. [Google Scholar] [CrossRef]
- Hajigholizadeh, M.M.; Hector, A.F. Erosion and Sediment Transport Modelling in Shallow Waters: A Review on Approaches, Models and Applications. Int. J. Environ. Res. Public Health 2018, 15, 518. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Green, T.R.; Beavis, S.G.; Zhang, L.; Dietrich, C.R.; Crapper, P.F. Modelling upland and instream erosion, sediment and phosphorus transport in a large catchment. Hydrol. Process. 1999, 13, 745–752. [Google Scholar] [CrossRef]
- Kuznetsov, M.S.; Gendugov, V.M.; Khalilov, M.S.; Ivanuta, A.A. An equation of soil detachment by flow. Soil Tillage Res. 1998, 46, 97–102. [Google Scholar] [CrossRef]
- Wei, H.; Nearing, M.A.; Stone, J.J.; Guertin, D.P.; Spaeth, K.E.; Pierson, F.B.; Nichols, M.H.; Moffet, C.A. A New Splash and Sheet Erosion Equation for Rangelands. Soil Sci. Soc. Am. J. 2009, 73, 1386–1392. [Google Scholar] [CrossRef]
- Iglesias, I.; Avilez-Valente, P.; Bio, A.; Bastos, L. Modelling the Main Hydrodynamic Patterns in Shallow Water Estuaries: The Minho Case Study. Water 2019, 11, 1040. [Google Scholar] [CrossRef]
- Marttila, H.; Klöve, B. Dynamics of erosion and suspended sediment transport from drained peatland forestry. J. Hydrol. 2010, 388, 414–425. [Google Scholar] [CrossRef]
- Ayele, G.T.; Teshale, E.Z.; Yu, B.; Rutherfurd, I.D.; Jeong, J. Streamflow and Sediment Yield Prediction for Watershed Prioritization in the Upper Blue Nile River Basin, Ethiopia. Water 2017, 10, 782. [Google Scholar] [CrossRef]
- García-Ruiz, J.M.; Beguería, S.; Nadal-Romero, E.; González-Hidalgo, J.C.; Lana-Renault, N.; Sanjuán, Y. A meta-analysis of soil erosion rates across the world. Geomorphology 2015, 239, 160–173. [Google Scholar] [CrossRef]
- Boyle, J.F.; Plater, A.J.; Mayers, C.; Turner, S.D.; Stroud, R.W.; Weber, J.E. Land use, soil erosion, and sediment yield at Pinto Lake, California: Comparison of a simplified USLE model with the lake sediment record. J. Paleolimnol. 2011, 45, 199–212. [Google Scholar] [CrossRef]
- Schmidt, J. A mathematical model to simulate rainfall erosion. Catena 1991, 19, 101–109. [Google Scholar]
- Green, W.H.; Ampt, G. Studies of soil physics: The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Von Werner, M. Erosion-3D: User Manual, version. 3.1.1; Michael von Werner Berlin: Berlin, Germany, 2006; p. 54. [Google Scholar]
- Campbell, G.S. Soil physics with basic: Transport models for soil-plant systems. DEV. Soil Sci. 1985, 14, 252–254. [Google Scholar]
- Von Werner, M. Erosion-3D Version 3.0 User Manual—Samples. 2003; GeoGnostics Software: Berlin, Germany, 2003; p. 34. [Google Scholar]
- Schmidt, J. Development and Application of a Physically Established Simulation Model for the Erosion of Agricultural Areas; Institute of Geographic Sciences: Berlin, Germany, 1996; p. 148. [Google Scholar]
- VODOTIKA. Polder Svacenický Creek. Bratislava, 10-01-2008; Project documentation; Vodotika: Bratislava, Slovak Republic, 2008; p. 35. [Google Scholar]
- Morgan, R.; Quinton, J.; Smith, R.; Govers, G.; Poesen, J.; Auerswald, K.; Chisci, C.; Torri, D.; Styczen, M.E. The European soil erosion model (EUROSEM)—A process-based approach for predicting sediment transport from fields and small catchments. Earth Surf. Proc. Land. 1998, 23, 527–544. [Google Scholar] [CrossRef]
- Laflen, J.M.; Elliot, W.J.; Flanagan, D.C.; Meyer, C.R.; Nearing, M.A. WEPP-predicting water erosion using a process-based model. J. Soil Water Conserv. 1997, 52, 96–102. [Google Scholar]
- De Roo, A.P.J.; Wesseling, C.G.; Ritsema, C.J. LISEM: A single event physically based hydrological and soil erosion model for drainage basins. I: Theory, input and output. Hydrol. Process. 1996, 10, 1107–1117. [Google Scholar] [CrossRef]
- Stocking, M.A.; Elwell, H.A. Rainfall erosivity over Rhodesia. Trans. Inst. Brit. Geogr. 1976, 1, 231–245. [Google Scholar] [CrossRef]
- Pasák, V. Soil Protection against Erosion, 1st ed.; State Agricultural Publishing House Prague: Prague, Czech, 1984; p. 164. [Google Scholar]
- Brychta, J.; Janeček, M. Determination of erosion rainfall criteria based on natural rainfall measurement and its impact on spatial distribution of rainfall erosivity in the Czech Republic. Soil Water Res. 2019, 14, 153–162. [Google Scholar] [CrossRef]
- Hucko, P.; Šumná, J. Verification of the System of Sediment Disposal from Water Management Reservoirs, 1th ed.; VÚVH: Bratislava, Slovak, 2003. [Google Scholar]
- Schindewolf, M.; Bornkampf, C.; von Werner, M.; Schmidt, J. Simulation of Reservoir Siltation with a Process-based Soil Loss and Deposition Model. In Effects of Sediment Transport on Hydraulic Structures; Vlassias, H., Ed.; Democritus University of Thrace: Xanthi, Greece, 2015; pp. 41–57. [Google Scholar] [CrossRef]
- Carvalho, D.F.; Eduardo, E.N.; de Almeida, W.S.; Santos, L.A.F.; Sobrinho, T.A. Water erosion and soil water infiltration in different stages of corn development and tillage systems. Rev. Bras. Eng. Agríc. Ambient. Agric. 2015, 19, 1072–1078. [Google Scholar] [CrossRef]
- Panagos, P.; Borelli, P.; Meusburger, K.; Alewell, C.; Lugato, E.; Montanarella, L. Estimating the soil erosion cover-management factor at the European scale. Land Use Policy 2015, 48, 38–50. [Google Scholar] [CrossRef]
- Bo, M.; Xiaoling, Y.; Fan, M.; Zhanbin, L.; Faqi, W. Effects of Crop Canopies on Rain Splash Detachment. PLoS ONE 2014, 9, 10. [Google Scholar] [CrossRef]
- Hugo, V.; Zuazo, D.; Rocío, C.; Pleguezuelo, R. Soil-erosion and runoff prevention by plant covers. A review. Agric. Sustain. Dev. 2008, 1, 65–86. [Google Scholar] [CrossRef]
- Ebabu, K.; Tsunekawa, A.; Haregeweyn, N.; Adgo, E.; Meshesha, D.T.; Aklog, D.; Masunaga, T.; Tsubo, M.; Sultan, D.; Fenta, A.A.; et al. Effects of land use and sustainable land management practices on runoff and soil loss in the Upper Blue Nile basin. Sci. Total Environ. 2019, 648, 1462–1475. [Google Scholar] [CrossRef] [PubMed]
- Knapen, A.; Poesen, J.; De Baets, S. Seasonal variations in soil erosion resistance during concentrated flow for a loess-derived soil under two contrasting tillage practices. Soil Tillage Res. 2007, 94, 425–440. [Google Scholar] [CrossRef]
- Uhrová, J.; Bachan, R.; Štěpánková, P. Determination of soil loss from erosion rills by method of digital photogrammetry and method of volumetric quantification. VTEI 2018, 6, 35–38. [Google Scholar]
- Uhrová, J.; Štěpánková, P.; Osičkovám, K. Complex system of natural water retention measures against erosion and flash floods. VTEI 2016, 4, 13–19. [Google Scholar]
- Michael, A. Anwendung des Physikalisch Begründeten Erosionsprognosemodells EROSION 2D/3D—Empirische Ansätze zur Ableitung der Modellparameter. Ph.D. Thesis, Technische Universität Bergakademie Freiberg, Freiberg, Germany, 2000. [Google Scholar]
- Zolina, O.; Simmer, C.; Kapala, A.; Shabanov, P.; Becker, P.; Mächel, H.; Gulev, S.; Groisman, P. Precipitation Variability and Extremes in Central Europe: New View from STAMMEX Results. Bull. Am. Met. Soc. 2014, 99, 995–1002. [Google Scholar] [CrossRef]
- Dolák, L.; Řezníčková, L.; Dobrovolný, P.; Štěpánek, P.; Zahradníček, P. Extreme precipitation totals under present and future climatic conditions according to regional climate models. In Climate Change Adaptation Pathways from Molecules to Society, 1st ed.; Vačkář, D., Ed.; Global Change Research Institute, Czech Academy of Sciences: Brno, Czech, 2017; pp. 27–37. [Google Scholar]
- Trnka, M.; Brázdil, R.; Vizina, A.; Dobrovolný, P.; Mikšovský, J.; Štěpánek, P.; Hlavinka, P.; Řezníčková, L.; Žalud, Z. Droughts and Drought Management in the Czech Republic in a Changing Climate. In Drought and Water Crises: Integrating Science, Management, and Policy, 1st ed.; Wilhite, D.A., Ed.; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2017; pp. 461–480. [Google Scholar]
- Slovak Hydrometeorological Institute (Increase in the Extremes of Total Rainfall Events in Slovakia). Available online: http://www.shmu.sk/sk/?page=2049&id=965 (accessed on 20 March 2019).
- Acuña, G.J.; Ávila, H.; Fausto, A.C. River Model Calibration Based on Design of Experiments Theory. A Case Study: Meta River, Colombia. Water 2019, 11, 1382. [Google Scholar] [CrossRef]
- Quinton, J. The Validation of Physically-based Erosion Models with Particular Reference to EUROSEM. Ph.D. Thesis, Cranfield University, Wharley End, UK, 1994. [Google Scholar]
- Favis-Mortlock, D.; Boardman, J.; Bell, M. Modelling long-term anthropogenic erosion of a loess cover: South Downs, UK. Holocene 1997, 7, 79. [Google Scholar] [CrossRef]
- Hrissanthou, V. Computation of Lake or Reservoir Sedimentation in Terms of Soil Erosion, In Sediment Transport in Aquatic Environments, 3rd ed.; Manning, A.J., Ed.; IntechOpen: London, UK, 2011; pp. 233–262. [Google Scholar] [CrossRef]
- Zhao, G.; Mu, X.; Jiao, J.; Gao, P.; Sun, W.; Li, E.; Wei, Y.; Huang, J. Assessing response of sediment load variation to climate change and human activities with six different approaches. Sci. Total Environ. 2018, 639, 773–784. [Google Scholar] [CrossRef]
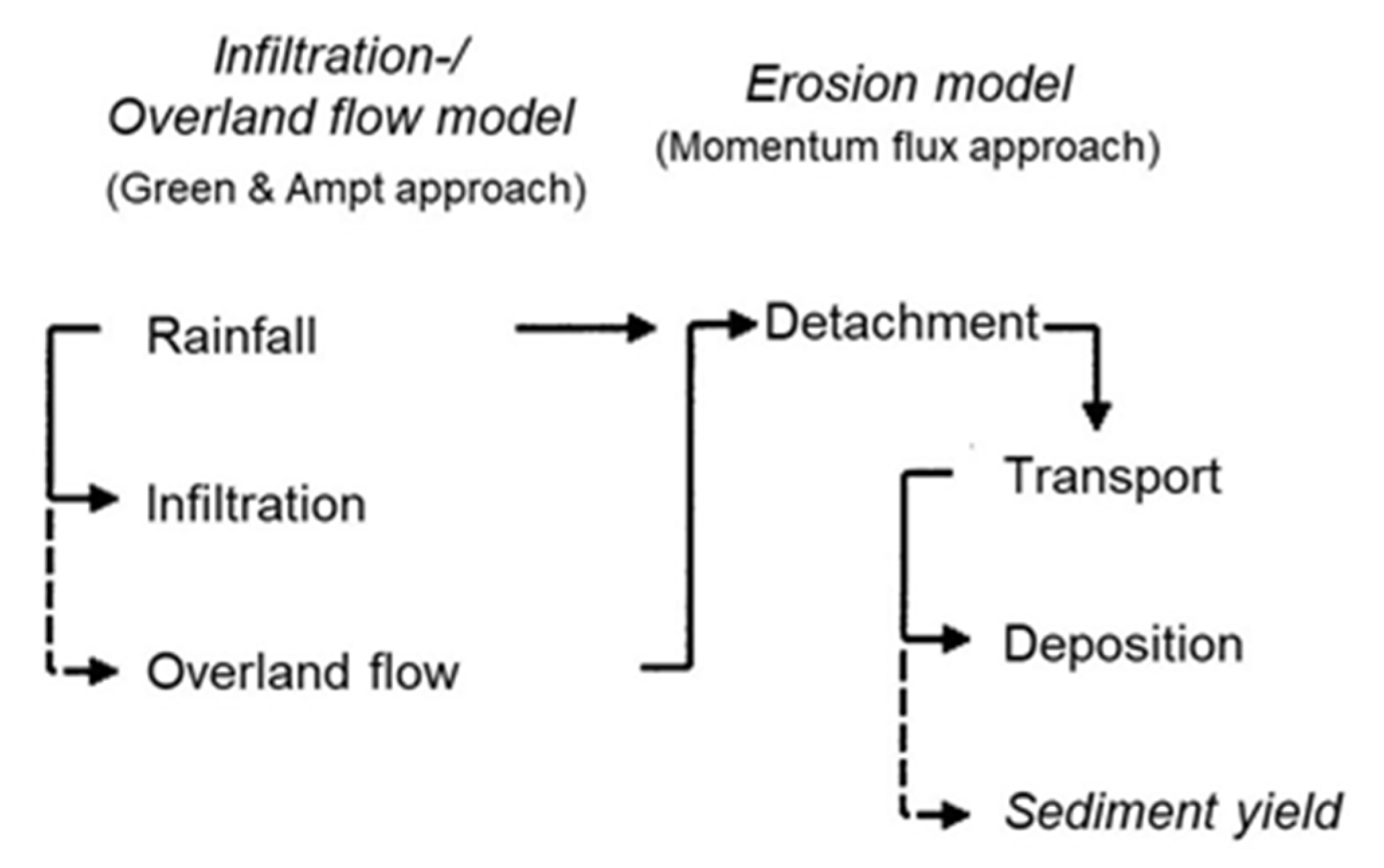
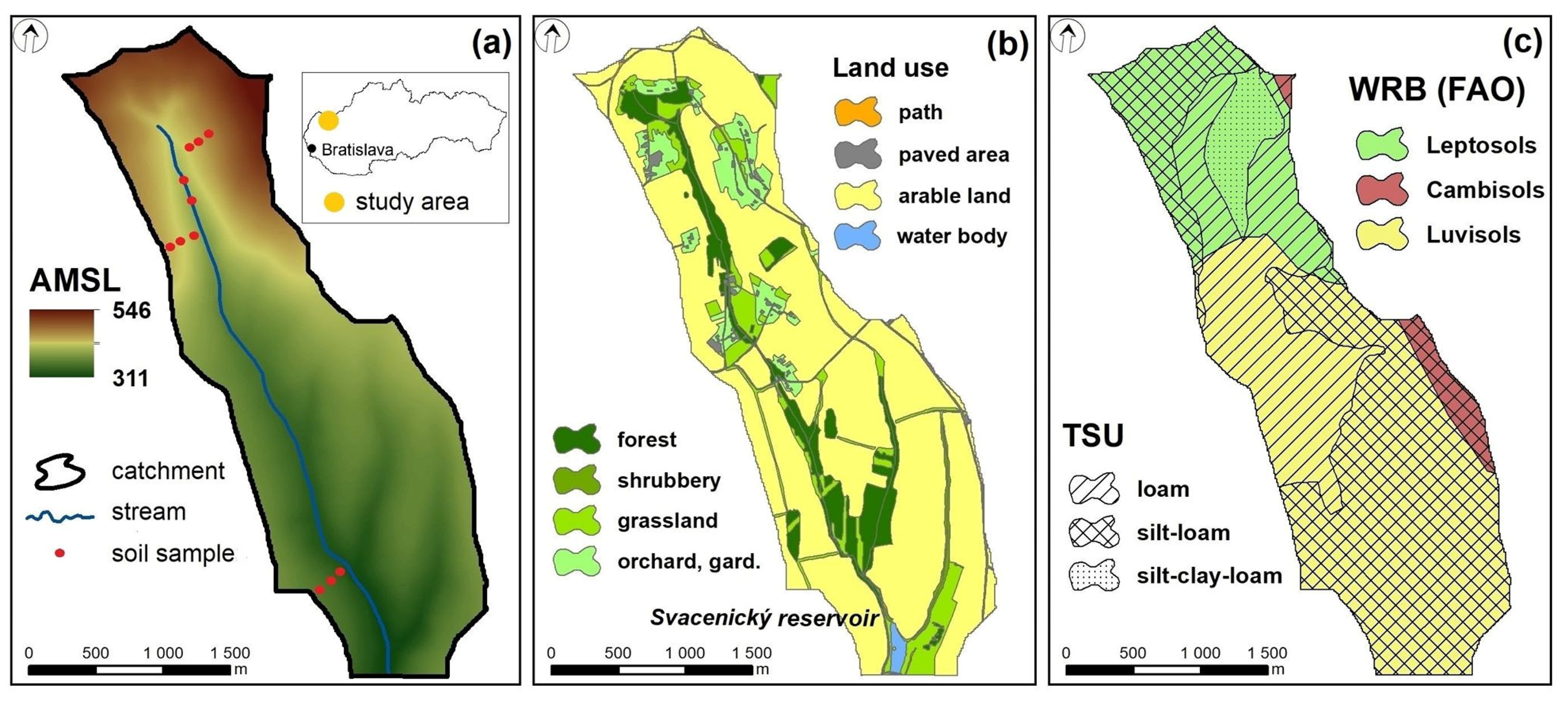
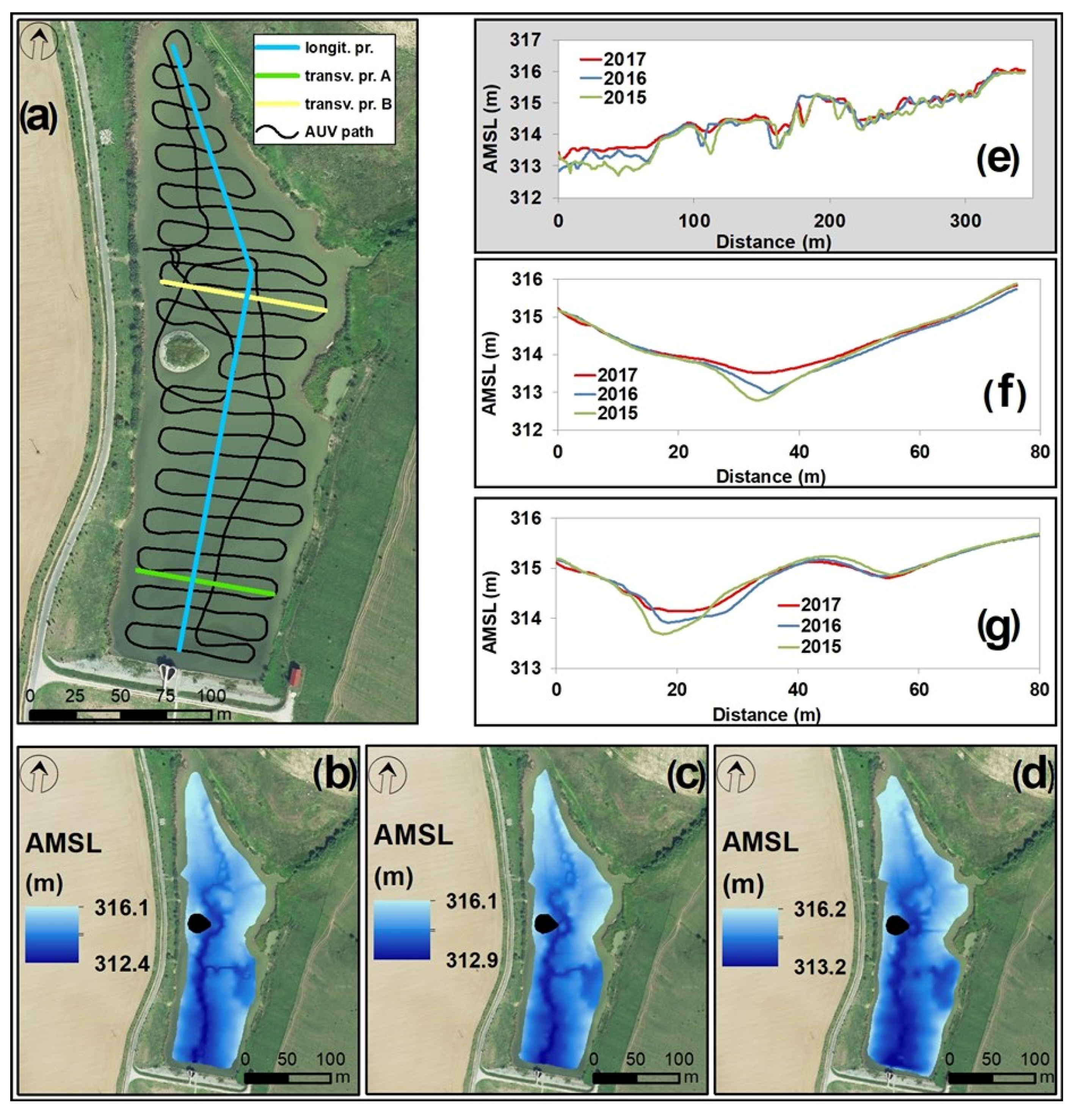
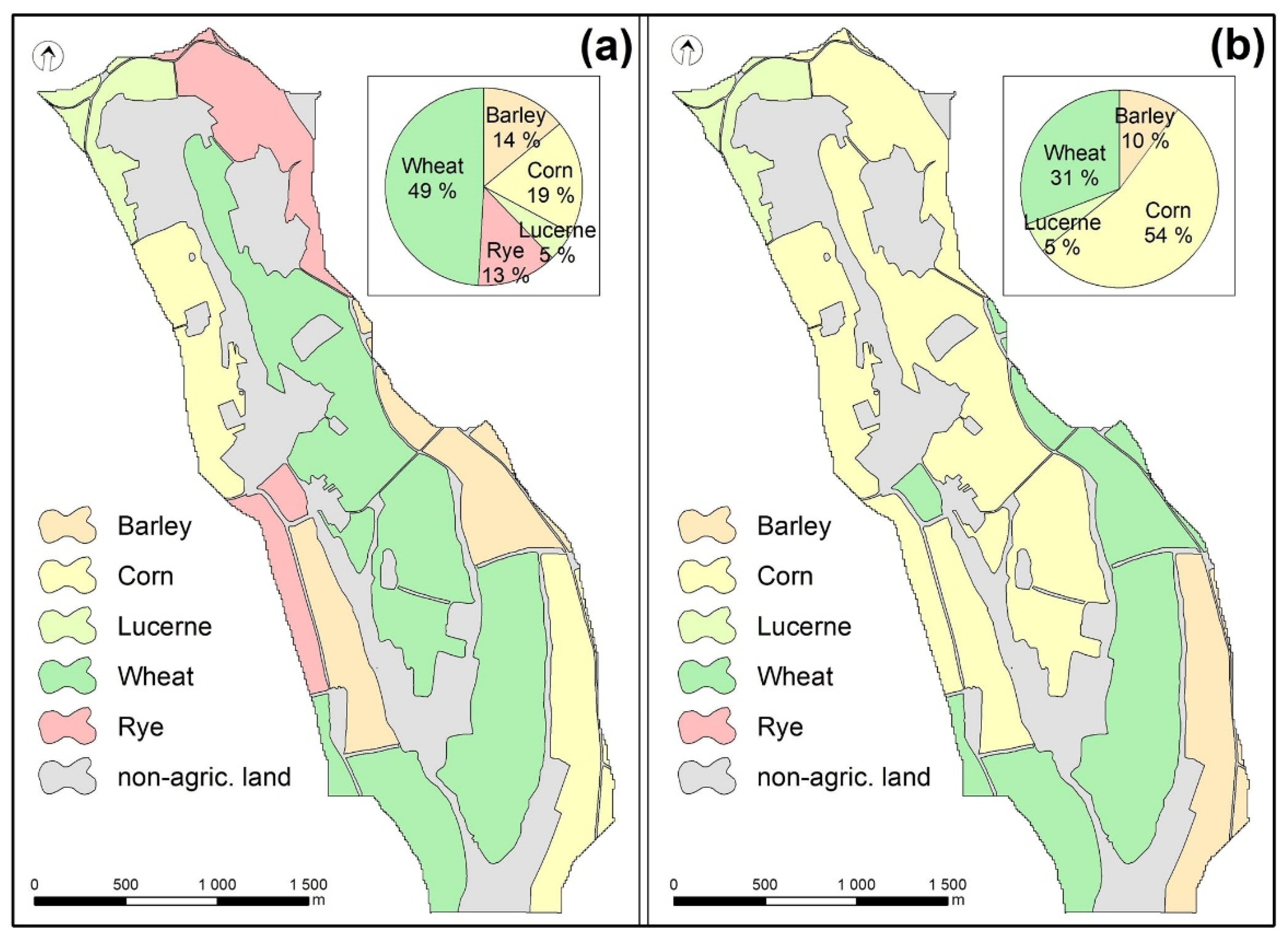
| Land Use Category | Total | Path | Paved Area | Arable Land | Water Body | Forest | Shrubbery | Grassland | Orchard, Garden |
|---|---|---|---|---|---|---|---|---|---|
| Area (km2) | 6.26 | 0.03 | 0.11 | 4.11 | 0.49 | 0.55 | 0.06 | 0.54 | 0.37 |
| Area (%) | 100 | 0.5 | 1.8 | 65.7 | 7.8 | 8.8 | 1.0 | 8.6 | 5.9 |
| Input Parameter | Unit | Data Source |
|---|---|---|
| Altitude (DEM) | (m) | Esprit, s. r. o. |
| Rainfall intensity per time step | (mm/min) | Slovak Hydrometeorological Institute |
| Bulk density | (kg/m3) | Field measurement |
| Organic carbon content | (%) | Field measurement |
| Grain size distribution | (%) | Field measurement |
| Skin factor | (−) | Parameter Catalogue |
| Surface roughness | (s/m1/3) | Parameter Catalogue |
| Initial soil moisture | (%) | Field measurement |
| Erosion resistance | (N/m2) | Parameter Catalogue |
| Soil ID | Soil Particle Size (%) | Organic Carbon Content (%) | Bulk Density (g/cm3) | ||
|---|---|---|---|---|---|
| Sand | Silt | Clay | |||
| 1 | 15.9 | 55.7 | 5.1 | 9.5 | 1.070 |
| 2 | 19.4 | 53.1 | 2.8 | 12.5 | 1.161 |
| 3 | 19.1 | 41.4 | 3.6 | 11.8 | 1.032 |
| 4 | 8.4 | 73.5 | 7.2 | 8.8 | 1.097 |
| 5 | 7.8 | 76.5 | 6.3 | 9.4 | 1.011 |
| 6 | 9.1 | 71.9 | 7.0 | 9.2 | 1.466 |
| 7 | 9.8 | 68.3 | 7.2 | 12.1 | 1.334 |
| 8 | 3.6 | 69.5 | 12.1 | 15.1 | 0.890 |
| 9 | 9.8 | 68.3 | 7.2 | 12.1 | 1.334 |
| 10 | 8.9 | 70.4 | 7.2 | 12.8 | 1.048 |
| 11 | 7.9 | 75.0 | 6.5 | 10.9 | 0.982 |
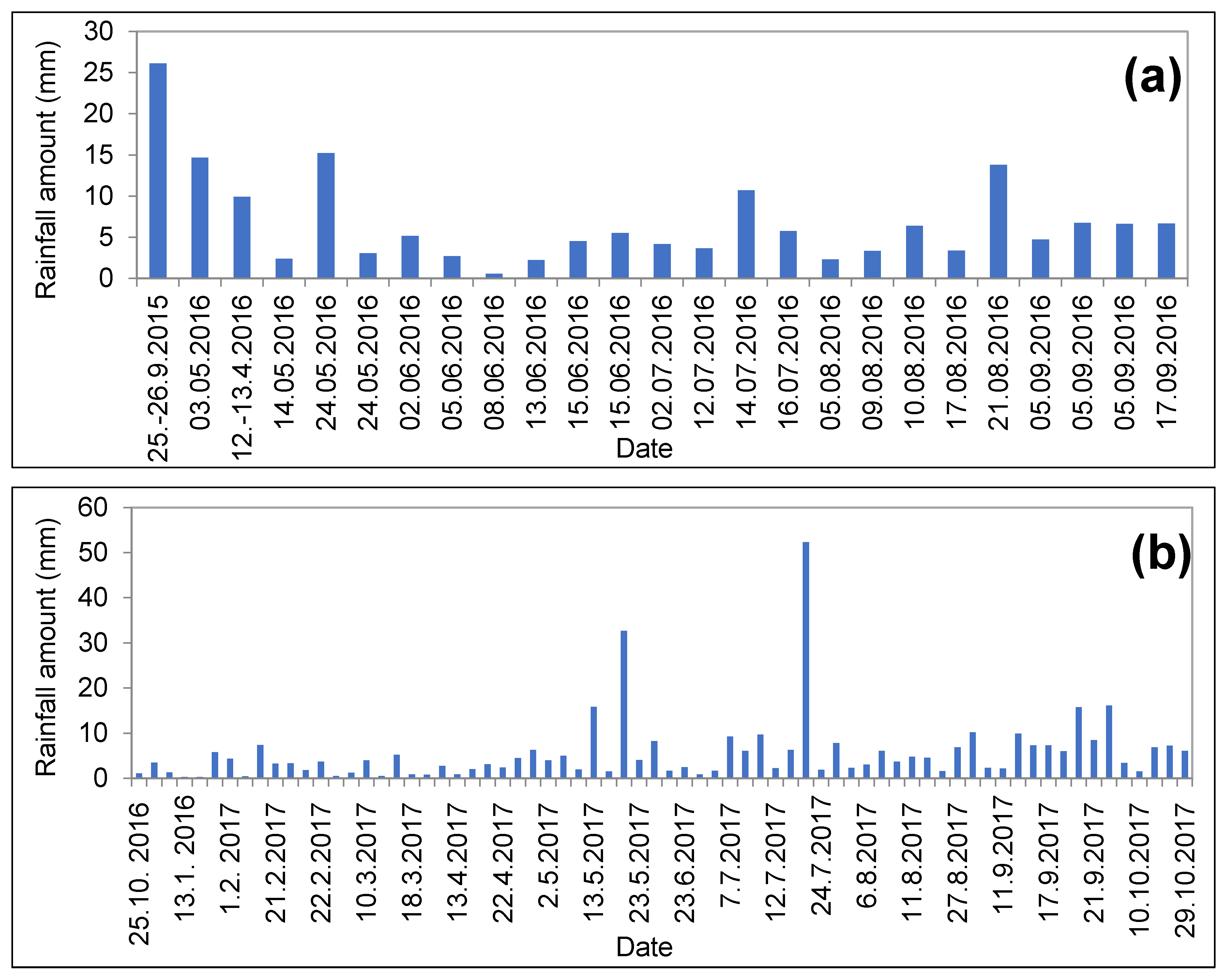
| Time Period | Duration (min) | Rainfall Amount (mm) | Rainfall Intensity (mm/min) |
|---|---|---|---|
| 2015–2016 | 1–1041 ( 141) | 0.57–26.11 ( 6.63) | 0.02–0.57 ( 0.12) |
| 2016–2017 | 10–504 (86) | 0.28–52.30 (5.59) | 0.02–0.71 ( 0.10) |
| Date | Duration (min) | Rainfall Amount (mm) | Rainfall Intensity (mm/min) | Surface Runoff (m3) | Erosion/Deposition Rate (t/ha) | Sediment Volume (m3) |
|---|---|---|---|---|---|---|
| 25–26 September 2015 | 1041 | 26.11 | 0.03 | 10.20 | 2.75 | 12.27 |
| 3 May 2016 | 206 | 14.66 | 0.07 | 6.25 | 0.35 | 15.66 |
| 24 May 2016 | 161 | 15.22 | 0.09 | 6.23 | 0.00 | 13.54 |
| 21 August 2016 | 79 | 13.8 | 0.18 | 4.33 | 0.18 | 7.60 |
| Total Sediment Production: | 49.07 | |||||
| 13 May 2017 | 51 | 15.8 | 0.31 | 4.20 | 1.36 | 1.19 |
| 23 May 2017 | 58 | 32.67 | 0.56 | 10.20 | 2.37 | 1.30 |
| 22 July 2017 | 74 | 52.3 | 0.71 | 22.30 | 2.36 | 1.41 |
| 21 September 2017 | 504 | 15.74 | 0.03 | 10.60 | 2.57 | 3.87 |
| 3 October 2017 | 226 | 16.07 | 0.07 | 0.50 | 0.21 | 1.23 |
| Total Sediment Production: | 9.00 | |||||
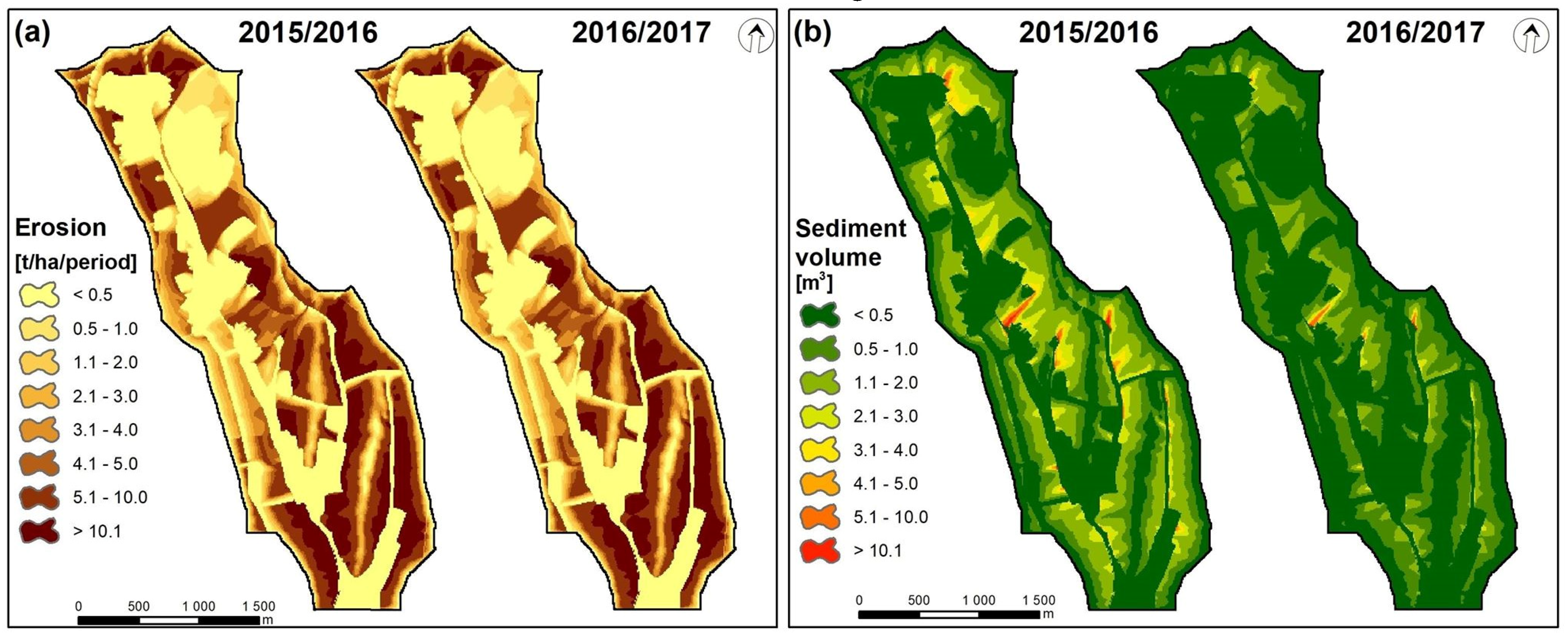
| Time Period | Predicted Sediment Volume (1) (m3) | Predicted Sediment Volume (2) (m3) | Observed Sediment Volume (m3) | Relative Error (%) | |
|---|---|---|---|---|---|
| 2015–2016 | 216.5 | 648.6 | 913.1 | −76.3 (1) | −28.9 (2) |
| 2016–2017 | 375.8 | 721.5 | 508.1 | −26.0 (1) | 41.9 (2) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Németová, Z.; Honek, D.; Kohnová, S.; Hlavčová, K.; Šulc Michalková, M.; Sočuvka, V.; Velísková, Y. Validation of the EROSION-3D Model through Measured Bathymetric Sediments. Water 2020, 12, 1082. https://doi.org/10.3390/w12041082
Németová Z, Honek D, Kohnová S, Hlavčová K, Šulc Michalková M, Sočuvka V, Velísková Y. Validation of the EROSION-3D Model through Measured Bathymetric Sediments. Water. 2020; 12(4):1082. https://doi.org/10.3390/w12041082
Chicago/Turabian StyleNémetová, Zuzana, David Honek, Silvia Kohnová, Kamila Hlavčová, Monika Šulc Michalková, Valentín Sočuvka, and Yvetta Velísková. 2020. "Validation of the EROSION-3D Model through Measured Bathymetric Sediments" Water 12, no. 4: 1082. https://doi.org/10.3390/w12041082
APA StyleNémetová, Z., Honek, D., Kohnová, S., Hlavčová, K., Šulc Michalková, M., Sočuvka, V., & Velísková, Y. (2020). Validation of the EROSION-3D Model through Measured Bathymetric Sediments. Water, 12(4), 1082. https://doi.org/10.3390/w12041082






