A Preliminary Assessment of the “Undercatching” and the Precipitation Pattern in an Alpine Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study and Data
2.2. Methodology
2.2.1. Historical Data Analyses and Processing
2.2.2. Preliminary Assessment of Precipitation and Temperature Fields (Geostatistical)
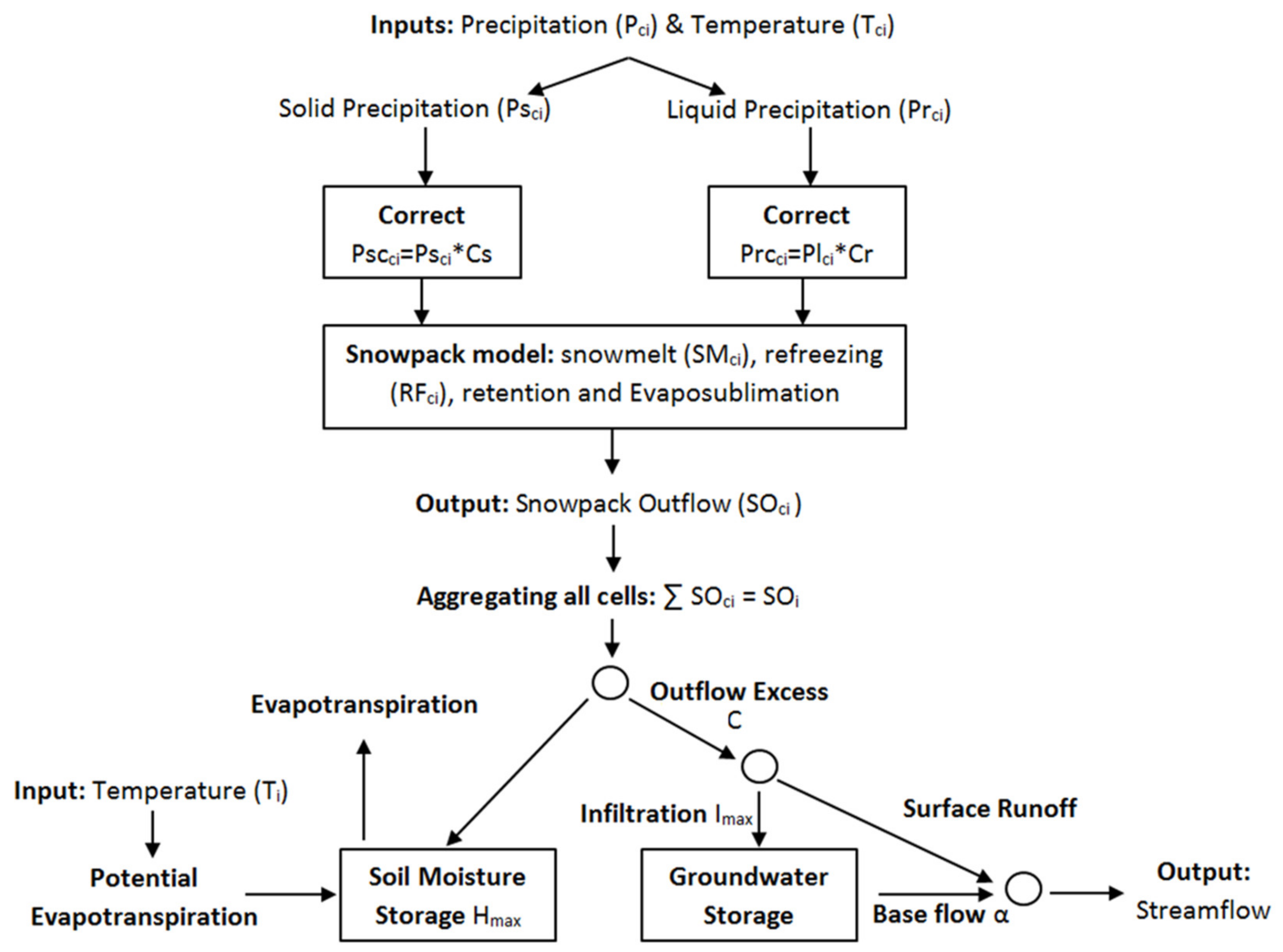
2.2.3. Definition of the Conceptual Hydrological Model
3. Results
3.1. Historical Data Analyses and Processing
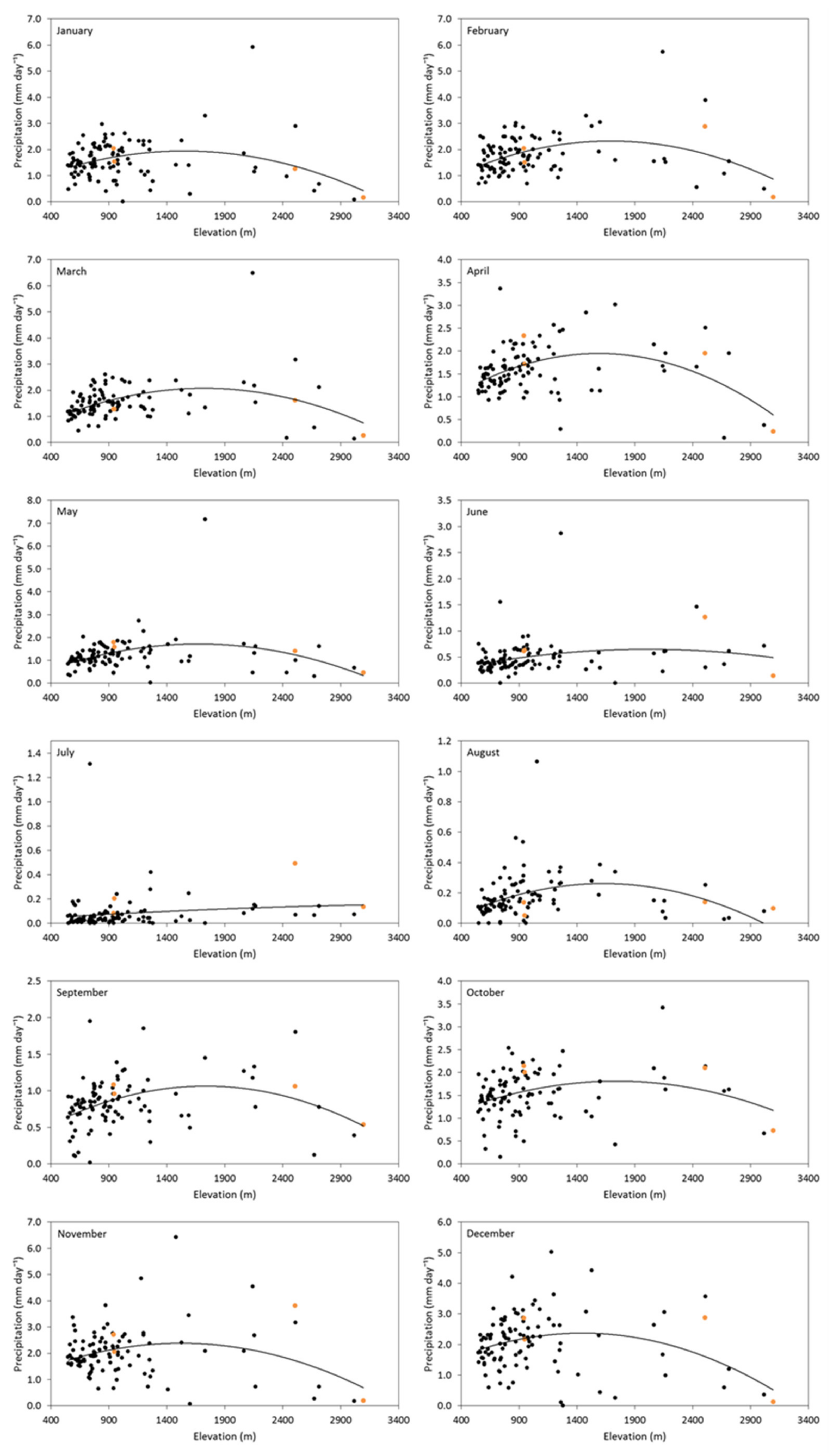
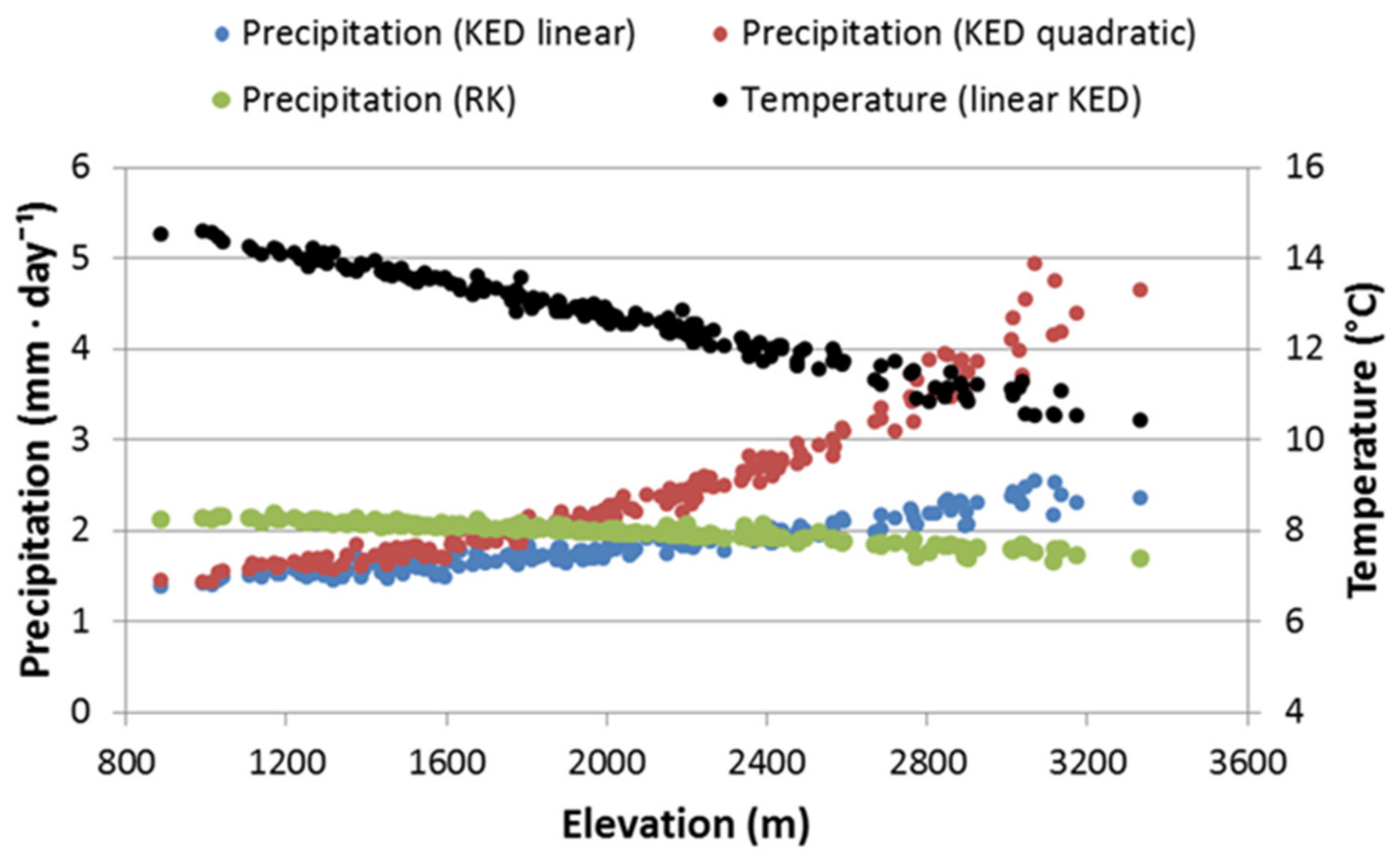
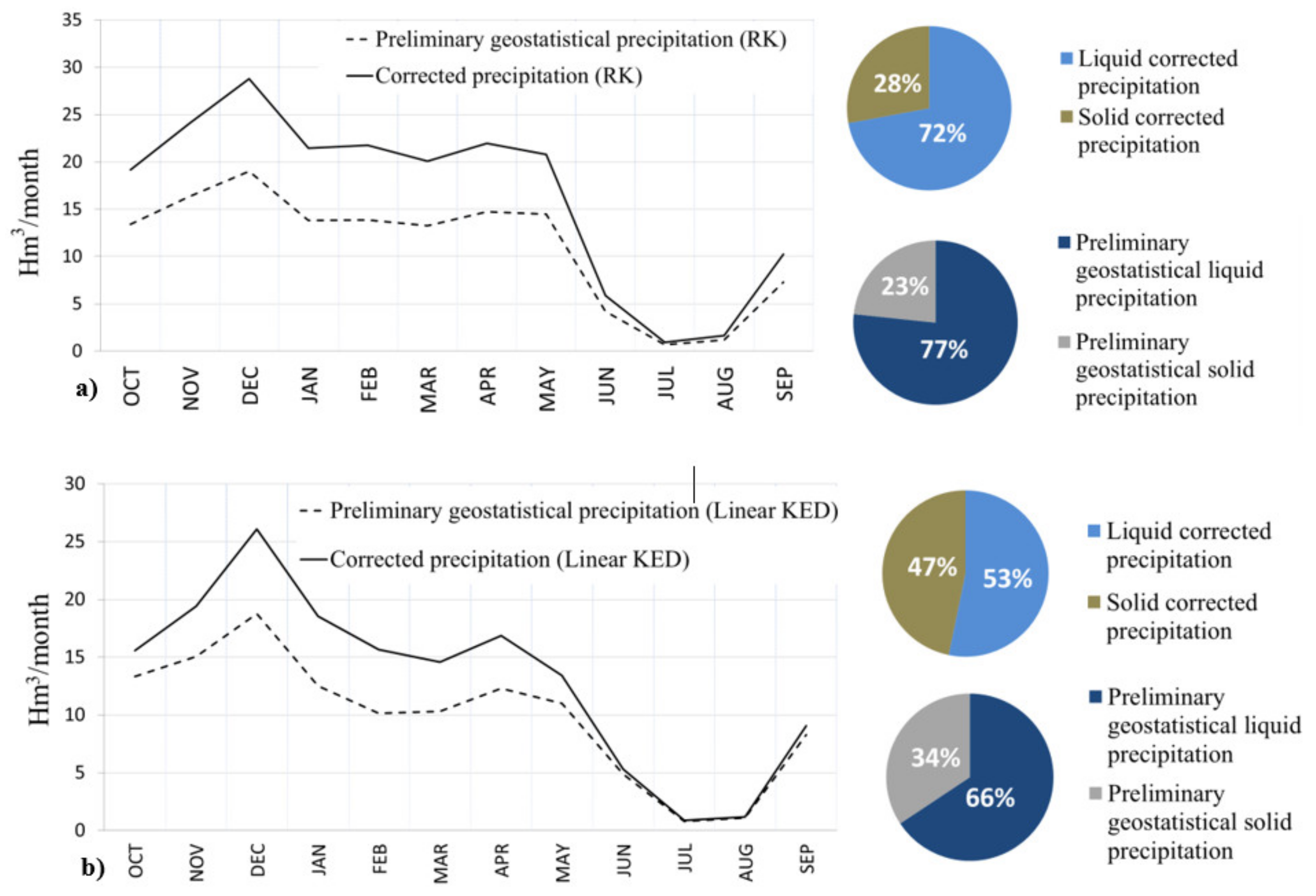
3.2. Preliminary Assessment of Precipitation Fields (Geostatistical)
3.3. Results of the Conceptual Hybrid Snow-Témez Model (STM)
4. Discussion
- In this preliminary approximation, we assume an invariant value of undercatch over space and time (correction factor) for solid and liquid precipitation. Future approximations might explore correction factors that area proportional to wind field intensity, for example.
- Although the model performance of the optimal combination of a hydrological model and geostatistical approach is satisfactory (in accordance with Moriasi et al. (2007) [69] criteria), there are some differences in the approximation of the runoff peaks. The proposed future works might improve in considering non-invariant value of the undercatch.
- The available climatic and streamflow data are quite limited in space and time in our case study. The uncertainty in the assessment would be significantly smaller if more gauge measurements were available.
- The assessment of the undercatch phenomenon is based on streamflow, assuming that our conceptual hydrological approach is valid.
- Although the snow model is distributed, a lumped hydrological balance model (Témez model) was employed to simulate streamflow. Other experiments using distributed hydrological models could be investigated.
- A hybrid degree-day method is employed to approximate the melt process within the snow model. Although it is not an energy balance approach, it considers the influence of some key variables related to the energy balance in a simplified way.
- The model is calibrated by minimizing differences with respect to natural streamflow observations. A multicriteria calibration could be explored in the future, considering also other hydrological variables such as the evolution of snow-covered area.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sevruk, B. Methodical Investigation of Systematic Error of Hellmann Rain Gauges in the Summer Season in Switzerland, in German; Trans. Versuchsanstalt für Wasserbau, Hydrologie und Glaziologie, Mitt. No. 52; ETH: Zürich, Switzerland, 1981. [Google Scholar]
- Groisman, P.Y.; Legates, D.R. The Accuracy of United States Precipitation Data. Bull. Am. Meteorol. Soc. 1994, 75, 215–227. [Google Scholar] [CrossRef]
- Goodison, B.; Louie, P.; Yang, D. WMO Solid Precipitation Measurement Intercomparison-Final Report; WMO: Geneva, Switzerland, 1998; Available online: https://globalcryospherewatch.org/bestpractices/docs/WMOtd872.pdf (accessed on 15 December 2019).
- Sevruk, B.; Ondrás, M.; Chvíla, B. The WMO precipitation measurement intercomparisons. Atmos. Res. 2009, 92, 376–380. [Google Scholar] [CrossRef]
- Rasmussen, R.; Baker, B.; Kochendorfer, J.; Meyers, T.; Landolt, S.; Fischer, A.P.; Black, J.; Thériault, J.M.; Kucera, P.; Gochis, D.; et al. How well are we measuring snow? The NOAA/FAA/NCAR winter precipitation test bed. Bull. Am. Meteorol. Soc. 2012, 93, 811–829. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Goodison, B.E.; Metcalfe, J.R.; Golubev, V.S.; Elomaa, E.; Gunther, T.; Bates, R.; Pangburn, T.; Hanson, C.L.; Emerson, D.; et al. Accuracy of Tretyakov precipitation gauge: Result of WMO intercomparison. Hydrol. Process. 1995, 9, 877–895. [Google Scholar] [CrossRef]
- Sevruk, B. Methods of Correction for Systematic Error in Point Precipitation Measurements for Operational Use; WMO: Geneva, Switzerland, 1982. [Google Scholar]
- Adam, J.C.; Lettenmaier, D. Adjustment of global gridded precipitation for systematic bias. J. Geophys. Res. 2003, 108, 4257. [Google Scholar] [CrossRef]
- Jevons, W.S. LIV. On the deficiency of rain in an elevated rain-gauge, as caused by wind. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1861, 22, 421–433. [Google Scholar] [CrossRef]
- Symons, G.J. Rain Gauges and Hints on Observing Them; British Rainfall: London, UK, 1864; pp. 8–13. [Google Scholar]
- Alter, J.C. Shielded storage precipitation gages. Mon. Weather Rev. 1937, 65, 262–265. [Google Scholar] [CrossRef]
- Wilson, W.T. Analysis of winter precipitation observations in the cooperative snow investigations. Mon. Weather Rev. 1954, 82, 183–195. [Google Scholar] [CrossRef]
- Benning, J.; Yang, D. Adjustment of daily precipitation data at Barrow and Nome Alaska for 1995-2001. Arct. Antarct. Alp. Res. 2005, 37, 276–283. [Google Scholar] [CrossRef] [Green Version]
- Buisán, S.T.; Earle, M.E.; Collado, J.L.; Kochendorfer, J.; Alastrué, J.; Wolff, M.; Smith, C.D.; López-Moreno, J.I. Assessment of snowfall accumulation underestimation by tipping bucket gauges in the Spanish operational network. Atmos. Meas. Tech. 2017, 10, 1079–1091. [Google Scholar] [CrossRef] [Green Version]
- Legates, D.R. A climatology of global precipitation. Publ. Climatol. 1987, 40, 85. [Google Scholar]
- Sevruk, B.; Hamon, W. International Comparison of National Precipitation Gauges with a Reference Pit Gauge; Instruments and Observing Methods Report; WMO: Geneva, Switzerland, 1984. [Google Scholar]
- SPICE: WMO Solid Precipitation Intercomparison Experiment (2012–2015). Available online: https://www.wmo.int/pages/prog/www/IMOP/intercomparisons/SPICE/SPICE.html (accessed on 17 February 2020).
- Nitu, R. Cold as SPICE: Determining the best way to measure snowfall. Meteorol. Technol. Int. 2013, 148–150. [Google Scholar]
- Wolff, M.A.; Isaksen, K.; Petersen-Overleir, A.; Odemark, K.; Reitan, T.; Braekkan, R. Derivation of a new continuous adjustment function for correcting wind-induced loss of solid precipitation: Results of a norwegian field study. Hydrol. Earth Syst. Sci. 2015, 19, 951–967. [Google Scholar] [CrossRef]
- Grossi, G.; Lendvai, A.; Peretti, G.; Ranzi, R. Snow Precipitation Measured by Gauges: Systematic Error Estimation and Data Series Correction in the Central Italian Alps. Water 2017, 9, 461. [Google Scholar] [CrossRef] [Green Version]
- Fekete, B.M.; Vörösmarty, C.J.; Roads, J.O.; Willmott, C.J. Uncertainties in precipitation and their impacts on runoff estimates. J. Clim. 2004, 17, 294–304. [Google Scholar] [CrossRef]
- Stisen, S.; Højberg, A.L.; Troldborg, L.; Refsgaard, J.C.; Christensen, B.S.B.; Olsen, M.; Henriksen, H.J. On the importance of appropriate precipitation gauge catch correction for hydrological modelling at mid to high latitudes. Hydrol. Earth Syst. Sci. 2012, 16, 4157–4176. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; Dai, A.; Yang, D.; Xie, Z. Effects of precipitation-biascorrections on surface hydrology over northern latitudes. J. Geophys. Res. 2007, 112, D14101. [Google Scholar] [CrossRef] [Green Version]
- Valéry, A.; Andréassian, V.; Perrin, C. Inverting the hydrological cycle: When streamflow measurements help assess altitudinal precipitation gradients in mountain areas. Iahs Publ. 2009, 333, 281–286. [Google Scholar]
- Bartolini, E.; Allamano, P.; Laio, F.; Claps, P. Runoff regime estimation at high-elevation sites: A parsimonious water balance approach. Hydrol. Earth Syst. Sc. 2011, 15, 1661–1673. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, M.; Wang, L.; Koike, T.; Tsutsui, H.; Xue, Y.; Hirabayashi, Y. Correcting basin-scale snowfall in a mountainous basin using a distributed snowmelt model and remote-sensing data. Hydrol. Earth Syst. Sci. 2014, 18, 747–761. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Beldring, S.; Xu, C.Y.; Huss, M.; Melvold, K.; Jain, S.K. Integrating a glacier retrea model into a hydrological model—Case studies of three glacierised catchments in Norway an Himalayan region. J. Hydrol. 2015, 527, 656–667. [Google Scholar] [CrossRef] [Green Version]
- Irannezhad, M.; Ronkanen A., K.; Kløve, B. Effects of climate variability and change on snowpack hydrological processes in Finland. Cold Reg. Sci. Technol. 2015, 118, 14–29. [Google Scholar] [CrossRef]
- Akanegbu, J.O.; Marttila, H.; Ronkanen, A.-K.; Kløve, B.J. A current precipitation index-based model for continuous daily runoff simulation in seasonally snow covered sub-arctic catchments. J. Hydrol. 2017, 545, 182–196. [Google Scholar] [CrossRef]
- Collados-Lara, A.J.; Pardo-Iguzquiza, E.; Pulido-Velazquez, D. Precipitation fields in an alpine Mediterranean catchment. Inversion of precipitation gradient with elevation or undercatch of snowfall? Int. J. Climatol. 2018, 38, 3565–3578. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Soto, J.; Pérez-Sánchez, J.; Garrido, J. A novel fuzzy clustering approach to regionalise watersheds with an automatic determination of optimal number of clusters. J. Hydrol. Hydromech. 2017, 65, 359–365. [Google Scholar] [CrossRef] [Green Version]
- Centre for Public Works Studies and Experimentation (CEDEX). Anuario de Aforos. Available online: http://ceh-flumen64.cedex.es/anuarioaforos/default.asp (accessed on 2 February 2020).
- Escriva-Bou, A.; Pulido-Velazquez, M.; Pulido-Velazquez, D. Economic value of climate change adaptation strategies for water management in Spain’s Jucar basin. J. Water Res. Plan. Asce 2017, 143, 7005. [Google Scholar] [CrossRef]
- Collados-Lara, A.-J.; Pardo-Igúzquiza, E.; Pulido-Velazquez, D. Spatiotemporal estimation of snow depth using point data from snow stakes, digital terrain models, and satellite data. Hydrol. Process. 2017, 31, 1966–1982. [Google Scholar] [CrossRef]
- Cantet, P. Mapping the mean monthly precipitation of a small island using kriging with external drifts. Theor. Appl. Climatol. 2017, 127, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Shtiliyanova, A.; Bellocchi, G.; Borras, D.; Eza, U.; Martin, R.; Carrére, P. Kriging-based approach to predict missing air temperature data. Comput. Electron. Agric. 2017, 142, 440–449. [Google Scholar] [CrossRef]
- Matheron, G. Principles of Geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Chiles, J.P.; Delfiner, P. Geostatistics: Modelling Spatial Uncertainty; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Lloyd, C.D. Assessing the effect of integrating elevation data into the estimation of monthly precipitation in Great Britain. J. Hydrol. 2005, 308, 128–150. [Google Scholar] [CrossRef]
- Richer, E.E.; Kampf, S.K.; Fassnacht, S.R.; Moore, C.C. Spatiotemporal index for analyzing controls on snow climatology: Application in the Colorado Front Range. Phys. Geogr. 2013, 34, 85–107. [Google Scholar] [CrossRef]
- Sexstone, G.A.; Fassnacht, S.R. What drives basin scale spatial variability of snowpack properties in the Front Range of Northern Colorado? Cryosphere 2014, 8, 329–344. [Google Scholar] [CrossRef] [Green Version]
- Pardo-Igúzquiza, E.; Collados-Lara, A.J.; Pulido-Velazquez, D. Estimation of the spatiotemporal dynamics of snow covered area by using cellular automata models. J. Hydrol. 2017, 550, 230–238. [Google Scholar] [CrossRef]
- Collados-Lara, A.J.; Pardo-Igúzquiza, E.; Pulido-Velazquez, D. A distributed cellular automata model to simulate potential future impacts of climate change on snow cover area. Adv. Water. Resour. 2019, 124, 106–119. [Google Scholar] [CrossRef]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Martinec, J.; Rango, A.; Roberts, R. Snowmelt Runoff Model (SRM) User’s Manual; New Mexico State University Press: Albuquerque, NM, USA, 2008. [Google Scholar]
- Şensoy, A.; Uysal, G. The value of snow depletion forecasting methods towards operational snowmelt runoff estimation using MODIS and Numerical Weather Prediction Data. Water Resour. Manag. 2012, 26, 3415–3440. [Google Scholar] [CrossRef]
- Bruland, O.; Maréchal, D.; Sand, K.; Killingtveit, A. Energy and water balance studies of a snow cover during snowmelt period at a high arctic site. Theor. Appl. Climatol. 2001, 70, 53–63. [Google Scholar] [CrossRef]
- Kuusisto, E. Snow Accumulation and Snow Melt in Finland; National Board of Waters: Helsinki, Finland, 1984; Volume 55. [Google Scholar]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Orozco-Medina, I. Modelación Parsimoniosa y Espacialmente Distribuida de los Procesos de Acumulación y Fusión de Nieve. Ph.D. Thesis, UPV, Valencia, Spain.
- Témez, J.R. Modelo Matemático de Transformación “Precipitación-Aportación”; Asociación de Investigación Industrial Eléctrica (ASINEL): Madrid, Spain, 1977. [Google Scholar]
- Smith, M.; Koren, V.; Zhang, Z.; Moreda, F.; Cui, Z.; Cosgrove, B.; Mizukami, N.; Kitzmiller, D.; Ding, F.; Reed, S.; et al. The distributed model intercomparison project—Phase 2: Experiment design and summary results of the western basin experiments. J. Hydrol. 2013, 507, 300–329. [Google Scholar] [CrossRef] [Green Version]
- Estrela, T.; Quintas, L. A distributed hydrological model for water resources assessment in large basins. In Proceedings of the Rivertech ’96-1st International Conference on New/Emerging Concepts for Rivers, Chicago, IL, USA, 22–26 September 1996; Volumes 1–2, pp. 861–868. [Google Scholar]
- Bejarano, M.D.; Marchamalo, M.; de Jalón, D.G.; del Tánago, M.G. Flow regime patterns and their controlling factors in the Ebro basin (Spain). J. Hydrol. 2010, 385, 323–335. [Google Scholar] [CrossRef] [Green Version]
- Jódar, J.; Cabrera, J.A.; Martos-Rosillo, S.; Ruiz-Constán, A.; González-Ramón, A.; Lambán, L.J.; Herrera, C.; Custodio, E. Groundwater discharge in high-mountain watersheds: A valuable resource for downstream semi-arid zones. The case of the Bérchules River in Sierra Nevada (Southern Spain). Sci. Total Environ. 2017, 593, 760–772. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; López-Ballesteros, A.; Pérez-Sánchez, J.; Segura-Méndez, F.J.; Pulido-Velazquez, D. Using Multiple Monthly Water Balance Models to Evaluate Gridded Precipitation Products over Peninsular Spain. Remote Sens. 2018, 10, 922. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Sánchez, J.; Senent-Aparicio, J.; Segura-Méndez, F.; Pulido-Velazquez, D.; Srinivasan, R. Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain. Sustainability 2019, 11, 2872. [Google Scholar] [CrossRef] [Green Version]
- Murillo, J.M.; Navarro, J.A. Aplicación del modelo de Témez a la determinación de la aportación superficial y subterránea del sistema hidrológico Cornisa-Vega de Granada para su implementación en un modelo de uso conjunto. Bol. Geol. Min. 2011, 122, 363–388. [Google Scholar]
- Hargreaves, G.H. Defining and using reference evapotranspiration. J. Irrig. Drain. Eng. 1994, 120, 1132–1139. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J.; Pulido-Velazquez, D. A Comparison of SWAT and ANN Models for Daily Runoff Simulation in Different Climatic Zones of Peninsular Spain. Water 2018, 10, 192. [Google Scholar] [CrossRef] [Green Version]
- Senent-Aparicio, J.; Jimeno-Sáez, P.; Bueno-Crespo, A.; Pérez-Sánchez, J.; Pulido-Velázquez, D. Coupling machine-learning techniques with SWAT model for instantaneous peak flow prediction. Biosyst. Eng. 2018, 177, 67–77. [Google Scholar] [CrossRef]
- Rosenbrock, H. An automatic method for finding the greatest or least value of a function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef] [Green Version]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, S.; Cai, Y.; Li, X.; Jiang, Y. Improvement of Hydrological Model Calibration by Selecting Multiple Parameter Ranges. Hydrol. Earth Syst. Sci. 2017, 21, 393–407. [Google Scholar] [CrossRef] [Green Version]
- Gupta, V.K.; Sorooshian, S. The Automatic Calibration of Conceptual Catchment Models Using Derivative-Based Optimization Algorithms. Water Resour. Res. 1985, 21, 473–485. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, J. A Microwave Wetland Surface Emissivity Calibration Scheme Using SCE-UA Algorithm and AMSR-E Brightness Temperature Data. Procedia Environ. Sci. 2011, 10, 2731–2739. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Am. Soc. Agric. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Kalin, L.; Isik, S.; Schoonover, J.E.; Lockaby, B.G. Predicting water quality in unmonitored watersheds using Artificial Neural Networks. J. Environ. Qual. 2010, 39, 1429–1440. [Google Scholar] [CrossRef]
- Estrela, T.; Cabezas, F.; Estrada, F. La evaluación de los recursos hídricos en el Libro Blanco del Agua en España. Ing. Del Agua 1999, 6, 125–138. [Google Scholar] [CrossRef] [Green Version]
- Herrero, J.; Polo, M.J. Evaposublimation from the snow in the Mediterranean mountains of Sierra Nevada (Spain). Cryosphere 2016, 10, 2981–2998. [Google Scholar] [CrossRef] [Green Version]
- Pulido-Velazquez, D.; Sahuquillo, A.; Andreu, J. A two-step explicit solution of the Boussinesq equation for efficient simulation of unconfined aquifers in conjunctive-use models. Water Resour. Res 2006, 42, W05423. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Sahuquillo, A.; Andreu, J.; Pulido-Velazquez, M. A general methodology to simulate groundwater flow of unconfined aquifers with a reduced computational cost. J. Hydrol. 2007, 338, 42–56. [Google Scholar] [CrossRef]
- Vehviläinen, B. Snow Cover Models in Operational Watershed Forecasting. Ph.D. Thesis, National Board of Waters and the Environment, Helsinki, Finland, 1992. [Google Scholar]
- Kochendorfer, J.; Nitu, R.; Wolff, M.; Mekis, E.; Rasmussen, R.; Baker, B.; Earle, M.E.; Reverdin, A.; Wong, K.; Smith, C.D.; et al. Analysis of single-Alter-shielded and unshielded measurements of mixed and solid precipitation from WMO-SPICE. Hydrol. Earth Syst. Sci. 2017, 21, 3525–3542. [Google Scholar] [CrossRef] [Green Version]




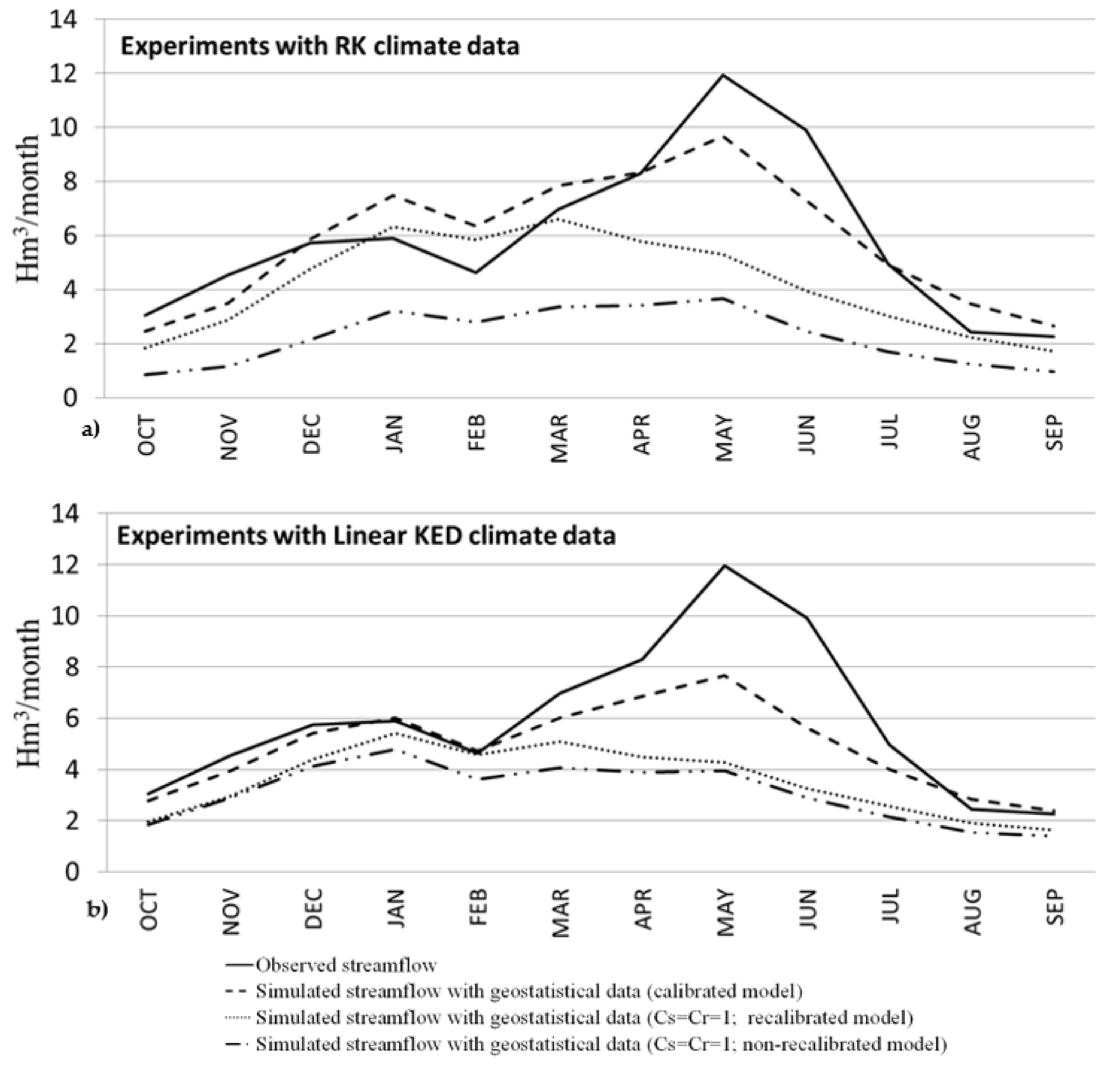


| Performance Rating | Daily | Monthly | ||
|---|---|---|---|---|
| NSE | PBIAS (%) | NSE | PBIAS (%) | |
| Very good | NSE ≥ 0.7 | |PBIAS|≤ 25 | 0.75 < NSE ≥ 1 | |PBIAS|≤ 10 |
| Good | 0.5 ≤ NSE < 0.7 | 25 <|PBIAS|≤ 50 | 0.65 < NSE ≤ 0.75 | 10 ≤|PBIAS|< 15 |
| Satisfactory | 0.3 ≤ NSE < 0.5 | 50 <|PBIAS|≤ 70 | 0.50 < NSE ≤ 0.65 | 15 ≤|PBIAS|< 25 |
| Unsatisfactory | NSE < 0.3 | |PBIAS|> 70 | NSE ≤ 0.5 | |PBIAS|≥ 25 |
| Period | Inflection Point (m) |
|---|---|
| Yearly | 1612.4 |
| January | 1549.6 |
| February | 1691.1 |
| March | 1721.3 |
| April | 1588.5 |
| May | 1672.5 |
| June | 2009.7 |
| July | - |
| August | 1629.0 |
| September | 1736.7 |
| October | 1741.2 |
| November | 1522.6 |
| December | 1448.0 |
| Variogram Analysis | Precipitation | Temperature | |||
|---|---|---|---|---|---|
| KEDQ | KEDL | RK | KEDL Tmin | OK Tmax − Tmin | |
| Yearly model | 23,519 | 10,440 | 12,387 | 5,977 | 10,886 |
| Monthly model | 21,386 | 10,194 | 12,347 | 6,043 | 10,786 |
| Parameter | Description | Lower Boundary 1 | Upper Boundary 1 | Optimal Value | |
|---|---|---|---|---|---|
| RK | Linear KED | ||||
| Hmax | Maximum soil moisture capacity (mm) | 40 | 300 | 102.84 | 50.04 |
| Imax | Maximum infiltration (mm) | 20 | 1000 | 450 | 550 |
| α1 | Discharge parameter of aquifer 1 (day−1) | 0.0003 | 0.03 | 0.005 | 0.007 |
| α2 | Discharge parameter of aquifer 2 (day−1) | 0.0003 | 0.03 | 0.030 | 0.029 |
| b | Distribution coefficient of aquifers | 0 | 1 | 0.54 | 0.61 |
| C | Threshold to generate runoff | 0.10 | 1 | 0.10 | 0.10 |
| H0 | Initial soil moisture (mm) | > 0 | 1 | 0.01 | |
| Q1,0 | Initial groundwater flow of aquifer 1 (mm) | > 0 | 1 | 0.01 | |
| Q2,0 | Initial groundwater flow of aquifer 0 (mm) | > 0 | 1.02 | 0 | |
| Tmelt | Snowmelt base temperature (ºC) | –6.10 | 2.10 | 2.04 | 0 |
| Tf | Refreezing base temperature (ºC) | –5.00 | –0.001 | –1.22 | –1.07 |
| Kd1 | Without rain | 0.01 | 15 | 0.93 | 4.56 |
| Kd2 | With rain | 0.01 | 15 | 1.69 | 1.11 |
| e | Exponent of refreezing | 0.001 | 1 | 1 | 1 |
| Ret | Liquid water retention capacity | 0.020 | 0.52 | 0.02 | 0.02 |
| E | Ratio of the evaposublimation versus total ablation | 0.10 | 0.50 | 0.10 | 0.10 |
| Tmin | Snowfall base temperature (°C) | –6.10 | 0.00 | −0.80 | 0.19 |
| Tmax | Rainfall base temperature (°C) | –0.10 | 5 | 4.23 | 5.00 |
| Cr | Rainfall correction coefficient | 1.01 | 1.40 | 1.40 | 1.07 |
| Cs | Snowfall correction coefficient | 1.05 | 1.80 | 1.78 | 1.8 |
| Approach | Cs | Cr | Scale | Calibration | Validation | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSE | R2 | RMSE | PBIAS | NSE | R2 | RMSE | PBIAS | |||||
| (1) | RK (calibrated model) | 1.78 | 1.4 | Daily | 0.56 | 0.58 | 0.15 | 1.91 | 0.48 | 0.52 | 0.12 | −0.35 |
| Monthly | 0.68 | 0.70 | 3.39 | 1.90 | 0.63 | 0.67 | 2.66 | −0.36 | ||||
| (2) | RK (non–recalibrated model) | 1 | 1 | Daily | 0.07 | 0.57 | 0.22 | 61.37 | 0.03 | 0.42 | 0.17 | 62.33 |
| Monthly | 0.06 | 0.70 | 5.79 | 61.37 | −0.001 | 0.55 | 4.37 | 62.33 | ||||
| (3) | RK (recalibrated model) | 1 | 1 | Daily | 0.38 | 0.51 | 0.18 | 30.18 | 0.32 | 0.40 | 0.14 | 26.39 |
| Monthly | 0.46 | 0.64 | 4.35 | 30.18 | 0.42 | 0.52 | 3.33 | 26.39 | ||||
| (1) | Linear KED (calibrated model) | 1.8 | 1.07 | Daily | 0.28 | 0.45 | 0.19 | 40.01 | 0.32 | 0.53 | 0.14 | −18.52 |
| Monthly | 0.57 | 0.43 | 4.80 | 40.00 | 0.71 | 0.57 | 3.29 | −18.49 | ||||
| (2) | Linear KED (non–recalibrated model) | 1 | 1 | Daily | −0.03 | 0.38 | 0.23 | 63.55 | 0.38 | 0.48 | 0.13 | 21.72 |
| Monthly | −0.08 | 0.48 | 6.15 | 63.55 | 0.49 | 0.62 | 3.11 | 21.74 | ||||
| (3) | Linear KED (recalibrated model) | 1 | 1 | Daily | 0.05 | 0.36 | 0.22 | 56.60 | 0.36 | 0.46 | 0.14 | 13.08 |
| Monthly | 0.04 | 0.45 | 5.82 | 56.60 | 0.47 | 0.60 | 3.18 | 13.11 | ||||
| Station | Elevation (m) | Mean Daily P Measurements (mm) | Mean Daily Estimated P Series (mm) | ||
|---|---|---|---|---|---|
| Linear KED | RK | Quadratic KED | |||
| 5501 | 940 | 1.36 | 1.39 | 2.12 | 1.45 |
| 5501O | 940 | 1.65 | 1.39 | 2.12 | 1.45 |
| 5511E | 2510 | 1.76 | 1.97 | 1.94 | 2.85 |
| PSN08 | 3100 | 0.27 | 2.18 | 1.70 | 4.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jimeno-Sáez, P.; Pulido-Velazquez, D.; Collados-Lara, A.-J.; Pardo-Igúzquiza, E.; Senent-Aparicio, J.; Baena-Ruiz, L. A Preliminary Assessment of the “Undercatching” and the Precipitation Pattern in an Alpine Basin. Water 2020, 12, 1061. https://doi.org/10.3390/w12041061
Jimeno-Sáez P, Pulido-Velazquez D, Collados-Lara A-J, Pardo-Igúzquiza E, Senent-Aparicio J, Baena-Ruiz L. A Preliminary Assessment of the “Undercatching” and the Precipitation Pattern in an Alpine Basin. Water. 2020; 12(4):1061. https://doi.org/10.3390/w12041061
Chicago/Turabian StyleJimeno-Sáez, Patricia, David Pulido-Velazquez, Antonio-Juan Collados-Lara, Eulogio Pardo-Igúzquiza, Javier Senent-Aparicio, and Leticia Baena-Ruiz. 2020. "A Preliminary Assessment of the “Undercatching” and the Precipitation Pattern in an Alpine Basin" Water 12, no. 4: 1061. https://doi.org/10.3390/w12041061






