Moisture Transfer and Formation of Separate Ice in the Freezing Process of Saturated Soils
Abstract
:1. Introduction
2. Analysis of Layering Process of Ice Lens
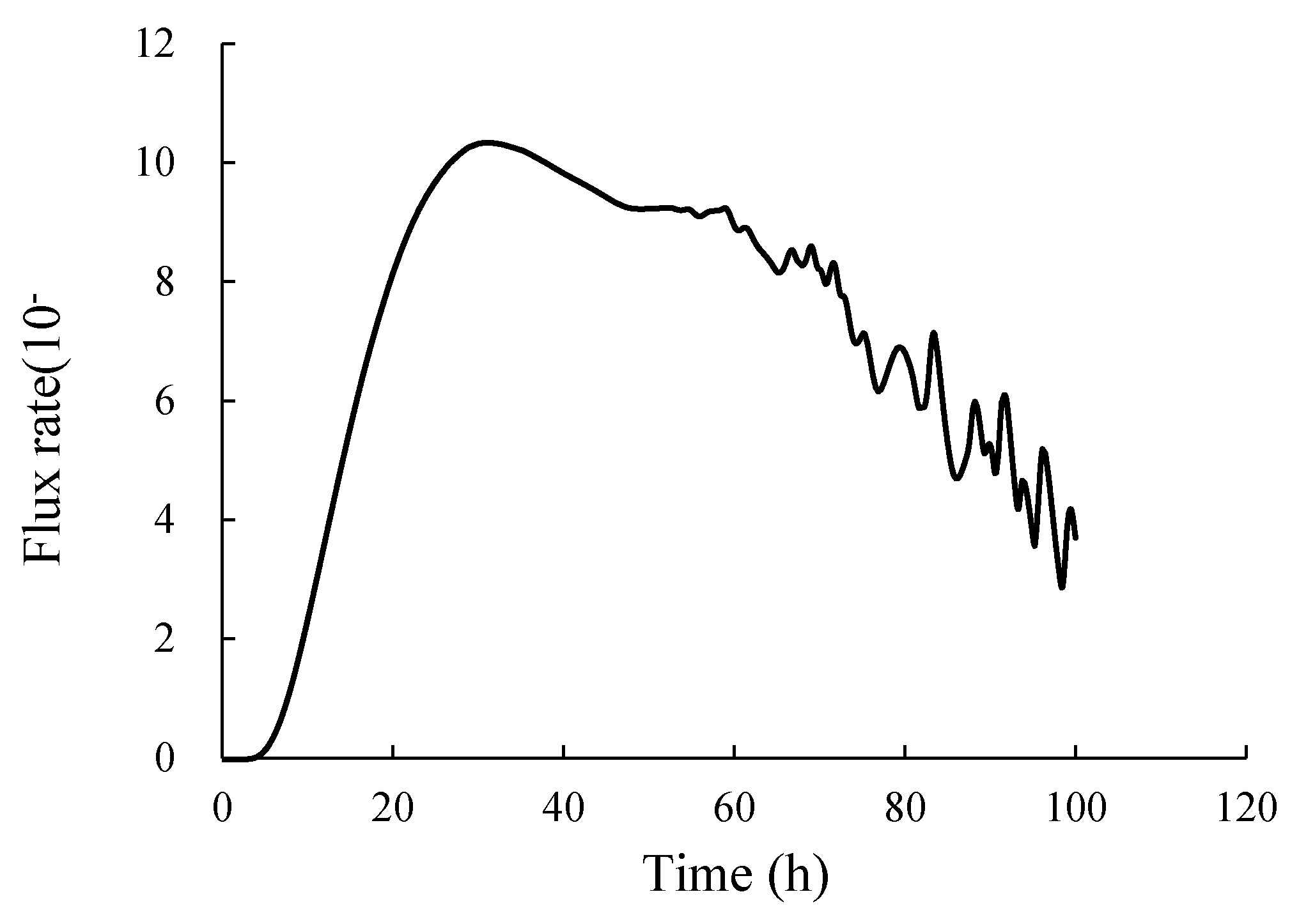
2.1. Analysis of Experimental Results of One-Side Freezing of Soil Columns in an Open System
2.2. Basic Assumptions for Ice Segregation on One-Side Freezing of Soil Columns in an Open System
2.3. Initial Stage of Freezing Process
2.4. Formation of First Layer of Ice Lenses
2.4.1. Migration of Water outside Unfrozen Water Film
2.4.2. Migration of Water inside Unfrozen Water Film
2.5. Formation of Second Layer of Ice Lens
2.6. Ending of Ice Lens Formation
3. Numerical Example and Analysis
3.1. Coupled Thermo–Hydro–Mechanical Equations
3.1.1. Moisture Transfer
3.1.2. Equation of Thermal Diffusion
3.1.3. Force Equilibrium
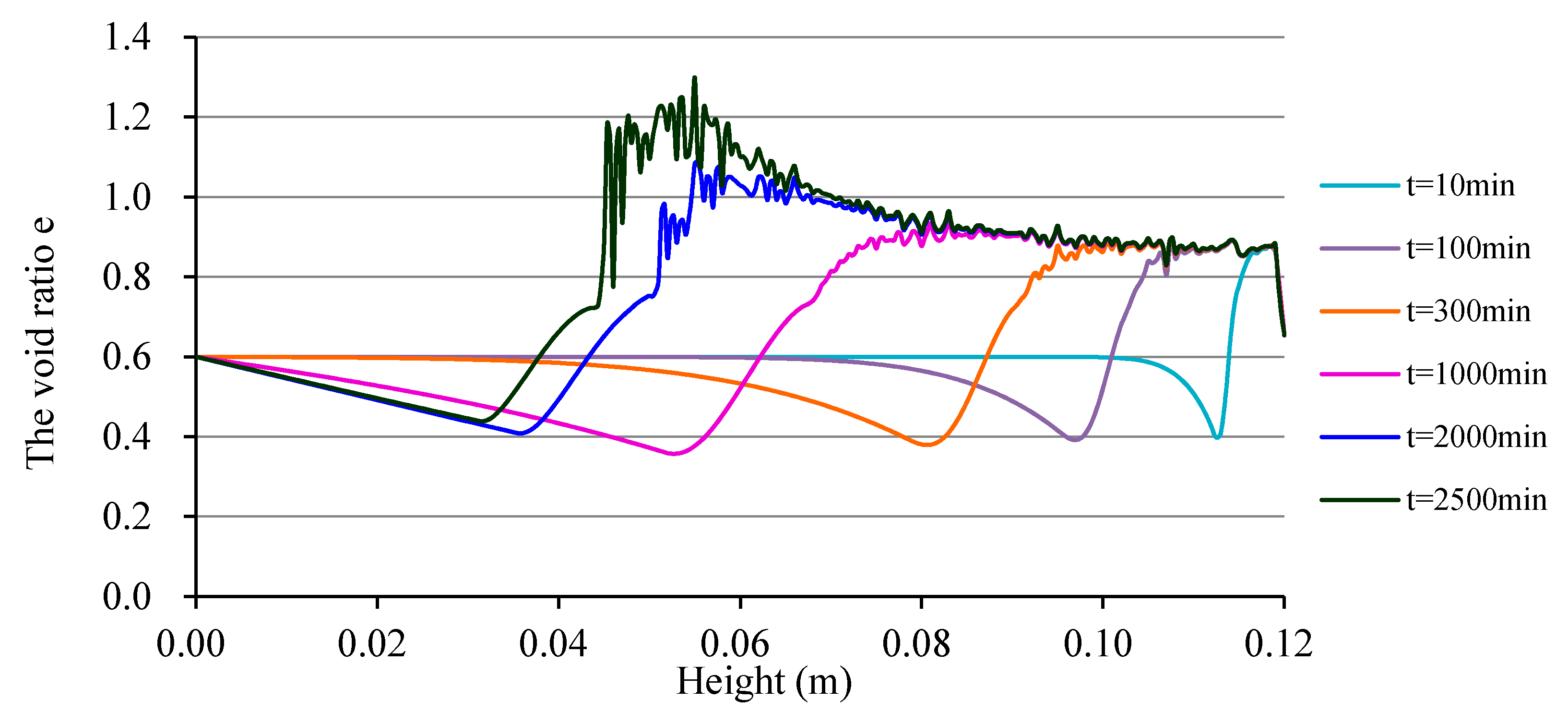
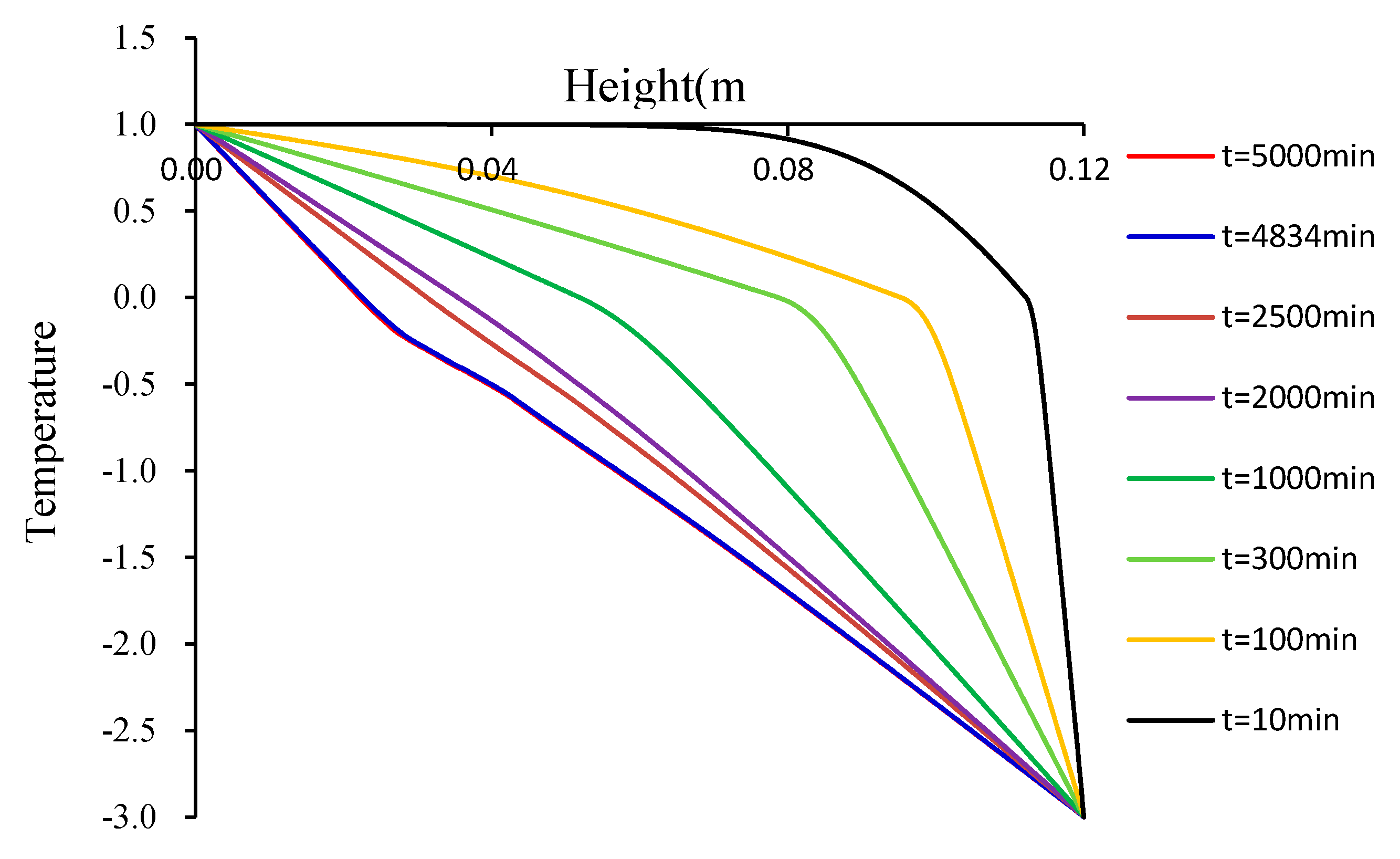
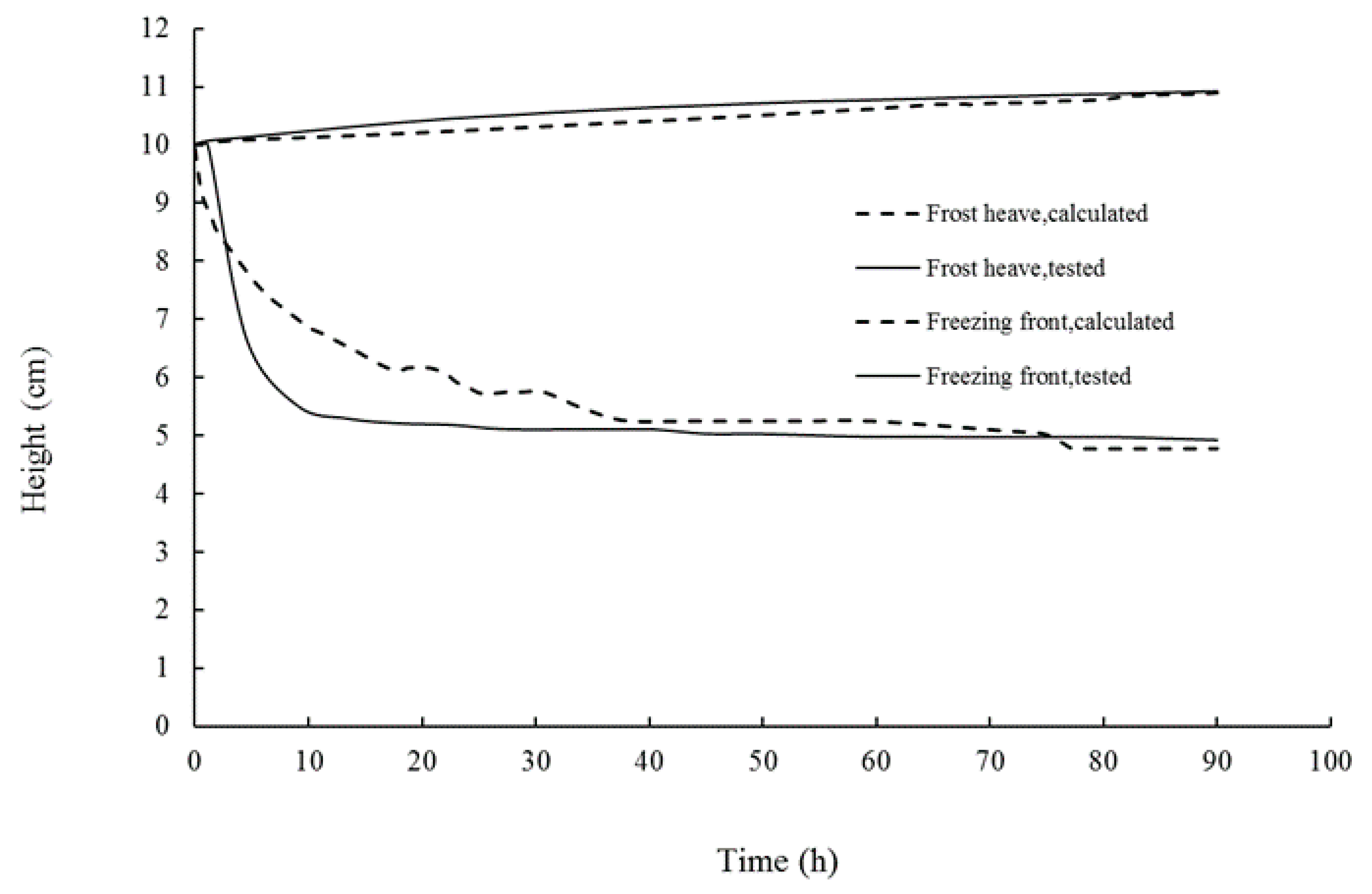
3.2. Numerical Simulation and Analysis of Moisture Migration and Layering of Ice Lens
3.3. Criterion for Formation of Ice Lens ahead of the Final Layer of Ice Lens
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, X.Z.; Wang, J.C.; Zhang, L.X. Physics of Frozen Soil; Science Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Konrad, J.M.; Morgenstern, N.R. The segregation potential of a freezing soil. Can. Geotech. J. 1981, 18, 482–491. [Google Scholar] [CrossRef]
- Miller, R.D. Lens initiation in secondary heaving. Proceedings of the International Symposium on Frost. Action Soils 1977, 2, 68–74. [Google Scholar]
- Konrad, J.M.; Morgenstern, N.R. A mechanistic theory of ice lens formation in fine grained soils. Can. Geotech. J. 1980, 1, 473–486. [Google Scholar] [CrossRef]
- Gilpin, R.R. A model for the prediction of ice lensing and frost heave in soils. Water Resour. Res. 1980, 16, 918–930. [Google Scholar] [CrossRef]
- Taber, S. Frost heaving. J. Geol. 1929, 42, 8–61. [Google Scholar] [CrossRef]
- Beskow, G. Soil freezing and frost heaving with special application to roads and railroads. Sver. Geol. Unders Ser. C 1935, 375, 91–123. [Google Scholar]
- Edlefsen, N.E.; Anderson, A.B.C. Thermodynamics of Soil Moisture; University of California: Berkeley, CA, USA, 1943. [Google Scholar]
- Nixon, J.F. Discrete ice lens theory for frost heave in soils. Can. Geotech. J. 1991, 28, 843–859. [Google Scholar] [CrossRef]
- Watanable, K. Experimental study on microstructure near freezing front during soil freezing. Trans. -Jpn. Soc. Irrig. Drain. Reclam. Eng. 1997, 5, 3–8. [Google Scholar]
- Thomas, H.R.; Cleall, P.; Li, Y.; Harris, C.; Kern-Luetschg, M. Modelling of cryogenic processes in permafrost and seasonally frozen soils. Geotechnique 2009, 59, 173–184. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Li, D.Q. Numerical analysis of coupled water, heat and stress in saturated freezing soil. Cold Reg. Sci. Technol. 2012, 72, 43–49. [Google Scholar] [CrossRef]
- O’Neill, K. The physics of mathematical frost heave models: A review. Cold Regions Sci. Technol. 1983, 6, 275–291. [Google Scholar] [CrossRef]
- Michalowski, R.L.; Zhu, M. Frost heave modelling using porosity rate function. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 703–722. [Google Scholar] [CrossRef] [Green Version]
- Nishimura, S.; Gens, A.; Olivella, S.; Jardine, R. THM-coupled finite element analysis of frozen soil: Formulation and application. Geotechnique 2009, 59, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.; Meschke, G. A three-phase thermo-hydro-mechanical finite element model for freezing soils. Int. J. Numer. Anal. Methods Geomech. 2009, 37, 3173–3193. [Google Scholar] [CrossRef]
- Zhang, Y.; Michalowski, R.L. Thermal-Hydro-Mechanical Analysis of Frost Heave and Thaw Settlement. J. Geotech. Geoenviron. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Liu, E.; Lai, Y.; Wong, H.; Feng, J. An elastoplastic model for saturated freezing soils based on thermoporomechanics. Int. J. Plast. 2018, 107, 246–285. [Google Scholar] [CrossRef]
- Lai, Y.M.; Pei, W.S.; Zhang, M.Y.; Zhou, J.Z. Study on theory model of hydro-thermal–mechanical interaction process in saturated freezing silty soil. Int. J. Heat Mass Transf. 2014, 78, 805–819. [Google Scholar] [CrossRef]
- Pei, W.S. Study of the hydro-thermal-mechanial interaction process of frozen soil and its numerical simulation. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2015. [Google Scholar]
- Terzaghi, K. A fundamental Fallacy in earth pressure computations. J. Boston Soc. Civil Eng. 1936, 23, 71–88. [Google Scholar]
- Bishop, A.W. The Principle of Effective Stress. Tecnisk Ukeblad 1959, 36, 859–863. [Google Scholar]
- Kadivar, M.; Manahiloh, K.N. Revisiting parameters that dictate the mechanical behavior of frozen soils. Cold Regions Sci. Technol. 2019, 163, 34–43. [Google Scholar] [CrossRef]
- Black, P.B. Applications of the Clapeyron Equation to Water and Ice in Porous Media; US Army Corps of Engineers, Cold Regions Research & Engineering Laboratory: Hanover, NH, USA, 1995. [Google Scholar]
- Chen, F.X.; Song, Z.P.; Li, N. Study on moisture migrating force model of freezing soil base on adsorption-flim moisture migration mechanism. J. Water Resour. Archit. Eng. 2006, 4, 1–4, (In Chinese with English abstract). [Google Scholar]
- Kay, B.D.; Groenevelt, P.H. On the interaction of water and heat transport in frozen and unfrozen soils:I. Basic theory; the vapor phase. Soil Sci. Soc. Am. J. 1974, 38, 395–400. [Google Scholar] [CrossRef]


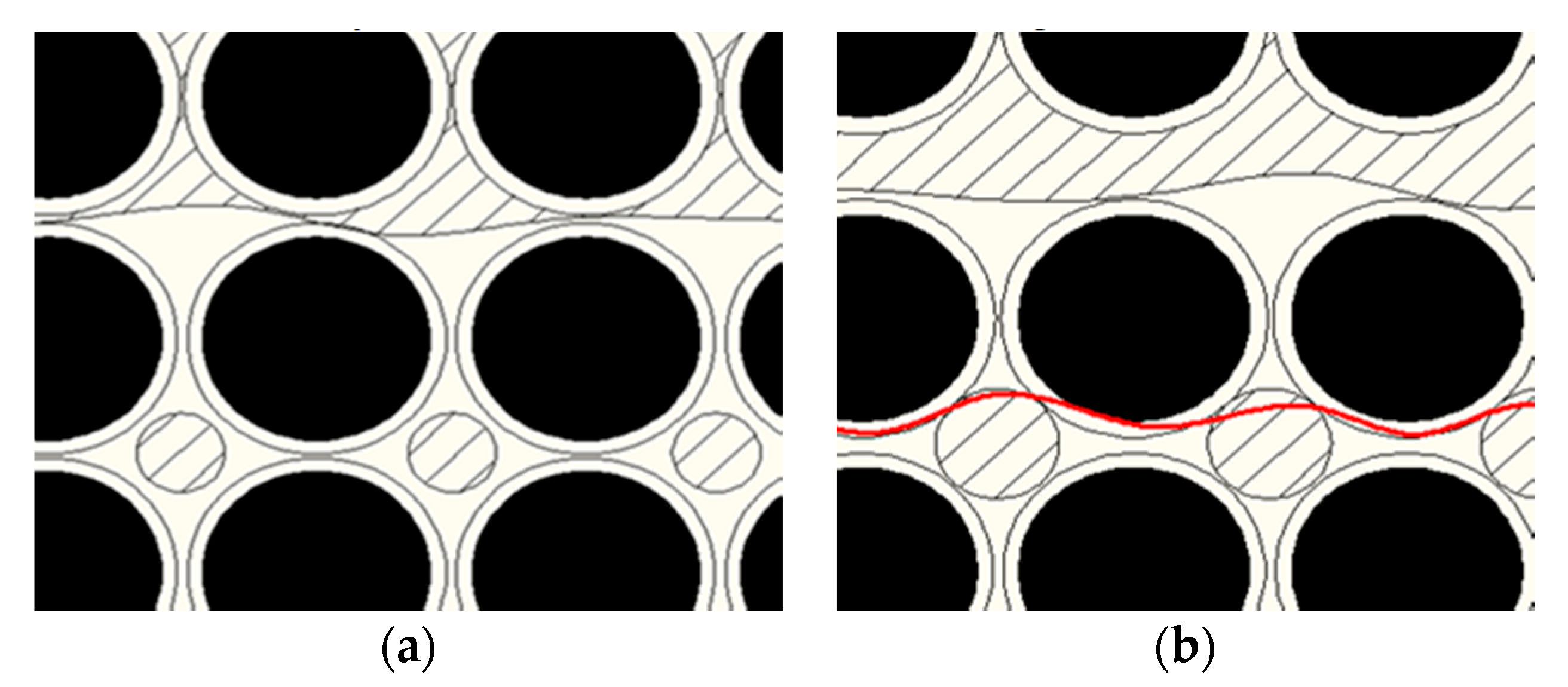



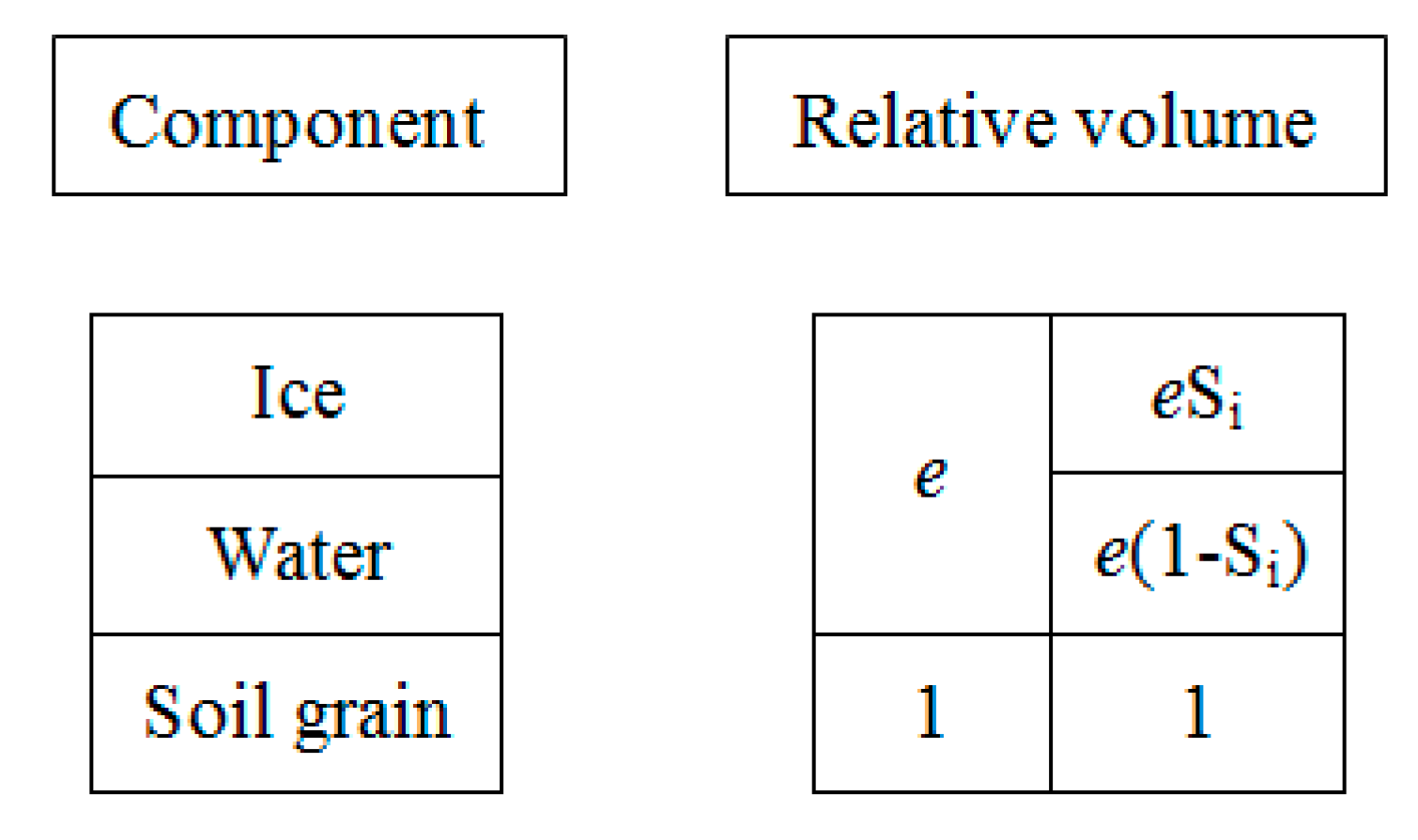



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| −5 | () | 1.20 | |
| −8 | () | 2.22 | |
| 2.5 | () | 0.58 | |
| 101 | () | 2160 | |
| () | 2.7 | () | 4180 |
| () | 0.917 | () | 1874 |
| () | 1.0 | L() | 334.56 |
| g() | 9.8 | esp | 1.2 |
| () | 0 |
| Parameter. | Value | Parameter | Value |
|---|---|---|---|
| −5 | () | 1.50 | |
| −8 | () | 2.22 | |
| 5.7 | () | 0.58 | |
| 101 | () | 2360 | |
| () | 2.36 | () | 4180 |
| () | 0.917 | () | 1874 |
| () | 1.0 | L() | 334.56 |
| g() | 9.8 | esp | 1.2 |
| () | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Luo, H.; Liu, E. Moisture Transfer and Formation of Separate Ice in the Freezing Process of Saturated Soils. Water 2020, 12, 1044. https://doi.org/10.3390/w12041044
Chen P, Luo H, Liu E. Moisture Transfer and Formation of Separate Ice in the Freezing Process of Saturated Soils. Water. 2020; 12(4):1044. https://doi.org/10.3390/w12041044
Chicago/Turabian StyleChen, Peishuai, Huiwu Luo, and Enlong Liu. 2020. "Moisture Transfer and Formation of Separate Ice in the Freezing Process of Saturated Soils" Water 12, no. 4: 1044. https://doi.org/10.3390/w12041044
APA StyleChen, P., Luo, H., & Liu, E. (2020). Moisture Transfer and Formation of Separate Ice in the Freezing Process of Saturated Soils. Water, 12(4), 1044. https://doi.org/10.3390/w12041044





