A Direct Approach for the Near-Optimal Design of Water Distribution Networks Based on Power Use

Abstract

In recent years, iterative computational techniques have been considered as the most effective methods to tackle the problem of Water Distribution System (WDS) minimum-cost design. Given their stochastic nature, these approaches involve a large number of hydraulic simulations in order to obtain suitable results. Herein, a WDS design methodology based entirely on hydraulic principles is presented. This methodology, named Optimal Power Use Surface (OPUS), focuses on both reaching low-cost designs and diminishing the number of hydraulic executions (iterations), by establishing efficient ways in which energy is dissipated and flow is distributed throughout the system. The algorithm was tested in four well known benchmark networks, previously reported in the literature. OPUS proved that following hydraulic principles is a fair choice to design WDS, showing plenty of potential in other water distribution mathematical modeling applications and offering an alternative for the extensive search process undertaken by metaheuristics.

1. Introduction

The optimal design of Water Distribution Systems (WDS) has been addressed internationally during the last decades. This is as a result of the need to make an efficient distribution of scarce economic resources without compromising the welfare of society. This problem is substantially magnified in the context of developing countries because the availability of resources is very limited, and there is a significant deficiency of WDSs that are capable of supplying water in appropriate conditions. To overcome these difficulties, it is important to use methodologies that are both efficient and effective in addressing the minimum-cost WDS design problem.

For instance, in developing countries it is common to find some cities that have WDS that cannot supply water continuously for 24 h a day. Thus, water utilities must find alternative ways to solve the water availability problem with intermittent water supply, which is not well-solved internationally [1]. Another problem found in developing countries is related to aging water networks, but few economic resources are available to perform proper maintenance and rehabilitation programs. In addition, there is increasing pressure on water supply because of climate change and population growth [2]: cities are requiring more water, but water is becoming scarcer. Hence, water utilities must find strategies to solve the problem. For instance, it is well-known that pressure control strategies over all of the network allows for reducing energy losses in water networks, as a workaround for making better use of energy resources. This reduces both energy consumption at pumping stations and water losses in pipes [2], which will allow water utilities to extend the lifespan of aging assets through the reduction of head-losses. Furthermore, the optimal selection of diameters for the equipment, pipes and pumps in WDSs have been found to achieve considerable energy reductions [3]. This increases the importance of making good decisions regarding energy losses in the network, as the objective of water distribution is to deliver water in the quantity required at adequate pressures with the maximum coverage possible at affordable costs [3].

For all these reasons, we find that it is important for water utilities to have several alternatives for the design of WDSs. As there is very little research on intermittent water supply, there is also a general lack in design methods that are straightforward and simple enough to be used by water utilities that lack the interest, the technology or the understanding required to apply state-of-the art design methods based on evolutionary algorithms. Thus, we propose this methodology as a workaround to solve design problems using an energy method, which will allow the designer to fully understand and control what is happening with the energy losses in the network, which we believe may be very useful to network designers in cities with few computation resources available, or cities where energy reduction is the main goal.

It has been shown that finding the optimal configuration of diameters is a NP-Hard problem (non-deterministic polynomial-time) [4], even for the simplest of branched networks, it is a highly constrained nonlinear optimization problem because of the need to satisfy node pressure and pipe flow restrictions. This means that finding an optimal solution using exhaustive and deterministic methods is not viable, hence, approximate methods are required to reach near optimal solutions. Most approximate methodologies are stochastic in nature, and currently most researchers use evolutionary algorithms. However, those approximate methodologies will try to search the whole solution space to find optimal and near-optimal solutions, making it necessary to reduce the search space and guide the heuristic methods to find the solution. For instance, Wu (2005) proposed self-adaptive penalties with Genetic Algorithms [5] and Montalvo (2010) proposed self-adaptive penalties with Particle Swarm Optimization [6].

So far, several authors have proposed approaches to solve the aforementioned problem, which have led to less expensive designs. In the 1970s and 1980s, engineers used traditional optimization methods such as enumeration [7], linear and nonlinear programming [8]. However, in the mid 1990s and beginnings of the 20th century, these approaches were slowly replaced by metaheuristic algorithms due to the greater ease of their implementation, more extensive exploration of the solution space, less dependence on the initial condition of the system, and the ability to integrate the discrete-sized diameter restrictions. Among the successful attempts in the literature, there are: Differential Evolution Algorithms [9], Genetic Algorithms [10], Simulated Annealing ([11,12]), Harmony Search [13], Scatter Search [14], Cross Entropy [15], and Particle Swarm [16]. Moreover, other authors have proposed combined approaches such as binary linear programming with differential evolution algorithm [17], as well as proposed approaches to increase the efficiency of the algorithm by reducing the search space, using afterwards a Genetic Algorithm [18].

Despite the advantages of these stochastic algorithms, they have an intrinsic limitation that exist in the requirement of an appropriate determination of several parameters inherent to each algorithm, which is a time-consuming and laborious task [19]. To accomplish this, metaheuristics use a large number of randomly-generated alternatives and use generic learning functions that progressively produce better results. However, these algorithms require the assessment of thousands of different design alternatives before they converge on a solution. For WDSs, testing each of these alternatives involves the use of a calculation engine, such as EPANET [20]. Thus, the computational effort required is considerable in most cases. For this reason, the number of iterations executed to obtain the final design of the WDS may be considered as an indicator of the efficiency of the tested methodologies.

One approach overshadowed by the rapid growth of metaheuristic techniques was based on the analysis of optimized designs for simple networks, to produce criteria that, combined with hydraulic principles, could produce optimized results in more complex systems. One of the first examples of this approach was Wu [21], who analyzed the behavior of the cost function in a series of pipes with uniform demands, establishing a criterion that indicates the target head-loss value for each pipe in the system to produce a minimum cost design. Featherstone and El-Jumaily [22] extended Wu’s criterion by suggesting its application to looped networks using the Euclidean distance as the main factor to assign the target Hydraulic Grade Line (HGL) at each node and, therefore, the target head-loss value per pipe. Based on the contributions of the aforementioned authors, the Optimal Power Use Surface (OPUS) methodology was first presented by Takahashi et al. [23], as a design methodology based on the target HGL criterion and the use of other hydraulic criteria to extend the concept to looped networks.

This paper describes the OPUS methodology for the optimal design of WDSs and tests its performance in different benchmark networks (Hanoi, Balerma, Taichung and Pescara). Several operational criteria, such as water quality, reliability and environmental impact, can be considered in an optimization problem related to WDS design and management. However, as a first step in the development on this alternative type of design method, the objective function considered in this manuscript is reduced to the construction costs of the system. A comparison against well tested metaheuristic algorithms shows promising results, both in the performance of the algorithm, as well as in the understanding of the physical principles of WDS design. The latter makes OPUS a suitable method for use in decision making at an urban scale, and can be easily understood by engineers. Finally, based on the obtained results, conclusions and future work guidelines are stated.

OPUS methodology, described in this paper, has become the basis for several applications to demand-driven models considering different topologies [24], and in pressure-driven models [25].

2. Optimal Hydraulic Grade Line (HGL) Criteria

Wu [21] analyzed the HGL generated by the global optimum design of pipes in a series system (drip irrigation main lines). He found that for flat topography, the optimal HGL was always a convex function. To characterize the function, Wu [21] used the straight HGL between the source and the last demand node, and defined the “sag” as the distance between that straight line and the function at the middle section. For his case study with uniform demands, the optimal sag was 15% of the total available head.

Using the linear programming method described by Alperovits and Shamir [8], it is possible to extend Wu’s [21] results for different demand distributions along the series of pipes, as well as different topography. As can be seen in Figure 1, the optimal HGL is always a convex function or a combination of adjacent convex functions with limits at nodes with high elevation (i.e., higher than the straight HGL). In these figures, the minimum HGL is composed of the elevation along the pipe series and the minimum pressure allowable. Hence, these figures show different combinations between topographic profiles and demand patterns.

A quadratic equation can be adjusted to the convex function found by Wu [21], as shown in Equation (1):

$$HGL\left(x\right)=4F\times \frac{\left(HG{L}_{max}-HG{L}_{min}\right)}{L^2}\times \left(x^2\right)-\left(1+4F\right)\times \frac{\left(HG{L}_{max}-HG{L}_{min}\right)}{L}\times x+HG{L}_{max}$$

(1)

where, HGL(x) is the hydraulic grade line at a distance x from the source, HGL_Max is the hydraulic grade line at the source, HGL_Min is the HGL at the final node and represents the minimum value allowable, F is the predefined sag as a percentage of (HGL_Max − HGL_Min), and L is the total length of the series [26].

Featherstone and El-Jumaily [22] extended the concept of optimal hydraulic grade line to lopped networks by setting x as the Euclidean distance from each node to the source, and L as the maximum value of x in the network (i.e., the furthest node). Using the Euclidean distance is a quick approach to extend Wu’s concept, but clearly the water needs to flow through longer distances according to the layout of the network. The OPUS methodology introduces a new method to define x and L using the topological distance in looped networks according to a cost-benefit optimal spanning tree.

3. Methodology

The Optimal Power Use Surface (OPUS) design methodology is composed of six steps, which are focused on understanding the flow of energy along the network. These steps are summarized in the flowchart shown in Figure 2, and described in detail in the subsequent sections.

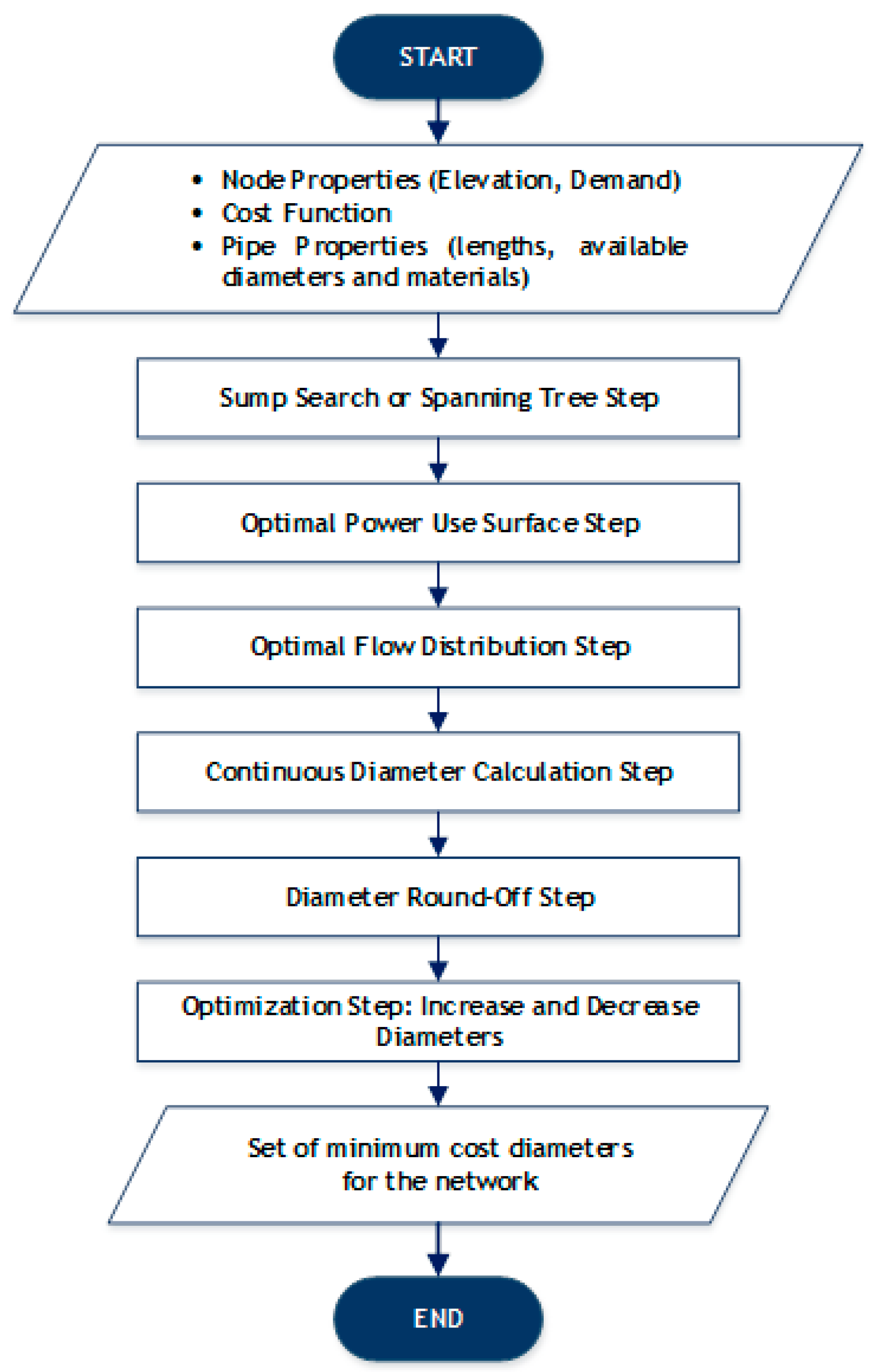
3.1. Sump Search or Spannin Tree Structure

The sump search, or the identification of the Spanning Tree structure, is based on two hydraulic principles: (1) In a least-cost WDS, the demand at the nodes should be supplied by transporting the water from the sources using a single route, and (2) As the pipes flow rates for design purposes increase, the marginal costs diminish.

For the first principle, it can be stated that redundancy is hydraulically inefficient, despite its benefits in terms of reliability. As a result, branched WDSs can manage to be less expensive compared to looped networks; thus, this step aims to decompose the looped system into an open tree-like structure. This leads to the identification of nodes in the original network that can be considered as sumps of a fictional branched network, meaning the nodes with the lowest hydraulic head among all its neighbors.

The second principle is based in the analysis of the relationship between the pipe diameter and its cost per length unit. A typical equation to represent the constructive cost of a pipe is given by Equation (2):

$$Cos{t}_i=K\times L_i\times d_i^x$$

(2)

where, $Cos{t}_i$ is the cost of pipe $i$; $K$ is the coefficient of the cost function; $L_i$ is the length of pipe $i$; $d_i$ is the diameter assigned to pipe $i$; and $x$ is the exponent of the cost function [21]. On the other hand, Hazen-Williams friction head losses equation relates to pipe diameters, friction head losses and flowrates as shown in Equation (3):

$$h_{fi}=\frac{10.67\times L_i\times Q_i^{1.85}}{C^{1.85}\times d_i^{4.87}}$$

(3)

where, $h_{fi}$ is the head-loss along pipe $i$ (m), $Q_i$ represents the volumetric flowrate on pipe $i$ ($m^3/s)$ and $C$ is the pipe roughness coefficient (dimensionless). Therefore, by solving Equation (3) for $d_i$ and then replacing it in Equation (2), an expression for the cost of the pipe as a function of $Q_i$ is obtained, as shown in Equation (4):

$$CostQ\left(Q_i\right)=Cos{t}_i=K^{\prime }\times L_i\times {\left(\frac{Q_i}{S_{fi}^{0.54}}\right)}^{x/2.63}$$

(4)

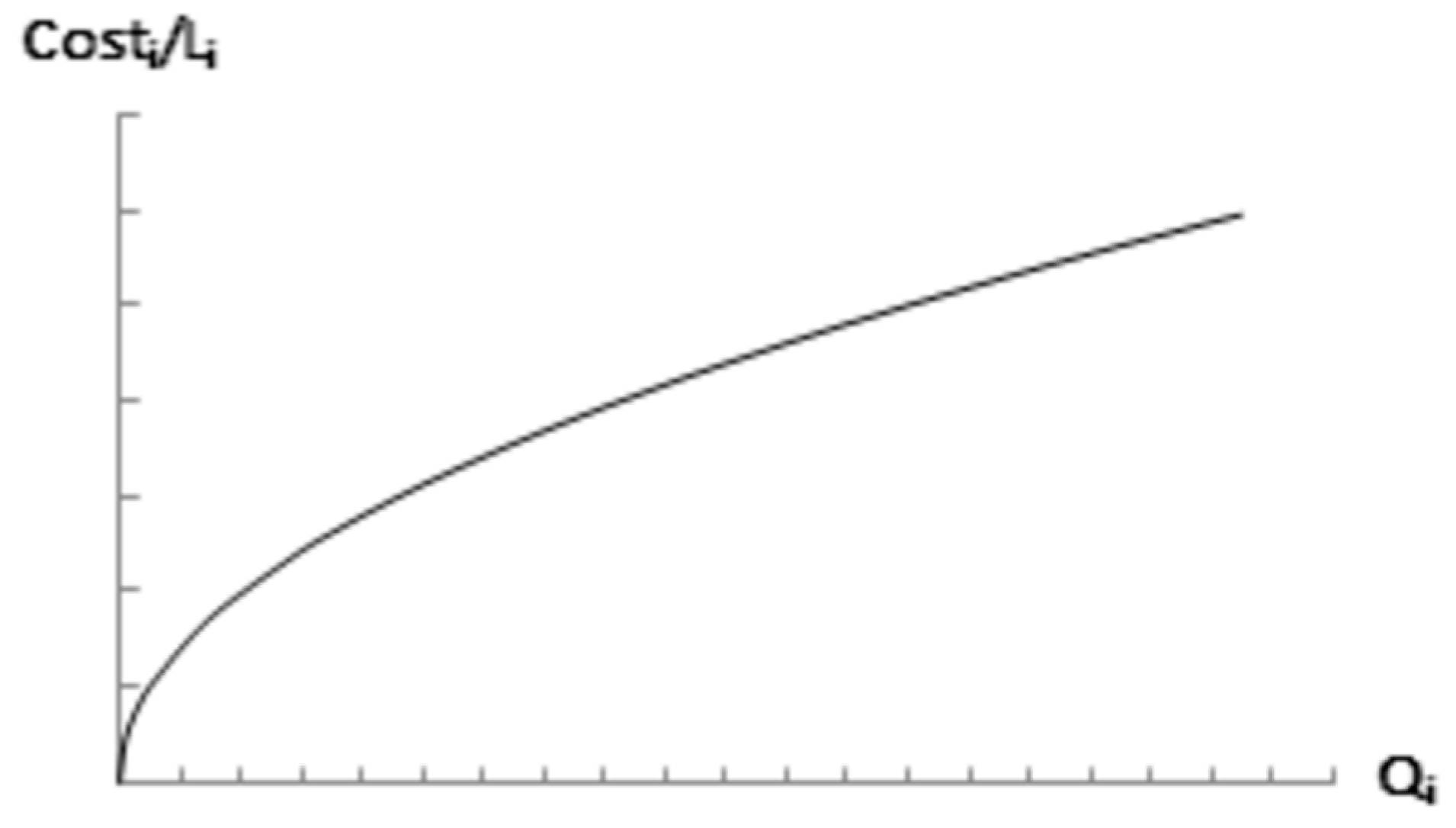
where, $K^{\prime }=K\times {\left(\frac{10.67}{C^{1.85}}\right)}^{x/4.87}$; and $S_{fi}$ is the friction slope for pipe $i$ defined by $h_{fi}/L_i$. Figure 3 shows the trend of this new expression, where it is shown that for typical values of $x$ (lower than 2.63), the marginal cost decreases as the design flowrate of a pipe increases.

Considering that WDS are represented as a set of junctions and links, the problem of obtaining a tree-like structure for the WDS is similar to the problem of finding a Minimum Spanning Tree (MST) for a weighted undirected graph. In this problem, the vertices of the graph are the nodes of the WDS, while the edges of the graph are the pipes (links) in the WDS. Prim [27] proposed an algorithm to find the MST that minimizes the sum of link lengths. For the OPUS methodology, Prim’s Algorithm can be modified to maximize a recursively updated Benefit-Cost ($B/C$) value for every link in the minimum spanning tree. This is equivalent to finding the MST for a graph weighted with the $B/C$ values, but with the $B/C$ values updated at each iteration of Prim’s Algorithm.

The spanning tree is initialized at the water source and grows by incorporating nodes from the selection front (set of adjacent nodes that are not yet connected to the spanning tree), ensuring the connection performed reaches the highest $B/C$ value possible among its set. This procedure is repeated until every node (demand and not demand nodes) in the network is connected to the tree.

If there is more than one water source in the network, there will be the same number of trees as sources in the system, since there should exist only one route to supply each node in the spanning tree structure. In that case, a tree will be initialized per water source, and the selection front will include any node not yet connected to a tree but adjacent to one.

The $B/C$ function of adding a pipe-node pair $i$ in the selection front, is calculated as the ratio between the demand of the node added to the tree and the marginal cost associated with its connection to the source [26], as shown in Equation (5). This marginal cost is computed as the sum of the total cost of the pipe $i$ and the cost difference related to the transportation of the additional flow through all of the upstream pipes [28].

$${\left(B/C\right)}_i=\frac{Outflo{w}_i}{CostQ\left(Outflo{w}_i\right)+{{\displaystyle \sum }}_{\begin{array}{c}j\in Upstream\\ pipes\end{array}}\left[CostQ\left(FlowRat{e}_j+Outflo{w}_i\right)-CostQ\left(FlowRat{e}_j\right)\right]}$$

(5)

where, ${\left(B/C\right)}_i$ is the Benefit–Cost value of adding the attached pipe-node pair $i$. $Outflo{w}_i$ is the flow demand of node $i$, which is the additional flow conveyed through the network, if pair $i$ was added to the tree. $FlowRat{e}_j$ is the flow that goes through pipe $j$ of the tree before inserting any adjacent pipe-node pairs. The first term in the denominator of Equation (5) stands for the cost of the new included pipe, while the sum corresponds to the marginal cost upstream [26]. This expression is computed using Equation (4) as the function $CostQ$.

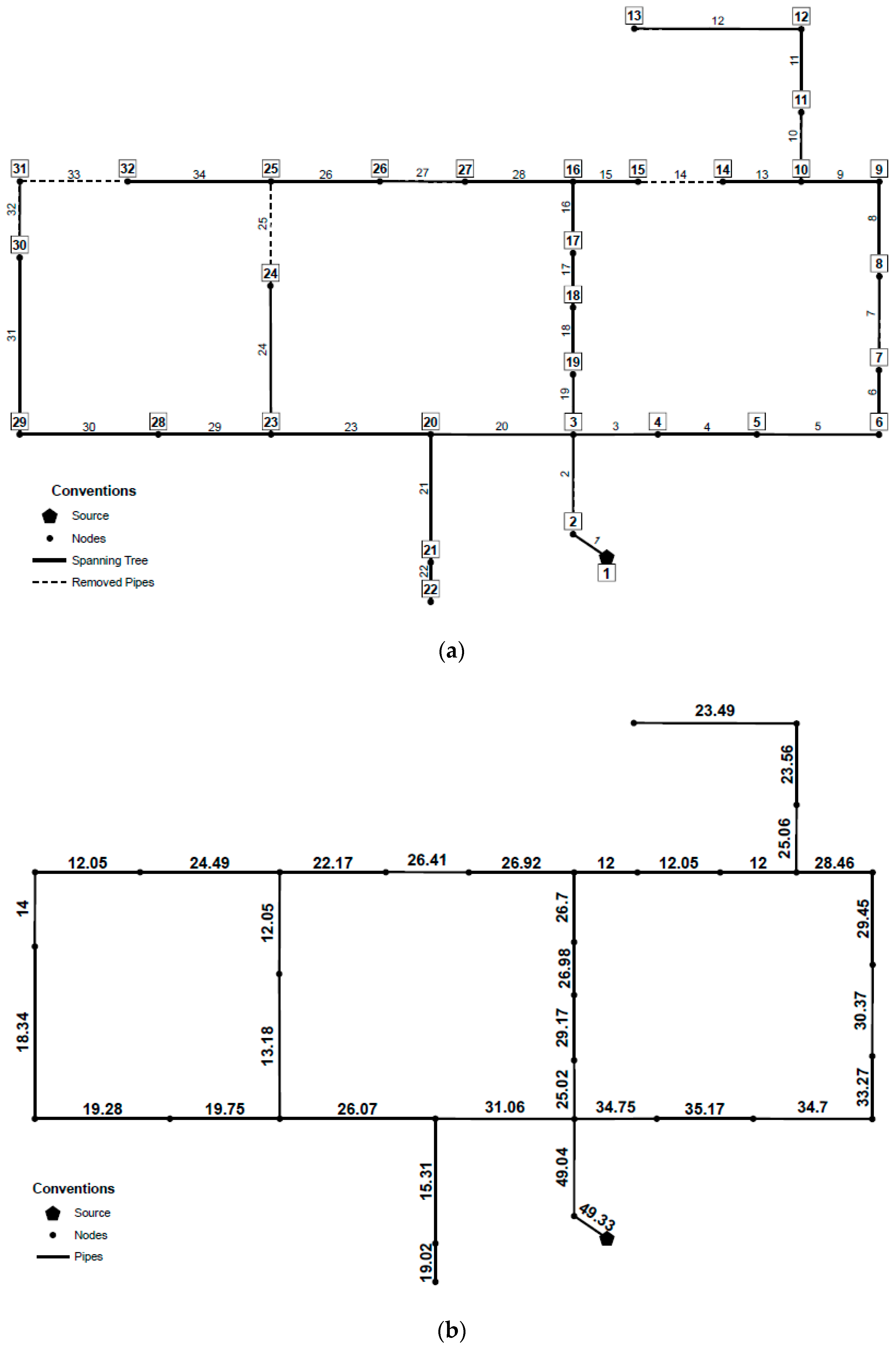
Given Pescara [29], the Italian WDS benchmark shown in Figure 4a, the sump search procedure will be developed as follows: Starting from the three sources (identified as 15, 43 and 65), each selection front is analyzed. In other words, the possible link-node pairs that can be added to Reservoir 65 are <90,76> (i.e., junction 90 and link 76) and <6,89>. Respectively, the link-node pairs <42,54> and <14,11> could be added to sources 43 and 15. To decide which source will be the root of the first tree, and consequently, which link–node pair will be added initially to the tree, the $B/C$ value is computed for each link–node pair, selecting the one that maximizes this criterion. This procedure is repeated until every node is connected to a tree. In Figure 4b, the minimum cost-spanning tree is shown for Pescara WDS, where each link maximized the $B/C$ value at each selection front. Dashed links are those who were not included in the spanning tree, but are present in the original WDS.

In particular, it must be noted that as the Pescara network is supplied by three different sources, it is expected that this tree-structure identification step will reach three different branched sub-systems, each one fed by a unique source. In general terms, for systems with n sources, the nodes in the original network will be grouped into a maximum number of n different tree structures. This is accomplished by seeking to maximize the $B/C$ relationship and ensuring that every node in the original network is assigned to a tree, except for the reservoirs that can be isolated given their $B/C$ relationship. Hence, for further steps in this methodology, the obtained trees are considered simultaneously.

Moreover, the values involved in this step are not actual costs, but values obtained proportionally from the relation presented in Figure 3. Configuring the tree using this cost-benefit function has an O(NN²) time complexity, where NN is the number of nodes. At the end, the status of the last nodes in each branch is set to ‘sumps’, which will be useful for the rest of the methodology [28].

3.2. Optimal Power Use Surface (OPUS)

The entire methodology is named after this specific step due to the close relation with the work developed by Wu [21]. This step consists of assigning a target HGL to each node in the network, which determines the head-losses for each pipe in advance [26].

In the proposed algorithm, the OPUS is computed using the tree structure, described in the previous section. Here, the Wu [21] concept of target HGL is used by setting the pressure of all of the sump nodes to the minimum admissible value [26], and calculating the intermediate nodes’ head for each path knowing the head in each reservoir. For this purpose, each node’s topological distance, measured along the path of pipes that connect the node with the source, must be computed previously. Then Equation (1) is used to compute the target HGL at every node.

Since Equation (1) depends on the parameter $F$ (sag), a sensitivity analysis to evaluate its effect in the final design cost was performed. The evaluated range was $F\in \left[0, 0.25\right]$. In order to represent a straight HGL, the minimum value was set to 0, since a negative sag results in a concave down parabolic HGL, opposite to Wu’s criterion [26]. The maximum value of the sag was obtained by finding the maximum $F$ in Equation (1) that produces a monotonically decreasing HGL for $x\in \left[0,L\right]$. It can be shown that a value of 0.25 is the maximum sag under this consideration (no increasing HGL).

The results of the sensitivity analysis showed that a second-order polynomial could be adjusted to the cost vs. $F$ relationship. Therefore, the design must be done three times with continuous diameters and the costs must be calculated to find the optimal target sag of a network. The criteria considered for the three designs are identical, apart from the general sag used. Subsequently, taking into account that cost vs. sag is a parabola, the optimal sag is determined by finding the minimum cost of a second-order polynomial regression obtained by the three cost vs. sag points previously calculated [26].

If the three designs are made using $F=\left\{0, 0.1, 0.25\right\}$ then the optimal target sag can be computed using Equation (6):

$$Optimal sag=\frac{21C_0-25C_{0.1}+4C_{0.25}}{40\left(3C_0-5C_{0.1}+2C_{0.25}\right)}$$

(6)

where, $C_x$ is the cost of the architecture obtained using a sag $F=x$ [26]. The procedure corresponding to this step is described in the pseudo-code shown in Figure 5.

The target sag $\left(F\right)$ must be recalculated at each intersection in an upstream analysis through the network, where the branches converge. In order to do so, the flow is weighted on each downstream course. It is essential to analyze the nodes with a high elevation, in order to avoid the assignment of a head value that does not fulfill the pressure demand [26].

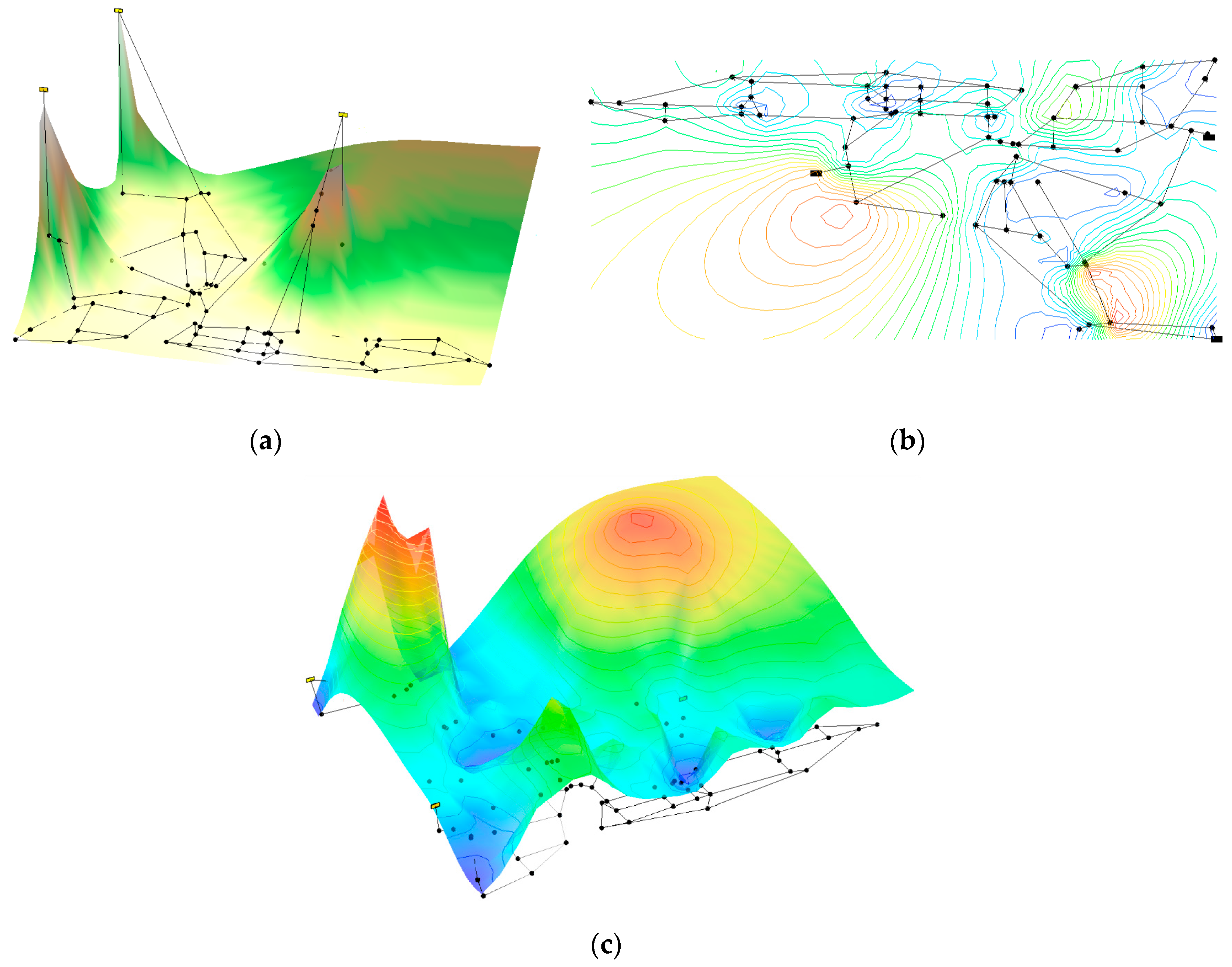
The optimal power use surface for the Pescara network is shown in Figure 6 as an example. The terrain of the network is shown in Figure 6a, while subsequent figures show the level curves for the HGL (Figure 6b), and its corresponding surface (Figure 6c). Note that, as mentioned before, for the water source, the HGL corresponds to the total head available in the reservoir, while in the sump nodes its value was assigned equal to the minimum pressure.

Once this step is concluded, all nodes must have an objective head value assigned. Thus, a flow value is required in order to calculate the diameter of each pipe in the network, using the process explained in the next section.

3.3. Optimal Flow Distribution

In a looped network, the same hydraulic gradient surface can be obtained by combining different configurations of diameters when the set of allowable pipe sizes is R⁺ (positive real numbers) [24]. Thus, this step is intended to find a unique flow distribution in the network that fits to the Optimal Power Use Surface (OPUS) previously defined, ensuring it satisfies the mass conservation at each node.

Since at this point the objective HGL has been assigned using Wu’s [16] criteria with the topological distance, the spanning tree structure is no longer required. Therefore, for further steps, the described procedures are done using the original graph (network).

The determination of the optimal flow distribution consists of the division of the flow demand into the upstream pipes, starting from the sumps. Three different criteria were explored for this procedure by Saldarriaga et al. [19]:

(1)

Uniform distribution: It assumes that all pipes have the same flow, which is calculated by dividing the total flow demand of each node into the number of upstream pipes connected to it [26].

(2)

Proportional distribution: For each pipe, the flow distributes proportionally to H/L², where H stands for the head losses in the pipe and L for its length.

(3)

All-in-one distribution: The conveyance capacity for all the pipes upstream of the analyzed node is computed assuming they have the minimum diameter available (d_min), and they are assigned as the design flows. If this is insufficient to transport the total flow demand, the residual flow is assigned to the one pipe with highest hydraulic favorability.

Depending on the used criterion, the reliability of the network varies. In this context, the reliability can be defined as the ability of the system to handle failures, and it can be measured through several approaches such as the Network Resilience Index (NRI), proposed by Prasad and Park [30]. Saldarriaga et al. [24] proved that the reliability of the network is magnified when the uniform distribution is used, contrasted to the other two criteria. However, in this paper only the All-in-one distribution is considered as it was found to be the one that produced least-cost networks [21].

There are multiple criteria to analyze the appropriateness of different pipes in order to define the main pipe, which is the one that transports the largest portion of the total flow demanded. Similar to the tree structure step, the pipe with the highest flow is determined through a function. This expression is Equation (7), which refers to the Hydraulic Favorability, where the pipe with the maximum value of this parameter is chosen. For nonsump nodes, the total demand is computed by adding its flow to the one required downstream. An Iterative-Recursive Algorithm (IRA) can be applied to perform all of the calculations with an O(NN) time complexity [26].

$$Hydraulic Favorabilit{y}_i=\frac{HG{L}_{up}-HG{L}_{down}}{L^2}$$

(7)

where, $HG{L}_{up}$ is the hydraulic grade line of the upstream node of pipe $i$, $HG{L}_{down}$ is the HGL of the downstream node of pipe $i$, and $L$ is the length of pipe $i$ [26]. At the end of the process, all of the pipes in the system must have been assigned an objective flow value. The subprocess is explained in detail in Figure 7.

3.4. Continuous Diameter Calculation

Once the assigned head-losses and the objective flow rate for each pipe are defined, the diameter required in a continuous range as the hydraulic design can be easily calculated in an explicit manner using the Hazen-Williams equation (solving for $Q$ on Equation (3)) and iteratively with the Darcy-Weisbach and Colebrook-White equations (Equations (8) and (9), respectively) [26]. Then, the obtained continuous diameter must be rounded to an available size to satisfy the constraints of the problem and turn an ideal optimal design into a low-cost feasible one.

In this equation, $Q$ represents the volumetric flowrate (${\mathrm{m}}^3/\mathrm{s})$, $h_f$ is the head loss over the length of pipe (m), $C$ is the pipe roughness coefficient (dimensionless), $d$ is the diameter of the pipe (m), and $L$ is the length of the pipe (m):

$$Q={\left(\frac{h_f\times g\times {\pi }^2\times d^5}{8f\times L}\right)}^{1/2}$$

(8)

where $g$ is the acceleration due to gravity ($\mathrm{m}/{\mathrm{s}}^2)$, and $f$ is the Darcy friction factor (dimensionless).

$$\frac{1}{\sqrt{f}}=-2{\log }_{10}\left(\frac{k_s}{3.7d}+\frac{2.51}{Re\sqrt{f}}\right)$$

(9)

where, $k_s$ is the roughness height of the pipe (m), and $Re$ is the Reynolds Number (dimensionless).

3.5. Diameter Round-off

As described before, the continuous diameters obtained in the previous step must be rounded to satisfy the commercial constraints of the problem. Therefore, in this step the continuous diameter of each pipe is rounded to a discrete value from the list of commercially available diameter sizes, which is represented by the set $\mathit{D}=\left\{D_1, \dots ,D_{ND}\right\}$ [26].

During this research, it has been found that using approaches for approximating the diameter based in either the nearest equivalent flow, as well as the nearest equivalent head-loss led to promising results. The latter is accomplished by raising the continuous diameter values to a power of 2.6 for the equivalent flow criterion (as explained in the Tree Structure step), or using a power of $-4.87$ in the case of the equivalent head-loss criterion. The aforementioned powers describe the relationship between the head-loss and the diameter, according to the Hazen-Williams equation calculated using the International System of Units. However, this action has a negative effect on the hydraulic performance of the network, requiring an additional step to post-optimize the current network.

3.6. Optimization

Finally, the optimization step has two central purposes: (1) To guarantee that all nodes have a pressure above the minimum required value; and (2) To find possible reductions in the capital cost of the network. The first objective is achieved by increasing diameters (if needed), setting as a starting point the ones with larger unit head-loss differences between real and target values [26]. The process is repeated until all the nodes in the system meet the minimum pressure requirement.

The second goal is reached with a double review over the pipes, decreasing the diameters if no constraint is violated. This two-way review starts at the reservoirs, heading towards the sumps in the direction of the flow, and then backwards. This means that the need of reducing the pipe’s diameter is verified twice. If any variation caused a pressure deficit in the system, it is reversed immediately, otherwise it remains [28].

Given that the diameter of one pipe is increased iteratively while some nodes are below the pressure demand, this step requires the highest percentage of iterations of the whole method because a hydraulic simulation must be run per pipe for each diameter variation. This single heuristic can be used alone to accomplish feasible designs, even though, it is strongly dependent on the initial pipe configuration [28].

4. Results and Discussion

The OPUS methodology was tested and validated using four well-known benchmark networks: Hanoi [31], Balerma [32], Taichung [33] and Pescara [29]. Different configurations of the parameters defined on each step of the methodology were tested, looking for optimal designs with discrete diameters (assigning only diameters commercially available). In some cases, there were assigned continuous values ($\mathit{D}=$ R⁺), where $\mathit{D}$ is the diameter of each pipe, to be considered as a theoretical solution giving the best costs that may be found with the methodology without the restriction of continuous diameter values. The input files corresponding to the optimal designs reported below are available in the supplementary files of this research.

4.1. Hanoi

The Hanoi network was first introduced by Fujiwara and Khang [31], and it has become a well-known benchmark WDS for the comparison of design methodologies since its appearance. For this network the Hazen-Williams equation is used to calculate the friction losses; a Hazen-Williams coefficient of $C=130$ is the value for this benchmark network. For the design process a 30 m minimum pressure was established and in order to calculate the network total cost, it is necessary to add the costs of all pipes using a potential function of each diameter. That function has a unit coefficient of $1.1/m and 1.5 as the exponent. The set of available design diameters are 12, 16, 20, 24, 30 and 40 inches [26], and their corresponding unit costs are shown in

Table 1. Unit Costs of Hanoi Network.

Diameter (in.)	12.0	16.0	20.0	24.0	30.0	40.0
Unit Cost ($/m)	45.73	70.40	98.39	129.33	180.75	278.28

. The network is composed of 34 pipes and 31 nodes configured in 3 loops. The whole system is supplied by 1 reservoir with a constant head of 100 m. A sag value of 0.25 was used in OPUS methodology, while both the layout of the network and the obtained spanning tree are shown in Figure 8a.

In OPUS, the Hanoi network was tested using continuous diameters, reaching a total cost of $5,535,888 and the pipe configuration shown in Figure 8b. As can be seen in the mentioned figure, higher values than the maximum allowable diameter (40 inches according to Fujiwara and Khang (1990)), are assigned to some pipes of the network. In order to consider the influence of the diameter restrictions on the final cost of the network, two different discrete designs were performed: the first one based on the original diameter list, and the second one considering the availability of a 50 inches diameter.

In the first scenario considering the original diameter list, the OPUS algorithm generated a total cost of $6,374,525 after 106 iterations, with the resulting pipe diameters (in inches) shown in Figure 8c. These iterations correspond to the total number of hydraulic simulations executed by the algorithm.

Although this is not the least cost reported, the number of hydraulic simulations needed to reach this result is three orders of magnitude smaller than that of other approaches, as is shown in

Table 2. Reported costs and number of iterations for the Hanoi WDS.

Algorithm	Cost (millions)	Number of Iterations
Genetic Algorithm [10]	$6.073	1,000,000
Simulated annealing [11]	$6.056	53,000
Harmony search [35]	$6.056	200,000
Shuffled frog leaping [36]	$6.073	26,987
Shuffled complex evolution [37]	$6.220	25,402
Genetic Algorithm [38]	$6.056	18,300
Ant colony optimization [39]	$6.134	35,433
Genetic Algorithms [32]	$6.081	50,000
Particle Swarm Optimization [40]	$6.093	6600
Genetic Algorithms [12]	$6.173	26,457
Simulated annealing [12]	$6.333	26,457
Simulated annealing with tabu search [12]	$6.353	26,457
Local search with simulated annealing [12]	$6.308	26,457
Harmony search [13]	$6.081	27,721
Cross entropy [15]	$6.081	97,000
Scatter search [33]	$6.081	43,149
Modified GA 1 [41]	$6.056	18,000
Modified GA 2 [41]	$6.190	18,000
Particle swarm harmony search [16]	$6.081	17,980
Heuristic based approach [42]	$6.701	70
Differential evolution [43]	$6.081	48,724
Honey-bee mating optimization [44]	$6.117	15,955
Heuristic based approach [45]	$6.232	259
Self-adaptive differential evolution [46]	$6.081	60,582
Pseudo-Genetic Algorithm [34]	$6.081	25,000
Linear Programming – Differential Evolution [17]	$6.081	33,148
B-GENOME (B-GA) [18]	$6.182	26,000
SOGH [47]	$6.337	94
OPUS (This research)	$6.374	106

. In regards to Hanoi, the least cost design used as benchmark was $6.081 million, given that lower cost results do not satisfy pressure constraints in EPANET2 as shown by [34]. To this end, OPUS reached a solution that has a difference of 4.81% with respect to the lowest value reported in a very low number of iterations.

In the second scenario considering the 50” diameter, the total cost of the design obtained following the OPUS algorithm was of only $5,533,393, due to the closer resemblance between the final hydraulic gradient surface and the target one, as shown in Figure 9. In this approach, the unit cost of the 50” pipe was extrapolated, resulting in a value of $388.91/m. Finally, the resulting diameters listed by their ID shown in Figure 8a are 50, 50, 40, 40, 40, 40, 40, 24, 24, 40, 20, 20, 12, 12, 12, 16, 20, 20, 20, 40, 16, 12, 40, 30, 24, 20, 12, 12, 12, 12, 12, 12, 12 and 20. These diameters are measured in inches.

4.2. Balerma

The Balerma network corresponds to an irrigation district in Almería, Spain [32], and is composed of a total of 454 pipes and 443 demand nodes which are supplied by 4 reservoirs. The topology of the network is presented in Figure 10.

The head-loss expression commonly used is the Darcy-Weisbach equation. The pipe diameters commercially available for its design are manufactured exclusively in PVC, with an absolute roughness coefficient of 0.0025 mm. The minimum pressure allowable is of 20 m, and it has 10 commercially available pipes, the costs of which are presented in

Table 3. Unit costs of Balerma network.

Diameter (mm)	113	126.6	144.6	162.8	180.8	226.2	285	361.8	452.2	581.8
Unit Cost (€/m)	7.22	9.10	11.92	14.84	18.38	28.60	45.39	76.32	124.64	215.85

. A sag value of 0.25 was used in the OPUS methodology, while both the general layout and the obtained spanning tree are shown in Figure 10a. In this figure, it is shown that if the network is fed by multiple sources, it will have a maximum of one spanning tree per reservoir. In this step, all nodes must be assigned to a spanning tree. However, a reservoir can be isolated given that it is not efficient in terms of $B/C$ to feed a part of the network.

Considering continuous diameters for this network, OPUS algorithm generated a design with a total cost of €1.755 million. After executing the Round-off and Optimization processes, the optimal discrete design reached a total cost of €2.015 million, requiring 1165 hydraulic simulations. The configuration of diameters in the OPUS design is shown in Figure 10b.

Table 4. Reported costs and number of iterations for the Balerma WDS.

Algorithm	Cost (€ millions)	Number of Iterations
Genetic algorithm [32]	2.302	10,000,000
Harmony search [13]	2.601	45,400
Harmony search [13]	2.018	10,000,000
Genetic algorithm [12]	3.738	45,400
Simulated annealing [12]	3.476	45,400
Simulated annealing with tabu search [12]	3.298	45,400
Local search with simulated annealing [12]	4.310	45,400
Hybrid discrete dynamically dimensioned search [48]	1.940	30,000,000
Harmony search with particle swarm [16]	2.633	45,400
SOGH [47]	2.100	1779
Memetic algorithm [49]	3.120	45,400
Genetic heritage evolution by stochastic transmission [50]	2.002	250,000
Differential evolution [46]	1.998	2,400,000
Self-adaptive differential evolution [46]	1.983	1,300,000
OPUS (this study)	2.015	1165

shows reported costs and number of iterations reached by several authors.

4.3. Taichung

Sung et al. [28] introduced the Taichung network, which is a WDS located in a city in Taiwan, Taichung. This WDS has 31 pipes and 20 nodes, included in 12 different loops. Water is supplied by one reservoir with 113.98 m as initial head.

Table 5. Unit costs of Taichung network.

Diameter (mm)	Unit Cost (NT Dollar/m)
100	860
150	1160
200	1470
250	1700
300	2080
350	2640
400	3240
450	3810
500	4400
600	5580
700	8360
800	10,400
900	12,800

presents the 13 commercial diameters and their costs [26]. For the design process a minimum head of 15 m was imposed and the friction loss equation is Hazen-Williams with 100 as the C coefficient [28]. The network’s topology is shown in Figure 11a.

The OPUS methodology reached a cost of $8,914,400 after 47 iterations, considering discrete diameters as shown in Figure 11b. Reported costs in literature, and its corresponding number of iterations for Taichung network are shown in

Table 6. Reported costs and number of iterations for the Taichung WDS.

Algorithm	Cost (NT Dollar)	Number of iterations
Tabu search [33]	8,774,900	Not Available
OPUS (this study)	8,914,400	47

.

4.4. Pescara Network

The Pescara network corresponds to the reduced version of the water distribution system of a medium-size city at Italy [29]. This WDS is composed of three reservoirs with a fixed head ranging between 53.08 m to 57.00 m, 99 pipes and 68 demand nodes.

The available pipes are made of cast iron represented by a uniform Hazen-Williams roughness coefficient of 130. The unitary costs of the available pipes are shown in

Table 7. Unit costs of Pescara network.

Diameter (mm)	Unit Cost (€/m)
100	27.7
125	38
150	40.5
200	55.4
250	75
300	92.4
350	123.1
400	141.9
450	169.3
500	191.5
600	246
700	319.6
800	391.1

. A sag value of 0.10 was used in the OPUS methodology. However, for this network the general layout and the obtained spanning tree for each reservoir are shown in Figure 4a.

The minimum pressure head of all demand nodes must be maintained at 20 m. However, this system has two additional constraints in its design: A set of maximum pressures at each demand node ranging between 28.5 m and 55.9 m, and a maximum velocity at each pipe of 2 m/s.

The OPUS methodology reached an optimal discrete design with a total cost of €2.161 million, requiring 206 hydraulic simulations. The configuration of the diameters obtained by OPUS methodology are shown in Figure 12a.

Table 8. Reported costs and number of iterations for the Pescara WDS.

Algorithm	Cost (€ millions)	Number of Iterations
Mixed Integer Linear Programming—MILP [29]	1.820	Not available—Time limit: 7200 s
OPUS (This research)	2.161	206

presents minimum costs and the number of iterations reached by several authors for Pescara Network.

The cost obtained using OPUS design is 18.7% higher than the reported by Bragalli et al. [29]; however, according to the authors, this result was the best solution they could reach within a time limit of 7200 s. In terms of computational efficiency, OPUS methodology requires 210 iterations, which represents less than one second in time, using an average desktop computer (we used a fourth-generation Intel Core i7 processor with 16 GB of RAM, however design software requirements are lower).

Finally, OPUS design fulfilled pressure constraints of the network, considering both the minimum pressure service as well as the maximum pressures allowable at each node. However, these results showed that 2 pipes (ID 84 and ID 103, the latter located downstream the reservoir 43 as shown in Figure 12b,c correspondingly) in the system did not meet the maximum velocity constraint.

4.5. Sensitivity Analysis OPUS Methodology—Sag

As described in the Optimal Power Use Surface (OPUS) step (Section 3.2) of this methodology, the optimal HGL is predefined using the sag, extending Wu (1975) criterion. In this context, the sag is a positive value between 0.0 and 0.50 that represents the difference, in percentage, between a straight HGL and the parabolic HGL that represents the minimum cost design.

To analyze the sensitivity of the resulting OPUS designs regarding the selected sag, several tests were developed considering values between 0.0 and 0.5, with increments of 0.05. In order to assess the performance of the methodology, two indexes were considered in addition to the cost (in millions) of the resulting designs for measuring the reliability of the system: the Resilience Index (RI) proposed by Todini [51], and the Network Resilience Index (NRI) proposed by Prasad and Park [30]. In first place, the RI measures the capacity to be prepared against the occurrence of sudden failures in the supply system based on the surplus of energy available at each junction; this is after demands and pressures have been satisfied. Second, the NRI considers the combined effect of both surplus power and reliable loops in the network as a measurement of resilience. NRI addressed the reliable loops as a consequence of having uniform diameters connected to a node.

In this analysis, Hanoi, Balerma, Taichung and Pescara networks were considered, leading to the results shown in Figure 13. As can be seen, in the case of Hanoi and Balerma, the least-cost design is obtained by using a sag of 0.25. In Taichung, the least-cost design is reached by using a sag value of 0.1 to 0.2, having an increase in the cost of the network of 0.88% when the sag value is 0.15. In Pescara, the near-optimal design is reached by using a sag value between 0.1 and 0.25. However, when a sag of 0.20 is used, an increase of 2.05% to the cost is obtained. Hence, it can be concluded that the least-cost designs are obtained when between 0.10 and 0.25 are used. Accordingly, the behavior shown by Pescara and Taichung may be a result of the rounding process, where small changes in the optimal power surface lead to some increase in pipe diameters.

In addition, for sag values higher than 0.25, the total costs of the network will be greater. The reason for this was first presented by Wu (1975), as for bigger sag values there will be a lower energy slope upstream (negative sag) or downstream (positive sag). Thus, cost will increase because of the need for use of larger sizes of pipe in those sections. Therefore, the costs curve will be convex, with the lower values being between the aforementioned range for sag values (0.10 and 0.25 depending on the network), and increasing above this threshold.

Regarding the comparison between the Resilience Index and the Network Resilience Index, it can be seen that they both decrease as the sag values increase. Given this, it can be inferred that for sag values above 0.25, the obtained results will be more expensive and less resilient. In addition, based on the topology of the networks, it can be seen that if the system tends to be more branched, the NRI will approach the RI. On the other hand, if the network tends to be more looped, the NRI will differ considerably from the RI.

The results presented for the Hanoi, Balerma and Pescara networks will be compared with some results available in literature to validate the performance of OPUS methodology in terms of the resilience of the network. As is presented in Figure 13, the Hanoi network has values ranging from 0.19 to 0.27 for the RI and 0.18–0.26 for the NRI. Similarly, the Balerma network has a RI between 0.30–0.44, and an NRI between 0.28 and 0.42. Finally, Pescara network has a RI ranging between 0.39 to 0.52, and an NRI between 0.32–0.43.

Several optimization approaches have been used for the design of water distribution networks. Reca, Martínez, Baños and Gil [52] used genetic algorithms to minimize the network investment cost, determining an optimal cost of approximately $6.1 million for the Hanoi network with an RI of 0.15. Reca et al. [52] also developed five different multi-objective optimization models for the design of water distribution networks, which are based on minimizing the investment cost and maximizing the RI. These methods proved to reach a lower cost for the same resilience index in comparison with other approaches. The resilience index interval found for the Hanoi network varies from 0.15 to 0.35 with cost ranging from around $5.6 million to $8 million [52]. On the other hand, Monsef (2019) reported an RI between 0.15 and 0.25, and an NRI ranging from 0.174 to 0.331 for the Hanoi network [53].

Regarding the Balerma network, the RI varies between 0.45–0.85 with cost ranging from around €2.9 million to €9.5 million [52]. The behavior of the pareto front of the Balerma network found by Reca et al. is similar to the results presented by other authors [54,55].

Furthermore, Wang, Savić and Kapelan [54] used different multi-objective metaheuristics to minimize the total cost and maximize the NRI of Pescara network resulting in an NRI varying from 0.4 to 0.99 with a cost ranging from 2 million to 18 million. On the other hand, multi-objective optimization based on decomposition presented values for NRI that ranged from 0.32 to 0.96, corresponding to costs of between 2 and 3.9 million [55].

Hence, through these comparisons, it can be concluded that OPUS is able to reach near-optimal designs that are comparable to those obtained by other authors in terms of costs, but also in terms of reliability and resilience. Finally, for reaching least cost designs, it is recommended to use sag values between 0.10 and 0.25, depending the complexity of the network, considering it in terms of its size, and also on whether the system tends to be more branched or more looped. As shown in this sensitivity analysis, using a sag value in this range ensures achieving near the minimum cost for the network.

5. Conclusions

The presented methodology was tested on four benchmark systems, previously mentioned in current literature: Hanoi, Balerma, Taichung and Pescara. In all cases, the OPUS algorithm reached near optimal results with the number of iterations up to five orders of magnitude smaller than other methodologies [26]. These results are noteworthy when considering that the methodology introduced here is entirely deterministic and thus, any user will obtain the same design, as opposed to metaheuristic methodologies that consider a stochastic component. OPUS algorithm takes into account an optimal distribution pattern of flow in the network as a way of spending energy properly. This approach differentiates it from metaheuristic methodologies that do not take into account hydraulic principles to search the solution space [28], proving that it is feasible to develop an entirely hydraulic method that provides near-optimal results.

In the case of the Hanoi network, OPUS achieved a difference of only of 4.81% higher than the lowest reported cost, requiring a number of iterations three orders of magnitude smaller. Regarding this network, the benchmark value in the literature was $6.081, given that lower solutions did not meet pressure constraints using EPANET2 [27]. Moreover, for establishing a comparison, the near-optimal solution reached by OPUS is located within a frequency of 2% of the most frequent solutions shown by Mora-Meliá et al. in the cited study. Hence, it can be seen that several authors report their best results in the literature, regardless of whether or not it is a result that can be obtained consistently. As for the Balerma network, it presented a difference of 3.86% in comparison to the lowest cost reported in previous works, but executed a number of iterations five orders of magnitude below. The Pescara network presented a difference of 18.73% with respect to the results reported previously, considering that this design presented a violation of velocity constraint in 2 pipes (ID 84 and ID 103). Finally, the Taichung network presented a difference of 1.59% when compared to the result reported in literature. Even though these results did not report the number of iterations required to reach the solution, with OPUS, we only required a total for 47 iterations to reach this near-optimal result, which does not demand a significant computational effort.

Regarding the sag value, it was demonstrated that least cost designs are obtained when this value is between 0.10 and 0.25. This can be compared to the Wu criterion [16], which uses a sag of 0.15 for series’ of irrigation pipes. A comparison using the Network Resilience Index (NRI) and the Resilience Index (RI) was done, resulting in a decreasing behavior for higher values of the sag. Similarly, the NRI and RI results were compared with values available in literature, finding that the results of the OPUS methodology were comparable to them. Hence, it can be concluded that for higher sag values, the resulting designs will be more expensive and less reliable. Meanwhile, both resilience indexes showed a similar behavior among them.

The OPUS methodology showed a good performance on real-size networks, leading to the minimization of constructive costs in a substantially low number of iterations in comparison to other methodologies. Conversely, because of the differences in hydraulic behavior between a tree-like network and a real-life looped network, when OPUS is used in small WDSs, the results are not as good as expected because that difference in hydraulics is higher in smaller networks. In addition, Giudicianni (2018) found that there are several topological differences between small, large and synthetic WDNs (Water Distribution Networks) [51,56], thus it is possible to state that one methodology fits for some kind of networks but not for others. In this case, the result was highly influenced by the optimization process and not by the steps based on hydraulic principles, as a result of the fact that the design is executed based on the branched network (spanning tree).

The algorithm described herein proves to be efficient and to achieve near-optimal solutions that resembles the costs and resilience of other evolutionary algorithm methodologies, but with running a lower number of iterations, based on understanding and applying the hydraulic principles that govern WDSs. Some of the results presented correspond to theoretical networks with some constraints that limited the design possibilities, as in the case of Hanoi. Therefore, it is highly recommended to test this methodology on real WDSs and include additional objectives in the procedure, such as maximizing the network reliability or minimizing leakages. Furthermore, energy approaches can be used for the calibration of models and design optimal system operation. The results obtained through the OPUS algorithm makes it a promising methodology to be used as a “hot start” for different metaheuristics. Namely, the pipe configuration obtained as a result of OPUS could be the initial configuration used by a stochastic methodology as a hot start to obtain even better results still with a small number of iterations.

Finally, despite the fact that the OPUS methodology was originally made to be applied on gravity-driven WDSs only, the algorithm could also be easily applied to the case of pump-driven networks. OPUS has not been applied to these cases, but one can speculate that the inclusion of pumps could be carried out with some minor adjustments to the algorithm. In those networks in which the water is pumped to an initial reservoir, the pumping effect could be easily introduced increasing the HGL at the entrance of the distribution system. A different case is when the pump is located in some node of the WDS downstream of the initial node. In this case, all nodes downstream of the pump must be changed to take into account the effect of a sudden increase in pressure. A decrease in the HGL of those downstream nodes should be included so that a simulation of a topological descent of the network can mimic the action of gravity. This means that the power surface must be changed because of the pressure addition at specific points of the network [26].