A Two-Dimensional Depth-Averaged Sediment Transport Mobile-Bed Model with Polygonal Meshes
Abstract
:1. Introduction
2. Governing Equations
2.1. Flow Equations
2.2. Sediment Transport Equations
2.3. Mobile-Bed Equations
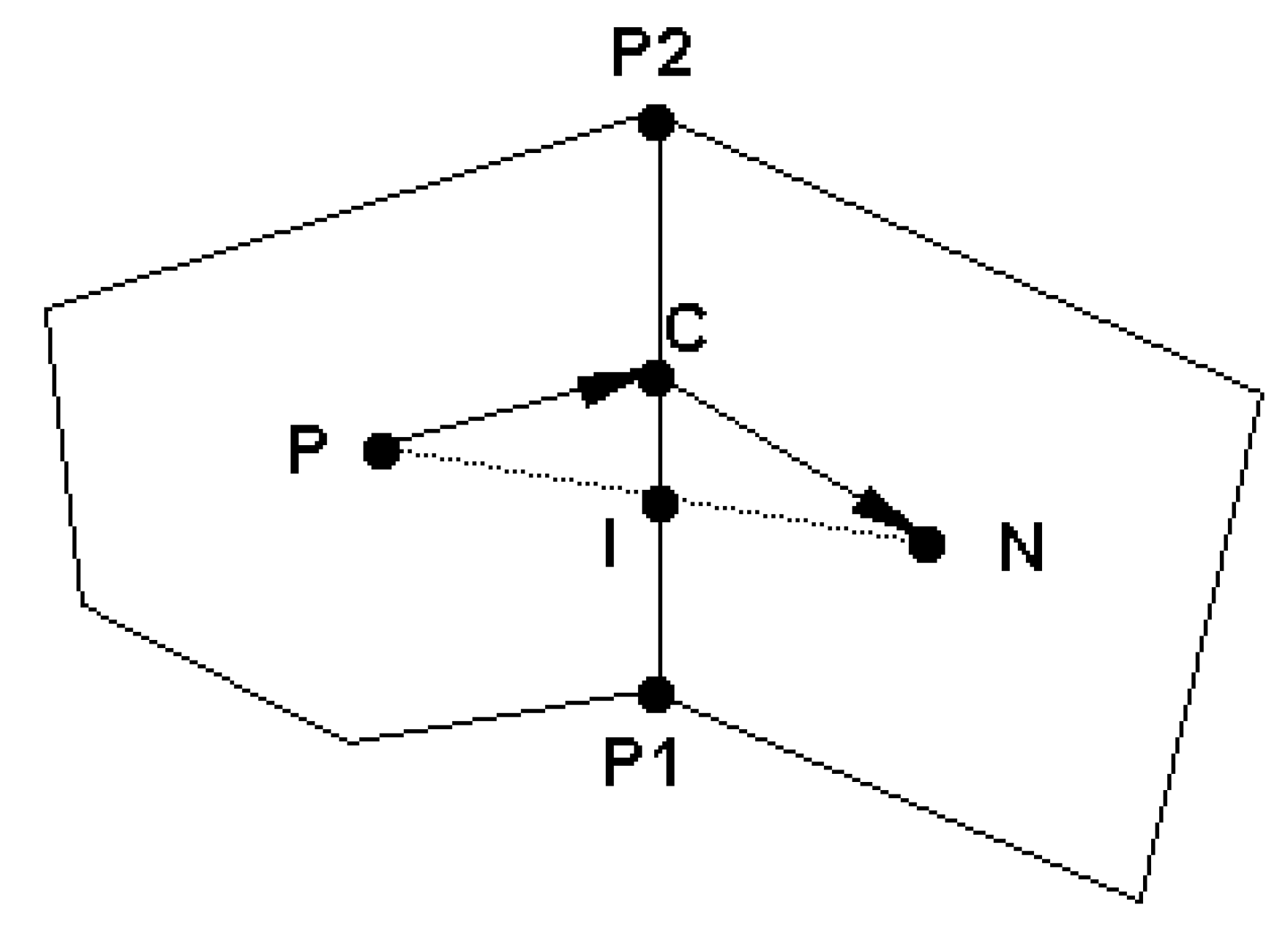
3. Numerical Methods
4. Model Verification and Validation
4.1. Aggradation in a Straight Channel
4.2. Erosion in a Straight Channel
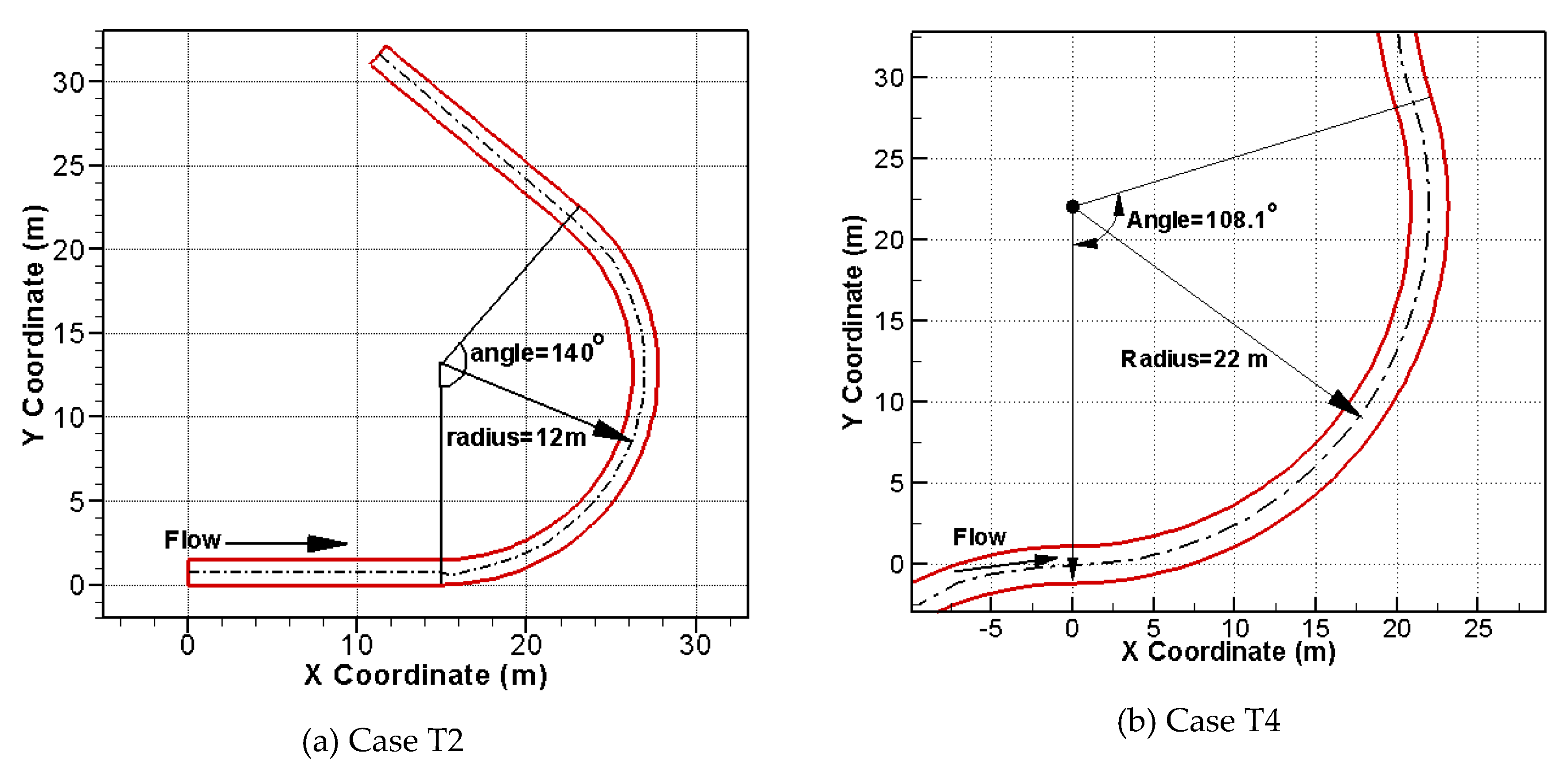
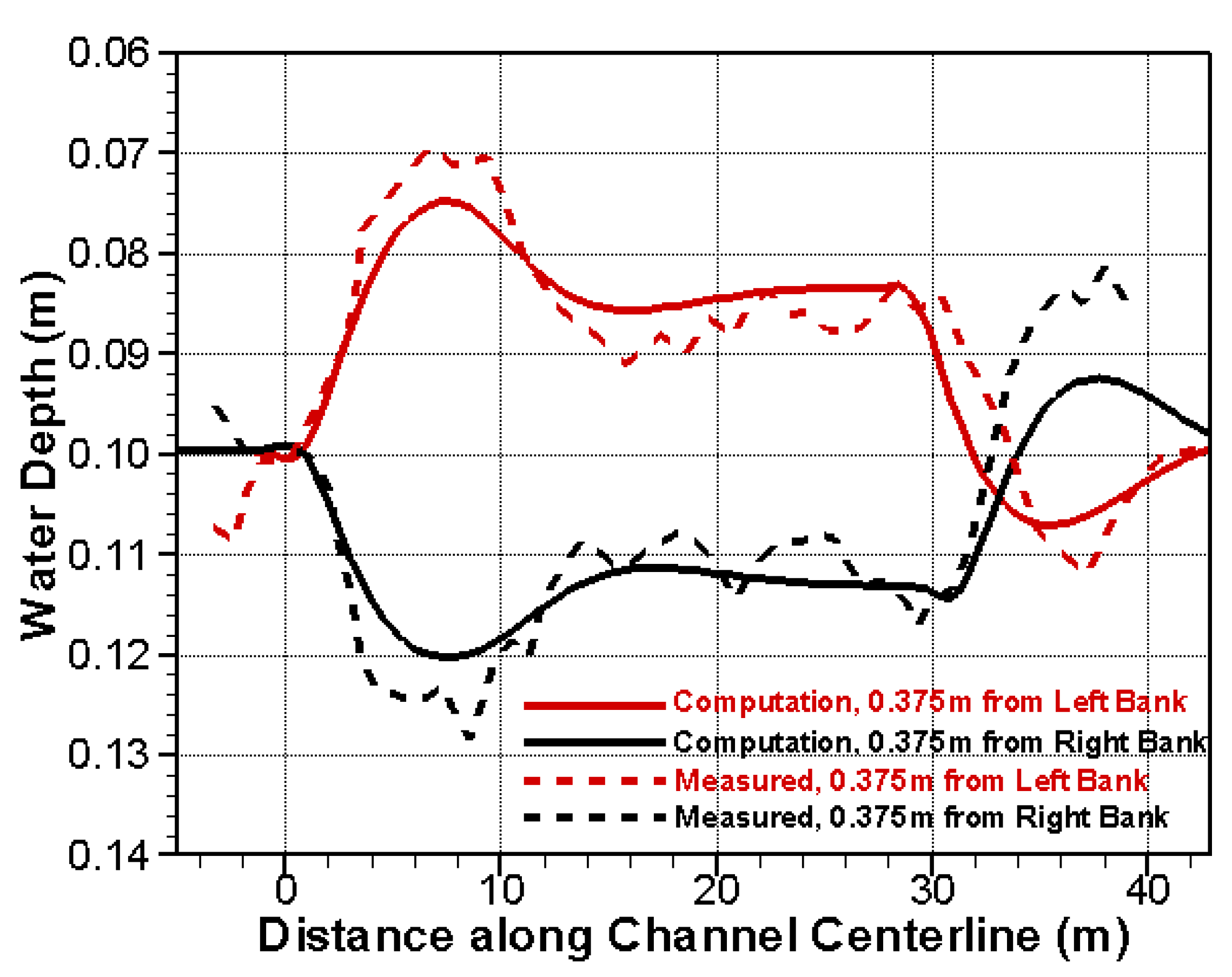
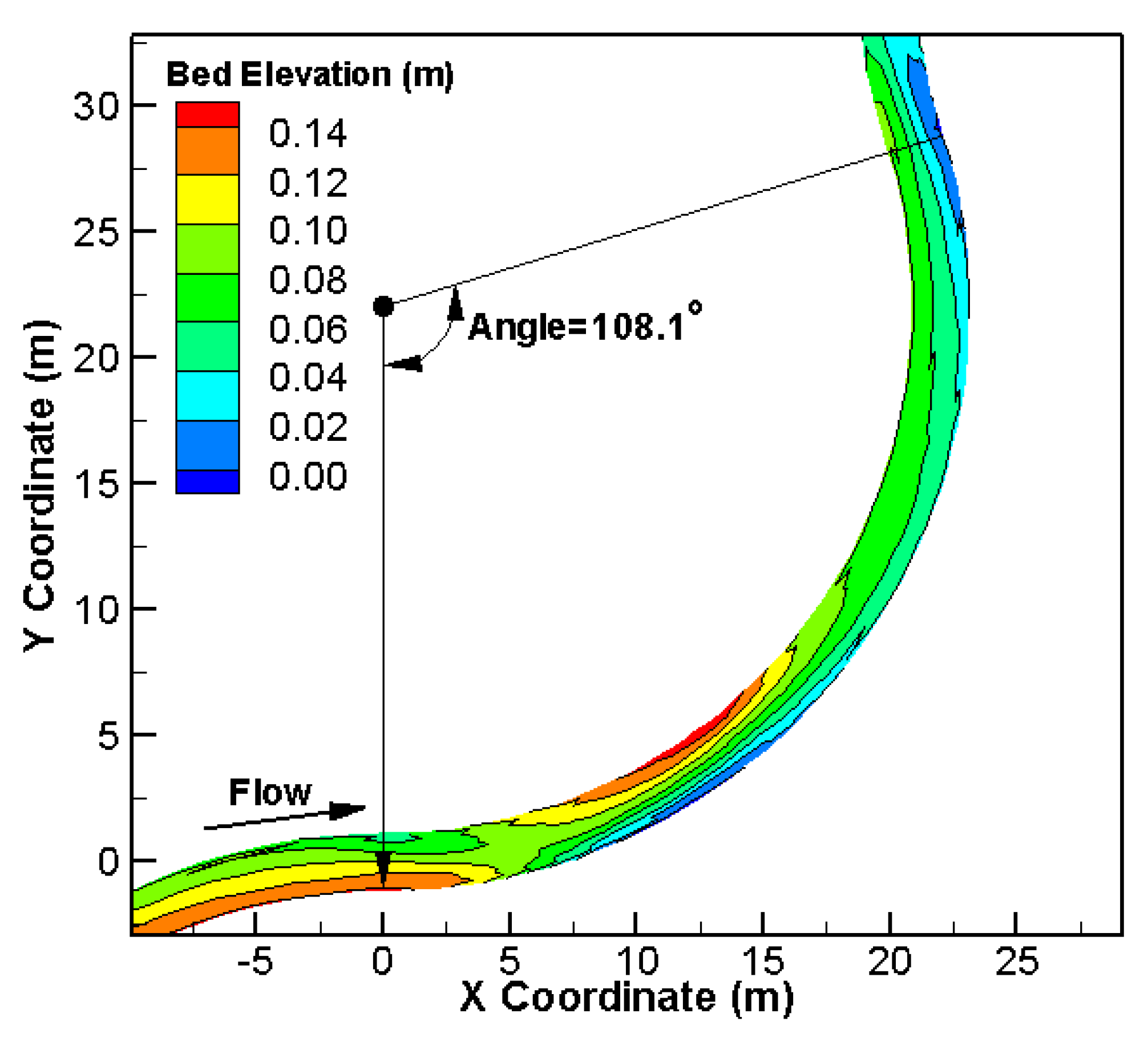
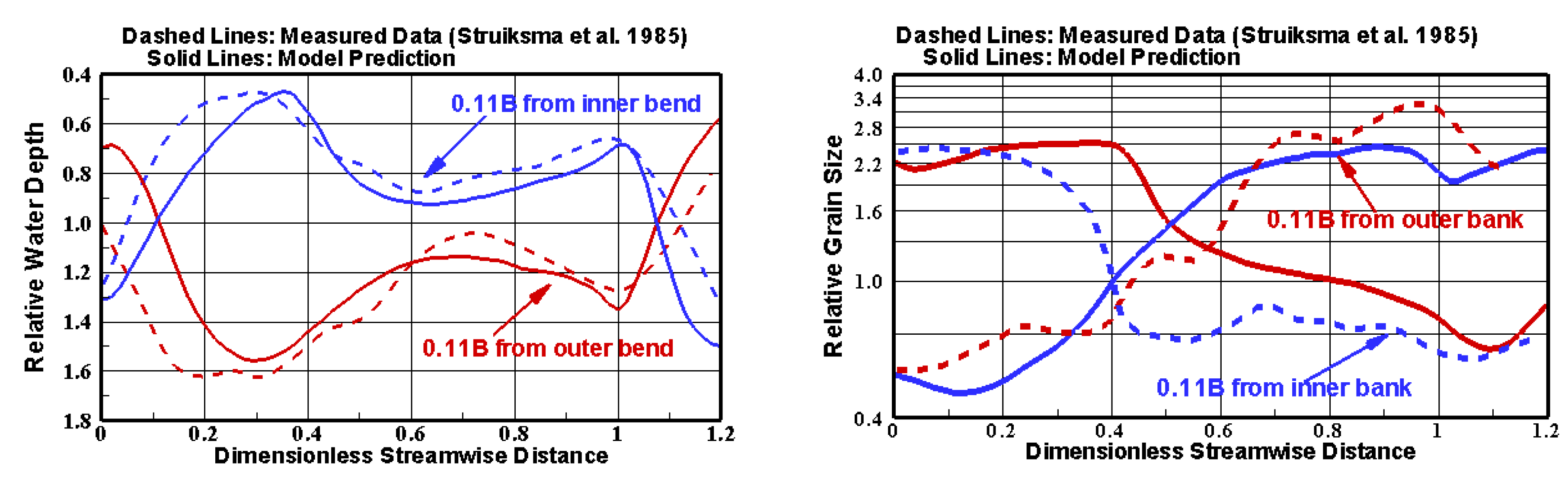
4.3. Erosion and Depostion in Bends
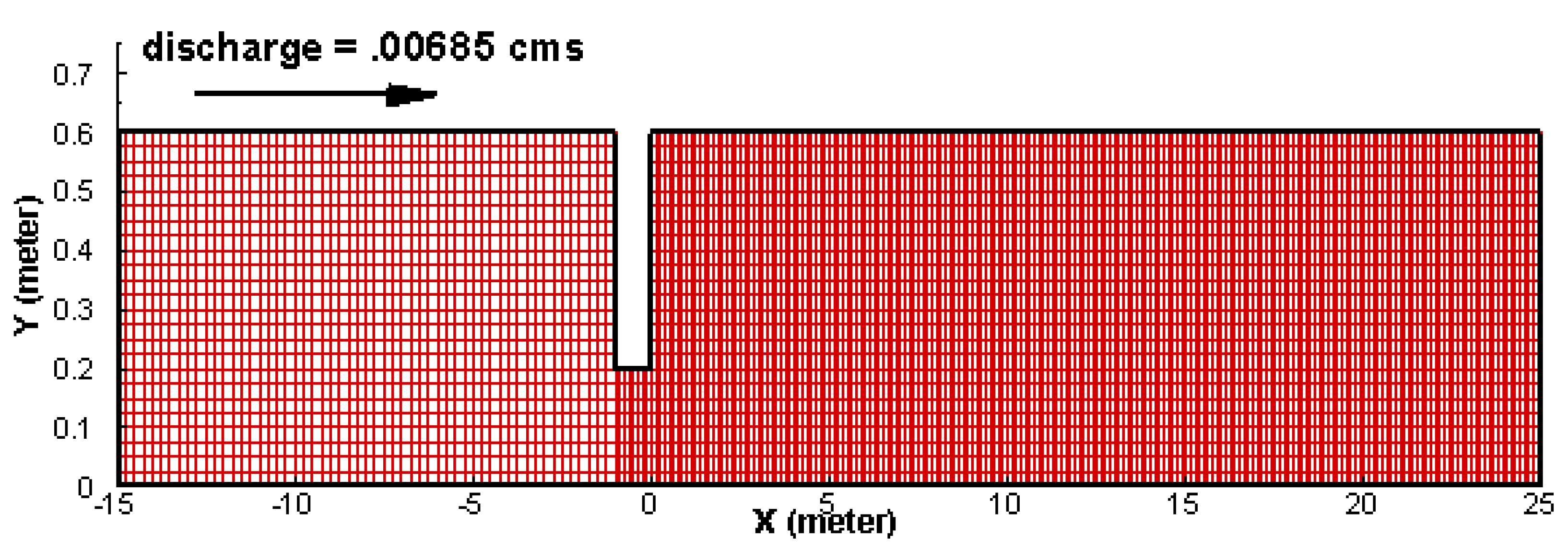
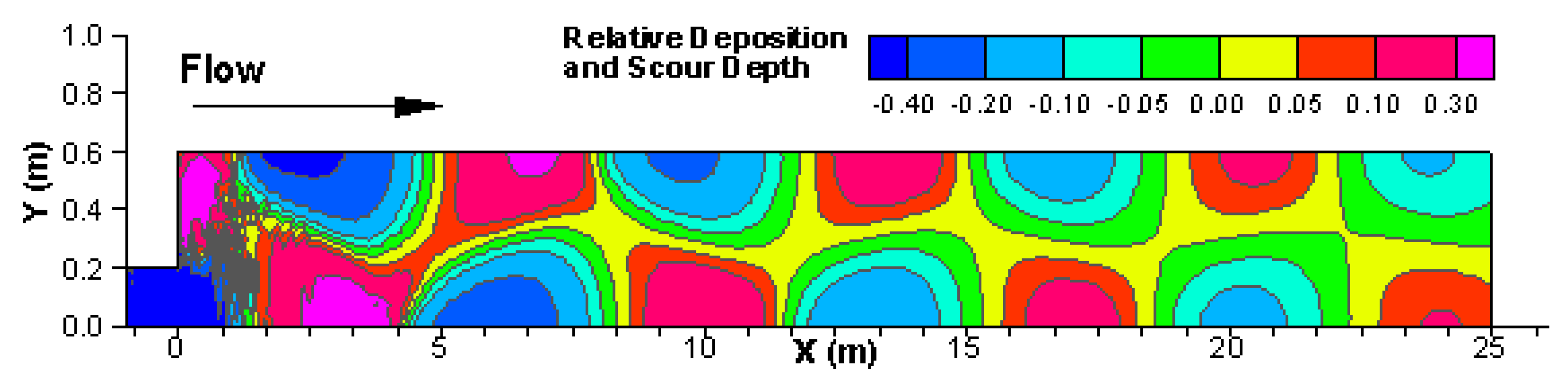
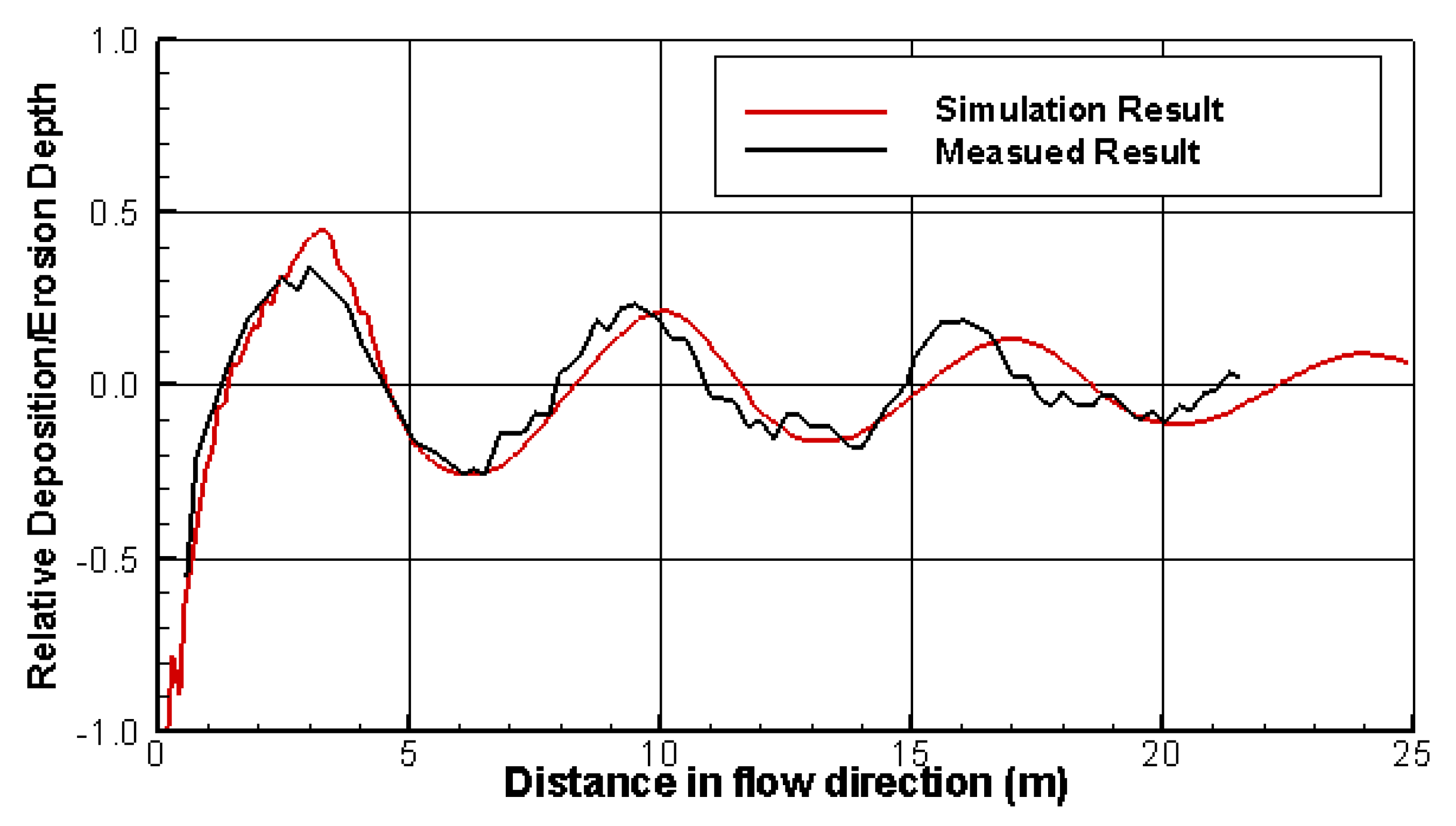
4.4. Alternating Bar Formation Downstream of an Inserted Dike
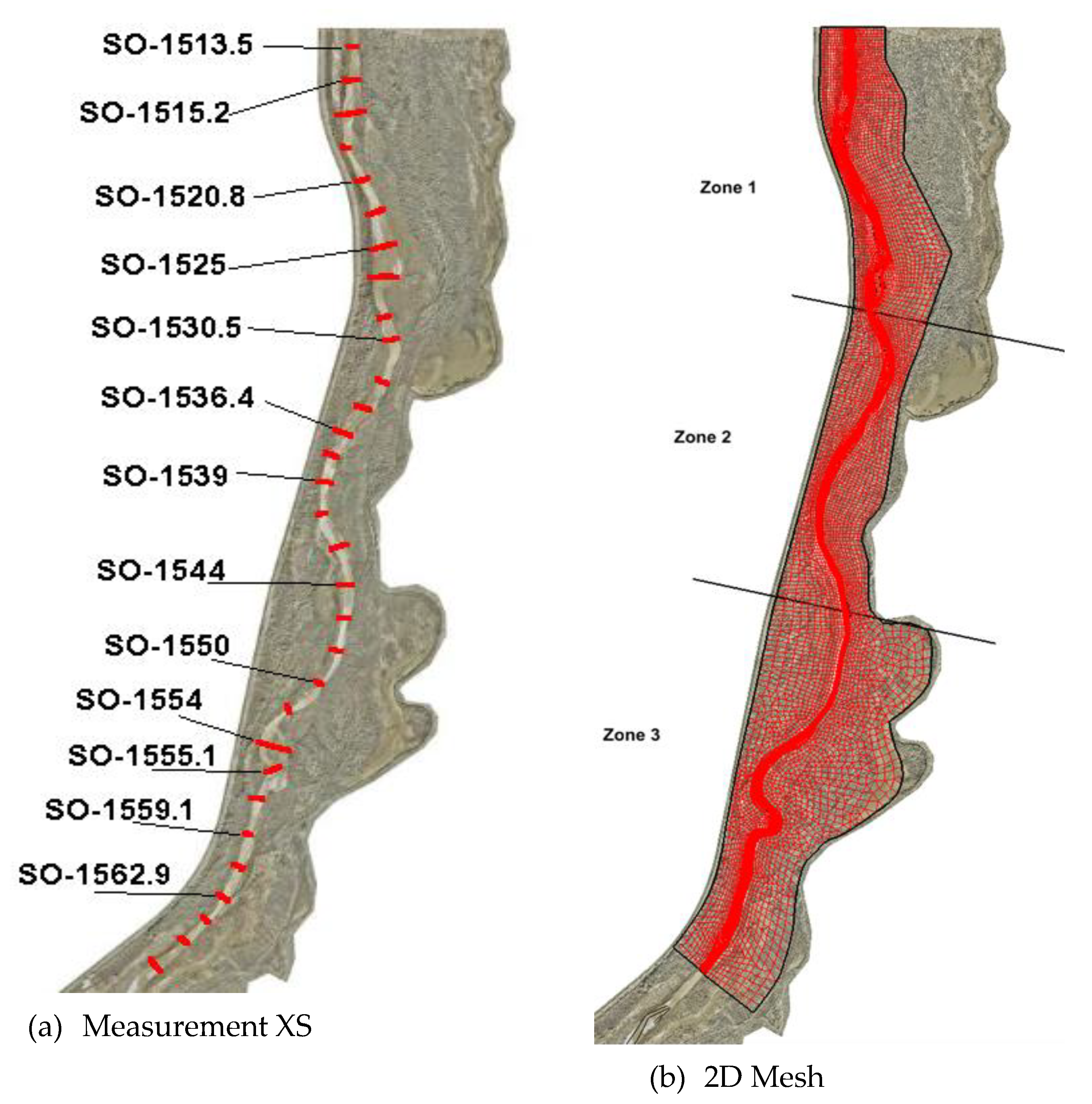
4.5. Erosion and Deposition on a Section of the Middle Rio Grande
5. Conclusions
Funding
Conflicts of Interest
References
- ASCE. Earthen embankment breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar] [CrossRef]
- Gibson, S.; Brunner, G.; Piper, S.; Jensen, M. Sediment Transport Computations in HEC-RAS. In Proceedings of the Eighth Federal Interagency Sedimentation Conference (8th FISC), Reno, NV, USA, 2–6 April 2006; pp. 57–64. [Google Scholar]
- USACE. New One-Dimensional Sediment Features in HEC-RAS 5.0 and 5.1. 2018. Available online: https://www.researchgate.net/publication/317073446_New_One-imensional_Sediment_Features_in_HEC-RAS_50_and_51 (accessed on 10 January 2020).
- DHI. MIKE 11. In Users Manual; Danish Hydraulic Institute: Horsholm, Denmark, 2005. [Google Scholar]
- Wu, W.; Vieira, D.A. One-Dimensional Channel Network Model CCHE1D Version 3.0.—Technical Manual; Technical Report No. NCCHE-TR-2002-1; National Center for Computational Hydroscience and Engineering, The University of Mississippi: Oxford, MS, USA, 2002. [Google Scholar]
- Huang, J.; Greimann, B.P. GSTAR-1D, General Sediment Transport for Alluvial Rivers—One Dimension; Technical Service Center, U.S. Bureau of Reclamation: Denver, CO, USA, 2007. [Google Scholar]
- FHWA. Evaluating Scour at Bridges, HEC-18, 5th ed.; Report, No. HIF-FHWA-12-003; Arneson, L.A., Zevenbergen, L.W., Lagasse, P.F., Clopper, P.E., Eds.; U.S. Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2012.
- Hogan, S.A. Advancements in Bridge Scour Assessment with 2D Hydraulic Modeling Using SRH-2D/SMS. In Proceedings of the 9th International Conference on Scour and Erosion, Taipei, Taiwan, 5–8 November 2018. [Google Scholar]
- Chow, V.T.; Ben-Zvi, A. Hydrodynamic modeling of two-dimensional watershed flow. J. Hydraul. Div. ASCE 1973, 99, 2023–2040. [Google Scholar]
- Kuipers, J.; Vreugdenhil, C.B. Calculation of Two Dimensional Horizontal Flow; Reports S163, Part 1; Deflt Hydraulics Lab.: Delft, The Netherlands, 1973. [Google Scholar]
- Celik, I.; Rodi, W. Modeling suspended sediment transport in nonequilibrium situations. J. Hydraul. Eng. 1998, 114, 1157–1191. [Google Scholar] [CrossRef]
- Spasojevic, M.; Holly, F.M., Jr. 2-D bed evolution in natural watercourses—New simulation approach. J. Waterw. Port Coast. Ocean Eng. 1990, 116, 425–443. [Google Scholar] [CrossRef]
- Minh Duc, B. Berechnung der Stroemung und des Sedimenttransorts in Fluessen Mit Einem Tieffengemittelten Numerischen Verfahren. Ph.D. Thesis, The University of Karlsruhe, Karlsruhe, Germany, 1998. (In German). [Google Scholar]
- Olsen, N.R.B. Two-dimensional numerical modeling of flushing processes in water reservoirs. J. Hydraul. Res. 1999, 37, 3–16. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S.Y.; Jia, T.; Robinson, K.M. Numerical simulation of two-dimensional headcut migration. In Proceedings of the 1999 International Water Resources Engineering Conference, on CD-ROM., ASCE, Seattle, WA, USA, 8–12 August 1999. [Google Scholar]
- Wu, W. Depth-averaged two-dimensional numerical modeling of unsteady flow and non-uniform sediment transport in open channels. J. Hydraul. Eng. 2004, 130, 1013–1024. [Google Scholar] [CrossRef]
- Hung, M.C.; Hsieh, T.Y.; Wu, C.H.; Yang, J.C. Two-dimensional nonequilibrium noncohesive and cohesive sediment transport model. J. Hydraul. Eng. 2009, 135, 369–382. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Cao, Z.; Pender, G.; Liu, Q.; Carling, P. Coupled flood and sediment transport modelling with adaptive mesh refinement. Sci. China Technol. Sci. 2015, 58, 1425–1438. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, S.S.Y. CCHE2D: Two-Dimensional Hydrodynamic and Sediment Transport Model for Unsteady Open Channel Flows Over Loose Bed; Technical Report: NCCHETR-2001-01; National Center for Computational Hydroscience and Engineering, The University of Mississippi: Oxford, MS, USA, 2001. [Google Scholar]
- Hervouet, J.-M. Hydrodynamics of Free Surface Flows; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007; pp. 1–360. [Google Scholar]
- Casulli, V.; Walters, R.A. An unstructured grid, three dimensional model based on the shallow water equations. Int. J. Numer. Methods Fluids 2000, 32, 331–348. [Google Scholar] [CrossRef]
- Bever, A.J.; MacWilliams, M.L. Simulating sediment transport processes in San Pablo Bay using coupled hydrodynamic, wave, and sediment transport models. Mar. Geol. 2013, 345, 235–253. [Google Scholar] [CrossRef]
- Deltares. Delft3D-FLOW. In Simulation of Multi-Dimensional Hydrodynamic Flow and Transport Phenomena, including Sediments–User Manual; Version 3.04, rev. 11114; Deltares: Delft, The Netherlands, 2010. [Google Scholar]
- Kernkamp, H.W.J.; Van Dam, A.; Stelling, G.S.; De Goede, E.D. Efficient scheme for the shallow water equations on unstructured grids with application to the Continental Shelf. Ocean Dynam. 2010, 29, 1175–1188. [Google Scholar] [CrossRef]
- Achete, F.M.; van der Wegen, M.; Roelvink, D.; Jaffe, B. A 2-D process-based model for suspended sediment dynamics: A first step towards ecological modeling. Hydrol. Earth Syst. Sci. 2015, 19, 2837–2857. [Google Scholar] [CrossRef] [Green Version]
- Deltares. D-Flow Flexible Mesh, Technical Reference Manual; Deltares: Delft, The Netherlands, 2014; 82p. [Google Scholar]
- Iverson, R.M.; Ouyang, C. Entrainment of bed material by earth-surface mass flows: Review and reformulation of depth-integrated theory. Rev. Geophys. 2015, 53, 27–58. [Google Scholar] [CrossRef]
- Cao, Z.; Xia, C.; Pender, G.; Liu, Q. Shallow water hydro-sediment-morphodynamic equations for fluvial processes. J. Hydraul. Eng. 2017, 143, 02517001. [Google Scholar] [CrossRef]
- Liu, X.; Infante Sedano, J.A.; Mohammadian, A. A coupled two-dimensional numerical model for rapidly varying flow, sediment transport and bed morphology. J. Hydraul. Res. 2015, 53, 609–621. [Google Scholar] [CrossRef]
- Greimann, B.P.; Lai, Y.G.; Huang, J.C. Two-dimensional total sediment load model equations. J. Hydraul. Eng. 2008, 134, 1142–1146. [Google Scholar] [CrossRef]
- Lai, Y.G. Modeling Stream Bank Erosion: Performance for Practical Streams and Future Needs. Water 2017, 9, 950. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.G. Two-Dimensional Depth-Averaged Flow Modeling with an Unstructured Hybrid Mesh. J. Hydraul. Eng. 2010, 136, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Rodi, W. Turbulence Models and Their Application in Hydraulics, 3rd ed.; IAHR Monograph: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Odgaard, A.J. Transverse bed slope in alluvial channel beds. J. Hydraul. Div. ASCE 1981, 107, 1677–1694. [Google Scholar]
- Struiksma, N.; Crosato, A. Analysis of a 2D bed topography model for rivers. In River Meandering; Ikeda, S., Parker, G., Eds.; AGU Water Resources Monograph 12: Washington, DC, USA, 1989. [Google Scholar]
- Talmon, A.M.; van Mierlo, M.C.L.M.; Struiksma, N. Laboratory measurements of the direction of sediment transport on transverse alluvial-bed slopes. J. Hydraul. Res. 1995, 33, 495–517. [Google Scholar] [CrossRef]
- Holly, F.M.; Rahuel, J.L. New Numerical/Physical Framework for Mobile-Bed Modeling, Part 1: Numerical and Physical Principles. J. Hydraul. Res. 1990, 28, 401–416. [Google Scholar] [CrossRef]
- Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Streams; Teknish Forlag, Technical Press: Copenhagen, Denmark, 1972. [Google Scholar]
- Parker, G. Surface-based bedload transport relation for gravel rivers. J. Hydraul. Res. 1990, 28, 417–428. [Google Scholar] [CrossRef]
- Andrews, E.D. Bed material transport in the Virgin River, Utah. Water Resour. Res. 2000, 36, 585–596. [Google Scholar] [CrossRef]
- Komar. Flow competence of the hydraulic parameters of floods. In Floods: Hydrological, Sedimentological and Geomorphological Implications; Beven, K., Carling, P., Eds.; John Wiley and Sons: Chichester, UK, 1989; pp. 107–134. [Google Scholar]
- Buffington, J.M.; Montgomery, D.R. A systematic Analysis of Eight Decades of Incipient Motion Studies, with special Reference to Gravel-Bedded Rivers. Water Resour. Res. 1997, 33, 1993–2029. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, P.R.; Crowe, J.C. Surface-Based Transport Model for Mixed-Size Sediment. J. Hydraul. Eng. 2003, 129, 120–128. [Google Scholar]
- Thuc, T. Two-Dimensional Morphological Computations Near Hydraulic Structures. Ph.D. Thesis, Asian Institute of Technology, Bangkok, Thailand, 1991. [Google Scholar]
- Rahuel, J.L.; Holly, F.M.; Chollet, J.P.; Belleudy, P.J.; Yang, G. Modeling of riverbed evolution for bedload sediment mixtures. J. Hydraul. Eng. 1989, 115, 1521–1542. [Google Scholar] [CrossRef]
- Gaeuman, D.; Sklar, L.; Lai, Y.G. Flume experiments to constrain bedload adaptation length. J. Hydrol. Eng. 2014, 20, 06014007. [Google Scholar] [CrossRef]
- Philips, B.C.; Sutherland, A.J. Spatial lag effect in bed load sediment transport. J. Hydraul. Res. 1989, 27, 115–133. [Google Scholar] [CrossRef]
- Han, Q.W. A study on the non-equilibrium transportation of suspended load. In Proceedings of the 1st International Symposium on River Sedimentation, IRTCES, Beijing, China, 24–29 March 1980. [Google Scholar]
- Han, Q.W.; He, M. A mathematical model for reservoir sedimentation and fluvial processes. Int. J. Sediment Res. 1990, 5, 43–84. [Google Scholar]
- Lai, Y.G.; Weber, L.J.; Patel, V.C. Non-Hydrostatic Three-Dimensional Method for Hydraulic Flow Simulation—Part I: Formulation and Verification. J. Hydraul. Eng. ASCE 2003, 129, 196–205. [Google Scholar] [CrossRef]
- Yanenko, N.N. The Method of Fractional Steps; Springer: New York, NY, USA, 1971. [Google Scholar]
- Soni, J.P. Laboratory study of aggradation in alluvial channels. J. Hydrol. 1981, 49, 87–106. [Google Scholar] [CrossRef]
- Ashida, K.; Michiue, M. An investigation of river bed degradation downstream of a dam. In Proceedings of the 14th IAHR Congress, Paris, France, 29 August–3 September 1971; Volume 3, pp. 247–256. [Google Scholar]
- Struiksma, N.; Olsen, K.W.; Flokstra, C.; De Vriend, H.J. Bed deformation in curved alluvial channels. J. Hydraul. Res. 1985, 23, 57–79. [Google Scholar] [CrossRef]
- Tetra Tech, Inc. Sediment Transport Analysis Total Load Report, June 2008, SO-1470.5 and EB-10 Lines, Tetra Tech Project No. T22541; Albuquerque Area Office, U.S. Bureau of Reclamation: Albuquerque, NM, USA, 2008.
- Lai, Y.G.; Collins, K.L. Sediment Plug Formation on the Rio Grande: A Review of Numerical Modeling; Technical Report No. SRH-2008-06; Technical Service Center, Bureau of Reclamation: Denver, CO, USA, 2008.
- Boroughs, C.B. Sediment Plug Computer Modeling Study, Tiffany Junction Reach, Middle Rio Grande Project; Albuquerque Aera Office, U.S. Bureau of Reclamation: Albuquerque, NM, USA, 2005; 122p.
- Collins, K.L. 2006 Middle Rio Grande Maintenance Modeling: San Antonio to Elephant Butte Dam. U.S. Bureau of Reclamation; Technical Service Center, Sedimentation and River Hydraulics Group: Denver, CO, USA, 2006.
- Bauer, T.R. 2006 Bed Material Sampling on the Middle Rio Grande, NM, U.S. Bureau of Reclamation; Technical Service Center, Sedimentation and River Hydraulics Group: Denver, CO, USA, 2006.





| Diameter Range (mm) | 0.2– 0.3 | 0.3– 0.4 | 0.4– 0.6 | 0.6– 0.8 | 0.8– 1.0 | 1.0– 1.5 | 1.5– 2.0 | 2.0– 3.0 | 3.0– 4.0 | 4.0– 6.0 | 6.0– 8.0 | 8.0– 10. |
| Content (%) | 7.45 | 12.4 | 15.9 | 4.4 | 3.6 | 6.79 | 4.0 | 9.18 | 10.2 | 18.1 | 6.0 | 2.0 |
| Flume Width (m) | Discharge (m3/s) | Water Depth (m) | Velocity (m/s) | Bed Slope | Froude Number | d50 (mm) | Manning’s Coefficient |
|---|---|---|---|---|---|---|---|
| 1.5 | 0.062 | 0.10 | 0.41 | 0.203% | 0.41 | 0.45 | 0.023 |
| Flume Width (m) | Discharge (m3/s) | Water Depth (m) | Velocity (m/s) | Bed Slope | Froude Number | d50 (mm) | Manning’s Coefficient |
|---|---|---|---|---|---|---|---|
| 2.3 | 0.121 | 0.12 | 0.44 | 0.128% | 0.41 | 0.60 | 0.02 |
| Flume Width (m) | Discharge (m3/s) | Water Depth (m) | Velocity (m/s) | Bed Slope | Froude Number | Manning’s Coefficient |
|---|---|---|---|---|---|---|
| 0.60 | 0.00685 | 0.044 | 0.26 | 0.3% | 0.39 | 0.0263 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Y.G. A Two-Dimensional Depth-Averaged Sediment Transport Mobile-Bed Model with Polygonal Meshes. Water 2020, 12, 1032. https://doi.org/10.3390/w12041032
Lai YG. A Two-Dimensional Depth-Averaged Sediment Transport Mobile-Bed Model with Polygonal Meshes. Water. 2020; 12(4):1032. https://doi.org/10.3390/w12041032
Chicago/Turabian StyleLai, Yong G. 2020. "A Two-Dimensional Depth-Averaged Sediment Transport Mobile-Bed Model with Polygonal Meshes" Water 12, no. 4: 1032. https://doi.org/10.3390/w12041032
APA StyleLai, Y. G. (2020). A Two-Dimensional Depth-Averaged Sediment Transport Mobile-Bed Model with Polygonal Meshes. Water, 12(4), 1032. https://doi.org/10.3390/w12041032





