Fluid-Structure Interaction Response of a Water Conveyance System with a Surge Chamber during Water Hammer
Abstract
:1. Introduction
2. Mathematical Model
2.1. Governing Equations
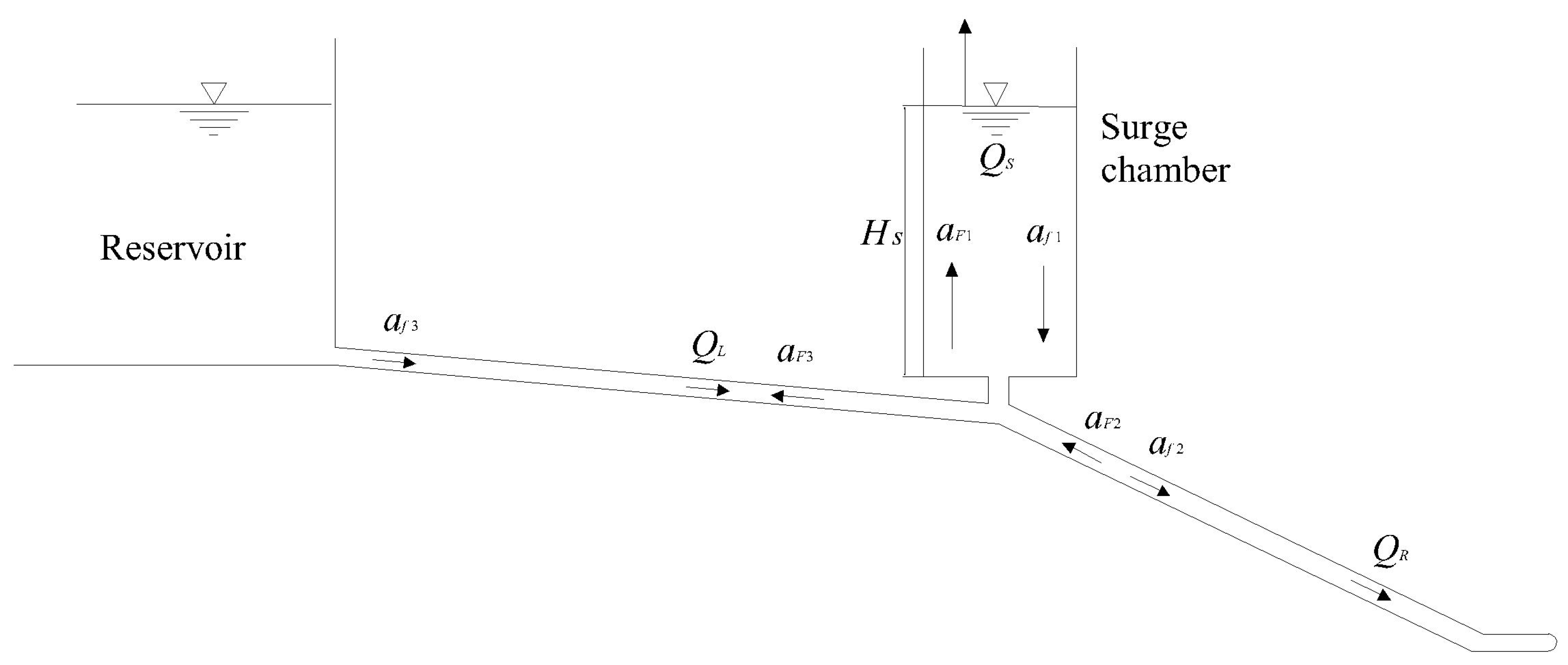
2.2. Surge Chamber
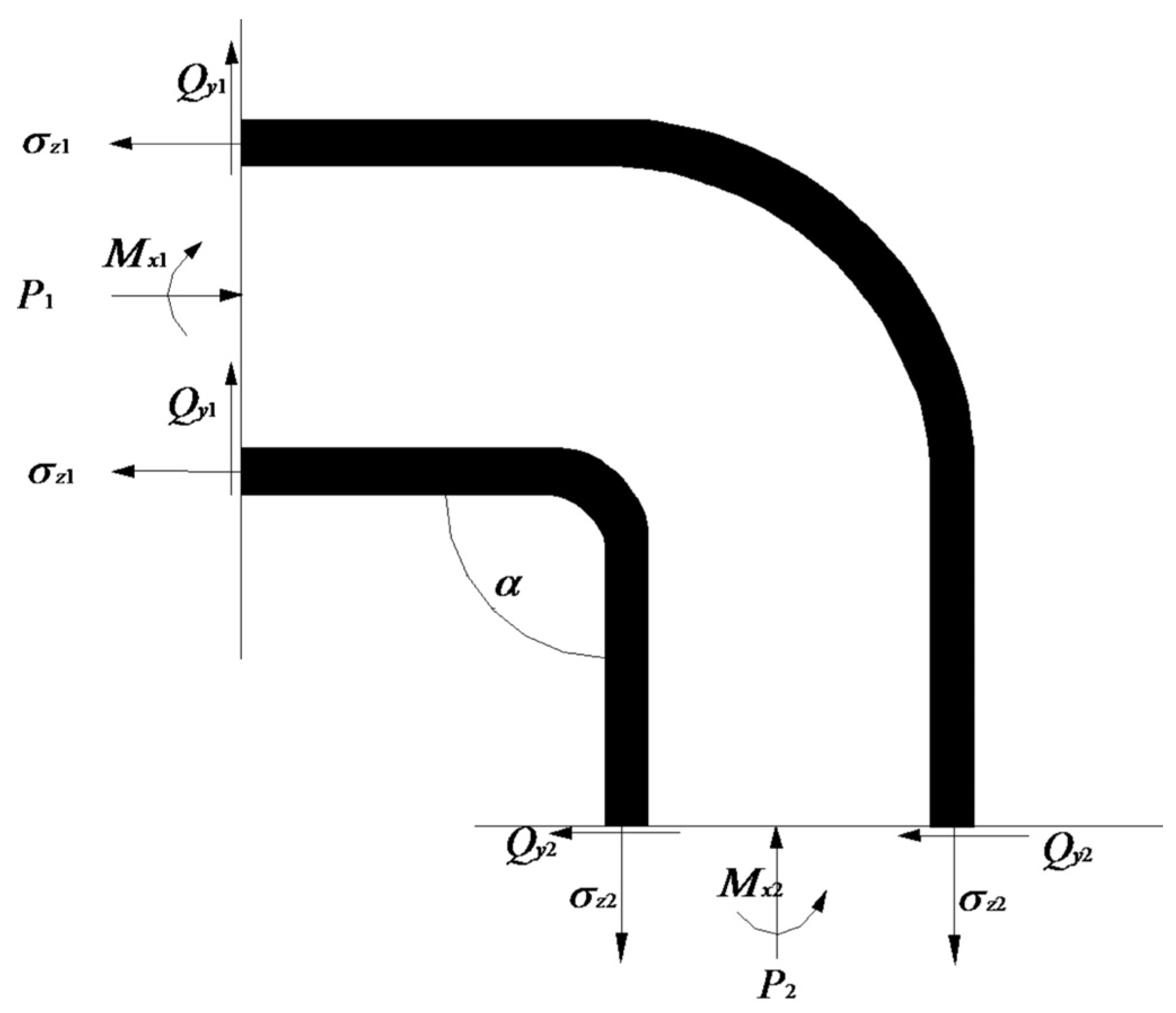
2.3. Elbow Tube
2.4. Outlet and Inlet Boundary
3. Solution Technique
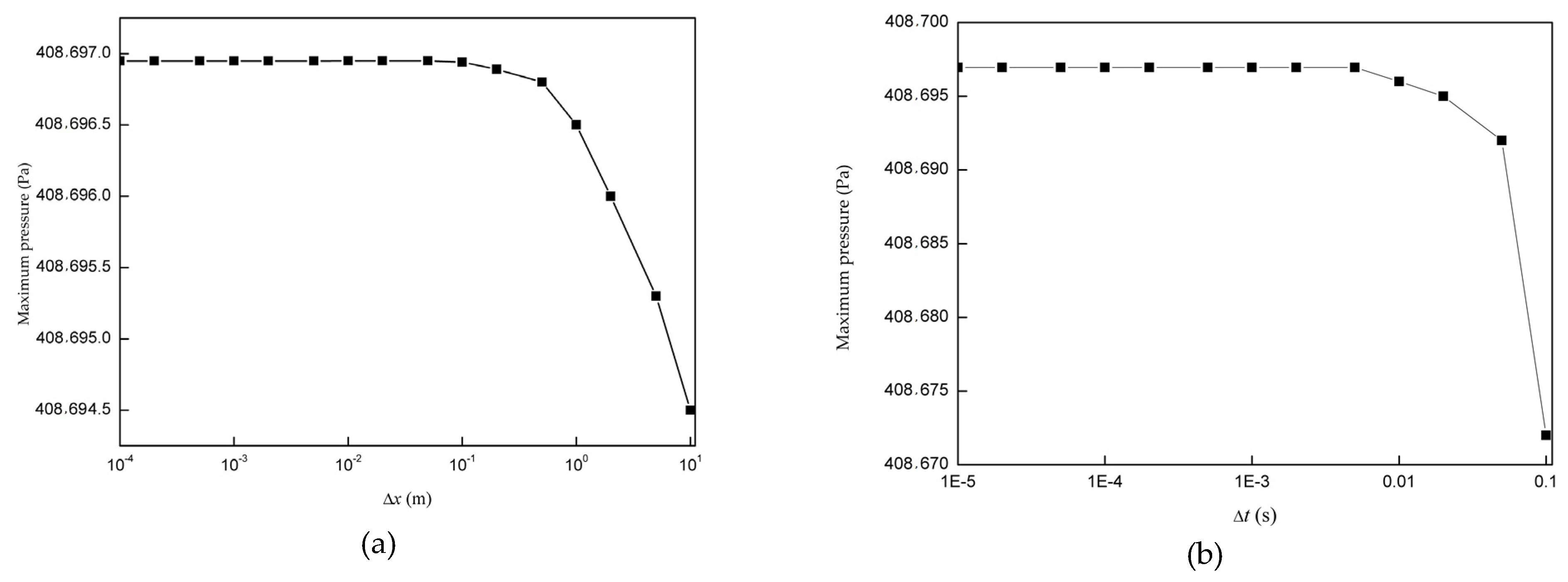
3.1. Finite Volume Method
3.2. Boundary Condition
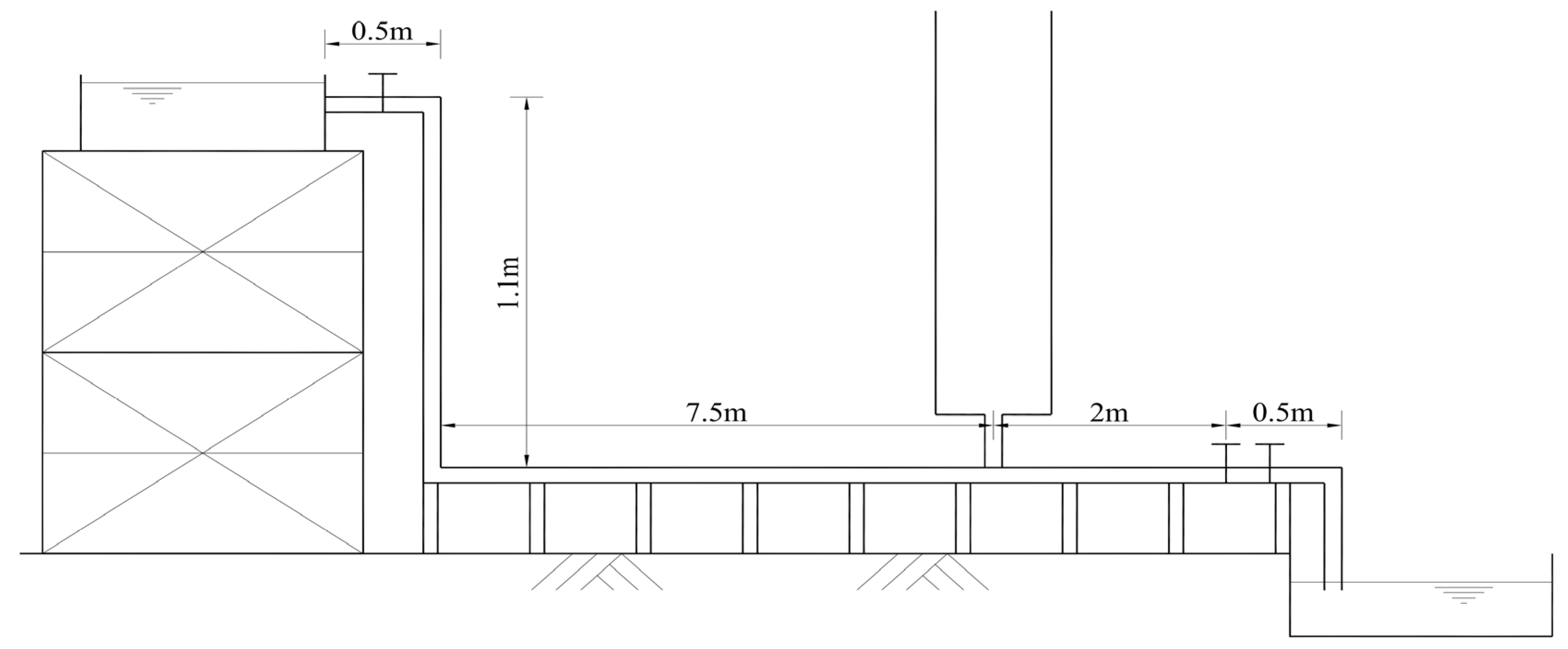
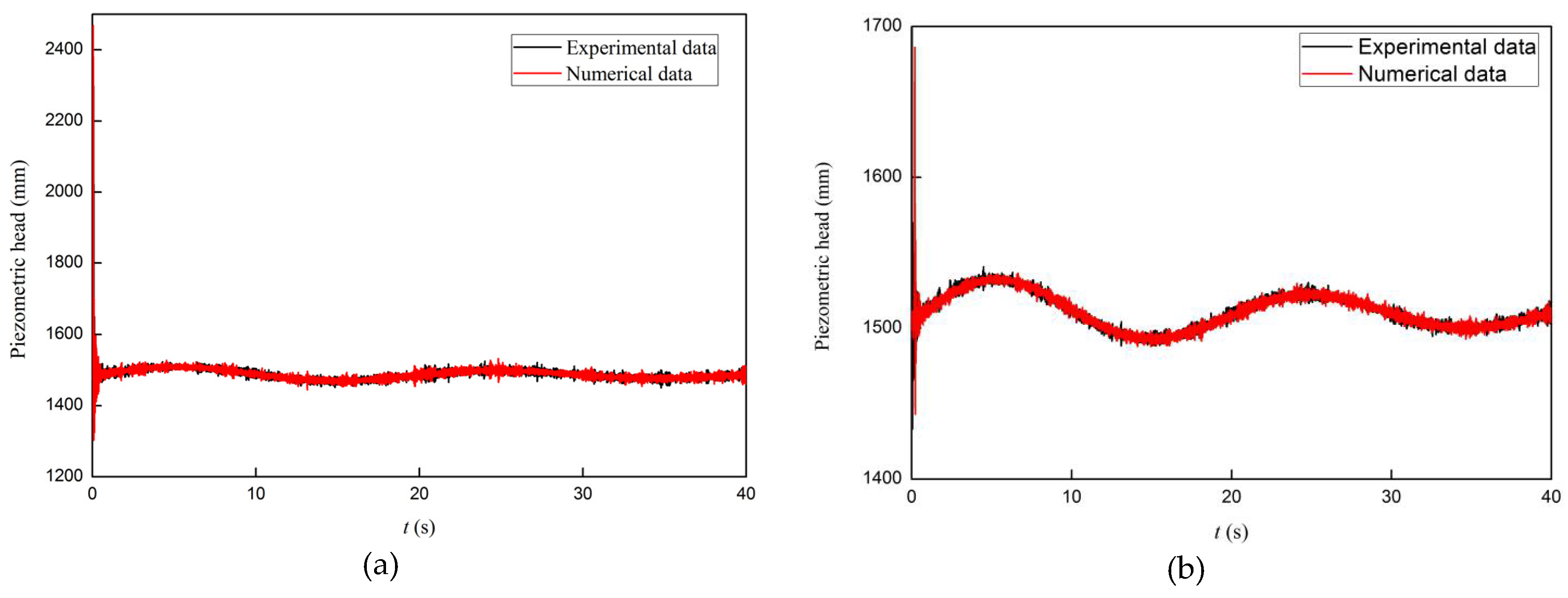
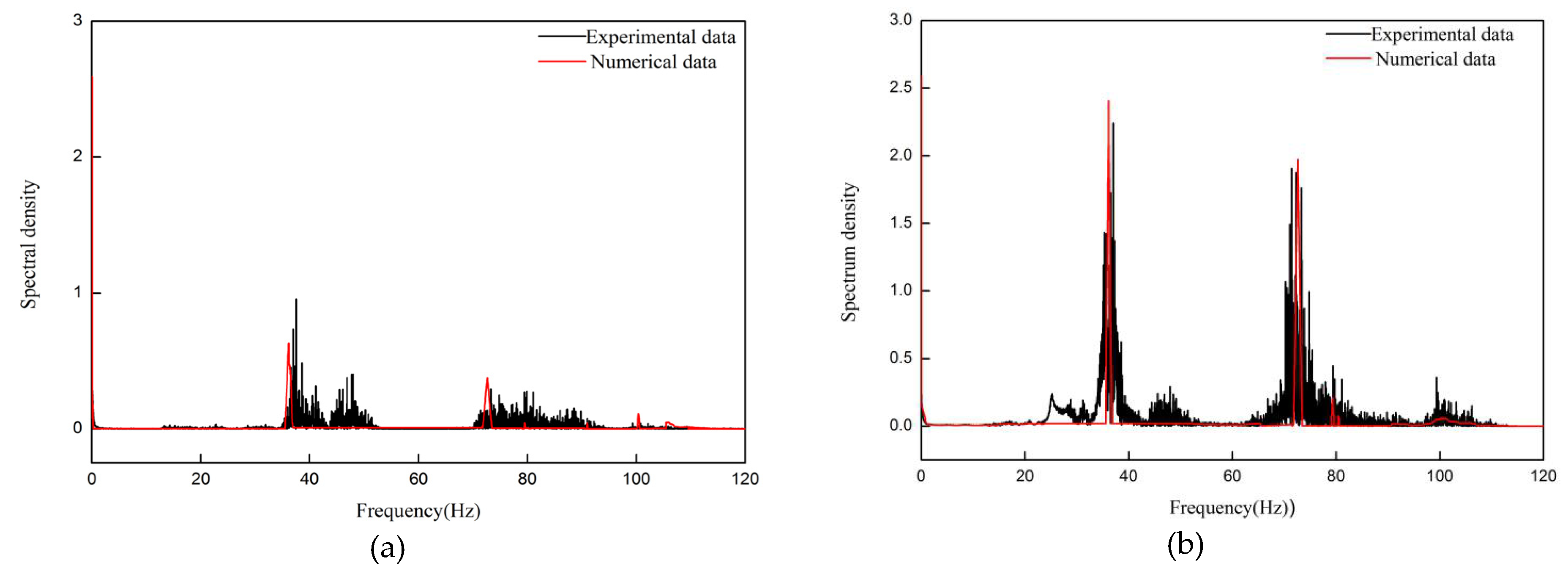
4. Experimental Verification
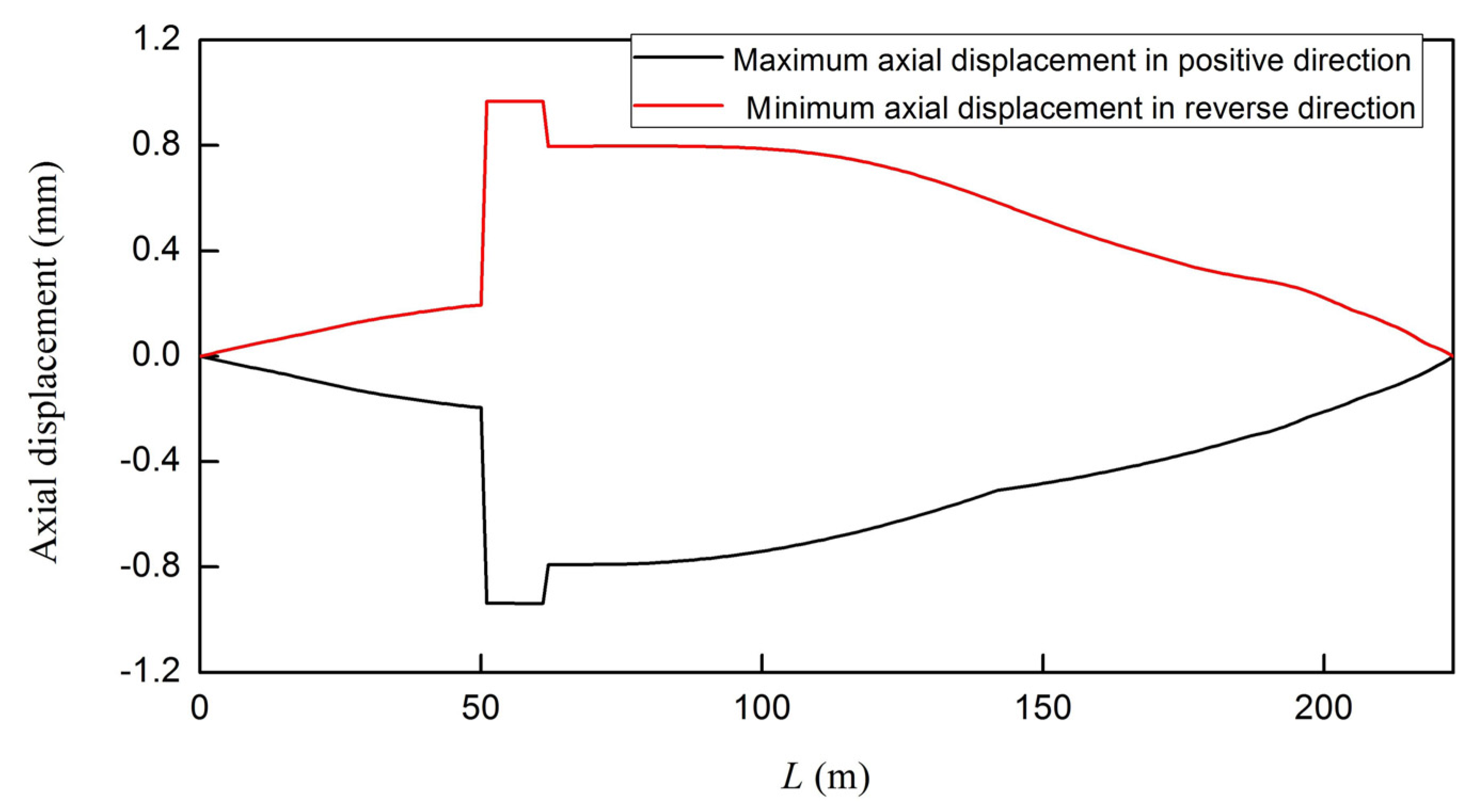
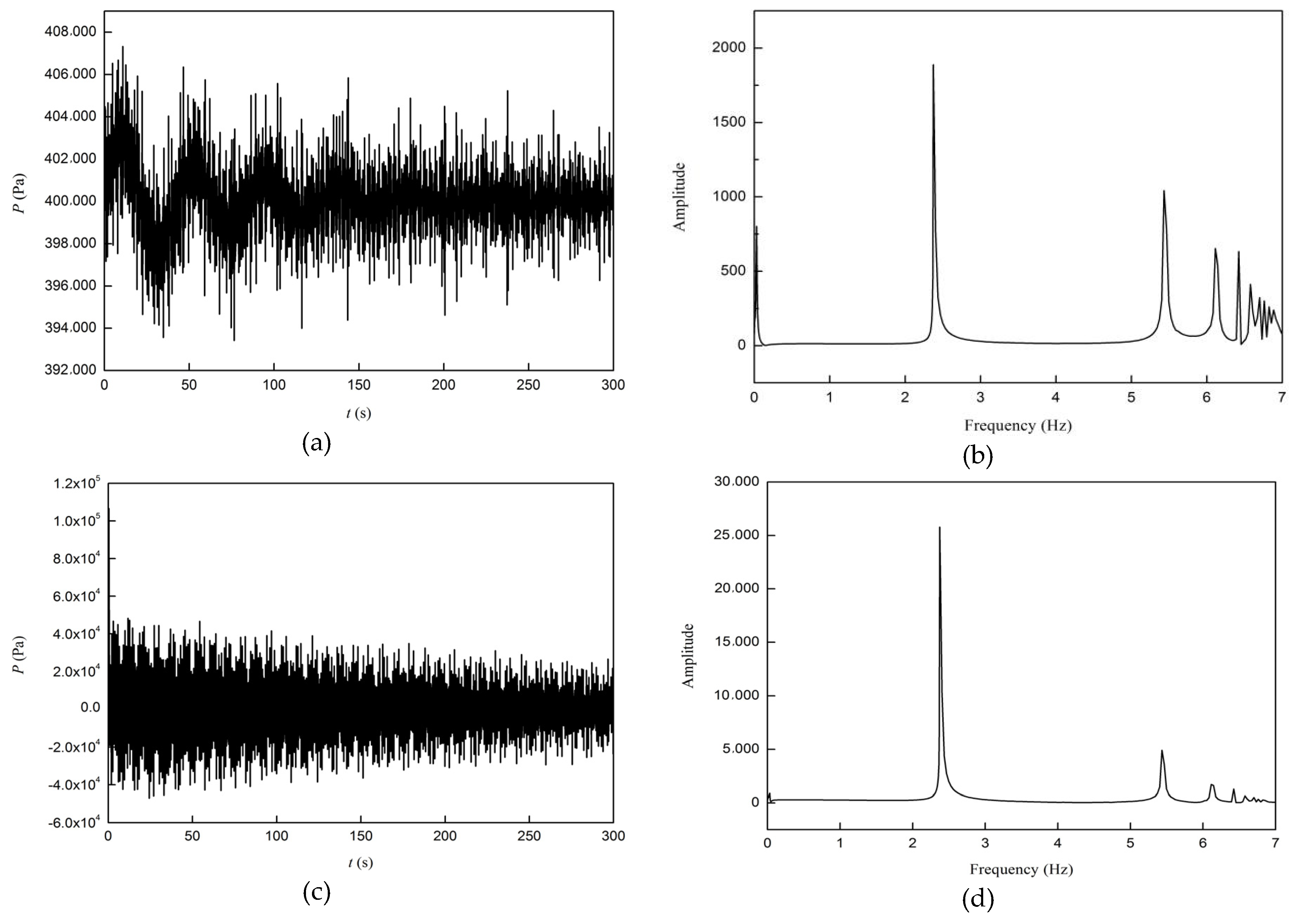
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Leishear, R.A. Fluid Mechanics, Water Hammer, Dynamic Stresses, and Piping Design; ASME: New York, NY, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- Olalla, G.; SasIrene, D.; Begoña, G. Liquid-liquid extraction of phenolic compounds from water using ionic liquids: Literature review and new experimental data using C2mim FSI. J. Environ. Manag. 2018, 78, 475–482. [Google Scholar] [CrossRef]
- Osama, M.; Theofilis, V.; Ahmed, E. Fluid Structure Interaction (FSI) Simulation Of the human eye under the air puff tonometry using CFD. In Proceedings of the Tenth International Conference on Computational Fluid Dynamics (ICCFD10), Barcelona, Spain, 9–13 July 2018. [Google Scholar]
- Bazilevs, Y.; Yan, J.; Deng, X. Simulating Free-Surface FSI and Fatigue Damage in Wind-Turbine Structural Systems. In Frontiers in Computational Fluid-Structure Interaction and Flow Simulation: Research from Lead Investigators under Forty; Springer: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Tijsseling, A.S.; Vardy, A.E. Time scales and FSI in unsteady liquid-filled pipe flow. In The 9th International on Pressure Surges; Chester, UK, 2004. [Google Scholar] [CrossRef]
- Wiggert, D.C.; Hatfield, F.J.; Stuckenbruck, S. Analysis of Liquid and Structural Transients in Piping by the Method of Characteristics. J. Fluids Eng. 1987, 109, 161–165. [Google Scholar] [CrossRef]
- Lavooij, C.S.W.; Tijsseling, A.S. Fluid–structure interaction in liquid-filled piping systems. J. Fluids Struct. 1991, 5, 573–595. [Google Scholar] [CrossRef]
- Ahmadi, A.; Keramat, A. Investigation of fluid–structure interaction with various types of junction coupling. J. Fluids Struct. 2010, 26, 1123–1141. [Google Scholar] [CrossRef]
- Liu, Y.; He, X.; Zhi, Y. Dynamical strength and design optimization of pipe-joint system under pressure impact load. Proceedings of the Institution of Mechanical Engineers, Part G. J. Aerosp. Eng. 2011, 226, 1029–1040. [Google Scholar] [CrossRef]
- Huang, S.; Zhou, B.; Bu, S.; Li, C.; Zhang, C.; Wang, H.; Wang, T. Robust fixed-time sliding mode control for fractional-order nonlinear hydro-turbine governing system. Renew. Energy 2019, 139, 447–458. [Google Scholar] [CrossRef]
- Zhai, H.; Wu, Z.; Liu, Y.; Yue, Z. In-plane dynamic response analysis of curved pipe conveying fluid subjected to random excitation. Nucl. Eng. Des. 2013, 256, 214–226. [Google Scholar] [CrossRef]
- Tijsseling, A.S.; Vardy, A.E.; Fan, D. Fluid-Structure Interaction and Cavitation in a Single-elbow Pipe System. J. Fluid Struct. 1996, 10, 395–420. [Google Scholar] [CrossRef]
- Mu, L.Z.; Li, X.Y.; Chi, Q.Z.; Yang, S.Q.; Zhang, P.D.; Ji, C.J.; He, Y.; Gao, G. Experimental and numerical study of the effect of pulsatile flow on wall displacement oscillation in a flexible lateral aneurysm model. Acta Mech. Sin. 2019, 39, 1120–1129. [Google Scholar] [CrossRef]
- Forbes, T.B.; Stephen, C.T. Dynamic Behavior of Complex Fluid-Filled Tubing Systems-Part ii: System Analysis. J. Dyn. Syst. Meas. 2001, 123, 78–84. [Google Scholar] [CrossRef]
- Altstadt, E.; Carl, H.; Prasser, H.M.; Weis, R. Fluid-structure interaction during artificially induced water hammers in a tube with a bend—Experiments and analyses. Multiph. Sci. Technol. 2008, 20, 213–238. [Google Scholar] [CrossRef]
- Wang, Y.G. Efficient prediction of wave energy converters power output considering bottom effects. Ocean Eng. 2019, 181, 89–97. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Miao, M.F.; Ma, J.M. Analytical study on water hammer pressure in pressurized conduits with a throttled surge chamber for slow closure. Water Sci. Technol. 2010, 3, 174–189. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, J.; Yu, X.D. Characterization of surge superposition following 2-stage load rejection in hydroelectric power plant. Can. J. Civ. Eng. 2016, 43, 844–850. [Google Scholar] [CrossRef]
- Guo, W.C.; Yang, J.D. Combined effect of upstream surge chamber and sloping ceiling tailrace tunnel on dynamic performance of turbine regulating system of hydroelectric power plant. Chaos Solitons Fractals 2017, 99, 243–255. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Niao, M.F. Explicit formulas for calculating surges in throttled surge chamber. J. Hydraul. Eng. 2012, 4, 467–472. (In Chinese) [Google Scholar]
- Wiggert, D.C.; Otwell, R.S.; Hatfield, F.J. The effect of elbow restraint on pressure transients. J. Fluid Eng. 1985, 107, 402–406. [Google Scholar] [CrossRef]
- Okosun, F.; Cahill1, P.; Hazra, B.; Pakrash, V. Vibration-based leak detection and monitoring of water pipes using output-only piezoelectric sensors. Eur. Phys. J. Spec. Top. 2019, 228, 1659–1675. [Google Scholar] [CrossRef]
- Tijsseling, A.S.; Wiggert, D.C. Fluid transients and fluid-structure interaction in flexible liquid-filled pipeing. Appl. Mech. Rev. 2001, 54, 455–481. [Google Scholar] [CrossRef]
- Wang, Y.H.; Zhang, J.H.; Ma, Z.X. Experimental determination of single-phase pressure drop and heat transfer in a horizontal internal helically-finned tube. Int. J. Heat Mass Transf. 2017, 104, 240–246. [Google Scholar] [CrossRef]
- Taitel, Y.; Dukler, A.E. A model for predicting flow regime transition in horizontal and near horizontal gas-liquid flow. AIChE J. 1976, 22, 47–55. [Google Scholar] [CrossRef]
- Meindlhumer, M.; Pechstein, A. 3D mixed finite elements for curved, flat piezoelectric structures. Int. J. Smart Nano Mater. 2019, 10, 249–267. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Sun, B. Study on fluid–structure interaction in liquid oxygen feeding pipe systems using finite volume method. Acta Mech Sin. 2011, 27, 706–712. [Google Scholar] [CrossRef]
- Ferras, D.; Manso, P.A.; Covas, D.I.C. Fluid–structure interaction in pipe coils during hydraulic transients. J. Hydraul. Res. 2017, 55, 491–505. [Google Scholar] [CrossRef]
- David, F.; Pedro, A.M.; Anton, J.S. Fluid-structure interaction in straight pipelines with different anchoring conditions. J. Sound Vib. 2017, 394, 348–365. [Google Scholar] [CrossRef]
- Banks, J.W.; Henshaw, W.D.; Schwen, D.W. A stable partitioned FSI algorithm for rigid bodies and incompressible flow in three dimensions. J. Comput. Phys. 2018, 73, 455–492. [Google Scholar] [CrossRef] [Green Version]
- Li, S.J.; Karney, B.W.; Liu, G.M. FSI research in pipeline systems-A review of the literature. J. Fluids Struct. 2015, 57, 277–297. [Google Scholar] [CrossRef]
- Ramírez, L.; Nogueira, X.; Ouro, P. A Higher-Order Chimera Method for Finite Volume Schemes. Arch. Comput. Methods Eng. 2018, 25, 691–706. [Google Scholar] [CrossRef] [Green Version]
- Hwang, Y.H.; Chung, N.M. A fast Godunov method for the water-hammer problem. Int. J. Numer. Methods Fluids 2002, 40, 799–819. [Google Scholar] [CrossRef]
- Sreejith, B.; Jayaraj, K.; Ganesan, N. Finite element analysis of fluid-structure interaction in pipeline systems. Nucl. Eng. Des. 2004, 227, 313–322. [Google Scholar] [CrossRef]
- Zhang, L.; Tijsseling, A.S.; Vardy, E.A. FSI analysis of liquid-filled pipes. J. Sound Vib. 1999, 224, 69–99. [Google Scholar] [CrossRef] [Green Version]



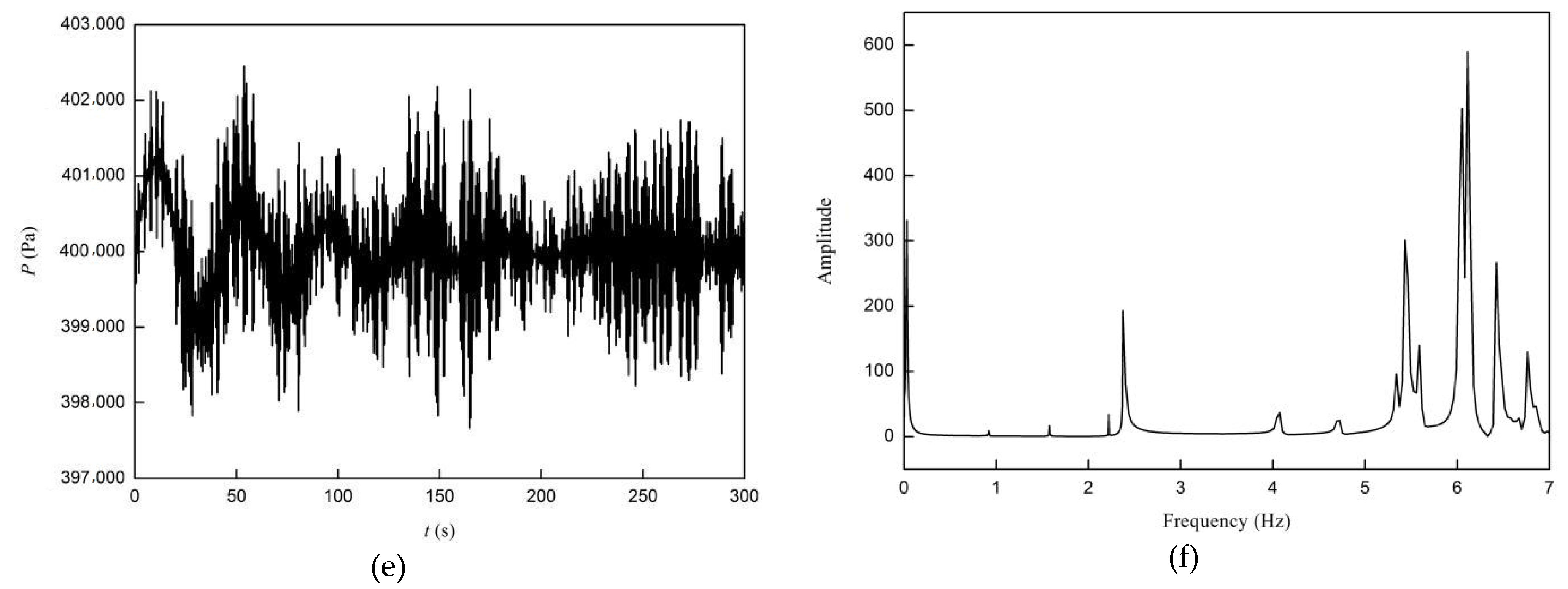
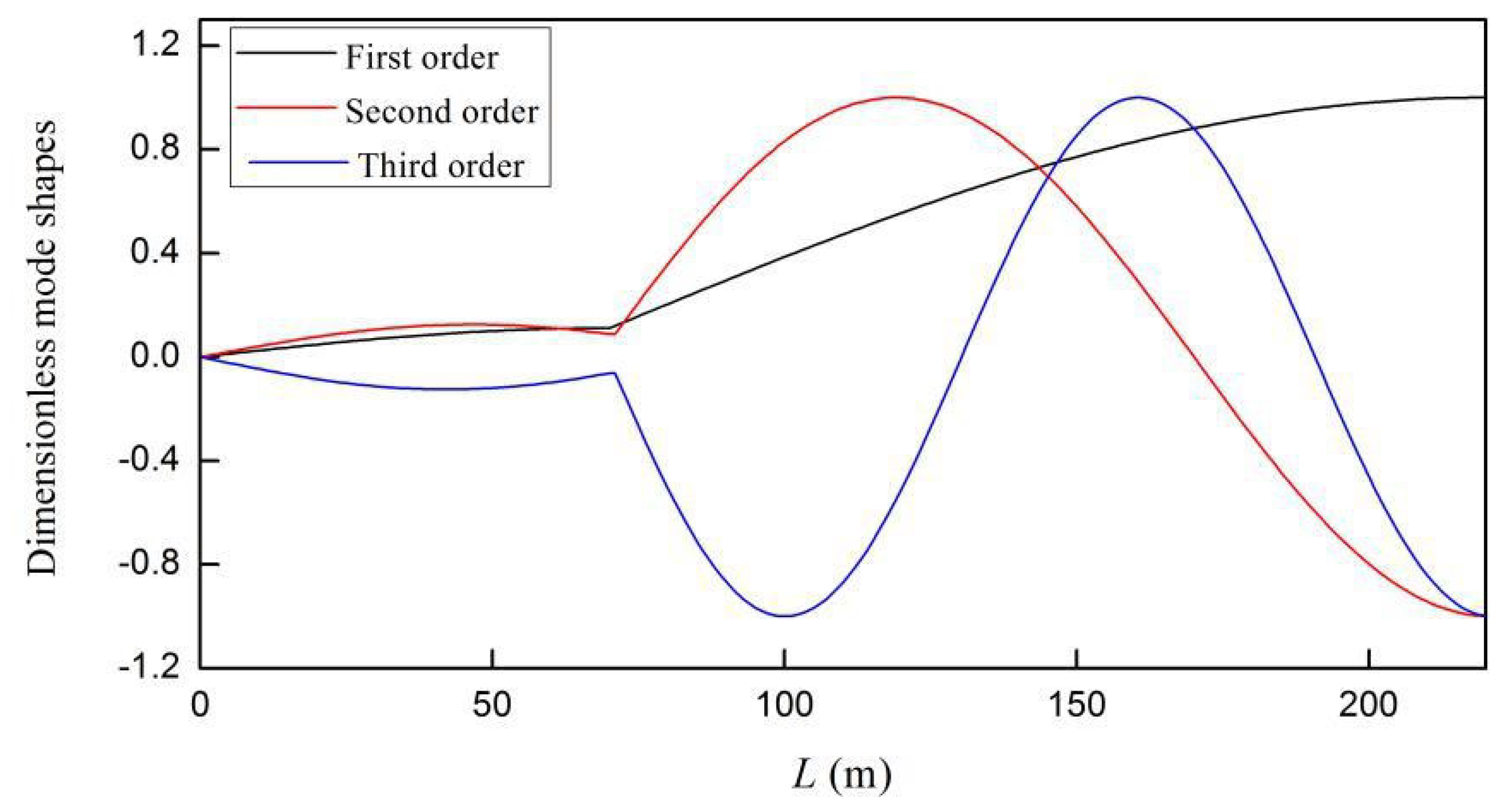
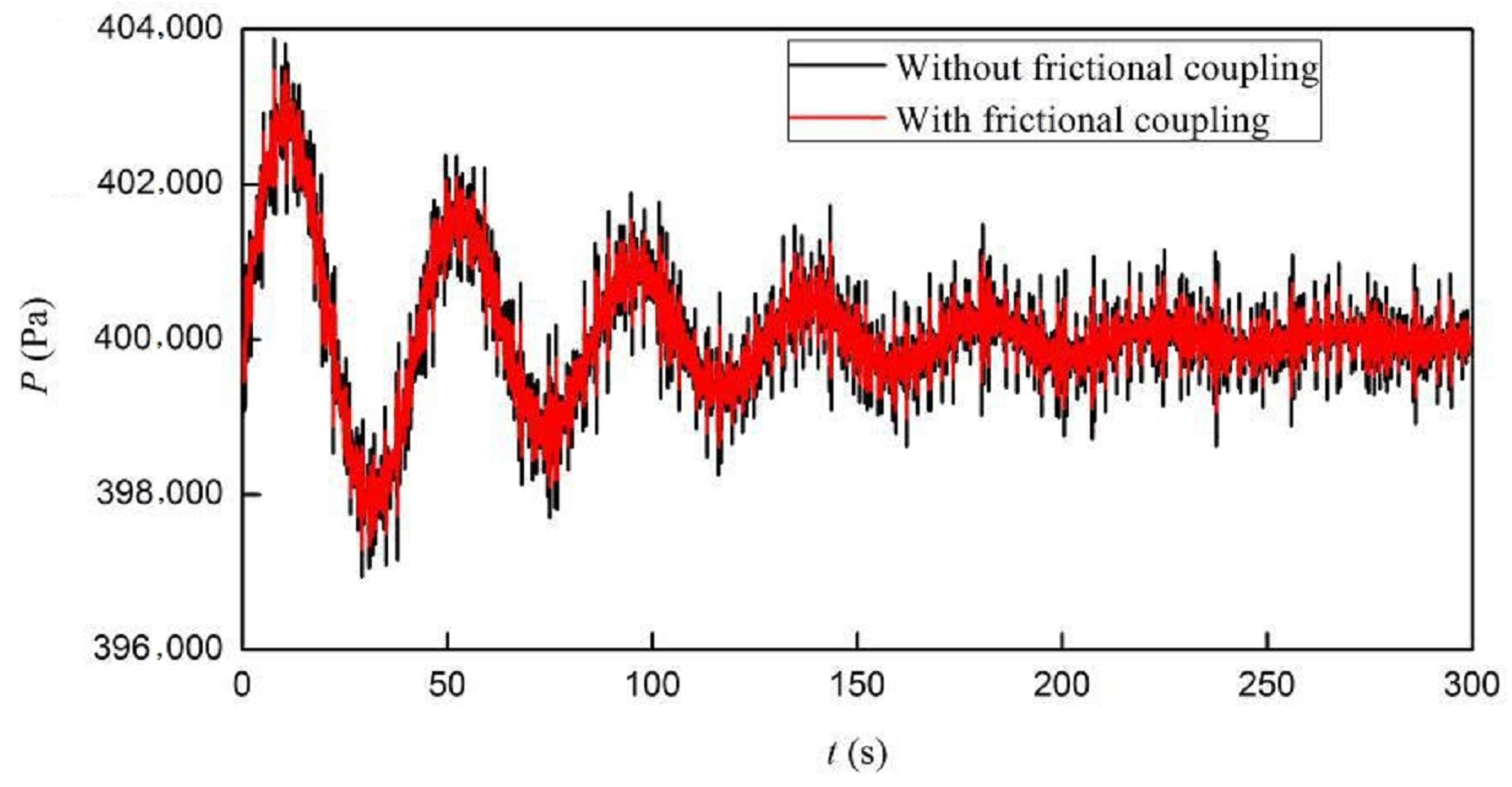
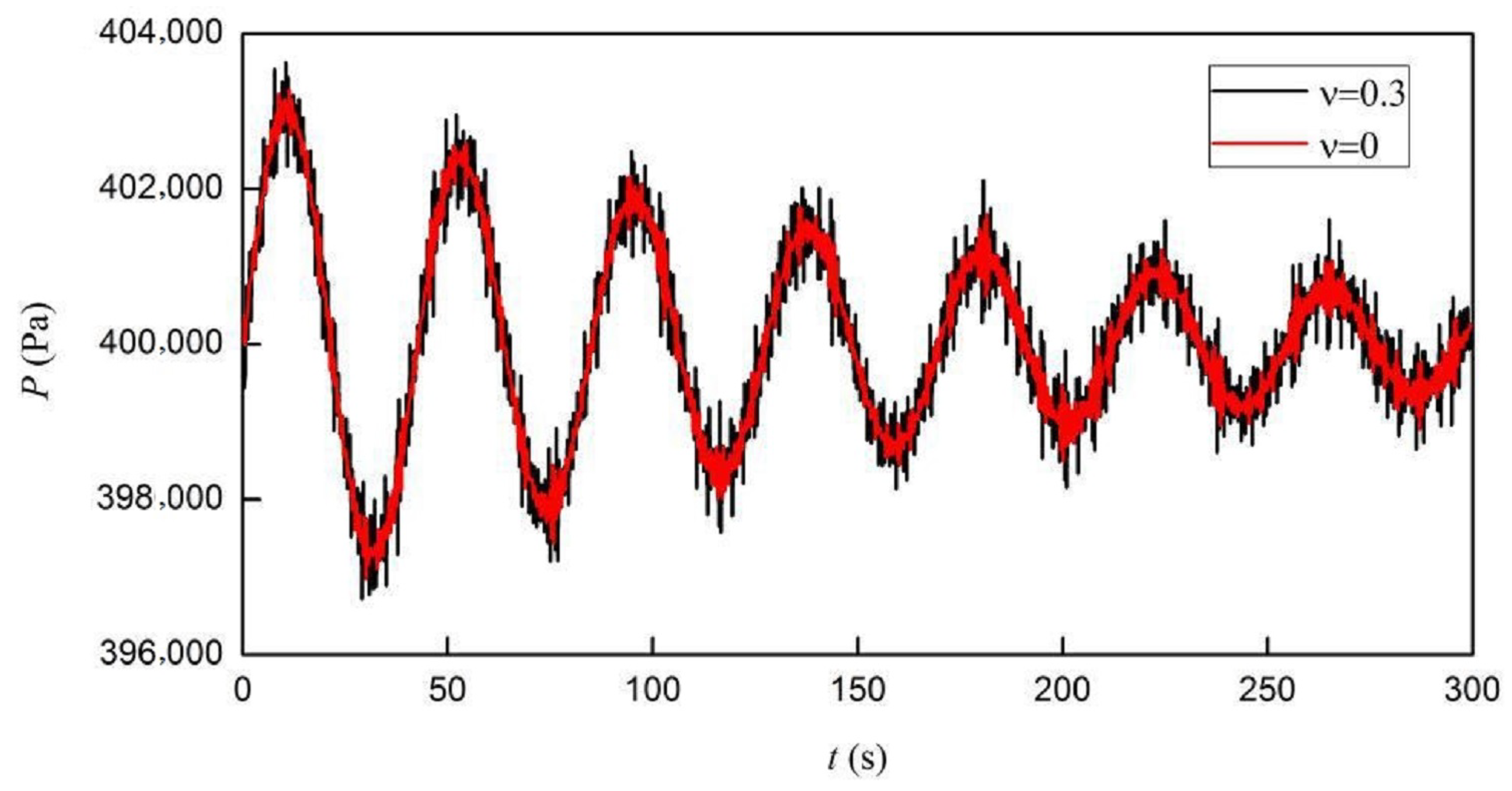
| ν | E | L | e | D | ρt |
|---|---|---|---|---|---|
| 0.3 | 3.88 Gpa | 11.1 m | 0.005 m | 0.05 m | 1378.57 kg/m3 |
| Mode | ν = 0.3 | ν = 0 |
|---|---|---|
| 1 | 2.1 Hz | 2.1 Hz |
| 2 | 5.8 Hz | 5.6 Hz |
| 3 | 9.3 Hz | 9.0 Hz |
| 4 | 13.1 Hz | 12.7 Hz |
| 5 | 17.0 Hz | 16.1 Hz |
| 6 | 20.5 Hz | 19.7 Hz |
| 7 | 21.2 Hz | 23.1 Hz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Zhou, J.; Li, Y.; Guan, X.; Liu, D.; Zhang, J. Fluid-Structure Interaction Response of a Water Conveyance System with a Surge Chamber during Water Hammer. Water 2020, 12, 1025. https://doi.org/10.3390/w12041025
Guo Q, Zhou J, Li Y, Guan X, Liu D, Zhang J. Fluid-Structure Interaction Response of a Water Conveyance System with a Surge Chamber during Water Hammer. Water. 2020; 12(4):1025. https://doi.org/10.3390/w12041025
Chicago/Turabian StyleGuo, Qiang, Jianxu Zhou, Yongfa Li, Xiaolin Guan, Daohua Liu, and Jian Zhang. 2020. "Fluid-Structure Interaction Response of a Water Conveyance System with a Surge Chamber during Water Hammer" Water 12, no. 4: 1025. https://doi.org/10.3390/w12041025
APA StyleGuo, Q., Zhou, J., Li, Y., Guan, X., Liu, D., & Zhang, J. (2020). Fluid-Structure Interaction Response of a Water Conveyance System with a Surge Chamber during Water Hammer. Water, 12(4), 1025. https://doi.org/10.3390/w12041025






