Model Analysis and System Parameters Investigation for Transient Wave in a Pump–Pipe–Valve System
Abstract
:1. Introduction
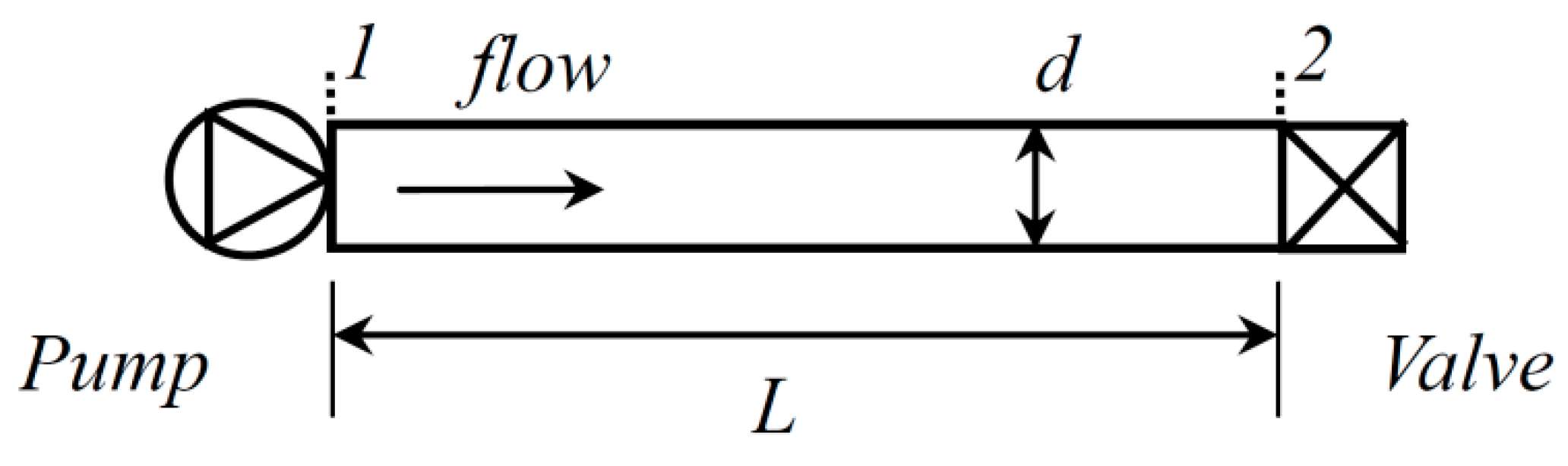
2. Pump–Pipe–Valve System
3. System Frequency Response
3.1. STMA Model
- (1)
- If ,
- (2)
- If ,
- (3)
- If ,
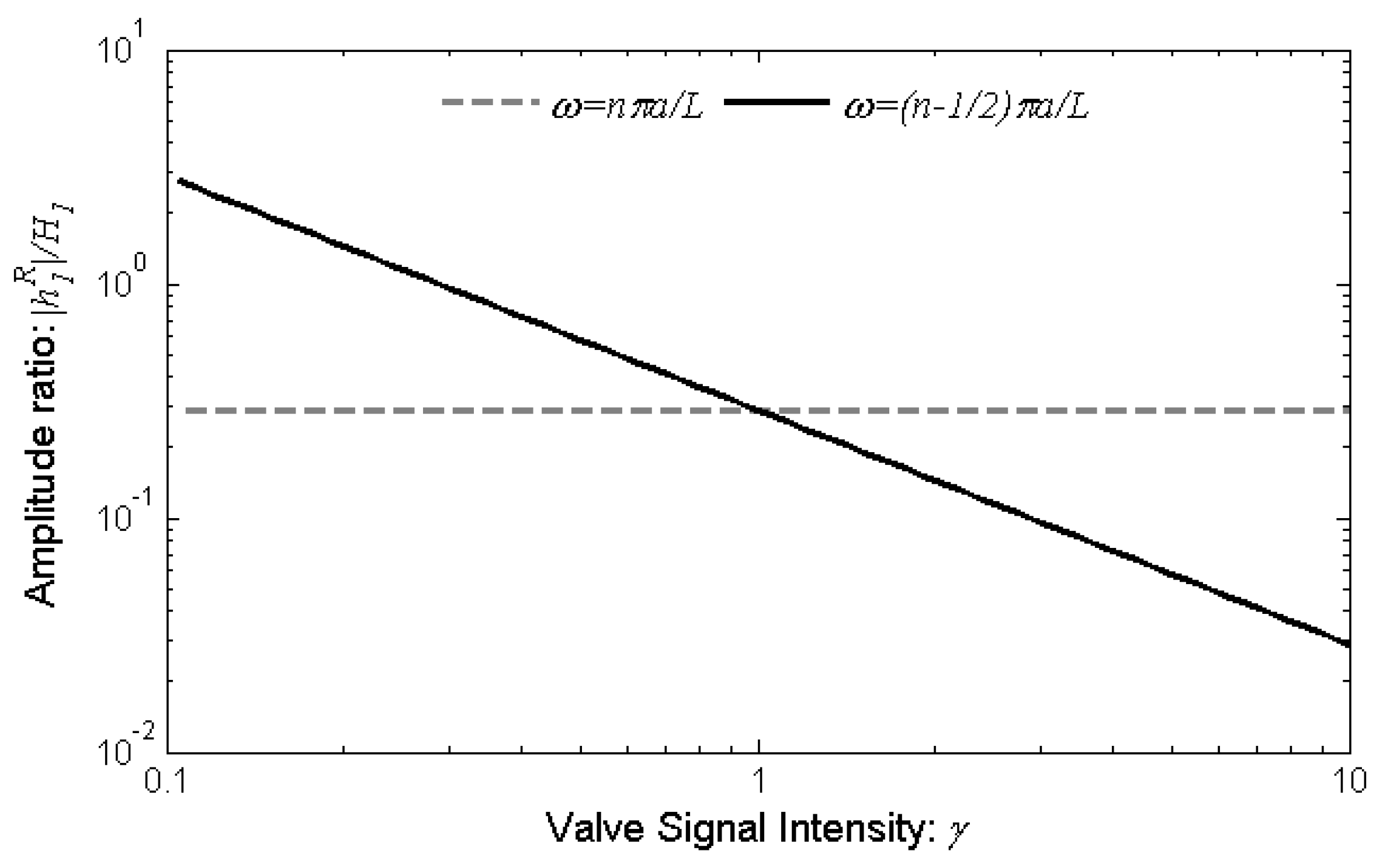
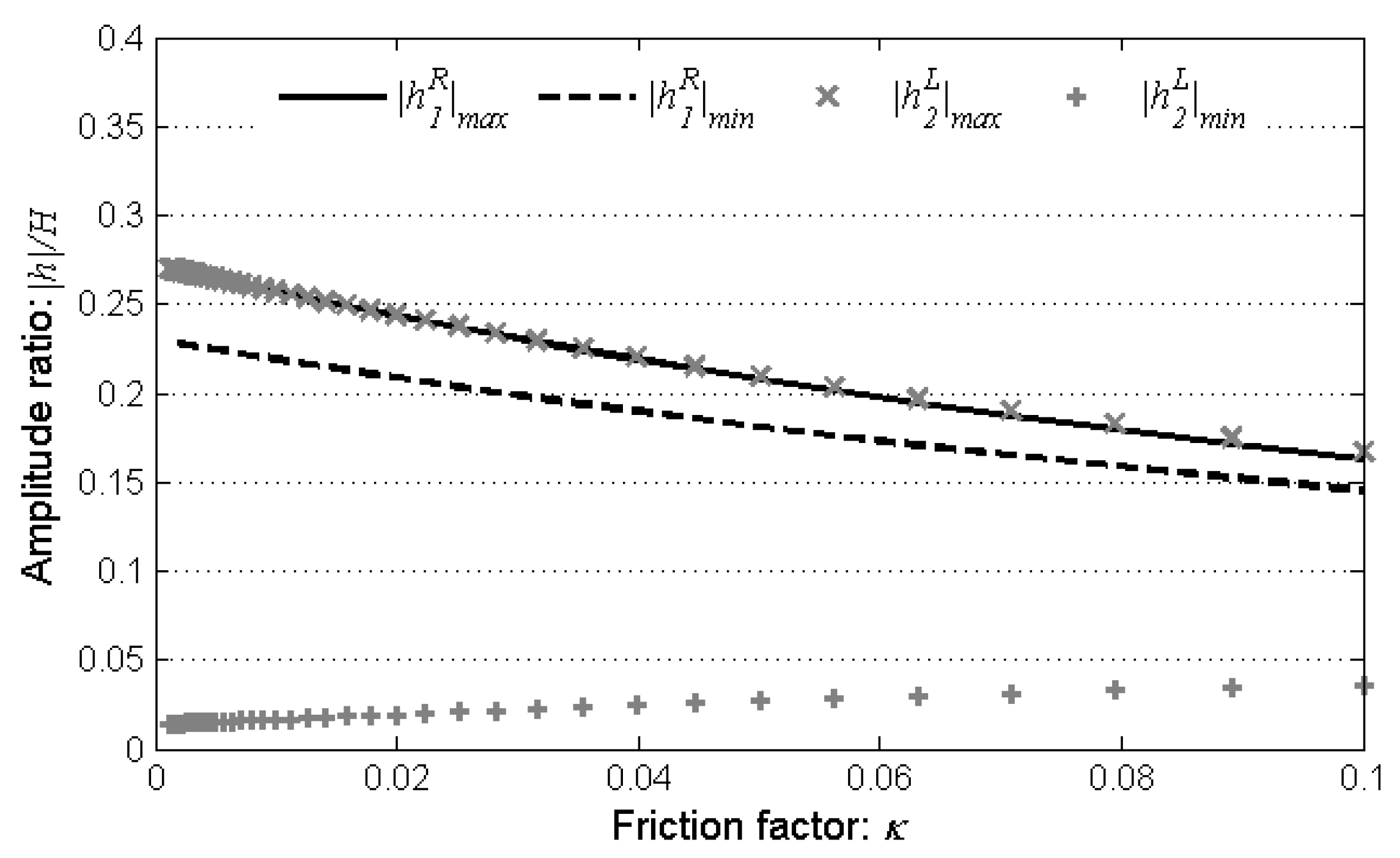
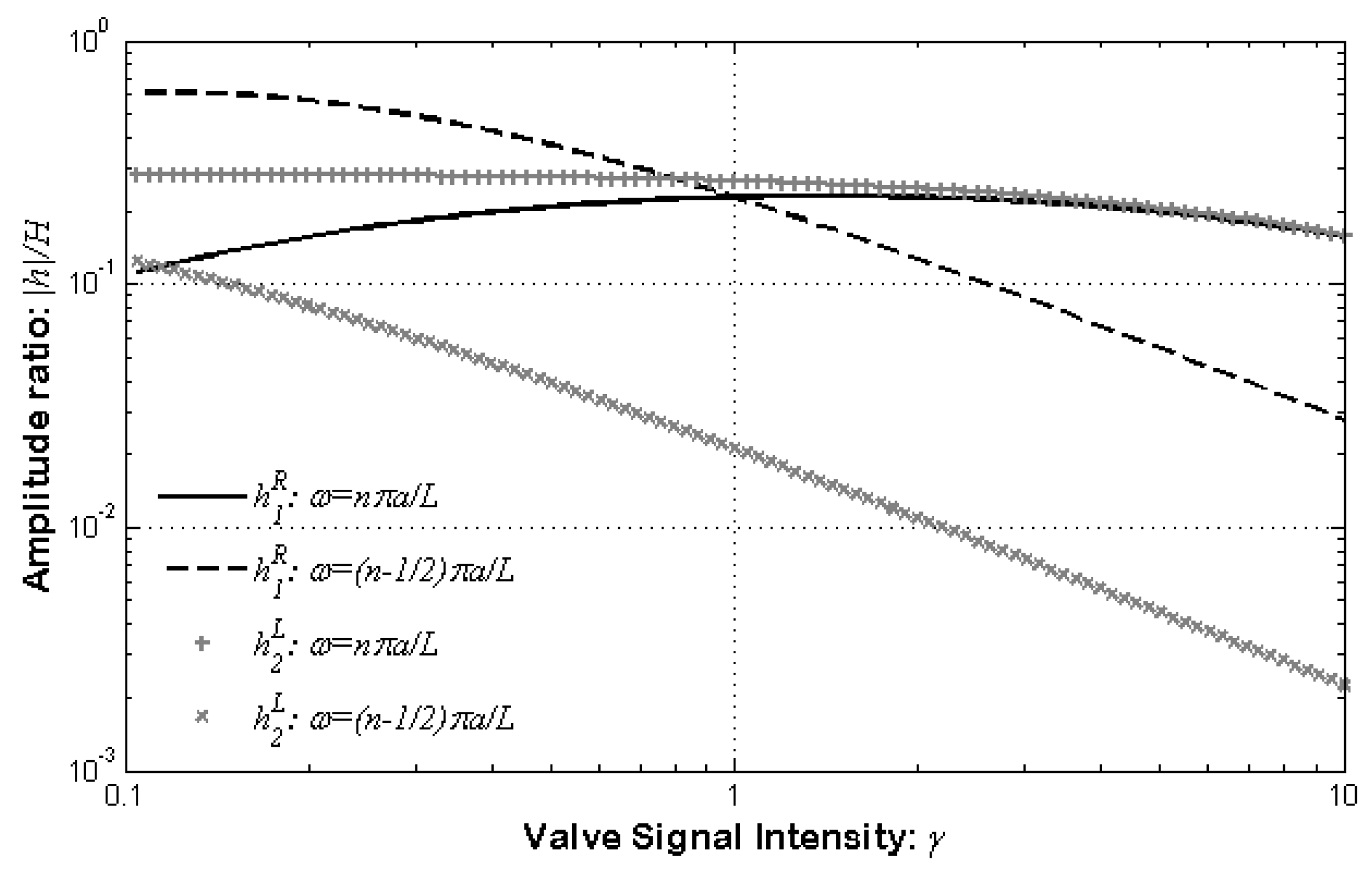
3.2. Frictionless Model
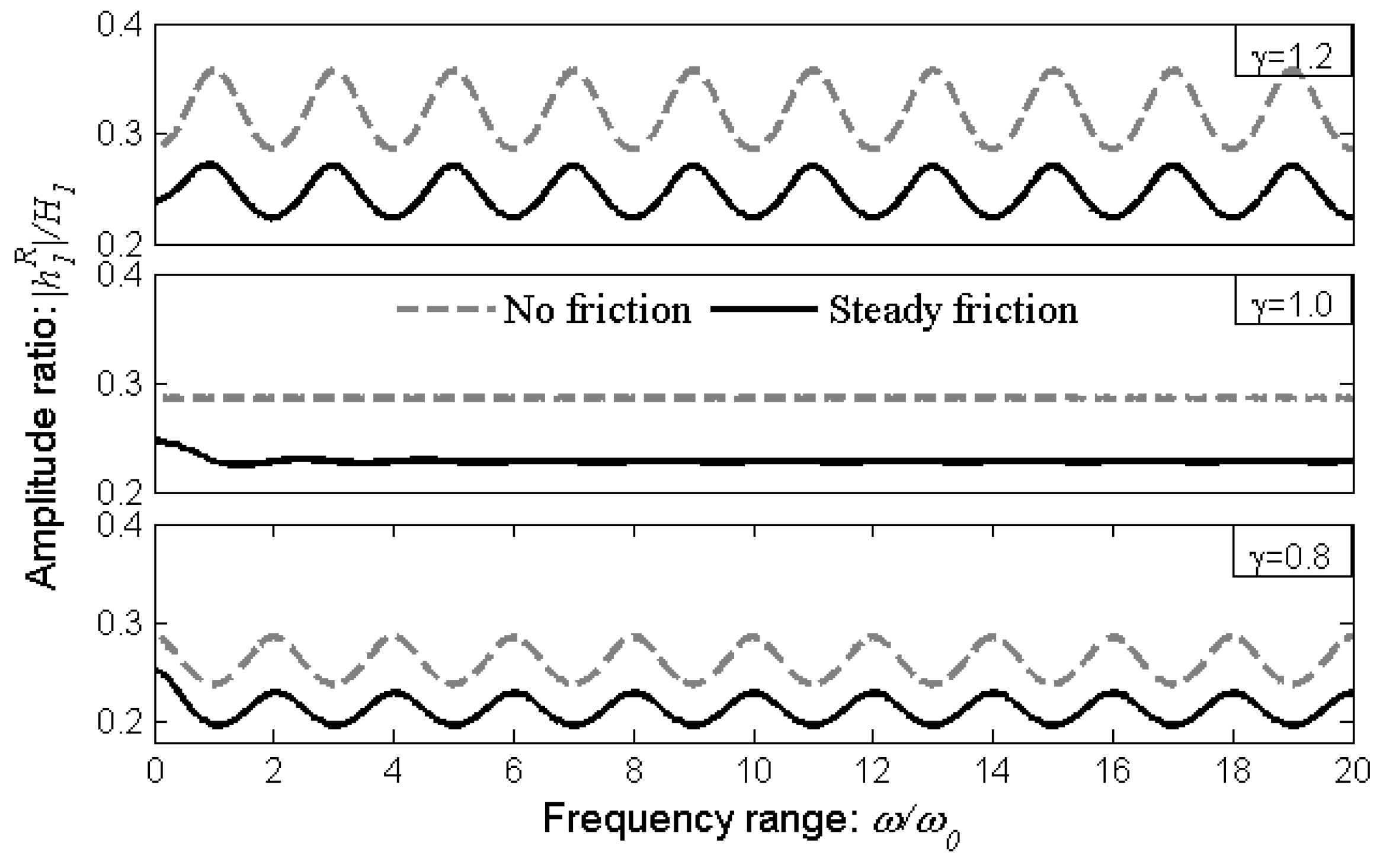
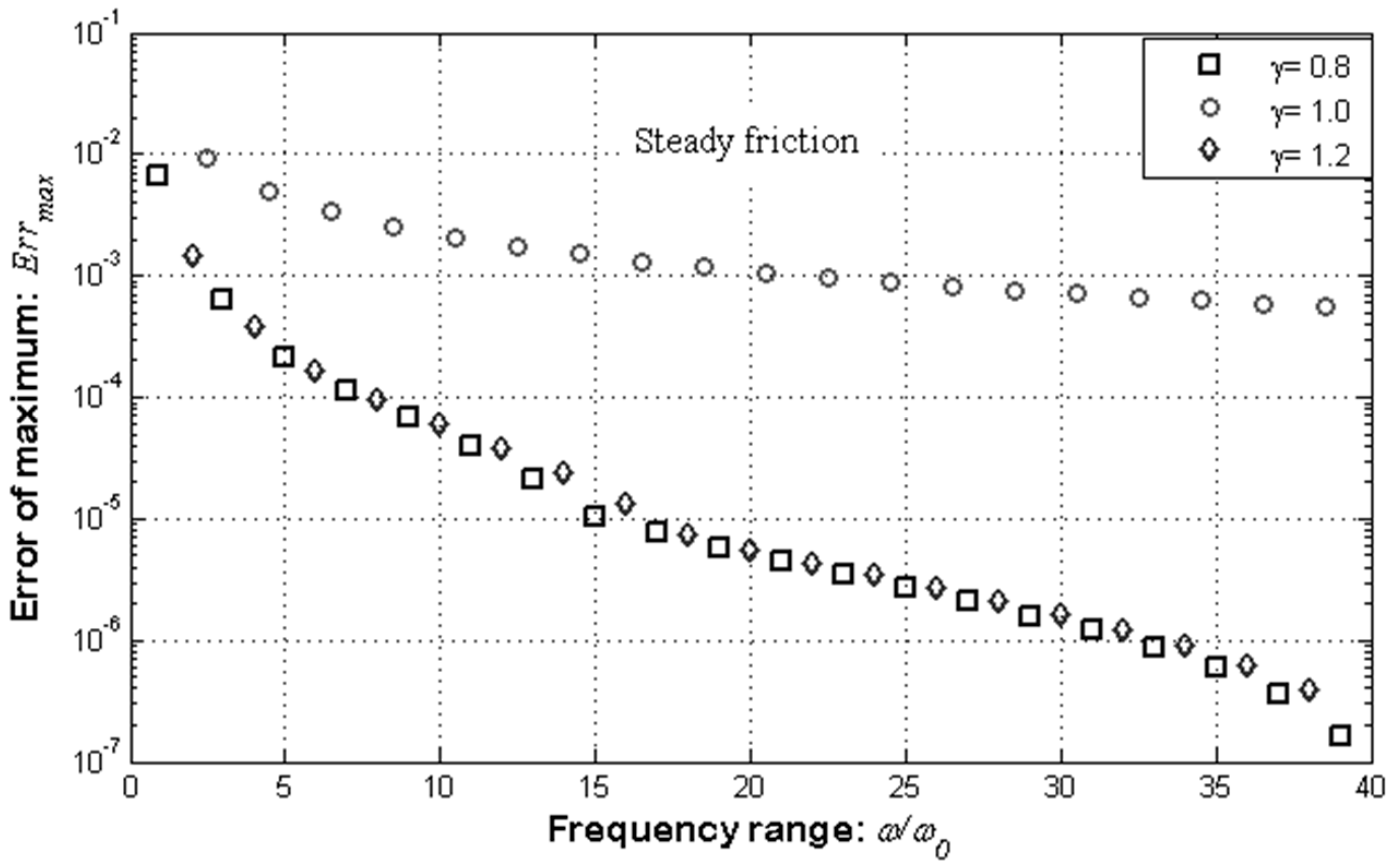
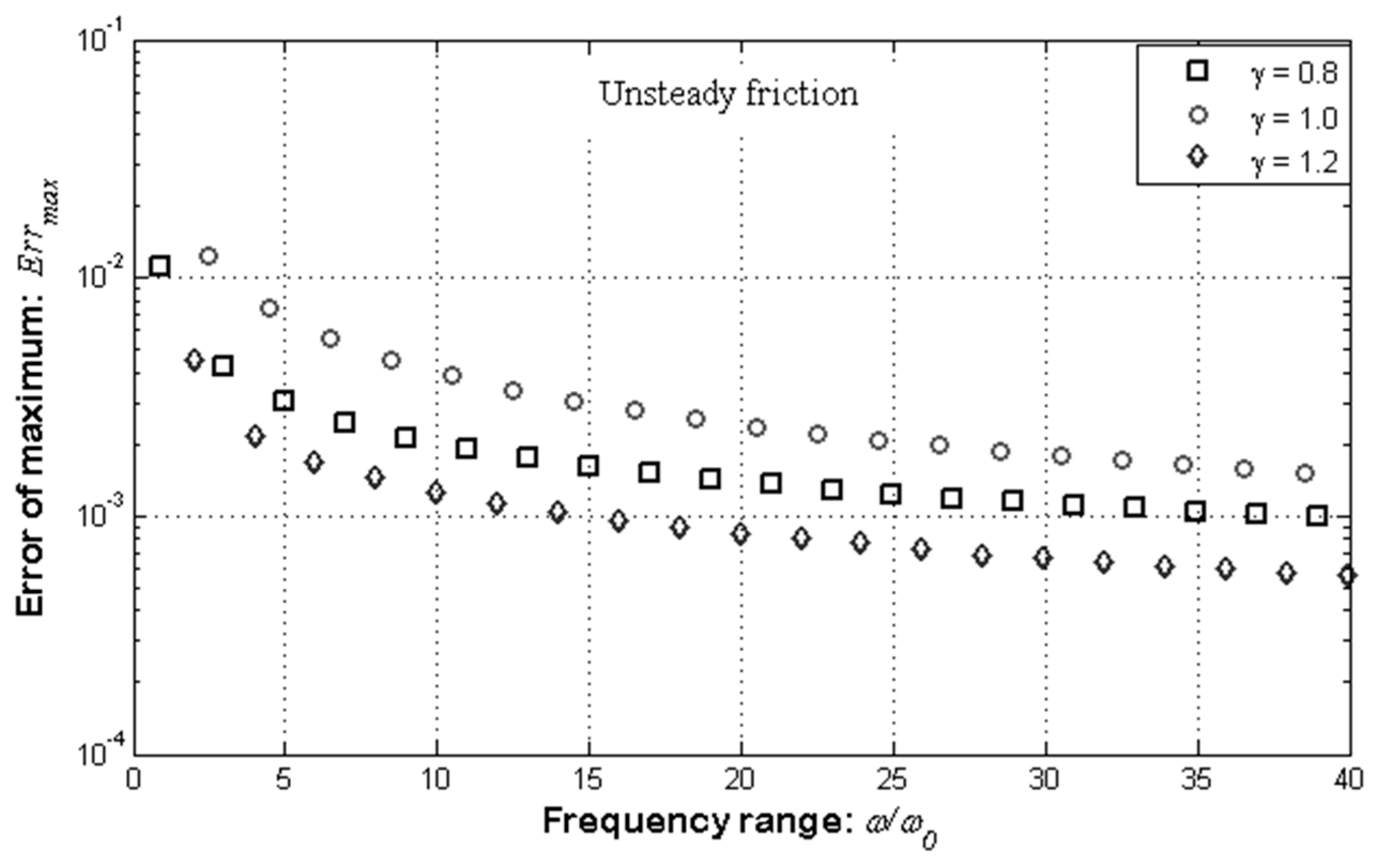
3.3. Steady and Unsteady Friction Models
- (1)
- If , then and
- (2)
- If , then and
- (3)
- If , then and
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schroeder, M.R. Determination of the geometry of the human vocal tract by acoustic measurements. J. Acoust. Soc. Am. 1967, 41, 1089–1100. [Google Scholar] [CrossRef] [PubMed]
- Mermelstein, P. Determination of the vocal-tract shape from measured formant frequencies. J. Acoust. Soc. Am. 1967, 41, 1283–1294. [Google Scholar] [CrossRef] [Green Version]
- Qunli, W.; Fergus, F. Estimation of blockage dimensions in a duct using measured resonance frequency shifts. J. Sound Vib. 1989, 133, 289–301. [Google Scholar] [CrossRef]
- Qunli, W. Reconstruction of blockage in a duct from single spectrum. Appl. Acoust. 1994, 41, 229–236. [Google Scholar] [CrossRef]
- De Salis, M.H.; Oldham, D.J. Determination of the blockage area function of a finite duct from a single pressure response measurement. J. Sound Vib. 1999, 222, 180–186. [Google Scholar] [CrossRef]
- De Salis, M.H.; Oldham, D.J. The development of a rapid single spectrum method for determining the blockage characteristics of a finite length duct. J. Sound Vib. 2001, 243, 625–640. [Google Scholar] [CrossRef]
- Çelik, H.; Cankurtaran, M.; Cakmak, O. Acoustic rhinometry measurements in stepped-tube models of the nasal cavity. Phys. Med. Biol. 2004, 49, 371–386. [Google Scholar] [CrossRef] [PubMed]
- Fredberg, J.J.; Wohl, M.E.; Glass, G.M.; Dorkin, H.L. Airway area by acoustic reflections measured at the mouth. J. Appl. Physiol. 1980, 48, 749–758. [Google Scholar] [CrossRef] [PubMed]
- Brooks, L.J.; Castile, R.G.; Glass, G.M.; Griscom, N.T.; Wohl, M.E.; Fredberg, J.J. Reproducibility and accuracy of airway area by acoustic reflection. J. Appl. Physiol. 1984, 47, 777–787. [Google Scholar] [CrossRef]
- Sharp, D.B.; Campbell, D.M. Leak detection in pipes using acoustic pulse reflectometry. Acta Acust. United Acust. 1997, 83, 560–566. [Google Scholar]
- Sharp, D.B. Increasing the length of tubular objects that can be measured using acoustic pulse reflectometry. Meas. Sci. Technol. 1998, 9, 1469–1479. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 249–326. [Google Scholar]
- Lee, P.J.; Vitkovsky, J.P.; Lambert, M.F.; Simpson, A.R.; Liggett, J.A. Frequency domain analysis for detecting pipeline leaks. J. Hydraul. Eng. 2005, 131, 596–604. [Google Scholar] [CrossRef] [Green Version]
- Mpesha, W.; Chaudry, M.N.; Gassman, S. Leak detection in pipes by frequency response method. J. Hydraul. Eng. 2001, 127, 137–147. [Google Scholar] [CrossRef]
- Ferrante, M.; Brunone, B. Pipe system diagnosis and leak detection by unsteady-state tests: Harmonic analysis. Adv. Water Resour. 2003, 26, 95–105. [Google Scholar] [CrossRef]
- Lee, P.J.; Vítkovský, J.P.; Lambert, M.F.; Simpson, A.R.; Liggett, J.A. Leak location using the pattern of the frequency response diagram in pipelines: A numerical study. J. Sound Vib. 2005, 284, 1051–1073. [Google Scholar] [CrossRef] [Green Version]
- Covas, D.; Ramos, H.; de Almeida, A.B. Standing wave difference method for leak detection in pipeline systems. J. Hydraul. Eng. 2005, 131, 1106–1116. [Google Scholar] [CrossRef]
- Verde, C.; Visairo, N.; Gentil, S. Two leaks isolation in a pipeline by transient response. Adv. Water Resour. 2007, 30, 1711–1721. [Google Scholar] [CrossRef]
- Guillen, M.; Dulhoste, J.F.; Besancon, G.; Rubio, S.I.; Santos, R.; Georges, D. Leak detection and location based on improved pipe model and nonlinear observer. In Proceedings of the European Control Conference, Strasbourg, France, 24–27 June 2014; pp. 958–963. [Google Scholar]
- Mohapatra, P.K.; Chaudhry, M.H.; Kassem, A.A.; Moloo, J. Detection of partial blockage in single pipelines. J. Hydraul. Eng. 2006, 132, 200–206. [Google Scholar] [CrossRef]
- Mohapatra, P.K.; Chaudhry, M.H.; Kassem, A.A.; Moloo, J. Detection of partial blockages in a branched piping system by the frequency response method. J. Fluids Eng. 2006, 128, 1106–1114. [Google Scholar] [CrossRef]
- Sattar, A.M.; Chaudhry, M.H.; Kassem, A. Partial blockage detection in pipelines by frequency response method. J. Hydraul. Eng. 2008, 134, 76–89. [Google Scholar] [CrossRef]
- Lee, P.J.; Vítkovský, J.; Lambert, M.; Simpson, A.; Liggett, J. Discrete blockage detection in pipelines using the frequency response diagram: Numerical study. J. Hydraul. Eng. 2008, 134, 658–663. [Google Scholar] [CrossRef] [Green Version]
- Duan, H.F.; Lee, P.J.; Ghidaoui, M.S.; Tung, Y.K. Extended blockage detection in pipelines by using the system frequency response analysis. J. Water Resour. Plan. Manag. 2012, 138, 55–62. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Kashima, A.; Lu, J.; Ghidaoui, M.S.; Tung, Y.K. Extended Blockage Detection in Pipes Using the System Frequency Response: Analytical Analysis and Experimental Verification. J. Hydraul. Eng. 2013, 139, 763–771. [Google Scholar] [CrossRef]
- Meniconi, S.D.; Duan, H.F.; Lee, P.J.; Brunone, B.; Ghidaoui, M.S.; Ferrante, M. Experimental investigation of coupled frequency and time-domain transient test-based techniques for partial blockage detection in pipelines. J. Hydraul. Eng. 2013, 139, 1033–1044. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J. Transient-Based Frequency Domain Method for Dead-End Side Branch Detection in Reservoir Pipeline-Valve Systems. J. Hydraul. Eng. 2015, 142, 04015042. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Che, T.C.; Ghidaoui, M.S.; Karney, B.W.; Kolyshkin, A.A. The influence of non-uniform blockages on transient wave behavior and blockage detection in pressurized water pipelines. J. Hydro-Environ. Res. 2017, 17, 1–7. [Google Scholar] [CrossRef]
- Louati, M.; Ghidaoui, M.S.; Meniconi, S.; Brunone, B. Bragg-type resonance in blocked pipe system and its effect on the eigenfrequency shift. J. Hydraul. Eng. 2018, 144, 04017056. [Google Scholar] [CrossRef] [Green Version]
- Che, T.C.; Duan, H.F.; Lee, P.J.; Meniconi, S.; Pan, B.; Brunone, B. Radial pressure wave behavior in transient laminar pipe flows under different flow perturbations. J. Fluids Eng. 2018, 140, 101203. [Google Scholar] [CrossRef]
- Ranginkaman, M.H.; Haghighi, A.; Lee, P.J. Frequency domain modelling of pipe transient flow with the virtual valves method to reduce linearization errors. Mech. Syst. Signal Process. 2019, 131, 486–504. [Google Scholar] [CrossRef]
- Pan, B.; Duan, H.F.; Meniconi, S.; Urbanowicz, K.; Che, T.C.; Brunone, B. Multistage Frequency-Domain Transient-Based Method for the Analysis of Viscoelastic Parameters of Plastic Pipes. J. Hydraul. Eng. 2020, 146, 04019068. [Google Scholar] [CrossRef]
- Lee, P.J.; Vítkovský, J.P. Quantifying linearization error when modeling fluid pipeline transients using the frequency response method. J. Hydraul. Eng. 2010, 136, 831–836. [Google Scholar] [CrossRef]
- Duan, H.F. Uncertainty analysis of transient flow modeling and transient-based leak detection in elastic water pipeline systems. Water Resour. Manag. 2015, 29, 5413–5427. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Jiao, Z.; Guan, C.; Xu, Y. Research on pulsation attenuation characteristics of expansion chamber in hydraulic systems. In IEEE International Conference on Industrial Informatics, Beijing, China, 25–27 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 735–739. [Google Scholar]
- Lee, P.J.; Duan, H.-F.; Ghidaoui, M.; Karney, B. Frequency domain analysis of pipe fluid transient behaviour. J. Hydraul. Res. 2013, 51, 609–622. [Google Scholar] [CrossRef]
- Lee, P.J.; Duan, H.; Tuck, J.; Ghidaoui, M. Numerical and experimental study on the effect of signal bandwidth on pipe assessment using fluid transients. J. Hydraul. Eng. 2015, 141, 04014074. [Google Scholar] [CrossRef]
- Vítkovský, J.P.; Bergant, A.; Lambert, M.F.; Simpson, A.R. Frequency-Domain Transient Pipe Flow Solution Including Unsteady Friction. In Proceedings of the Pumps, Electromechanical Devices and Systems: Applied to Urban Water Management, Valencia, Spain, 22–25 April 2003; pp. 773–780. [Google Scholar]
- Duan, H.F.; Che, T.C.; Lee, P.J.; Ghidaoui, M.S. Influence of nonlinear turbulent friction on the system frequency response in transient pipe flow modelling and analysis. J. Hydraul. Res. 2018, 56, 451–463. [Google Scholar] [CrossRef]
- Creaco, E.; Campisano, A.; Franchini, M.; Modica, C. Unsteady Flow Modeling of Pressure Real-Time Control in Water Distribution Networks. J. Water Resour. Plann. Manag. 2017, 143, 04017056. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Pan, D.; Qu, F.; Hu, J. Model Analysis and System Parameters Investigation for Transient Wave in a Pump–Pipe–Valve System. Water 2020, 12, 1014. https://doi.org/10.3390/w12041014
Liu Z, Pan D, Qu F, Hu J. Model Analysis and System Parameters Investigation for Transient Wave in a Pump–Pipe–Valve System. Water. 2020; 12(4):1014. https://doi.org/10.3390/w12041014
Chicago/Turabian StyleLiu, Zubin, Dingyi Pan, Fengzhong Qu, and Jianxin Hu. 2020. "Model Analysis and System Parameters Investigation for Transient Wave in a Pump–Pipe–Valve System" Water 12, no. 4: 1014. https://doi.org/10.3390/w12041014
APA StyleLiu, Z., Pan, D., Qu, F., & Hu, J. (2020). Model Analysis and System Parameters Investigation for Transient Wave in a Pump–Pipe–Valve System. Water, 12(4), 1014. https://doi.org/10.3390/w12041014




