1. Introduction
Scientists and managers currently lack reliable climate projections at the temporal and spatial resolution required to perform traditional flood risk analyses. Furthermore, there is no consensus on methods to incorporate multiple, uncertain future scenarios into such analyses. Climate model output has served as the starting point and basis of most studies of climate risk [
1,
2,
3]. However, the output from climate models is often ill-suited for this role for several interrelated reasons that include:
Misalignment with the designed purpose of General Circulation Models (GCMs) and to evaluate global policies concerning greenhouse gases and its application to regional planning and decision-making [
4,
5];
Incompatible spatial and temporal resolution between reliable GCM output and water resource specialists’ needs [
6,
7]; and
Cascading, increasing uncertainty through bias correction and downscaling to achieve desired spatial and temporal resolution [
8].
Importantly, advances in modeling and downscaling techniques will not ameliorate the concerns listed above. While new generations of GCMs, Coupled Model Intercomparison Project (CMIP) output, Regional Climate Models (RCMs), and downscaling techniques all possess the potential to better characterize uncertainty, these new models and techniques will by no means eliminate uncertainty, and instead may increase uncertainty in future climate projections [
9,
10]. Current approaches to flood frequency analysis (e.g., Bulletin 17B used in the United States [
11]), that rely on a single, reliable, long-term hydrologic record and assume stationarity are ill-suited for assessing flood risk using multiple, highly uncertain climate change projections.
To date, top-down, scenario-led impact assessments have dominated thinking on climate change impacts and evaluation of potential adaptation measures (e.g., [
1,
2,
3]). However, the dependence of these approaches on a small set of deeply uncertain, downscaled GCM output limits their ability to reliably assess the full range of future flood risk. Currently, no agreement exists on a universally appropriate method to temporally and spatially downscale GCM output to the resolution required for flood frequency analysis (e.g., catchment scale and daily or sub-daily time step) [
12,
13]. At the same time, the choice of downscaling method can have significant implications for flood frequency analysis [
6]. Alternatively, RCMs can be used to indirectly derive regional climate from GCM output, though RCMs have their own issues [
14]. In either case, calculating the resulting streamflow requires further modeling efforts to force hydrologic models with the output from the climate models. As a result, uncertainty is cascaded down the various steps reaching the point where the streamflow impacts can span wide, confounding ranges, which may even include opposite signs, e.g., an increase or decrease in flood magnitude [
8,
15]. Few studies take the additional step of combining the hydrologic projections with damage projections, regardless of how these damages are characterized, in order to assess vulnerability and flood risk [
8,
15], which adds another layer of uncertainty to the results. Demonstrating an approach to accomplish this is the primary innovation of this effort.
Approaching flood risk assessment from the bottom-up can overcome some of the limitations of top-down decision-making. With bottom-up approaches, assessments are tailored to address a specific flood management decision within the limitations of the available data. Bottom-up approaches take several names and forms, including: Scenario-neutral approaches [
15], decision scaling [
16,
17], climate risk informed decision analysis [
18,
19], and robust decision-making [
8,
20]. These approaches reverse the order of typical impact and vulnerability assessment used in top-down approaches, as well as the order in which projected hydrologic information is used to inform decision-making. Top-down approaches first generate a limited set of downscaled climate scenarios from which to assess impacts and then vulnerability to those limited scenarios. In contrast, bottom-up assessments generally start with an identified management concern, around which system sensitivity and vulnerability to climate are characterized. Bottom-up approaches acknowledge the limits of uncertain climate model output and downscaling approaches, and as such they only consider GCMs in the later stages of the risk assessment process, alongside other available climate data, such as observations and paleontological data.
We present a methodology for bottom-up assessment of flood damages based on existing frameworks [
16,
21] that require first defining the decision context for assessing climate impacts on water systems. The decision context refers to identifying the assessment goals and relevant parameters in the context of a specific management or policy decision, and it is established before choosing and analyzing models and data [
21]. Focusing on the specific management decision or policy at hand, bottom-up approaches scale and tailor climate information to inform that decision, usually through a sensitivity and vulnerability analysis. We began our analysis with a sensitivity and vulnerability assessment that does not consider climate projections, but is intended to help water managers better understand the hydrologic conditions that push their systems into a vulnerable state. For this bottom-up flood risk assessment, sensitivity is defined in terms of how much Expected Annual Damages (EAD) change under different climatic conditions. A system’s vulnerability to exceeding an acceptable flood risk is defined by the extent to which a system is unable to maintain EAD below a threshold risk level. As part of the sensitivity and vulnerability analyses, several studies [
15,
16,
22] have developed functions to describe climate response (e.g., increase in peak flows) as a function of changes in mean annual precipitation and seasonal variation. We took this work a step further by describing climate response in terms of flood risk, a function of both changes in peak flows and the damages associated with those flows [
23]. While other flood damage assessment techniques exist, with active research on the topic ongoing, this is not the focus of this effort. Rather, the proposed innovation can be applied to any existing or emerging technique.
The climate response surfaces, describing sensitivity and vulnerability, in combination with plausible climate impacts, can be used to compare the future performance of different management actions and determine the climate scenarios that favor certain strategies over others. The metrics used to assess system performance differ in bottom-up and top-down approaches. Top-down approaches tend to seek an optimum solution based on the probability of future scenarios occurring and the expected value of different decisions under those scenarios. However, in the face of uncertain climatic changes, rather than seeking optimal performance, a growing body of literature advocates for seeking robust strategies that perform reasonably well over a wide range of uncertain, yet plausible future scenarios [
7,
8,
20,
24,
25,
26]. By using robustness criterion in combination with a vulnerability and impact assessment, managers can evaluate: Whether actions towards adaptations are needed [
16], the conditions that cause a particular decision to be favored over another [
22], or the robustness of a policy [
15].
We present a climate risk and adaptation assessment of the flood management system in the American River basin, CA, USA with the objectives of: (1) Developing a bottom-up methodology for the assessment of flood management decisions in which uncertainty and nonstationarity of flood frequencies are directly considered and (2) applying the methodology to the flood management system in the American River to characterize its vulnerabilities to flood damages under different climate and management scenarios. This second objective aims to respond directly to specific planning efforts conducted as part of the Central Valley Flood Protection Plan (CVFPP). Using a bottom-up approach, we began by framing this decision context around a key question water resources managers have been investigating [
27]: Given climate change, what is the most robust strategy to take for managing flood risk in the American River basin? To inform this decision, we (1) identified the sensitivity of the American River flood system to different climates, defined in terms of changes in EAD; (2) identified a vulnerability range of flood regimes under which the current system cannot maintain flood risk (EAD) below an acceptable threshold; (3) determined potential changes in flood frequency and flood risk under climate change by stochastically generating a set of plausible future flood regimes; and (4) evaluated the robustness of the flood management scenarios under plausible future conditions in terms of their ability to maintain flood risk below a threshold EAD and maintain a benefit-cost ratio (BCR) above a cost-effectiveness threshold.
Study Area: American River Basin, CA, USA
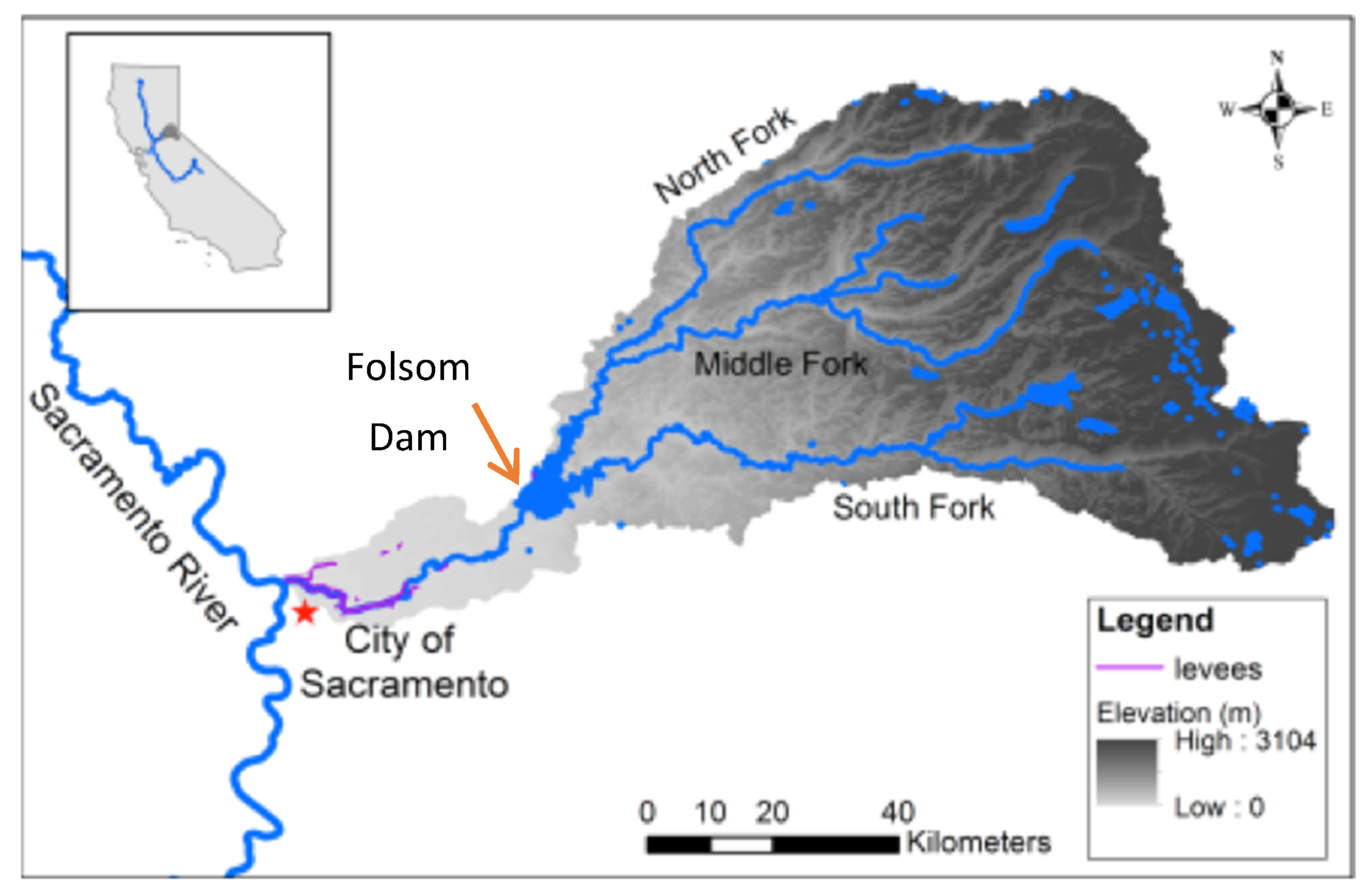
From its headwaters in the western slopes of the Sierra Nevada mountain range in Northern California, the American River flows southwest towards its confluence with the Sacramento River at the City of Sacramento (
Figure 1). This study focused on flood risk in the highly populated portion of the basin to the south of the American River. The American River drains an area of 4975 km
2, from elevations of 3170 m. along the Sierra crest to 7 m. above sea level at the confluence with the Sacramento River. Forty percent of the basin lies above the snowline, which occurs at an elevation of approximately 1500 m. The basin has a Mediterranean climate, with 90% of annual precipitation falling in 2–3 winter months [
3]. Wintertime rainfall and snowmelt runoff comprises about two-thirds of the American River streamflow, with less than one-third derived from springtime snowmelt runoff [
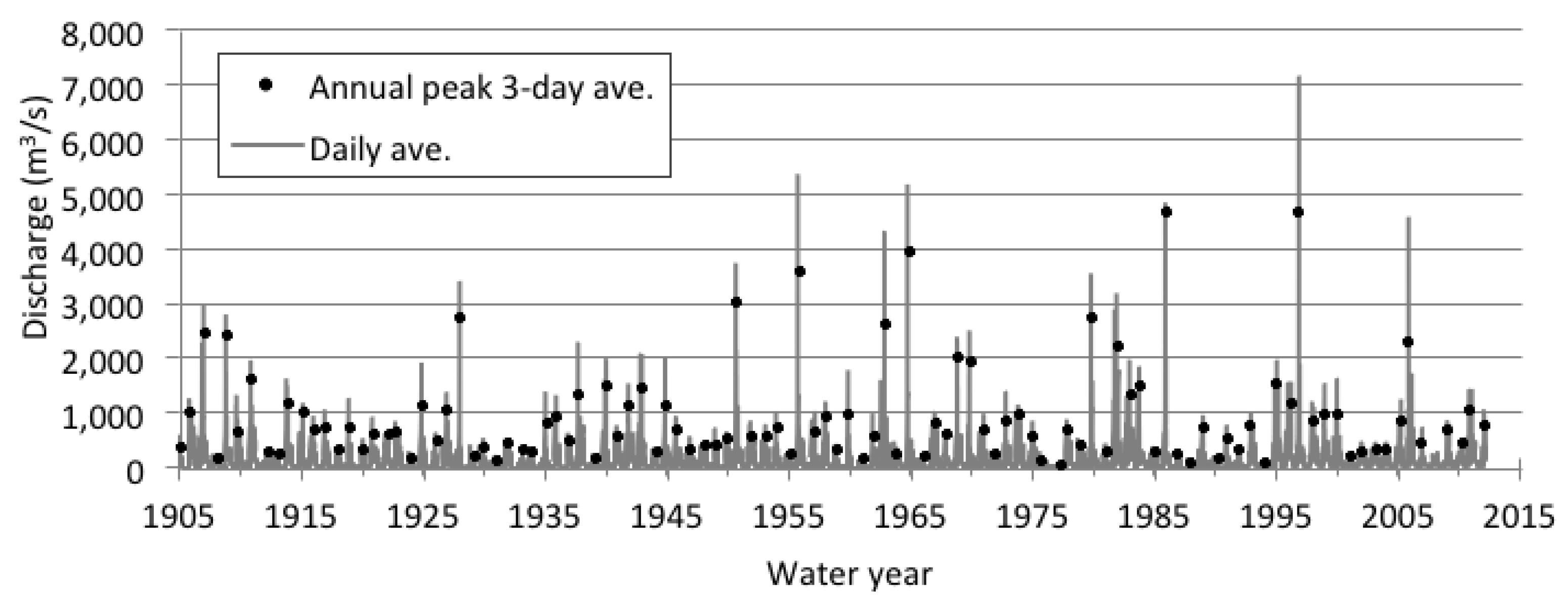
28]. The American River experiences large variations in annual precipitation and streamflow (
Figure 2). Much of this variation results from water years that include a few large storms fueled by the landfall of atmospheric rivers. Known informally as “Pineapple Express” storms in the Pacific region, these events produce a narrow corridor of concentrated moisture that travels northeast over the Pacific Ocean from an area near Hawaii to California [
29]. As the moist air and orography interact over land, the events can generate substantial portions of a basin’s annual precipitation and runoff (e.g., up to 50% for California [
29]) over the course of a few days, often leading to substantial flood hazards.
The history of flooding on the American and Sacramento Rivers pre-dates European settlement; In 1808 the Spanish explorer Ensign Gabriel Moraga observed evidence that the rivers created “one immense sea, leaving only scattered eminences which art of nature have produced, as so many islets or spots of refuge” (in [
30]). Attempts to control the floodwaters of the American River necessarily coincided with settlement and continue to this day. The State Plan for Flood Control (SPFC) descriptive document produced in 2010 [
31], represented California’s first large-scale coordinated effort to manage floods at the state level. The SPFC is comprised of: Facilities (levees, weirs, dams, pumping plants, bypass basins, etc.); lands (fee title, easements, and land use agreements); operations and maintenance (O&M) requirements of SPFC facilities, conditions (terms, Memorandums of Understanding, regulations, etc.); and programs and plans. Major SPFC works in the American River basin include Folsom Reservoir and Dam, located at the confluence of the American River’s two main tributaries (
Figure 1); levees on both banks of much of lower portions of the river below Folsom; and three pumping plants [
32]. About the SPFC, the California Department of Water Resources (CA-DWR) [
32] has concluded that:
It has prevented billions of dollars in flood damages since its inception;
some SPFC facilities face an unacceptably high chance of failure; and
an unintended consequence of the long-term effort to reduce flooding is that development and population growth behind levee-protected areas have increased flood damages over time.
Thus, although the probability of flooding has decreased, the damages when floods occur are much higher today than they were in the past, resulting in a net long-term increase in flood risk [
27]. The City of Sacramento faces some of the highest flood risk in the United States and the developed world [
33], which is one of the reasons many prior research efforts [
23,
28,
34,
35] and financial investments have attempted to help manage flood risk in the American River basin. In this study, we expanded upon previous flood management work in the basin to include a bottom-up climate impact assessment.
2. Data and Methods
The developed methodology for conducting the climate risk assessment is in line with other bottom-up studies, but it uniquely tailors the approach to the specific decision context in the American River basin, uses only existing models and available data, and incorporates a Bayesian approach to developing a plausible range of future climates. We undertook the following steps to conduct a bottom-up risk assessment of a retrospective decision regarding future flood management strategies for the American River basin:
Establish the decision context
Assess the sensitivity of the system to changes in climate and flood regimes
Assess the vulnerability of the system to flood regime changes
Determine a plausible range of future flood regimes
Assess the robustness of management strategies
2.1. Establishment of the Decision Context
In response to increasing flood damages, highlighted during flooding in the 1990s, the California State Legislature directed the CA-DWR to prepare a Central Valley Flood Protection Plan (CVFPP) and supporting documentation [
27] as an enhancement to the SPFC. The primary goal of the 2012 CVFPP is to improve flood risk management, though the plan also includes supplemental goals to improve operations and maintenance of project facilities, promote ecosystem functions, improve institutional support, and promote multi-benefit projects. It is important to note that the current study is designed to supplement, not critique the CVFPP. As such, the CVFPP provided the decision context for the proposed innovation related to adapting flood management plans more generally to changing climatic conditions.
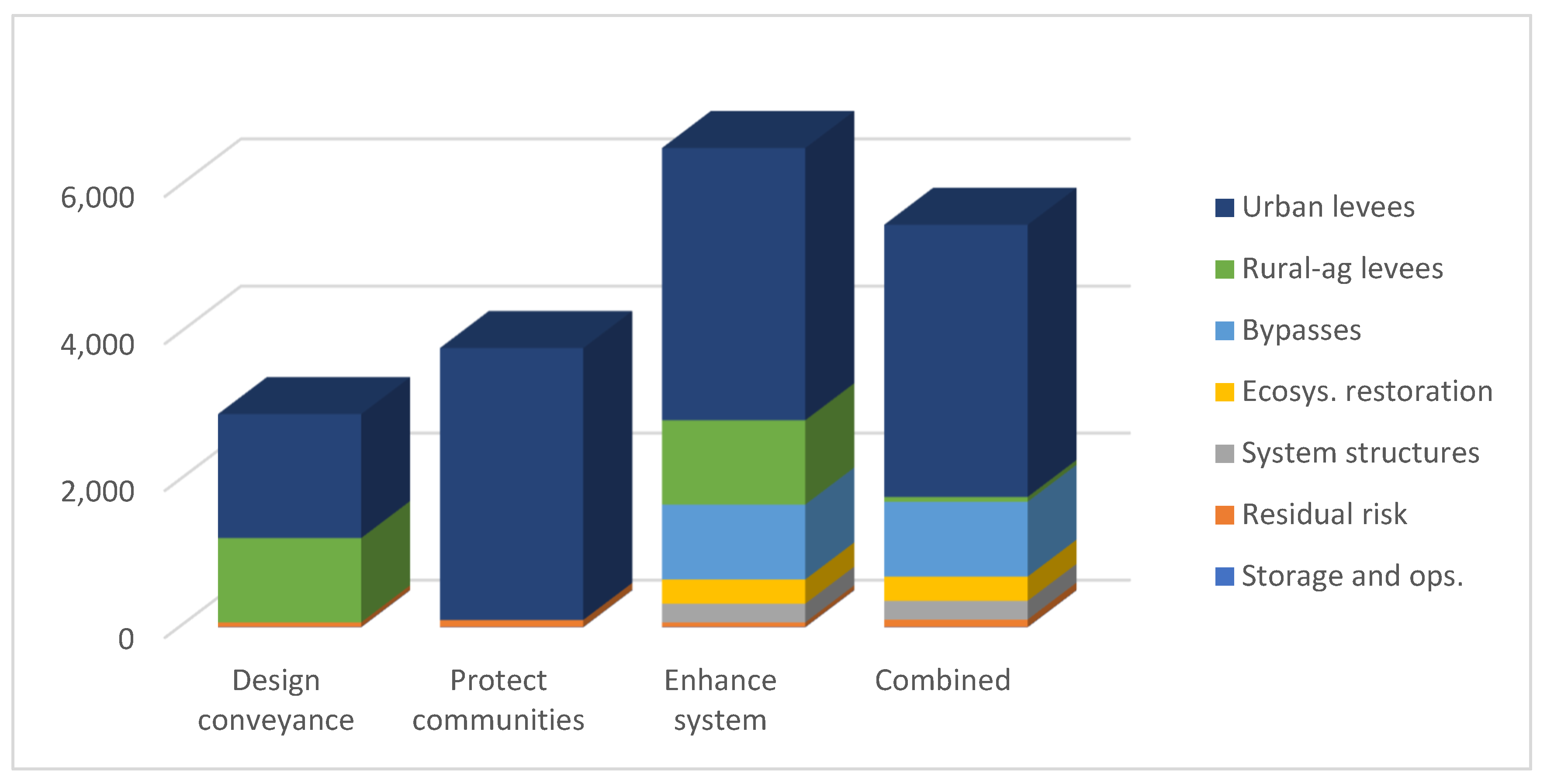
The plan developed for the CVFPP outlines three preliminary strategies for addressing the problems identified in the current SPFC as well as a fourth strategy that combines the strength of each of the preliminary strategies (
Table 1). The Without Project baseline describes a continuation of existing conditions and projects currently authorized, e.g., current construction efforts to raise Folsom Dam. The Design Capacity (SPFC) strategy splits its budget between improvements to existing urban and rural SPFC levees so that they can convey their design flow (
Figure 3). Alternatively, the strategy designed to Protect High Risk Communities (PHRC) focuses almost exclusively on urban levees in the Sacramento metro area. The third preliminary strategy took a more holistic approach to Enhance the Flood System Capacity (EFSC) and sought out opportunities to achieve multiple benefits throughout the basin. The EFSC strategy includes the levee improvements of the SPFC and PHRC strategies, but also a wide variety of additional management actions, including the inclusion of nature-based strategies, such as: Expansion of bypasses, conjunctive use, groundwater recharge, and ecosystem restoration (including floodplain restoration). A fourth strategy, the State Systemwide Investment Approach (SSIA) was then developed to combine the strengths of the three strategies above. The SSIA includes much of the same management actions as the EFSC, but reduces expenditures dedicated to rural levee improvements (
Figure 3) (For a more detailed description of specific management actions included in each strategy, see the 2012 CVFPP [
27]).
The CVFPP assessed each of the strategies, along with the baseline Without Project conditions, based on effectiveness in contributing to the CVFPP goals and other quantitative and qualitative performance measures, including: Level of flood protection, population with less than 100-year protection, EAD and reduction in EAD, capital costs, O&M requirements, opportunity for ecosystem restoration, opportunity for multi-benefit projects, ability to meet objectives in flood legislation, social sustainability, and climate change adaptability. The CVFPP analysis concluded that the Enhance System strategy, which includes the greatest extent of nature-based strategies, best meets CVFPP goals. However, it also requires the highest level of investment and significant institutional changes. Thus, CA-DWR adopted the Combined strategy to incorporate many of the beneficial features in the three preliminary strategies, including nature-based strategies such as widening channels to expand flood conveyance capacities and restoring floodplains, at a more reasonable cost and implementation time. This is the policy context in which the current effort attempted to introduce novel notions to planning in the face of climate change.
To add a climate change dimension to the CA-DWR analysis, we assessed the robustness of the management strategies in terms of their ability to meet the primary goal of flood risk reduction under a plausible range of future climates. Consistent with the CVFPP analysis and the U.S. Army Corps of Engineers (USACE) evaluation procedures for flood risk management plans [
36,
37], we based our climate risk metrics on EAD and reduction in EAD through management actions. This allows for consideration of climate change within the same decision context used in the CVFPP analysis, conveying information regarding future flood risks to decision makers using a familiar and well understood metric. While damages monetized through the EAD assessment only described a limited portion of flood risk, the methods presented herein could be applied to any of the performance measures included in the CVFPP, or others, e.g., population in the 100-year floodplain, loss of life, etc., or even metrics associated with the supplemental goals of the CVFPP. In addition to EAD, we also assessed the cost-effectiveness of the CVFPP strategies in terms of the benefit–cost ratio (BCR) over a wide range of plausible climate futures.
2.2. Sensitivity of the Current System to Flood Regime Changes
We assessed the current flood management system’s sensitivity to climate change by evaluating the relationship between flood risk, in terms of EAD, and changes in the hydrologic flood regime. EAD is a function of the probability of a flood event occurring multiplied by the damages expected to result from such an event [
23]. Integrating flood damages over the probability of all possible flood events in a given year yields EAD (Equation (1)):
where, D(p) is the expected damages, D, in dollars, based on the probability of event (p).
Again, consistent with the CVFPP, our assessment only examined hydrologic changes and did not incorporate changes in the damage function, D(p), which could result, for example, from development and land use changes in the floodplain.
For flood risk management, the most important input to characterize hydrology is the probability distribution of annual peak flows, known as the flood-frequency curve [
38]. In the U.S., flood forecasting by federal agencies follows the analysis techniques outlined in the Guidelines for Determining Flood Flow Frequency Bulletin 17B, commonly referred to as “Bulletin 17B”. Bulletin 17B recommends fitting a log-Pearson type III (LP3) distribution to observed annual maximum streamflow data using the method-of-moments to estimate the mean (μ), standard deviation (σ), and the skew coefficient (ϒ) [
11]. In terms of potential changes to the flood frequency curve: Higher values of μ indicate larger expected values of flood magnitudes in any given year; higher values of σ indicate larger inter-annual variability in flood magnitude; and higher values of ϒ steepen the upper tail of the distribution, resulting in larger extreme events.
We based our initial flood frequency curve analysis on historic observations of daily streamflow gauge records collected on the American River at Fair Oaks gauge (USGS 11446500), located 11 km downstream of Folsom Dam, from 1905–2012. However, direct gauge data after the construction of Folsom Dam in 1955 represents regulated flow. Thus, we replaced the gauge data with estimated natural flows for the 1955–2012 period (Northwest River Forecast Center (NWRFC), unpublished data), which were calculated based on upstream gauges, storage volume, and release rates at Folsom. In this study, we assumed a skew parameter of zero for the LP3 distribution, which is a reasonable assumption for the historic period considering that the calculated station skew at Fair Oaks gauge is −0.035 with a standard deviation of 0.233 [
39]. While this assumption may not hold into the future, limited historical records already result in unstable skew parameters [
40], and projections of future skew are even more uncertain than mean and standard deviation. In addition, the zero-skew assumption simplifies the Bayesian analysis and does not detract from the methodological focus of the study.
To assess the sensitivity of the current flood management system to different climates, we first developed a climate response function that describes the relationship between EAD and log-normal flood frequency curve parameter sets of μ and σ for the peak 3-day average discharge at Fair Oaks gauge. The mean daily unregulated inflow at Folsom Dam is one of the primary determinates of downstream flood risk, as there are no major inputs or outputs between Folsom and the City of Sacramento. We calculated EAD with a modeling suite that included the CVFPP using the USACE Hydrologic Engineering Center’s Flood Damage Assessment software (HEC-FDA) [
27,
33]. The HEC-FDA model uses stage-exceedance probability curves and damage-stage curves to estimate EAD (
Figure 4). For the CVFPP, the stage-exceedance probability curves represent the downstream floodplain stage associated with flows entering Folsom reservoir, i.e., unmodified 99.9-, 10-, 4-, 2-, 1-, 0.5-, and 0.2-percent exceedance events flows at the Fair Oaks gauge (
Figure 4a). Development of these stage-exceedance curves required the routing of flows through Folsom Reservoir and then to downstream regions using HEC Reservoir Simulation (RES-SIM) and HEC River Analysis System (RAS) models, respectively. Using in-channel stage and probability of levee failure curves, flood flows were then routed through a FLO-2D model to determine downstream floodplain stage. The damage associated with different floodplain stages (
Figure 4b) considered:
Residential, commercial, industrial, and governmental structure and contents damage;
Agricultural/crop losses; and
Business production losses. See CVFPP 2012 [
27] Attachment 8F for a full description of the Flood Damage Analysis and associated models.
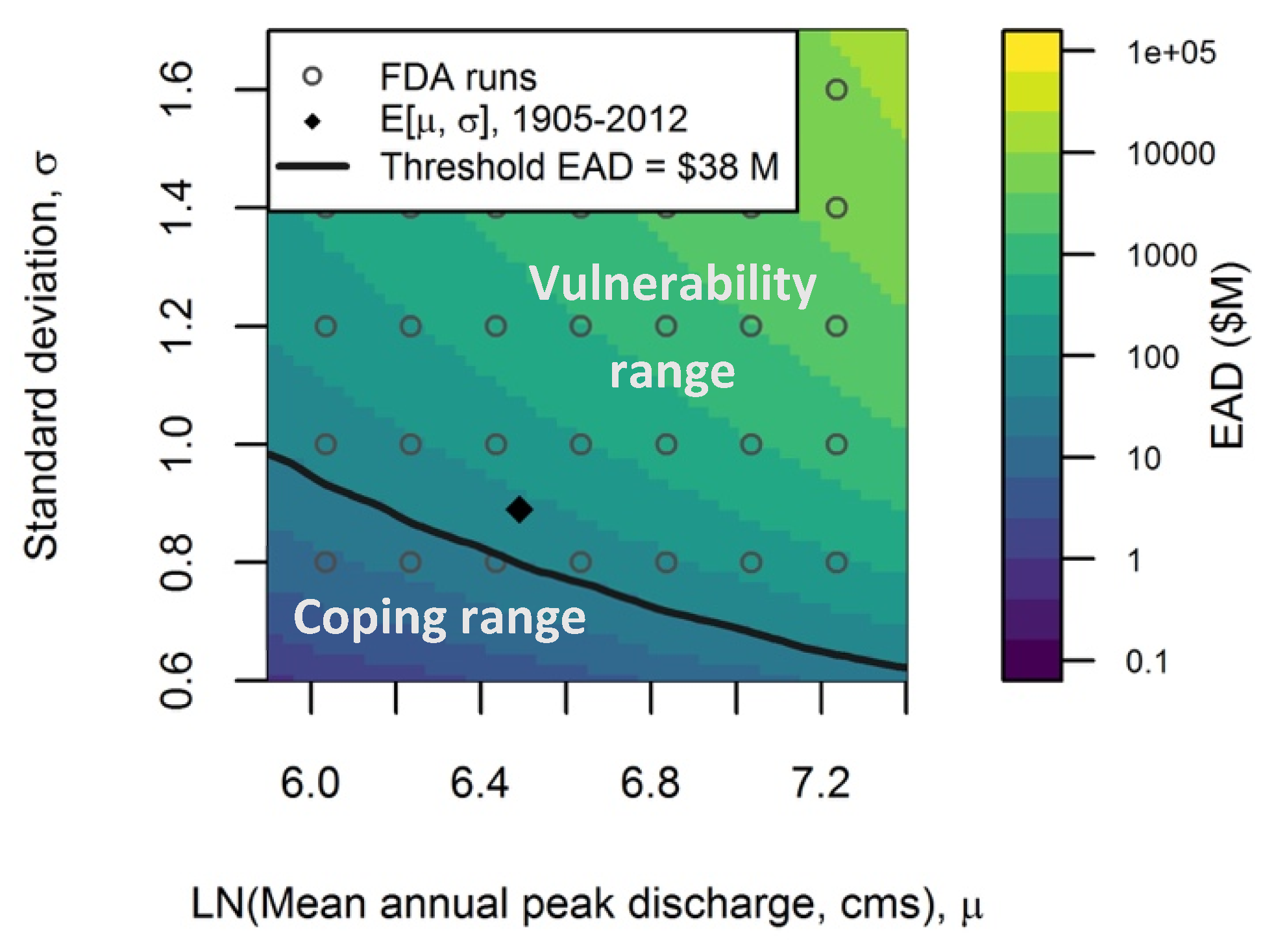
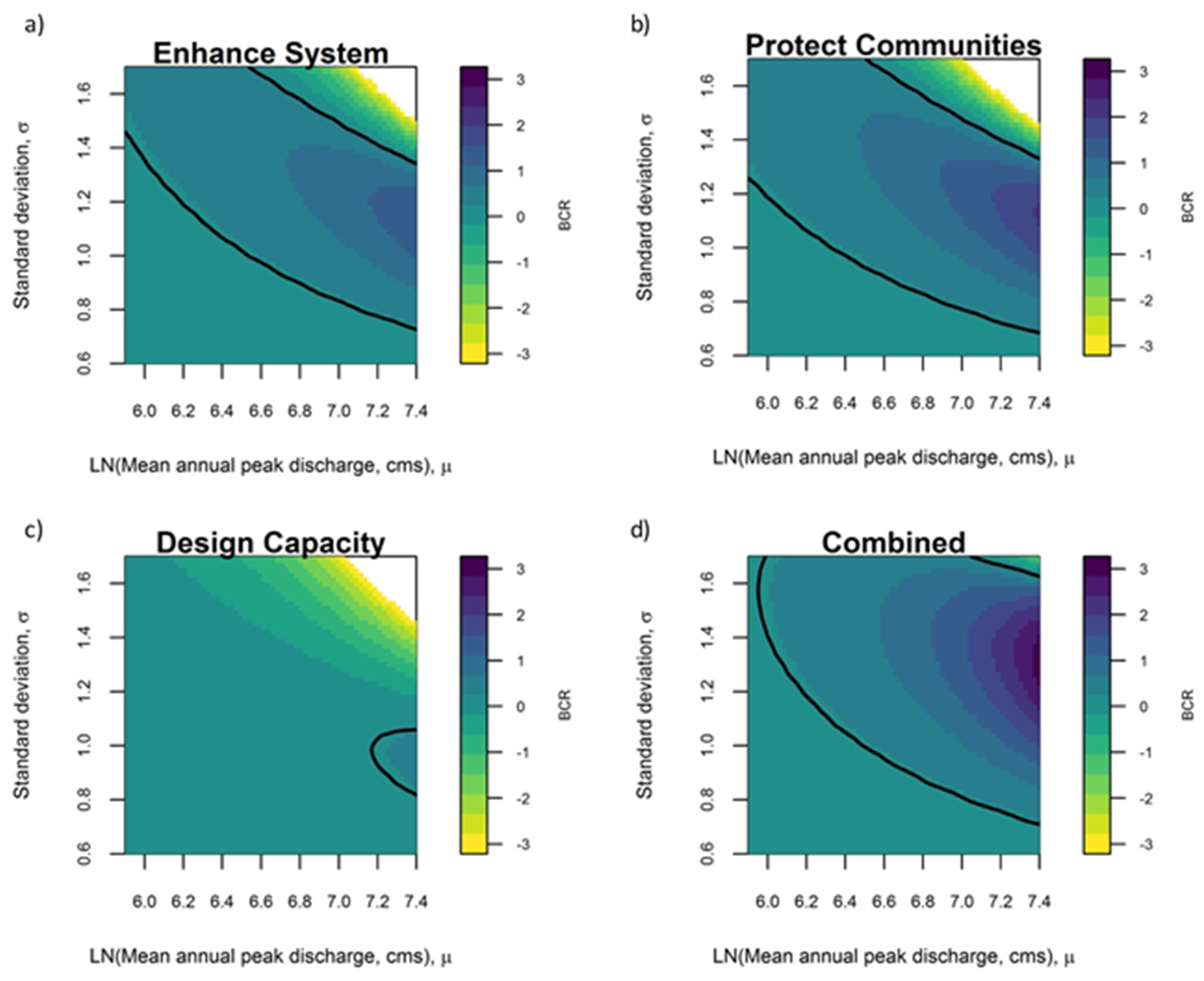
Using the HEC-FDA model, we assessed EAD across a gridded range of μ and σ parameter sets representing different flood frequency curves (
Figure 5). For each parameter set, we calculated the probability of exceeding the river stage associated with the historic 99.9-, 10-, 4-, 2-, 1-, 0.5-, and 0.2 exceedance events (dotted line in
Figure 4a) and combined this with the stage-damage curve (
Figure 4b) to develop damage-exceedance plots (
Figure 4c) and EAD values for each gridded parameter set (open circle locations in
Figure 5). Due to the stepwise nature of the damage functions, where flooding and damages only occur after a certain flood magnitude, low (μ, σ) combinations produce EAD values of
$0, or no damage. We concentrated on the portion of the EAD functions that produce damages, i.e., those with σ values of 0.8 and above. To assess how EAD responds to changes in the flood frequency curve, we developed a continuous climate response surface for the Without Project conditions by fitting a linear climate response function to the discrete flood frequency curve parameter sets (Equation (2)):
where, EAD is Expected annual damages (
$); μ is the mean of the 3-day peak flow; σ is the standard deviation; and β
i are regression coefficients.
We developed climate response surfaces using Equation (2) to examine the sensitivity of EAD to changes in μ and σ (shaded background in
Figure 5).
2.3. Vulnerability of System to Flood Regime Changes
After developing the climate response surfaces, we identified the range of flood frequency regimes under which the system is vulnerable to exceeding an acceptable flood risk. We accepted a threshold for acceptable flood risk as the EAD (
$38 million/year) under the Combined strategy that was selected as the CVFPP management strategy moving forward [
27]. As such, the system was considered vulnerable when mean and standard deviation combinations yield EAD above the threshold of
$38 million. We termed the region above the threshold the “vulnerability range” and below the threshold the “coping range” [
41], and used historical gauge data to assess the extent to which the current system is vulnerable to exceeding the threshold EAD (
Figure 5).
2.4. Plausible Range of Future Flood Regimes
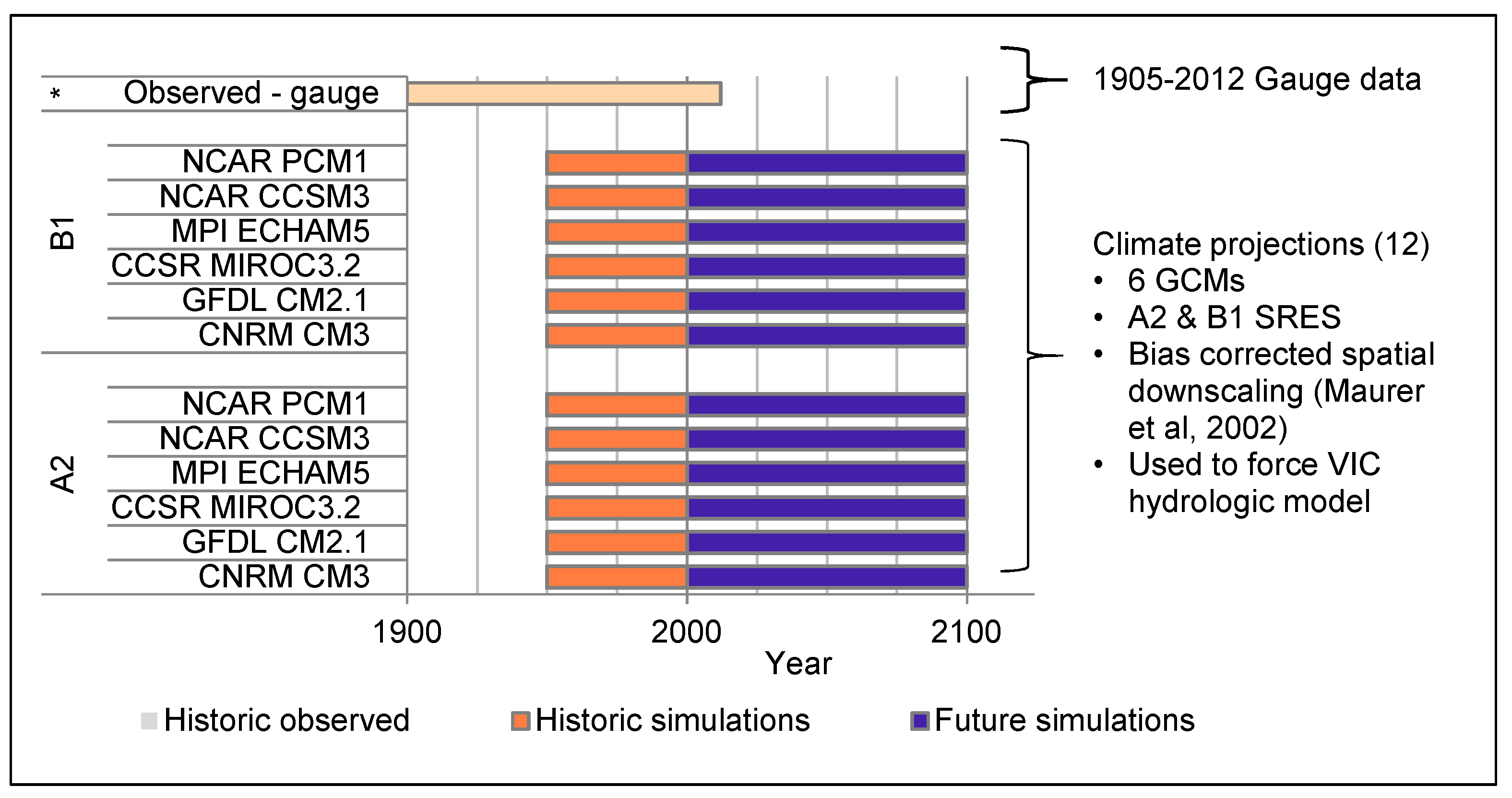
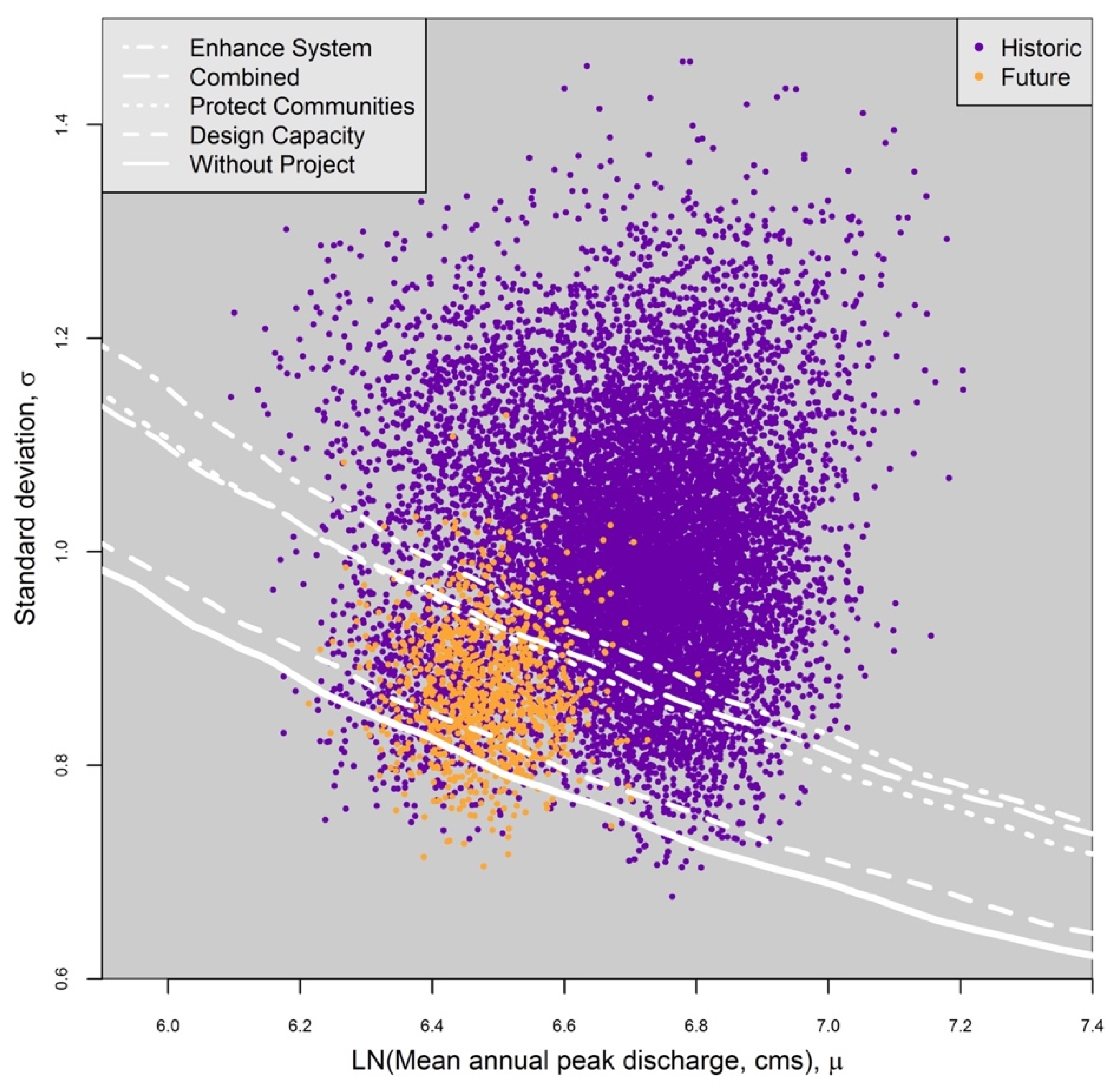
After assessing the sensitivity and vulnerability of the current system based on historic data, we then developed a plausible range of future flood regimes based on GCM simulations of future peak flow. We also used historic observations and historic GCM simulations to inform our confidence in the future simulations (
Figure 6). In addition to the historical Fair Oaks gauge dataset, we assessed GCM-derived projections based on daily streamflow output from a Variable Infiltration Capacity (VIC) model of the Sacramento Basin, forced with Bias Corrected Spatially Downscaled (BCSD) output from two runs each of six GCMs [
42,
43]. We used streamflow simulations at a VIC index point on the American River at Folsom Dam, 11 km upstream of Fair Oaks and without significant inflow/outflow between the two locations. VIC output from 1950 to 1999 represent a forcing of the GCMs with observed atmospheric variables, downscaled and input into the hydrologic model. For the future time period (2000–2100), each GCM was forced with two climate change emissions scenarios (A2 and B1), totaling twelve sets of daily streamflow projections from 1950 to 2099.
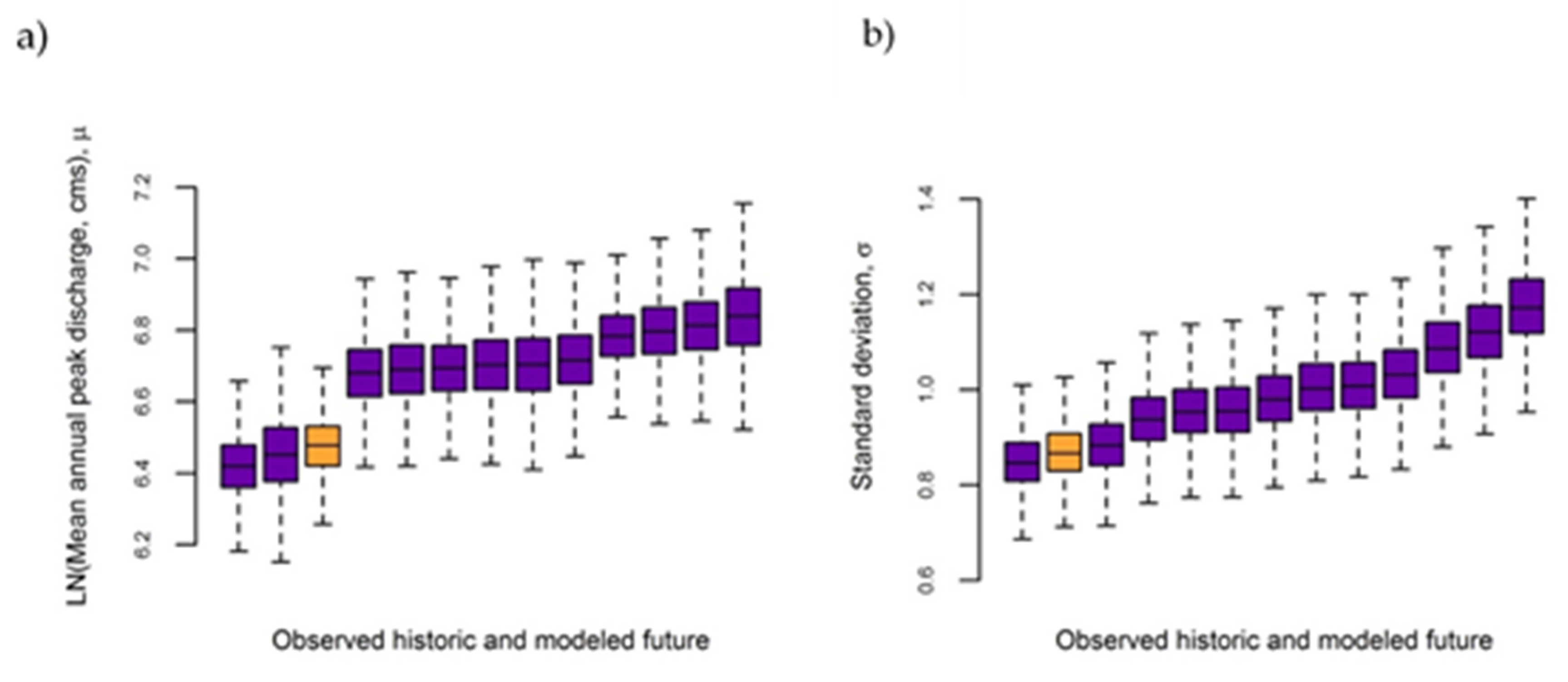
We evaluated flood frequency parameters (μ, σ) for each of the historic and future flow datasets to both characterize plausible climate impacts on flood regimes and to qualitatively assess the reliability and uncertainty in the climate projections. This analysis included:
Examining trends in flood frequency parameters based in the observed historic data (1905–2012);
Comparing flood frequency parameters based on historic observations (1950–1999) and historic GCM simulations (1950–1999); and
Comparing flood frequency parameters based on historic observations (1905–2012) and future GCM simulations (2000–2100).
In conducting the flood frequency analyses, we incorporated two major modifications to the methods outlined in Bulletin 17B. The first was the inclusion of future projections in addition to historic observations in the analysis. Secondly, we used Bayesian statistical techniques to develop plausible ranges of historic and future flood regime projections rather than Frequentist techniques. Bayes Theorem [
44] treats the parameters of the probability distribution as variables themselves, which allowed for describing the parameters of fitted flood frequency curves (μ, σ) in terms of their own probabilistic distributions, conducive to developing our desired range of plausible impacts. For this analysis, using WinBUGS [
45] we fit a log-normal Bayesian model with non-informative priors to the observed and simulated peak annual 3-day average flood discharge datasets. For each dataset, we used a Gibbs sampling Markov Chain Monte Carlo (MCMC) algorithm to produce 11,000 iterations, with the first 1000 used for burn in, to determine posterior intervals of the flood frequency parameters. To check convergence, we ensured that the Gelman-Rubin diagnostic results in
values less than 1.05.
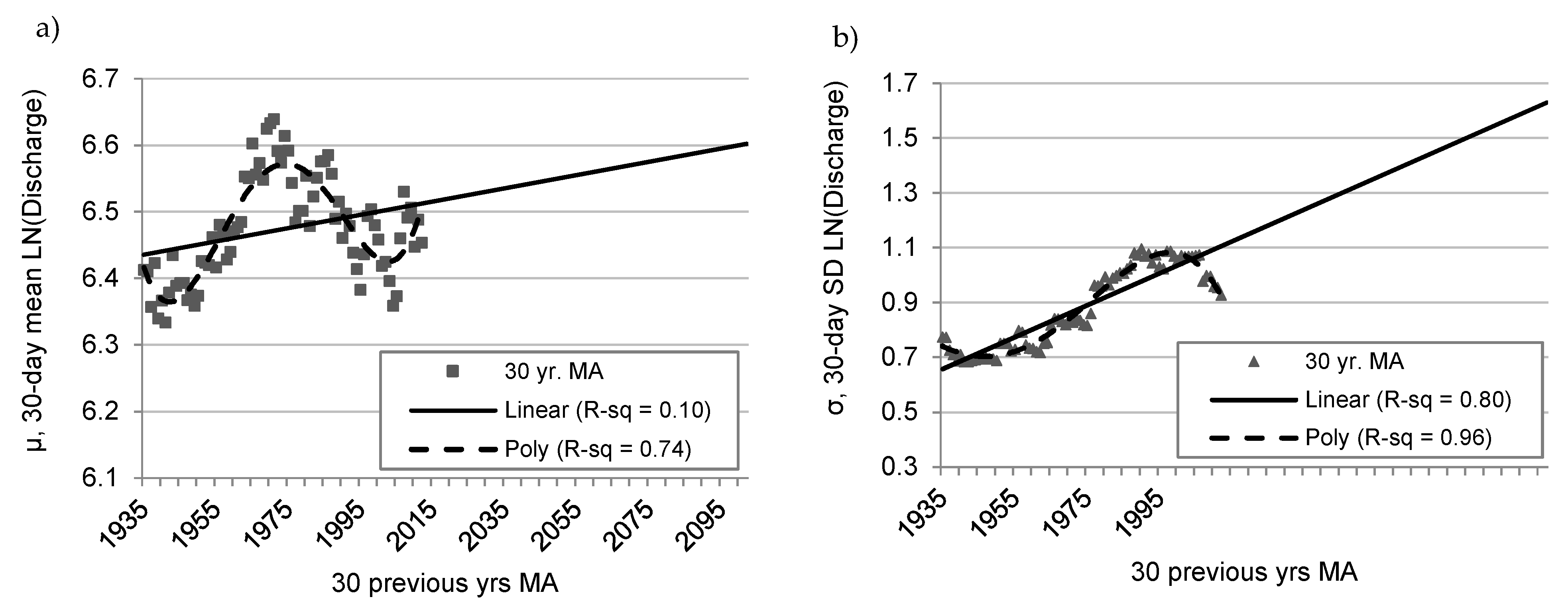
2.4.1. Trends in Mean and Standard Deviation of Flood Flows for the Historic Period (1905–2012)
We examined trends in the historical data, and projections based on those trends, to help establish a level of confidence in the future GCM-based projections. Studies examining climate trends often describe the factor of interest (e.g., precipitation, temperature, streamflow, etc.) in terms of the mean and variability over a period of time, typically 20 to 40-year intervals (e.g., [
46,
47]). As such, we fit log-normal flood frequency curves to moving 30-year time periods and examine trends in the fitted parameters over the historic period. Since flood frequency methods in Bulletin 17B generally only use the peak flow in any given year, the number of data points was low and equivalent to the number of years analyzed. The small sample size associated with extreme events made conclusive trend analysis difficult [
48]. As a result, while we examined a 30-year moving average of the μ and σ of the peak discharge to investigate historical trends, results remain highly uncertain.
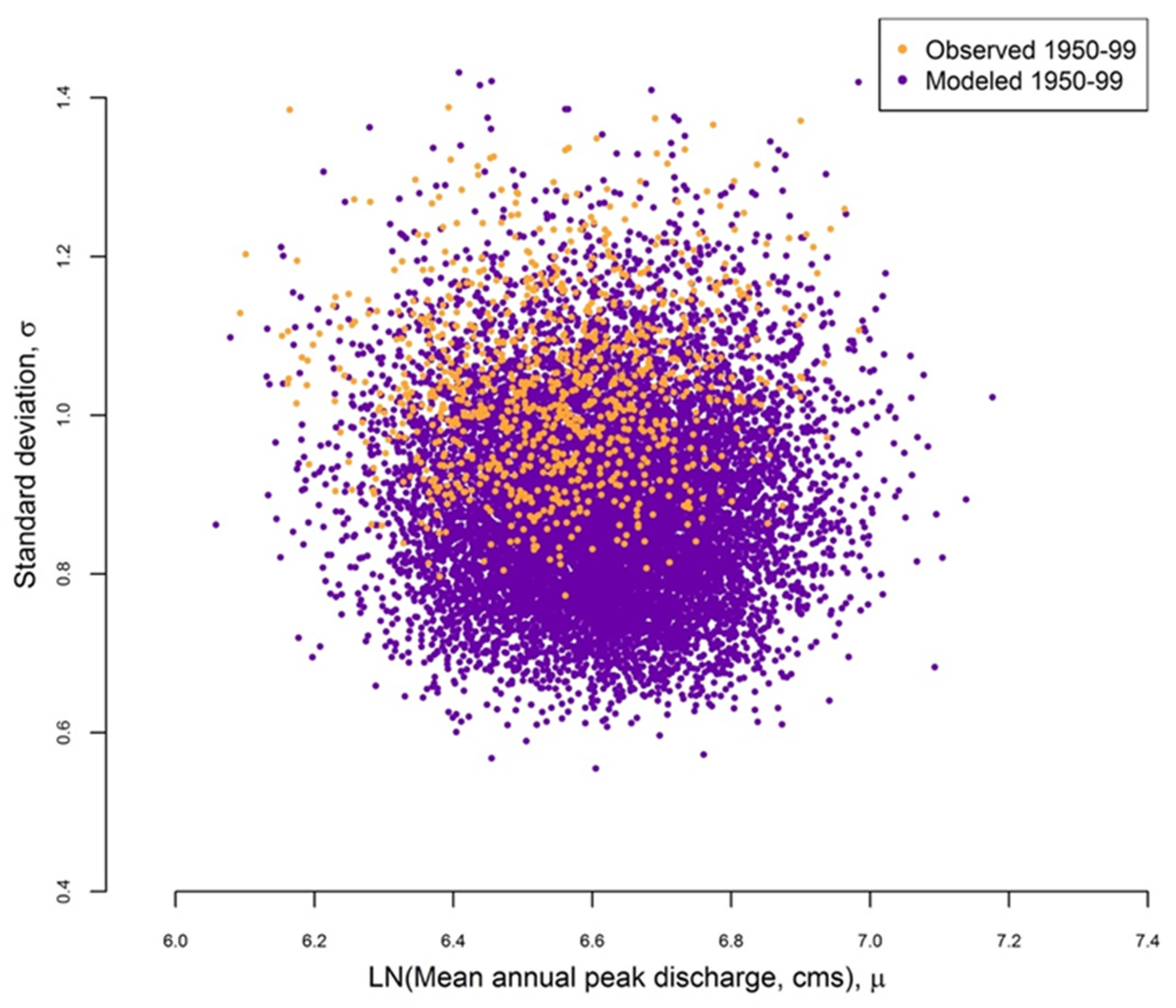
2.4.2. Comparison of Historic Observations and Historic GCM Simulations (1950–1999)
To assess the reliability of the GCM projections in projecting observed conditions, we compared the posterior intervals of the Bayesian flood frequency parameters (μ and σ) fit to the gauge observations and those fit to the GCM projections forced with observed historical emissions scenarios from 1950–1999.
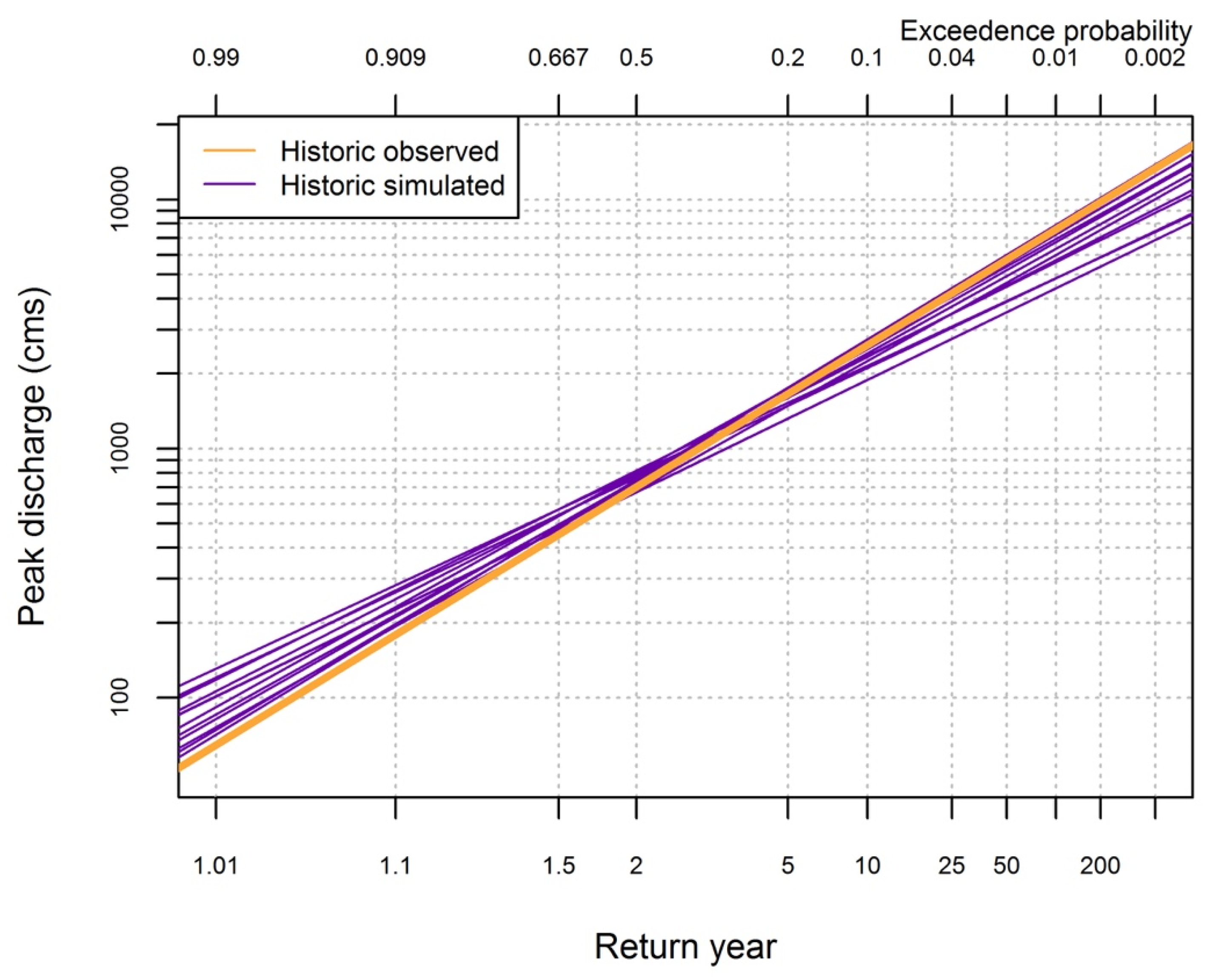
2.4.3. Comparison of Historic Observations (1905–2012) and GCM Projections (2000–2099)
Lastly in developing the plausible impact range, for the historic observed and twelve future projected peak flow datasets (
Figure 6), we generated 10,000 Markov chain samples of (μ, σ) combinations representing flood frequency curves. The resulting 120,000 parameter sets derived from the future GCM projections defined our plausible range of future flood regimes. We compared the posterior intervals of the parameter sets derived from future GCMs to those derived from the historic record to assess potential hydrologic responses to climate change.
2.5. Robustness of Current Systems and Management Strategies
In the last step of the bottom-up decision-making approach, we combined the vulnerability and impact assessment to determine the robustness of the current system and proposed management strategies. Consistent with Lempert, et al. [
20] we defined robust strategies as those that perform reasonably well compared to the alternatives across a wide range of plausible scenarios. As an indicator of the robustness, we calculated the percentage of the draws from the posterior flood frequencies parameter sets below an established vulnerability threshold (Equation (3)):
A robustness value of one indicates that the full range of flood regimes lies below the threshold, and thus the system is not vulnerable to exceeding the decision threshold. On the other end of the spectrum, a robustness value of zero indicates that the system fails to meet the performance threshold under any of the plausible scenarios, making it extremely vulnerable to future conditions.
We used two different robustness thresholds, one a measure of flood risk (EAD) and the other a measure of cost-effectiveness (BCR). We assessed the robustness of the current system and management strategies in terms of the EAD threshold of
$38 million, by first developing EAD response functions for each of the management strategies using the same methods described in
Section 2.2. We then determined how many MCMC parameter sets lie above and below the threshold. In addition, we developed climate response surfaces of the BCR (Equation (4)) for each of the management strategies under different flood regimes, to assess their cost-effectiveness:
where BCR is the benefit–cost ratio (
$/
$), EAD
WO is the EAD under Without Project conditions, EAD
manage is the EAD under one of the management strategies, r is the discount rate, t is life of the strategy, and cost is the cost of the management strategy.
Assessment of the BCR presented difficulties when trying to align the spatial extent of costs and benefits. We measured benefits in terms of EAD reduction within the American River Basin, however the cost estimates [
27] included all projects located within the lower Sacramento region, of which the American River is a sub-basin. As such, the cost estimates included projects outside of the American basin, some of which would influence EAD within the American basin (e.g., expansion of Yolo Bypass) and some of which only produce benefits outside the American basin (e.g., mainstem levee improvements downstream of the confluence of the American). In addition, the projects included in the costs produce benefits outside of the American Basin, which are not included in the benefits calculation. To roughly address the incongruence with costs and benefits, similar to the EAD threshold, we set the BCR decision threshold to the BCR of the Combined strategy under historical flood conditions, namely 0.2 [
27].
We set the discount rate to 7%, as recommended by the Federal Emergency Management Agency for public investments [
49], and the life of the project to 50 years based on the CVFPP planning horizon [
50]. Further, we conservatively used the high cost estimate for each strategy (
Table 2).
4. Discussion
The potential for changes in flood regimes due to climate change, in combination with the deep limitations of climate projections, necessitates rethinking how we make flood risk management decisions. While bottom-up climate assessments hold promises as a new way to view water resources management under climate change, few studies have carried out a full bottom-up approach to flood risk management in practice. In addition, many options exist within the broadly outlined approaches in the literature [
5,
15,
16,
17,
20] that need to be explored further. In developing a bottom-up climate assessment of flood risk for the American River flood management system, we identified several key ideas about both the bottom-up methodology and about flood risk within the American River system, with the goal of establishing a methodology that will aid water managers everywhere to better understand the hydrologic conditions that push a flood management system into a vulnerable state. We begin our discussion around the methodology employed, and then discuss the results for the American River basin in particular.
The methods used for the sensitivity and vulnerability assessment allow water managers to identify the hydrologic conditions that shift the system into a vulnerable state, using only the historic data and models currently available in the American River basin. Our method of fitting EAD response curves to a grid of flood frequency curve parameters (μ, σ) provides a computationally efficient method to assess the sensitivity of a system to a large range of potential flood regimes. However, this method does have limitations. Some accuracy is lost in fitting a linear model to a relatively small number of HEC-FDA runs, particularly at the lowest and highest range of μ, σ combinations. However, the R2 value for these equations fitted to the FDA model runs, range from 0.79 to 0.87, providing an adequate fit for a reconnaissance level pre-project planning analysis, such as presented in the 2012 CVFPP.
We used the EAD under the CVFPP strategy moving forward as a simple, justifiable method to determine the EAD vulnerability threshold, but many bottom-up approaches emphasize the importance of including stakeholders in process, particularly the vulnerability assessment [
51,
52,
53]. Such a process might have revealed metrics of performance beyond EAD that could have been evaluated using the methodology developed through this research. Unfortunately, the time required to collaboratively establish acceptable risk thresholds is beyond the scope of our work. We acknowledge the lack of stakeholder participation as a shortcoming in our case study.
To capture some of the uncertainty associated with the future projections and incorporate it into the decision-making process, we used Bayesian techniques to develop a wide range of plausible flood frequency regimes characterized by their statistical parameters, μ and σ. Using draws from the posterior parameter sets in combination with the climate response surfaces enabled us to quickly calculate the EAD under thousands of plausible future flood regimes. The Bayesian analysis also lends itself to a variety of techniques to combine the historical and future data depending on its uncertainty and the decision at hand. For example, while we used non-informative priors throughout the study, it is possible to inform future flood frequency parameters with prior information based on the historical data or to weight GCMs based on their performance in projecting historic flood regimes, or other criteria. Determination of the plausible range of future scenarios would then incorporate, and place weight on, the historical record. In addition, rather than examining the 12 sets of future projections in isolation, we could use a hierarchical Bayesian model to combine the projections from different GCMs and emissions scenarios, and then examine the hyper-parameters that guide μi and σi, the posterior flood frequency parameters for each set of future projections. Furthermore, adding the skew parameter, ϒ, to the Bayesian analysis in order to fit LP3 distributions to the historic and future data, could improve the fit of the distribution, but it could also add more uncertainty with the additional parameter.
Assessing the proposed management strategies based on two different robustness parameters demonstrated how the climate response surfaces can be adjusted for different metrics, as well as the importance of examining all pertinent criteria for decision-making. Our assessment based on EAD demonstrated the extent to which the management strategies increase the robustness of the systems, but it only examines flood risk benefits without examining cost of the strategies. Adding costs into the analysis, as well as the net benefits over the life of the project, rather than average damages (EAD), provided an alternate perspective on the cost-effectiveness of the projects. Nonetheless, these two metrics only address the primary goal of the CVFPP, to reduce flood risk, and neglect to consider the three sub-goals, namely to improve operations and maintenance; promote ecosystem functions; improve institutional support; and promote multi-benefit projects. Similar climate response surfaces could be developed for metrics to assess the three sub-goals of the CVFPP.
Our case study demonstration of a bottom-up methodology also revealed interesting points regarding flood risk within the American River system and the robustness of proposed management actions. We found that the EAD of the American River flood management system is highly sensitive to small changes in the flood frequency parameters, which brings up two points of concern. First, real changes in the flood regime due to nonstationarity could result in very different damage scenarios for the basin. Secondly, considering the uncertainty associated with flood frequency parameters, even those calculated with observed gauge records, water managers must use caution in basing decisions on the median or mean EAD without considering the uncertainty of the calculation and sensitivity of EAD to the frequency parameters.
In terms of vulnerability, we found that the current system operates in a vulnerable state with a median EAD above the threshold EAD, as expected. The vulnerability of the flood management system to current conditions provided the impetus to invest in improving the system through the CVFPP management strategy.
To increase the utility of the vulnerability assessment, we used historic observed and future project hydrologic data to develop a plausible range of future flood regimes and establish our confidence in that range. Our results demonstrated poor skill in the ability of GCM model runs forced with observed parameters to capture the statistical parameters of the observed historic flood regime of the American River. It may be possible to improve the model skill by applying a bias correction aimed specifically at addressing the errors in projecting extreme precipitation events.
Some correlation was found between future model projections and trends in the historic data; however, trends based on the historic data exhibit a high degree of uncertainty due to the limited length of the gauge record. Further, we in no way demonstrate that the historic trend in increased flood regime intensity is linked to anthropogenic climatic changes. Nonetheless, both the future GCM projections and historic data trends indicate a similar increase in the flood frequency mean and standard deviation over time. These results are also in agreement with the physical science governing floods under climate change and direct output from the GCMs, which suggest warmer winters with more precipitation in the Sierra Nevada mountain range [
2,
54,
55].
Our results also highlight differences in the robustness of different flood management strategies in the CVFPP, depending on whether robustness is measured in terms of flood risk (EAD) or cost-effectiveness (BCR). The Enhance System strategy, which included the greatest focus on nature-based strategies, provides the greatest robustness in terms of EAD, and is also the most expensive strategy. Taking project costs into consideration, the Protect Communities strategy exhibits the greatest robustness in terms its ability to maintain a BCR above the threshold for the largest portion of the plausible future range. The Combined strategy exhibited the second highest robustness indicator values for both metrics, and is also the second most expensive strategy.
The results of the robustness assessment lead to important planning considerations. While all of the proposed strategies offer substantial gains in EAD robustness under historic hydrological conditions, the robustness drops drastically when considering the plausible range of future climate impacts. As such, decision-making processes that neglect to consider future impacts run the danger of implementing strategies that do not reduce risk as much as expected. Alternatively, the cost-effectiveness of the management strategies initially increases in value under more extreme flood conditions. As such, some management strategies may become more financially appealing when future hydrologic conditions are taken into consideration.
While our results describe the conditions that may favor one strategy over another, the uncertainty associated with climate change and the wide plausible range of future conditions say little to nothing about which conditions we expect to occur in the future. However, over the course of the long implementation time (15–40 years) for the CVFPP strategies, advances in modeling, data, and analysis methods may allow us to track changes in observed flood frequency, narrow the plausible range of future conditions by decreasing uncertainty, and/or better describe uncertainty and associate probabilities with future conditions. As we gain such knowledge, we can adapt our decision-making process and management strategies to the expected future conditions.
5. Conclusions
The bottom-up methodology addresses arguably the two largest challenges facing future flood management, namely, the lack of: (1) Climate projections that can reliably represent historic conditions at the temporal and spatial resolution required for flood frequency analysis, and (2) methods to tailor climate projections into information useful to flood managers. Beginning the climate assessment process from the bottom-up enabled us to describe the sensitivity and vulnerability of the system to changes in flood regime, using only historic data. The climate response surfaces provide flood mangers with a visual representation of the sensitivity and vulnerability of the system. On their own, these response surfaces can be used to assess whether the current system is operating above or below vulnerability thresholds, how flood risk might change under different flood regimes, as well as how different management strategies might affect system vulnerabilities. Furthermore, by combining the response surfaces with future climate projections, we can assess the robustness of the current system and management strategies in terms of their ability to meet a performance threshold under a large portion of the plausible range of future conditions.
Our case study of the CVFPP in the American River basin provided an opportunity to demonstrate the utility of bottom-up methods, while yielding insight into the sensitivity, vulnerability, and robustness of the American River basin and management strategies proposed in the CVFPP. Our analysis intentionally limited data sources and models to those already included in the 2012 CVFPP, making it relatively easy to expand to the larger Central Valley planning region and/or narrow for more detailed robustness assessments of the refined set of management actions included in the Updated 2017 CVFPP [
56]. As the planning and implementation process for the CVFPP moves forward and more money is at stake, the importance of considering climate impacts increases, along with the consequences of not considering climate impacts.
While bottom-up approaches hold promise for future water resources decision-making, very few applications exist in practice and many questions remain regarding the specific methods to use. This leads the way for many potential avenues of future work related specifically to this study and bottom-up climate assessment more generally. In relation to climate risk assessment for the CVFPP, we recommend further work to: (a) Include public participation in identifying threshold metrics and levels; (b) include other metrics besides those focused on EAD (i.e., those that address the sub-goals of the CVFPP); (c) consider different methods to combine historic and future data (i.e., informative priors of future projections based on historical data); and (d) consider other sources of uncertainty and nonstationarity (e.g., population growth and land change). More generally, the field of climate adaptation could benefit tremendously from more on-the-ground examples of climate risk assessment and adaptation planning.