Sustainable Water Resources Management in an Arid Area Using a Coupled Optimization-Simulation Modeling

Abstract

Severe water scarcity in recent years has magnified the economic, social, and environmental significance of water stress globally, making optimal planning in water resources necessary for sustainable socio-economic development. One of the regions that is most affected by this is the Sistan region and its Hamoun wetland, located in south-east Iran. Water policies are essential to sustain current basin ecosystem services, maintaining a balance between conflicting demands from agriculture and the protection of wetland ecosystems. In the present study, a multi-objective optimization model is linked with the Water Evaluation and Planning (WEAP) software to optimize water allocation decisions over multiple years. We formulate and parameterize a multi-objective optimization problem where the net economic benefit from agriculture and the supply of environmental requirements were maximized, to analyze the trade-off between different stakeholders. This problem is modeled and solved for the study area with detailed agricultural, socio-economic, and environmental data for 30 years and quantification of ecosystem services. By plotting Pareto sets, we investigate the trade-offs between the two conflicting objectives and evaluate a possible compromise. The results are analyzed by comparing purely economic versus multi-objective scenarios on the Pareto front. Finally, the disadvantages and advantages of these scenarios are also qualitatively described to help the decision process for water resources managers.

1. Introduction

Approximately 30% of the world’s total land resources consist of arid and semi-arid regions, and water scarcity is a major barrier to social and economic development in these areas [1]. The main concerns in the allocation of water resources within the sustainable development goals (SDG) approach are achieving maximum use for society, the environment, and the economy while minimizing conflicts among different stakeholders. Health, environmental, political, social, economic, and sustainability concerns increase the need to integrate these problems into management solutions [2]. This relevance of better water management to achieve SDGs is increasingly important globally, where according to [3], half a billion people now live under severe water scarcity, and 4 billion in water scarcity at least one month a year.

To increase the efficiency of water resources consumption for different purposes, applying compromise policies for water allocation in a form of modeling multi-objective systems is necessary. Simulation is recognized as a fast and efficient means for evaluating the performance of water resources systems including water transfer projects. Presently, there are various types of simulation models in interactive graphics interfaces available for studying river planning and management issues that are also available to facilitate stakeholder participation in the planning and decision process [4]. Much research has been done to plan resource management strategies in each of these models, such as Modeling and Simulation (MODSIM) [5,6], MIKE BASIN [7], River Basin Simulation Model (RIBASIM) [8,9,10], and Water Evaluation and Planning system (WEAP) [11,12,13,14]. They usually adopt predefined reservoir operation rules or single-period optimization programs to allocate optimal water resources among conflicting consumers. Hence, they cannot use multi-period optimization to determine the optimum size and performance of system components [15].

In recent years, multi-period optimization methods and the introduction of the meta-heuristic methods has been used in water resources management [16,17]. Heuristics are more easily programmed, and can determine a near-optimal solution. However, in some cases, the results may be far from optimal solution and adaptation to new situations is difficult [18]. Also, in water allocation issues where the complexities of the system are high and the system involves a large number of physical components as well as resource supply priorities and consumer demand priorities, the use of optimization models alone faces difficulties. Hence, the water resource systems modeling may be extended beyond the optimization of water allocation in a multi-supply and/or multi-demand system for which the solution approaches demand more detailed simulation models need to be accounted for [19].

Meta-heuristic optimization algorithms can easily be linked to computer-aided Decision Support Systems (DSS) to simulate water system processes without the need for variables, functions, and relevant computer codes to be consistent and accessible to users [20]. These features make it possible to use more accurate simulation models that can better represent simulated hydrological, environmental, legal, administrative, and economic processes. In recent years, researchers have applied linkage between optimization and simulation tools in water resources management. Mousavi et al. [15] linked WEAP simulation model, benefiting from fast, single-period linear programming, to the multi-objective particle swarm optimization (MOPSO) for multi-period optimization. The objective functions were minimizing the sizes of the project’s infrastructures and maximizing the reliability of supplying water to agricultural lands. In the study presented by [21], the WEAP-NSGA-II coupling model was developed in order to apply the hedging policy in a two-reservoir system, including Gavoshan and Shohada dams, located in the west of Iran. Trying to better represent socio-economic issues, hydro-economic modeling has been linked with simulation modules for guiding and implementing various water policy issues such as climate change impacts on water resources and agricultural production [22], optimizing infrastructural projects and measures and operation policies [23], sizing the planed water storage and transfer components of a river basin system and to allocate water resources [24]. However, hydro-economic models can be poor tools to simulate actual water markets since individual agent behavior and transaction costs cannot be represented easily for some non-monetary human and environmental health [25]. This paper presents a multi-objective optimization-simulation tool for analyzing the economic as well as ecological conditions of the Sistan arid-region, and for optimizing water allocation. This goal was achieved by linking a Multi-Objective Genetic Algorithm (MOGA) and the WEAP water allocation decision support system. The design variables of the problem consist of the cultivated area, cropping pattern and wetland inflow requirements. A multi-objective optimization has been applied in scenarios involving two incompatible objectives, maximizing long-term net economic benefit and maximizing water flow to the wetland.

The proposed WEAP-MOGA simulation-optimization approach takes advantage of both positive aspects of WEAP and a multi-objective meta-heuristic optimization algorithm. WEAP is a well-known and widely used decision support system employing a priority-based water allocation scheme. Therefore, it is sufficiently general, easy to use and reliable because there are several features in WEAP that can be tweaked depending on the problem under consideration. From an algorithmic perspective, the meta-heuristic approach used in this optimization modeling framework is a hybrid approach that combines fast linear programming (i.e. uses linear programs to solve single-period water allocation problems in WEAP), and multi-period optimization in a multi-objective genetic algorithm. This hybrid algorithm is a novel and practical solution to solve large-scale, nonlinear optimization problems common in real-world water management problems.

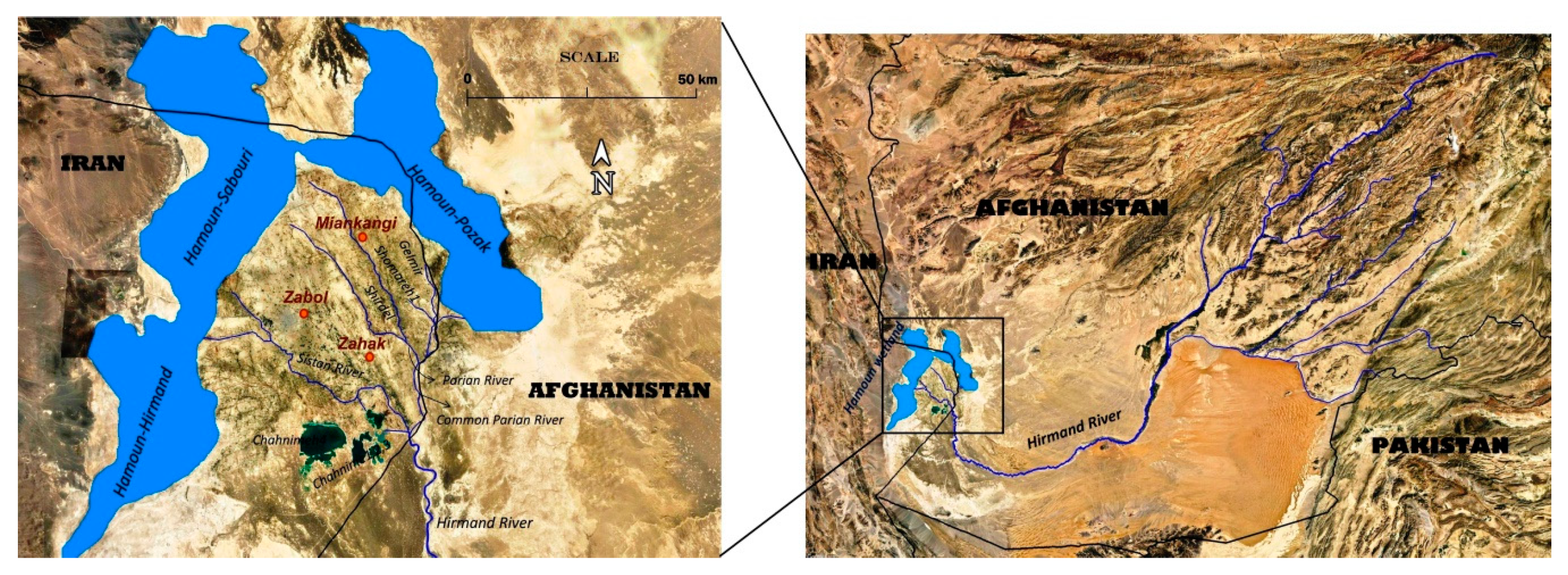
Study Area

The Sistan region is located close to the Iranian border with Pakistan and Afghanistan, in the south-eastern part of Iran, Figure 1.

The climate of the region is almost arid. The annual average precipitation is less than 60 mm, and the mean potential evaporation rate exceeds 4000 mm per year [26]. The Sistan region, in which the Hamoun wetlands are located, has attracted many researchers in recent years. For centuries, water demands of the region have been supplied by the Hirmand river (also known as Helmand), which begins in Helmand Province of Afghanistan [27]. At the point before the border between Iran and Afghanistan, the Hirmand river is divided into two branches: the Parian border river and the Sistan River. The Parian river supplies the water demand of the Miankangi land and also the cities and villages located in the catchment, and the water of the Sistan River is consumed by the Zahak and Zabol lands and residents of the cities and villages of these two catchments. The remaining water of these rivers eventually flows into the Hamoun wetland.

The region’s three water user groups include domestic, agricultural and environmental uses (Hamoun wetland). The Hirmand river is the domestic water supplier for around one million people in the area. Chah-Nimeh storages are one of the other important sources of water in the Sistan region. Chah-Nimeh reservoirs contain natural and big cavities and a synthetic storage in the south-eastern of Sistan Plain. Natural storages are called Chah-Nimeh123 and artificial storage is called Chah-Nimeh4 connected with a canal. Since these storages supply drinking water to cities and villages in the region, they play an important role in the regional water resources system. Agriculture is the main occupation of the people of Sistan, which is heavily influenced by the Hirmand river. Hamoun wetland, the largest freshwater ecosystem on the Iran plateau, is one of the first wetlands defined by the Ramsar Convention (The Convention on Wetlands, called the Ramsar Convention, is the intergovernmental treaty that provides the framework for the conservation and wise use of wetlands and their resources. (https://www.ramsar.org/)). Hamoun wetland has different ecological services. One of the most important services is sandstorm prevention. The dust storm in the Sistan area affects air quality, human health, ecosystems, and the environment. This phenomenon is commonly known as the "wind of 120 days," which causes heavy dust storms throughout the region between May and August [28]. The severe water deficit in recent years has multiplied the economic and environmental significance of water resources in the study area. A well-designed water resource planning can play a key role in providing a path to sustainable socio-economic development.

As the main water user, the agricultural sector of the region has significant impacts on socio-economic and ecological conditions. On the one hand, lack of desirable conditions in agriculture development indices [29], and the fact that current cropping patterns in the area are not optimal with respect to water use [30]. On the other hand, recent droughts in Hamoun wetland with high importance for its ecosystem services have highlighted the undesirable conditions for these two important competing sectors [31]. In recent years, some studies have attempted to optimize the allocation of water resources in the Sistan region to achieve the optimal cropping pattern and greater agricultural productivity [32,33]. There are also studies that aim to address the environmental challenges and drought hazard and strategize to revitalize the Hamoon Wetland [34,35,36]. Nevertheless, the interaction of water use between the agricultural and environmental needs has not been investigated for the Sistan region. In the present study, a model-based optimization is used to analyze the trade-off between agricultural and environmental systems.

Due to the complexity of prioritizing demands over the whole Sistan region, time-varying hydrological features, lack of accurate information on water requirements, inaccuracy of some effective parameters such as water consumption and return flow, recent studies have been conducted either for short periods and have modeled only a small part of the region [33,37]. To overcome these complexities in Sistan region, a multi-objective optimization model is linked with the integrated water resources management model (WEAP) to make a coupled model [11,38]. We formulate and use a multi-objective function, where the net economic benefit of the region and the supply of environmental requirements were maximized, in order to analyze the competition between different stakeholders. The problem is modeled and implemented for the study area with detailed socio-economic and environmental data. Since reliable future predictions are not available because of dynamic upstream development scenarios and climate change, we use past water inflow data to represent future variation, based on an approximately thirty-year climate period. Hence, the historical water inflow data of the past 30 years have been used to model the next 30 years. Sensitivity analysis was also performed to investigate the sensitivity of the results to the inflow water values. Since the aim here in is not real-time control of water systems but that of strategic planning for water resources management, this back casting is insightful also in understanding past possibilities.

2. Methods and Materials

In this section, the WEAP model and multi-objective optimization model are described in detail separately. We described the WEAP model with various components of water system (Section 2.1). In Section 2.2, multi-objective model is described in detail which includes the economic (Section 2.2.1) and the environmental (Section 2.2.2) objective functions, and the algorithm used in this study to solve two-objective optimization (Section 2.2.3). The constraints applied to the model implementation process are described in Section 2.3. Finally, coupled simulation-optimization model is presented in Section 2.4 with explanation of variables and parameters applied.

2.1. WEAP Model

The WEAP software tool developed by the Stockholm Environmental Institute is based on water balance and is capable of simulating some of the water system components such as supply sources, rainfall-runoff, water demands, water quality, and system constraints. The model is comprehensive, straightforward and user friendly that even stakeholders (e.g., water managers) can easily participate in the modeling process [39].

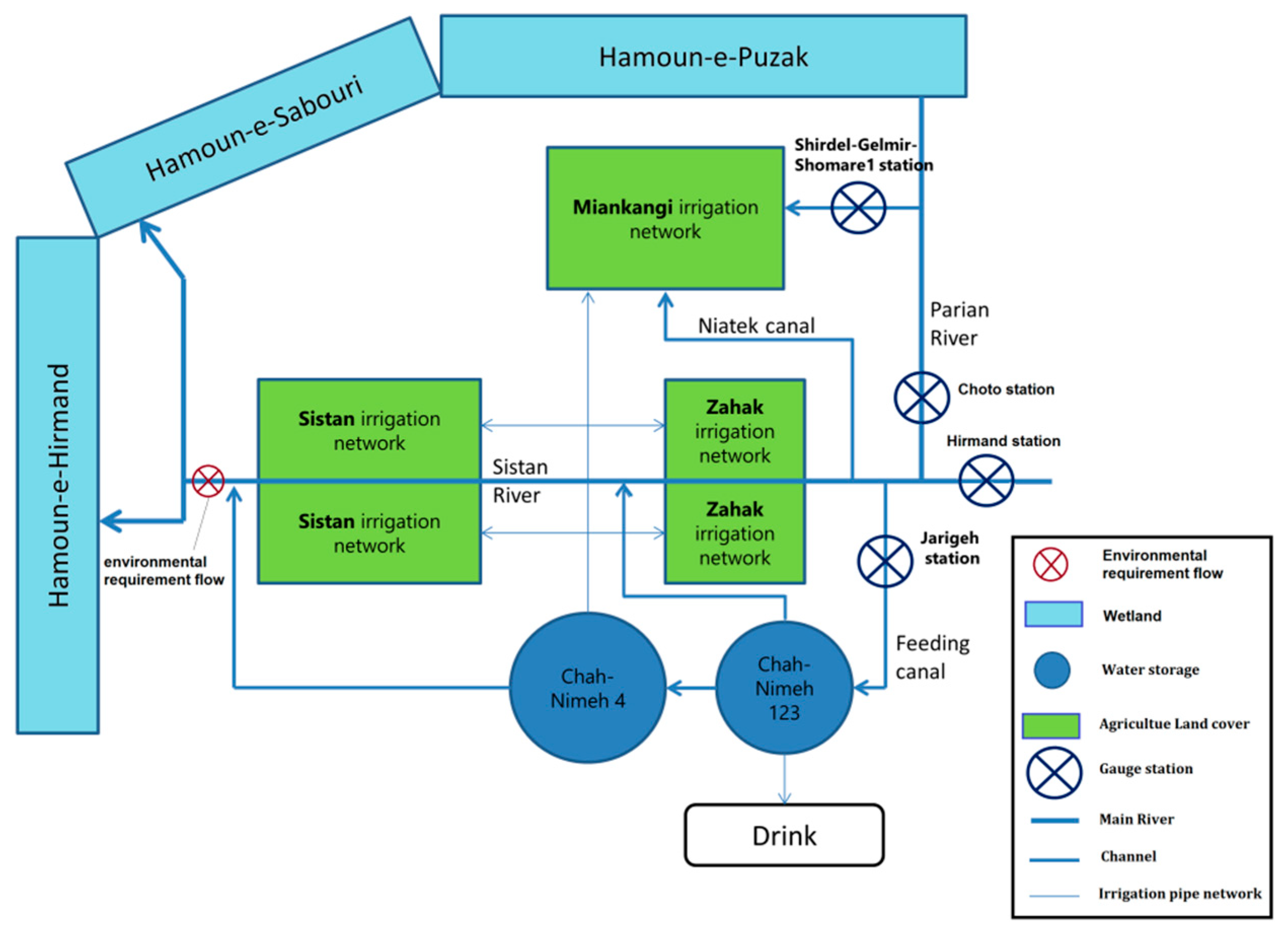
In this research, WEAP data requirements are reservoir physical and operational characteristics, hydrological parameters, land use, crop data, climatic data, irrigation, different water demand, and demographic details. For modeling purposes, the Hirmand river basin located in Iran contains three agricultural catchment nodes according to channels and supply resources for each catchment node and drainage network; see also Figure 2. Each catchment node was subdivided into individual crop types. According to extremely low precipitation (50 mm/yr.) of the region and lack of essential data, the “Irrigation Demands Method” version of the “Simplified Coefficient Approach” is chosen to simulate the catchment processes. In this method, crop requirements are calculated assuming a demand site with simplified agro-hydrological processes such as precipitation, evapotranspiration, and rainfed agriculture. Non-agricultural land classes can be included as well [40]. The Chah-Nimeh storages were implemented as a “Reservoir node” with required inputs such as storage capacity, volume-elevation curve, monthly evaporation rate, and operation data entered into WEAP. A minimum flow requirement was defined as the minimum flow required along a river to meet water quality, fish and wildlife, navigation, recreation, downstream the Sistan River. This demand was set with a “flow requirement node” where water flows into the Hamoun wetland. Figure 2 indicates the schematic model of the water system in Sistan region, Iran.

WEAP monthly calculations follow the order including (1) Annual demand and monthly supply requirements for each water user sector and flow requirement (2) Inflows and outflows of water for every node and link in the system. The WEAP model calculates a water balance for every node and link in the system at each time step. Nodes are connected by flow links that represent the natural or synthetic water conduits such as river channels, canals, and pipelines. These lines include rivers, diversions, and transmission links, and return flow links. Each period is independent of the previous, except for reservoir storage. It means that all the water entering the system in a given period is either stored in a river, a reservoir, or leaves the system by the end of that period. All flows are assumed to occur instantaneously and a demand section can withdraw water from the river, consume some, and return the remaining to the river, all in the same time step [14]. In the case of Sistan region, monthly time steps were chosen to run the model. The model computes water inflows to and outflows from every node and link in the system for a given month. This includes calculating withdrawals from supply sources to meet demands. A mixed-integer linear program (MILP) is solved to maximize the demand satisfaction of different sectors, subject to demand priorities, supply preferences, mass balance, and other constraints. WEAP uses an open source linear program solver called LPSolve.

The WEAP model was calibrated on 14-year historical streamflow data of two stations for the period 1995–2000. The period 2001–2008 was then used for validation. Calibration parameters were domestic consumption and effective precipitation. Domestic consumption is the percentage of water consumed by domestic users that is lost to the system. A uniform monthly rate of consumption was used in our case. According to the experts’ opinions at the University of Sistan and Balouchestan and Zabol Agriculture Bureau, domestic consumption is between 10% to 20% of total water supply. Thus, we used this range to calibrate the model.

Effective precipitation is the percentage of rainfall available for evapotranspiration. Mohammadghasemi et al. [41] neglected to value of the effective rainfall for different crops in Sistan region due to no information available on soil moisture. US Bureau of Reclamation Method [42], which does not require soil moisture information, is suggested for arid and semi-arid regions and estimates effective precipitation based on mean monthly precipitation of the five past consecutive years. The parameter was applied in monthly time series. Since there is no significant difference among various monthly precipitation means during the modeling years, the calibration range for different months was set the same, between 75% and 100% [42]. All other parameters included climatic data, historical inflow data, historical agriculture land cover, crops yields, prices and costs, human population, domestic consumption rate, and storages and wetland characteristics were obtained from reports from the Agriculture-Jahad Organization, Plan and Budget Organization, the Regional Water Company, as well as reports from the Ministry of Energy and also interviews with the governmental experts.

2.2. Multi-Objective Optimization Model

The formulated multi-objective optimization model includes two objectives: (1) the economic and (2) environmental objectives.

2.2.1. Economic Objective (${\mathrm{F}}_1$)

The economic function, in terms of net income in US dollar equivalents, consists of two sub-divisions of agriculture profits and Hamoun wetland’s ecological services profits.

$${\mathrm{F}}_1={\mathrm{E}}_{\mathrm{Agr}}+{\mathrm{E}}_{\mathrm{Wetland}},$$

(1)

where ${\mathrm{F}}_1$ is the economic function, ${\mathrm{E}}_{\mathrm{Agr}}$ stands for net agriculture profits, and ${\mathrm{E}}_{\mathrm{Wetland}}$ is wetland profits contains consolidation of soil against wind and fisheries.

Agriculture Profits (${\mathrm{E}}_{\mathrm{Agr}}$)

The profit from agricultural activities for wheat, barley, grapes, melons, sorghum, tomatoes, and alfalfa in the Miankangi, Zahak, and Sistan lands is defined as:

$${\mathrm{E}}_{\mathrm{Agr}}={\sum }_{\mathrm{t}}\left[{\sum }_{\mathrm{i}}{\sum }_{\mathrm{cr}}\left({\mathrm{A}}_{\mathrm{i},\mathrm{cr},\mathrm{t}}\times \left({\mathrm{Y}}_{\mathrm{i},\mathrm{cr},\mathrm{t}}\times {\mathrm{P}}_{\mathrm{i},\mathrm{cr},\mathrm{t}}-{\mathrm{C}}_{\mathrm{i},\mathrm{cr},\mathrm{t}}\right)\right)\right],$$

(2)

where t is the time step, i is the parameter related to different agricultural catchments, cr is the crop type parameter, Y is the crop yield (kg/ha), P is the crop price (US/kg), A is the crop cultivated area, C is the cost of crop production. The crop yield Y (kg/ha) is calculated as:

$$\mathrm{Y}={\mathrm{Y}}_{\mathrm{p}}\times \left(1-{\mathrm{k}}_{\mathrm{y}}\left(1-\frac{{\mathrm{Et}}_{\mathrm{a}}}{{\mathrm{Et}}_{\mathrm{p}}}\right)\right),$$

(3)

where ${\mathrm{Et}}_{\mathrm{a}}$ is actual crop evapotranspiration (mm), ${\mathrm{k}}_{\mathrm{y}}$ is the seasonal factor (Non-dimensional) that defines how the yield changes under water stress conditions (i.e., when ${\mathrm{Et}}_{\mathrm{a}}$ is less than ${\mathrm{Et}}_{\mathrm{p}}$), Yp is the maximum potential yield given optimal supplies of water (Kg/ha), and Y is the actual yield given the available evapotranspiration (Kg/ha).

Wetland Profits (${\mathrm{E}}_{\mathrm{Wetland}}$)

Wetlands have unique environmental features that provide many products and services for habitats [43]. The methods for determining economic benefits associated with the environment are highly complex [44]. In engineering optimization approaches, the benefit objective function is used in many studies [17,45,46,47,48]. However, few of them have explicitly included environmental economic benefits [16,49,50,51]. One of the ways to create an environmental benefit objective function is to use the values obtained from the economic valuation of ecological and environmental services [49]. In this research, the results of a project carried out in [52] and research which has been supported by the Delft Cluster program [53] are used. In [39], the valuation of ecological services in different hydrological conditions of the Hamoun wetland was carried out. On the other hand, Meijer et al. [53] presented quantification of Hamoun wetland ecosystem services and made a relationship between the Hamoun wetland ecosystem and the Hamoun hydrology. Wetland services consist of two parts, (a) indirect use in prevention of sandstorms and (b) direct use by fisheries.

(a) Consolidation of Soil Against the Wind

According to the atmospheric conditions of the study area, an important function of the wetland is to prevent the formation of sandstorms. The notorious 120-days wind blows around May, June, July, and August at a wind force of 4–6 Beaufort [54]. The wetland ecosystem, by water covering on the surface of the wetland prevents sand harvesting by wind directly from the wetland bed. The perspective of ecosystem functions valuation by [52] is based on the lost interests and values method. To mitigate the damage caused by the storm, the government has taken actions such as planting tamarisk trees and mulching in part of the wetland that are not permanently inundated. For this reason, the costs avoided by the state for protecting one hectare of wetland areas from wind erosion were considered to be a benefit of this function. Also, Shahraki et al. [12] specified 50,000 hectares of Hamoun were exposed during a peak in crisis dust. According to a report by the Hamoon International Wetland Institute and the Zabol University, 25,000 hectares of this area is ranked first in the dewatering prioritization based on sandstorm control [55]. In this way, a relation was created between Hamoun benefits and inundated area of Hamoun during May, June, July, and August.

(b) Benefits from Fisheries

An approach similar to the drift method was used to establish a relationship between hydrology and ecology of the Hamoun wetland [54]. In this approach, hydrological parameters and ecological conditions were assessed for a reference scenario in which the wetland is in its fully appropriated water condition. The dynamic condition of fisheries is then expressed as a percentage of the reference condition for each combination of parameter values. To define the well-condition of Hamoun wetland, the data in 1975 was considered to be a reference. With assumption by [52], the maximum fish caught in full-water condition of the wetland is estimated around 9000 tons per year. Thus, the benefit from fisheries for each year is computed as a fraction of reference situation multiplied by the fish market value with respect to hydrologic condition and its parameter values. Based on an analysis of the reference situation (1970s), Beek et al. [56] identified hydrological parameters of key importance for the ecosystem condition. Because the ecosystem conditions cannot be determined for all possible values of these parameters, thresholds that delineate classes of parameter values are identified. The parameters identified as determinants for the fish ecosystem conditions are drought, spring flood, and fall area. The thresholds for each of these parameters have been determined. Drought is a moment that the total area of Hamoun (${\mathrm{A}}_{\mathrm{w}}$) is less than 10% of the maximum wetland area possible (${\mathrm{A}}_{\mathrm{t}}$). For spring flood, the total volume which should be entering the wetland between February and June is put at 2000 Million Cubic Meters (MCM). The fall area parameter is defined as the inundated area during October-January. A suitable threshold is that preferably 40% or more of the area should be inundated [54]. This is the result of the size of an average spring flood in the previous hydrological year. When the inundated area is below 40% of the total area, but still above 20% the effects on the ecosystem are less severe, than when the inundated area falls below 20%. Combining all parameters and thresholds considered in the present study led to 12 theoretical hydrological situations shown in

Table 1. Estimated effects for combination of parameter values [54].

Drought	Flood Spring	Area Fall	Percentage of Fish Harvested Relative to the Reference Situation
Aw < 0.1 At	>2000 MCM		Lower Boundary * (%)	Upper Boundary * (%)
Yes	Yes	>40%	100	100
		20%–40%	90	100
		<20%	20	90
	No	>40%	**	**
		20%–40%	30	80
		<20%	20	70
No	Yes	>40%	0	50
		20%–40%	0	50
		<20%	0	50
	No	>40%	**	**
		20%–40%	0	50
		<20%	0	50

* Boundaries are expressed in percentage of the fully appropriated 1975 reference situation. ** Assumed to be infeasible combinations of parameters.

; however, two of these are not considered possible in reality.

2.2.2. Environmental Objective (${\mathrm{F}}_2$)

The normalized Environmental function in Equation (4) is defined by the ratio of Hamoun wetland water inflow in the modeling period (${\mathrm{Q}}_{\mathrm{wet},\mathrm{t}}$, in cubic meters) to the total amount of water inflow into study area (${\mathrm{Q}}_{\mathrm{T}}$, in cubic meters) during modeling years of length T.

$${\mathrm{F}}_2=\left(\frac{{\sum }_{\mathrm{t}=1}^{\mathrm{T}}{\mathrm{Q}}_{\mathrm{wet},\mathrm{t}}}{{\mathrm{Q}}_{\mathrm{T}}}\right).$$

(4)

The variable ${\mathrm{Q}}_{\mathrm{T}}$ is data for the optimization representing total inflow into the considered case, set to historical inflow data from Hirmand station (Figure 2) and ${\mathrm{Q}}_{\mathrm{wet},\mathrm{t}}$ is a decision variable calculated by our WEAP implementation. Then, this value is imported in the optimization model to compute the environmental objective (${\mathrm{F}}_2$) and represents the amount directed into the Hamoun wetland in the same years. The model used in this study, by maximizing the function ${\mathrm{F}}_2$, seeks to optimize the water inflow of the Hamoun wetland during the modeled period.

2.2.3. Multi-Objective Genetic Algorithm (MOGA)

The multi-objective optimization problem is solved using a MOGA in MATLAB [57], which uses a weighted sum of the multiple objective functions to convert them to a scalar fitness function. Since the characteristic feature of the MOGA is that the weights of multi-objective functions are not constant, those are determined randomly for each selection. Accordingly, the search path in MOGA is not constant. A set of optimal Pareto solutions called a “tentative set” is maintained in the implementation of the MOGA, and only a certain number of individuals in these solutions are inherited for the next generation as elite individuals.

This algorithm consists of various steps including initialization, evaluation, selection, mutation, elitist strategy, termination test, and user selection. Each of these steps is briefly described below:

• Initialization: An initial population with a given number (${\mathrm{N}}_{\mathrm{pop}}=500$) of strings is generated.
• Evaluation: The values of the objective functions for each string are calculated in the second step and a tentative set of Pareto-optimal solutions is updated. It is worth noting that the algorithm and the WEAP software are linked in this step.
• Selection: The fitness function for each string is evaluated. Then, ${\mathrm{N}}_{\mathrm{pop}}/2$ pairs of strings from the population are selected based on following selection probability. Selection probability P(x) of a string x in a population pop is determined as:

$$\mathrm{P}\left(\mathrm{x}\right)=\frac{\mathrm{f}\left(\mathrm{x}\right)-{\mathrm{f}}_{\min }\left(\mathrm{pop}\right)}{{\sum }_{\mathrm{x}\in \mathrm{pop}}\left\{\mathrm{f}\left(\mathrm{x}\right)-{\mathrm{f}}_{\min }\left(\mathrm{pop}\right)\right\}},$$

(5)

where f(x) is the scalar fitness (i.e., objective) function consisting of weighted sum of the objective functions ${\mathrm{F}}_1$ and ${\mathrm{F}}_2$, and x contains the decision variables:

$${\mathrm{f}}_{\min }\left(\mathrm{x}\right)=\min \left\{\mathrm{f}\left(\mathrm{x}\right)| \mathrm{x}\in \mathrm{pop}\right\}$$

(6)

• Crossover: For each selected pair, two new strings are generated using the crossover operation. In this way, ${\mathrm{N}}_{\mathrm{pop}}$ new strings are generated at this step.
• Mutation: For a small sample of strings produced in the previous step, a mutation operation with a predetermined mutation probability is used.
• Elitist strategy:${ \mathrm{N}}_{\mathrm{elite}}$ strings produced by the jump operation are randomly removed and replaced by ${\mathrm{N}}_{\mathrm{elite}}$ strings randomly selected from a tentative set of Pareto-optimal solutions.
• Termination test: If predetermined stopping criteria are not satisfied, the algorithm will return to the evaluation step.
• User selection: The final set of Pareto-optimal solutions is shown to the decision makers (DMs). A selection of the solutions is carried out based on the preferences of DMs and stakeholders and the problem condition.

2.3. Model Constraints

The model constraints in the study area include structural, environmental, and crop-related constraints that are presented in the following.

2.3.1. Hydrological Classification of Basin Inflow in the Modeling Period

The hydrological classification is an objective process that is easily interpretable, explicitly handles uncertainty with methodological robustness, and provides definable class boundaries and target group membership [58]. The classifications represent the structure of relationships among groups with different stream flow. Hydrological classes provide a template for the generalization of hydrological responses to disturbances and classify the research and management needs [59]. This method can be applied to place individual streams into an interval concept to handle the uncertainty of the streamflow.

Due to the fact that the cropping pattern, land cover of cultivation and wetland environmental life are strongly dependent on the hydrological conditions of the region, it seems that presentation of the cropping pattern and ecological demands can be optimized and determined in different hydrological classifications. It means that same cropping patterns are assigned for same year types during the optimization process. In other words, the optimization algorithm generates the same variables for years with the same classification.

The hydrological conditions of the study area were classified according to the Streamflow Drought Index (SDI) presented by [60] in different years, and the cropping pattern of Sistan region was presented based on each classification. According to the SDI, it is assumed that a time series of monthly streamflow volumes ${\mathrm{Q}}_{\mathrm{ij}}$ is available where i denotes the hydrological year and j the month within that hydrological year (j = 1 for October and j = 12 for September).

$${\mathrm{q}}_{\mathrm{i}}={\displaystyle \sum }_{\mathrm{j}=1}^{12}{\mathrm{Q}}_{\mathrm{ij}},$$

(7)

where ${\mathrm{q}}_{\mathrm{i}}$ is the cumulative streamflow volume for the i-th hydrological year, i = 1,2, …, T, T is the number of years studied which is 30 years in this study. Based on cumulative streamflow volumes ${\mathrm{q}}_{\mathrm{i}}$ the SDI is defined for each of the i-th hydrological years as:

$${\mathrm{SDI}}_{\mathrm{i}}=\frac{{\mathrm{I}}_{\mathrm{i}}- \overline{\mathrm{I}}}{{\mathsf{\sigma }}_{\mathrm{I}}},$$

(8)

where ${\mathrm{I}}_{\mathrm{i}}=\ln {\mathrm{q}}_{\mathrm{i}}$ is the natural logarithm of cumulative streamflow with mean $\overline{\mathrm{I}}$ and standard deviation ${\mathsf{\sigma }}_{\mathrm{I}}$ as these statistics are estimated over a long period. Four states are considered which are denoted by an integer number ranging from 0 (non-drought) to 3 (extreme drought) and are defined through the criteria of

Table 2. Different states of hydrological drought based on SDI [60].

State	Description	Criterion
0	Non-drought	$\mathrm{SDI}\ge 0.0$
1	Mild drought	$-0.1\le \mathrm{SDI}\le 0.0$
2	Severe drought	$-2.0\le \mathrm{SDI}\le -1.0$
3	Extreme drought	$-2.0\ge \mathrm{SDI}$

.

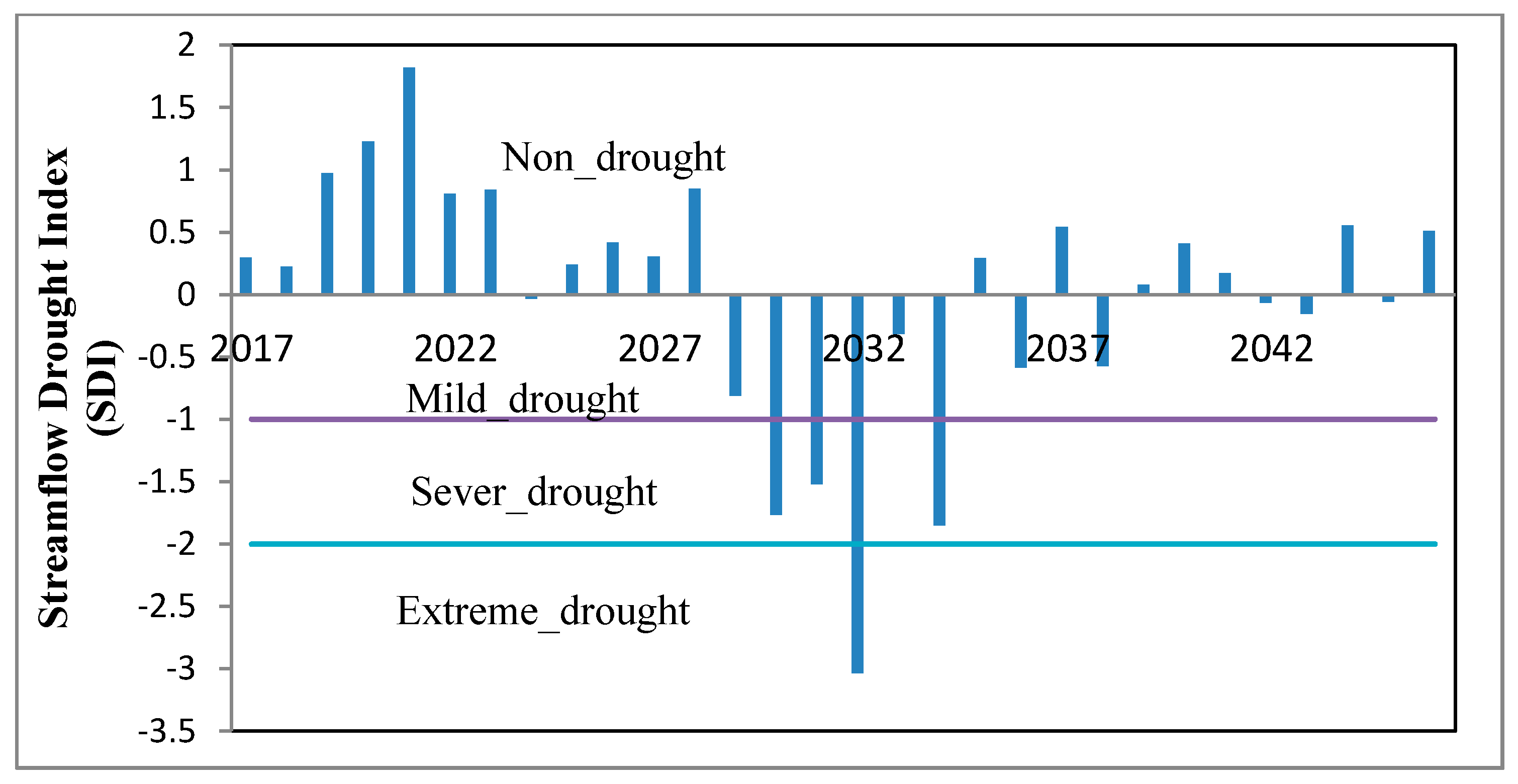
As noted, historical river flow data were used for future modeling. Therefore, the proposed model was implemented for the years 2017–2046 using the inflow water data of the Hirmand river from the years 1987–2017. According to the SDI, a hydrological classification was carried out for these 30 years of streamflow into the Sistan region. Based on these results, as shown in Figure 3, 18 years were found to be non-drought years (all years between 2017 and 2023, between 2025 and 2028, and in 2035, 2037, 2039, 2040, 2041, 2044, and 2046). The volume of annual inflow into the region in these hydrological conditions ranges from 1275 to 8594 MCM. It is also a mild drought for eight years (2024, 2033, 2036, 2038, 2039, 2042, 2043 and 2045) has an annual inflow of 519 to 1159 MCM. Also, severe droughts in 2030, 2031, 2034, and extreme drought in 2032 were calculated. Annual inflow in each of these years is 187, 244, 171, and 48 MCM, respectively.

2.3.2. Agricultural Constraints

The three irrigable lands in Sistan region are Sistan, Zahak and Miankangi lands with area 54,000, 49,000 and 32,000 hectares, respectively. Crops cultivated consist of wheat, barley, grapes, melon, sorghum, and vegetables. Sistan basin also has an irrigation efficiency of 34% [61].

According to four hydrological types in modeling period and seven crops, twenty-eight (4 × 7 = 28) decision variables (${\mathrm{CropArea}}_{\mathrm{H},\mathrm{cr}}$) have been used to optimize the crop area. ${\mathrm{CropArea}}_{\mathrm{H},\mathrm{L},\mathrm{cr}}$ expresses the cultivated area of crop “cr” during the years with hydrological class “H”. It is also assumed that different irrigable lands (Sistan, Zahak and Miankangi) have same crop mix or

$${\mathrm{CropArea}}_{\mathrm{H},\mathrm{L},\mathrm{cr}}={\mathrm{CropArea}}_{\mathrm{H},\mathrm{cr}}\frac{{\mathrm{IrrArea}}_{\mathrm{L}}}{{\sum }_{\mathrm{L}}{\mathrm{IrrArea}}_{\mathrm{L}}},$$

(9)

where ${\mathrm{IrrArea}}_{\mathrm{L}}$ is irrigable area in land “L”. This approach in effect certifies spatial equity among the agricultural lands in terms of production and opportunity for profit [62].

2.3.3. Environmental Goals in Reservoirs and Hamoun Wetland

The storage in the area includes two reservoirs called Chah-Nimeh123 and Chah-Nimeh4. According to the decisions of water resource planning managers, for the maintenance of environmental conditions, the minimum values for these two reservoirs are considered. Thus, the minimum reservoir of water in the Chah-Nimeh123 with a capacity of 670 MCM is 300 MCM, and in the Chah-Nimeh4 with a volume of 820 MCM, this amount is 200 MCM.

The annual flow requirements of Hamoun wetland are considered to be decision variable. These variables are assigned to the different hydrological classes during the optimization process. Therefore, four decision variables are generated to optimize the flow requirement of the wetland according to the four hydrological classes of modeled period. Based on the research presented by [63], the ideal environmental requirement of the Hamoun wetland was estimated at 1250 MCM per year. On the other hand, the environmental water right of the Hamoun wetland from the Chah-Nimeh reservoirs is 60 MCM. This amount has been set and authorized by the Ministry of Energy’s Water Allocation Committee with the request of the Environmental Protection Agency. In this way, the values of 60 and 1250 MCM were set as lower and upper values of decision variables.

2.3.4. Water Channels Transportation Capacity for Agriculture Use

Based on this constraint, which is set in the WEAP, the maximum capacity of the canals from different sources to different agricultural lands is set. Thus, Sistan lands, which are supplied from the Sistan River and the Chah-Nimeh4, are 2180 and 128 MCM per year, respectively. The Zahak lands also supplied from the same resources, respectively, have conduit capacity of 1730 and 116 MCM per year, respectively. The Miankangi lands, which are supplied from the Parian river, the Niatek Canal, and the Chah-Nimeh4, have capacities of 2200, 18,900 and 76 MCM per year.

2.3.5. Water Transport Pipeline Capacity for Domestic Uses

Domestic water consumption of cities and villages in the Sistan region is provided by the Chah-Nimeh reservoirs. In connection with the constraints on the transfer capacity of this section, the maximum amount of water for domestic consumption should not exceed 2.66 MCM per month. This constraint is set in the WEAP model.

2.3.6. Priority

Although the volume of drinking water consumed is low compared to other sectors of consumption, the drought in recent years has affected the consumers in this sector which includes 1 million inhabitants. In the case of drinking water shortages, the government makes arrangements for transporting water with tanker trucks to villages and cities based on the amount of water shortages (Figure 4). According to the estimate of the water tank trucks for transfer, the cost of water supply to the cities and villages of the study area is 4.1 USD/m³. In other words, in the case of supplying drinking water to the region, the government benefits from the method of lost interests and values method equal to 4.1 USD/m³. Unsurprisingly, this is an expensive way of transporting water and the costs are much higher compared to the profit from each agricultural crop per cubic meter of water. Moreover, drinking water is a basic need for a healthy society and has a higher priority socio-politically. Thus, the provision of this sector was considered to be the single priority in the WEAP model. This is in line with what is practically being implemented in the study area [64].

Currently, the second priority is the agriculture sector and the last priority is given to the Hamoun wetland as the environmental sector, in line with the governmental policy in the study area [64]. In the present study, in order to analyze the competition between agricultural and environmental sectors, as well as because the change in water consumption in these two sectors has a significant effect on the changes in the two-objective functions, these two consumption sectors were set with equal priority in the model, i.e., second priority after drinking water.

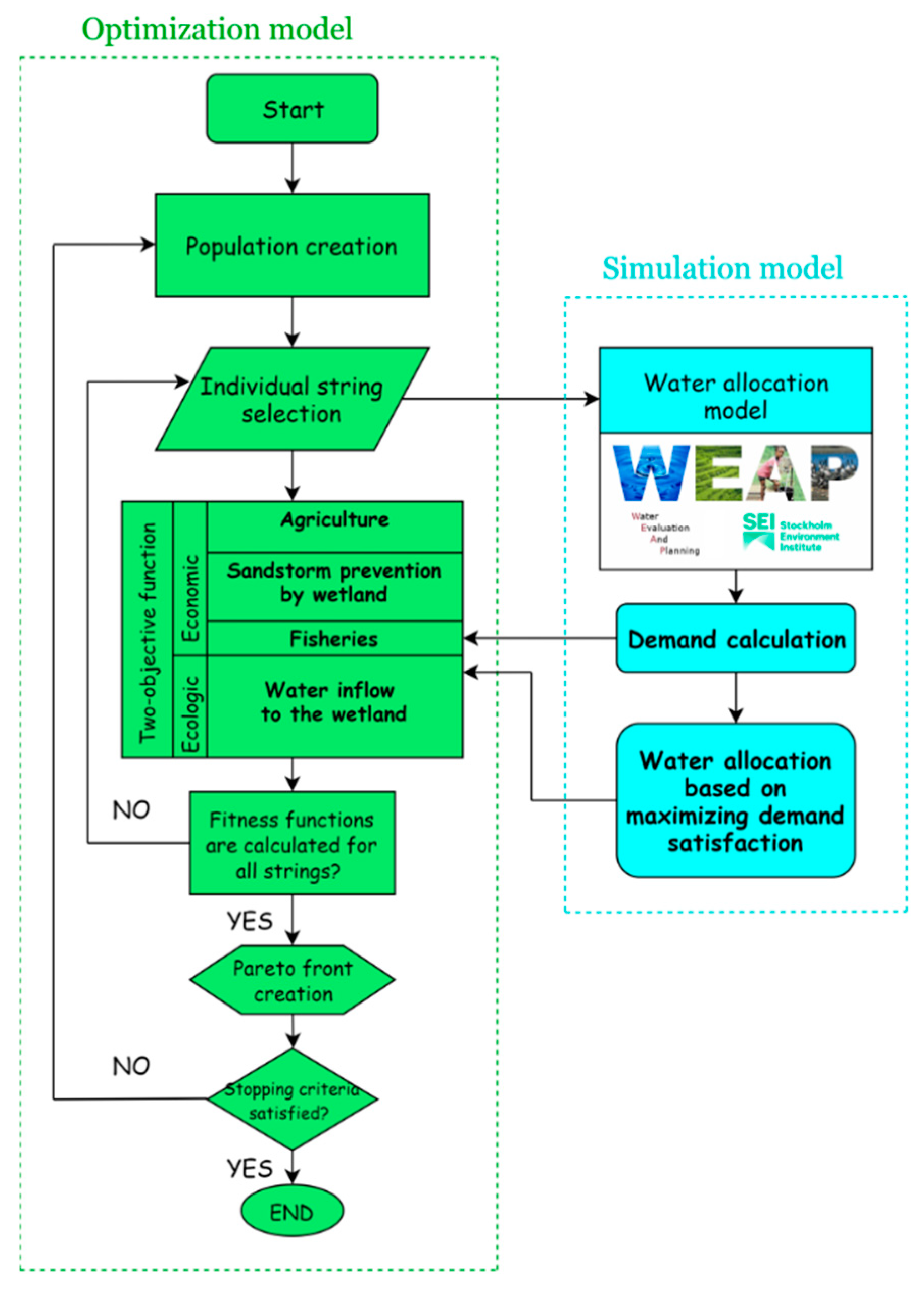
2.4. Coupled Simulation-Optimization Model

In this section, we show how a WEAP model is built, parameterized, and coupled with a multi-objective optimization model Figure 5. We use Pareto-optimal sets to investigate the trade-offs between the two conflicting objectives and present optimal compromises. We approximate the Pareto front using the weighted sum scalarization technique [65]. Our approach relies on the solution of a series of single-objective optimization problems which weigh the two conflicting objectives of economic and ecological benefits. For the solution of each single-objective optimization problem, we use a Genetic Algorithm constrained by a simulation using WEAP [57].

The steps of the coupled model are that the optimization model generates its population (subset of solutions in the current generation) for a given set of weights for the two objectives, which contain as decision variables the land cover area of different crops and the flow requirement of the Hamoun wetland. After that, an individual string is imported into the WEAP model to run the simulation. An individual is characterized by a set of parameters (variables) known as genes. Genes are joined into a string to form a Chromosome (solution). In a genetic algorithm, the set of genes of an individual is represented using a string, in terms of an alphabet. WEAP then constrains the string by water availability, reducing land allocated, or flow requirements as needed. The feasible simulation results of this string are then sent to the optimization model to calculate the constrained fitness function (a particular type of objective function that is used to summarize, as a single figure of merit, how close a given design solution is to achieving the set aims). Then the next string from the population of the optimization model is imported into the simulation model and the process is repeated until all strings of the population are simulated. If the optimization stopping criterion is not satisfied, the optimization model generates the next population; otherwise, a point on the Pareto front is made using the final optimization results for the given weights. The process is repeated for multiple weights to build a complete Pareto front (set of allocation of resources for which it is impossible to reallocate so as to make any one individual or preference criterion better off without making at least one individual or preference criterion worse off [65]).

The variables and parameters are shown in

Table 3. Implementation of model components and flows in WEAP-MOGA.

Component	Parameter	Description
Decision variables	Cropping area (ha)	Generated in MOGA, Imported in WEAP
	Environmental requirement (m3)
Hydrologic and Climatic	Reference evapotranspiration (mm/month)	Adjusted in WEAP
	Precipitation (mm/month)	Adjusted in WEAP
	Water inflow (m3/s)	Adjusted in WEAP
Demographic	Population and growth rate	Adjusted in WEAP
	Annual consumption rate (m3/person)	Adjusted in WEAP
Storages	Physical and operational characteristics	Adjusted in WEAP
Agriculture	Crop coefficient (kc)	Adjusted in WEAP
	Potential evaporation (mm), actual evaporation (mm)	Calculated by WEAP, Imported in MOGA
	Crop yield (kg/ha), prices (USD/kg), costs (USD/kg)	Identified in MOGA
	Agriculture benefit (USD)	Calculated by MOGA
Wetland	Physical characteristics	Identified in MOGA
	Wetland benefit (USD)	Calculated by MOGA
	Water inflow (m3/s)	Calculated by WEAP, Imported in MOGA
Objective function	${\mathrm{F}}_1$ = Agriculture benefit + Wetland benefit	Calculated by MOGA
	${\mathrm{F}}_2$ = wetland water inflow (m3)/study area inflow (m3)

. It gives an overview of how each component of the water system is presented in coupled simulation-optimization model.

3. Results and Discussion

3.1. WEAP Model

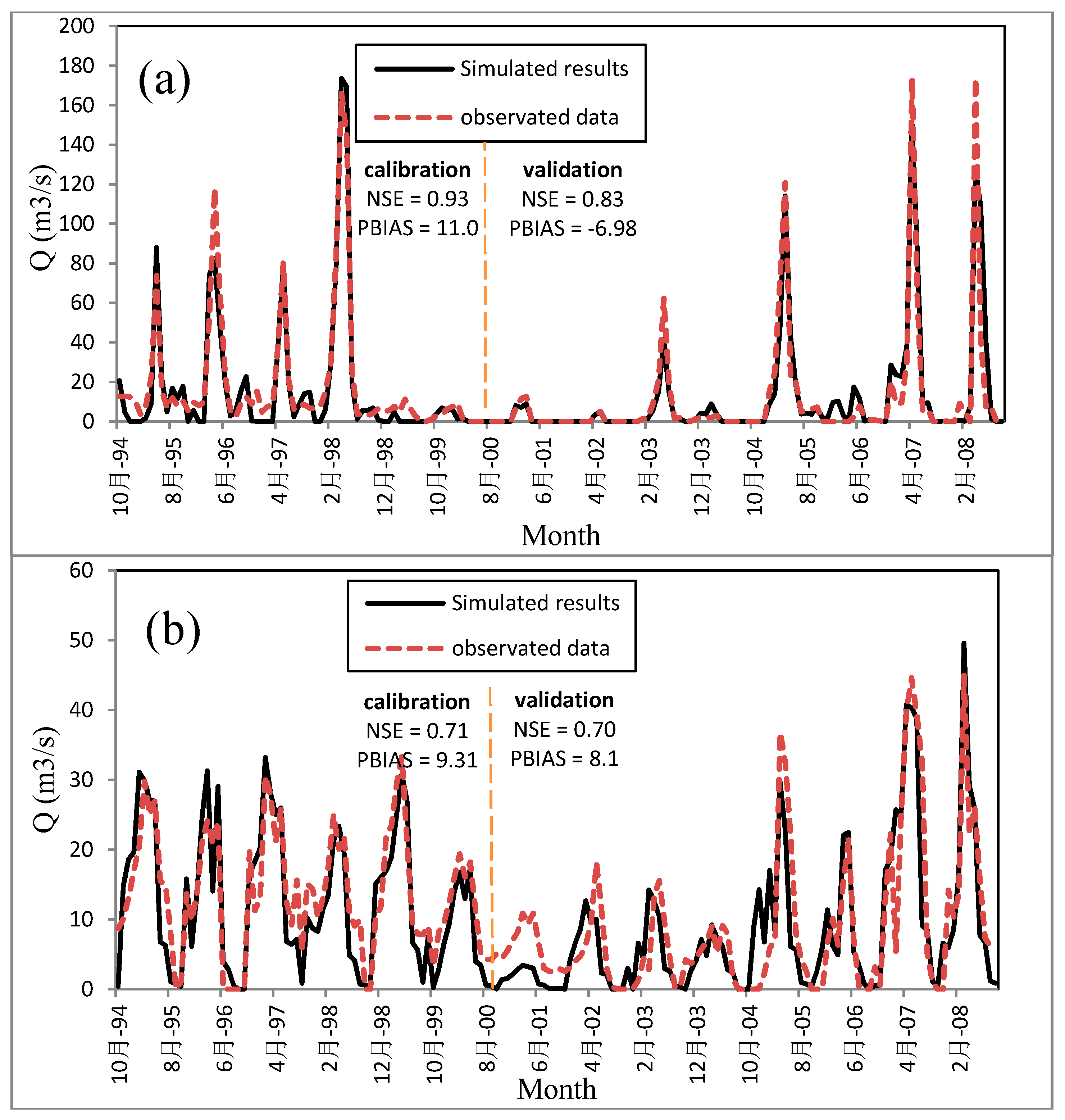
Graphical results during calibration and validation (Figure 6) indicated adequate calibration and validation over the range of streamflow. Nash–Sutcliffe (NSE) values for the monthly streamflow calibration and validation were 0.93 and 0.83 in Jarigeh station (Figure 6a) and 0.71 and 0.70 in Shirdel-Gelmir-Shomare1 station (Figure 6b), respectively. According to the model evaluation guidelines (

Table 4. General performance rating the stream flow for PBIAS and Nash–Sutcliffe for a monthly time step [66].

Performance Rating	Nash–Sutcliffe	BIAS (%)
Very good	$0.75<\mathrm{NSE}\le 1$	$\mathrm{Bias}<\pm 10$
Good	$0.65<\mathrm{NSE}\le 0.75$	$\pm 10\le \mathrm{Bias}<\pm 15$
Satisfactory	$0.5<\mathrm{NSE}\le 0.65$	$\pm 15\le \mathrm{Bias}<\pm 25$
Unsatisfactory	$\mathrm{NSE}\le 0.5$	$\mathrm{Bias}\ge \pm 25$

), the WEAP model simulated the streamflow trends “well” to “very well”, as shown by the statistical results which are in agreement with the graphical results. The percent bias (PBIAS) values for calibration and validation were obtained 11.4% and −6.98% in Jarigeh station and from 9.31% to 8.1% in Shirdel-Gelmir-Shomare1 station, respectively. The magnitudes of simulated monthly streamflow values were within the good and very good range for each station during calibration and validation. Model predictions for the Shirdel-Gelmir-Shomare1 station are less accurate (Figure 6b). The explanation lies in the somewhat low quality of the inflow data for Parian river, as upstream of this station, which introduces inaccuracy in the simulated streamflow.

3.2. Application of Multi-Objective Optimization

Figure 7 shows results for multi-objective optimization run where the environmental objective (${\mathrm{F}}_2$) is plotted over the long-term profits objective (${\mathrm{F}}_1$) for all solutions which are calculated during the optimization procedure.

The blue squares comprise the Pareto-optimal data set, i.e., the Pareto front. The yellow circles represent specific optimal solutions. The circle labeled as “Long-term profit scenario” presents the solution in which only economic profits are decision-making’s criterion of the case study and environmental objectives are less important. Different solutions along the Pareto front are multi-objective type and represent potential compromises between conflicting objectives, depending on the relationship of the two objectives. The circle labeled “A multi-objective scenario”, the solution representing the multi-objective scenario, was selected with economic (${\mathrm{F}}_1$) and environmental (${\mathrm{F}}_2$) considerations. Agriculture profit in this solution is around 1.8 times the average annual income of agriculture activities in the past 30 years (Statistical yearbooks of Sistan and Baluchistan). In addition, a significant amount of water is allocated to the Hamoun wetland, in which the ecological requirements of the wetland have more satisfaction coverage than long-term profit solution.

The shape of the Pareto front may be divided into two different ranges between specific solutions. Within the first part—between the solutions labeled as “A multi-objective scenario” and “Long-term profit scenario”, respectively—an increase of the agricultural land cover is associated with a larger change wetland inflow, which means a higher risk of damaging the wetland ecosystem. The second part comprises the range between the single solution, where only (${\mathrm{F}}_2$) is considered, and the solution labeled as “multi-objective scenario”. In this range, only moderate changes in wetland hydrological conditions lead to relatively large changes in the region’s economic profits.

3.3. Cropping Patterns on the Pareto-Optima

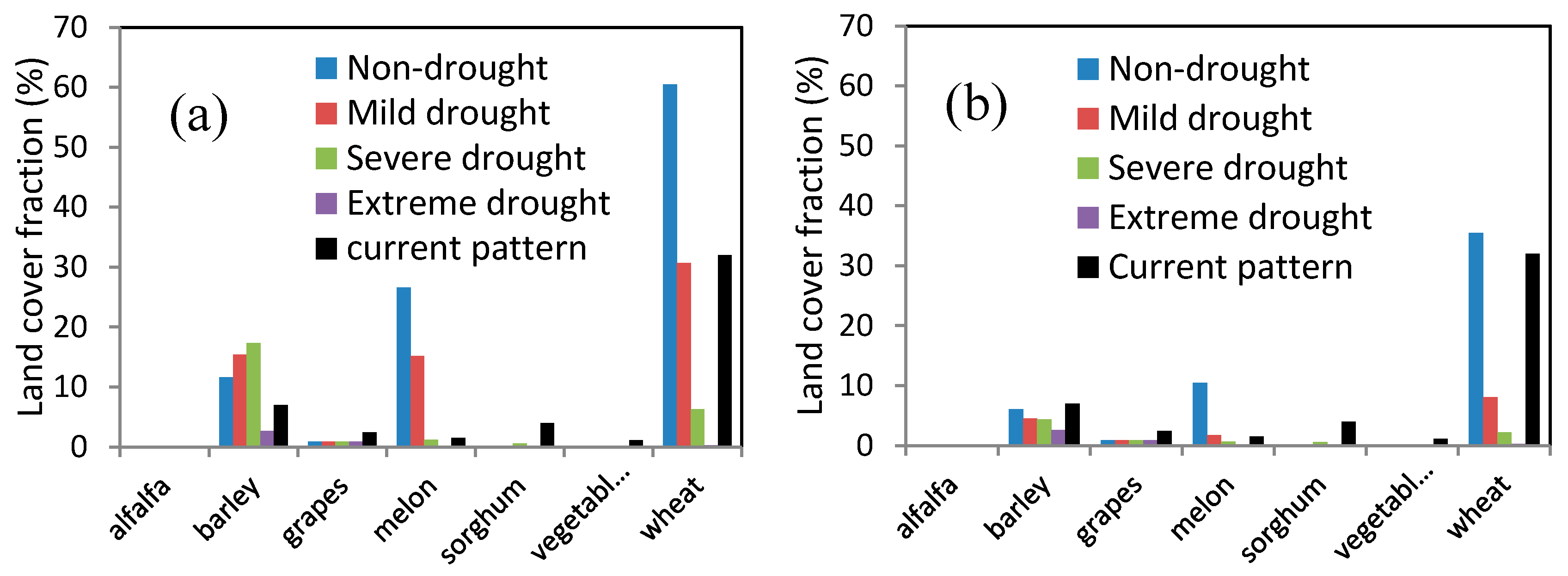
Figure 8 presents the crop pattern area for the specific solutions “the long-term profit scenario” (a), and “multi-objective scenario” (b). As shown in Figure 8, different cropping patterns were presented for each of the different hydrologic conditions which are classified in Section 3.1, as well as current cropping pattern based on the report presented by the [64]. Also, the most effective crops for the objectives specified in the study are wheat, barley, and melon.

3.3.1. Extreme Drought

In the overall view and comparison between the two scenarios, the sharp decline in agricultural lands from Scenario (a) to Scenario (b) can be seen. Both scenarios, in the extreme-drought conditions that occur only in 2032, have the same pattern of cultivation. In this hydrologic condition, the cultivated area is very low, with 2.6% barley and 0.3% wheat as the optimal pattern. The reason for the very low agricultural area this year is that the total volume of region water inflow in this year is about 50 MCM, which is the majority of this amount, is allocated for supplying drinking water. The results obtained from the study carried out by [37] also demonstrated the significant irrigated area reduction in Sistan region with the drought scenario. Their cropping pattern results in the drought scenario show that the cultivated area would experience an 86.9% loss. Ibrahimzadeh and Esmaelnejad [67] also showed the significant effect of drought on reducing the cultivation area in Sistan region.

3.3.2. Severe Drought

In these conditions, wheat, barley, and small area of melon are cultivated in both scenarios. The amount of wheat, barley and melon in these years in the Scenario (a) is 6.3, 17.4 and 1.2 respectively and in Scenario (b), these values are reduced to 4.4, 4.4 and 0.65, respectively.

3.3.3. Mild Drought

In these hydrological conditions, the crop pattern shows a different situation for the two scenarios. Due to the tendency to profitability in Scenario (a), the optimization model increases the area of the melon over its area under severe and extreme-drought conditions. This is due to the high profitability of melon in terms of sufficient water availability. In Scenario (b), although there is an increase in melon, this increase is not noticeable. This is due to ecological consideration in the scenario. Since the water consumption of melon is high, the model will achieve its environmental goal by not cultivating melon more. The current hydrological condition is in mid-drought category based on the SDI. Therefore, comparing the current crop patterns with the two scenarios, we can find that the current policy of the region is more economic oriented than environmental. Also, it could be improved by increasing the melon and barley areas.

3.3.4. Non-Drought

In these years, which include 19 of the modeling years, the land cover fraction for wheat, barley, and melon in long-term profit scenario are 60.4%, 11.6%, and 26.6%, respectively. For the multi-objective scenario the corresponding land cover fraction are 35.5%, 6%, and 10.4%, respectively.

3.4. Long-Term Scenario Analysis

The results (Figure 9) show that agricultural activities play the most important role in the economy of Sistan region.

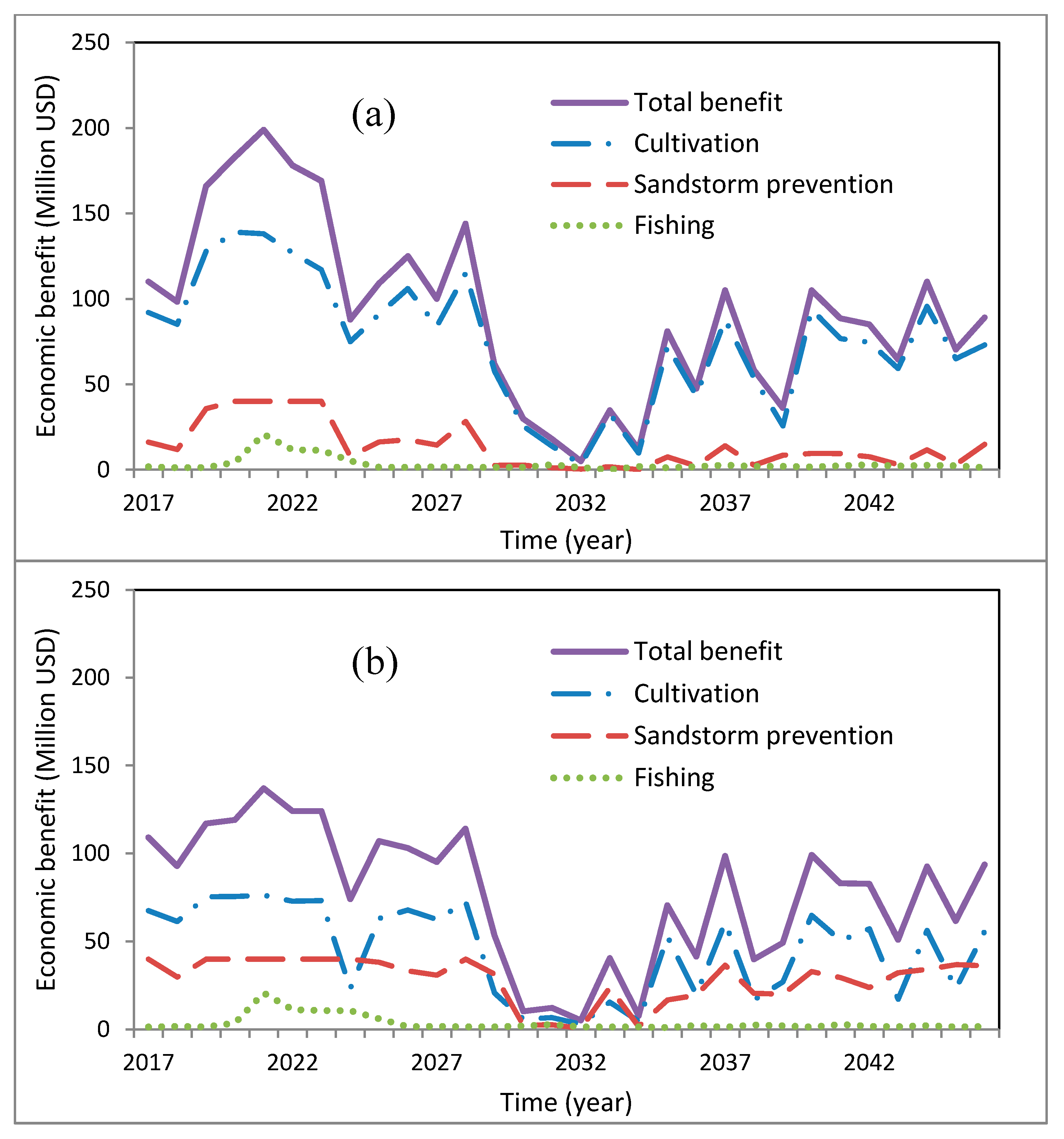
In the long-term scenario (Figure 9a), the benefits of wetland ecosystem services, except in the 2019–2023 period in which a large flood occurred in the region, is very low in most modeling years. In the flood years, this amount is also about one third of agricultural profits. In this regard, as shown in

Table 5. Comparison of different section Benefits for three scenarios.

Scenario	Agriculture Benefit (Million USD)	Sandstorm Prevention Benefit (Million USD)	Fishing Benefit (Million USD)	Total Benefit (Million USD)
Economic	2260.84	410.97	97.86	2770.42
Multi-objective	1348.3	853.7	104.89	2307.63

, the total economic profit of the region in this scenario is 2770 Million USD, which is 2261 Million USD in agricultural activity and 509 Million USD in profit form wetland services.

To compare the results with those obtained in [37], we calculated the annual average agricultural profit 77.4 million USD for the non-drought and mild-drought years, and 9.7 million USD for the severe- and extreme-drought years. Dahmardeh Ghaleno et al. [37] obtained 66.5 and 5.9 million USD for agriculture profits of Sistan in wet and drought years, respectively. 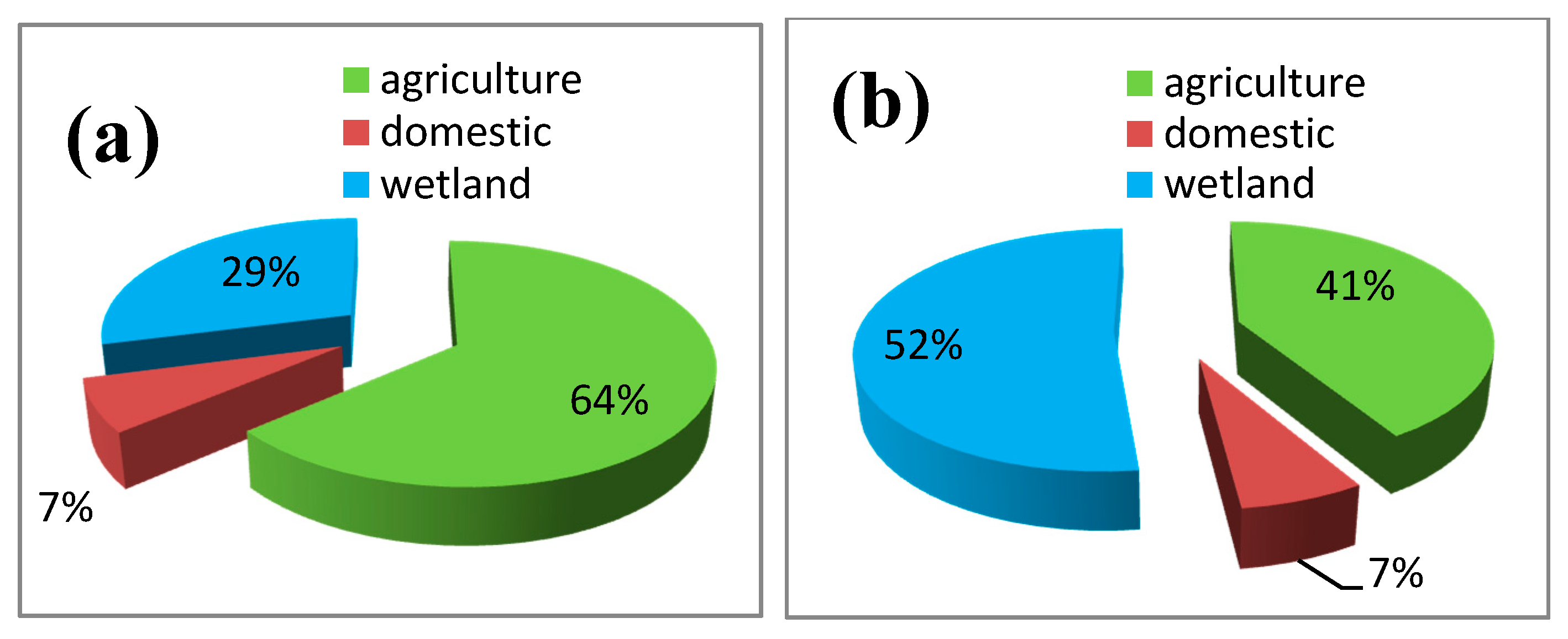On the other hand, in this scenario, the damage risk of the Hamoun wetland might increase because the long-term annual average of water allocated to the Hamoun wetland is 29% of the long-term annual average of water allocated to all sectors (Figure 10a), which does not adequately meet the environmental requirements of the Hamoun wetland. To confirm this, Figure 11 shows that in this scenario, the average wetland inundated between May and August is more than the supercritical area (25,000 hectares) only during six years of the 30 year modeling period. Based on the results, the annual average water inflow into the Hamoun wetland during the study period is 668 MCM per year. That is only 53% of the environmental requirement of the Hamoun wetland.

The change from Scenario (a) to Scenario (b) in Figure 10 reduces overall economic profits in the region by 17% (Table 5). By assessing the profits of different sectors, the sharp decline in agricultural profits from 2261 to 1374 Million USD can be seen, but this sharp decline is somewhat moderated by increasing environmental profits. In the Scenario (b), which follows a multi-objective approach, the profits of the wetland sector are increased. Profit from sandstorm prevention has risen 411 to 854 Million USD. This increase in profit is because the number of years in which the wetland inundated area is above the threshold of the supercritical area has increased from 6 years in the long-term profit scenario to 20 years in the multi-objective scenario (see Figure 11). To prove the results, one can refer to the annual damage caused by the sandstorm in the Sistan area, the field study provided by [68]. They revealed that the annual losses in terms of physical damage and loss of productive person-hours have been estimated at 25 Million USD when the Hamoun wetland is in drought. Given the relative improvement of the Hamoun wetland in 14 years with the multi-objective scenario (Figure 11), the results of the increase in profits in this study seem plausible. In terms of water inflow to the wetland, the ratio of the long-term annual average of water allocated to the Hamoun wetland over the long-term annual average of total water allocated increases by 51% in this scenario (Figure 10b). This amount is 1140 MCM per year, which is 91.2% of the environmental requirement of the Hamoun wetland. In terms of wetland profits, fishing profits show no significant increase (98 to 105 Million USD). This might be a result of the fishing profits dependency on the three hydrological parameters. As presented in Table 1, to achieve high profits, all three conditions must be in a desirable situation. This situation occurs only during the flood years. Dahmardeh et al. [69] evaluated the fishing profits in three water conditions wet, average, and dry. They obtained 3.95, 1.65, and 0.12 Million USD in different conditions, respectively. Expanding these results over the modeling period based on the hydrological classification presented in the study, the fishing profit is estimated at 87 Million USD. If we consider this estimation as a representative of reference fishing profits, it is observed that using the Scenario (a) and (b), fishing profit increases by 12.4% and 21%, respectively.

It is worth noting that in the multi-objective scenario, the amount of water allocated to the agricultural sector is drastically reduced (Figure 10), as it assigns lower priority to the activities of farmers who account for a large part of the region’s occupation.

3.5. Sensitivity Analysis

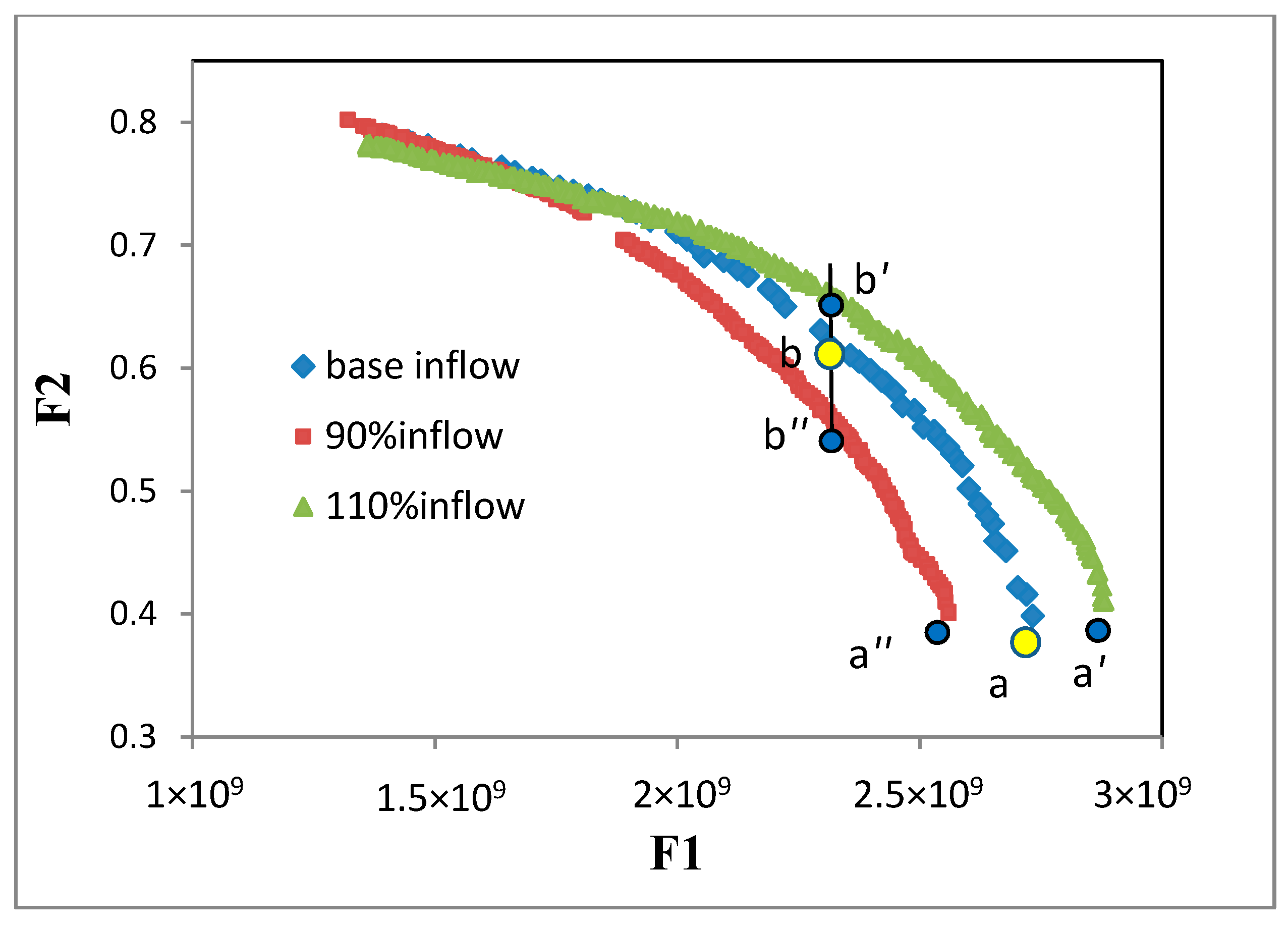
Figure 12 shows the sensitivity of the Pareto front generated by the proposed model to the variations of the water inflow. The results shown in Figure 12 are due to a decrease and increase of 10% in the inflow of water into the study area. This range was chosen so that the hydrological classification of modeling years as one of the principles of the proposed model does not change. Optimal solutions ${\mathrm{a}}^{\prime }$ and ${\mathrm{a}}^{″}$ are used to analyze the results of the long-term profit scenario for the increased and decreased inflow scenario, respectively. The solutions ${\mathrm{b}}^{\prime }$ and ${\mathrm{b}}^{″}$ are solutions that have balanced economic profit value in the multi-objective scenario. This analysis shows how changes in the parameters of the proposed model arise because of the change in the streamflow and preserving the region’s economy.

Table 6. Sensitivity Analyses, Various Parameters.

Parameter	Economic Scenario		Multi-Objective Scenario
	Baseline Model (a)	Interval (% of Baseline Value) $({\mathbf{a}}^{″},{\mathbf{a}}^{\prime })$	Baseline Model (a)	Interval (% of Baseline Value) $({\mathbf{b}}^{″},{\mathbf{b}}^{\prime })$
Total profit (M USD)	2770	(93, 104)	2307	-
Irrigation profit (M USD)	2261	(89, 101)	1348	(110, 91)
Prevention of sandstorm profit (M USD)	411	(98, 128)	854	(84, 111)
Fisheries profit (M USD)	97.5	(92, 100)	105	(93, 127)
Cropping land cover 1 (ha)	103,520	(99, 103)	51,600	(130, 68)
Wheat area 1 (ha)	54,703	(104, 95)	33,186	(144, 44)
Barley area 1 (ha)	17,246	(88, 122)	5,344	(117, 40)
Melon 1 (ha)	30,081	(97, 105)	13,572	(90, 102)
Wetland water inflow (MCM)	21,740	(94, 113)	34,196	(84, 116)
Wetland inundated 2 (ha)	24,774	(91, 124)	41,921	(78, 114)

¹ The values of these parameters are based on the average long-term annual cultivation area. ² Average long-term wetland inundated between May and August (The most effective ecological services of the Hamoun wetland depend on its hydrological conditions in the months mentioned).

. presents a series of sensitivity analyses for the baseline optimization scenario. As can be seen, in solution ${\mathrm{a}}^{″}$, a 10% reduction in water inflow reduces the total profit of water uses by 7% when compared to the model outcomes using the baseline flow input. This decline is mainly due to an 11% decline in agricultural productivity. Considering that the changes in the cultivated area are negligible, it can be concluded that the reason for reducing irrigation profits is to reduce the yield of the crops.

At inflow levels of 110% (${\mathrm{a}}^{\prime }$), total economic profits from water consumption increase to 104%. Most of this change is due to a 28% increase in profits from sandstorm prevention. This is a result of an increase of 13% in the water inflow into the Hamoun wetland and consequently an increase of 24% in the inundated area.

By analyzing the range of changes in the output parameters, it can be derived that although changes in the total irrigation area are negligible, barley cultivation is very sensitive to fluctuations in the inflow of water, and melons and wheat are more stable.

In the multi-objective solution (${\mathrm{b}}^{″}$), a 10% reduction in the inflow of water, with the condition of maintaining total profits, leads to an increase in agricultural activity. There is a 30% increase in cultivated land, which includes a 44% increase in wheat area, a 17% increase in barley and a 10% reduction in the area of melon. In this condition, there is a 16% decrease in the water inflow to the wetland and consequently a 22% decrease in the inundated area, which reduces by 16% and 7% in profits from the sandstorm prevention and fisheries profits, respectively.

In contrast, the ${\mathrm{b}}^{\prime }$ solution has a 10% increase in water flow. As shown, even with a 32% reduction in the total cultivated area, the profit is obtained corresponding to the multi-objective (b) solution. This has many reasons, such as not changing in the cultivated area of melons as the most beneficial crop, an increase of 11% and 27% respectively in the profits from preventing lagoons and fishing, increasing the yield of products.

In general, the results of this section showed that the output parameters of this model are sensitive to the water inflow; moreover, it confirmed the importance of the hydrological classification in the robustness in the allocation decisions.

In addition, this inflow parameter faces many uncertainties such as climate change, Afghanistan’s population and agricultural land changes, and the political relations between the two transboundary river countries, Afghanistan and Iran. Hence it is recommended for future studies to carry out climate change projection and use different types of scenarios to better predict the future Iran water inflow.

4. Conclusions

In the present study, we studied the trade-offs between environmental water demand and economic benefits using a multi-objective optimization model. Two optimal solutions from the Pareto front were presented representing so-called “long-term economic” and multi-objective scenarios. In the long-term profit scenario, a large portion of the total economic profits derived from the agricultural activities of the people of the region. In the multi-objective scenario, a 17% decrease in economic profit is seen compared to the long-term profit scenario as water is diverted for ecological services from the wetland. The predominant occupations of the region are the jobs related to agriculture activity. Other common occupations of the region include fishing, animal husbandry, birds hunting, handicraft sellers, etc. The long-term profit scenario optimizes conditions for irrigated agriculture, while other jobs that more directly linked to the ecological services of Hamoun wetland almost disappear. This is the opposite of the multi-objective scenario in which farmers face a serious challenge with a sharp decline in agricultural land. As such, this case can be considered to be showing an example of clear trade-offs in the water-food-ecosystem-land nexus.

One of the most important criteria for sustainable development is the environmental aspect of natural resources. Sandstorm phenomenon is the parameter that influences the social well-being of the region’s people. The resulting sandstorms have reportedly completely covered houses. Also, numerous people suffer from skin, lung, and eye complaints because of the dust. Women suffer even more because the dusty circumstances require frequent cleaning. In addition to the heavy costs imposed on the government to protect the bed soil of the wetland against the wind, this phenomenon has social consequences such as respiratory diseases and migrations of the inhabitants of the area. As the results show, the focus on the wetland sector in the multi-objective scenario is much greater than the long-term profit scenario. Therefore, the long-term annual average of water allocated to this sector has increased from 29% in the economic scenario to 51% in the multi-objective scenario. As a result, better conditions for ecological services are provided and the migration of residents who are exposed to the dangers of sandstorms and the lack of proper living conditions is likely to be prevented.

In water management, it is often not possible to make a perfect decision that satisfies all stakeholders. In this regard, the results from the scenarios considered in this study are no exception. Each direction along the Pareto front comes with disadvantages and advantages. It is worth noting that the modeling of the research is presented with the current conditions in the region, with the difference that the amount of agricultural land has been optimized for Pareto-optimal solutions. In other words, existing management policies and decisions have not been used to generate these solutions and could in principle be below the Pareto curve. Our findings confirmed that if water resources management policies are not improved in the region, at least one of the two sectors considered, agricultural and environmental will be under tension in drought years. Therefore, considering the potential of the study area in the application of some efficient policies such as reducing evaporation of storages, increasing irrigation efficiency, using optimized deficit irrigation, population control, and cultivable lands reduction, it seems to be necessary to study and evaluate the scenarios that include these policies. Furthermore, to deal with large hydrological uncertainty, it is worth testing future climate and socio-economic development scenarios for the region. These scenarios could be effective in assessing risks and improving the socio-economic and environmental conditions of the region for sustainable development.