Seasonal and Diurnal Variations in the Priestley–Taylor Coefficient for a Large Ephemeral Lake
Abstract
1. Introduction
2. Background and General Definitions
3. Data and Processing
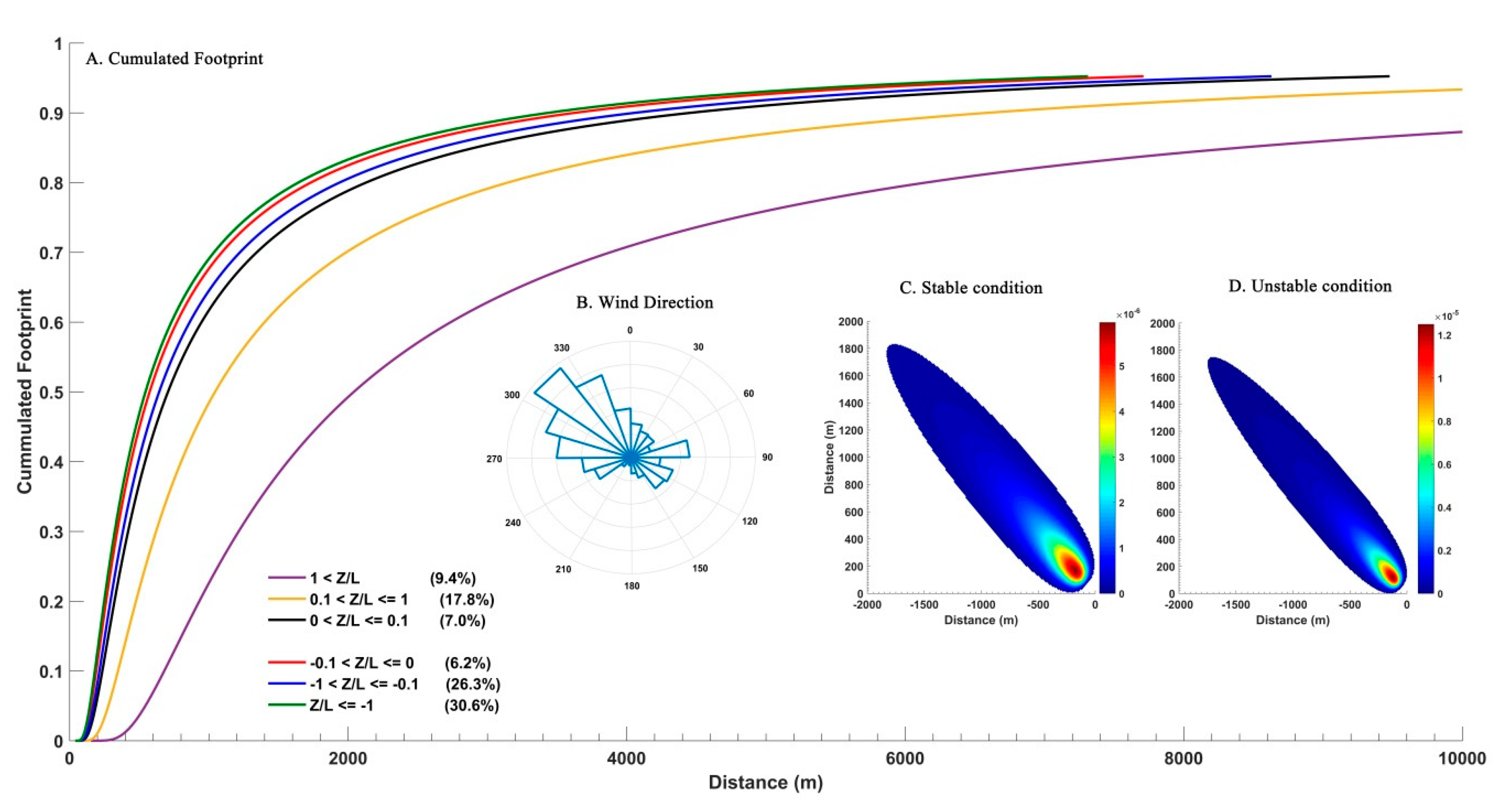
3.1. Site Description
3.2. Data Processing
4. Results and Discussion
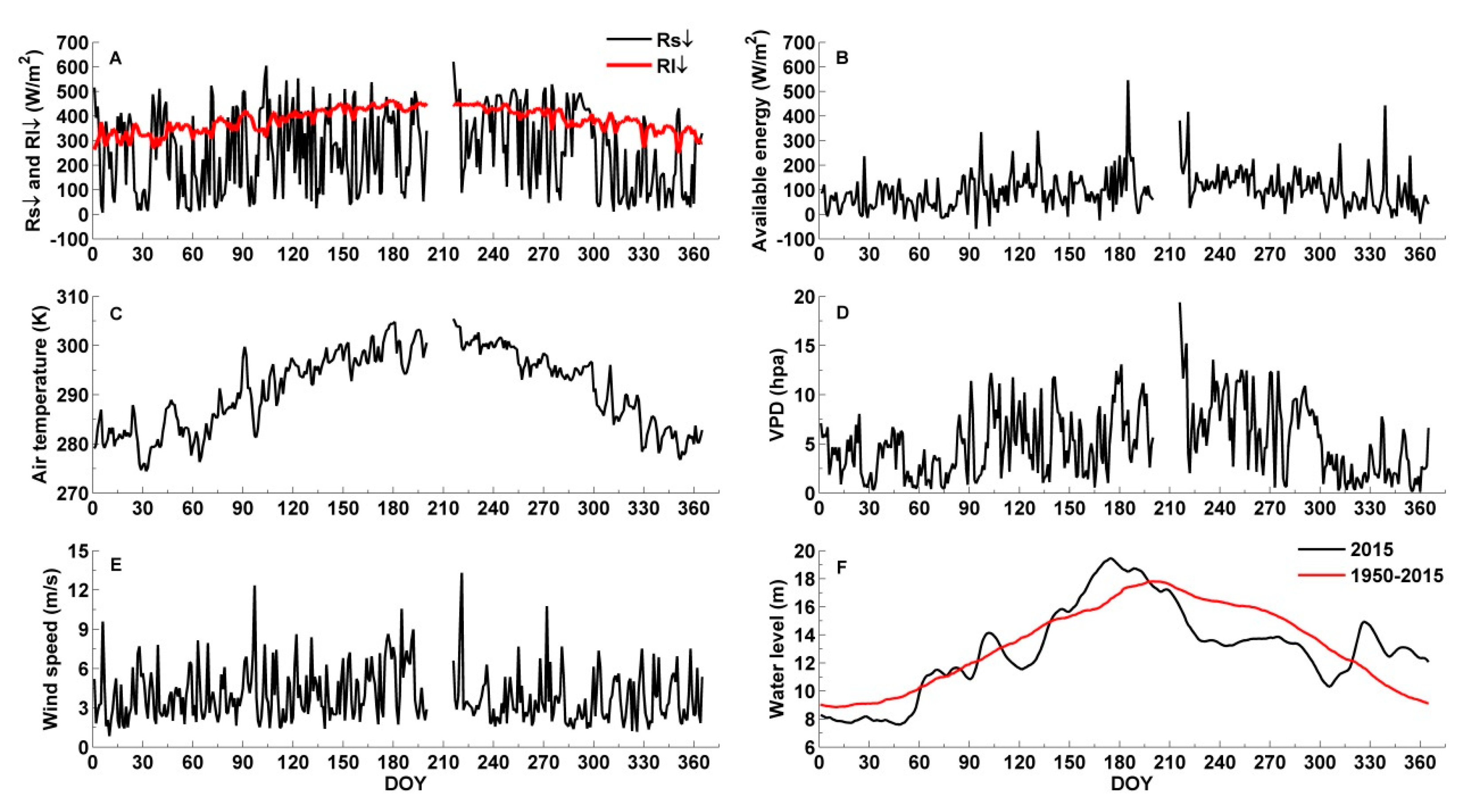
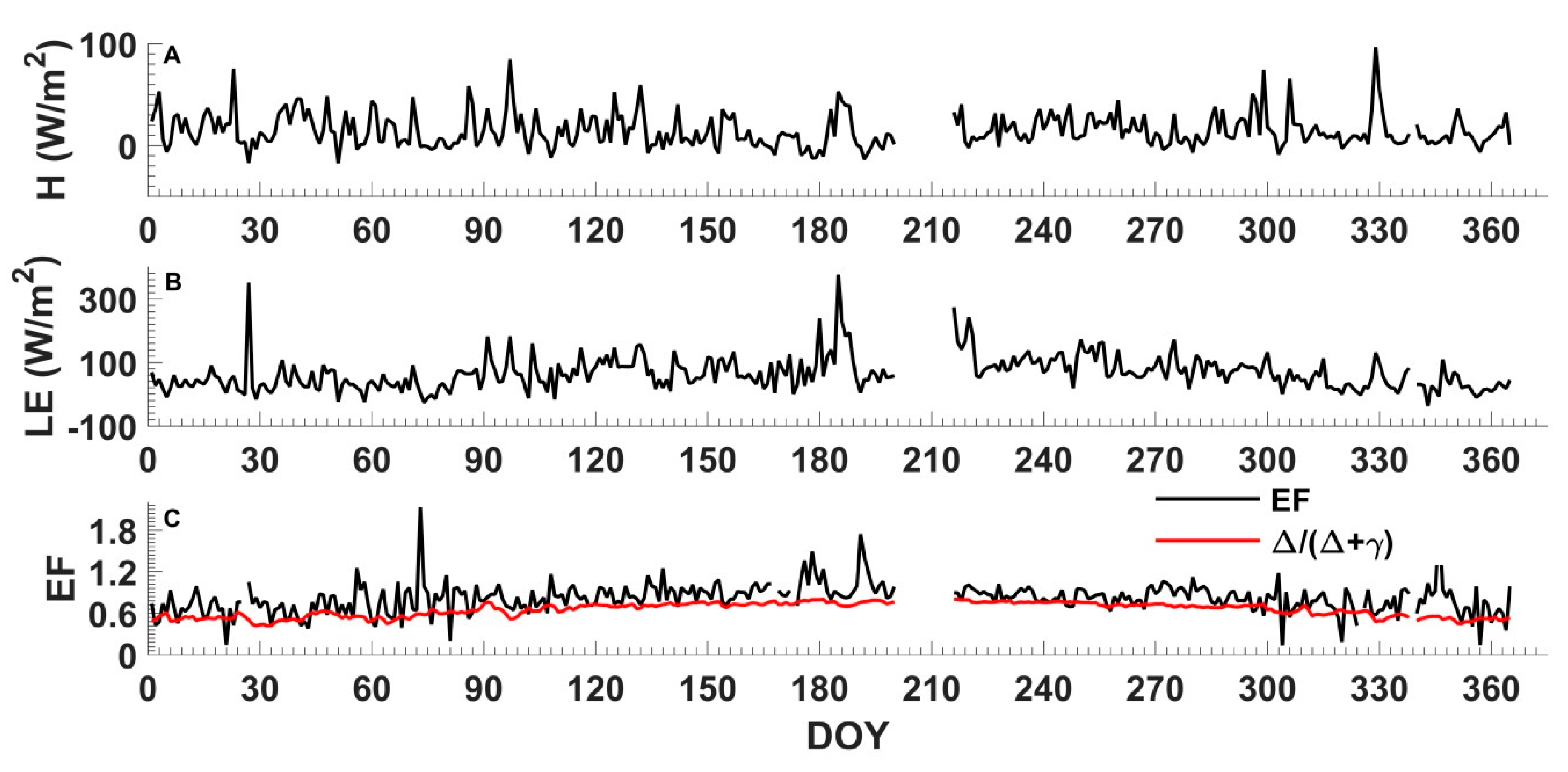
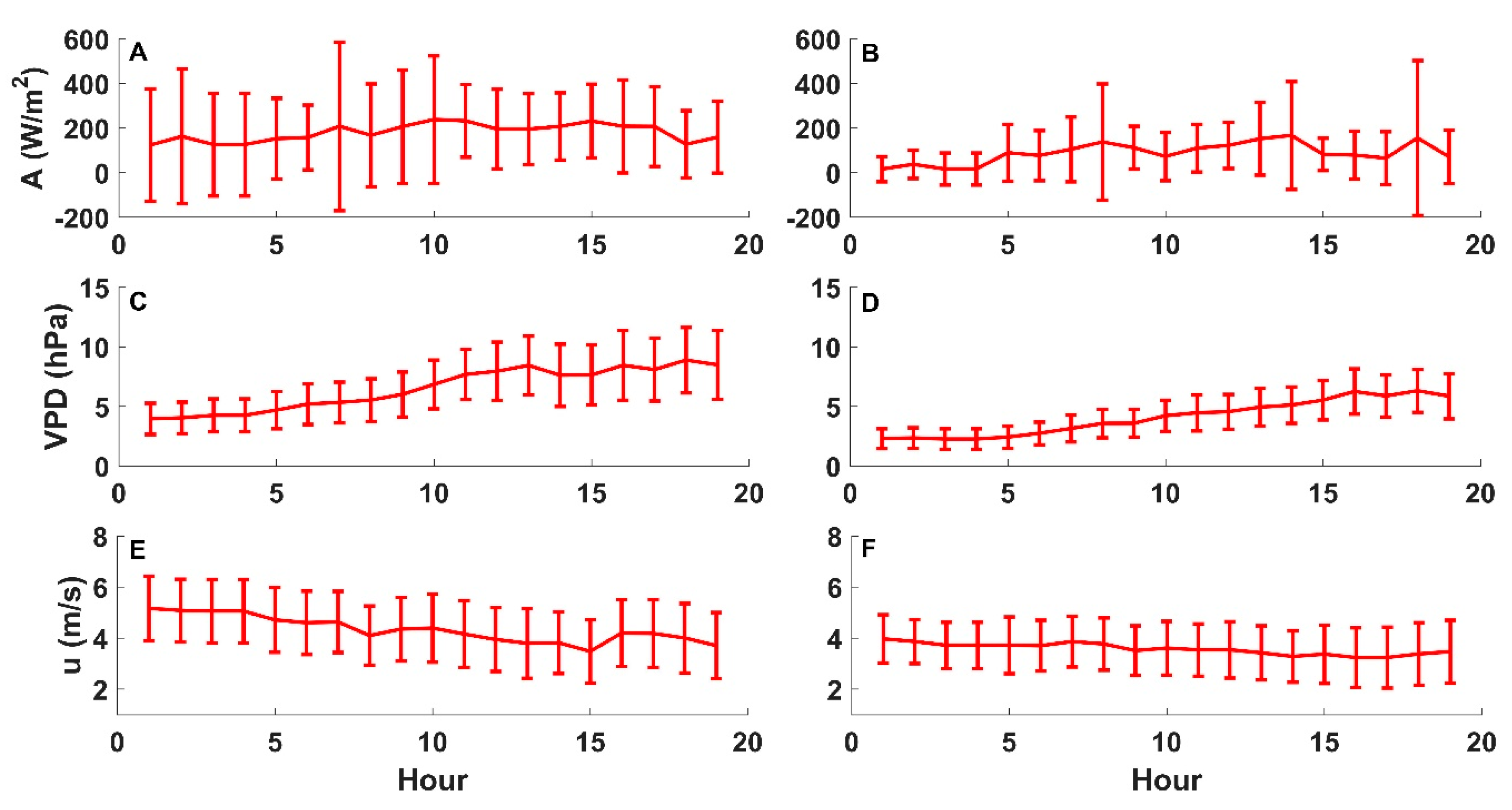
4.1. Environmental Conditions and Energy Fluxes
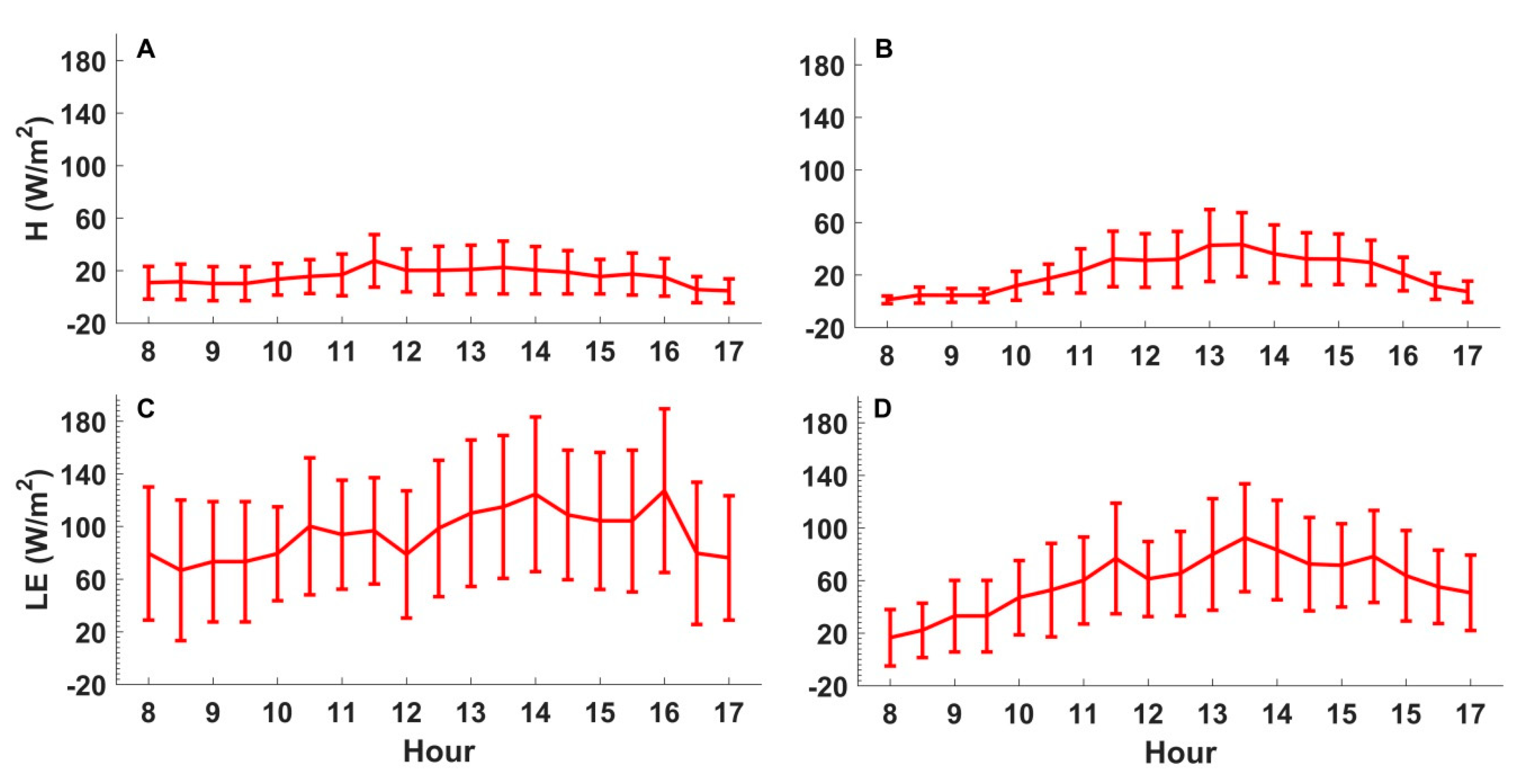
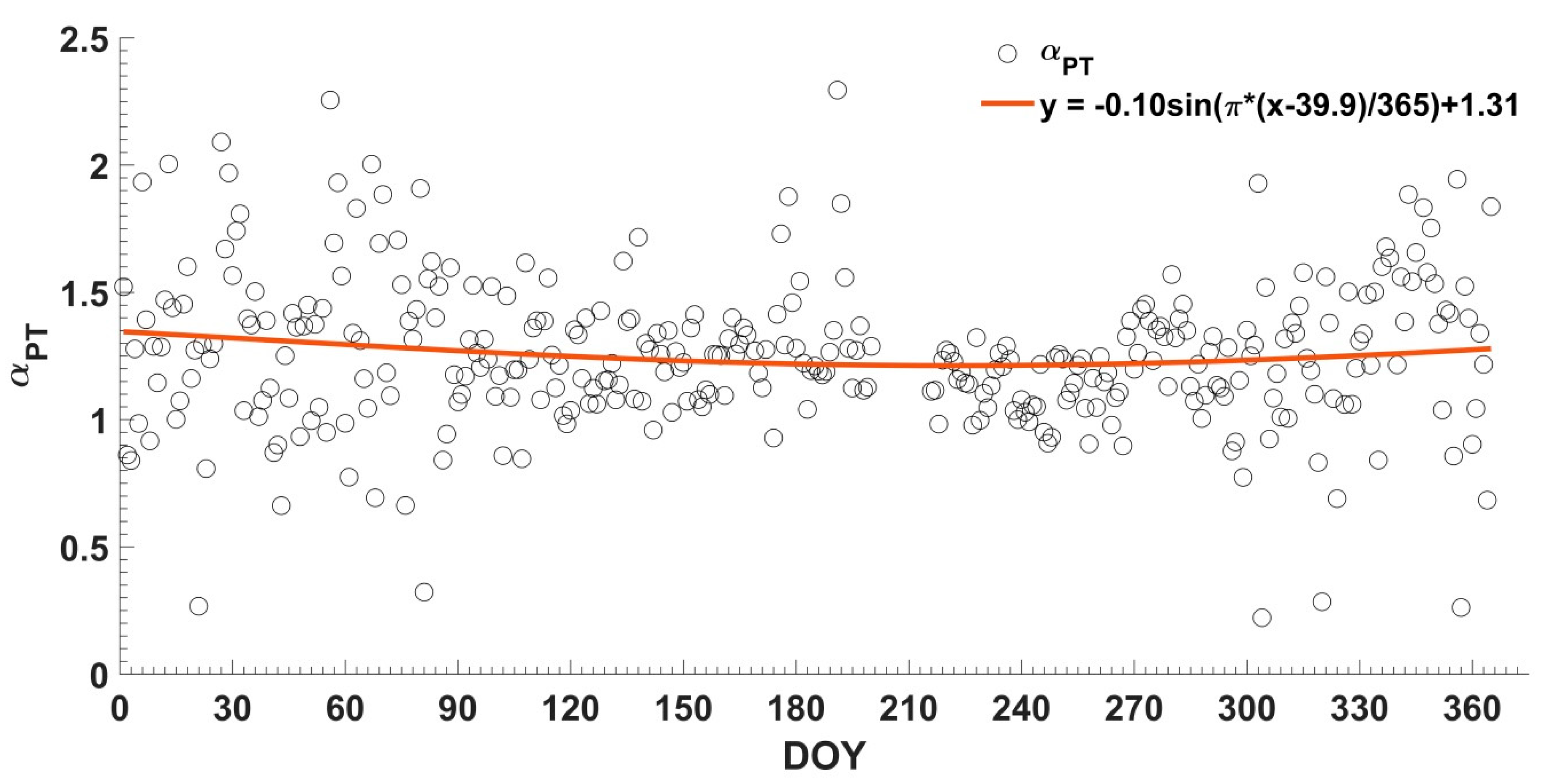
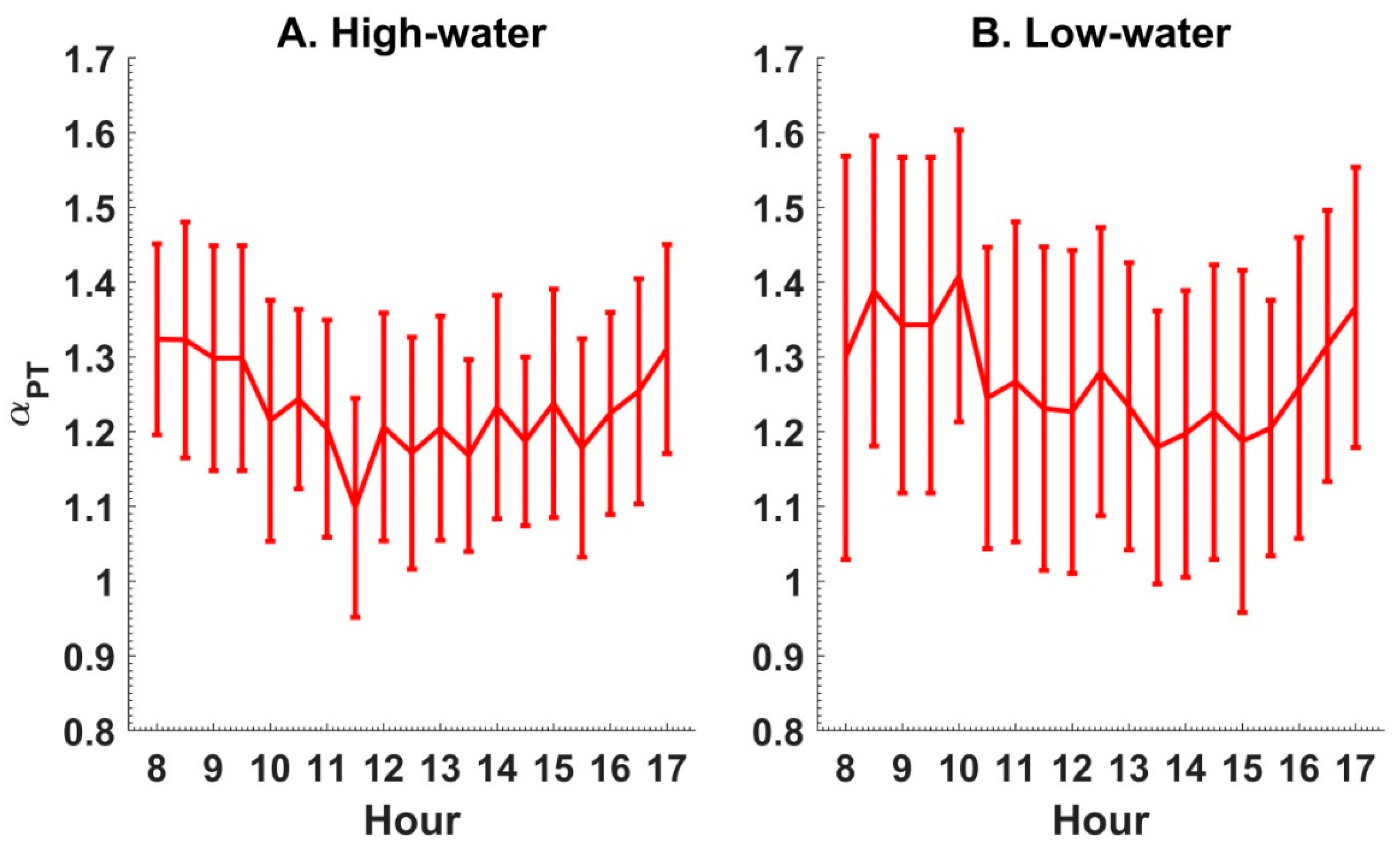
4.2. Seasonal and Diurnal Variations in α
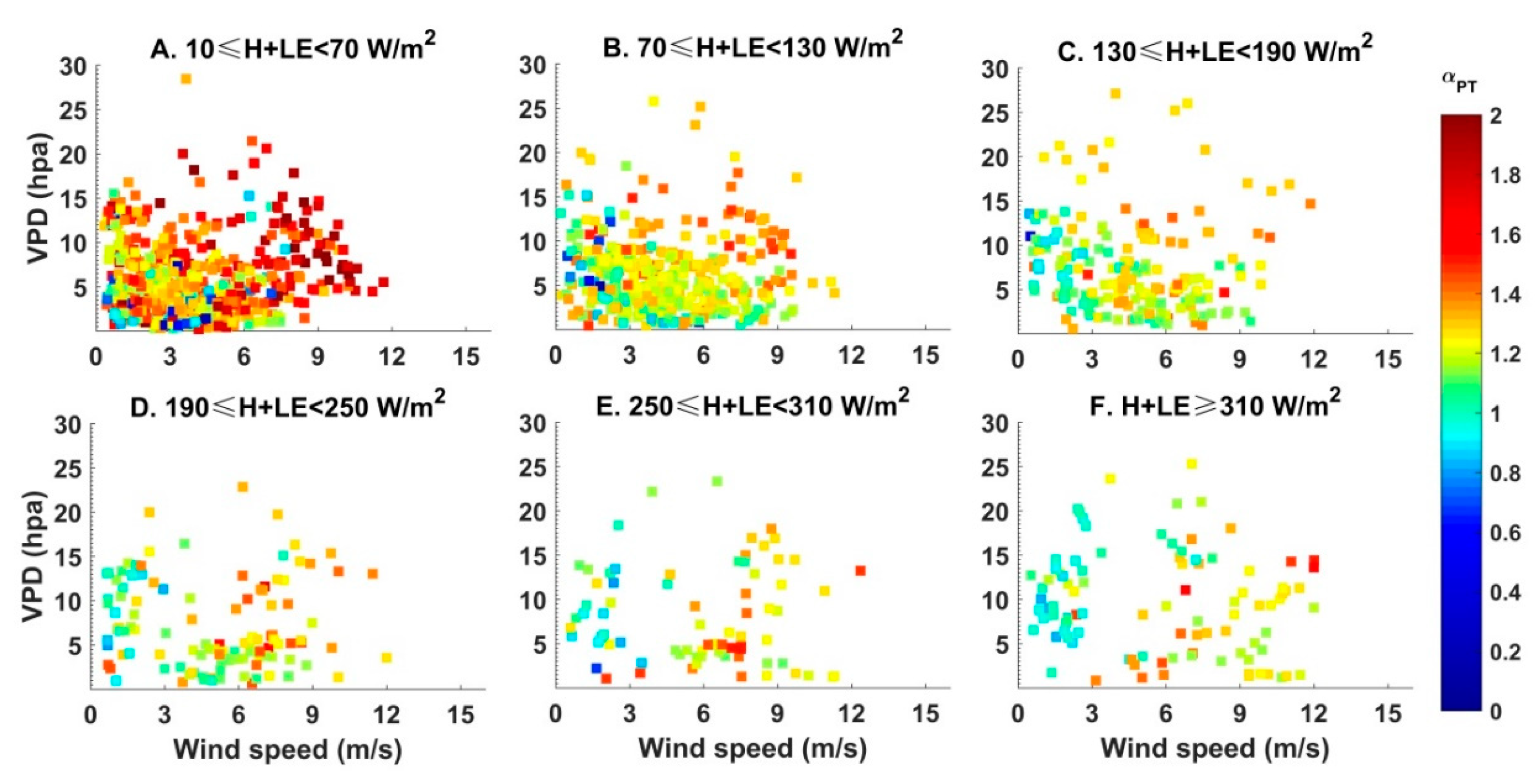
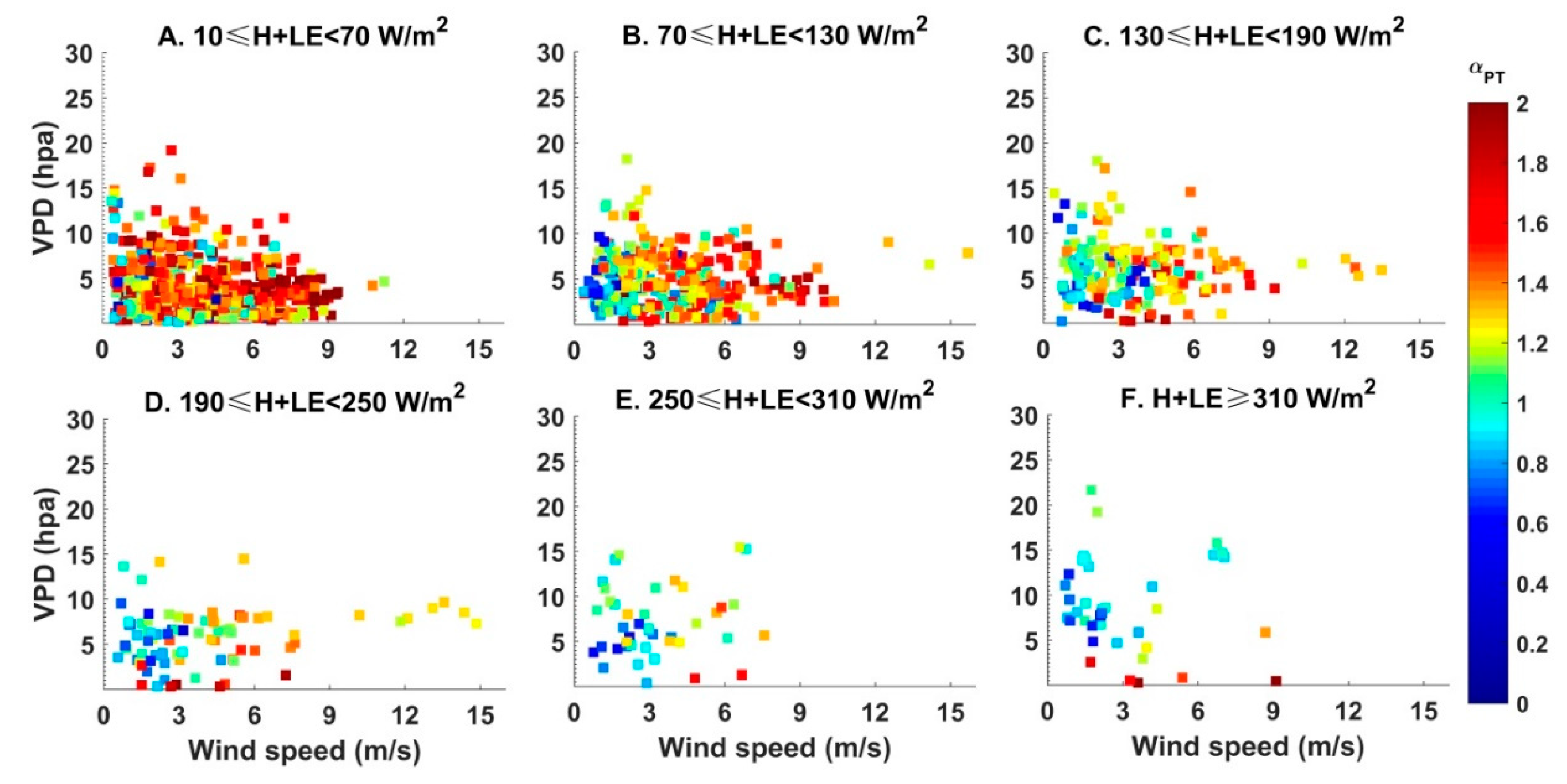
4.3. The Controlling Factors of Parameter α
5. Discussion
5.1. Contributions of Local Advection and Energy Control to the α Variations
5.2. Use of the PT Equation in Changing Surface Conditions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Downing, J.A.; Prairie, Y.T.; Cole, J.J.; Duarte, C.M.; Tranvik, L.J.; Striegl, R.G.; McDowell, W.H.; Kortelainen, P.; Caraco, N.F.; Melack, J.M.; et al. The global abundance and size distribution of lakes, ponds, and impoundments. Limnol. Oceanogr. 2006, 51, 2388–2397. [Google Scholar] [CrossRef]
- Polsenaere, P.; Deborde, J.; Detandt, G.; Vidal, L.O.; Perez, M.A.P.; Marieu, V.; Abril, G. Thermal enhancement of gas transfer velocity of CO2 in an Amazon floodplain lake revealed by eddy covariance measurements. Geophys. Res. Lett. 2013, 40, 1734–1740. [Google Scholar] [CrossRef]
- Long, Z.; Perrie, W.; Gyakum, J.; Caya, D.; Laprise, R. Northern lake impacts on local seasonal climate. J. Hydrometeorol. 2007, 8, 881–896. [Google Scholar] [CrossRef]
- Sharma, A.; Hamlet, A.F.; Fernando, H.J.S.; Catlett, C.E.; Horton, D.E.; Kotamarthi, V.R.; Kristovich, D.A.R.; Packman, A.I.; Tank, J.L.; Wuebbles, D.J. The Need for an Integrated Land-Lake-Atmosphere Modeling System, Exemplified by North America’s Great Lakes Region. Earths Future 2018, 6, 1366–1379. [Google Scholar] [CrossRef]
- Rouse, W.R.; Oswald, C.J.; Binyamin, J.; Spence, C.R.; Schertzer, W.M.; Blanken, P.D.; Bussieres, N.; Duguay, C.R. The role of northern lakes in a regional energy balance. J. Hydrometeorol. 2005, 6, 291–305. [Google Scholar] [CrossRef]
- Beyrich, F.; Leps, J.P.; Mauder, M.; Bange, J.; Foken, T.; Huneke, S.; Lohse, H.; Ludi, A.; Meijninger, W.M.L.; Mironov, D.; et al. Area-averaged surface fluxes over the litfass region based on eddy-covariance measurements. Bound. Layer Meteorol. 2006, 121, 33–65. [Google Scholar] [CrossRef]
- Xue, P.F.; Pal, J.S.; Ye, X.Y.; Lenters, J.D.; Huang, C.F.; Chu, P.Y. Improving the Simulation of Large Lakes in Regional Climate Modeling: Two-Way Lake-Atmosphere Coupling with a 3D Hydrodynamic Model of the Great Lakes. J. Climate 2017, 30, 1605–1627. [Google Scholar] [CrossRef]
- Dutra, E.; Stepanenko, V.M.; Balsamo, G.; Viterbo, P.; Miranda, P.M.A.; Mironov, D.; Schar, C. An offline study of the impact of lakes on the performance of the ECMWF surface scheme. Boreal. Environ. Res. 2010, 15, 100–112. [Google Scholar]
- Gu, H.P.; Jin, J.M.; Wu, Y.H.; Ek, M.B.; Subin, Z.M. Calibration and validation of lake surface temperature simulations with the coupled WRF-lake model. Clim. Chang. 2015, 129, 471–483. [Google Scholar] [CrossRef]
- McDonald, C.P.; Rover, J.A.; Stets, E.G.; Striegl, R.G. The regional abundance and size distribution of lakes and reservoirs in the United States and implications for estimates of global lake extent. Limnol. Oceanogr. 2012, 57, 597–606. [Google Scholar] [CrossRef]
- Liu, Y.B.; Wu, G.P.; Zhao, X.S. Recent declines in China’s largest freshwater lake: Trend or regime shift? Environ. Res. Lett. 2013, 8. [Google Scholar] [CrossRef]
- Liu, Y.B.; Song, P.; Peng, J.; Fu, Q.N.; Dou, C.C. Recent increased frequency of drought events in Poyang Lake Basin, China: Climate change or anthropogenic effects? Hydro-Climatol. Var. Chang. 2011, 344, 99–104. [Google Scholar]
- Granger, R.J.; Hedstrom, N. Modelling hourly rates of evaporation from small lakes. Hydrol. Earth Syst. Sci. 2011, 15, 267–277. [Google Scholar] [CrossRef]
- Lenters, J.D.; Kratz, T.K.; Bowser, C.J. Effects of climate variability on lake evaporation: Results from a long-term energy budget study of Sparkling Lake, northern Wisconsin (USA). J. Hydrol. 2005, 308, 168–195. [Google Scholar] [CrossRef]
- Bouin, M.N.; Caniaux, G.; Traulle, O.; Legain, D.; Le Moigne, P. Long-term heat exchanges over a Mediterranean lagoon. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Nordbo, A.; Launiainen, S.; Mammarella, I.; Lepparanta, M.; Huotari, J.; Ojala, A.; Vesala, T. Long-term energy flux measurements and energy balance over a small boreal lake using eddy covariance technique. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Assouline, S.; Tyler, S.W.; Tanny, J.; Cohen, S.; Bou-Zeid, E.; Parlange, M.B.; Katul, G.G. Evaporation from three water bodies of different sizes and climates: Measurements and scaling analysis. Adv. Water Resour. 2008, 31, 160–172. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. Assessment of Surface Heat-Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81. [Google Scholar] [CrossRef]
- Debruin, H.A.R. A Model for the Priestley-Taylor Parameter-Alpha. J. Clim. Appl. Meteorol. 1983, 22, 572–578. [Google Scholar] [CrossRef]
- Eichinger, W.E.; Parlange, M.B.; Stricker, H. On the concept of equilibrium evaporation and the value of the Priestley-Taylor coefficient. Water Resour. Res. 1996, 32, 161–164. [Google Scholar] [CrossRef]
- Keskin, M.E.; Terzi, O. Evaporation estimation models for Lake Egirdir, Turkey. Hydrol. Process. 2006, 20, 2381–2391. [Google Scholar] [CrossRef]
- Delclaux, F.; Coudrain, A.; Condom, T. Evaporation estimation on Lake Titicaca: A synthesis review and modelling. Hydrol. Process. 2007, 21, 1664–1677. [Google Scholar] [CrossRef]
- Guo, X.F.; Liu, H.P.; Yang, K. On the Application of the Priestley-Taylor Relation on Sub-daily Time Scales. Bound. Layer Meteorol. 2015, 156, 489–499. [Google Scholar] [CrossRef]
- Assouline, S.; Li, D.; Tyler, S.; Tanny, J.; Cohen, S.; Bou-Zeid, E.; Parlange, M.; Katul, G.G. On the variability of the Priestley-Taylor coefficient over water bodies. Water Resour. Res. 2016, 52, 150–163. [Google Scholar] [CrossRef]
- Soucha, C.; Wolfe, C.P.; Grimmtind, C.S.B. Wetland evaporation and energy partitioning: Indiana Dunes National Lakeshore. J. Hydrol. 1996, 184, 189–208. [Google Scholar] [CrossRef]
- Drexler, J.Z.; Snyder, R.L.; Spano, D.; Paw, K.T.U. A review of models and micrometeorological methods used to estimate wetland evapotranspiration. Hydrol. Process 2004, 18, 2071–2101. [Google Scholar] [CrossRef]
- Zhao, X.S.; Liu, Y.B. Phase transition of surface energy exchange in China’s largest freshwater lake. Agr. For. Meteorol. 2017, 244, 98–110. [Google Scholar] [CrossRef]
- Zhao, X.S.; Liu, Y.B. Variability of Surface Heat Fluxes and Its Driving Forces at Different Time Scales Over a Large Ephemeral Lake in China. J. Geophys. Res. Atmos. 2018, 123, 4939–4957. [Google Scholar] [CrossRef]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Raupach, M.R. Combination theory and equilibrium evaporation. Q. J. Roy Meteorol. Soc. 2001, 127, 1149–1181. [Google Scholar] [CrossRef]
- Blanken, P.D.; Spence, C.; Hedstrorn, N.; Lenters, J.D. Evaporation from Lake Superior: 1. Physical controls and processes. J. Great Lakes Res. 2011, 37, 707–716. [Google Scholar] [CrossRef]
- Spence, C.; Blanken, P.D.; Hedstrom, N.; Fortin, V.; Wilson, H. Evaporation from Lake Superior: 2 Spatial distribution and variability. J. Great Lakes Res. 2011, 37, 717–724. [Google Scholar] [CrossRef]
- Spence, C.; Blanken, P.D.; Lenters, J.D.; Hedstrom, N. The Importance of Spring and Autumn Atmospheric Conditions for the Evaporation Regime of Lake Superior. J. Hydrometeorol. 2013, 14, 1647–1658. [Google Scholar] [CrossRef]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. R. Soc. Lon. Ser. A 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Wu, G.P.; Liu, Y.B. Capturing variations in inundation with satellite remote sensing in a morphologically complex, large lake. J. Hydrol. 2015, 523, 14–23. [Google Scholar] [CrossRef]
- Wu, G.P.; Liu, Y.B. Combining Multispectral Imagery with in situ Topographic Data Reveals Complex Water Level Variation in China’s Largest Freshwater Lake. Remote Sens. 2015, 7, 13466–13484. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, G. Hydroclimatological influences on recently increased droughts in China’s largest freshwater lake. Hydrol. Earth Syst. Sci. 2016, 20, 93–107. [Google Scholar] [CrossRef]
- Li, P.; Feng, Z.M.; Jiang, L.G.; Liu, Y.; Hu, J.W.; Zhu, J.P. Natural Water Surface of Poyang Lake Monitoring Based on Remote Sensing and the Relationship with Water Level. J. Nat. Resour. 2013, 28, 1556–1568. [Google Scholar]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model. Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple parameterisation for flux footprint predictions. Bound. Layer Meteorol. 2004, 112, 503–523. [Google Scholar] [CrossRef]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of Net Ecosystem Exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Granger, R.J.; Gray, D.M. Evaporation from Natural Nonsaturated Surfaces. J. Hydrol. 1989, 111, 21–29. [Google Scholar] [CrossRef]
- Gentine, P.; Entekhabi, D.; Chehbouni, A.; Boulet, G.; Duchemin, B. Analysis of evaporative fraction diurnal behaviour. Agr. For. Meteorol. 2007, 143, 13–29. [Google Scholar] [CrossRef]
- Lhomme, J.P.; Elguero, E. Examination of evaporative fraction diurnal behaviour using a soil-vegetation model coupled with a mixed-layer model. Hydrol. Earth Syst. Sci. 1999, 3, 259–270. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Garcia, M.; Sandholt, I.; Ceccato, P.; Ridler, M.; Mougin, E.; Kergoat, L.; Morillas, L.; Timouk, F.; Fensholt, R.; Domingo, F. Actual evapotranspiration in drylands derived from in-situ and satellite data: Assessing biophysical constraints. Remote Sens. Environ. 2013, 131, 103–118. [Google Scholar] [CrossRef]
- Liu, Y.B.; Hiyama, T.; Yasunari, T.; Tanaka, H. A nonparametric approach to estimating terrestrial evaporation: Validation in eddy covariance sites. Agr. For. Meteorol. 2012, 157, 49–59. [Google Scholar] [CrossRef]
- Gao, Y.C.; Gan, G.J.; Liu, M.F.; Wang, J.F. Evaluating soil evaporation parameterizations at near-instantaneous scales using surface dryness indices. J. Hydrol. 2016, 541, 1199–1211. [Google Scholar] [CrossRef]
- Gan, G.J.; Gao, Y.C. Estimating time series of land surface energy fluxes using optimized two source energy balance schemes: Model formulation, calibration, and validation. Agr. For. Meteorol. 2015, 208, 62–75. [Google Scholar] [CrossRef]
- Gan, G.; Kang, T.; Yang, S.; Bu, J.; Feng, Z.; Gao, Y. An optimized two source energy balance model based on complementary concept and canopy conductance. Remote Sens. Environ. 2019, 223, 243–256. [Google Scholar] [CrossRef]

| Variables | The Entire Period | High-Water Period | Low-Water Period | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | |
| H (W·m−2) | −17.5 | 96.8 | 16.3 | −13.8 | 96.8 | 11.3 | −17.5 | 75.4 | 16.9 |
| LE (W·m−2) | −26.9 | 376.1 | 68.9 | −12.6 | 376.1 | 80.9 | −26.9 | 351.1 | 45.8 |
| EF (-) | −3.78 | 2.13 | 0.81 | −1.07 | 1.73 | 0.86 | −3.78 | 2.13 | 0.71 |
| Time scales | The Entire Period | High-Water Period | Low-Water Period | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | |
| Daily | 0.22 | 2.29 | 1.27 | 0.69 | 2.29 | 1.25 | 0.22 | 2.26 | 1.29 |
| Subdaily | 0.01 | 2.12 | 1.29 | 0.16 | 2.11 | 1.27 | 0.01 | 2.12 | 1.30 |
| Timescales | Variables | Statistics for Coefficients | Statistics for the Regression Equation | |||
|---|---|---|---|---|---|---|
| Daily | High-water | Coefficients | Status | Pcoeff | RMSE | r |
| A | −0.0016 | In | <0.001 | 0.146 | 0.66 | |
| VPD | 0.0148 | In | 0.001 | |||
| u | 0.0465 | In | <0.001 | |||
| Constant | 1.102 | |||||
| Low-water | Coefficients | Status | Pcoeff | RMSE | R2 | |
| A | −9.503 × 10−4 | Out | 0.106 | 0.256 | 0.58 | |
| VPD | −0.0340 | In | <0.001 | |||
| u | 0.084 | In | <0.001 | |||
| Constant | 1.096 | |||||
| 30 min | High-water | Coefficients | Status | Pcoeff | RMSE | R2 |
| A | −8.730 × 10−4 | In | <0.001 | 0.214 | 0.46 | |
| VPD | 0.0098 | In | <0.001 | |||
| u | 0.0317 | In | <0.001 | |||
| Constant | 1.168 | |||||
| Low-water | Coefficients | Status | Pcoeff | RMSE | R2 | |
| A | −0.0015 | In | <0.001 | 0.329 | 0.47 | |
| VPD | −0.0065 | In | 0.02 | |||
| u | 0.0573 | In | <0.001 | |||
| Constant | 1.197 | |||||
| Variables | Daily | 30 min | ||
|---|---|---|---|---|
| High-Water | Low-Water | High-Water | Low-Water | |
| VPD | 0.06 | −0.08 | 0.05 | −0.02 |
| u | 0.11 | 0.16 | 0.08 | 0.13 |
| A | −0.12 | 0 | −0.09 | −0.12 |
| Time Scales | High-Water | Low-Water | ||||
|---|---|---|---|---|---|---|
| RMSE (W·m−2) | Bias (W·m−2) | Mean (W·m−2) | RMSE (W·m−2) | Bias (W·m−2) | Mean (W·m−2) | |
| Daily | 11.2 | 3.4 | 105.9 | 19.1 | 1.5 | 70.4 |
| 30 min | 23.3 | 4.1 | 105.9 | 28.4 | 4.2 | 70.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, G.; Liu, Y.; Pan, X.; Zhao, X.; Li, M.; Wang, S. Seasonal and Diurnal Variations in the Priestley–Taylor Coefficient for a Large Ephemeral Lake. Water 2020, 12, 849. https://doi.org/10.3390/w12030849
Gan G, Liu Y, Pan X, Zhao X, Li M, Wang S. Seasonal and Diurnal Variations in the Priestley–Taylor Coefficient for a Large Ephemeral Lake. Water. 2020; 12(3):849. https://doi.org/10.3390/w12030849
Chicago/Turabian StyleGan, Guojing, Yuanbo Liu, Xin Pan, Xiaosong Zhao, Mei Li, and Shigang Wang. 2020. "Seasonal and Diurnal Variations in the Priestley–Taylor Coefficient for a Large Ephemeral Lake" Water 12, no. 3: 849. https://doi.org/10.3390/w12030849
APA StyleGan, G., Liu, Y., Pan, X., Zhao, X., Li, M., & Wang, S. (2020). Seasonal and Diurnal Variations in the Priestley–Taylor Coefficient for a Large Ephemeral Lake. Water, 12(3), 849. https://doi.org/10.3390/w12030849






