1. Introduction
Sustainable Urban Drainage Systems (SUDs) have gained relevancy as efficient solutions for optimal water management in urban areas. While traditional management seeks to rapidly harvest runoff to be treated and discharged to watercourses, SUDs represent a new paradigm that seeks to handle runoff locally. SUDs encompass different types of facilities such as green roofs, permeable pavements, infiltration trenches, detention areas, rain gardens, etc.
Several initiatives have recently been developed to install SUDs in urban areas [
1,
2,
3,
4]. Scientific literature has widely focused on this topic [
5,
6,
7], some studies have addressed the optimal SUD combination at the urban planning stage [
8,
9,
10,
11,
12], while others have studied possible locations or have proposed multi-objective functions for determining the optimal SUDs location [
13,
14,
15,
16].
Despite the number of studies addressing SUDs, some unsolved questions remain. First, a detailed definition of the SUD design aim has not been thoroughly discussed by the literature that, in most cases, does not go beyond simple goals such as minimizing runoff, maximizing aquifer recharge, or minimizing cost functions. From a theoretical point of view, this target has to be considered in close relation to the set of variables involved in the whole hydrological system since SUDs alter several processes involved. For example, runoff detainment reduces surface discharge to watercourses which, although desired above certain levels, undoubtedly limits streamflow which can affect ecological flows. Otherwise, infiltration of stored runoff into vegetated soils through for example infiltration trenches without further consideration of evapotranspiration could lead to water losses by deep percolation.
Similarly, SUDs design criteria have traditionally relied on the same design standards of traditional draining infrastructures. Standards of SUDs design usually seek to mimic the hydrology of the pre-development state [
17] setting up limits of peak flow and runoff volume for different storm events. In line with such guidelines, studies aimed at either defining general planning strategies or particular SUDs design, often use specific extreme events for analyzing SUDs behavior. Several authors have discussed the validity of using extreme storm events for SUDs design based on the fact that such facilities are not aimed at collecting runoff with security purposes but for managing runoff [
18].
Otherwise, studies aimed at finding the optimal SUDs combination at the planning stage usually chose among a set of enclosed alternatives encompassing a reduced type of SUDs whose set-up was previously defined, (see, for example, [
19]). Studies tackling SUDs design comprising all possible combinations, even the absence, of SUDs to deduce the optimal solution are still lacking.
The present paper proposes a method for determining the optimal SUDs combination at a city scale encompassing the complete hydrological system. A comprehensive set of SUDs categories comprising infrastructures aimed at either detaining and locally reusing runoff or infiltrating precipitation is considered. For that purpose, hydrological dynamics are modeled with a water balance. A multi-criteria decision process encompassing both economic and hydrological aims completes the framework.
2. Materials and Methods
The state equation for a linear hydrological system (Equation (1)) relates inputs (
IP), outputs (
O) and internal system variation (
S) as time functions:
For the proposed urban hydrological cycle, the soil water content (
θ) varies as a result of evapotranspiration (
ETk), precipitation (
P), aquifers recharge (
D) and runoff (
R).
Three types of SUD categories comprising most of the SUD facilities were considered:
1. SUDs aimed at detaining and storing runoff for local reuse
The set of SUDs aimed at detaining and storing runoff are defined in the present model as
ki rates of runoff detained at each
i land use, while the remaining portion of
R goes to conventional urban draining infrastructure (
CUD).
The summation in (3) represents the volume of water stored (VSUD) for local reuse. The maximum value for the summation in Equation (3) represents the maximum volume of water to be stored which in turn represents the SUDs design parameter (VSUDMAX). Storing tanks or ponds for local reuse, infiltration trenches or wells, infiltration cells, rain gardens, etc. can be included within this SUDs category.
2. SUDs aimed at easing the direct infiltration of precipitation
Porous pavements, or equivalent facilities, are included in the model by the particular definition of the infiltration properties of each land use. For that purpose, kppi rates representing the portion of the total area occupied by porous pavements were defined for each i land use, and specific infiltration properties were assigned to these areas.
3. Green roofs
Green roofs were incorporated as green areas where runoff directly goes to CUD, infiltrated water stores within the soil up to saturation level, infiltrated water after the saturation is reached discharges to CUD, plants consume the soil water at ETk rate and the potential water deficit is covered with I. Similarly, kgri rates define the proportions of each land use occupied by green roofs.
Upon this general structure, the water balance (Equation (2)) simulations were run with the following assumptions.
After an initial soil water content (θ0) was defined, the subsequent estimation of θ allowed determining the daily irrigation requirements by comparison between the estimated θ and the triggering irrigation threshold (θr). If θ < θr, then VSUD, if any, was used to increase θ to θFC. In the event of VSUD to be insufficient to increase θ to θFC, external irrigation (I) was provided.
Daily potential evapotranspiration and precipitation were used to run the model daily. For a data series of several years, the daily average value of a sort of median interval (values within the interval mean ± 1.5×standard deviation) was used. Therefore, a representative climatic year was selected to run the water balance.
The incoming water to VSUD exceeding its storage capacity (VSUDMAX) discharged to CUD.
The aquifer was recharged (D) by the water infiltrated into the vegetated soil after θ equals saturation (θs) and by the infiltrated water, if any, in paved areas. In green roofs, runoff and excess of infiltrated water when θ exceeds saturation level also discharged to CUD.
To avoid problems arising with regard to the duration of storm events, and to simplify the incorporation of porous pavements and green roofs to the water balance, the Soil Conservation System curve number method was used to estimate runoff volumes. Each daily precipitation value was supposed to define a unique storm event.
The water balance was computed, for each possible combination of SUDs implemented by
ki,
kgri and
kppi, daily, with daily
P and
ETk (a crop coefficient
kcc = 1 was considered to transform
ET0 into
ETk) data and supposing
θ0 to be 0.2. The annual aggregated
D,
I and
CUD were estimated and the following cost function was computed for each SUDs combination. The sets of SUDs minimizing
CT (Aggregated cost) and complying with the constraints were selected.
where:
VSUDMAX represents the runoff storing capacity.
CUVSUD is the unitary cost (€/m3) of the storing elements.
CUSUDi is the unitary cost (€/m3) of detaining, storing and reusing runoff at each land use.
CUCUD represents the unitary cost (€/m3) of managing runoff through conventional draining facilities.
CUI is the unitary cost of irrigating (€/m3).
CUpp is the unitary cost of porous pavements (€/m2).
CUgr represents the unitary cost of green roofs (€/m2).
Σkppi × Si and Σkgri × Si represent the areas occupied by either porous pavements or green roofs.
Two hydrological objectives were added to economic criteria:
D ≥ Dmin: the aquifer to be recharged above a given limit seeking to either comply with environmental objectives or to replenish water withdrawals.
CUDmin ≤ CUD ≤ CUDmax: supposed that CUD finally goes to watercourses, this constraint seeks to maintain ecological flows but not exceeding an upper limit to prevent flooding risks.
The unknowns of the optimization problem were VSUDMAX and kppi, kgri, and ki rates.
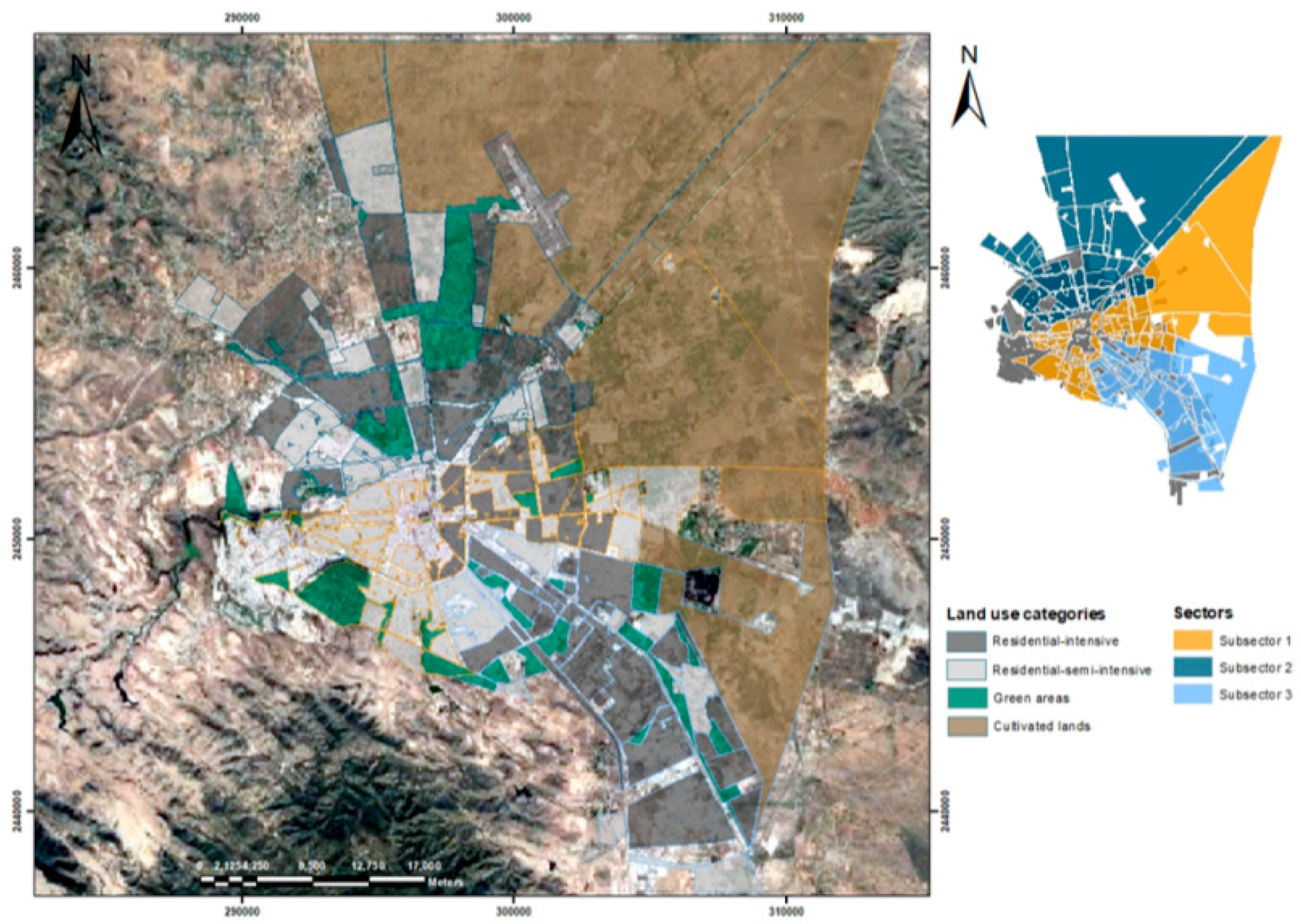
Case Study
The Metropolitan Area of San Luis Potosí is located approximately 400 km north-west of México City at the south-east end of the Sierra Madre Occidental with an area of 2409.2 km
2 (see
Figure 1).
The region has a semiarid climate with mean temperature, precipitation, and potential evapotranspiration around 17 °C, 400 mm, and 2033 mm, respectively [
20]. The valley of San Luis Potosí, located at the hydrological region 37 “El Salado,” has no natural perennial surface drainage. The total availability of surface water stored in dams to supply the Metropolitan Area of San Luis Potosí is 10.176 Mm
3 [
21]. Yearly average groundwater extraction amounts to approximately 125.6 Mm
3 per year distributed as follows (see
Table 1).
The installed capacity of wastewater treatment plants is 1889.4 L/s (
Table 2) and the treated flow 1575.89 L/s [
22].
Three catchments were delineated in the metropolitan area of San Luis Potosí for analyzing SUDs alternatives.
Figure 2 depicts the identified catchments and
Table 3 presents the land use areas within each catchment.
3. Results
Table 4 presents the costs used in the optimization model.
CUCUD,
CUI, and
CUVSUD were retrieved from [
18];
CUSUDin,
CUSUDsin,
CUSUDzzvv,
CUSUDag,
CUpp, and
CUgr were defined with the aid of local agents. These costs, in particular the ones for porous pavements and green roofs, agree with the SUDs costs in other studies, for example in [
18]. The costs were updated at a hypothetical starting project date and include both building and operation costs.
Table 5 presents the Curve Number values (
CNs) used for runoff estimation.
Table 6 and
Table 7 present the estimates obtained with Equation (2) for, respectively, the current land use distribution presented in
Table 3 and the hypothetical original situation where the entire land would be completely occupied by rural areas.
For finding the optimal combination of SUDs the cost function was defined as follows.
Potential areas suitable for porous pavements and green roofs do not reach the total area of each land use (kppi, kgri ≤ 0.3) as such facilities can only be installed at certain zones (green roofs at buildings and porous pavements out of buildings and unpaved areas). In addition, it was assumed that only at in and sin land uses green roofs can be installed while only in, sin and zzvv lands are suitable for porous pavements. On the contrary, kin, ksin, kzzvv, and kag were let to vary between zero and one as it was assumed that the runoff detention rate can perfectly vary between zero and one. VSUDMAX was limited to the maximum runoff appearing if the maximum precipitation (historical data series) falls.
Replenishing water withdrawals was considered for limiting
D. For each catchment,
D was imposed to be larger than the proportional rate (according to the area of each catchment over the total area of San Luis Potosí) of the annual aquifer extractions estimated to be 1.25 × 10
6 m
3/year (see
Table 1).
The amount of runoff conveyed to
CUD to feed watercourses was imposed to be smaller than the pre-development values (
Table 6) and larger than the supposedly original ones (
Table 7) to ensure that SUD implementation keeps potential ecological flow rates without increasing the actual flooding risk.
Table 8 summarizes the limits for
D and
CUD.
The multi-objective problem was solved to find the combination of
kin,
ksin,
kzzvv,
kag,
kppin,
kppsin,
kppzzvv,
kgrin,
kgrsin, and
VSUDMAX complying with the proposed restrictions and minimizing the cost function. All possible combinations of these variables were checked computing the water balance and
CT, and the optimal values were obtained (
Table 9).
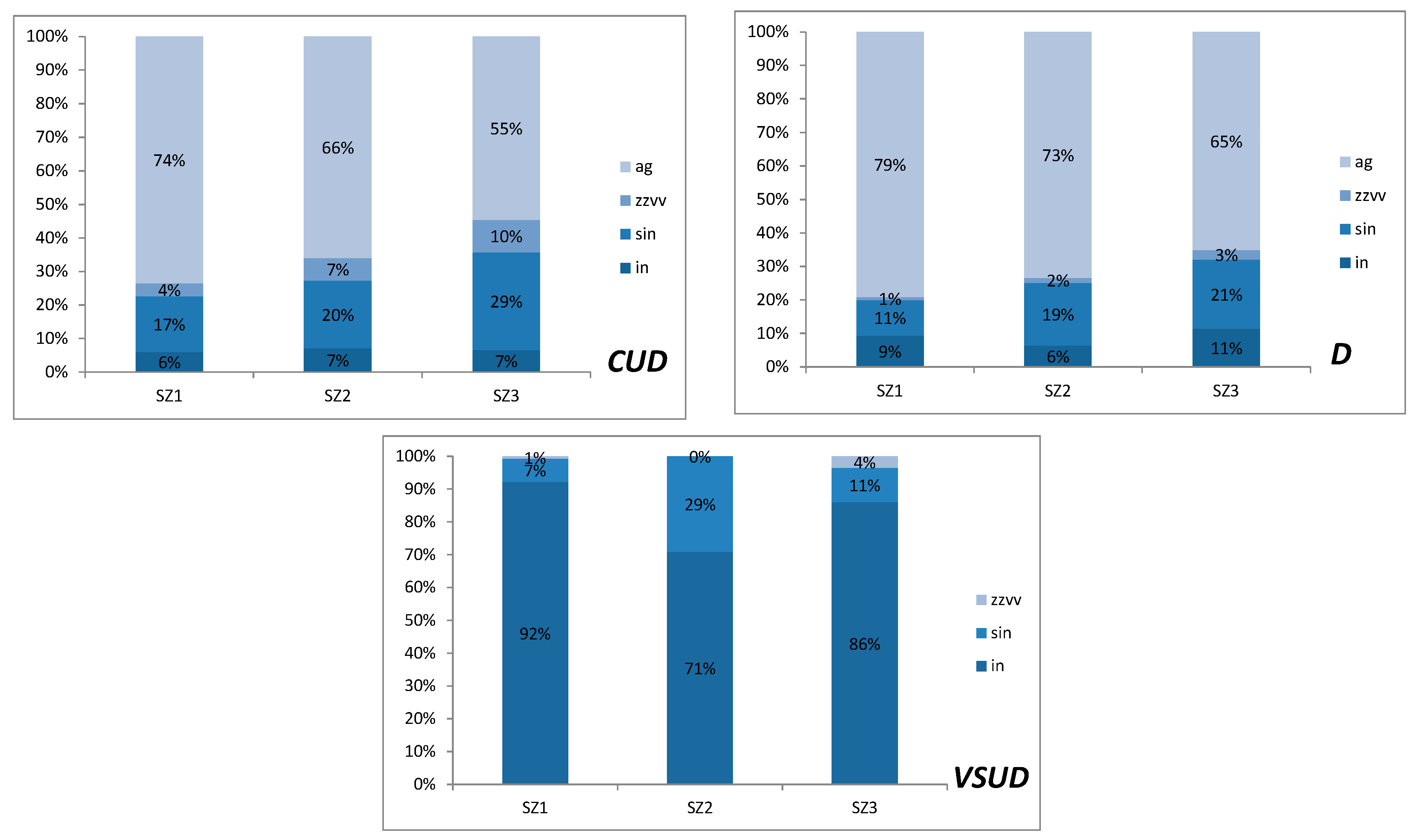
From
Table 9, it can be observed that green roofs and porous pavements are penalized by their larger cost in comparison with the costs of the facilities aimed at collecting and reusing runoff.
Table 10 present the main variables of the water balance for the optimal SUDs combinations.
As it could be expected, the optimal SUDs combinations managed to reduce
CUD to practically reach the pre-development state while
D largely exceeds the established minimum thresholds.
D and
CUD mostly come from rural areas while runoff stored in
VSUD is almost entirely detained in intensive and semi-intensive land use (
Figure 3).
Different scenarios were studied for each catchment (
Table 11) either developing residential intensive areas at the expense of rural lands (keeping constant semi-intensive and green zones) or developing semi-intensive areas on rural lands (keeping constant intensive and green zones). The considered scenarios are presented in
Table 11.
Figure 4 shows
D and
CUD calculated for each scenario together with their proposed thresholds (
Dmin,
CUDmin,
CUDmax).
Continuous lines displayed in
Figure 4 represent
D and
CUD for the optimal SUDs combinations (
Table 3). Developing semi-intensive urban areas at the expense of rural lands does not imply failing in the proposed objectives except in SZ1 and SZ2 where
CUD exceeds the upper limit for developments larger than those considered in scenarios 2 and 6, respectively. On the contrary, intensive developments more frequently break the objectives:
CUD above scenario 2 and
D above scenario 9 in SZ1;
CUD above scenario 2 and
D above scenario 7; SZ2 and
CUD above scenario 4 and
D above scenario 3 in SZ3.
Dashed lines presented in
Figure 4 display
D and
CUD for the new optimal (cheapest) combination of either
kgrin,
kppin, and
kin (intensive developments) or
kgrsin,
kppsin, and
ksin (semi-intensive developments) required for the developments for the entire catchment to comply with the original constraints. That is, each new urban development altering the water balance to fail in meeting the objectives for
D and/or
CUD, shall be required to provide a SUD combination such that the whole catchment complies with the original targets.
Table 12 presents the new optimal (minimum cost) SUDs combination required for the new developments for the catchment to meet the original objectives.
Urban developments are mainly required to detain and reuse runoff and, when necessary, porous pavements and green roofs are also required to preserve the limits for D and CUD.
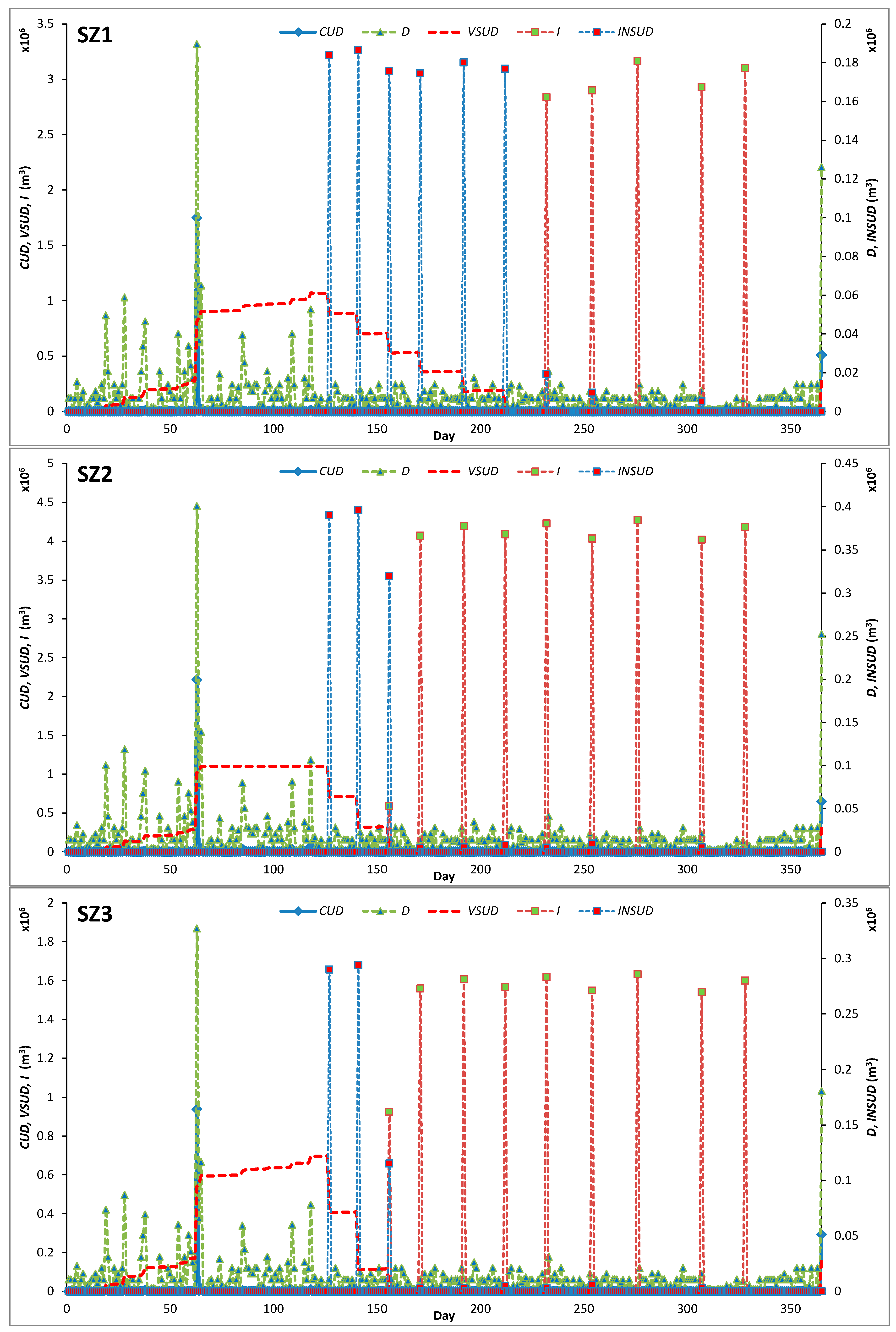
Figure 5 presents the expected evolution of the main water balance variables throughout the representative year using daily climatological data,
θ0 = 0.2 and
VSUDMAX = 0 at
t = 0.
Similar patterns were observed in the three analyzed catchments: VSUD is filling during the initial part of the year, supplying water to fulfill the irrigation requirements of three irrigation events (INSUD) at SZ2 and SZ3 and six at SZ1. VSUDMAX almost empties after days 210 (SZ1), 150 (SZ2) and 160 (SZ3), from which irrigation is mostly provided by external sources.
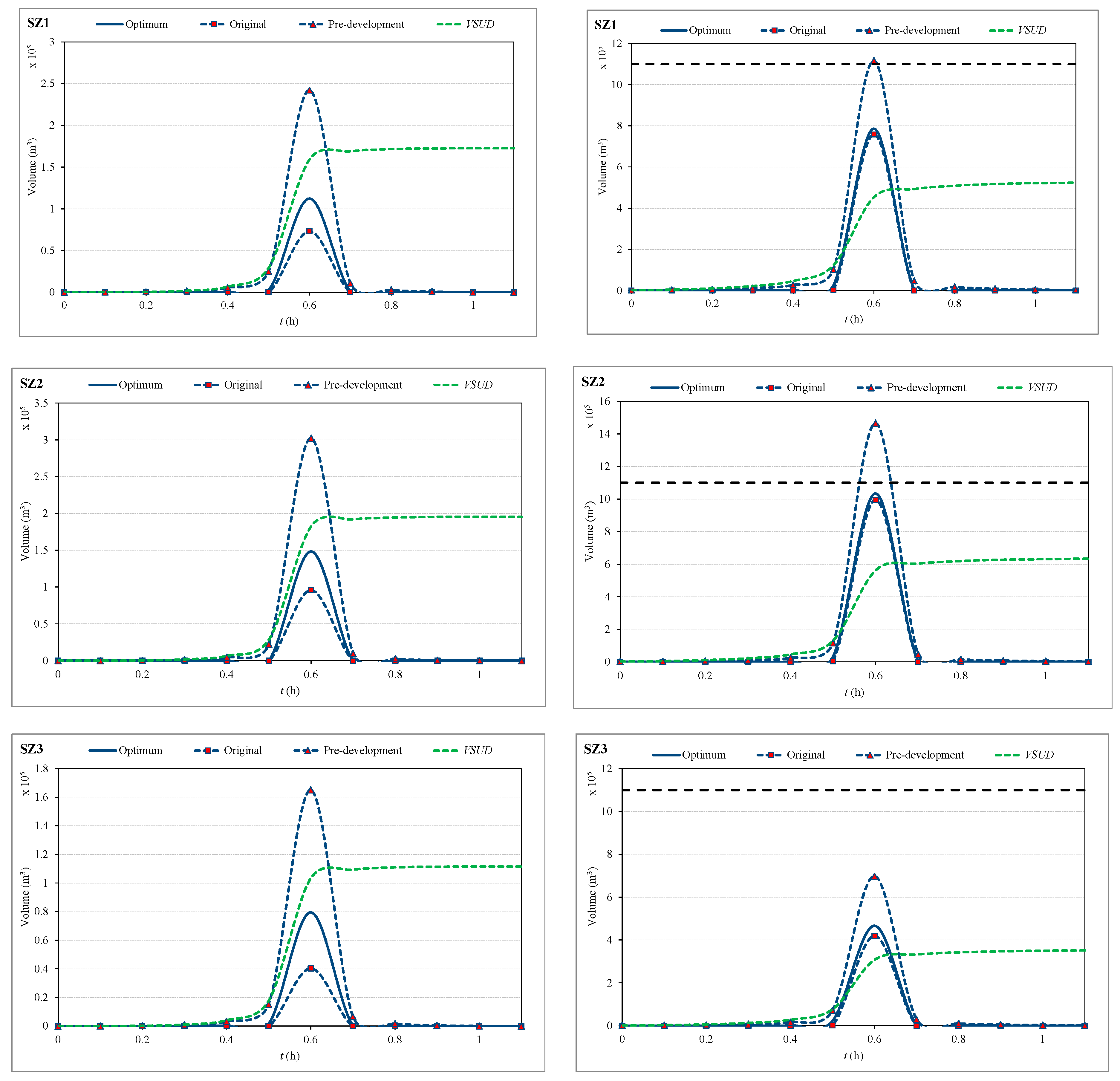
Figure 6 presents the operation of the SUDs storing elements and
CUD for a 1.1 h duration storm event of either 5 or 100 years return period and for the optimal SUDs combinations. The expected evolution of
CUD in the pre-development (actual) and the runoff discharge to watercourses in the supposedly original (only rural areas) states have also been depicted in
Figure 6.
The presence of SUDs helps reduce the peak flow at any catchment and return period compared to the actual (pre-development) situation.
VSUDMAX does not fill in any case. The peak flow observed with the optimal SUDs combination is not delayed with respect to the original or pre-development cases because runoff is not completely collected and thus it is continuously discharging to
CUD.
Figure 7 presents the
CUD increase, or reduction, for the analyzed storm events as a result of the SUDs implementation and the stored volume at
VSUD during the studied events as well.
From
Figure 7, it can also be observed that the proposed optimal solutions help mimic the original situation with regards to the discharged volume so the traditional requirements for SUD design (see, for example, [
18]) would be met.
4. Discussion
We have addressed the study of the optimal SUDs combination to comply with both economic and hydrological goals. For this purpose, we have developed a Python code instead of using other models as SWMM [
23,
24]. It provided us with greater flexibility to perform specific studies such as the requirements for new developments to ensure the initial hydrological objectives are met. Although the Metropolitan Area of San Luis Potosí does not have a monitoring network for calibration and validation of the results, the estimates agree with the information of the treatment plants which could be considered an indirect validation of the model performance. Ideally, validation processes are needed to ensure the suitability of the assumptions and they must be incorporated if available.
We focused on the optimal SUDs provision from an open insight without more limitations than those related to costs, aquifer recharge, and contribution to watercourses. This approach seeks to provide the best SUDs combination aimed at mimicking the pre-development status. Other authors have focused on either finding the best SUDs combination among the enclosed set of SUD combinations [
24,
25] or determining the optimal SUDs location [
26]. In this paper, we are not delivering guidelines on where to locate SUDs facilities or proposing enclosed SUDs packages. We focus on the entire urban catchment and define the optimal solution in terms of minimum cost, required aquifer recharge, and watercourses contribution.
We considered three groups of SUDs comprising the majority of SUDs facilities aimed at either detaining and locally reusing runoff or increasing infiltration rates. Other particular SUD facilities could also be incorporated by properly defining their effect on each variable of the water balance. The method yielded the optimal SUDs combination for the catchment by comparing the results of each potential SUD combination with both the actual status and the supposedly original configuration before the urban area was developed. It allowed us to propose general criteria to be met by any other future urban development within the catchment to preserve the original targets. As a result of it, the optimal SUDs combination required for any potential urban development for ensuring that the entire catchment meets the original criteria was estimated.
The solution is sensitive to costs and the resulting optimal SUDs combinations presented in this paper are only valid for the Metropolitan Area of San Luis Potosí. The particular costs, even the set of costs, considered in this work might not be completely suitable for other regions. The issues of the cost function have to be carefully analyzed for each case-study and their temporal consistency must be ensured. The theoretical framework, based on a multi-criteria approach encompassing both economic and hydrological goals, is, however, valid for any other location.
It can be assumed that, on average, the deduced optimal SUDs rates (ki, kgri, and kppi) generate the estimated I, CUD, and D values as we used representative climatic data. However, the real I, CUD, and D volumes with the optimal SUD combinations strongly depend on climatic variables. Occasionally, real values could deviate from estimates as average climatic data were used to deduce the optimal combinations. However, the aggregated results should not differ from the estimates provided that the average values were calculated using data representative of local weather conditions. In this paper, we use the average value of the median interval as we assumed that this metric better represented the nature of the data series. Any other method of providing representative values should be valid.
Other authors have also presented different multi-objective [
27] or multi-criteria [
13,
24] routines but to the author’s best knowledge none of them come up with comprehensive constraints comparable to those considered in the present paper. Most of the previous studies pose simple minimization criteria for costs or flooding, for example. On the contrary, we incorporate criteria/objectives aimed at minimizing costs and mimicking the pre-development status. It implies defining an upper limit for flooding to prevent damages, a lower limit also for flooding (or more to the point for watercourses discharge) to ensure ecological river levels and finally a minimum aquifer recharge to cover extraction rates.
The approach presented in this paper differs from those considered in various standards for example [
17] that only define thresholds of peak flow and volume for particular storm events. The methodology developed in this paper does not focus on storm events but the daily evolution of the selected variables. Despite the different design approaches, the deduced optimal solutions were also checked to comply with the proposed goals for two storm events yielding satisfactory results.
5. Conclusions
A multi-objective decision model comprising economic and hydrological criteria is proposed to estimate the optimal SUDs combination at the urban catchment scale. Economic criteria were incorporated by a cost function encompassing costs of SUDs installation and operation. Hydrological criteria consisted of thresholds for ensuring a minimum groundwater recharge rate and both upper and lower limits for runoff to prevent flooding damages and ensure a minimum runoff contribution to watercourses. A conceptual method based on a volumetric water balance was performed to estimate the daily evolution of hydrological processes.
The method is based on urban catchments and yields the optimal SUD combination considering detention and local reuse facilities (infiltration facilities, rain gardens, or similar), green roofs, and porous pavements. The method, and the theoretical general framework, were probed for validity to find the optimal SUD combination in three urban catchments at the Metropolitan Area of San Luis Potosí (México). In this case, the optimal solutions promoted surface runoff detention and reuse over porous pavements and green roofs.
Some key points to be customized for each application have to be carefully considered, in particular: identifying representative statistics for incorporating climatic information and defining the proper set of representative costs ensuring their temporal consistency. The requirements for future urban developments for the entire catchment to keep accomplishing the original hydrological targets were estimated. It allows incorporating comprehensive SUD planning criteria for the sustainability of urban catchments to be preserved by new potential developments.
It must be remarked that the real operation of the SUD facilities could differ from the model estimates as average climatological data were used. Despite this, SUD operating conditions during particular storm events were checked and the results showed their suitability to practically mimic the pre-development status for both 5 and 100 years return period and 1.1 h duration storm events.