Modeling of the Free-Surface Vortex-Driven Bubble Entrainment into Water
Abstract
1. Introduction
2. Model Description
2.1. The GENTOP Concept
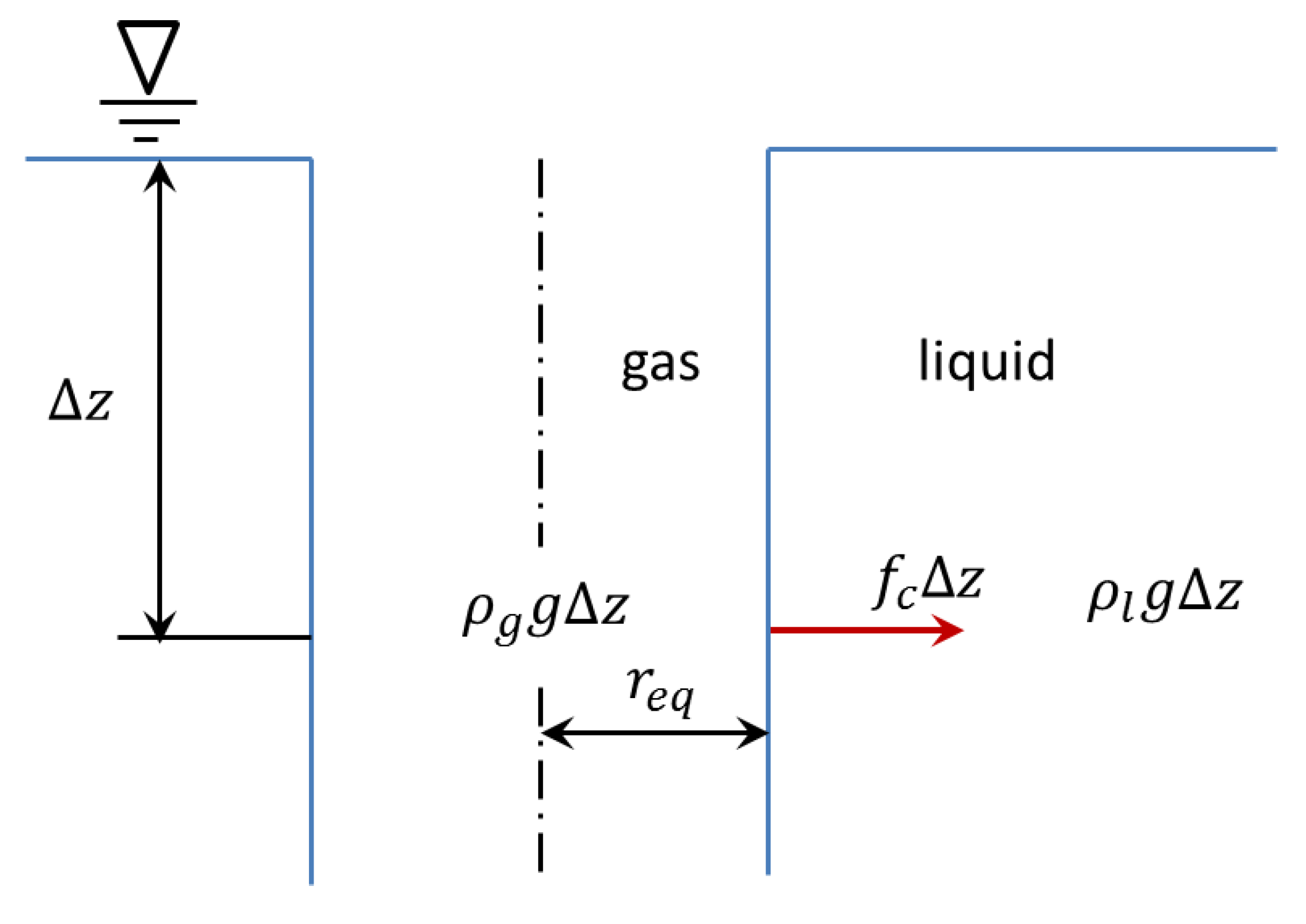
2.2. The New Entrainment Model
2.3. The Turbulence Model
3. CFD Set-Up
4. Results and Discussion
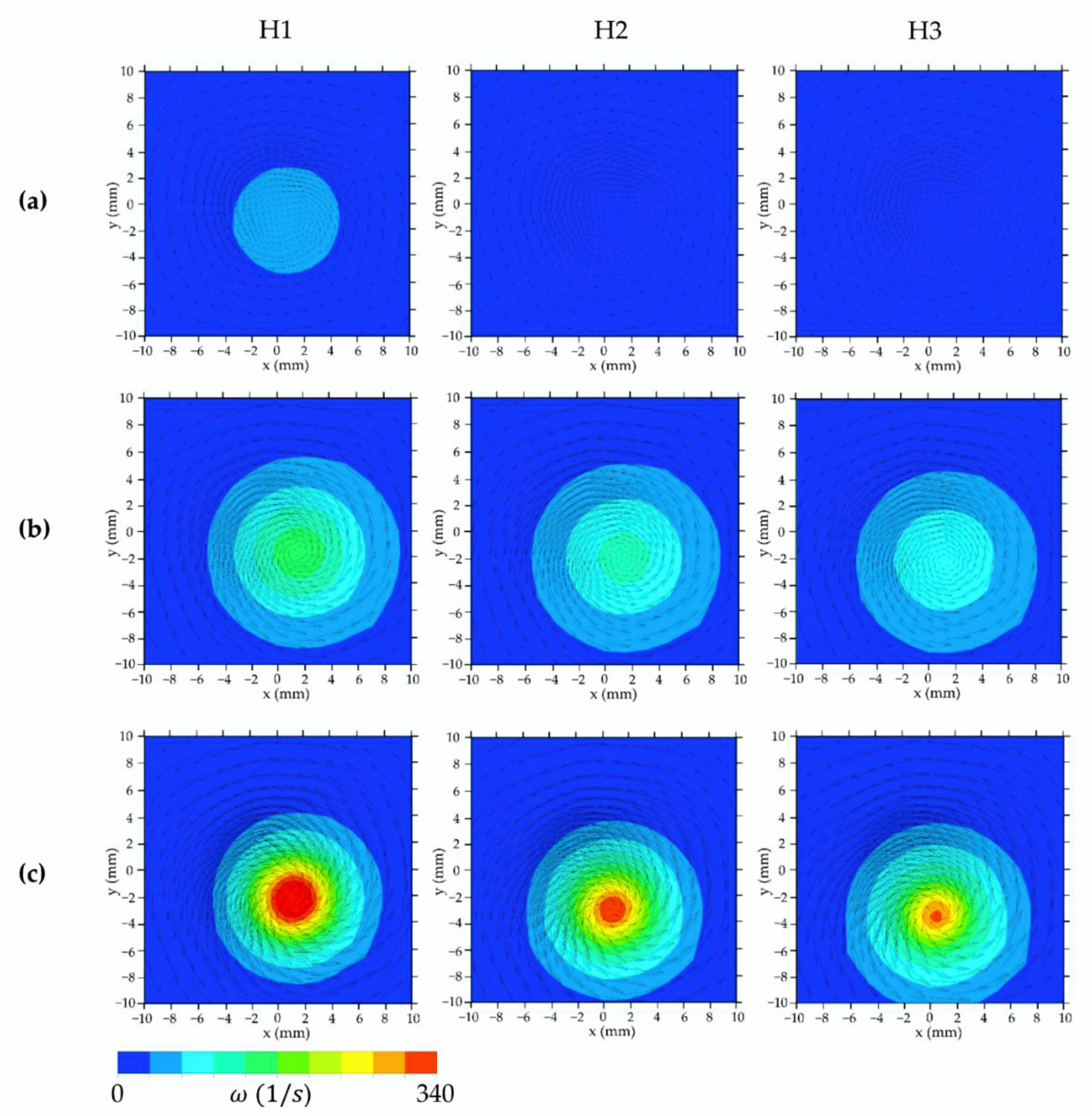
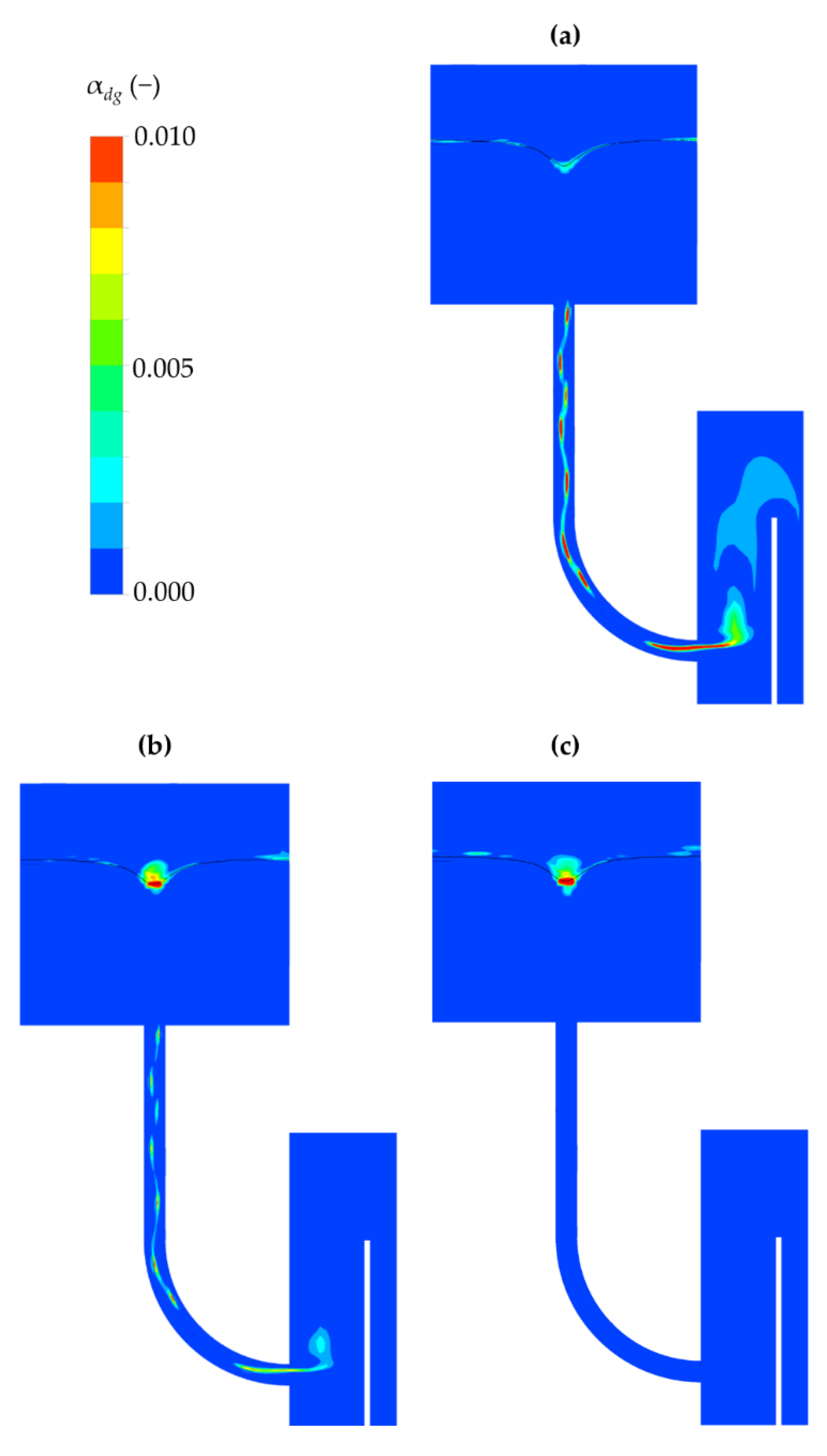
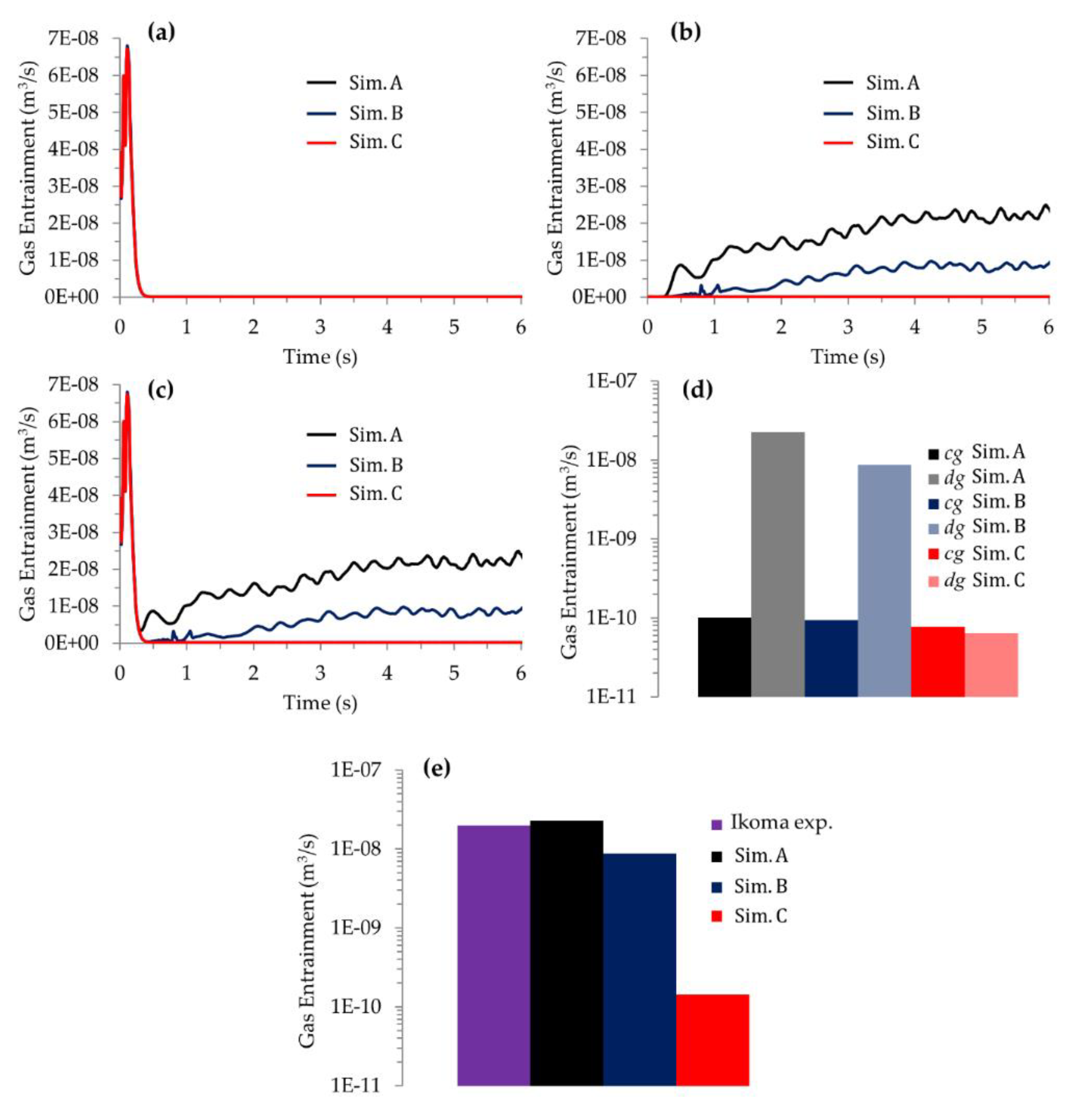
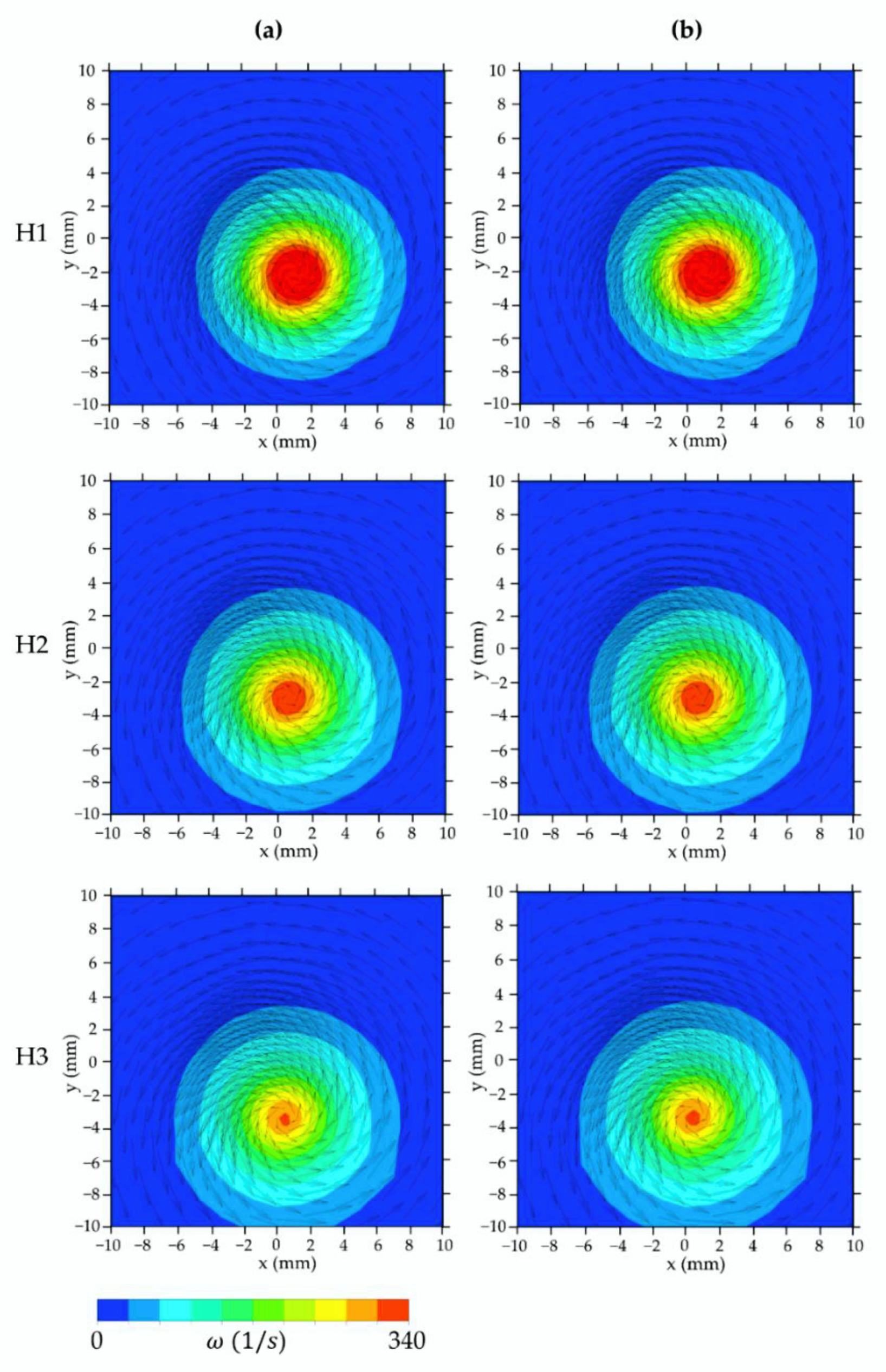
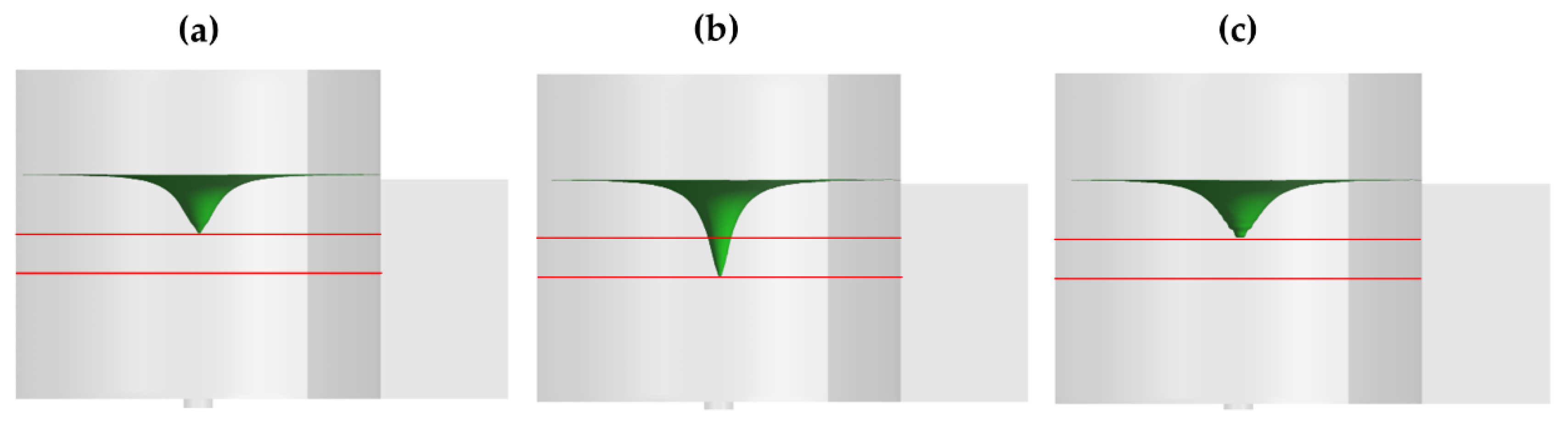
4.1. The Influence of the Turbulence Model
4.2. The Influence of Entrained Bubble Size Distribution
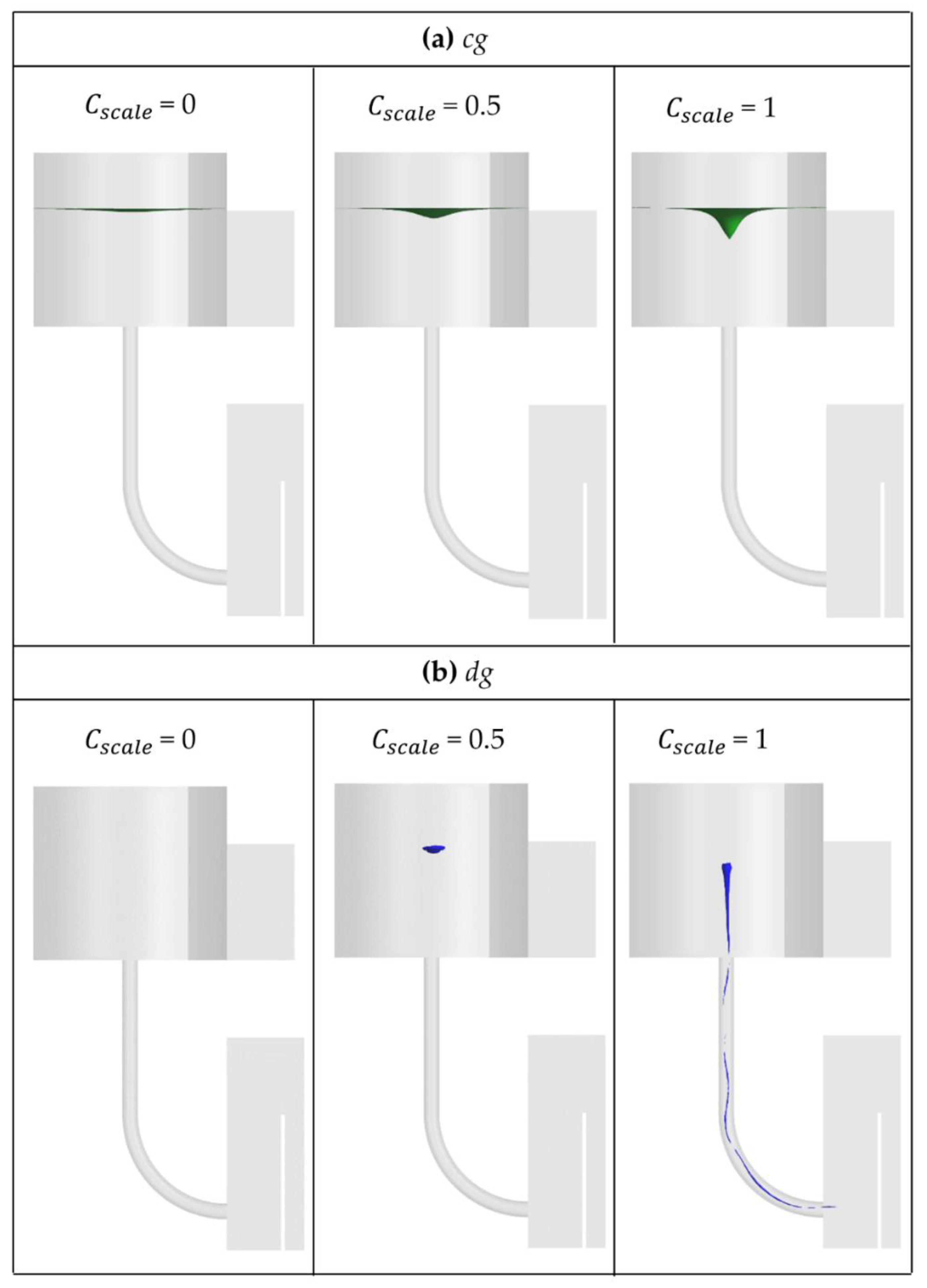
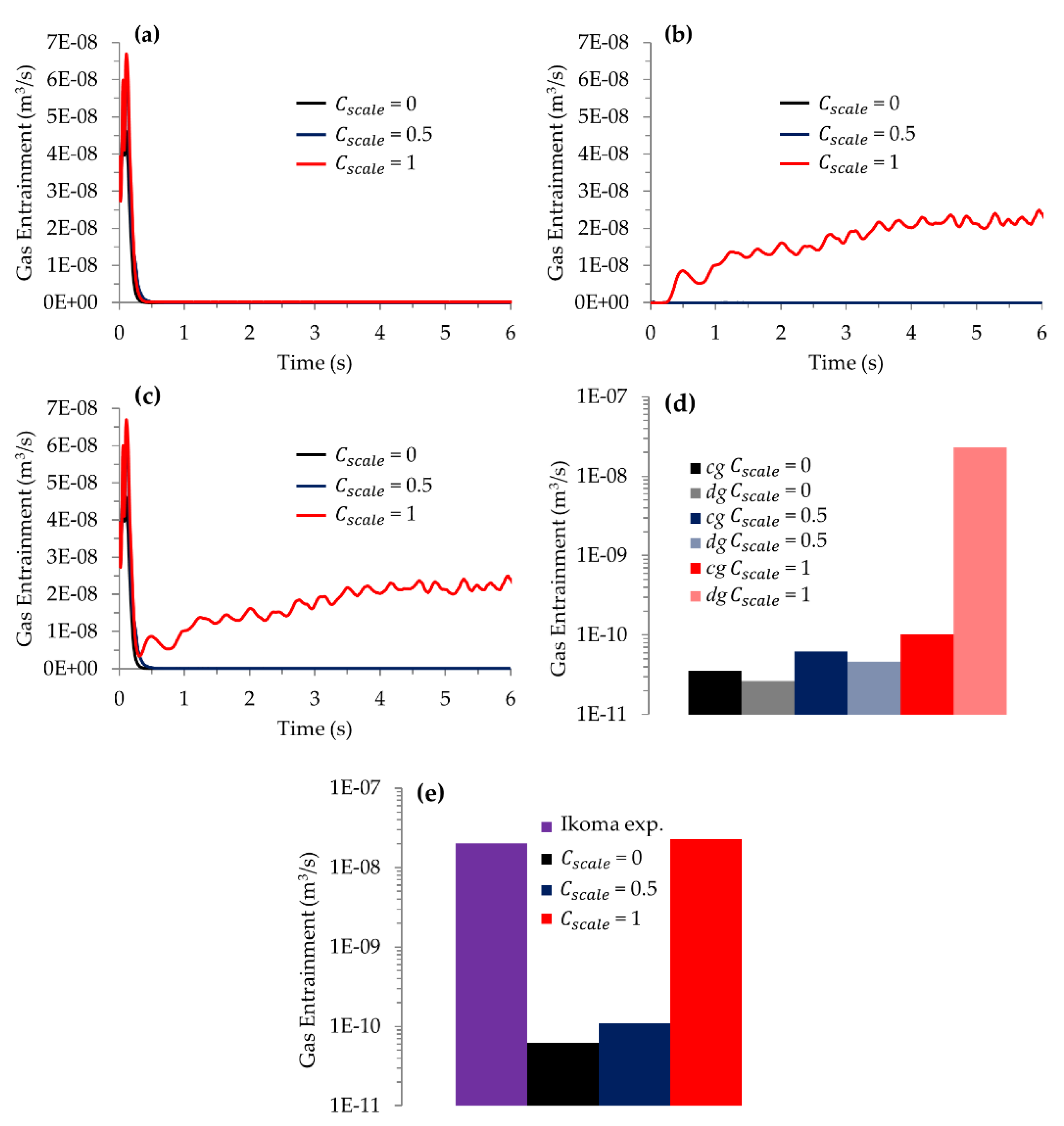
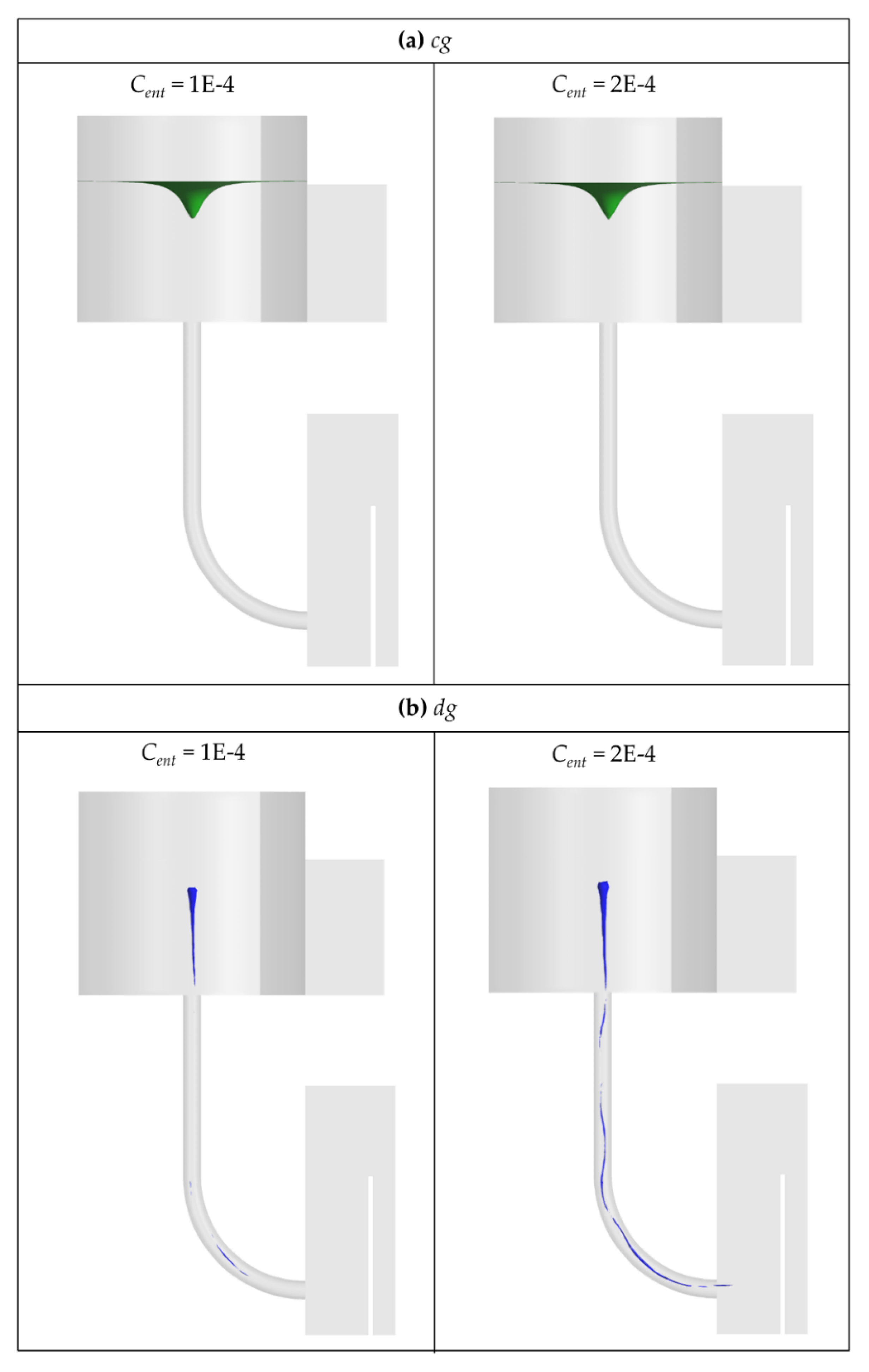
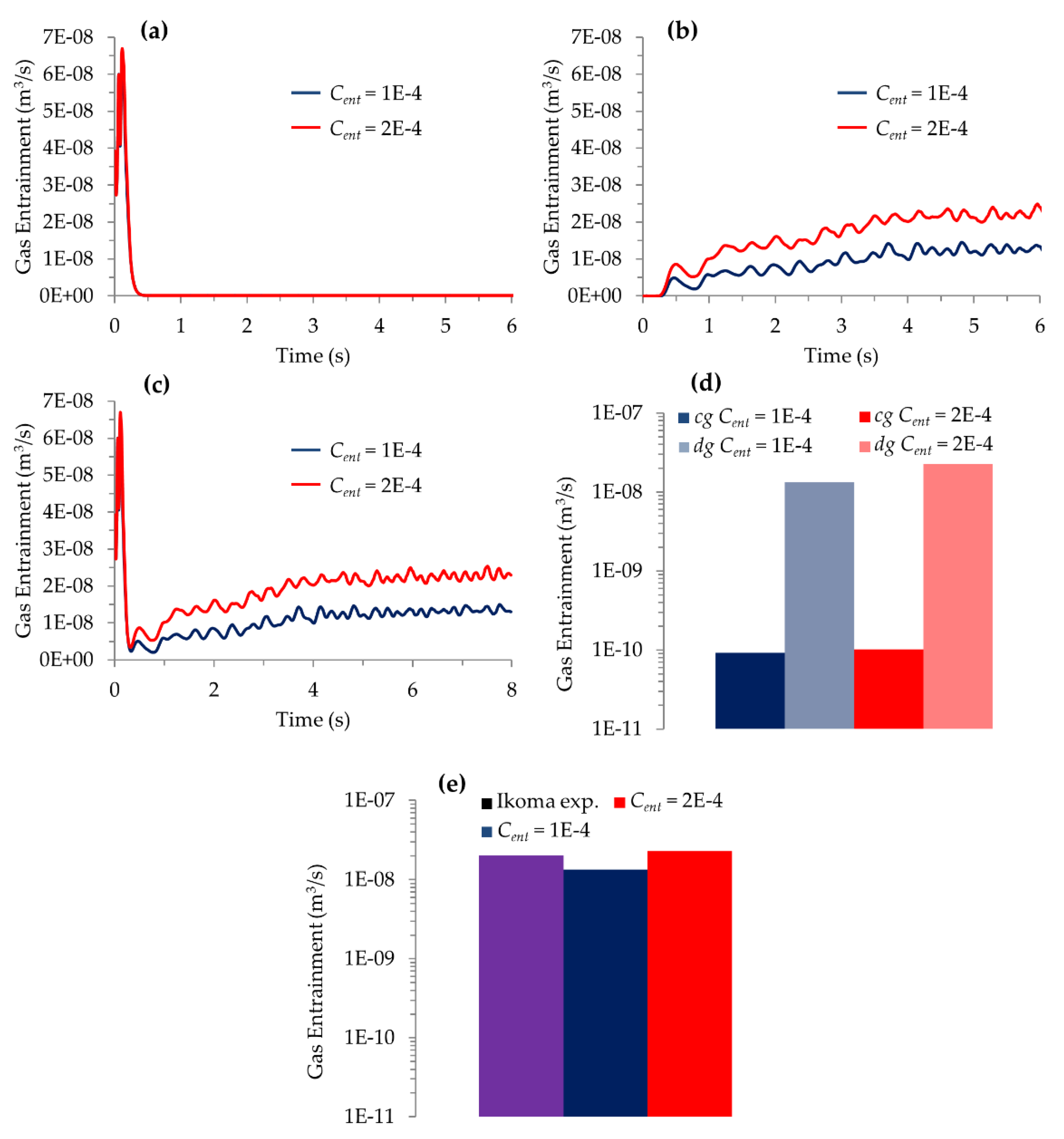
4.3. The Influence of the Entrainment Coefficient
4.4. The Influence of the Computational Cell Size
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin symbols | |
| interfacial area density (m−1) | |
| drag coefficient (dimensionless) | |
| entrainment coefficient (m s−1) | |
| lift coefficient (dimensionless) | |
| scaling coefficient of curvature correction (dimensionless) | |
| virtual mass coefficient (dimensionless) | |
| wall force coefficient (dimensionless) | |
| shear-induced turbulence coefficient (dimensionless) | |
| D | pipe diameter (m) |
| bubble diameter (m) | |
| maximum horizontal dimension of a bubble (m) | |
| Eötvös number (dimensionless) | |
| modified Eötvös number (dimensionless) | |
| force (N m−3) | |
| gravitational acceleration (m2 s−2) | |
| momentum transfer term (kg m−2 s−2) | |
| pressure (Pa) | |
| Reynolds number (dimensionless) | |
| momentum source due to external body forces (kg m−2 s−2) | |
| mean velocity magnitude (m s−1) | |
| velocity vector (m s−1) | |
| time (s) | |
| y | distance to the wall (m) |
| axial distance (m) | |
| Greek symbols | |
| volume fraction (dimensionless) | |
| characteristic cell length scale (m) | |
| dynamic viscosity (Pa s) | |
| density (kg m−3) | |
| surface tension (N m−1) | |
| turbulent Schmidt number (dimensionless) | |
| blending function (dimensionless) | |
| Subscripts and superscripts | |
| free surface | |
| phase index | |
| gas | |
| liquid | |
| virtual mass | |
| wall | |
References
- Shapiro, A.H. Bath-Tub Vortex. Nature 1962, 196, 1080–1081. [Google Scholar] [CrossRef]
- Forbes, L.K.; Hocking, G.C. The bath-plug vortex. J. Fluid Mech. 1995, 284, 43–62. [Google Scholar] [CrossRef]
- Andersen, A.; Bohr, T.; Stenum, B.; Rasmussen, J.J.; Lautrup, B. The bathtub vortex in a rotating container. J. Fluid Mech. 2006, 556, 121–146. [Google Scholar] [CrossRef]
- Gjevik, B.; Moe, H.; Ommundsen, A. Sources of the Maelstrom. Nature 1997, 388, 837–838. [Google Scholar] [CrossRef]
- Jain, A.K.; Raju, K.G.R.; Ramachandra, G.J. Vortex formation at vertical pipe intakes. Asce J. Hydraul. Div. 1978, 104, 1429–1445. [Google Scholar]
- Odgaard, A.J. Free-surface air core vortex. J. Hydraul. Eng. 1986, 112, 610–620. [Google Scholar] [CrossRef]
- Rindels, A.J.; Gulliver, J.S. An experimental study of critical submergence to avoid free-surface vortices at vertical intakes. In Project Report No. 224 University of Minnesota St. Anthony Falls Hydraulic Laboratory, Minneapolis; University of Minnesota: Minneapolis, MN, USA, 1983. [Google Scholar]
- Denny, D.F. An experimental study of air-entraining vortices in pump sumps. Proc. Inst. Mech. Eng. 1956, 106–125. [Google Scholar] [CrossRef]
- Chuang, W.L.; Hsiao, S.C.; Hwang, K.S. Numerical and experimental study of pump sump flows. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Yang, J.; Andreasson, P.; Högström, C.-M.; Teng, P. The Tale of an Intake Vortex and Its Mitigation Countermeasure: A Case Study from Akkats Hydropower Station. Water 2018, 10, 881. [Google Scholar] [CrossRef]
- Banerjee, I.; Sundararajan, T.; Sangras, R.; Velusamy, K.; Padmakumar, G.; Rajan, K.K. Development of gas entrainment mitigation devices for PFBR hot pool. Nucl. Eng. Des. 2013, 258, 258–265. [Google Scholar] [CrossRef]
- Satpathy, K.; Velusamy, K.; Patnaik, B.S.V.; Chellapandi, P. Numerical simulation of liquid fall induced gas entrainment and its mitigation. International Journal of Heat and Mass Transfer 2013, 60, 392–405. [Google Scholar] [CrossRef]
- Baum, M.R. Gas entrainment at the free surface of a liquid: Entrainment inception at a laminar vortex. J. Br. Nucl. Energy Soc. 1974, 13, 203–209. [Google Scholar]
- Tenchine, D. Some thermal hydraulic challenges in sodium cooled fast reactors. Nucl. Eng. Des. 2010, 240, 1195–1217. [Google Scholar] [CrossRef]
- Takahashi, M.; Inoue, A.; Aritomi, M.; Takenaka, Y.; Suzuki, K. Gas entrainment at free surface of liquid, (I). J. Nucl. Sci. Technol. 1988, 25, 131–142. [Google Scholar] [CrossRef][Green Version]
- Yamaguchi, A.; Tatsumi, E.; Takata, T.; Ito, K.; Hiroyuki Ohshima, H. Gas entrainment allowance level at free surface and gas dynamic behavior of sodium-cooled fast reactor. Nucl. Eng. Des. 2011, 241, 1627–1635. [Google Scholar] [CrossRef]
- Sakai, T.; Eguchi, Y.; Monji, H.; Iwasaki, T.; Ito, K.; Ohshima, H. Proposal of design criteria for gas entrainment from vortex dimples based on a computational fluid dynamics method. Heat Transfer Eng. 2010, 29, 731–739. [Google Scholar] [CrossRef]
- Kimura, N.; Ezure, T.; Tobita, A.; Kamide, H. Experimental study on gas entrainment at free surface in reactor vessel of a compact sodium-cooled fast reactor. J. Nucl. Sci. Technol. 2008, 45, 1053–1062. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Takata, T.; Tatsumi, E.; Ito, K.; Ohshima, H.; Kamide, H. Rationalization of gas entrainment allowance level at free surface of Sodium-cooled fast reactor. In Proceedings of the NUTHOS-7: The 7th International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Operation and Safety, Seoul, Korea, 5–9 October 2008. [Google Scholar]
- Ito, K.; Kunugi, T.; Ohshima, H.; Kawamura, T. Formulations and validations of a high-precision volume-of-fluid algorithm on nonorthogonal meshes for numerical simulations of gas entrainment phenomena. J. Nucl. Sci. Technol. 2009, 46, 366–373. [Google Scholar] [CrossRef]
- Ito, K.; Sakai, T.; Eguchi, Y.; Monji, H.; Ohshima, H.; Uchibori, A.; Xu, Y. Improvement of gas entrainment prediction method-introduction of surface tension effect. J. Nucl. Sci. Technol. 2010, 47, 771–778. [Google Scholar] [CrossRef]
- Kimura, N.; Ezure, T.; Miyakoshi, H.; Kamide, H.; Fukuda, T. Experimental study on gas entrainment due to nonstationary vortex in a sodium cooled fast reactor-comparison of onset conditions between sodium and water. J. Eng. Gas Turbines Power 2010, 132, 102908. [Google Scholar] [CrossRef]
- Koizumi, Y.; Ito, K.; Ohshima, H.; Ohtake, H. Study on gas entrainment rate into liquid from free surface by Vortex. In Proceedings of the ASME, International Mechanical Engineering Congress and Exposition, Vancouver, BC, Canada, 12–18 November 2010. [Google Scholar]
- Monji, H.; Shinozaki, T.; Kamide, H.; Sakai, T. Effect of experimental conditions on gas core length and downward velocity of free surface vortex in cylindrical vessel. J. Eng. Gas Turbines Power 2010, 132, 012901. [Google Scholar] [CrossRef]
- Ezure, T.; Kimura, N.; Miyakoshi, H.; Kamide, H. Experimental investigation on bubble characteristics entrained by surface vortex. Nucl. Eng. Des. 2011, 241, 4575–4584. [Google Scholar] [CrossRef]
- Ito, K.; Ohshima, H.; Nakamine, Y.; Imai, Y. Study on turbulent modeling in gas entrainment evaluation method. J. Power Energy Syst. 2012, 6, 151–164. [Google Scholar] [CrossRef]
- Koizumi, Y.; Ohte, N.; Hideki, K.; Ohno, S.; Ito, K. Measurement of gas entrainment rate from free surface by vortex. In Proceedings of the 2012 20th International Conference on Nuclear Engineering collocated with the ASME 2012 Power Conference, ICONE20-POWER2012, Anaheim, CA, USA, 30 July–3 August 2012. [Google Scholar]
- Ito, K.; Ezure, T.; Ohno, S.; Kamide, H. Evaluation model of bubble-type gas entrainment. In Proceedings of the the 15th International Topical Meeting on Nuclear Reactor Thermal-Hydraulics, NURETH15, Pisa, Italy, 12–17 May 2013. [Google Scholar]
- Ito, K.; Kunugi, T.; Ohshima, H. High-precision numerical scheme for vortical flow. Appl. Math. 2013, 4, 17–25. [Google Scholar] [CrossRef][Green Version]
- Naosuke, O.; Koizumi, Y.; Hideki, K.; Ohno, S.; Ito, K. Effect of physical properties on gas entrainment rate from free surface by vortex. In Proceedings of the 2013 21st International Conference on Nuclear Engineering ICONE21, Chengdu, China, 29 July–2 August 2013. [Google Scholar]
- Winterton, R.H.S. Cover-gas bubbles in recirculating sodium primary coolant. Nucl. Eng. Des. 1972, 22, 262–271. [Google Scholar] [CrossRef]
- Eguchi, Y.; Yamamoto, K.; Funada, T.; Tanaka, N.; Moriya, S.; Tanimoto, K. Gas entrainment in the IHX vessel of top-entry. Nucl. Eng. Des. 1994, 146, 373–381. [Google Scholar] [CrossRef]
- Patwardhan, A.W.; Mali, R.G.; Jadhao, S.B.; Bhor, K.D.; Padmakumar, G.; Vaidyanathan, G. Argon entrainment into liquid sodium in fast breeder reactor. Nucl. Eng. Des. 2012, 249, 204–211. [Google Scholar] [CrossRef]
- Tenchine, D.; Fournier, C.; Dolias, Y. Gas entrainment issues in sodium cooled fast reactors. Nucl. Eng. Des. 2014, 270, 302–311. [Google Scholar] [CrossRef]
- Kim, S.N.; Jang, W.H. A study on the free surface vortex in the pipe system. J. Korean Nucl. Soc. 1992, 24, 311–319. [Google Scholar]
- Blömeling, F. Final Report: Generische numerische Untersuchungen zur Bestimmung der Mindestüberdeckung von Pumpenzuläufen zur Vermeidung von Luftmitriss; TÜV NORD SysTec GmbH & Co. KG: Hamburg, Germany, 2014. [Google Scholar]
- Pandazis, P.; Babcsány, B. Numerical and experimental investigation of surface vortex formation in coolant reservoirs of reactor safety systems. Kerntechnik 2016, 81, 477–483. [Google Scholar] [CrossRef]
- Škerlavaj, A.; Lipej, A.; Ravnik, J.; Škerget, L. Turbulence model comparison for a surface vortex simulation. Iop Conf. Ser. Earth Environ. Sci. 2010, 12, 012034. [Google Scholar] [CrossRef]
- Škerlavaj, A.; Škerget, L.; Ravnik, J.; Lipej, A. Predicting Free-Surface Vortices with Single-Phase Simulations. Eng. Appl. Comput. Fluid Mech. 2014, 8, 193–210. [Google Scholar] [CrossRef]
- Merzari, E.; Ninokata, H.; Wang, S.; Baglietto, E. Numerical Simulation of Free-Surface Vortices. Nucl. Technol. 2009, 165, 313–320. [Google Scholar] [CrossRef]
- Shi, X.M.; Yang, F.; Dai, R.; Chen, T.J.; Wu, Y.L. Simulation of free-surface vortex produced by a rotating cylindrical wall below a static barrel. Iop Conf. Ser. Earth Environ. Sci. 2012, 15, 052034. [Google Scholar] [CrossRef]
- Gauss, F.; Lucas, D.; Krepper, E. Grid studies for the simulation of resolved structures in an Eulerian two-fluid framework. Nucl. Eng. Des. 2016, 305, 371–377. [Google Scholar] [CrossRef]
- Cristofano, L.; Nobili, M.; Romano, G.P.; Caruso, G. Investigation on bathtub vortex flow field by Particle Image Velocimetry. Exp. Therm. Fluid Sci. 2016, 74, 130–142. [Google Scholar] [CrossRef]
- Hänsch, S.; Lucas, D.; Krepper, E.; Höhne, T. A multi-field two-fluid concept for transitions between different scales of interfacial structures. Int. J. Multiph. Flow 2012, 47, 171–182. [Google Scholar] [CrossRef]
- Hänsch, S.; Lucas, D.; Höhne, T.; Krepper, E. Application of a new concept for multi-scale interfacial structures to the dam-break case with an obstacle. Nucl. Eng. Des. 2014, 279, 171–181. [Google Scholar] [CrossRef]
- Montoya, G.A. Development and validation of advanced theoretical modeling for churn-turbulent flows and subsequent transitions. In Wissenschaftlich-Technische Berichte, Hemholtz-Zentrum Dresden-Rossendorf (HZDR); HZDR: Dresden, Germany, 2015. [Google Scholar]
- Höhne, T.; Krepper, E.; Lucas, D.; Montoya, G. A Multiscale Approach Simulating Boiling in a Heated Pipe Including Flow Pattern Transition. Nucl. Technol. 2019, 205, 48–56. [Google Scholar] [CrossRef]
- Höhne, T.; Krepper, E.; Montoya, G.; Lucas, D. CFD-simulation of boiling in a heated pipe including flow pattern transitions using the GENTOP concept. Nucl. Eng. Des. 2017, 322, 165–176. [Google Scholar] [CrossRef]
- ANSYS. ANSYS CFX-Solver Theory Guide, Release 19.2; ANSYS: Canonsburg, PA, USA, 2019. [Google Scholar]
- Lucas, D.; Rzehak, R.; Krepper, E.; Ziegenhein, T.; Liao, Y.; Kriebitzsch, S.; Apanasevich, P. A strategy for the qualification of multi-fluid approaches for nuclear reactor safety. Nucl. Eng. Des. 2016, 299, 2–11. [Google Scholar] [CrossRef]
- Putra, R.A.; Schäfer, T.; Neumann, M.; Lucas, D. CFD studies on the gas-liquid flow in the swirl generating device. Nucl. Eng. Des. 2018, 332, 213–225. [Google Scholar] [CrossRef]
- Putra, A.R.; Neumann-Kipping, M.; Schäfer, T.; Lucas, D. Comparison of Gas–Liquid Flow Characteristics in Geometrically Different Swirl Generating Devices. Energies 2019, 12, 4653. [Google Scholar] [CrossRef]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. Aiche J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Ẑun, I. The transverse migration of bubbles influenced by walls in vertical bubbly flow. Int. J. Multiph. Flow 1980, 6, 583–588. [Google Scholar] [CrossRef]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse migration of single bubbles in simple shear flows. Chem. Eng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Wellek, R.M.; Agrawal, A.K.; Skelland, A.H.P. Shape of liquid drops moving in liquid media. Aiche J. 1966, 12, 854–862. [Google Scholar] [CrossRef]
- Antal, S.P.; Lahey, R.T.; Flaherty, J.E. Analysis of phase distribution in fully developed laminar bubbly two-phase flow. Int. J. Multiph. Flow 1991, 17, 635–652. [Google Scholar] [CrossRef]
- Tomiyama, A.; Sou, A.; Zun, I.; Kanami, N.; Sakaguchi, T. Effects of Eötvös number and dimensionless liquid volumetric flux on lateral motion of a bubble in a laminar duct flow. Multiphase flow 1995 1995, 1995, 3–15. [Google Scholar]
- Hosokawa, S.; Tomiyama, A.; Misaki, S.; Hamada, T. Lateral Migration of Single Bubbles Due to the Presence of Wall. In Proceedings of the ASME Joint U.S.-European Fluids Engineering Division Conference. FEDSM 2002, Montreal, QC, Canada, 14–18 July 2002. [Google Scholar]
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.-M. The Favre Averaged Drag Model for Turbulence Dispersion in Eulerian Multi-Phase Flows; ICMF2004: Yokohama, Japan, 2004. [Google Scholar]
- Auton, T.R.; Hunt, J.C.R.; Prud’Homme, M. The force exerted on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 2006, 197, 241–257. [Google Scholar] [CrossRef]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Magnaudet, J.; Rivero, M.; Fabre, J. Accelerated flows past a rigid sphere or a spherical bubble. Steady straining flow. J. Fluid Mech. 2006, 284, 97–135. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Ma, J.; Oberai, A.A.; Drew, D.A.; Lahey, R.T., Jr.; Hyman, M.C. A comprehensive sub-grid air entrainment model for RANS modeling of free surface bubbly flows. J. Comput. Multiph. Flows 2011, 3, 16. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. Aiaa J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Smirnov, P.E.; Menter, F.R. Sensitization of the SST Turbulence Model to Rotation and Curvature by Applying the Spalart–Shur Correction Term. J. Turbomach. 2009, 131, 041010. [Google Scholar] [CrossRef]
- Spalart, P.R.; Shur, M. On the sensitization of turbulence models to rotation and curvature. Aerosp. Sci. Technol. 1997, 1, 297–302. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. Bubble-induced turbulence: Comparison of CFD models. Nucl. Eng. Des. 2013, 258, 57–65. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. CFD modeling of bubble-induced turbulence. Int. J. Multiph. Flow 2013, 55, 138–155. [Google Scholar] [CrossRef]
- Ikoma, Y.; Koizumi, Y.; Ito, K.; Ohshima, H. Bubble-Type Gas Entrainment into Liquid from Free Surface by Vortex. In Proceedings of the ICONE-19 the 19th International Conference on Nuclear Engineering, Osaka, Japan, 24–25 October 2011. [Google Scholar]
- Ito, K.; Koizumi, Y.; Ohshima, H.; Kawamura, T. Physics-basis simulation of bubble pinch-off. Mech. Eng. J. 2016. [Google Scholar] [CrossRef][Green Version]
- Zidouni, F.; Krepper, E.; Rzehak, R.; Rabha, S.; Schubert, M.; Hampel, U. Simulation of gas–liquid flow in a helical static mixer. Chem. Eng. Sci. 2015, 137, 476–486. [Google Scholar] [CrossRef]


| Force | Formulation | Ref. | No. |
|---|---|---|---|
| Drag | [53] | (5) | |
| , | (6) | ||
| , , | |||
| Lift | [54] | (7) | |
| [55] | (8) | ||
| (9) | |||
| (10) | |||
| [56] | (11) | ||
| Wall lubrication | [57] | (12) | |
| [58] | (13) | ||
| [59] | (14) | ||
| Turbulent dispersion | [60] | (15) | |
| [49] | (16) | ||
| Virtual mass | [61,62,63] | (17) | |
| (18) |
| Velocity Groups | dg | cg | |||
|---|---|---|---|---|---|
| Morphology | Polydispersed | Continuous | |||
| Bubble classes | G1 | G2 | G3 | G4 | G5 |
| Diameter [mm] | 1 | 3 | 5 | 7 | ≥9 |
| Entrainment fraction (Sim. A) | 1 | 0 | 0 | 0 | −1 |
| Entrainment fraction (Sim. B) | 0.50 | 0.50 | 0 | 0 | −1 |
| Entrainment fraction (Sim. C) | 0.25 | 0.25 | 0.25 | 0.25 | −1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Putra, R.A.; Lucas, D. Modeling of the Free-Surface Vortex-Driven Bubble Entrainment into Water. Water 2020, 12, 709. https://doi.org/10.3390/w12030709
Putra RA, Lucas D. Modeling of the Free-Surface Vortex-Driven Bubble Entrainment into Water. Water. 2020; 12(3):709. https://doi.org/10.3390/w12030709
Chicago/Turabian StylePutra, Ryan Anugrah, and Dirk Lucas. 2020. "Modeling of the Free-Surface Vortex-Driven Bubble Entrainment into Water" Water 12, no. 3: 709. https://doi.org/10.3390/w12030709
APA StylePutra, R. A., & Lucas, D. (2020). Modeling of the Free-Surface Vortex-Driven Bubble Entrainment into Water. Water, 12(3), 709. https://doi.org/10.3390/w12030709





