Modeling of the Free-Surface-Pressurized Flow of a Hydropower System with a Flat Ceiling Tail Tunnel
Abstract
1. Introduction
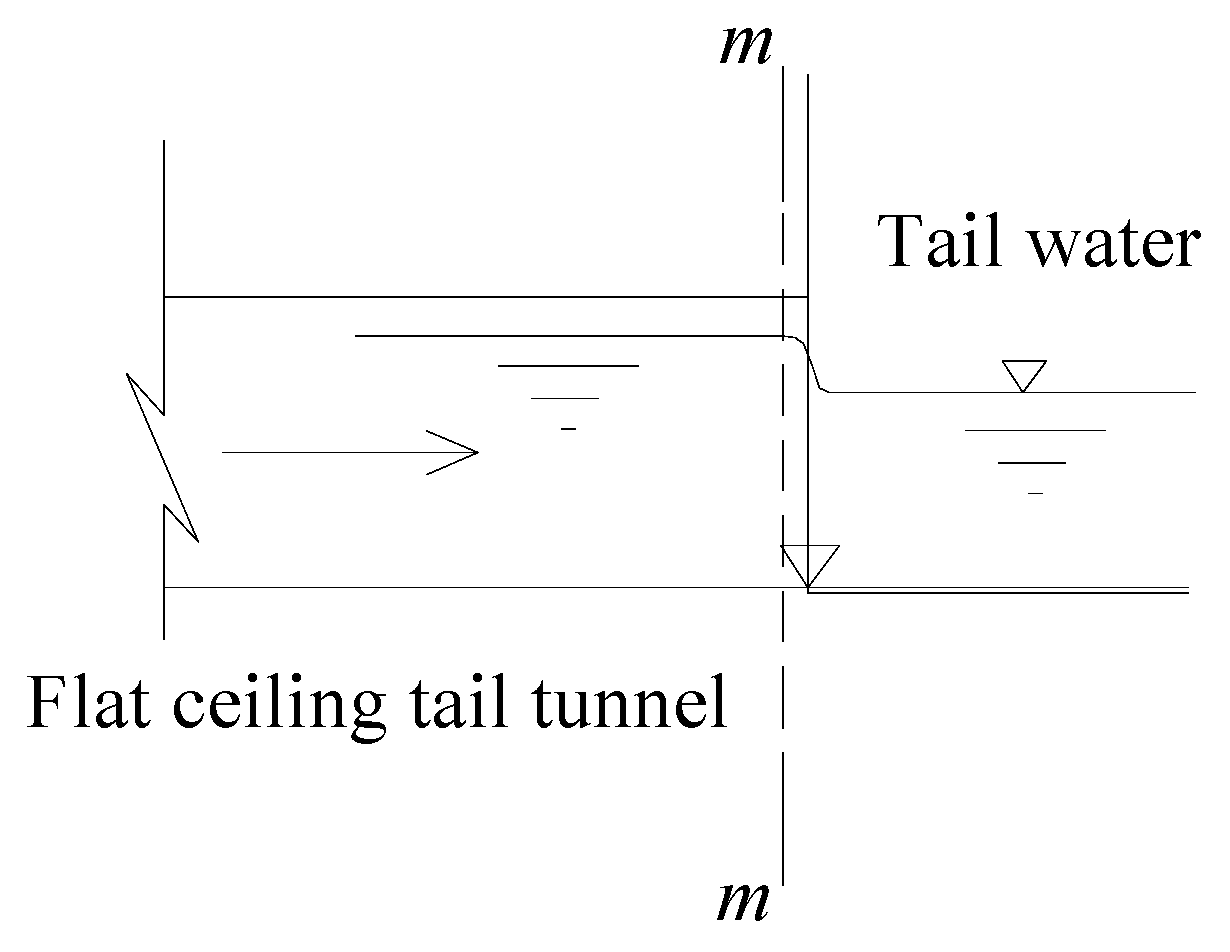
- Pressurized flow. If the tail water level is higher than the top elevation of the tail tunnel outlet, the flat ceiling tail tunnel is always in a typical pressurized state.
- Free-surface-pressurized flow. If the tail water level is obviously lower than the top elevation of the tail tunnel outlet, the flat ceiling tail tunnel is always in free channel flow under both steady and transient states, and a unique interface between pressurized flow and free surface flow is located along the connecting tunnel. Particularly as the tail water level is slightly lower than the top elevation of tail tunnel outlet, the interface between the pressurized flow and the free surface flow is located along the flat ceiling tail tunnel under steady states, and possible mixed free-surface-pressurized flow will inevitably happen under transient states, with one or more air masses existing along the crown of the tail tunnel in some cases.
2. Material and Methods
2.1. Governing Equations
2.2. Characteristic Implicit Format
2.3. Boundary Conditions
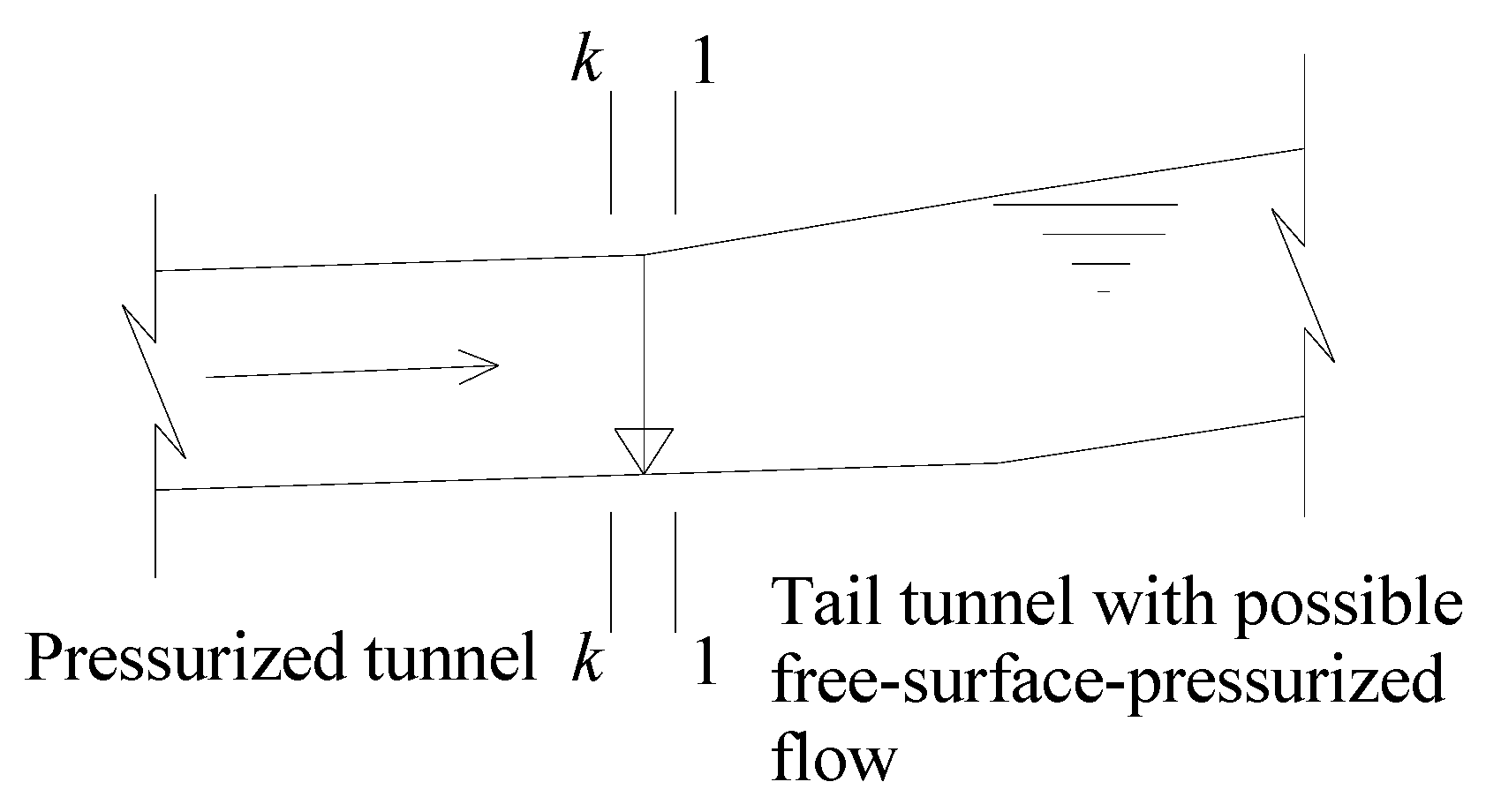
2.3.1. Inlet Section
2.3.2. Gate Shaft in Mid-Section of the Flat Ceiling Tail Tunnel
2.3.3. Outlet of the Flat Ceiling Tail Tunnel
2.4. Analysis Model of Transient Flow in System
3. Results and Discussions
3.1. Experimental Research
3.1.1. Experiment Description
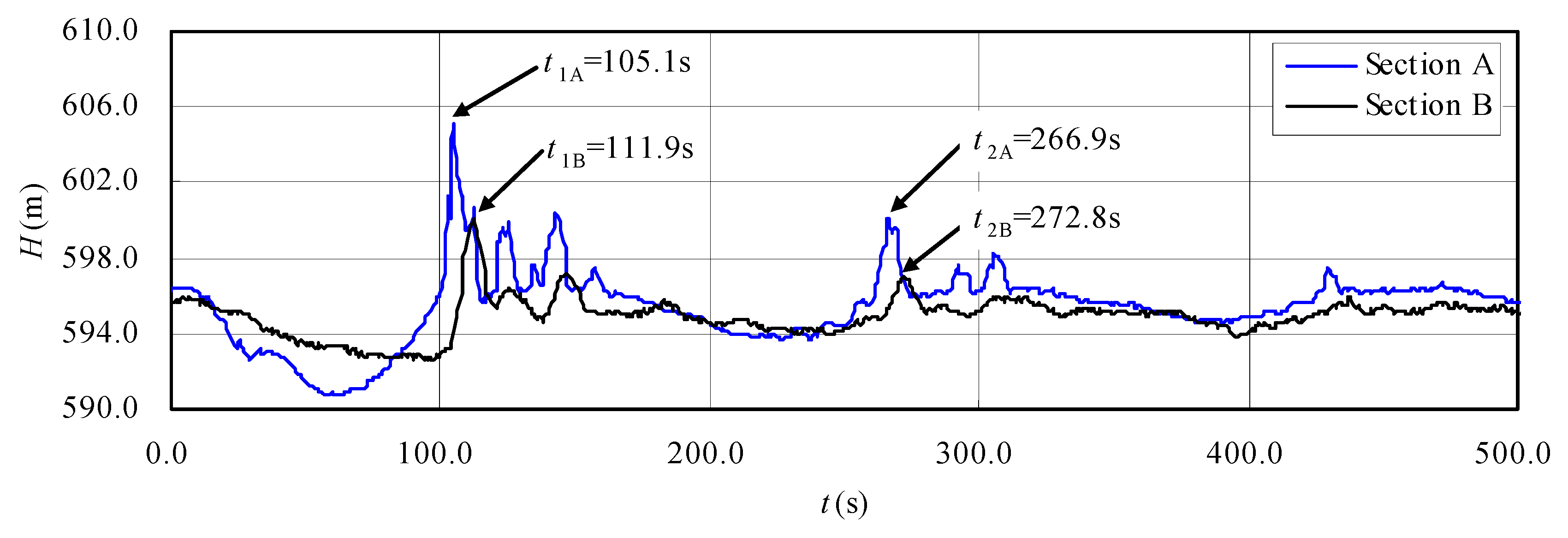
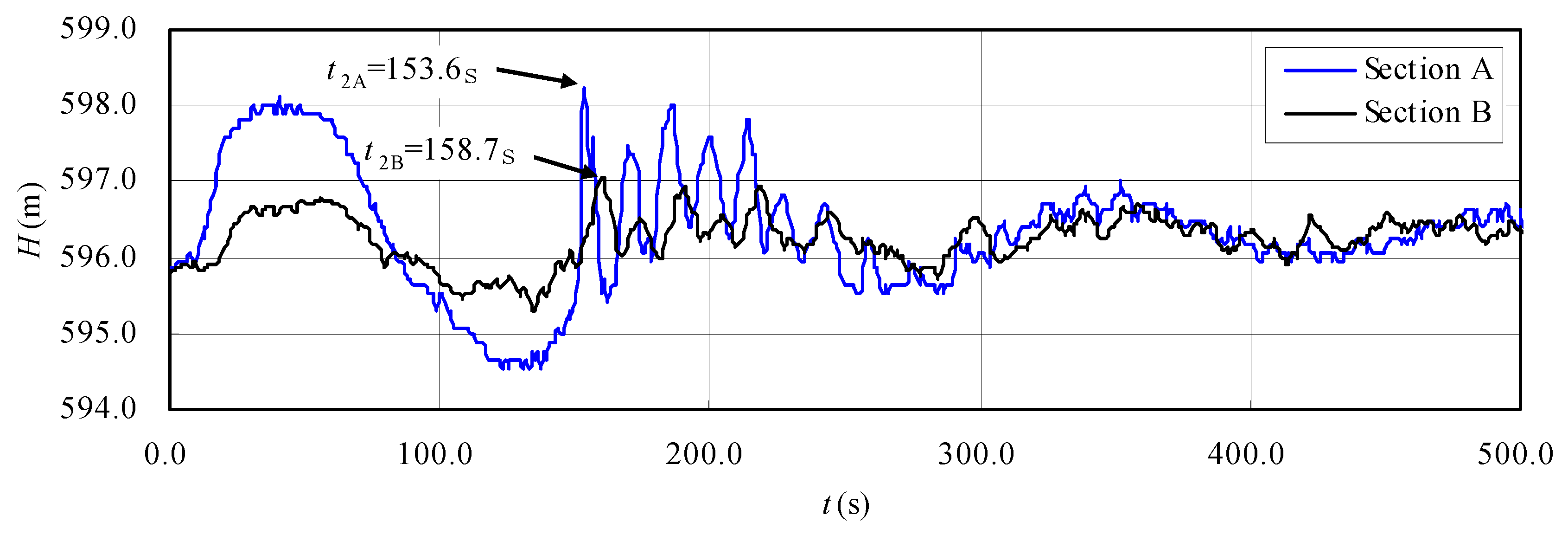
3.1.2. Wave Speed Analysis along the Flat Ceiling Tail Tunnel
3.2. Numerical Simulation by Using the Characteristic Implicit Method
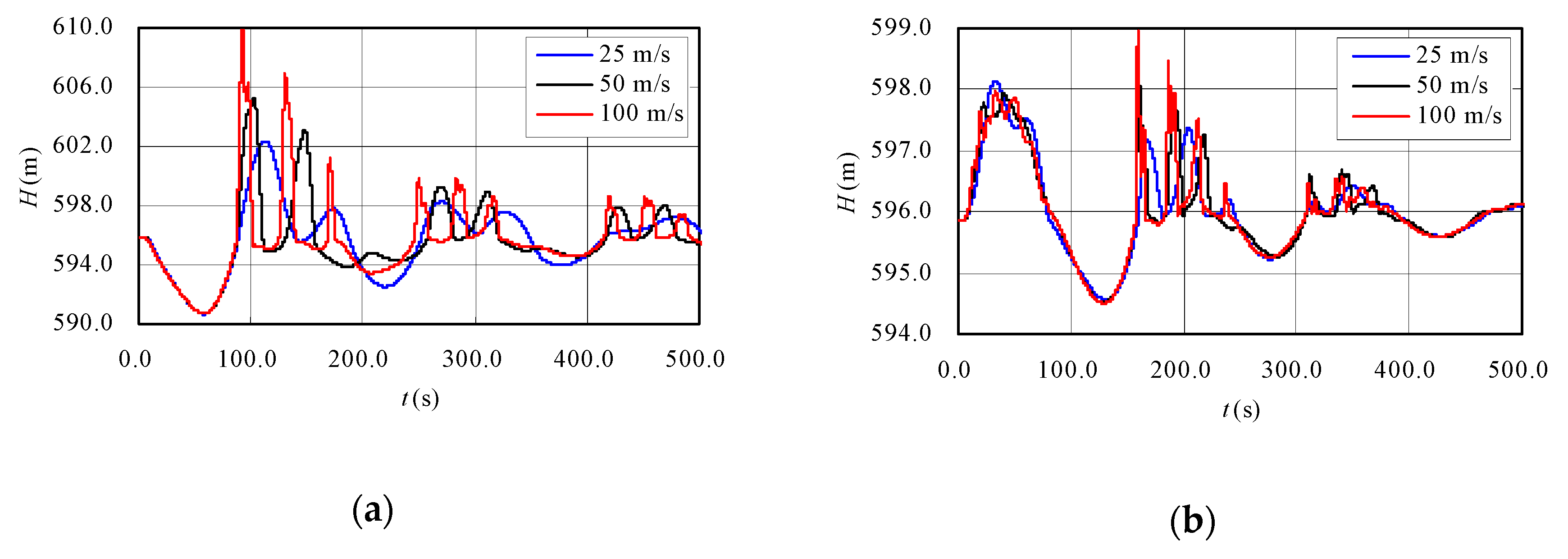
3.2.1. Effect of Wave Speed on Transient Process
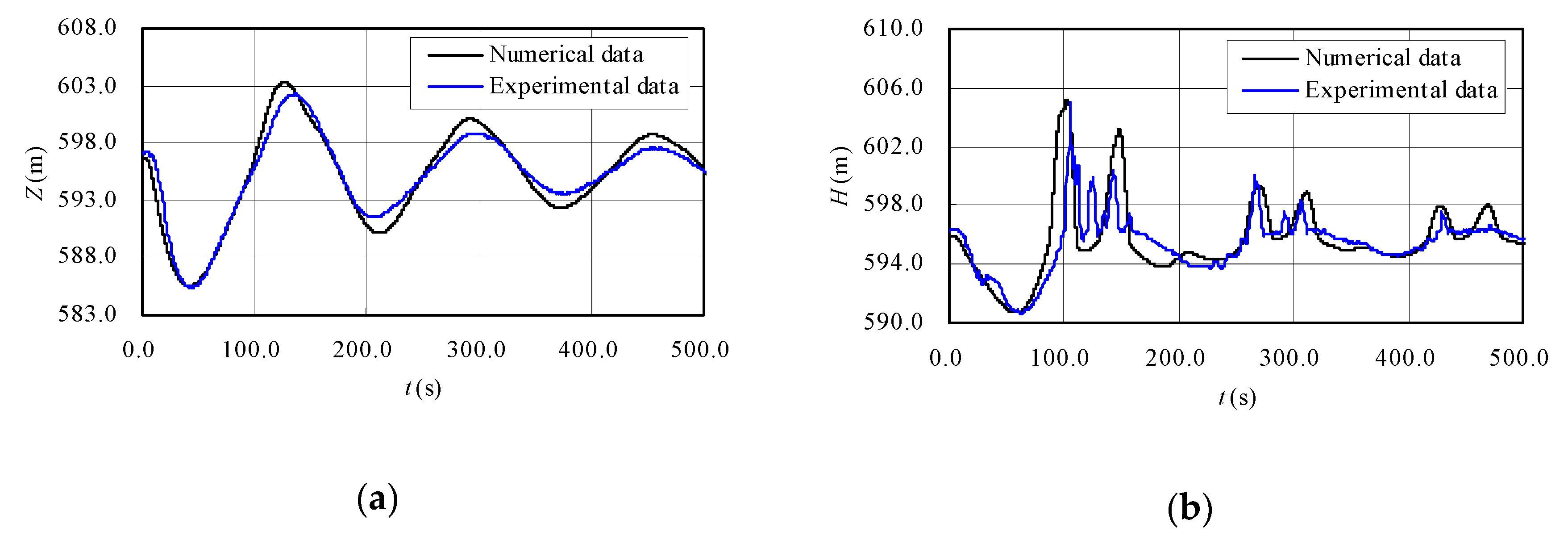
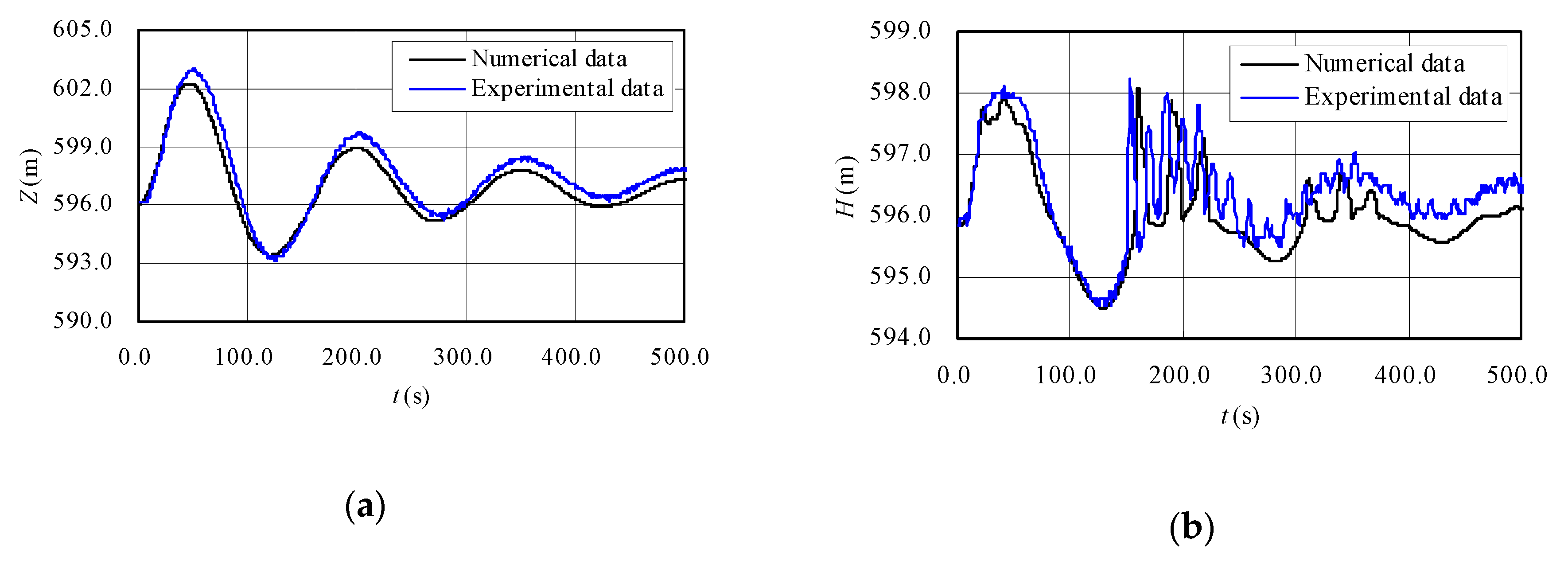
3.2.2. Comparative Analysis with Experimental Results
4. Conclusions
- Based on the characteristic implicit method for modeling of the free-surface-pressurized flow in the tail tunnel together with Newton–Raphson linearization, the linear algebraic equations with a band coefficient matrix are constructed, with the introduction of necessary boundary conditions for transient simulation of the free-surface-pressurized flow. Then, a unified mathematical model is established for hydraulic transient analysis of the given hydropower systems. This unified model can accurately reveal typical water behaviors in the water-surface-pressurized flow.
- With the built experimental setup in the lab and further data analysis, considering the dynamic curves of the piezometric head at two typical reference sections along the flat ceiling tail tunnel, the wave speed af for the free-surface-pressurized flow is experimentally analyzed, which is used for the correctness in the unified model. It is found that the wave speed af for the mixed water-surface-pressurized flow in the flat ceiling tail tunnel is close to 50 m/s.
- After the sensitivity analysis of wave speed af in the free-surface-pressurized flow, the detailed hydraulic characteristics of the free-surface-pressurized flow in the flat ceiling tail tunnel are further investigated and then confirmed by comparative analysis with experimental data. With appropriate correctness of wave speed af, the numerical results are in good agreement with the experimental results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Bousso, S.; Daynou, M.; Fuamba, M. Numerical modeling of mixed flows in storm water systems: Critical review of literature. J. Hydraul. Eng. 2012, 139, 385–396. [Google Scholar] [CrossRef]
- Bousso, S.; Daynou, M.; Fuamba, M. Mixed flows with depressurizing wavefront in circular pipe. J. Irrig. Drain. Eng. 2014, 140, 04013007. [Google Scholar] [CrossRef]
- Trajkovic, B.; Ivetic, M.; Calomino, F.; D'Ippolito, A. Investigation of transition from free surface to pressurized flow in a circular pipe. Water Sci. Technol. 1999, 39, 105–112. [Google Scholar] [CrossRef]
- Vasconcelos, J.G.; Wright, S.J. Experimental investigation of surges in a stormwater storage tunnel. J. Hydraul. Eng. 2005, 131, 853–861. [Google Scholar] [CrossRef]
- Ferreri, G.B.; Ciraolo, G.; Lo Re, C. Storm sewer pressurization transient—an experimental investigation. J. Hydraul. Res. 2014, 52, 666–675. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, R.; Jia, Z. Study on free-surface-pressurized-flow of pressure spillway tunnel under different submerged depth. In Proceedings of the 3rd International Conference on Civil, Architectural and Hydraulic Engineering, Hangzhou, China, 30–31 July 2014; pp. 332–335. [Google Scholar]
- Zhou, F.; Hicks, F.; Steffler, P. Observations of air-water interaction in a rapidly filling horizontal pipe. J. Hydraul. Eng. 2002, 128, 635–639. [Google Scholar] [CrossRef]
- Bashiri-Atrabi, H.; Hosoda, T.; Shirai, H. Propagation of an air-water interface from pressurized to free-surface flow in a circular pipe. J. Hydraul. Eng. 2016, 142, 04016055. [Google Scholar] [CrossRef]
- da Silva, J.K.; Vasconcelos, J.G.; Maestri, R.D.; Borges, A.L.D. Experimental investigation of air-water interactions during rapid filling process in an urban stormwater system model. In Proceedings of the 18th Annual World Environmental and Water Resources Congress of the Environmental-and-Water-Resources-Institute (EWRI), Minneapolis, MN, USA, 3–7 June 2018. [Google Scholar]
- Zhang, W.; Cai, F.; Zhou, J.; Hua, Y. Experimental investigation on air-water interaction in a hydropower station combining a diversion tunnel with a tailrace tunnel. Water 2017, 9, 274. [Google Scholar] [CrossRef]
- Crnkovic, B.; Crnjaric-Zic, N.; Kranjcevic, L. Improvements of semi-implicit schemes for hyperbolic balance laws applied on open channel flow equations. Comput. Math. Appl. 2009, 58, 292–309. [Google Scholar] [CrossRef][Green Version]
- Trieu Dong, N. Numerical method to calculate a free-surface, or pressurized, or partially free-surface and partially pressurized unsteady flow. Houille Blanch. 1990, 45, 149–158. [Google Scholar] [CrossRef]
- Hosoda, T.; Tada, A.; Inoue, K.; Kitahara, M. Hydraulic analysis of unsteady flows with propagation of an interface between free surface flow and pressurized flow. Doboku Gakkai Ronbunshu 1994, 503, 89–97. [Google Scholar] [CrossRef]
- Arai, K.; Yamamoto, K.; Saitou, M.; Fukumoto, S. Transient analysis of mixed free-surface-pressurized flows with modified slot model (Part 1: Computational model and experiment). In Proceedings of the 4th ASME/JSME Joint Fluids Engineering Conference, Honolulu, HI, USA, 6–10 July 2003. [Google Scholar]
- Arai, K.; Yamamoto, K.; Saitou, M.; Fukumoto, S. Transient analysis of mixed free-surface-pressurized flows with modified slot model (Part2: Similarity law and eigenvalue problem). In Proceedings of the 4th ASME/JSME Joint Fluids Engineering Conference, Honolulu, HI, USA, 6–10 July 2003. [Google Scholar]
- León, A.S.; Ghidaoui, M.S.; Schmidt, A.R.; García, M.H. Application of Godunov-type schemes to transient mixed flows. J. Hydraul. Res. 2009, 47, 147–156. [Google Scholar] [CrossRef]
- Ferreri, G.B.; Freni, G.; Tomaselli, P. Ability of Preissmann slot scheme to simulate smooth pressurization transient in sewers. Water Sci. Technol. 2010, 62, 1848–1858. [Google Scholar] [CrossRef] [PubMed]
- Fern´dez-Pato, J.; García-Navarro, P. A pipe network simulation model with dynamic transition between free surface and pressurized flow. Procedia Eng. 2014, 70, 641–650. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.; Wu, Z. and Zeng, X. Study on free-surface-pressurized flow mathematical model for urban drainage networks. Chin. J. Hydrodyn. 2016, 31, 210–218. (In Chinese) [Google Scholar]
- Fan, H.; Chen, N.; Liu, L.; Li, H. Simulation of transient mixed free surface pressure flow. J. Tsinghua Univ. Sci. Technol. 2000, 40, 63–66. (In Chinese) [Google Scholar]
- Deng, M.; Liu, D.; Zhou, J. Transient flow calculation for sloping ceiling tail water tunnels and their body-type design for hydropower stations. J. Hohai Univ. Nat. Sci. 2003, 31, 436–439. (In Chinese) [Google Scholar]
- Zhou, J.; Zhang, J.; Liu, D. Hydraulic turbulence calculation for tailwater tunnel system with a sloping ceiling shared by two units. J. Hohai Univ. Nat. Sci. 2004, 32, 661–664. (In Chinese) [Google Scholar]
- Fan, H.; Chen, N.; Yang, L. Simulation of transient mixed free-surface-pressure f lows for all kinds of tunnel network topologies in hydropower stat ions. J. Tsinghua Univ. Sci. Technol. 2005, 45, 1126–1129, 1133. (In Chinese) [Google Scholar]
- Kabiri Samani, A.R.; Borghei, S.M.; Saidi, M.H. Entrapped air in long water tunnels during transition from a pressurized to free-surface flow regime. Sci. Iran. 2006, 13, 174–186. [Google Scholar]
- Cheng, Y.; Li, J.; Yang, J. Free surface-pressurized flow in ceiling-sloping tailrace tunnel of hydropower plant: Simulation by vof model. J. Hydraul. Res. 2007, 45, 88–99. [Google Scholar] [CrossRef]
- León, A.S.; Liu, X.; Ghidaoui, M.S.; Schmidt, A.R.; García, M.H. Junction and drop-shaft boundary conditions for modeling free-surface, pressurized, and mixed free-surface pressurized transient flows. J. Hydraul. Eng. 2010, 136, 705–715. [Google Scholar]
- Moradi Ajam, S.; Wang, Y.; Oberlack, M. Mathematical Optimization of Water Networks: Modeling of Channel Flows with Transition Interface Separating Free Surface and Pressurized Channel Flows; Springer: Basel, Switzerland, 2012. [Google Scholar]
- Wang, C.; Yang, J.; Nilsson, H. Simulation of water level fluctuations in a hydraulic system using a coupled liquid-gas model. Water 2015, 7, 4446. [Google Scholar] [CrossRef]
- Zhu, F.; Cheng, Y. Transient flows in headrace system combining open channel and shaft for hydropower stations. Eng. J. Wuhan Univ. 2015, 48, 744–750. (In Chinese) [Google Scholar]
- Liu, J.; Zhang, S.; Xu, D.; Bai, M.; Liu, Q. Coupled simulation and validation with fully implicit time scheme for free-surface-pressurized water flow in pipe/channel. Trans. Chin Soc. Agric. Eng. 2017, 33, 124–130. (In Chinese) [Google Scholar]
- Nomeritae, N.; Bui, H.H.; Daly, E. Modeling Transitions between Free Surface and Pressurized Flow with Smoothed Particle Hydrodynamics. J. Hydraul. Eng. 2018, 144, 04018012. [Google Scholar] [CrossRef]
- Hu, D.; Li, S.; Yao, S. and Jin, Z. A simple and unified linear solver for free-surface and pressurized mixed flows in hydraulic systems. Water 2019, 11, 1979. [Google Scholar] [CrossRef]
- Li, Q.; Liang, Q. and Xia, X. A novel 1D-2D coupled model for hydrodynamic simulation of flows in drainage networks. Adv. Water Resour. 2020, 137, 103519. [Google Scholar] [CrossRef]

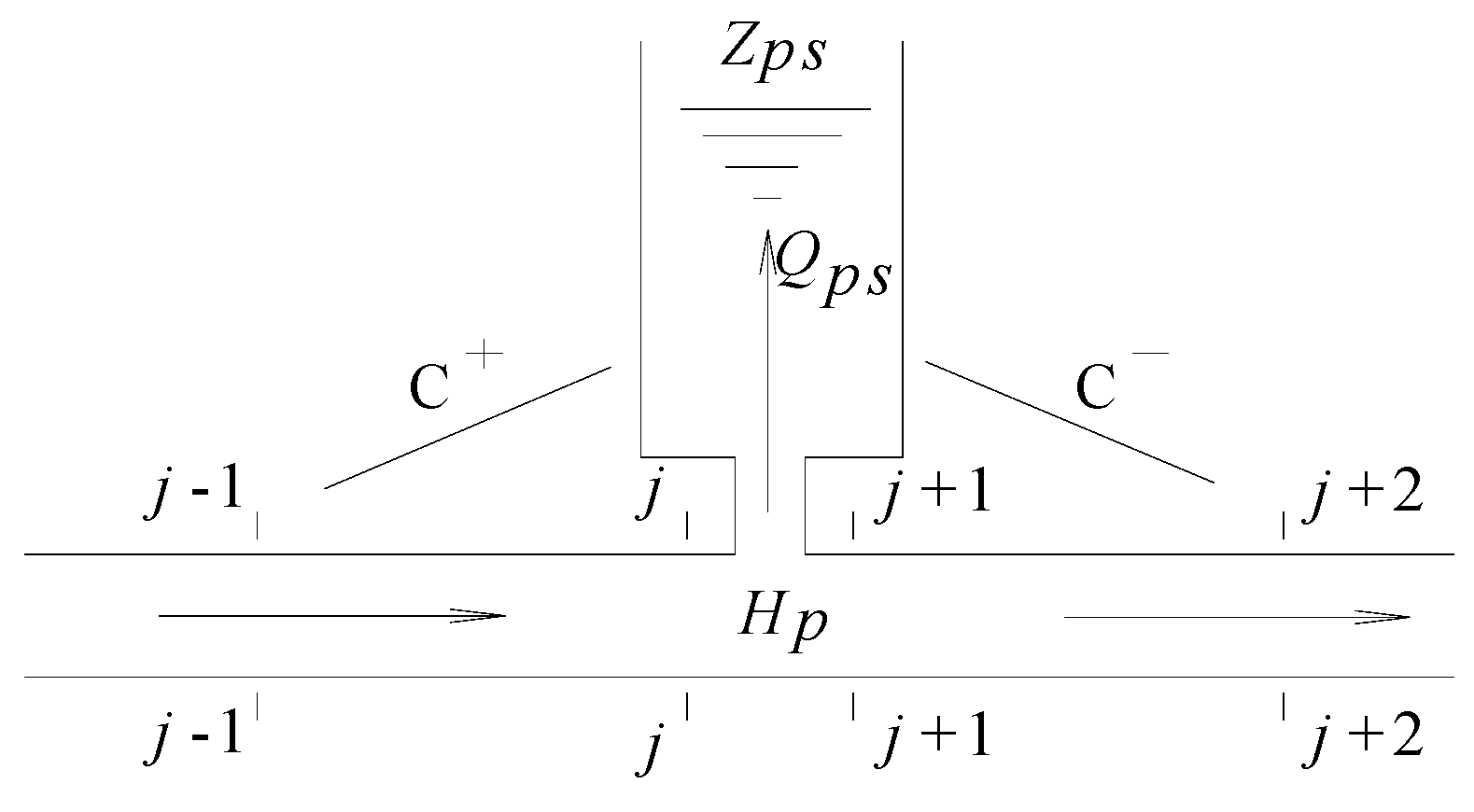

| Typical Cases | Reference Period | Peak Time (s) | Propagating Time (s) | Wave Speed, af (m/s) | |
|---|---|---|---|---|---|
| Section A | Section B | ||||
| C1: Load rejection | 1st pressure increase period | 105.1 | 111.9 | 6.8 | 42.2 |
| 2nd pressure increase period | 266.9 | 272.8 | 5.9 | 48.6 | |
| C2: Load acceptance | 1st pressure increase period | —— | —— | —— | —— |
| 2nd pressure increase period | 153.6 | 158.7 | 5.1 | 56.2 | |
| Typical Cases | Transient Variables | Experimental Data | Numerical Data | Error | |
|---|---|---|---|---|---|
| C1: Load rejection | Water level in surge tank (m) | Max. | 602.32 (134.9) | 603.29 (126.8) | 0.97 |
| Min. | 585.33 (43.9) | 585.49 (41.8) | 0.16 | ||
| Piezometric head in section A (m) | Max. | 605.10 (105.1) | 605.18 (103.0) | 0.08 | |
| Min. | 590.69 (62.0) | 590.72 (57.9) | 0.03 | ||
| C2: Load acceptance | Water level in surge tank (m) | Max. | 602.98 (50.3) | 602.25 (46.8) | −0.73 |
| Min. | 593.17 (126.0) | 593.42 (120.6) | 0.25 | ||
| Piezometric head in section A (m) | Max. | 598.22(153.6) | 598.09(160.3) | −0.13 | |
| Min. | 594.52(125.2) | 594.51(128.6) | −0.01 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Li, Y. Modeling of the Free-Surface-Pressurized Flow of a Hydropower System with a Flat Ceiling Tail Tunnel. Water 2020, 12, 699. https://doi.org/10.3390/w12030699
Zhou J, Li Y. Modeling of the Free-Surface-Pressurized Flow of a Hydropower System with a Flat Ceiling Tail Tunnel. Water. 2020; 12(3):699. https://doi.org/10.3390/w12030699
Chicago/Turabian StyleZhou, Jianxu, and Yongfa Li. 2020. "Modeling of the Free-Surface-Pressurized Flow of a Hydropower System with a Flat Ceiling Tail Tunnel" Water 12, no. 3: 699. https://doi.org/10.3390/w12030699
APA StyleZhou, J., & Li, Y. (2020). Modeling of the Free-Surface-Pressurized Flow of a Hydropower System with a Flat Ceiling Tail Tunnel. Water, 12(3), 699. https://doi.org/10.3390/w12030699




