Abstract
Climate change has effects on hydrological change in multiple aspects, particularly in the headwaters of the Yellow River (HWYR), which is widely covered by climate-sensitive frozen ground. In this study, the annual runoff was partitioned into four runoff compositions: winter baseflow, snowmelt runoff, rainy season runoff, and recession flow. In addition, the effects of global warming, precipitation change, and frozen ground degradation were considered in long-term variation analyses of the runoff compositions. The moving t-test was employed to detect change points of the hydrometeorological data series from 1961 to 2013, and flow duration curves were used to analyze daily runoff regime change in different periods. It was found that the abrupt change points of cold season runoff, such as recession flow, winter baseflow, and snowmelt runoff, are different from that of the rainy season runoff. The increase in winter baseflow and decrease in snowmelt runoff at the end of 1990s was closely related to global warming. In the 21st century, winter baseflow presented a larger relative increase compared to rainy season runoff. The correlation analyses indicate that winter baseflow and snowmelt runoff are mainly controlled by water-resource-related factors, such as rainy season runoff and the accumulated precipitation in cold season. To analyze the global warming impacts, two runoff coefficients—winter baseflow discharge rate (Rw) and direct snowmelt runoff coefficients (Rs)—were proposed, and their correlation with freezing–thawing indices were analyzed. The increase of Rw is related to the increase in the air temperature thawing index (DDT), but Rs is mainly controlled by the air temperature freezing index (DDF). Meanwhile, the direct snowmelt runoff coefficient (Rs) is significantly and positively correlated to DDF and has decreased at a rate of 0.0011/year since 1980. Under global warming, the direct snowmelt runoff (runoff increment between March to May) of the HWYR could decrease continuously in the future due to the decrease of accumulative snow in cold season and frozen ground degradation. This study provides a better understanding of the long-term runoff characteristic changes in the HWYR.
1. Introduction
Hydrological impacts of climate change have drawn worldwide concern, especially in cold regions due to the existence of the climate-sensitive cryospheric hydrogeology environment, such as frozen ground, seasonal snowpack, etc. [1,2,3,4,5]. Climate change impacts the hydrological change of cold regions, both directly through changes in climate forcing (precipitation and evaporation) and indirectly through changes in runoff generation caused by the degrading cryosphere, which has increased the uncertainties and complexities of hydrological studies in cold regions [6,7].
As an important component of the cryosphere, frozen ground is a unique hydrogeological composition related to runoff generation processes in cold regions [3,8,9]. Frozen ground, which consists of seasonally frozen ground and permafrost, is defined as a subsurface region with a temperature below 0 °C. The part of the frozen ground which remains in a frozen state (≤0 °C) for at least two consecutive years is further defined as permafrost [10]. With global warming, the frozen depth of the active layer has decreased, leading taliks to form above the permafrost table, which will increase groundwater discharge to the river in winter [11,12]. In previous studies, increasing baseflow and the changing recession process induced by frozen ground degradation in cold-region basins have been reported worldwide [13,14,15,16]. Meanwhile, recession-flow characteristics, annual minimum flow, and winter baseflow were used to indicate and estimate frozen ground degradation rates in cold-region basins [17,18]. As another important component of cryosphere, seasonal snowpack is a key surface water resource of cold regions, which accumulates in winter and releases in spring and summer. Changes of snowpack under the warming climate have been altering the hydrological regime and hydrograph characteristics in cold regions [19]. Meanwhile, frozen ground is characterized as having a low permeability, which limits the water infiltration [20,21], making the direct runoff ratio as well as the snowmelt runoff ratio higher in cold regions compared to temperate regions [22]. The existence of frozen ground impedes snowmelt infiltration, resulting in spring floods [23,24,25]. Snowmelt runoff is mainly feed by seasonal snowpack, meanwhile, its generation processes are also related to frozen ground. Therefore, the hydrological impacts of cryosphere degradation on snowmelt runoff under the changing climate are more complex and merit investigation. In conclusion, the cold season runoff, such as recession flow, winter baseflow, and spring runoff, is sensitive to climate change and cryosphere degradation. However, the interactions and alternations between recession flow, winter baseflow, and spring runoff under the changing climate are rarely studied.
The Tibetan Plateau is known as the third pole of the world, with an extremely cold environment and widely distributed cryosphere. The headwaters of the Yellow River (HWYR) are situated in the east of the Tibetan Plateau where there is a transitional area of permafrost and seasonally frozen soil. Under the warming climate, frozen ground has dramatically degraded, which has manifested as a shrinking permafrost area, a warming permafrost temperature, a decreasing frozen depth, a reducing frozen duration of seasonally frozen ground, and a formation of taliks [26,27,28]. The runoff of the HWYR has undergone tremendous changes since the 1990s. The runoff change in the headwaters of the Yellow River is primarily caused by climate change rather than land use transition [29]. The climatic impacts on long-term variations and water balance of annual runoff of the HWYR have been extensively discussed at an annual scale [29,30,31]. The long-term variations of annual runoff of the HWYR can be generally divided into three periods: a pre-change period (1961–1990), a decrease period (the 1990s), and a recovery period (the 21st century) [30,31]. Compared to the pre-change period (1961–1990), the annual mean runoff of the headwater basins decreased by 20% in the 1990s, but demonstrated a recovery in the 21st century, especially in the sub-basin above Jimai station where runoff increased by 6.2% relative to the pre-change period [32]. The frozen ground degradation effects on the hydrological change have also drawn concern in this area recently, but have only been discussed at an annual scale [16,32,33,34]. Although long-term annual runoff characteristic changes have been extensively discussed and investigated in previous studies, the long-term variations of runoff in different seasons are still unknown. Moreover, the ways in which runoff in cold seasons—such as the snowmelt runoff, recession flow, and the winter baseflow—responds to climate change, such as temperature increase, changes in precipitation types, have not been thoroughly studied. However, to understand how climate change directly alters the runoff in different seasons and how the hydrological processes respond to the changing cryosphere under the climate change, it is imperative to analyze the long-term variations of runoff in different seasons.
This study analyzed the long-term runoff changes in the HWYR, with the aims to (1) characterize the long-term runoff variations of different seasons in different change periods, (2) analyze the potential causes of runoff change in considering global warming, precipitation change, and frozen degradation, (3) analyze frozen ground degradation impacts on cold season runoff; and (4) provide a better understanding of runoff response to climate change in the HWYR.
2. Study Area and Data Processing
2.1. Study Area
The Yellow River originates from the east of the Tibetan Plateau. The catchment above Jimai station, possessing a large permafrost area and a cold climate, was selected to analyze hydrological change of the headwaters of the Yellow River (HWYR). The study area, with a drainage area of about 45,000 km2, is embraced by the Bayan Har mountains, the Buqing mountains, and Animaqing mountain from the south, west, to northeast, with elevation ranges from 3951 to 5345 m (Figure 1a). Two major large lakes, Gyaring and Ngoring, are located in the Northwest of the catchment. Two meteorological stations, Maduo and Dari, are located in this area to observe climate change. The Jimai hydrological station is located at the outlet of the catchment and gauges the runoff change. As no water-supply-related glacier existed in the study area, the cryosphere mentioned in this study focused on frozen ground and seasonal snowpack. The study area is fully underlain by frozen ground, including seasonally frozen soil and permafrost. The distribution of the frozen ground in the study area in the 1980s (Figure 1b) and the 1990s (Figure 1c) were obtained from the Map of Snow, Ice and Frozen Ground in China (1988) and the Map of Permafrost on the Qinghai-Tibetan Plateau [35], respectively. The two maps were provided by the Environmental and Ecological Science Data Center for West China, National Natural Science Foundation of China (http://westdc.westgis.ac.cn). According to these two maps, frozen soil of the study area was briefly classified as seasonally frozen soil and permafrost. As shown in Figure 1b,c, permafrost distribution in the study area has shrunken significantly since the 1980s.
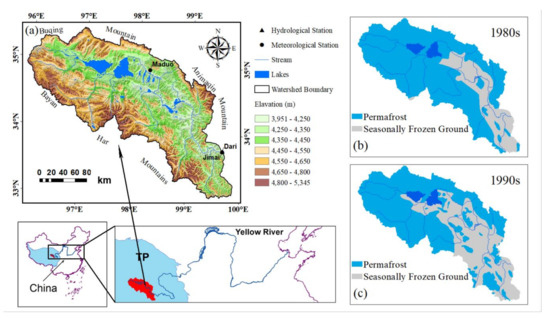
Figure 1.
(a) Relative location of the study area in the Yellow River basin, distribution of the meteorological stations, and the outlet hydrological station; (b) frozen ground distribution in the 1980s; (c) frozen ground distribution in the 1990s.
2.2. Data Processing
Two kinds of datasets—hydrometeorological data and remote sensing data—were used in this study. Note that we defined a freezing–thawing year and a hydrological year in the following data processing and analyses, since the time cycles of the freeze–thaw process and hydrological process are different from each other. When calculating the accumulative snow in winter, using the freezing index (DDF) and thawing index (DDT), we regarded the period from September to the following August as a freezing–thawing year (FTY). However, we took March to the following February as a hydrological year (HY) when analyzing the runoff changes in different seasons.
2.2.1. Hydrometeorological Data
The daily precipitation and temperature data from HY 1961 to 2013 at Dari and Maduo meteorological stations were provided by the China Meteorological Administration (CMA). The daily runoff from 1961 to 2013 (lack of 1990 daily runoff data) and monthly runoff from 1961 to 2013 at the Jimai outlet hydrological station were provided by the Yellow River Conservancy Commission (YYCC). The annual precipitation (P, mm), annual mean air temperature (T, °C), and precipitation intensity (I, mm/day) were obtained from the daily meteorological data and used in the following analyses. The precipitation intensity (I) is defined as the ratio of the total annual precipitation amount to the total number of days of rain in a hydrological year.
2.2.2. Snow and Frozen Ground
A simple threshold method was used to divide the precipitation into rain, snow, and sleet in this study (described in Section 3.1). The rain, snow, and sleet were calculated separately with the respective daily temperature and precipitation of the two meteorological stations by the threshold method. The accumulative snow from September to May was used to indicate the seasonal snowpack. The Moderate Resolution Imaging Spectroradiometer (MODIS) snow product—the MOD10A2 dataset (the MODIS/Terra Snow Cover 8-day L3 Global 500 m Grid) is the most widely used snow product. The MOD10A2 dataset is produced and distributed by the National Aeronautics and Space Administration (NASA) Distributed Active Archive Center (DAAC) and is available at the website of the National Snow and Ice Data Center (NSIDC) (http://nsidc.org/). The MOD10A2 dataset was used to validate the obtained snow by the proposed method in this study. The MOD10A2 dataset from 2001 to 2013, with 8-day temporal resolution and 500 m spatial resolution, was collected and used to detect the snow cover seasonal variations in the HWYR. As MOD10A2 is an 8-day composite dataset, the cloud cover effects were effectively minimized. Many studies have proved the validity and efficiency of the MOD10A2 in mapping snow cover [36,37]. The percentage snow cover area of each image was defined as the ratio of snow cover area to the whole basin area. The mean value of the snow cover area of every same date image from 2001 to 2013 was used to represent the snow cover distribution of the date.
The air temperature freezing index (DDF) and air temperature thawing index (DDT), as commonly used and easily obtained indices, were used to indicate the frozen depth and thawed depth variations of frozen ground in this study. The DDF and DDT were defined as the absolute accumulative negative air temperature and the accumulative positive air temperature in a freeze–thaw year (FTY) (from September to August), respectively. The physical basis of using DDF and DDT to indicate the frozen ground is derived from the commonly used active layer frozen-thawed depth simulation model Stefan equation [38]. The DDF and DDT were calculated separately with the daily air temperature obtained from the respective station.
The mean value of DDF (or DDT) of the two meteorological stations was used to represent the frozen (or thawed) ground depth of the study area. All climate factors, such as P, T, I, rain, sleet, and snow, used in the following analyses were the mean value of the two stations.
3. Methods
In this study, we proposed a simple but efficient way to distinguish snow, sleet, and rain by using only daily precipitation and daily air temperature (Section 3.1). We used the moving t-test (Section 3.2) to detect abrupt change points and used flow duration curves (Section 3.3) to detect runoff characteristics changes. Then correlation analyses were applied to reveal relationships and interactions between runoff, climatic factors, and freezing–thawing indices.
3.1. Identification of Precipitation Types
The snow, sleet, and rain records are available only from 1956 to 1979 in the two meteorological stations. We analyzed the snow, sleet, and rain distribution from the data, along with air temperature, and the results are shown in Figure 2.
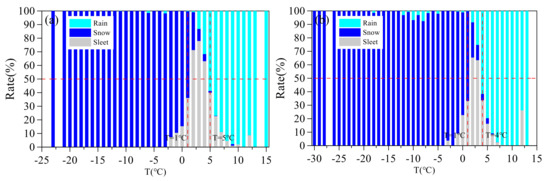
Figure 2.
Snow, sleet, and rain distribution along with air temperature; (a) Jimai station, (b) Maduo station.
Snow rate increased as temperature decreased, and rain rates increased as temperature increased. Sleet rate showed a normal distribution in relation to temperature (Figure 2). Using 50% (the horizontal red dashed line in Figure 2) as a critical value, we were able to find the critical temperature for snow, sleet, and rain. According to the obtained results, we defined a simple method to distinguish snow, sleet, and rain at the two stations, as indicated in Table 1.

Table 1.
Critical temperature of snow, sleet, and rain.
The obtained critical temperature (1 °C) of snow is a commonly used threshold value in distinguishing snow and rain in previous studies in the HWYR [39,40]. The obtained critical temperature of snow, sleet, and rain was used to distinguish precipitation types in the two meteorological stations, respectively, and the mean values of snow, sleet, and rain of the two stations were used in the following analyses. The correlation coefficient between obtained snow and sleet, and observed snow and sleet is 0.75 and 0.56 at an annual scale.
3.2. The Moving t-Test
The original t-test is an efficient and valid way to assesses whether the mean values of two subsamples are significantly different from each other. For the original t-test, there are two major statistic values, t and s, which are defined as follows [29]:
As shown in the above Equations (1) and (2), , s, and ni are the mean value, standard deviation, and the size of the two independent samples (i = 1, 2). The moving t-test applies the original t-test to a subseries with a given length n before and after the potential change points (n = n1 = n2). Therefore, the length of the moving window is set as 2n to detect if the middle point is an abrupt change point. If the calculated t-value is larger than the critical value tα, then the middle point of the moving window is accepted as a change point at the significant level α. In this study, n = 10, and the critical value was tα = 2.1 for α = 0.05. The moving t-test was employed to detect the abrupt change points of the long-term runoff and climate factors series.
3.3. Flow Duration Curves
FDC has been generally used since approximately 1915, which provides a simple and efficient way to show the runoff distribution in different percentage of exceedance (Pe) ranges [41,42]. To plot the FDC, firstly, the runoff in the corresponding period should be sorted from large values to small values. Then, the percentage of exceedance (Pe) of the corresponding runoff is calculated by the following equation:
where j is the sequence number of the sorted runoff series in the corresponding period and m is the total number of the runoff series. In this study, the daily runoff from 1961 to 2013 was divided into three periods according to the long-term runoff variations pattern (described in Section 4.1). The daily runoff in the corresponding period was integrated into one-year mean daily runoff to represent the daily runoff change regime in the corresponding period. In this study, to maintain the consistence of the length of daily runoff series in each year, the last daily runoff of a leap year was removed and the m in Equation (3) was set as 365.
4. Results
4.1. Runoff Characteristics and Variation Analyses
4.1.1. Runoff Compositions and Their Correlations
The moving t-test was employed to detect the change points of the long-term annual mean runoff (AMR) variations. As shown in Figure 3a, there are two abrupt change points, 1989 and 2002, dividing the long-term runoff change into three periods: I. pre-change period (1961–1989); II. 1990s (1990–2002); and III. 2000s (2003–2013). The abrupt change points obtained in this study are similar to previous studies in the Yellow River sub-basins using other approaches [43,44]. The intra-annual variations of daily runoff in the three periods are displayed in Figure 3b. Compared to the pre-change period, period II is a low-flow period, and period III is a recovery period. Although runoff volume changed significantly in the three periods, the seasonal patterns showed similarity.
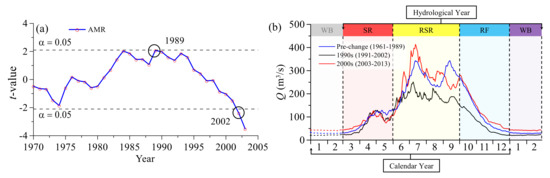
Figure 3.
(a) The change points of annual mean runoff detected by moving t-test (b) comparison of daily runoff regime of the three periods and the definition of hydrological year.
Daily runoff intra-annual variations can be generally divided into four stages: winter baseflow (WB) (January–February), snowmelt runoff (SR) (March–May), rainy season runoff (RSR) (June–September), and recession flow (RF) (October–December) account for 4%, 15%, 61%, and 20% of annual runoff, respectively. As runoff variations from October to the following February can be integrated into a full recession process, we defined March to the following February as a hydrological year (HY) in following runoff change analyses (Figure 3b). The correlation analyses were applied to reveal the four runoff composition interactions (Table 2).

Table 2.
The correlation matrix of runoff compositions.
Rainy season runoff is a major runoff composition before cold season runoff and has continuous effects on recession flow (RF), winter baseflow (WB), and snowmelt runoff (SR). The correlation coefficients between rainy season runoff (RSR) and RF, WB, and SR are 0.85, 0.80, and 0.54, respectively, reducing along with the hydrological processes. The correlation coefficient between RSR and SR is relatively lower due to depletion of recession processes and disturbance of snowmelt recharge. However, SR still showed a high correlation with RSR (0.54), RF (0.68), and WB (0.60), as the continuous groundwater discharge from recession processes affects SR. To remove groundwater discharge impacts on SR, we defined direct snowmelt runoff (DSR) as the difference of SR and WB. As shown in Table 2, the correlations of DSR and RSR, and RF and WB are obviously lower compared to the correlation of SR and RSR, and RF and WB. The impacts of RSR, RF, and WB are effectively removed. The correlation coefficient between DSR and WB is negative; however, the value is low (−0.08), thus the correlation is negligible.
4.1.2. The Changes of Runoff Compositions
Flow duration curves (FDC) of the three periods are shown in Figure 4a, and the relative runoff variations of period II (1990s) and period III (2000s) to period I (the pre-change period) are displayed in Figure 4b. Points in red, yellow, blue, and purple indicate spring (SR), rainy season runoff (RSR), recession flow (RF), and winter baseflow (WB), respectively. Dots in the blue line, square points in the black line, and triangle points in the red line represent FDC of period I, period II, and period III, respectively. Percentage of exceedance (Pe) of RSR and WB range from 0% to 30% and 80% to 100%, respectively. Pe values of SR and RF range from 30% to 80%.
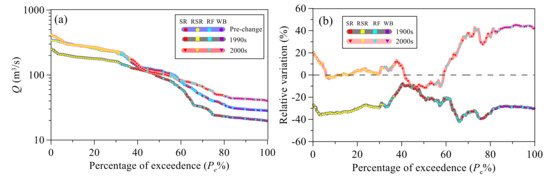
Figure 4.
(a) Comparison of flow duration curves of the three periods (b) Relative changes of different percentile runoff in different periods.
The runoff of period II is lowest among the three periods in almost all ranges of Pe. Runoff of period III returned as a same level as period I, but WB showed a relatively larger increase (Figure 4a). Using period I as a benchmark, the relative changes of period II and period III are presented in Figure 4b. For period II, both high flow (Pe < 30%) and low flow (Pe > 70%) decreased by 30–40%, medium flow (30% < Pe < 70%) decreased by 10–20%. The runoff of period III showed a recovery; the high flow and a part of the medium flow increased by 0–20%. However, the low flow, which was dominated by winter baseflow (WB), increased by more than 40%. Meanwhile, a part of the medium flow (40% < Pe <60%), which was dominated by SR showed a 10% reduction. The abrupt change points of snowmelt runoff (SR), rainy season runoff (RSR), recession flow (RF), winter baseflow (WB), annual mean runoff (AMR), and direct snowmelt runoff (DSR) are detected by the moving t-test (Figure 5).
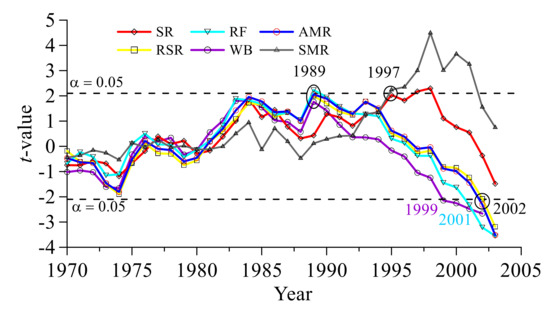
Figure 5.
The moving t-test results of different runoff compositions.
As mentioned above, variations of AMR from 1961 to 2013 can be divided into three periods by two abrupt change points: 1989 and 2002. RSR, as the major runoff composition, has two change points (1989, 2002) which are exactly the same as AMR. WB has two abrupt change points: 1989 and 1999. RF has two abrupt change points: 1989 and 2001. SR and DSR have only one abrupt change point: 1997. These abrupt change points are circled in Figure 5.
Runoff long-term inter-annual variations can be partitioned into different periods by these obtained abrupt change points. The mean values, relative changes to reference periods, and change rates in different periods of different runoffs are shown in Table 3. In the 1990s, AMR and RSR decreased by 28.15% and 29.57% relative to the reference period (1961–1989), respectively. In the 21st century, RSR and AMR increased by 3–5% relative to the reference period. The mean value of WB decreased by 20% in the 1990s, but presented a significant increase trend (at 5% level) with a rate of 1.10 m3/s/year. In the 21st century, WB continuously increased at a rate of 3.66 m3/s/year and presented a larger increase (42.03%) compared to the recovery of RSR and AMR. The RF showed a reduction in both the 1990s (6.9%) and 21st century (6.4%), however, increased significantly (p < 0.01) in the 21st century at a rate of 6.04 m3/s/year. SR deceased by 8.64% in the period 1998–2013, however, DSR showed a more considerable decrease (31.21%). Both SR and DSR showed no significant change in trend during the period 1998–2013.

Table 3.
Runoff changes in respective periods.
4.2. Climate Change and Frozen Ground Degradation
4.2.1. Precipitation Changes
In this section, we investigate precipitation changes, including the changes of precipitation amount, precipitation intensity, and precipitation types. For precipitation types, we used a threshold method mentioned in Section 3.1 to distinguish snow, sleet, and rain. The intra-annual snow variations and inter-annual snow variations in the HWYR are shown in Figure 6a,b, respectively.
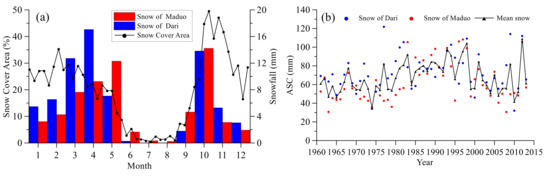
Figure 6.
(a) Intra-annual variation of snow and snow cover area; (b) inter-annual variation of annual accumulative snow in cold season (ASC).
The monthly snow of Maduo and Jimai stations is derived from daily precipitation from HY 1961 to 2013. The 8-day snow cover variations in one year was obtained from 2001 to 2013 from the MOD10A2 dataset. The time span of snow obtained from the observation station is different from the remote sensing dataset. As indicated in Figure 6a, however, the intra-annual variations of snow and snow cover area are consistent with each other, mutually proving the efficiency of the data. As indicated by Figure 6a, snow starts accumulating in September and begins melting in March, and is completely melted during June to July, and no permanent snowpack exists in this area. The percentage snow cover area ranges from 30% to 50% in winter. The accumulative snow from September to May is defined as accumulative snow in the cold season (ASC) and is taken as seasonal snowpack in this study. The long-term variations of ASC are displayed in Figure 6b; the ASC showed a slight increase from 1980 to 1997 and then decreased during the period 1998–2013.
We focused our study on analyzing snow, sleet, and rain in the cold season, which are more related to cold season runoff; moreover, 98% of snow happened in the cold season (September–May). To investigate the snowmelt runoff and winter baseflow changes, we summarized sleet and rain from September to February, and March to May, separately. The moving t-test results of precipitation amount, precipitation intensity, and precipitation types are shown in Figure 7, and the respective mean values, relative changes, and change rates are summarized in Table 4.
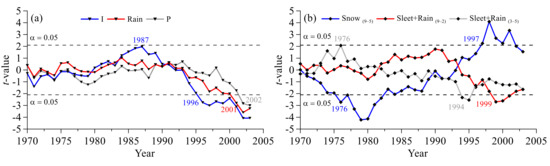
Figure 7.
The change points of precipitation intensity (I), rain, and precipitation (P); and (b) cold season precipitation detected by moving t-test.

Table 4.
Precipitation changes in respective periods.
The long-term variations of precipitation and rain are divided into two periods. Precipitation and rain increased by 12.12% and 16.09% in the 21st century. Although a decrease in precipitation in the 1990s in the HWYR was reported by previous studies [31,32], the decrease is not significant, as there is only one change point (2002) detected by the moving t-test (Figure 7). However, precipitation intensity decreased by 8.36% in period 1988–1995 and increased by 4.49% in period 1996–2013. To consider the impact of changes in precipitation types on cold-season runoff, we identified cold-season precipitation into three groups: (Snow) (9–5) , (Sleet + Rain) (9–2), and (Sleet + Rain) (3–5), indicating snow happened in the cold season, sleet and rain happened between September and the following February, and sleet and rain happened between March and the following May.
The (Sleet + Rain) (9–2) group can provide an extra supplement to recession flow and winter baseflow besides groundwater discharge. The (Sleet + Rain) (3–5) group can provide an extra supplement to snowmelt runoff and direct snowmelt runoff besides snowmelt. Compared to the reference period (1961–1976), snow of the cold season increased by 36.88% in the period 1988-1995 and increased significantly (p < 0.05) at a rate of 0.90 mm/year. (Sleet + Rain) (9–2) increased by 6.35% in period 2000–2013 and (Sleet + Rain) (3–5) increased by 24.16% in the period 1995–2013. (Sleet + Rain) (3–5) decreased by 14.21% in the period 1997–1994 when snow significantly increased.
4.2.2. The Changes of Temperature and Freezing–Thawing Indices
In this study, we used annual mean air temperature to indicate global warming and freezing–thawing indices (DDF, DDT) to indicate frozen ground degradation following global warming.
As shown in Figure 8, air temperature (T) and thawing index (DDT) have two abrupt change points, and freezing index (DDF) has only one abrupt change point.
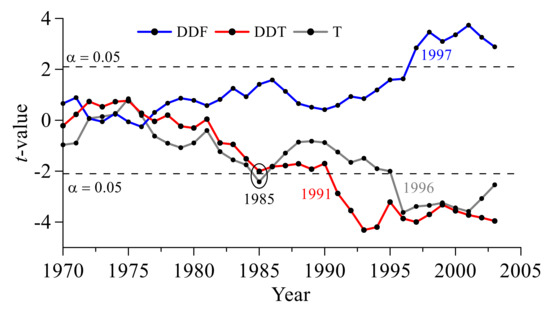
Figure 8.
Change points of freezing–thawing indices and annual mean temperature detected by moving t-test.
As seen in Table 5, both T and DDT have two increase periods. T showed a slight increase (0.52 °C) in the period 1986–1996 but a substantial increase (1.27 °C) in the period 1997–2013, with a significant increase rate 0.07 °C/year (p < 0.05). Similar to T, DDT increased by 3.26% in the period 1986–1991 and increased by 14.29% with a significant increase rate of 11.42 °C·day/year in the period 1992–2013 (p < 0.01). The abrupt change point (1997) of DDF is relatively late compared to DDT and air temperature. DDF showed a 14.99% reduction in the period 1998–2013 compared to the period 1961–1997.

Table 5.
Temperature and freezing–thawing indices changes in respective periods.
5. Discussion
In previous studies, the decrease of annual mean runoff (AMR) and rainy season runoff (RSR) in the low-flow period (1990–2002) is generally attributed to decreases in precipitation, and increases in evaporation [29,31]. Meanwhile, the significantly decreased precipitation intensity is also a crucial factor that resulted in an evaporation increase in the 1990s. The increase in precipitation after 2002 offset the effects of increased evaporation, and is the main reason leading to a recovery of the runoff in the recovery period (2003–2013) [31,32].
This study focused on the cold season runoff changes. The cold season runoff, recession flow (RF), and winter baseflow (WB) shared one abrupt change point (1989) with rainy season runoff (RSR). It is a rational result, as RF and WB are results from the recession of RSR. In addition, RSR, RF, and WB are highly correlated with each other (Table 2). However, the second abrupt change points of RF and WB have a three-year (1999) deviation and a one-year (2001) deviation compared to RSR (2002), indicating the runoff supplement and runoff processes changed during the 1990s (Figure 5). Both cold season precipitation and freezing–thawing indices showed abrupt changes in the 1990s (Table 4 and Table 5). The potential reasons for the inconsistent variations of RSR, WB, and RF are the changes of cold season precipitation and frozen ground. Meanwhile, previous studies reported that the existence of frozen ground impedes infiltration, resulting in higher direct flow ratio [23,24,25]. However, the ways in which the snowmelt runoff changes along with cold season precipitation changes and frozen ground degradation are still unknown. In this section, the precipitation change impacts on cold season runoff and the potential hydrological effects of frozen ground degradation are discussed.
5.1. Precipitation Change Impacts on Cold Season Runoff
The correlations between cold season runoff and cold season precipitation are shown in Table 6. By comparing Table 2 and Table 6, we found that the winter baseflow (WB) is mainly controlled by recession flow (RF) and rainy season runoff (RSR) but is also affected by (Sleet + Rain) (9–2). Snowmelt runoff (SR) is mainly controlled by (Snow (9–5) + (Sleet + Rain) (9–2)), RF, and WB. After removing the WB impacts on SR, the correlation coefficient between direct snowmelt runoff (DSR) and Snow (9–5) increased to 0.54. The correlation coefficient between direct snowmelt runoff (DSR) and Snow (9–5) + (Sleet + Rain) (9–2) is 0.55. The correlation coefficient between direct snowmelt runoff (DSR) and Snow (9–5) + (Sleet + Rain) (3–5) is 0.29. Therefore, DSR is mainly fed by the snowmelt from the accumulative snow in cold season (ASC), therefore, the changes of precipitation types between September and May have little impacts on direct snowmelt runoff change. The recession flow (RF) has a relatively weak correlation with cold season precipitation, which is mainly controlled by rainy season runoff (Table 2).

Table 6.
Correlations between cold season runoff and cold season precipitation.
The increased (Sleet + Rain) (9–2), caused by the increase of air temperature in the 1990s, is an extra supplement for RF and WB compared to the pre-change period (1961–1989). RSR and RF showed a decrease trend in the 1990s, however, WB increased significantly at a rate of 1.10 m3/s/year (Table 3). In addition, (Sleet + Rain) (9–2) showed no significant change until 1999, indicating that the change of supplement could not fully explain the gradually increase phenomenon of WB in the 1990s. Therefore, another important factor, frozen ground degradation, should be involved in the explanation of WB changes. In the 2000s, both RF and WB showed a significant increase trend, partly because the extra supplement, (Sleet + Rain) (9–2), increased by 6.35% from 2000 to 2013. The continuous effects of frozen ground degradation on WB increase in the 2000s are further discussed in the following section.
5.2. Frozen Ground Degradation Impacts on Cold Season Runoff
5.2.1. Frozen Ground Degradation Impacts on Winter Baseflow
As indicated by the obtained results in Table 2, winter baseflow is significantly correlated to rainy season runoff (RSR) and recession flow (RF). Recession flow is a depletion process of rainy season runoff, in which surface runoff gradually decreased and was replaced by groundwater discharge. Winter baseflow is mainly fed by groundwater discharge, which is related to the water stored in the active layer and aquifer (WRSQ) in the rainy season [45]. Due to the lack of groundwater observation data, RSR was used as an index to indicate volume of WRSQ in this study. Additionally, assume that RSR is linearly related with WRSQ when the aquifer characteristic does not evidently change. To investigate the variations of winter baseflow (WB), the related correlation analyses are plotted in Figure 9a,b. The rainy season runoff (RSR) and winter baseflow (WB) showed similar variations, as shown in Figure 9a. As shown in Figure 9b, WB is significantly positively correlated with RSR (R2 = 0.65, p < 0.01) which supports the theory that winter baseflow is fed by water resources stored in aquifers in the rainy season. If we assume that aquifer characteristics, such as hydrological conductivity and storage capacity, have not undergone dramatic change, WB and RSR could show the same variation. As analyzed in Section 4.1, however, the moving t-test results indicate the abrupt change point of WB appeared three years earlier than RSR, indicating the change of the relationship between WB and RSR at the end of 1990s.
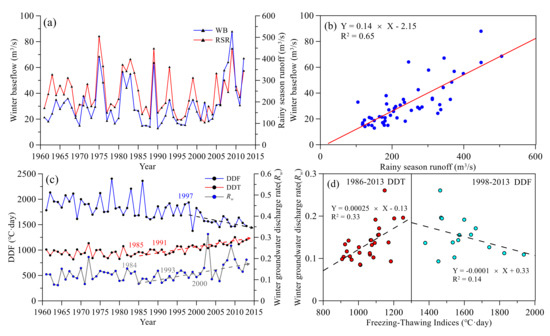
Figure 9.
(a) Inter-annual variation of rainy season runoff and winter baseflow (b) correlation of winter baseflow and rainy season runoff (c) Inter-annual variation of freezing–thawing indices (DDF, DDT) and winter groundwater discharge rate (Rw) (d) The correlation between freezing–thawing indices (DDF, DDT) and winter groundwater discharge rate (Rw).
To analyze the effects of frozen ground degradation to winter baseflow (RSR) change, we defined winter groundwater discharge rate as the ratio of WB to RSR. The long-term variations of freezing–thawing indices and winter groundwater discharge rate (Rw) are shown in Figure 9c. The labelled years indicate the abrupt change points of freezing–thawing indices and Rw detected by the moving t-test. DDT showed a continuous significant increase (R2 = 0.70, p < 0.01) since 1986, DDF remained stable between 1985 and 1997 but showed a significantly decrease (R2 = 0.22, p < 0.01) in the period 1997–2013. The results indicate permafrost thawed depth significantly increased since 1985, and frozen depth significantly decreased since 1997. The enlarged thawed depth provided more room for water storage in the active layer in the rainy season. Meanwhile, the decrease of frozen depth leads to taliks formation which provided extra groundwater discharge channels. The combination effects of thawed depth and frozen depth changes lead more grounder water discharge in winter. The Rw remains about 0.1–0.2 but gradually significantly increased (R2 = 0.34, p < 0.01) since 1985 and reached about 0.2–0.3 in the 21st century.
The correlation of Rw and freezing–thawing indices after temperature significantly increased (1985) are plotted in Figure 9d. The Rw is significantly and negatively (R2 = 0.14, p < 0.01) correlated with DDF, and is significantly and positively (R2 = 0.33, p < 0.01) correlated with DDT. This finding indicates the increase in thawed depth and decrease in frozen depth will increase winter groundwater discharge rate, which is consistent with the understanding that under the warming climate the deeper permafrost table and the reduction frozen depth of active layer will lead more groundwater discharge in the winter [12,46]. The higher correlation coefficient between DDT and Rw (R2 = 0.33, p < 0.01) indicated that the deeper thawed depth played a more important role in influencing groundwater discharge rate change. However, the correlation coefficient between thawing-freezing indices and Rw (R2 = 0.33, R2 = 0.14) is lower than the correlation coefficient of RSR and WB (R2 = 0.65, p < 0.01), which indicates water resources stored in the rainy season is the main controlling factor of WB, and global warming induced frozen ground degradation altered the relationship between WB and WRSQ. Meanwhile, Rw in the period 2000–2013 presented a more distinct fluctuation compared to period the 1985–2000 (Figure 9c). This may be related to the increased sleet and rain from September to February since 1999, which provided an extra supplement to the winter baseflow.
5.2.2. Frozen Ground Degradation Impacts on Direct Snowmelt Runoff
The correlation analyses matrix between cold season runoff and cold season precipitation indicates that direct snowmelt runoff is mainly fed by accumulative snow in the cold season (ASC) (Table 6). The direct snowmelt runoff (DSR) and respective runoff coefficient changes are plotted in Figure 10a,b, respectively.
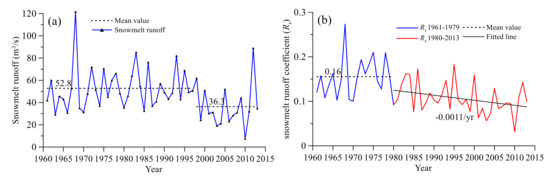
Figure 10.
The inter-annual variation of (a) direct snowmelt runoff and (b) direct snowmelt runoff coefficient (Rs).
The direct snowmelt runoff coefficient (Rs) was defined as the ratio of direct snowmelt runoff depth (mm) to accumulative snow in the cold season (ASC) (mm). As shown in Figure 10a, the DSR slightly increased in the period 1961–1997 and decreased in the period 1998–2013, presenting a similar variations pattern with ASC plotted in Figure 8b. The change pattern can be generally divided into two periods; a pre-change period (1961–1997) and a decrease period (1998–2013). The DSR remains at the same level (mean value 52.76 m3/s) during the period 1986–1997 but sharply decreased to 36.30 m3/s during the period 1998–2013. The decrease in the DSR (31.21%) is three times larger than the decrease in SR (8.64%) after removing the increasing winter baseflow (WB) impacts (Table 3). Due to the impacts of gradually increased WB in the 1990s, SR presented a slight increase trend during the 1990s, although snow decreased.
Notably, the Rs of DSR shown in Figure 10b displayed a different variation pattern; the Rs was approximately 0.16 from 1961 to 1980 but decreased with a rate of 0.0011/year from 1981 to 2013 (significant at 10% level (p < 0.1)). The variation in the direct snowmelt runoff coefficient (Rs) is different from direct snowmelt runoff, indicating there is another factor controlling snowmelt runoff generation besides accumulative snow in cold season (ASC). Since frozen ground is characterized as having low permeability, one possible reason for the Rs decrease is the decreased frozen depth and shortened frozen duration, leading to more snowmelt infiltration in the ground in spring rather than directly contributing to the runoff. As indicated by previous studies, the hillslopes produce more runoff than those without permafrost, moreover, snowmelt runoff in cold regions has a higher direct runoff ratio than the storm runoff in watersheds without frozen ground [22,47,48].
To analyze frozen ground degradation impacts on direct snowmelt runoff generation, DDF and DDT were used to represent the frozen depth and thawed depth of the frozen ground. The correlations between freezing–thawing indices and direct snowmelt runoff coefficient (Rs) are shown in Figure 11.
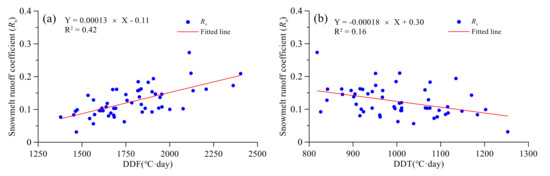
Figure 11.
The correlation between direct snowmelt runoff coefficient and freezing–thawing indices (DDF (a), DDT (b)).
As indicated by the comparison of Figure 11a,b, the direct snowmelt runoff coefficient (Rs) is more related to DDF (0.42, p < 0.01) rather than to DDT (0.16, p < 0.01). This indicates that ground frozen depth in winter controlled direct snowmelt runoff generation, and with the deeper frozen depth and the longer frozen duration in the winter, more direct snowmelt runoff will be produced in the spring. The results indicate frozen ground degradation will reduce direct snowmelt runoff generation.
5.3. Frozen Ground Degradation Impacts on Water Balance
In this study, we ignored frozen ground degradation impacts on water balance in the HWYR and focused on its impacts on winter baseflow and snowmelt runoff. Nevertheless, the frozen ground degradation impacts have been considered in long-term water balance analyses lately [7,32,34]. Duan [7] used a sensitive-based method to analyze permafrost effects on runoff change of watersheds in north-eastern China and concluded that permafrost thaw increased runoff, but it is difficult to separate the permafrost degradation impacts from complex driving factors. Based on a modified decomposition method, Wu [32] also found that the permafrost degradation presented a positive effect, which is contrary to temperature impacts on runoff change in the headwaters of the Yellow River (HWYR). Sun [49] used a water balance simulation model to simulate and quantify the runoff change in the HWYR. The study found that total permafrost degradation will increase discharge at an annual scale. However, Wang [34] reported a different conclusion based on the Budyko framework, indicating that frozen ground degradation decreases the runoff of the HWYR by about 34%. In addition, Zheng [50] and Zhang [51] used a physical based model with different freeze–thaw process scenarios to simulate runoff in cold regions, and the results showed that the simulated runoff generally reduced when the soil freeze–thaw mechanism is not considered.
As described above, the conclusions of frozen ground degradation’s contribution to water balance are still debatable. Meanwhile, as indicated by the moving t-test and the statistical results, the change in precipitation, precipitation intensities, and temperature can explain the annual mean runoff changes. The results agree with most previous studies that the long-term annual runoff change in the HWYR is mainly controlled by climate changes (decrease in precipitation and increase in evaporation) [29,30,31,32]. Furthermore, it is difficult to separate the frozen ground degradation impacts on water balance, because the increase in temperature affects actual evaporation and the frozen ground at the same time [32]. Considering frozen ground degradation impacts on water balance by a statistical method is out the scope of this study. However, frozen ground impacts on annual water balance is still an unsolved question which deserves further analyses in future research.
6. Conclusions
In order to investigate hydrological change and its relationship with the changing climate, and degrading frozen ground in the HWYR, we analyzed the long-term variations of runoff compositions, climate factors, and degrading frozen ground. Moreover, we further discussed the correlations between hydrological change and climate change, especially degrading frozen ground following climate change in this study. According to the obtained results, several conclusions can be drawn:
- (1)
- The long-term annual runoff variations can generally be divided into three periods: I. a pre-change period (1961–1989), II. a low-flow period (1990–2002), and III. a recovery period (2003–2013). In period II, the decrease in high flow (Pe < 30%) and low flow (Pe > 70%) presented the same levels (about 30%) as period I. In period III, however, low flow increased by 40% but high flow increased by less than 20% relative to period I.
- (2)
- The intra-annual variations of runoff in the HWYR can be divided into winter baseflow (January to February), snowmelt runoff (March to May), rainy season runoff (June to September), and recession flow (October to December), which account for 4%, 15%, 61%, and 20% of annual runoff, respectively.
- (3)
- The winter baseflow is mainly controlled by rainy season runoff, but the frozen ground degradation altered the relationship between rainy season runoff and winter baseflow. Frozen ground degradation increased ground water discharge rate in winter.
- (4)
- Direct snowmelt runoff remained at the same level during the period 1961–1997 but decreased 31.21% in the period 1997–2013 relative to the period 1961–1997. The direct snowmelt runoff coefficient (Rs) has been linearly decreasing at a rate of 0.0011/year since 1980, which is significantly controlled by DDF.
According to the obtained conclusions summarized above, we can deduce that with the decreasing accumulative snow in the cold season and the degrading frozen ground, the direct snowmelt runoff of the HWYR may decrease continuously under a warming climate in the future.
Author Contributions
Conceptualization, P.W. and S.L.; methodology, P.W.; validation, X.-S.W., S.L. and Y.F.; formal analysis, P.W. and Y.F.; writing—original draft preparation, P.W.; writing—review and editing, S.L., X.-S.W. and J.M.M.; supervision, S.L. and J.M.M.; project administration, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
Supports from the strategic priority research program of Chinese Academy of Sciences (XDA20100103), National Nature Science Foundation of China (41330634, 41072191, 91125011) and China Geological Survey (DD20191006) are gratefully acknowledged.
Acknowledgments
The authors are grateful for the insightful and constructive comments from the two anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yamazaki, Y.; Kubota, J.; Ohata, T.; Vuglinsky, V.; Mizuyama, T. Seasonal changes in runoff characteristics on a permafrost watershed in the southern mountainous region of Eastern Siberia. Hydrol. Process. 2010, 20, 453–467. [Google Scholar] [CrossRef]
- Haldorsen, S.; Heim, M.; Dale, B.; Landvik, J.Y.; van der Ploeg, M.; Leijnse, A.; Salvigsen, O.; Hagen, J.O.; Banks, D. Sensitivity to long-term climate change of subpermafrost groundwater systems in svalbard. Quat. Res. 2010, 73, 393–402. [Google Scholar] [CrossRef]
- Lyon, S.W.; Destouni, G. Changes in catchment-scale recession flow properties in response to permafrost thawing in the Yukon river basin. Int. J. Climatol. 2010, 30, 2138–2145. [Google Scholar] [CrossRef]
- Andermann, C.; Longuevergne, L.; Bonnet, S.; Crave, A.; Davy, P.; Gloaguen, R. Impact of transient groundwater storage on the discharge of Himalayan rivers. Nat. Geosci. 2012, 5, 1–6. [Google Scholar] [CrossRef]
- Qin, Y.; Yang, D.; Gao, B.; Wang, T.; Chen, J.; Chen, Y.; Wang, Y.; Zheng, G. Impacts of climate warming on the frozen ground and eco-hydrology in the yellow river source region, China. Sci. Total Environ. 2017, 605, 830–841. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef]
- Duan, L.; Man, X.; Kurylyk, B.L.; Cai, T.; Li, Q. Distinguishing streamflow trends caused by changes in climate, forest cover, and permafrost in a large watershed in Northeastern China. Hydrol. Process. 2017, 31, 1938–1951. [Google Scholar] [CrossRef]
- Liu, J.; Hayakawa, N.; Lu, M.; Dong, S.; Yuan, J. Hydrological and geocryological response of winter streamflow to climate warming in northeast china. Cold Regions Sci. Technol. 2003, 37(1), 15–24. [Google Scholar] [CrossRef]
- Wang, G.; Mao, T.; Chang, J.; Song, C.; Huang, K. Processes of runoff generation operating during the spring and autumn seasons in a permafrost catchment on semi-arid plateaus. J. Hydrol. 2017, 550, 307–317. [Google Scholar]
- Zhou, Y.; Guo, D.; Qiu, G.; Cheng, G. Geocryology in China; Science Press: Beijing, China, 2000; 450p. (In Chinese) [Google Scholar]
- Ge, S.; Mckenzie, J.; Voss, C.; Wu, Q. Exchange of groundwater and surface-water mediated by permafrost response to seasonal and long term air temperature variation. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Gao, B.; Yang, D.; Qin, Y.; Wang, Y.; Li, H.; Zhang, Y.; Zhang, T. Change in frozen soils and its effect on regional hydrology in the upper heihe basin, the Northeast Qinghai-Tibetan Plateau. Cryosphere 2018, 12, 1–55. [Google Scholar] [CrossRef]
- Walvoord, M.A.; Striegl, R.G. Increased groundwater to stream discharge from permafrost thawing in the Yukon river basin: Potential impacts on lateral export of carbon and nitrogen. Geophys. Res. Lett. 2007, 34, L12402. [Google Scholar] [CrossRef]
- Wang, G.; Hu, H.; Li, T. The influence of freeze–thaw cycles of active soil layer on surface runoff in a permafrost watershed. J. Hydrol. 2009, 375, 438–449. [Google Scholar] [CrossRef]
- Jacques, J.M.S.; Sauchyn, D.J. Increasing winter baseflow and mean annual streamflow from possible permafrost thawing in the northwest territories, Canada. Geophys. Res. Lett. 2009, 36, 329–342. [Google Scholar] [CrossRef]
- Qin, Y.; Gao, B.; Yang, D.; Lei, H.; Fan, W.; Wang, Y.; Cong, Z.; Fan, W. Long-term change in the depth of seasonally frozen ground and its ecohydrological impacts in the qilian mountains, northeastern tibetan plateau. J. Hydrol. 2016, 542(C), 204–221. [Google Scholar] [CrossRef]
- Lyon, S.W.; Destouni, G.; Giesler, R.; Humborg, C.; Mörth, C.M.; Seibert, J.; Karlsson, J.; Troch, P.A. Estimation of permafrost thawing rates in a sub-arctic catchment using recession flow analysis. Hydrol. Earth Syst. Sci. 2009, 13, 595–604. [Google Scholar] [CrossRef]
- Sjöberg, Y.; Frampton, A.; Lyon, S.W. Using streamflow characteristics to explore permafrost thawing in northern swedish catchments. Hydrogeol. J. 2013, 21, 121–131. [Google Scholar] [CrossRef]
- Stewart, I.T.; Prowse, T.D. Changes in snowpack and snowmelt runoff for key mountain regions. Hydrol. Process. 2010, 23, 78–94. [Google Scholar] [CrossRef]
- Haupt, H.F. Infiltration, overland flow, and soil movement on frozen and snow-covered plots. Water Resour. Res. 1967, 3, 145–161. [Google Scholar] [CrossRef]
- Walvoord, M.A.; Kurylyk, B.L. Hydrologic impacts of thawing permafrost—A review. Vadose Zone J. 2016, 15, 1–20. [Google Scholar] [CrossRef]
- McNamara, J.P.; Kane, D.L.; Hinzman, L.D. An analysis of streamflow hydrology in the Kuparuk River Basin, arctic Alaska: A nested watershed approach. J. Hydrol. 1988, 206, 39–57. [Google Scholar] [CrossRef]
- Kane, D.L.; Stein, J. Water movement into seasonally frozen soils. Water Resour. Res. 1983, 19, 1547–1557. [Google Scholar] [CrossRef]
- Hayashi, M.; Kamp, G.V.D.; Schmidt, R. Focused infiltration of snowmelt water in partially frozen soil under small depressions. J. Hydrol. 2003, 270, 214–229. [Google Scholar] [CrossRef]
- Shanley, J.B.; Chalmers, A. The effect of frozen soil on snowmelt runoff at Sleepers River, Vermont. Hydrol. Process. 1999, 13, 1843–1857. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T. Recent permafrost warming on the Qinghai-Tibetan Plateau. J. Geophys. Res. Atmos. 2008, 113, D13108. [Google Scholar] [CrossRef]
- Jin, H.J.; He, R.X.; Cheng, G.D.; Wu, Q.B.; Wang, S.L.; Chang, X.L. Changes in frozen ground in the source area of the yellow river on the Qinghai-Tibet Plateau, China, and their eco-environmental impacts. Environ. Res. Lett. 2009, 4, 045206. [Google Scholar] [CrossRef]
- Cheng, G.; Jin, H. Permafrost and groundwater on the Qinghai-Tibet Plateau and in northeast China. Hydrogeol. J. 2013, 21, 5–23. [Google Scholar] [CrossRef]
- Cuo, L.; Zhang, Y.; Gao, Y.; Hao, Z.; Cairang, L. The impacts of climate change and land cover/use transition on the hydrology in the upper Yellow River Basin, China. J. Hydrol. 2013, 502, 37–52. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Liu, C.; Shao, Q.; Fukushima, Y. Changes in stream flow regime in headwater catchments of the Yellow River basin since the 1950s. Hydrol. Process. 2007, 21, 886–893. [Google Scholar] [CrossRef]
- Meng, F.; Su, F.; Yang, D.; Tong, K.; Hao, Z. Impacts of recent climate change on the hydrology in the source region of the yellow river basin. J. Hydrol. Reg. Stud. 2016, 6, 66–81. [Google Scholar] [CrossRef]
- Wu, P.; Liang, S.; Wang, X.S.; Feng, Y.; Mckenzie, J. A new assessment of hydrological change in the source region of the yellow river. Water 2018, 10, 877. [Google Scholar] [CrossRef]
- Chang, G.; Lin, L.I.; Zhu, X.; Wang, Z.; Xiao, J.; Fengxia, L.I. Changes and influencing factors of surface water resources in the source region of the yellow river. Acta Geogr. Sin. 2007, 62, 312–320. [Google Scholar]
- Wang, T.; Yang, H.; Yang, D.; Qin, Y.; Wang, Y. Quantifying the streamflow response to frozen ground degradation in the source region of the yellow river within the budyko framework. J. Hydrol. 2018, 558, 301–313. [Google Scholar] [CrossRef]
- Li, S.D.; Cheng, G.D. Map of Permafrost on the Qinghai-Tibet Plateau (1:3,000,000); Gansu Culture Press: Lanzhou, China, 1996. (In Chinese) [Google Scholar]
- Liang, T.G.; Huang, X.D.; Wu, C.X.; Liu, X.Y.; Li, W.L.; Guo, Z.G.; Ren, J.Z. An application of modis data to snow cover monitoring in a pastoral area: A case study in northern Xinjiang, China. Remote Sens. Environ. 2008, 112, 1514–1526. [Google Scholar] [CrossRef]
- Pu, Z.; Xu, L.; Salomonson, V.V. MODIS/Terra observed seasonal variationss of snow cover over the Tibetan Plateau. Geophys. Res. Lett. 2007, 34, L06706. [Google Scholar] [CrossRef]
- Riseborough, D.; Shiklomanov, N.; EtzelmÜLler, B.; Gruber, S.; Marchenko, S. Recent advances in permafrost modelling. Permafr. Periglac. Process. 2010, 19, 137–156. [Google Scholar] [CrossRef]
- Sato, Y.; Ma, X.; Xu, J.; Matsuoka, M.; Zheng, H.; Liu, C.; Fukushima, Y. Analysis of long-term water balance in the source area of the Yellow River basin. Hydrol. Processes 2008, 22, 1618–1629. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Woods, R.A.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Chang. 2014, 4, 583–586. [Google Scholar] [CrossRef]
- Searcy, J.K. Flow-duration curves. Water Supply Paper, U.S. Geol. Survey Water-Supply Paper 1542-A. 33p, 1960. [Google Scholar]
- Smakhtin, V.U. Restoration of natural daily flow time-series in regulated rivers using non-linear spatial interpolation technique. Regul. Rivers Res. Manag. 1999, 15, 311–323. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Zhu, R.; Liu, C.; Sato, Y.; Fukushima, Y. Responses of streamflow to climate and land surface change in the headwaters of the yellow river basin. Water Resour. Res. 2009, 45(7), 587–595. [Google Scholar] [CrossRef]
- Tang, Y.; Tang, Q.; Tian, F.; Zhang, Z.; Liu, G. Responses of natural runoff to recent climatic variationss in the Yellow River basin, China. Hydrol. Earth Syst. Sci. 2013, 17, 4471–4480. [Google Scholar] [CrossRef]
- Streletskiy, D.A.; Tananaev, N.I.; Opel, T.; Shiklomanov, N.I.; Nyland, K.E.; Streletskaya, I.D.; Shiklomanov, A.I. Permafrost hydrology in changing climatic conditions: Seasonal variability of stable isotope composition in rivers in discontinuous permafrost. Environ. Res. Lett. 2015, 10, 095003. [Google Scholar] [CrossRef]
- Lamontagne-Hallé, P.; McKenzie, J.M.; Kurylyk, B.L.; Zipper, S.C. Changing groundwater discharge dynamics in permafrost regions. Environ. Res. Lett. 2018, 13, 084017. [Google Scholar] [CrossRef]
- Carey, S.K.; Woo, M.K. Hydrology of two slopes in subarctic Yukon, Canada. Hydrol. Processes 1999, 13, 2549–2562. [Google Scholar] [CrossRef]
- Carey, S.K.; Woo, M.K. Slope runoff processes and flow generation in a subarctic, subalpine catchment. J. Hydrol. 2001, 253, 110–129. [Google Scholar] [CrossRef]
- Sun, A.; Yu, Z.; Zhou, J.; Acharya, K.; Ju, Q.; Xing, R.; Huang, D.; Wen, L. Quantified hydrological responses to permafrost degradation in the headwaters of the Yellow River (HWYR) in High Asia. Sci. Total Environ. 2020, 712, 135632. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Cheng, G.; Li, X.; Jin, H.; Yang, D.; Flerchinger, G.N.; Chang, X.; Bense, V.F.; Han, X.; Liang, J. Influences of frozen ground and climate change on hydrological processes in an alpine watershed: A case study in the upstream area of the Hei’he River, Northwest China. Permafr. Periglac. Process 2017, 28, 420–432. [Google Scholar] [CrossRef]
- Zheng, D.; Rogier, V.D.V.; Su, Z.; Wen, J.; Wang, X.; Yang, K. Impact of soil freeze–thaw mechanism on the runoff dynamics of two Tibetan rivers. J. Hydrol. 2018, 563, 382–394. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).