Enhancing Physical Similarity Approach to Predict Runoff in Ungauged Watersheds in Sub-Tropical Regions
Abstract
1. Introduction
2. Materials and Methods
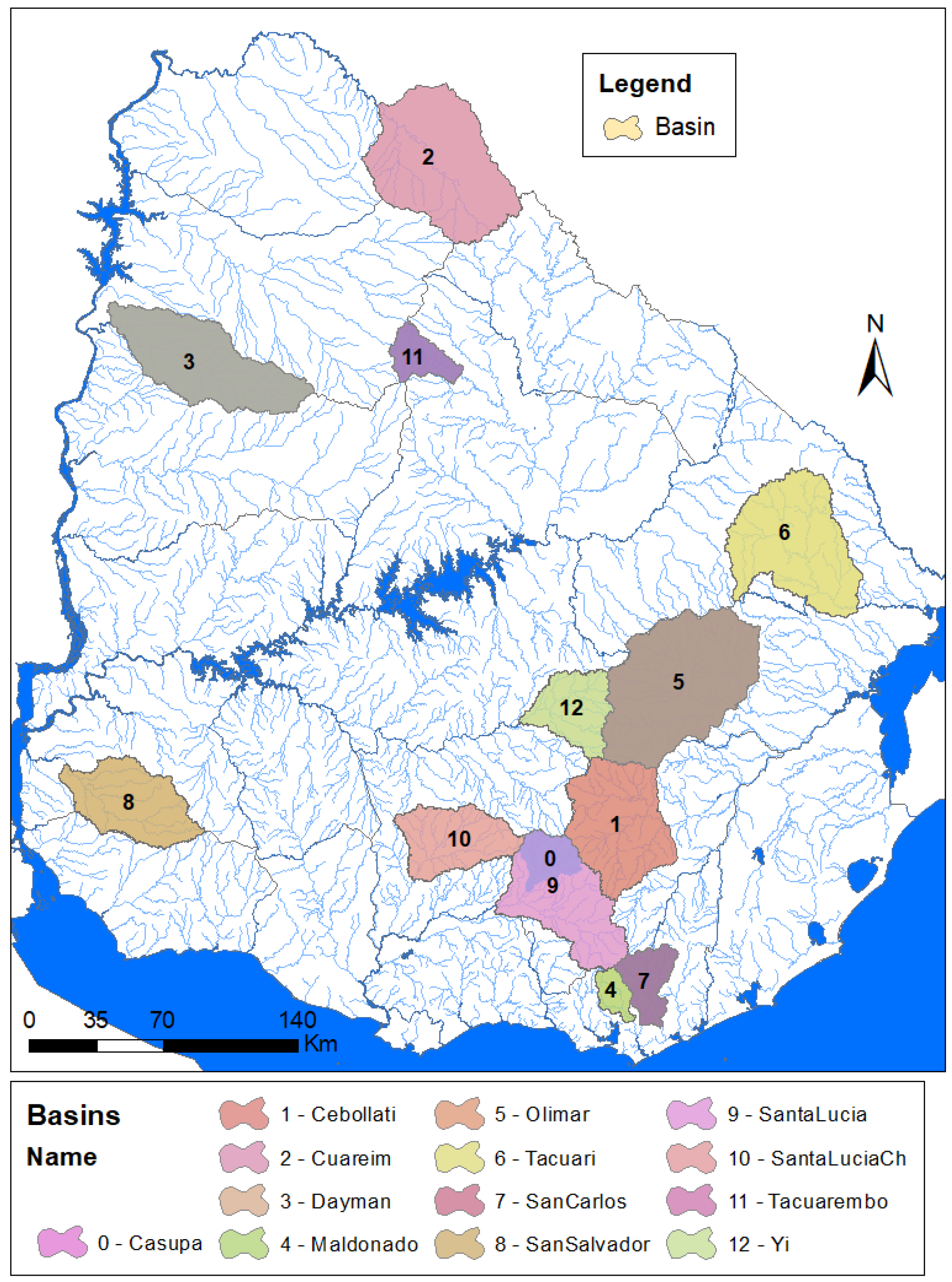
2.1. Study Area
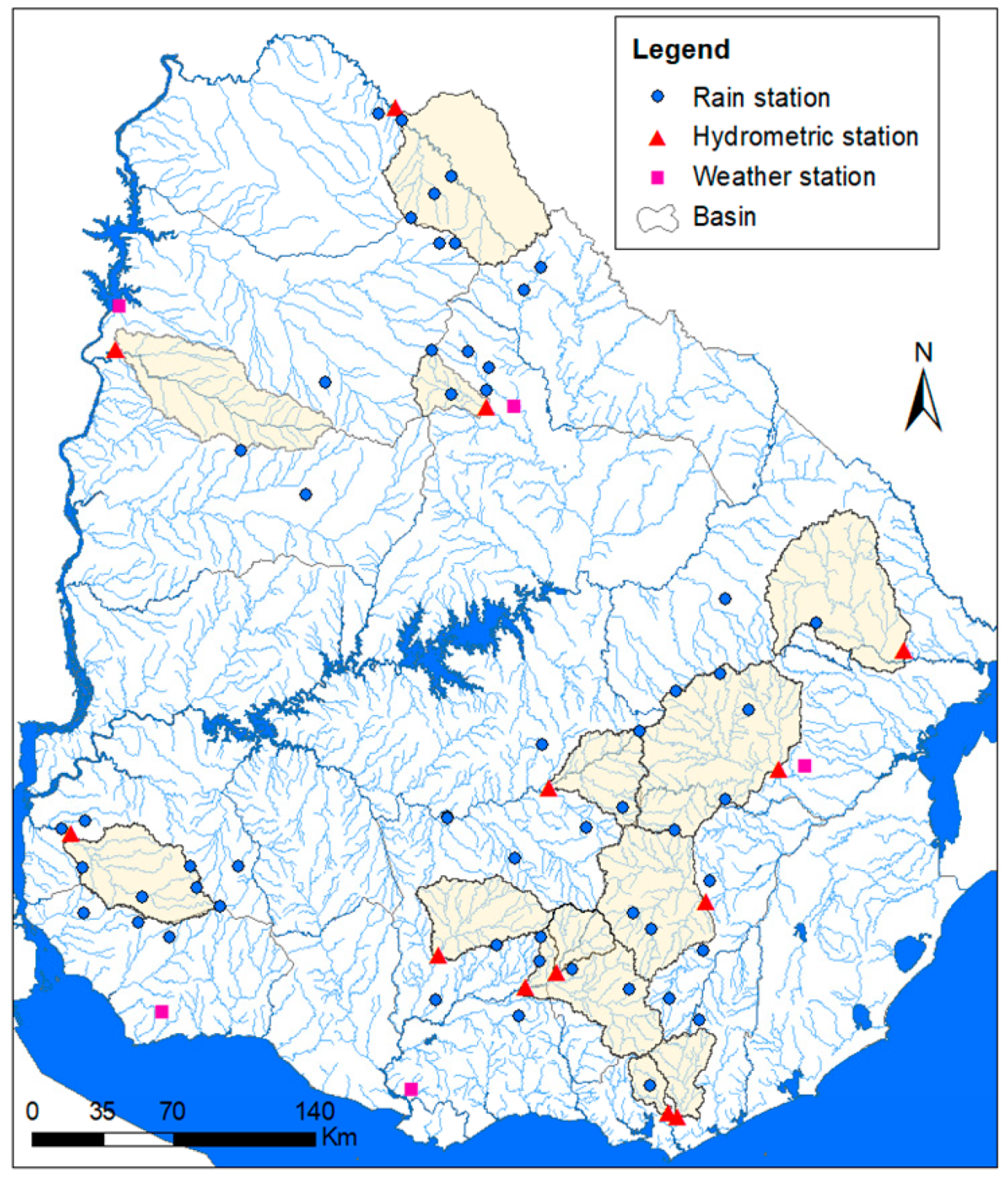
2.2. Data Collection
2.2.1. Precipitation, Climate, and Streamflow
2.2.2. Soil Type
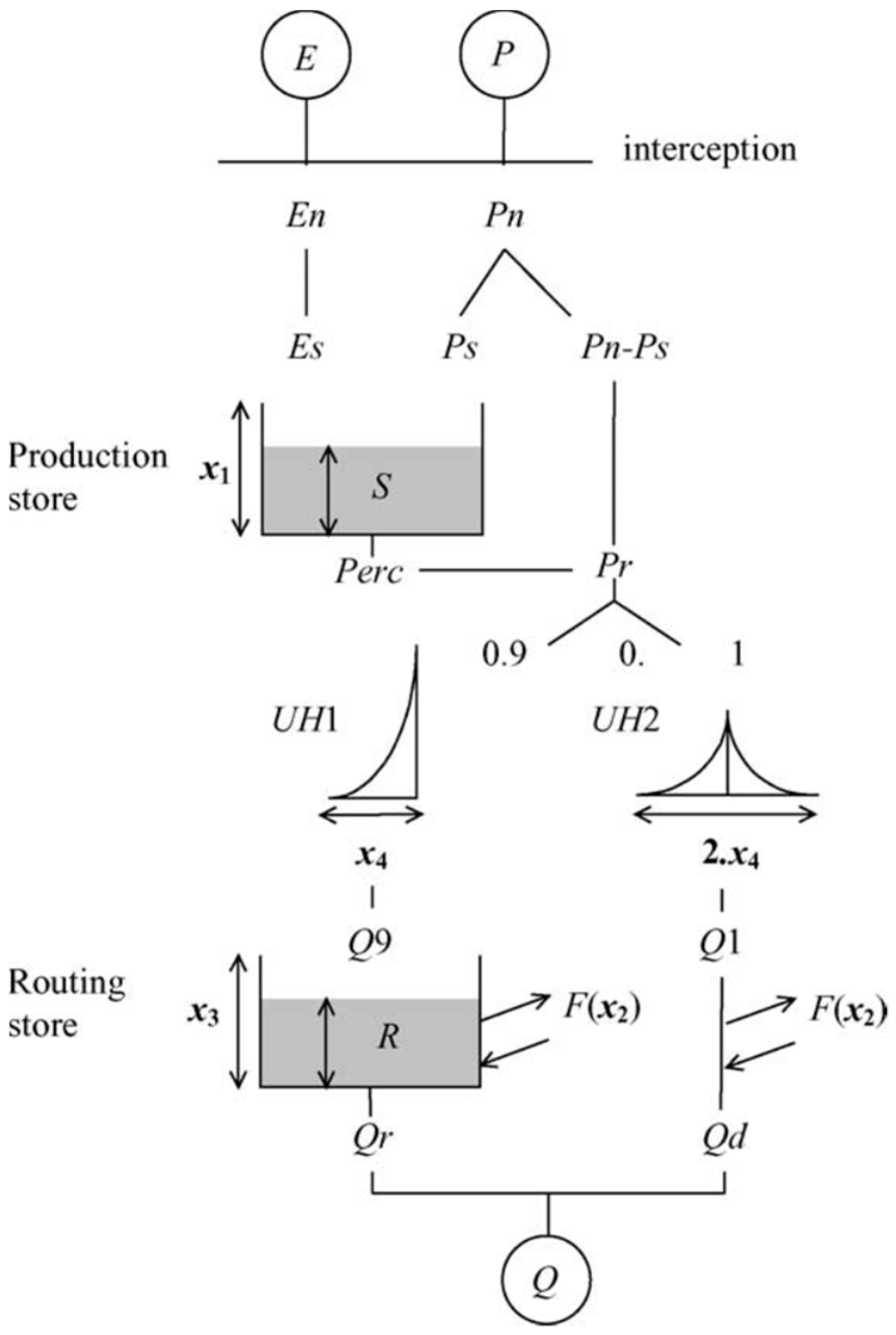
2.3. Rainfall-Runoff Model
2.4. Cluster Analysis for Watershed Selection
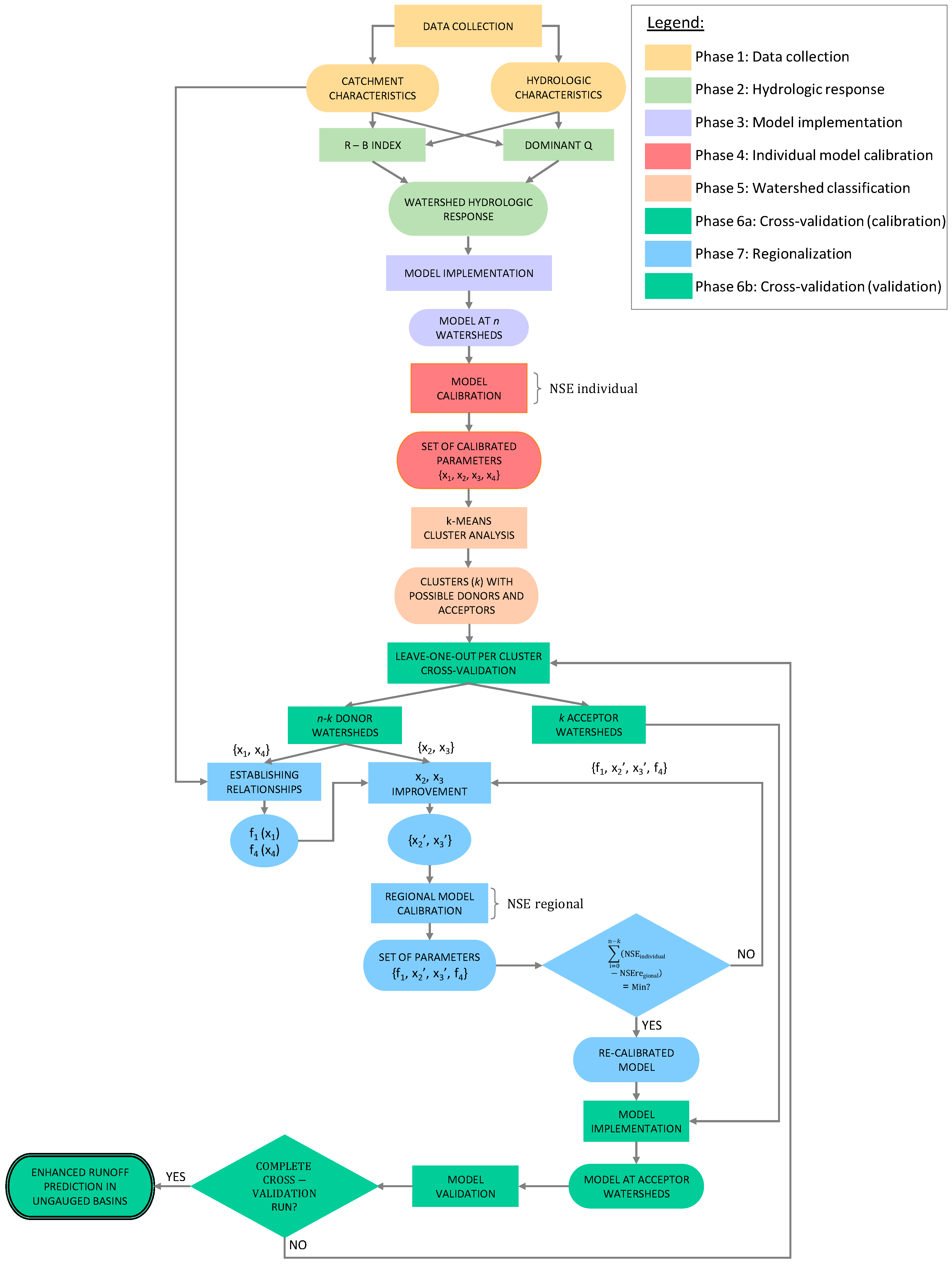
2.5. Regionalization Approach
3. Results and Discussion
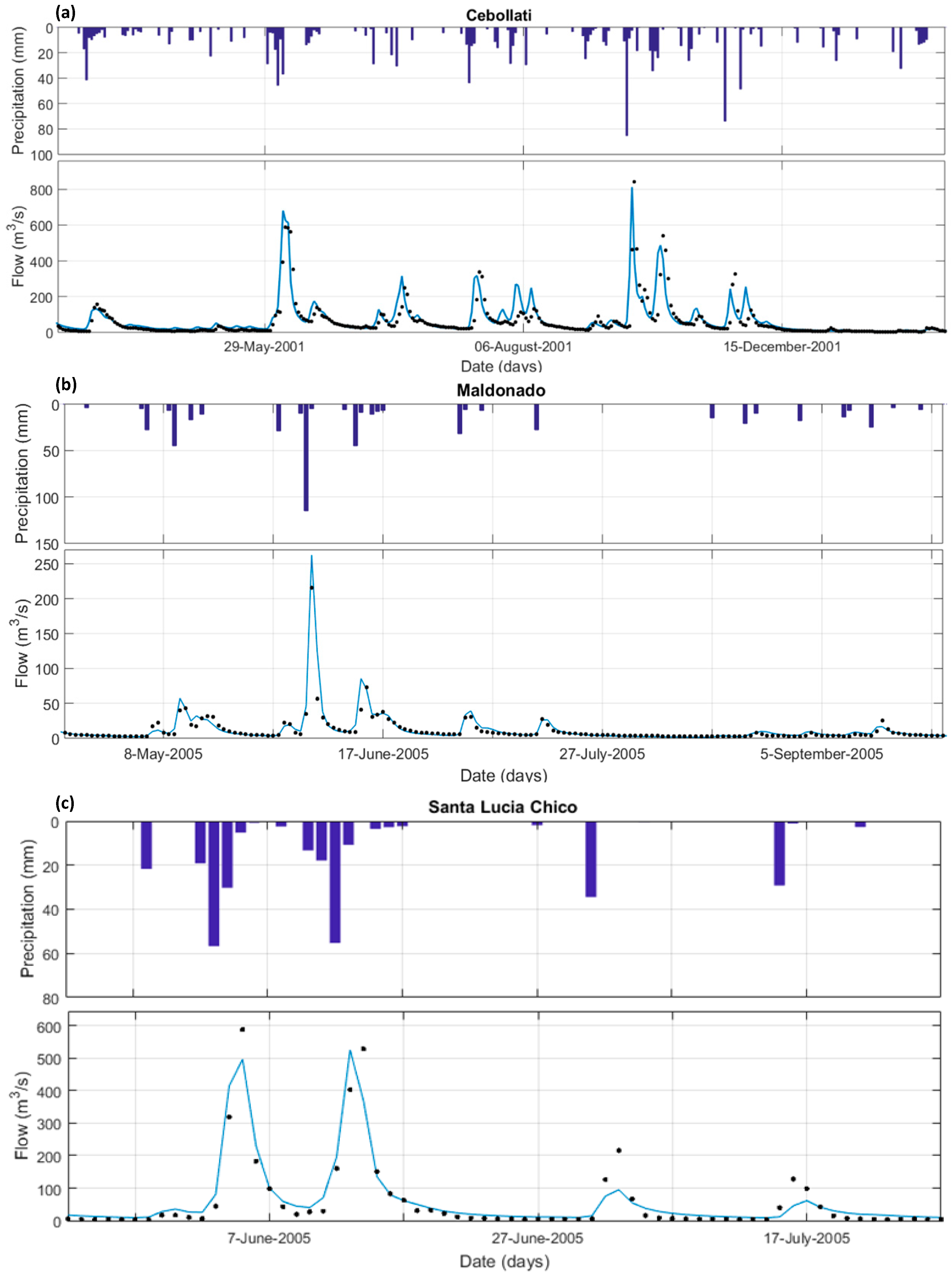
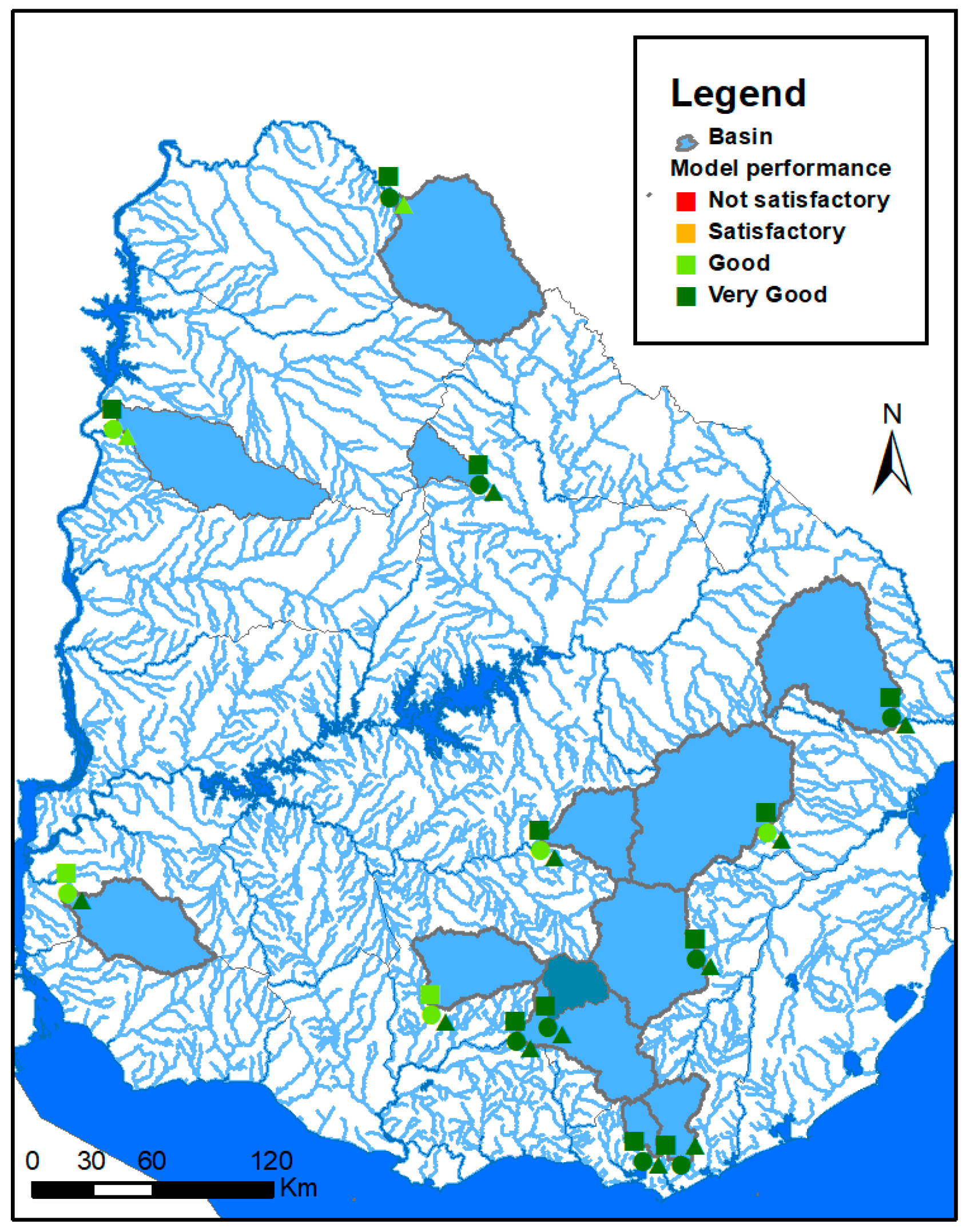
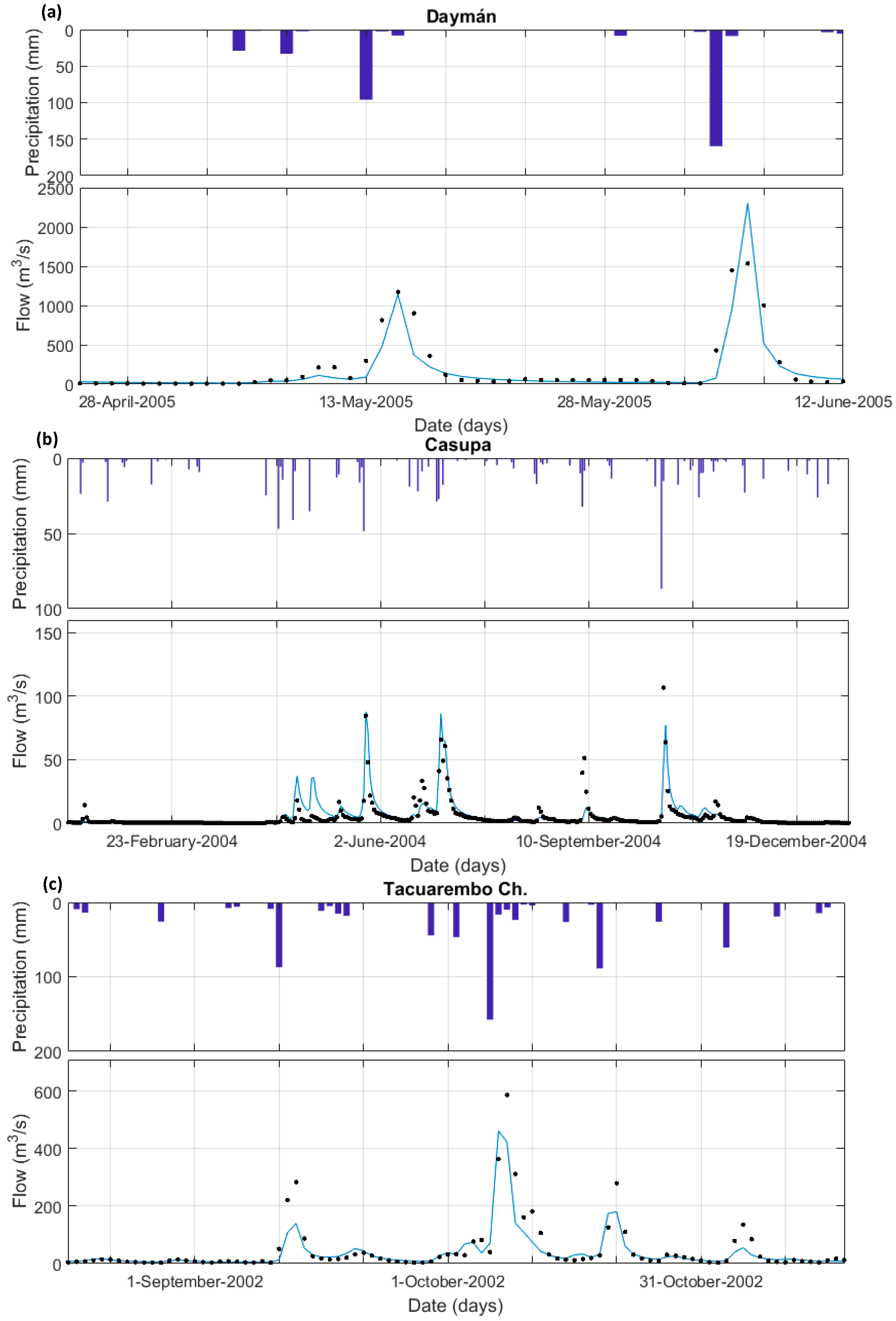
3.1. Rainfall-Runoff Model Performance
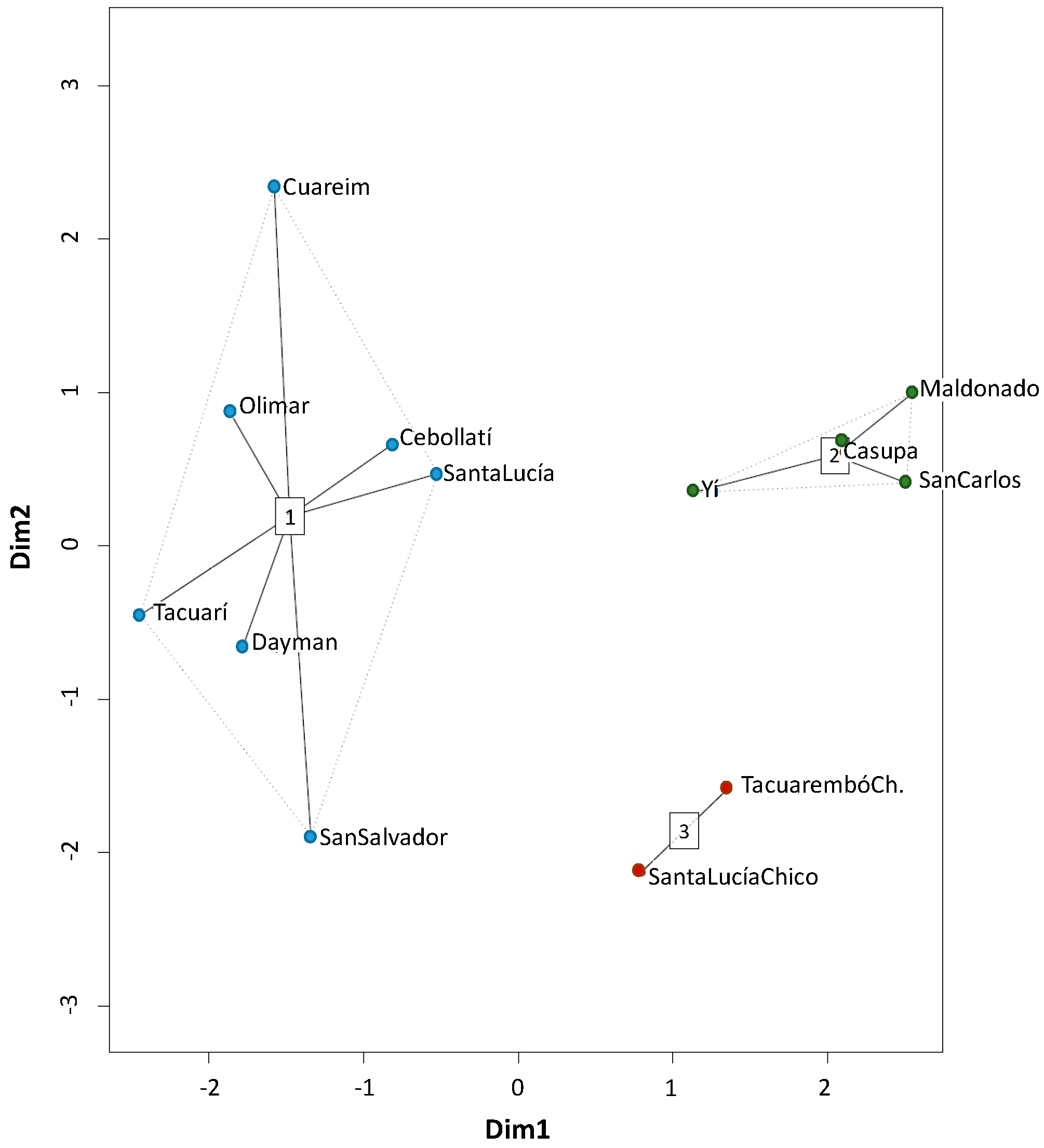
3.2. Donor and Acceptor Catchment Selection
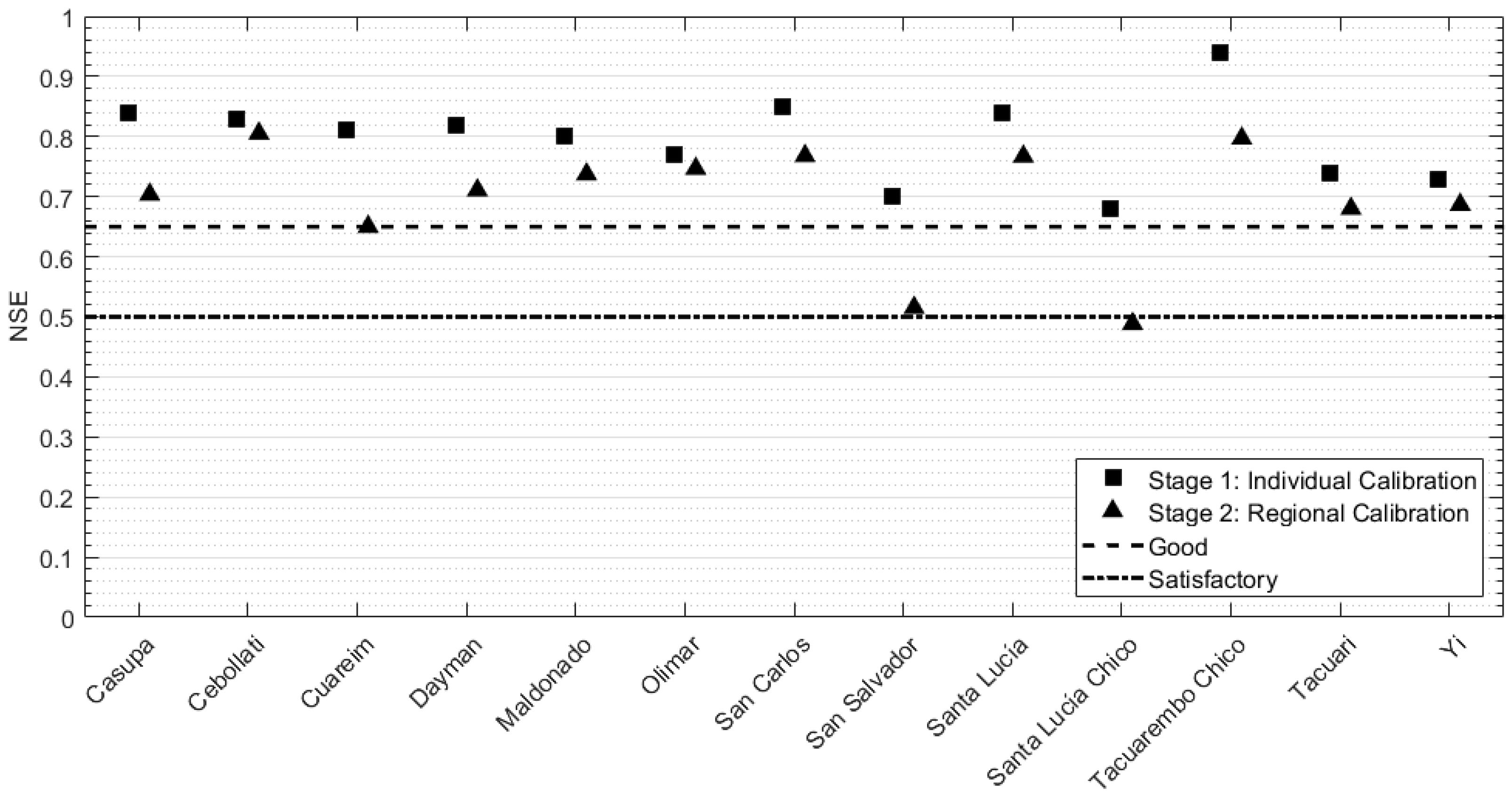
3.3. Calibration and Model Parameter Regionalization
3.4. Cross-Validation of the Regionalization Process
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yang, X.; Magnusson, J.; Xu, C.-Y. Transferability of regionalization methods under changing climate. J. Hydrol. 2019, 568, 67–81. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Gioia, A.; Iacobellis, V. A Framework for Assessing Modeling Performance and Effects of Rainfall-Catchment-Drainage Characteristics on Nutrient Urban Runoff in Poorly Gauged Watersheds. Sustainability 2019, 11, 4933. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Bombardelli, F.A.; Pitton, B.J.L.; Oki, L.R.; Haver, D.L.; Young, T.M. Uncertainty in the parameterization of sediment build-up and wash-off processes in the simulation of water quality in urban areas. Environ. Model. Softw. 2019, 111, 170–181. [Google Scholar] [CrossRef]
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.J.; Mendiondo, E.M.; O’Connell, P.E.; et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Tsegaw, A.T.; Alfredsen, K.; Skaugen, T.; Muthanna, T.M. Predicting hourly flows at ungauged small rural catchments using a parsimonious hydrological model. J. Hydrol. 2019, 573, 855–871. [Google Scholar] [CrossRef]
- Nearing, G.S.; Ruddell, B.L.; Bennett, A.R.; Prieto, C.; Gupta, H. Does Information Theory Provide a New Paradigm for Earth Science? Hypothesis Testing. Water Resour. Res. 2020, 56, e2019WR024918. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. A comparison of regionalization methods for catchment model parameters. Hydrol. Earth Syst. Sci. Discuss. 2005, 2, 509–542. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial proximity, physical similarity, regression and ungaged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Reichl, J.P.C.; Western, A.W.; McIntyre, N.R.; Chiew, F.H.S. Optimization of a similarity measure for estimating ungauged streamflow. Water Resour. Res. 2009, 45, 1–15. [Google Scholar] [CrossRef]
- He, Y.; Bárdossy, A.; Zehe, E. A review of regionalization for continuous streamflow simulation. Hydrol. Earth Syst. Sci. 2011, 15, 3539–3553. [Google Scholar] [CrossRef]
- Samuel, J.; Coulibaly, P.; Metcalfe, R.A. Estimation of continuous streamflow in Ontario ungauged basins: Comparison of regionalization methods. J. Hydrol. Eng. 2011, 16, 447–459. [Google Scholar] [CrossRef]
- Razavi, T.; Coulibaly, P. Streamflow prediction in ungauged basins: Review of regionalization methods. J. Hydrol. Eng. 2013, 18, 958–975. [Google Scholar] [CrossRef]
- Salinas, J.L.; Laaha, G.; Rogger, M.; Parajka, J.; Viglione, A.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins-Part 2: Flood and low flow studies. Hydrol. Earth Syst. Sci. 2013, 17, 2637–2652. [Google Scholar] [CrossRef]
- Viglione, A.; Parajka, J.; Rogger, M.; Salinas, J.L.; Laaha, G.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins-Part 3: Runoff signatures in Austria. Hydrol. Earth Syst. Sci. 2013, 17, 2263–2279. [Google Scholar] [CrossRef]
- Bastola, S.; Ishidaira, H.; Takeuchi, K. Regionalisation of hydrological model parameters under parameter uncertainty: A case study involving TOPMODEL and basins across the globe. J. Hydrol. 2008, 357, 188–206. [Google Scholar] [CrossRef]
- Götzinger, J.; Bárdossy, A. Comparison of four regionalisation methods for a distributed hydrological model. J. Hydrol. 2007, 333, 374–384. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, J.; Liu, J.; Fu, G.; Wang, G.; He, R.; Yan, X.; Jin, J.; Liu, H. Comparison of regionalization approaches based on regression and similarity for predictions in ungauged catchments under multiple hydro-climatic conditions. J. Hydrol. 2012, 466, 37–46. [Google Scholar] [CrossRef]
- Zhang, Y.; Vaze, J.; Chiew, F.H.; Teng, J.; Li, M. Predicting hydrological signatures in ungauged catchments using spatial interpolation, index model, and rainfall–runoff modelling. J. Hydrol. 2014, 517, 936–948. [Google Scholar] [CrossRef]
- Swain, J.B.; Patra, K.C. Streamflow estimation in ungauged catchments using regionalization techniques. J. Hydrol. 2017, 554, 420–433. [Google Scholar] [CrossRef]
- Yang, X.; Magnusson, J.; Rizzi, J.; Xu, C.-Y. Runoff prediction in ungauged catchments in Norway: Comparison of regionalization approaches. Hydrol. Res. 2018, 49, 487–505. [Google Scholar] [CrossRef]
- Kay, A.L.; Jones, D.A.; Crooks, S.M.; Calver, A.; Reynard, S.N. A comparison of three approaches to spatial generalization of rainfall-runoff models. Hydrol. Process. 2006, 20, 3953–3973. [Google Scholar] [CrossRef]
- Samaniego, L.; Bárdossy, A.; Kumar, R. Streamflow prediction in ungauged catchments using copula-based dissimilarity measures. Water Resour. Res. 2010, 46, W02506. [Google Scholar] [CrossRef]
- Ayzel, G.V. Runoff predictions in ungauged Arctic basins using conceptual models forced by reanalysis data. Water Resour. 2018, 45, S1–S7. [Google Scholar] [CrossRef]
- Prieto, C.; Le Vine, N.; Kavetski, D.; García, E.; Medina, R. Flow Prediction in Ungauged Catchments Using Probabilistic Random Forests Regionalization and New Statistical Adequacy Tests. Water Resour. Res. 2019, 55, 4364–4392. [Google Scholar] [CrossRef]
- Bulygina, N.; McIntyre, N.; Wheater, H. Bayesian conditioning of a rainfall-runoff model for predicting flows in ungauged catchments and under land use changes. Water Resour. Res. 2011, 47, W02503. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Addor, N.; Nearing, G.; Prieto, C.; Newman, A.J.; Le Vine, N.; Clark, M.P. A Ranking of Hydrological Signatures Based on Their Predictability in Space. Water Resour. Res. 2018, 54, 8792–8812. [Google Scholar] [CrossRef]
- Tegegne, G.; Kim, Y.-O. Modelling ungauged catchments using the catchment runoff response similarity. J. Hydrol. 2018, 564, 452–466. [Google Scholar] [CrossRef]
- Cazes-Boezio, G.; Robertson, A.W.; Mechoso, C.R. Seasonal dependence of ENSO teleconnections over South America and relationships with precipitation in Uruguay. J. Clim. 2003, 16, 1159–1176. [Google Scholar] [CrossRef]
- Talento, S.; Terra, R. Basis for a streamflow forecasting system to Rincón del Bonete and Salto Grande (Uruguay). Theor. Appl. Climatol. 2013, 114, 73–93. [Google Scholar] [CrossRef]
- García, N.O.; Mechoso, C.R. Variability in the discharge of South American rivers and in climate. Hydrol. Sci. J. 2005, 50, 478. [Google Scholar] [CrossRef]
- Pisciottano, G.; Díaz, A.; Cazes, G.; Mechoso, C.R. El Niño-Southern Oscillation Impact on Rainfall in Uruguay. J. Clim. 1994, 7, 1286–1302. [Google Scholar] [CrossRef]
- Diaz, A.F.; Studzinski, C.D.; Mechoso, C.R. Relationships between precipitation anomalies in Uruguay and southern Brazil and sea surface temperature in the Pacific and Atlantic Oceans. J. Clim. 1998, 11, 251–271. [Google Scholar] [CrossRef]
- National Environmental Observatory of Uruguay (OAN). Available online: https://www.dinama.gub.uy/oan/ (accessed on 8 May 2019).
- Baker, D.B.; Richards, R.P.; Loftus, T.T.; Kramer, J.W. A New Flashiness Index: Characteristics and Applications to Midwestern Rivers and Streams. J. Am. Water Resour. Assoc. 2004, 40, 503–522. [Google Scholar] [CrossRef]
- García, M.H. Sedimentation Engineering. In Processes, Management, Modeling, and Practice; ASCE Manuals and Reports on Engineering Practice No. 110; American Society of Civil Engineers: Reston, VA, USA, 2008; ISBN 13: 978-0-7844-0814-8. [Google Scholar]
- Molfino, J. Estimation of Available Water in the CONEAT Groups-Methodology Used. 2009. Available online: http://www.mgap.gub.uy/sites/default/files/multimedia/estimacion_de_agua_disponible_en_los_grupos_coneat_metodologia_empleada.pdf (accessed on 24 April 2019). (In Spanish).
- Fernández, J.C. Estimaciones de densidad aparente, retención de agua a tensiones de–1/3 y–25 bar y agua disponible en el suelo a partir de la composición granulométrica y porcentaje de materia orgánica. In 2da Reunión Técnica; Facultad de Agronomía, Universidad de la República: Montevideo, Uruguay, 1979. (In Spanish) [Google Scholar]
- Silva, A.; Ponce de León, J.; García, F.; Durán, A. Aspectos metodológicos en la determinación de la capacidad de retener agua en los suelos del Uruguay. In Boletín de Investigación, 10; Facultad de Agronomía: Montevideo, Uruguay, 1988. (In Spanish) [Google Scholar]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Edijatno, N.; Michel, C. Un modèle pluie-débit journalier à trois paramétres. La Houille Blanche 1989, 2, 113–121. (In French) [Google Scholar]
- Nascimento, N.O. Appréciation à L’aide D’un Modéle Empirique Des Effets D’action Anthropiques Sur La Relation Pluie-Débit à L’échelle Du Bassin Versant. Ph.D. Thesis, CERGRENE/ENPC, Paris, France, 1995; p. 550. (In French). [Google Scholar]
- Edijatno; Nascimento, N.O.; Yang, X.; Makhlouf, Z.; Michel, C. GR3J: A daily watershed model with three free parameters. Hydrol. Sci. J. 1999, 44, 263–277. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Crisci, M.; Kayser, R.H.; Chreties, C.; Collischonn, W. A New Scenario-Based Framework for Conflict Resolution in Water Allocation in Transboundary Watersheds. Water 2019, 11, 1174. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Gioia, A.; Iacobellis, V.; Piccinni, A.F.; Ranieri, E. A rationale for pollutograph evaluation in ungauged areas, using daily rainfall patterns: Case studies of the Apulian region in Southern Italy. Appl. Environ. Soil Sci. 2016, 2016, 1–16. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Bombardelli, F.A.; Pitton, B.J.L.; Oki, L.R.; Haver, D.L.; Young, T.M. Role of Sediments in Insecticide Runoff from Urban Surfaces: Analysis and Modeling. Int. J. Environ. Res. Public Health 2018, 15, 1464. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Silveira, L. Large scale basins with small to negligible slopes. Part I: Generation of runoff. Nord. Hydrol. 2000, 31, 15–26. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Soil Water Div. Asabe 2007, 50, 885–900. [Google Scholar]
- Chen, H.; Luo, Y.; Potter, C.; Moran, P.J.; Grieneisen, M.L.; Zhang, M. Modeling pesticide diuron loading from the San Joaquin watershed into the Sacramento-San Joaquin Delta using SWAT. Water Res. 2017, 121, 374–385. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.R-project.org/ (accessed on 30 April 2019).
- Mpelasoka, F.S.; Chiew, F.H.S. Influence of rainfall scenario construction methods on runoff projections. J. Hydrometeorol. 2009, 10, 1168–1183. [Google Scholar] [CrossRef]
- Parajka, J.; Andréassian, V.; Archfield, S.A.; Bárdossy, A.; Blöschl, G.; Chiew, F.; Duan, Q.; Gelfan, A.; Hlavcova, K.; Merz, R.; et al. Predictions of runoff hydrographs in ungauged basins. In Predictions in Ungauged Basins: Synthesis across Processes; Blöschl, G., Sivapalan, S., Wagener, T., Savenije, H., Eds.; Cambridge University Press, Places and Scales: Cambridge, UK, 2013; Chapter 10; pp. 227–268. [Google Scholar]
- Li, F.; Zhang, Y.; Xu, Z.; Liu, C.; Zhou, Y.; Liu, W. Runoff predictions in ungauged catchments in southeast Tibetan Plateau. J. Hydrol. 2014, 511, 28–38. [Google Scholar] [CrossRef]

| Criteria for Watershed Selections | |
|---|---|
| Data Quality | Quality and availability of streamflow observations. |
| Simultaneous precipitation and flow data. | |
| Spatial Distribution | Watersheds distributed all over the country. |
| Elevation covers the entire national range. | |
| Precipitation and temperature cover the entire national ranges. | |
| Different soil characteristics (dominant) considered. | |
| Model Hypothesis | Adequate surface to the model-unit hydrograph. |
| No presence of reservoirs. | |
| Basin | Catchment Characteristics | Hydrologic Characteristics | |||||
|---|---|---|---|---|---|---|---|
| ID | Name | Area (km2) | Slope (%) | Tc (h) | AD (mm) | R-B Index | Dominant Q (m3/s/km2) |
| 0 | Casupa | 689 | 5.4 | 16 | 77 | 0.50 | 0.14 |
| 1 | Cebollati | 2884 | 6.2 | 38 | 76 | 0.43 | 0.34 |
| 2 | Cuareim | 4568 | 4.4 | 50 | 37 | 0.50 | 0.13 |
| 3 | Dayman | 3183 | 2.5 | 44 | 78 | 0.46 | 0.51 |
| 4 | Maldonado | 366 | 8.4 | 12 | 72 | 0.45 | 0.24 |
| 5 | Olimar | 4679 | 6.6 | 43 | 86 | 0.35 | 0.37 |
| 6 | Tacuari | 3544 | 5.1 | 54 | 107 | 0.32 | 0.49 |
| 7 | San Carlos | 803 | 8.3 | 18 | 74 | 0.61 | 0.28 |
| 8 | San Salvador | 2151 | 2.4 | 38 | 125 | 0.48 | 0.39 |
| 9 | Santa Lucia | 2754 | 6.0 | 36 | 81 | 0.50 | 0.27 |
| 10 | Santa Lucía Ch. | 1749 | 3.3 | 26 | 99 | 0.78 | 0.44 |
| 11 | Tacuarembo Ch. | 660 | 6.8 | 23 | 77 | 0.63 | 0.71 |
| 12 | Yi | 1380 | 4.2 | 26 | 76 | 0.50 | 0.21 |
| Parameter | Description | Unit |
|---|---|---|
| x1 | Maximum capacity of the production store | mm |
| x2 | Groundwater exchange coefficient | mm |
| x3 | Capacity of the nonlinear routing store | mm |
| x4 | Unit-hydrograph time base | day |
| Parameter | 80% Confidence Interval |
|---|---|
| x1 (mm) | [100, 1200] |
| x2 (mm) | [−5, 3] |
| x3 (mm) | [20, 300] |
| x4 (day) | [1.1, 2.9] |
| Basin | x1 | x2 | x3 | x4 |
|---|---|---|---|---|
| Casupa | 91 | −2.5 | 70.0 | 2.0 |
| Cebollati | 90 | 0.5 | 70 | 2.7 |
| Cuareim | 105 | 1 | 25 | 2.4 |
| Dayman | 91 | 0.5 | 80.0 | 2.4 |
| Maldonado | 70 | 1 | 34 | 2.2 |
| Olimar | 105 | 0.5 | 80 | 3 |
| San Carlos | 100 | 0 | 30 | 2.3 |
| San Salvador | 130 | 1 | 15 | 2.6 |
| Santa Lucia | 100 | −1 | 30 | 2.5 |
| Santa Lucía Ch. | 101 | −2.5 | 49 | 2.3 |
| Tacuarembo Ch | 60 | 2 | 34.0 | 2.5 |
| Tacuari | 130 | −2 | 110 | 3.3 |
| Yi | 100 | −2.5 | 80 | 2.5 |
| Basin | NSE | R2 | d |
|---|---|---|---|
| Casupa | 0.84 | 0.68 | 0.74 |
| Cebollati | 0.83 | 0.91 | 0.84 |
| Cuareim | 0.81 | 0.90 | 0.74 |
| Dayman | 0.82 | 0.66 | 0.77 |
| Maldonado | 0.80 | 0.90 | 0.81 |
| Olimar | 0.77 | 0.92 | 0.77 |
| San Carlos | 0.85 | 0.92 | 0.84 |
| San Salvador | 0.70 | 0.84 | 0.79 |
| Santa Lucía | 0.84 | 0.93 | 0.86 |
| Santa Lucía Chico | 0.68 | 0.83 | 0.76 |
| Tacuarembó Chico | 0.94 | 0.75 | 0.81 |
| Tacuari | 0.74 | 0.86 | 0.77 |
| Yi | 0.73 | 0.86 | 0.80 |
| Performance Rating | R2 | NSE | d |
|---|---|---|---|
| Very good | 0.75 < R2 ≤ 1.00 | 0.75 < NSE ≤ 1.00 | 0.75 < d ≤ 1.00 |
| Good | 0.65 < R2 ≤ 0.75 | 0.65 < NSE ≤ 0.75 | 0.65 < d ≤ 0.75 |
| Satisfactory | 0.50 < R2 ≤ 0.65 | 0.50 < NSE ≤ 0.65 | 0.50 < d ≤ 0.65 |
| Unsatisfactory | R2 ≤ 0.50 | NSE ≤ 0.50 | d ≤ 0.50 |
| Basin | NSE Max | NSE Min |
|---|---|---|
| Casupa | 0.72 | 0.64 |
| Cebollati | 0.82 | 0.80 |
| Cuareim | 0.65 | 0.49 |
| Dayman | 0.73 | 0.70 |
| Maldonado | 0.77 | 0.72 |
| Olimar | 0.76 | 0.74 |
| San Carlos | 0.81 | 0.75 |
| San Salvador | 0.57 | 0.50 |
| Santa Lucía | 0.78 | 0.75 |
| Santa Lucía Chico | 0.52 | 0.48 |
| Tacuarembó Chico | 0.82 | 0.79 |
| Tacuari | 0.70 | 0.63 |
| Yi | 0.69 | 0.62 |
| Basin | NSE | R2 | d |
|---|---|---|---|
| Casupa | 0.70 | 0.84 | 0.74 |
| Cebollati | 0.81 | 0.90 | 0.82 |
| Cuareim | 0.65 | 0.68 | 0.76 |
| Dayman | 0.71 | 0.82 | 0.78 |
| Maldonado | 0.74 | 0.87 | 0.77 |
| Olimar | 0.75 | 0.90 | 0.82 |
| San Carlos | 0.77 | 0.88 | 0.81 |
| San Salvador | 0.52 | 0.73 | 0.78 |
| Santa Lucía | 0.77 | 0.87 | 0.82 |
| Santa Lucía Chico | 0.49 | 0.67 | 0.78 |
| Tacuarembo Ch. | 0.80 | 0.94 | 0.82 |
| Tacuari | 0.68 | 0.80 | 0.79 |
| Yi | 0.69 | 0.87 | 0.80 |
| R2 | NSE | d | Area | Slope | Tc | AD | R-B index | Dominant Q | |
|---|---|---|---|---|---|---|---|---|---|
| R2 | 1.0 | ||||||||
| NSE | 0.9 | 1.0 | |||||||
| d | 0.8 | 0.7 | 1.0 | ||||||
| Area | −0.3 | 0.0 | 0.2 | 1.0 | |||||
| Slope | 0.7 | 0.7 | 0.4 | −0.3 | 1.0 | ||||
| Tc | −0.3 | −0.1 | 0.2 | 0.9 | −0.5 | 1.0 | |||
| AD | −0.1 | −0.5 | 0.0 | −0.1 | −0.3 | 0.1 | 1.0 | ||
| R-B index | −0.3 | −0.4 | −0.4 | −0.5 | −0.1 | −0.5 | −0.1 | 1.0 | |
| Dominant Q | 0.2 | 0.0 | 0.3 | 0.0 | −0.1 | 0.2 | 0.5 | 0.2 | 1.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narbondo, S.; Gorgoglione, A.; Crisci, M.; Chreties, C. Enhancing Physical Similarity Approach to Predict Runoff in Ungauged Watersheds in Sub-Tropical Regions. Water 2020, 12, 528. https://doi.org/10.3390/w12020528
Narbondo S, Gorgoglione A, Crisci M, Chreties C. Enhancing Physical Similarity Approach to Predict Runoff in Ungauged Watersheds in Sub-Tropical Regions. Water. 2020; 12(2):528. https://doi.org/10.3390/w12020528
Chicago/Turabian StyleNarbondo, Santiago, Angela Gorgoglione, Magdalena Crisci, and Christian Chreties. 2020. "Enhancing Physical Similarity Approach to Predict Runoff in Ungauged Watersheds in Sub-Tropical Regions" Water 12, no. 2: 528. https://doi.org/10.3390/w12020528
APA StyleNarbondo, S., Gorgoglione, A., Crisci, M., & Chreties, C. (2020). Enhancing Physical Similarity Approach to Predict Runoff in Ungauged Watersheds in Sub-Tropical Regions. Water, 12(2), 528. https://doi.org/10.3390/w12020528






