Streamflow Variability in Colombian Pacific Basins and Their Teleconnections with Climate Indices
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Streamflow Data
2.3. Climate Indices
2.4. Filling Missing Data
2.5. Principal Component Analysis
2.6. Kendall’s Tau and Pearson Correlation Coefficient
2.7. Wavelet Transform
3. Results and Discussion
3.1. Completing the Missing Data
3.2. Principal Component Analysis
3.3. Kendall’s Tau Correlation and Cross-Correlation with Climate Indices
3.4. Wavelet Analysis
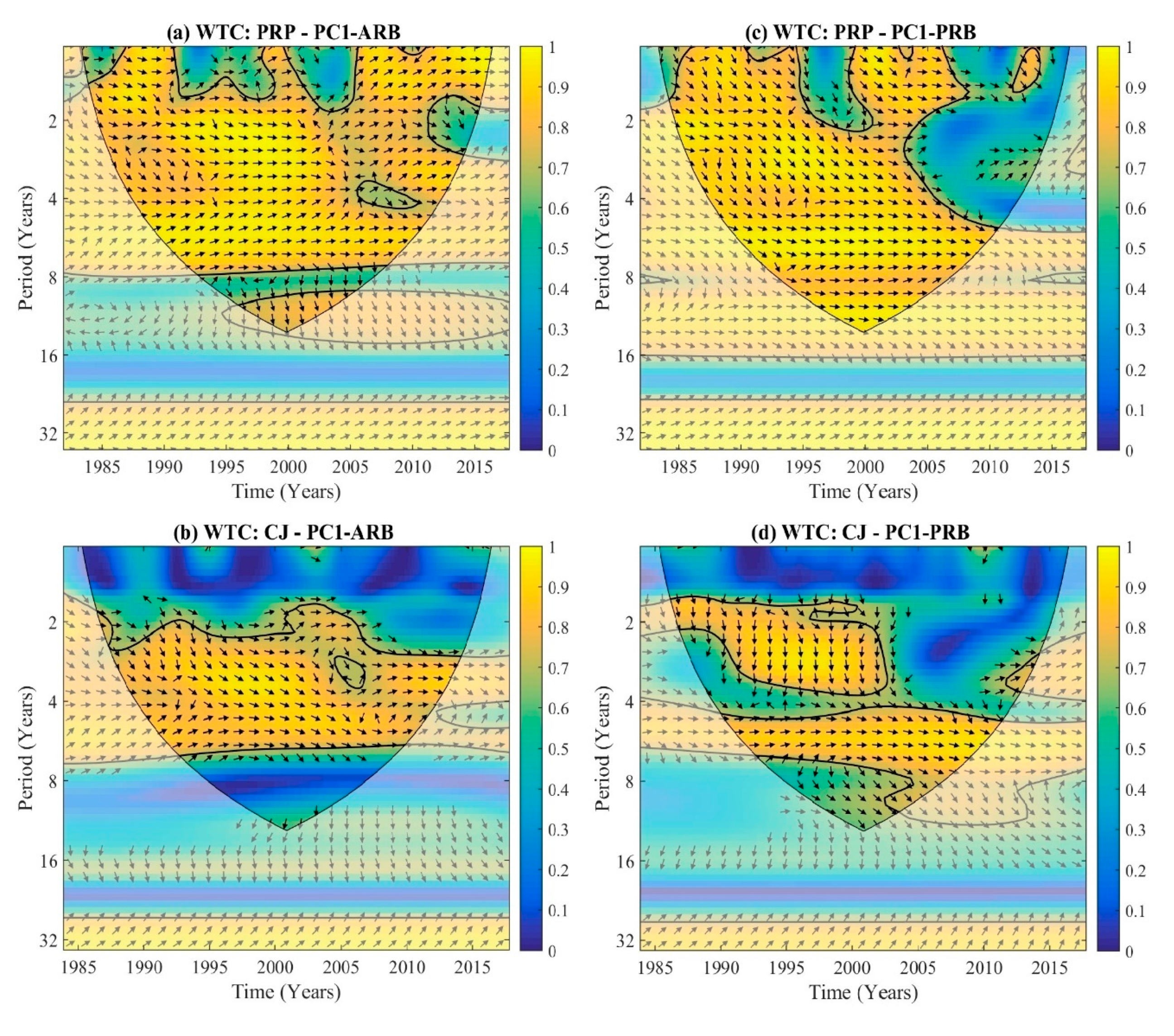
3.5. Wavelet Coherence and Phase Difference
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Coulibaly, P. Spatial and temporal variability of Canadian seasonal precipitation (1900–2000). Adv. Water Resour. 2006, 29, 1846–1865. [Google Scholar] [CrossRef]
- Jiang, R.; Gan, T.Y.; Xie, J.; Wang, N. Spatiotemporal variability of Alberta’s seasonal precipitation, their teleconnection with large-scale climate anomalies and sea surface temperature. Int. J. Climatol. 2014, 34, 2899–2917. [Google Scholar] [CrossRef]
- Pasquini, A.I.; Depetris, P.J. Discharge trends and flow dynamics of South American rivers draining the southern Atlantic seaboard: An overview. J. Hydrol. 2007, 333, 385–399. [Google Scholar] [CrossRef]
- Coulibaly, P.; Burn, D.H. Wavelet analysis of variability in annual Canadian streamflows. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Capozzoli, C.R.; Cardoso, A.d.O.; Ferraz, S.E.T. River flow variability patterns in Main Brazilian basins and association with climate indices. Revista Brasileira de Meteorologia 2017, 32, 243–254. [Google Scholar] [CrossRef][Green Version]
- Eltahir, E.A. El Niño and the natural variability in the flow of the Nile River. Water Resour. Res. 1996, 32, 131–137. [Google Scholar] [CrossRef]
- Siam, M.S.; Eltahir, E.A. Explaining and forecasting interannual variability in the flow of the Nile River. Hydrol. Earth Syst. Sci. 2015, 19, 1181–1192. [Google Scholar] [CrossRef]
- Sagarika, S.; Kalra, A.; Ahmad, S. Interconnections between oceanic–atmospheric indices and variability in the US streamflow. J. Hydrol. 2015, 525, 724–736. [Google Scholar] [CrossRef]
- Tamaddun, K.A.; Kalra, A.; Bernardez, M.; Ahmad, S. Multi-scale correlation between the western US snow water equivalent and ENSO/PDO using wavelet analyses. Water Resour. Manag. 2017, 31, 2745–2759. [Google Scholar] [CrossRef]
- Konapala, G.; Veettil, A.V.; Mishra, A.K. Teleconnection between low flows and large-scale climate indices in Texas River basins. Stoch. Environ. Res. Risk Assess. 2018, 32, 2337–2350. [Google Scholar] [CrossRef]
- Tamaddun, K.A.; Kalra, A.; Ahmad, S. Spatiotemporal Variation in the Continental US Streamflow in Association with Large-Scale Climate Signals Across Multiple Spectral Bands. Water Resour. Manag. 2019, 33, 1–22. [Google Scholar] [CrossRef]
- Handorf, D.; Dethloff, K. Atmospheric teleconnections and flow regimes under future climate projections. Eur. Phys. J. Spec. Top. 2009, 174, 237–255. [Google Scholar] [CrossRef]
- Mihaila, D.; Briciu, A.-E. Climatic teleconnections with influence on some rivers from south-eastern Europe. Boletin de la Asociacion de Geografos Espanoles 2015, 69, 37–62. [Google Scholar]
- Rodríguez Fonseca, B.; Casado Calle, M.J.; Barriopedro, D. Modes of Variability Affecting Southwestern Europe. CLIVAR Exchanges 2017, 73, 24–31. [Google Scholar]
- Kim, J.S.; Jain, S.; Yoon, S.K. Warm season streamflow variability in the Korean Han River Basin: Links with atmospheric teleconnections. Int. J. Climatol. 2012, 32, 635–640. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, T. Investigation of hydrological variability in the Korean Peninsula with the ENSO teleconnections. Proc. Int. Assoc. Hydrol. Sci. 2016, 374, 165–173. [Google Scholar] [CrossRef]
- Mechoso, C.R.; Iribarren, G.P. Streamflow in southeastern South America and the southern oscillation. J. Clim. 1992, 5, 1535–1539. [Google Scholar] [CrossRef]
- Poveda, G.; Mesa, O.J. Feedbacks between hydrological processes in tropical South America and large-scale ocean–atmospheric phenomena. J. Clim. 1997, 10, 2690–2702. [Google Scholar] [CrossRef]
- Poveda, G.; Gil, M.M.; Quiceno, N. El ciclo anual de la hidrología de Colombia en relación con el ENSO y la NAO. Bulletin de l’Institut Français d’études Andines 1998, 27, 721–731. [Google Scholar]
- Poveda, G.; Álvarez, D.M.; Rueda, Ó.A. Hydro-climatic variability over the Andes of Colombia associated with ENSO: A review of climatic processes and their impact on one of the Earth’s most important biodiversity hotspots. Clim. Dyn. 2011, 36, 2233–2249. [Google Scholar] [CrossRef]
- Enciso, A.M.; Carvajal-Escobar, Y.; Sandoval, M.C. Hydrological analysis of historical floods in the upper valley of Cauca river: Análisis hidrológico de las crecientes históricas del río Cauca en su valle alto. Ingeniería y Competitividad 2016, 18, 47–58. [Google Scholar]
- Navarro, E.; Vieira, C.; Arias, P. Spatiotemporal variability of the precipitation in Colombia during ENSO events. XV Seminario Iberoamericano de Redes de Agua y Drenaje SEREA2017 2017, 1, 1–8. [Google Scholar]
- Ávila, Á.; Guerrero, F.C.; Escobar, Y.C.; Justino, F. Recent Precipitation Trends and Floods in the Colombian Andes. Water 2019, 11, 379. [Google Scholar] [CrossRef]
- Navarro, E.; Arias, P.A.; Vieira, S.C. El Niño-Oscilación del Sur, fase Modoki, y sus efectos en la variabilidad espacio-temporal de la precipitación en Colombia. Revista de la Academia Colombiana de Ciencias Exactas Físicas y Naturales 2019, 43, 120–132. [Google Scholar] [CrossRef]
- Loaiza Cerón, W.; Toshie Kayano, M.; Andreoli, R.V.; Avila, A.; Canchala, T.; Francés, F.; Ayes Rivera, I.; Alfonso-Morales, W.; Ferreira de Souza, R.A.; Carvajal-Escobar, Y. Streamflow Intensification Driven by the Atlantic Multidecadal Oscillation (AMO) in the Atrato River Basin, Northwestern Colombia. Water 2020, 12, 216. [Google Scholar] [CrossRef]
- Poveda, G. La hidroclimatología de Colombia: Una síntesis desde la escala inter-decadal hasta la escala diurna. Rev. Acad. Colomb. Cienc 2004, 28, 201–222. [Google Scholar]
- Hurtado, M.A.F.; Mesa, S.Ó.J. Reconstrucción de los campos de precipitación mensual en Colombia. Escuela de Geociencias y Medio Ambiente 2014, 81, 251–258. [Google Scholar]
- Poveda, G.; Jaramillo, L.; Vallejo, L.F. Seasonal precipitation patterns along pathways of South American low-level jets and aerial rivers. Water Resour. Res. 2014, 50, 98–118. [Google Scholar] [CrossRef]
- Mittermeier, R.A.; Turner, W.R.; Larsen, F.W.; Brooks, T.M.; Gascon, C. Global biodiversity conservation: The critical role of hotspots. In Biodiversity Hotspots; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–22. [Google Scholar]
- Velásquez-Restrepo, M.; Poveda, G. Estimación del balance hídrico de la región Pacífica Colombiana. DYNA 2019, 86, 297–306. [Google Scholar] [CrossRef]
- Montealegre, E.J.; Pabón, J.D. La variabilidad climática interanual asociada al ciclo El Niño-La Niña-Oscilación del Sur y su efecto en el patrón pluviométrico de Colombia. Meteorología Colombiana 2000, 2, 7–21. [Google Scholar]
- Tedeschi, R.G.; Cavalcanti, I.F.; Grimm, A.M. Influences of two types of ENSO on South American precipitation. Int. J. Climatol. 2013, 33, 1382–1400. [Google Scholar] [CrossRef]
- Tedeschi, R.G.; Grimm, A.M.; Cavalcanti, I.F. Influence of Central and East ENSO on extreme events of precipitation in South America during austral spring and summer. Int. J. Climatol. 2015, 35, 2045–2064. [Google Scholar] [CrossRef]
- Loaiza, W.; Carvajal-Escobar, Y.; Andreoli, R.V.; Kayano, M.T.; Gonzáles, N. Spatio-temporal varibility of the droughts in Cali, Colombia and their relationships with the El Niño-Southern Oscillation (ENSO) between 1971 and 2011. Atmósfera 2020, 33, 51–69. [Google Scholar] [CrossRef]
- Arias, P.A.; Martínez, J.A.; Vieira, S.C. Moisture sources to the 2010–2012 anomalous wet season in northern South America. Clim. Dyn. 2015, 45, 2861–2884. [Google Scholar] [CrossRef]
- Hoyos, I.; Dominguez, F.; Cañón-Barriga, J.; Martínez, J.; Nieto, R.; Gimeno, L.; Dirmeyer, P. Moisture origin and transport processes in Colombia, northern South America. Clim. Dyn. 2018, 50, 971–990. [Google Scholar] [CrossRef]
- Jaramillo, L.; Poveda, G.; Mejía, J.F. Mesoscale convective systems and other precipitation features over the tropical Americas and surrounding seas as seen by TRMM. Int. J. Climatol. 2017, 37, 380–397. [Google Scholar] [CrossRef]
- Bedoya-Soto, J.; Aristizabal, E.; Carmona, A.M.; Poveda, G. Seasonal Shift of the Diurnal Cycle of Rainfall Over Medellin’s Valley, Central Andes of Colombia (1998–2005). Front. Earth Sci. 2019, 7, 92. [Google Scholar] [CrossRef]
- Poveda, G.; Vélez, J.; Mesa, O.; Hoyos, C.; Mejía, J.F.; Barco, O.J.; Correa, P.L. Influencia de fenómenos macroclimáticos sobre el ciclo anual de la hidrología colombiana: Cuantificación lineal, no lineal y percentiles probabilísticos. Meteorología Colombiana 2002, 6, 121–130. [Google Scholar]
- Cadavid, J.M.; Salazar, J.E. Generación de series sinteticas de caudales usando un Modelo Matalas con medias condicionadas. Avances en Recursos Hidráulicos 2008, 17, 17–24. [Google Scholar]
- Tootle, G.A.; Piechota, T.C.; Gutiérrez, F. The relationships between Pacific and Atlantic Ocean sea surface temperatures and Colombian streamflow variability. J. Hydrol. 2008, 349, 268–276. [Google Scholar] [CrossRef]
- Rojo, J.D.; Carvajal, L.F. Predicción no lineal de caudales utilizando variables macroclimáticas y análisis espectral singular. Tecnología y Ciencias del Agua 2010, 1, 59–73. [Google Scholar]
- Rodríguez-Rubio, E. A multivariate climate index for the western coast of Colombia. Adv. Geosci. 2013, 33, 21–26. [Google Scholar] [CrossRef][Green Version]
- Córdoba-Machado, S.; Palomino-Lemus, R.; Gámiz-Fortis, S.R.; Castro-Díez, Y.; Esteban-Parra, M.J. Influence of tropical Pacific SST on seasonal precipitation in Colombia: Prediction using El Niño and El Niño Modoki. Clim. Dyn. 2015, 44, 1293–1310. [Google Scholar] [CrossRef]
- Cuadrado, P.B.; Blanco, R.J. Teleconexiones y eventos extremos de sequía en áreas protegidas del norte de Colombia. Revista de Climatología 2015, 15, 27–38. [Google Scholar]
- Rodríguez-Fonseca, B.; Polo, I.; García-Serrano, J.; Losada, T.; Mohino, E.; Mechoso, C.R.; Kucharski, F. Are Atlantic Niños enhancing Pacific ENSO events in recent decades? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Mosquera-Machado, S.; Ahmad, S. Flood hazard assessment of Atrato River in Colombia. Water Resour. Manag. 2007, 21, 591–609. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. El Niño/Southern Oscillation behaviour since 1871 as diagnosed in an extended multivariate ENSO index (MEI. ext). Int. J. Climatol. 2011, 31, 1074–1087. [Google Scholar] [CrossRef]
- L’Heureux, M.L.; Collins, D.C.; Hu, Z.-Z. Linear trends in sea surface temperature of the tropical Pacific Ocean and implications for the El Niño-Southern Oscillation. Clim. Dyn. 2013, 40, 1223–1236. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1080. [Google Scholar] [CrossRef]
- Hurrel, J.W.; Kushnir, Y.; Ottersen, G.; Visbeck, M. The North Atlantic oscillation: Climatic significance and environmental impact. Geophys. Monogr. 2003, 134. [Google Scholar] [CrossRef]
- Poveda, G.; Mesa, O.J. On the existence of Lloró (the rainiest locality on Earth): Enhanced ocean-land-atmosphere interaction by a low-level jet. Geophys. Res. Lett. 2000, 27, 1675–1678. [Google Scholar] [CrossRef]
- Serna, L.M.; Arias, P.A.; Vieira, S.C. Las corrientes superficiales de chorro del Chocó y el Caribe durante los eventos de El Niño y El Niño Modoki. Revista de la Academia Colombiana de Ciencias Exactas Físicas y Naturales 2018, 42, 410–421. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, D.P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Carvajal, Y.; Grisales, C.; Mateus, J. Correlación de variables macroclimáticas del Océano Pacífico con los caudales en los ríos interandinos del Valle del Cauca (Colombia). Revista Peruana de Biología 1999, 6, 9–17. [Google Scholar] [CrossRef][Green Version]
- Díaz, Á.J.Á.; Escobar, Y.C.; Serna, S.E.G. Análisis de la influencia de El Niño y La Niña en la oferta hídrica mensual de la cuenca del río Cali. Tecnura 2013, 18, 120–133. [Google Scholar]
- Puertas; Carvajal. Incidence of El Niño southern oscillation in the precipitation and the temperature of the air in Colombia, using Climate Explorer. Ingeniería y Desarrollo 2008, 23, 104–118. [Google Scholar]
- Tootle, G.A.; Piechota, T.C. Relationships between Pacific and Atlantic ocean sea surface temperatures and US streamflow variability. Water Resour. Res. 2008, 42. [Google Scholar] [CrossRef]
- Poveda, G.; Mesa, O. La Oscilación del Atlántico Norte y su influencia sobre el clima de Colombia. In Proceedings of the Memorias XVII Congreso Latino-Americano de Hidráulica e Hidrología, IAHR, Guayaquil, Ecuador, 21 October 1996; pp. 343–354. [Google Scholar]
- Hurtado, A. Estimación de los campos mensuales históricos de precipitación en el territorio colombiano. MSc Thesis, Posgrado en Aprovechamiento de Recursos Hidráulicos, Facultad de Minas, Universidad Nacional de Colombia sede Medellín, Colombia, 2009; pp. 1–104. [Google Scholar]
- Hoyos, I.; Baquero-Bernal, A.; Jacob, D.; Rodríguez, B.A. Variability of extreme events in the Colombian Pacific and Caribbean catchment basins. Clim. Dyn. 2013, 40, 1985–2003. [Google Scholar] [CrossRef]
- Poveda, G.; Mesa, O. La corriente de chorro superficial del Oeste (“del Chocó”) y otras dos corrientes de chorro en Colombia: Climatología y variabilidad durante las fases del ENSO”. Revista Académica Colombiana de Ciencia 1999, 23, 517–528. [Google Scholar]
- Sierra, J.P.; Arias, P.A.; Vieira, S.C. Precipitation over northern South America and its seasonal variability as simulated by the CMIP5 models. Adv. Meteorol. 2015, 2015. [Google Scholar] [CrossRef]
- Durán-Quesada, A.; Reboita, M.; Gimeno, L. Precipitation in tropical America and the associated sources of moisture: A short review. Hydrolo. Sci. J. 2012, 57, 612–624. [Google Scholar] [CrossRef]
- Scholz, M.; Kaplan, F.; Guy, C.L.; Kopka, J.; Selbig, J. Non-linear PCA: A missing data approach. Bioinformatics 2005, 21, 3887–3895. [Google Scholar] [CrossRef]
- Miró, J.J.; Caselles, V.; Estrela, M.J. Multiple imputation of rainfall missing data in the Iberian Mediterranean context. Atmos. Res. 2017, 197, 313–330. [Google Scholar] [CrossRef]
- Canchala, T.; Carvajal-Escobar, Y.; Alfonso-Morales, W.; Loaiza, W.; Caicedo, E. Estimation of missing data of monthly rainfall in southwestern Colombia using artificial neural networks. Data Brief. 2019, 104517. [Google Scholar] [CrossRef]
- Scholz, M.; Fraunholz, M.; Selbig, J. Nonlinear principal component analysis: Neural network models and applications. In Principal Manifolds for Data Visualization and Dimension Reduction; Springer: Berlin/Heidelberg, Germany, 2008; pp. 44–67. [Google Scholar]
- Rousi, Ε.; Anagnostopoulou, C.; Tolika, K.; Maheras, P. Representing teleconnection patterns over Europe: A comparison of SOM and PCA methods. Atmos. Res. 2015, 152, 123–137. [Google Scholar] [CrossRef]
- Tošić, I.; Zorn, M.; Ortar, J.; Unkašević, M.; Gavrilov, M.B.; Marković, S.B. Annual and seasonal variability of precipitation and temperatures in Slovenia from 1961 to 2011. Atmos. Res. 2016, 168, 220–233. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Phil. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Helena, B.; Pardo, R.; Vega, M.; Barrado, E.; Fernandez, J.M.; Fernandez, L. Temporal evolution of groundwater composition in an alluvial aquifer (Pisuerga River, Spain) by principal component analysis. Water Res. 2000, 34, 807–816. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis; Springer: New York, NY, USA, 1986; Volume 271, pp. 129–155. [Google Scholar]
- Preisendorfer, R. Principal Component Analysis in Meteorology and Oceanography; Elsevier Science Publisher: Amsterdam, The Netherlands, 1988; Volume 17, p. 425. [Google Scholar]
- Carvajal, Y.; Segura, J.B.M. Análisis de variabilidad de datos medioambientales aplicando funciones ortogonales empíricas o componentes principales. Ingeniería de Recursos Naturales y del Ambiente 2004, 1, 4–11. [Google Scholar]
- Knight, W.R. A computer method for calculating Kendall’s tau with ungrouped data. J. Am. Stat. Assoc. 1966, 61, 436–439. [Google Scholar] [CrossRef]
- Banimahd, S.A.; Khalili, D. Factors influencing Markov chains predictability characteristics, utilizing SPI, RDI, EDI and SPEI drought indices in different climatic zones. Water Resour. Manag. 2013, 27, 3911–3928. [Google Scholar]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Labat, D. Wavelet analysis of the annual discharge records of the world’s largest rivers. Adv. Water Resour. 2008, 31, 109–117. [Google Scholar] [CrossRef]
- Schulte, J.A.; Najjar, R.G.; Li, M. The influence of climate modes on streamflow in the Mid-Atlantic region of the United States. J. Hydrol. Reg. Stud. 2016, 5, 80–99. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y.; Shao, D. Wavelet analysis of precipitation extremes over Canadian ecoregions and teleconnections to large-scale climate anomalies. J. Geophys. Res. Atmos. 2016, 121. [Google Scholar] [CrossRef]
- Andreoli, R.V.; Kayano, M.T. Multi-scale variability of the sea surface temperature in the Tropical Atlantic. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Proc. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P.J. Interdecadal changes in the ENSO–monsoon system. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Diaz, L.G.; Morales, M.A. Estadística Multivariada: Inferencia y Métodos; Universidad Nacional de Colombia: Bogota, Colombia, 2002. [Google Scholar]
- Trenberth, K. The climate data guide: Nino SST indices (Nino 1 + 2, 3, 3.4, 4; ONI and TNI). 2019. Available online: https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni (accessed on 6 September 2019).
- Hoyos, N.; Escobar, J.; Restrepo, J.; Arango, A.; Ortiz, J. Impact of the 2010–2011 La Niña phenomenon in Colombia, South America: The human toll of an extreme weather event. Appl. Geogr. 2013, 39, 16–25. [Google Scholar] [CrossRef]
- Rueda, O.; Poveda, G. Variabilidad espacial y temporal del chorro del “Chocó” y su efecto en la hidroclimatología de la región del pacífico colombiano. Meteorol. Col 2006, 10, 132–145. [Google Scholar]
- Poveda, G.; Jaramillo, A.; Gil, M.M.; Quiceno, N.; Mantilla, R.I. Seasonally in ENSO-related precipitation, river discharges, soil moisture, and vegetation index in Colombia. Water Resour. Res. 2001, 37, 2169–2178. [Google Scholar] [CrossRef]
- Kayano, M.T.; Andreoli, R.V. Clima da região Nordeste do Brasil. Cavalcanti, Iracema FA et al. Tempo e Clima no Brasil. São Paulo: Oficina de Textos 2009, 1, 212–233. [Google Scholar]
- Andreoli, R.V.; Kayano, M.T. ENSO-related rainfall anomalies in South America and associated circulation features during warm and cold Pacific decadal oscillation regimes. Int. J. Climatol. 2005, 25, 2017–2030. [Google Scholar] [CrossRef]
- Rasmusson, E.M.; Arkin, P.A. Interannual climate variability associated with the El Niño/Southern Oscillation. Elsevier Oceanogr. Ser. 1985, 40, 697–725. [Google Scholar]
- Kousky, V.E.; Kagano, M.T.; Cavalcanti, I.F. A review of the Southern Oscillation: Oceanic-atmospheric circulation changes and related rainfall anomalies. Tellus A 1984, 36, 490–504. [Google Scholar] [CrossRef]
- Eslava, J. Climatology of colombian pacific (in spanish). Academia Colombiana de Ciencias Geofísicas, Colección Eratóstenes 1994, 1, 1–79. [Google Scholar]
- Sánchez, Ó.J.M.; Vélez, V.M.P. Complejidad de la estructura espacio-temporal de la precipitación. Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales 2015, 39, 304–320. [Google Scholar] [CrossRef]
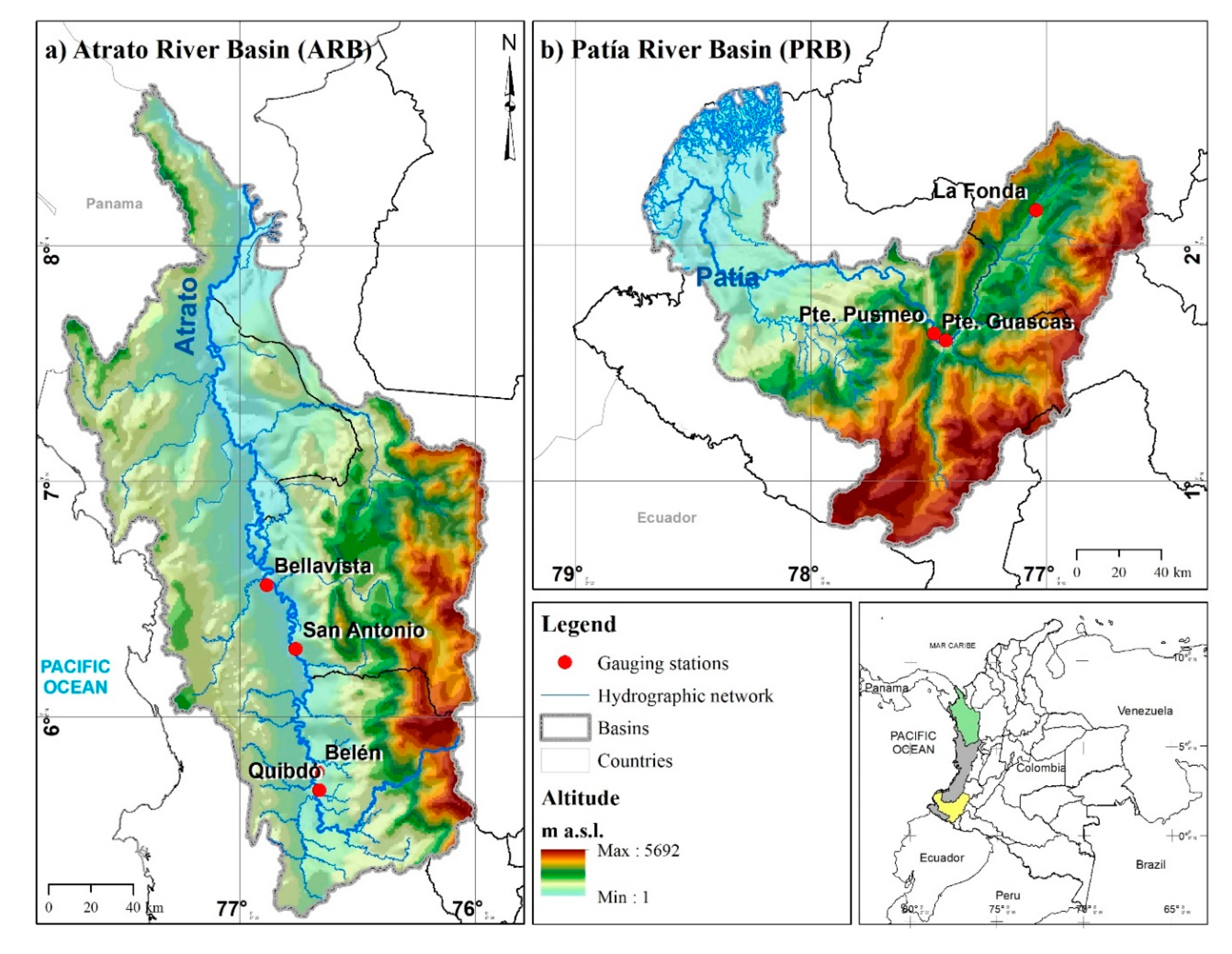
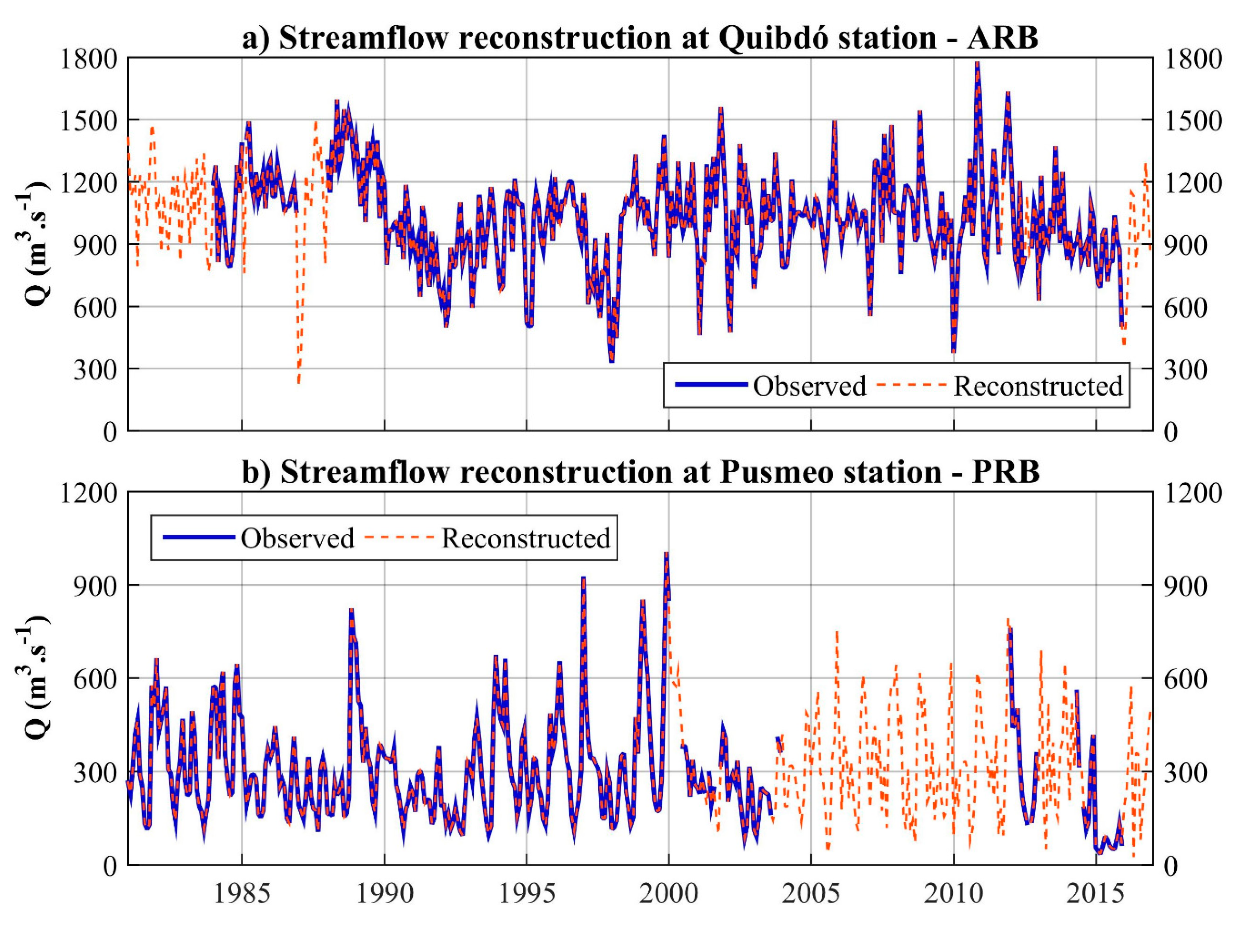

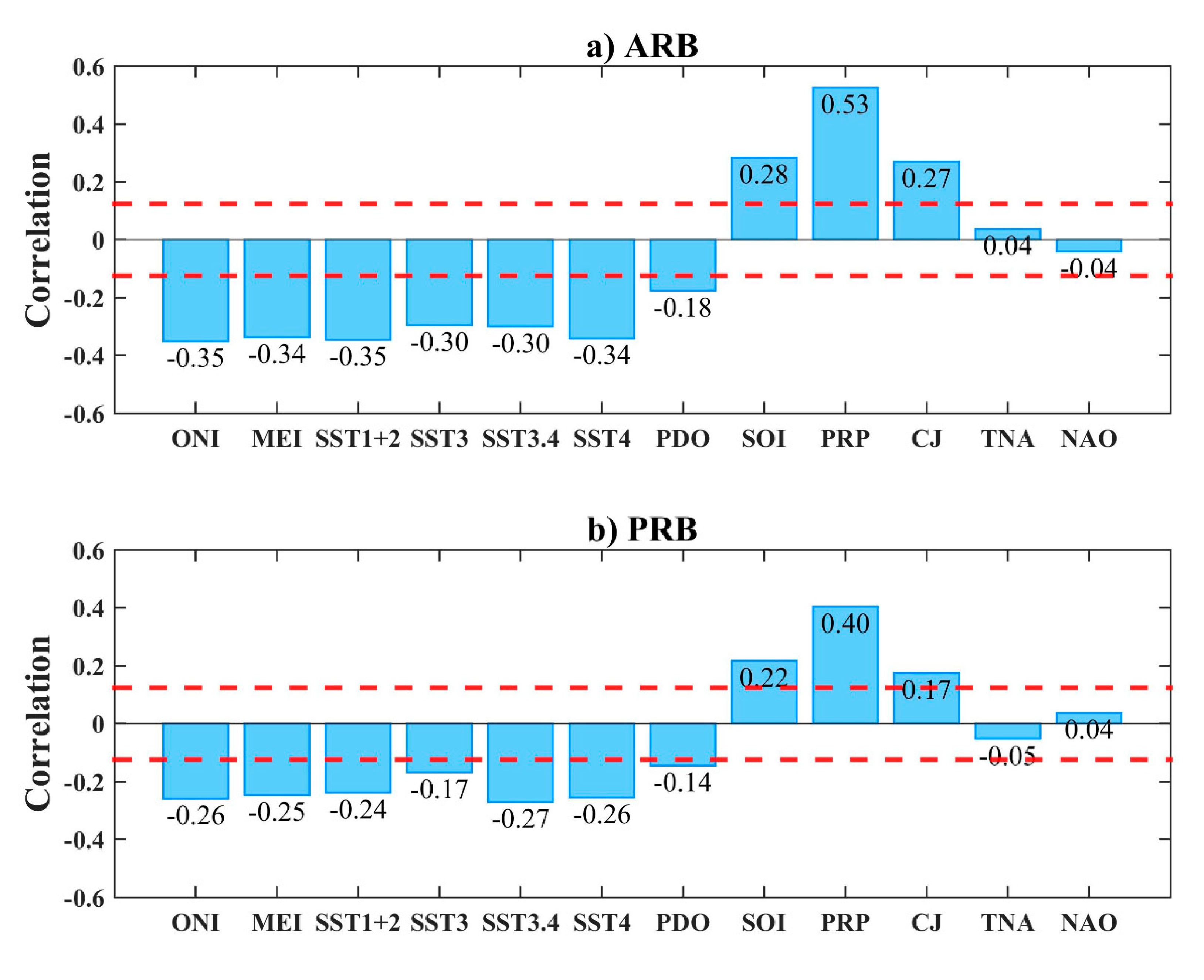
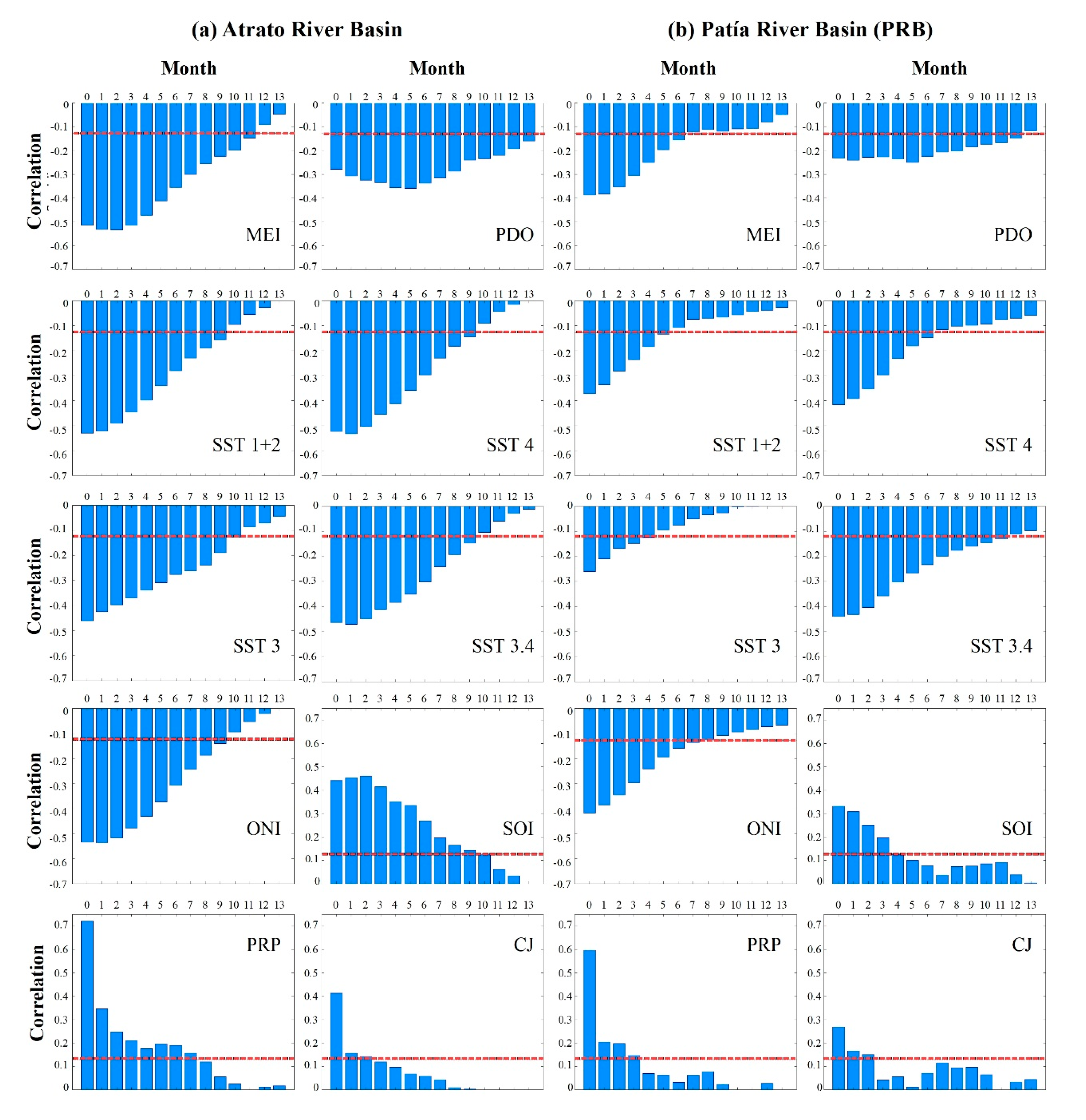
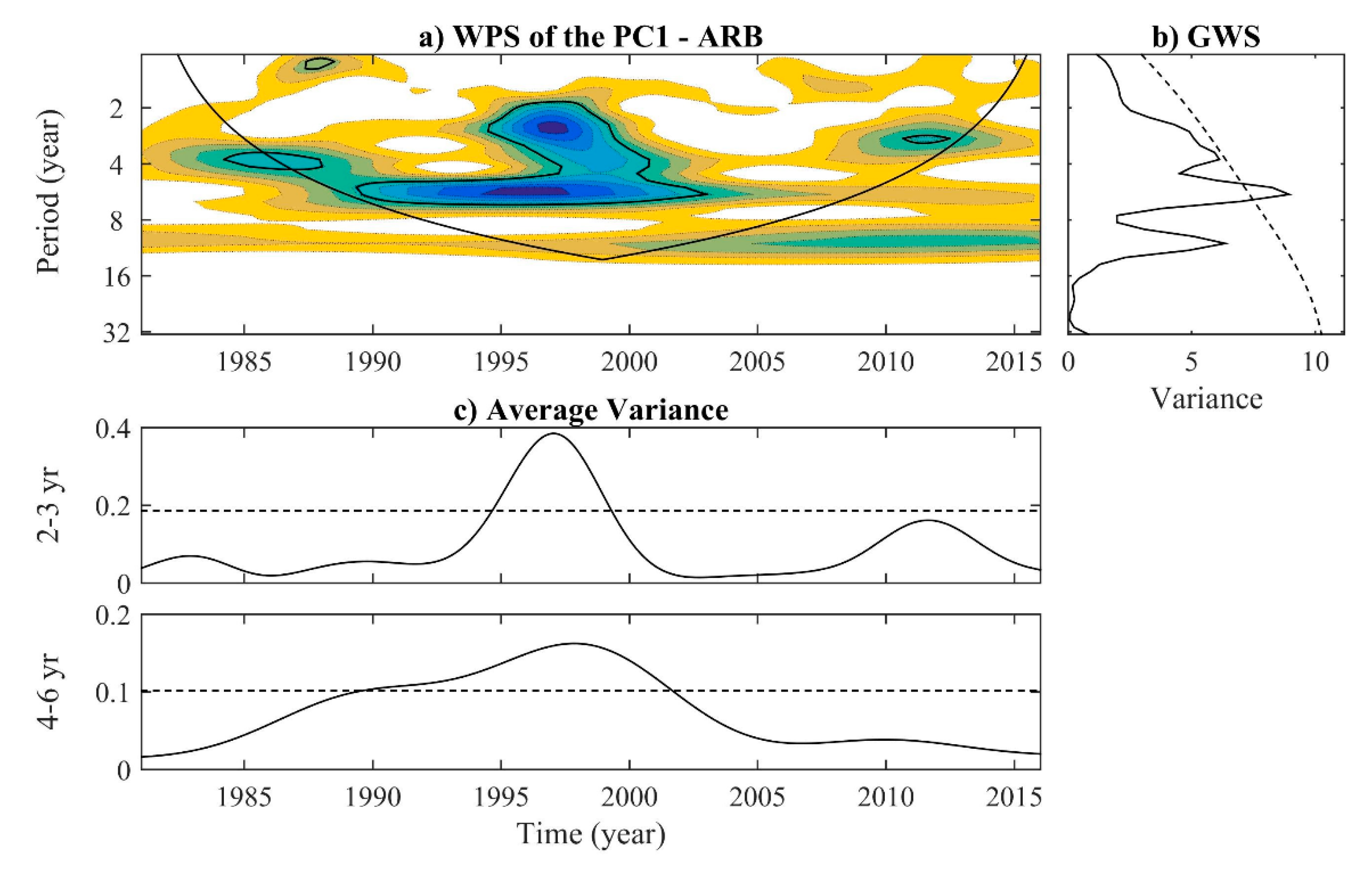
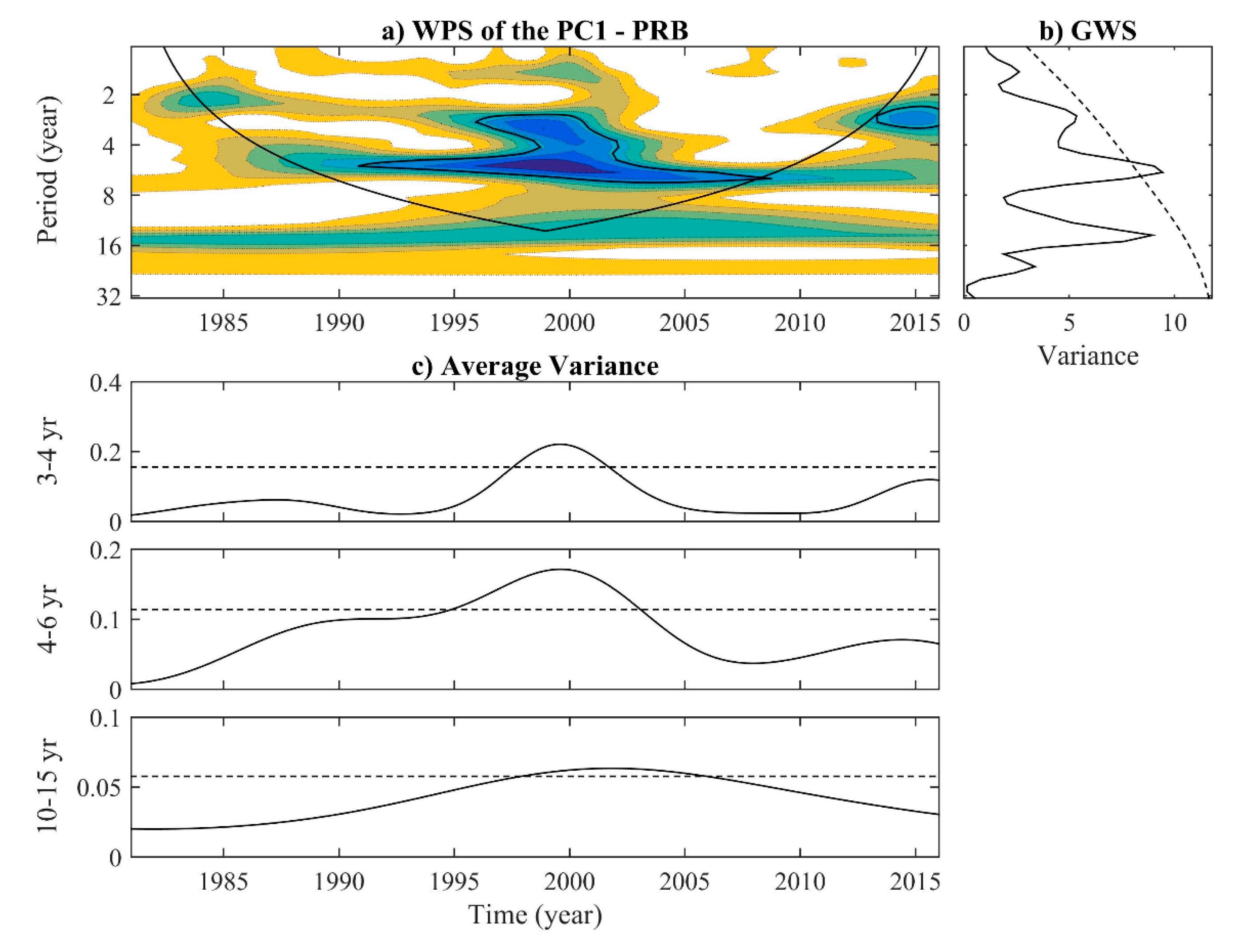
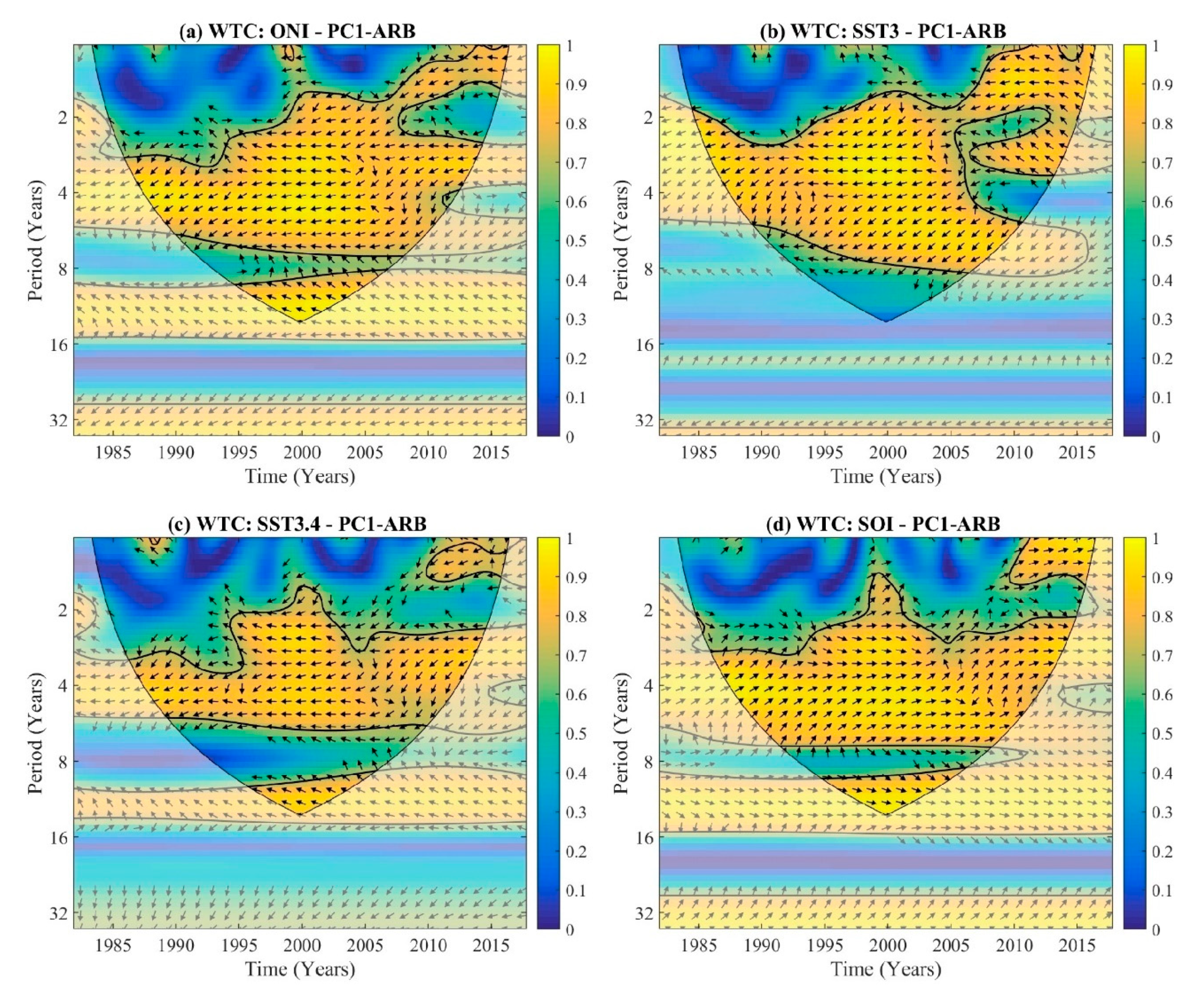
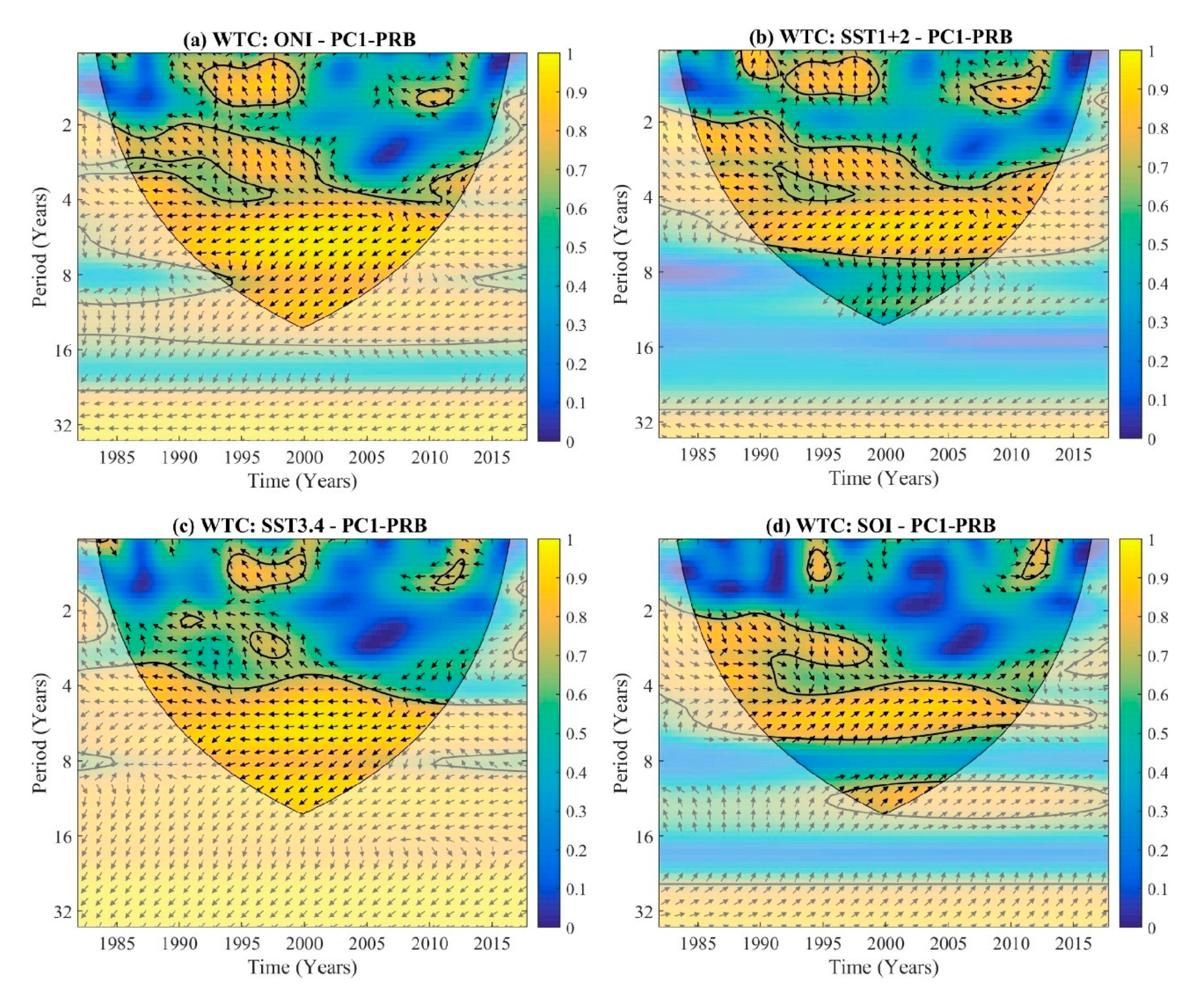
| Station | ID | Mean (m3·s−1) | Std. Dev. (m3·s−1) | Coef. of Var. | Missing Data % | River Basin | Drainage Area (km2) |
|---|---|---|---|---|---|---|---|
| Belén | BEL | 1062.5 | 257.9 | 0.25 | 5.3 | Atrato (37,731.8 km2) | 617.3 |
| Quibdó | QUI | 1023.1 | 229.0 | 0.22 | 14.8 | 4845.5 | |
| San Antonio | SAN | 1937.0 | 431.2 | 0.22 | 4.4 | 560.8 | |
| Bellavista | BELL | 2524.0 | 626.3 | 0.25 | 2.8 | 6207.3 | |
| Guascas | GUA | 203.2 | 130.4 | 0.64 | 30.6 | Patía (23,909.5 km2) | 15,177.4 |
| La Fonda | FON | 62.4 | 47.8 | 0.77 | 17.6 | 1444.1 | |
| Pusmeo | PUS | 299.5 | 165.3 | 0.55 | 31.5 | 4112.6 |
| Climate Indices | References |
|---|---|
| SOI | Carvajal et al. [56], Poveda et al. [39], Rojo and Carvajal, [42], Ávila et al. [57] |
| MEI | Poveda et al. [39], Poveda, [26], Puertas and Carvajal, [58], Ávila et al. [57], Loaiza et al. [34] |
| ONI | Ávila et al. [57], Enciso et al. [21], Loaiza et al. [34] |
| SST1+2 | Puertas and Carvajal, [58], Rodríguez-Rubio, [43] |
| SST3 | Carvajal et al. [56], Poveda et al. [20], Rodríguez-Rubio, [43] |
| SST3.4 | Carvajal et al. [56], Tootle et al. [59], Puertas and Carvajal, [58], Ávila et al. [57], Loaiza et al. [34] |
| SST4 | Carvajal et al. [56], Puertas and Carvajal, [58], Poveda et al. [20] |
| PDO | Poveda and Mesa, [60], Poveda et al. [19], Poveda et al. [39], Tootle et al. [59], Loaiza et al. [34] |
| NAO | Poveda et al. [39], Hurtado, [61], Hoyos et al. [62] |
| TNA | Carvajal et al. [56] |
| CJ | Poveda and Mesa, [63], Poveda, [26], Sierra et al. [64], Durán-Quesada et al. [65] |
| PCs | ARB | PRB | ||
|---|---|---|---|---|
| Exp. Var (%) | Eigenvalue | Exp. Var (%) | Eigenvalue | |
| 1 | 75.48 | 3.02 | 79.03 | 2.37 |
| 2 | 15.41 | 0.61 | 19.16 | 0.57 |
| 3 | 6.4 | 0.25 | 1.81 | 0.05 |
| PC1 | ONI | MEI | SST1+2 | SST3 | SST3.4 | SST4 | PDO | SOI | PRP | CJ | TNA | NAO | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARB | Annual | −0.52 | −0.45 | −0.48 | −0.40 | −0.40 | −0.49 | −0.28 | 0.47 | 0.54 | 0.33 | 0.12 | −0.08 |
| Maximum | −0.30 | −0.25 | −0.27 | −0.20 | −0.30 | −0.32 | −0.15 | 0.32 | 0.3 | 0.23 | 0.10 | −0.10 | |
| Minimum | −0.42 | −0.39 | −0.42 | −0.39 | −0.33 | −0.40 | −0.30 | 0.36 | 0.44 | 0.22 | 0.03 | 0.02 | |
| PRB | Annual | −0.35 | −0.37 | −0.36 | −0.23 | −0.32 | −0.37 | −0.25 | 0.29 | 0.55 | 0.22 | −0.02 | 0.09 |
| Maximum | −0.40 | −0.38 | −0.34 | −0.21 | −0.37 | −0.41 | −0.23 | 0.35 | 0.57 | 0.31 | 0.09 | −0.04 | |
| Minimum | −0.11 | −0.14 | −0.19 | −0.12 | −0.11 | −0.12 | −0.05 | 0.03 | 0.27 | 0.03 | −0.39 | 0.30 |
| Indices | ARB | PRB | ||||
|---|---|---|---|---|---|---|
| Scale | Lags (Months) | Scale | Lags (Months) | |||
| Interannual | Decadal | Interannual/Decadal | Interannual | Decadal | Interannual/Decadal | |
| ONI | 2–7 years (-) | 8–16 years (-) | 0–5/5–9 | 4–8 years (-) | 8–14 years (-) | 0–5/5–9 |
| MEI | 2–7 years (-) | 8–16 years (-) | 0–5/5–9 | 2–7 years (-) | 10–14 years (-) | 0–7/ |
| SST1+2 | 2–7 years (-) | 8–12 years (-) | 0–5/5–9 | 2–7 years (-) | 0–7/ | |
| SST3 | 2–7 years (-) | 0–5/ | 2–7 years (-) | 0–7/ | ||
| SST3.4 | 3–6 years (-) | 10–12 years (-) | 2–4/3–4 | 4–8 years (-) | 8–14 years (-) | 0/8–14 |
| SST4 | 2–7 years (-) | 10–14 years (-) | 0–5/5–9 | 4–8 years (-) | 8–14 years (-) | 0–5/5–9 |
| PDO | 5–7 years (-) | 2–7/ | ||||
| SOI | 2–7 years (+) | 10–14 years (+) | 0–5/3–5 | 4–7 years (+) | 10–12 years (+) | 0–5/15–18 |
| PRP | 2–8 years (+) | 10–14 years (+) | 0–3/15–21 | 2–8 years (+) | 8–14 years (+) | 0–12/0–5 |
| CJ | 2–7 years (+) | 3–11/ | 2–3 years and 4–6 years (+) | 0–2 and 6–9/ | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Canchala, T.; Loaiza Cerón, W.; Francés, F.; Carvajal-Escobar, Y.; Andreoli, R.V.; Kayano, M.T.; Alfonso-Morales, W.; Caicedo-Bravo, E.; Ferreira de Souza, R.A. Streamflow Variability in Colombian Pacific Basins and Their Teleconnections with Climate Indices. Water 2020, 12, 526. https://doi.org/10.3390/w12020526
Canchala T, Loaiza Cerón W, Francés F, Carvajal-Escobar Y, Andreoli RV, Kayano MT, Alfonso-Morales W, Caicedo-Bravo E, Ferreira de Souza RA. Streamflow Variability in Colombian Pacific Basins and Their Teleconnections with Climate Indices. Water. 2020; 12(2):526. https://doi.org/10.3390/w12020526
Chicago/Turabian StyleCanchala, Teresita, Wilmar Loaiza Cerón, Félix Francés, Yesid Carvajal-Escobar, Rita Valéria Andreoli, Mary Toshie Kayano, Wilfredo Alfonso-Morales, Eduardo Caicedo-Bravo, and Rodrigo Augusto Ferreira de Souza. 2020. "Streamflow Variability in Colombian Pacific Basins and Their Teleconnections with Climate Indices" Water 12, no. 2: 526. https://doi.org/10.3390/w12020526
APA StyleCanchala, T., Loaiza Cerón, W., Francés, F., Carvajal-Escobar, Y., Andreoli, R. V., Kayano, M. T., Alfonso-Morales, W., Caicedo-Bravo, E., & Ferreira de Souza, R. A. (2020). Streamflow Variability in Colombian Pacific Basins and Their Teleconnections with Climate Indices. Water, 12(2), 526. https://doi.org/10.3390/w12020526








