Performance of Satellite-Based Evapotranspiration Models in Temperate Pastures of Southern Chile
Abstract
1. Introduction
2. Study Area and Datasets
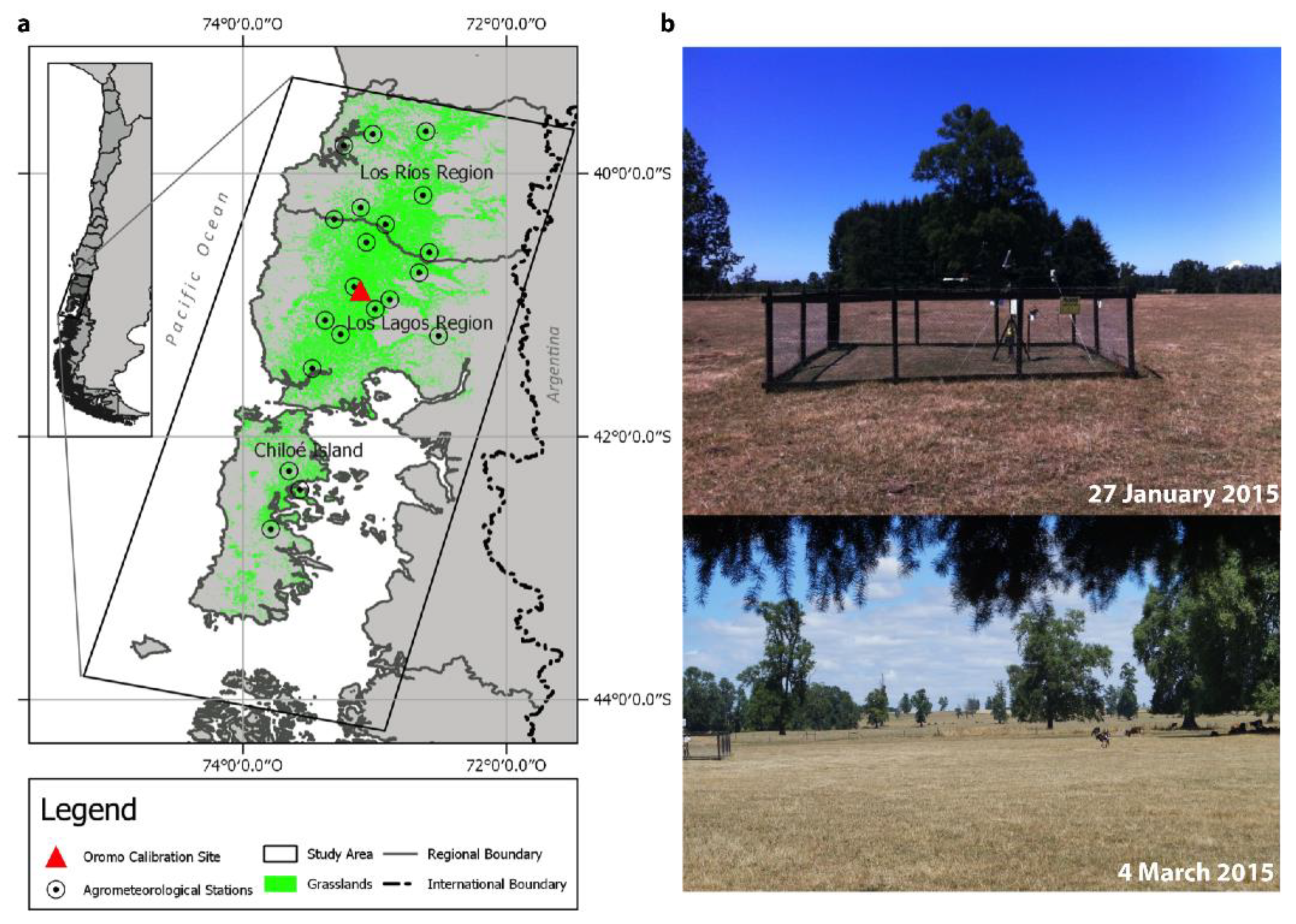
2.1. Study Area
2.2. Satellite and Ancillary Data Used to Drive the Models
2.3. Global Evapotranspiration Products
2.4. Ground Data
3. Methods
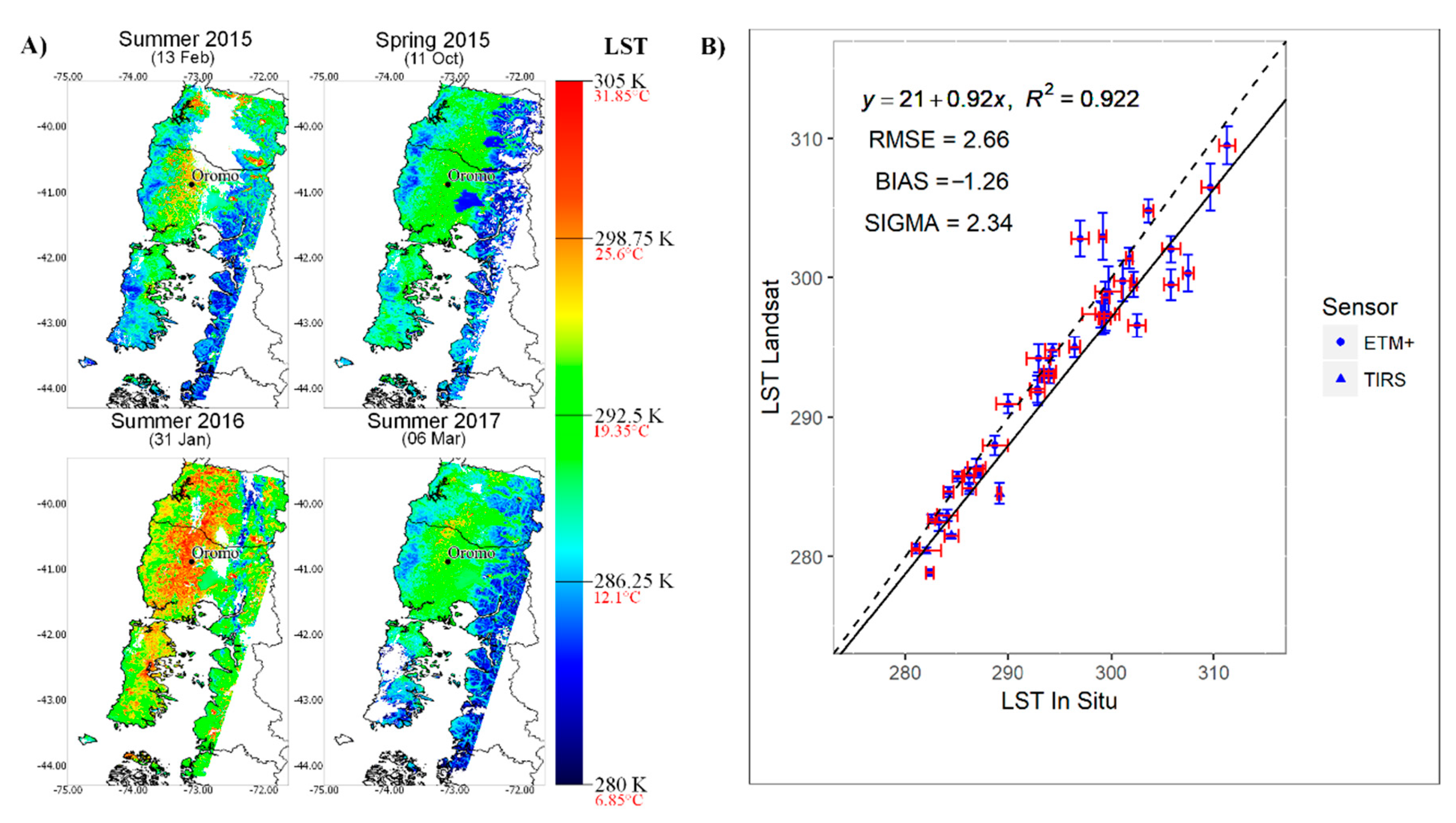
3.1. Surface Temperature (Ts) Estimation
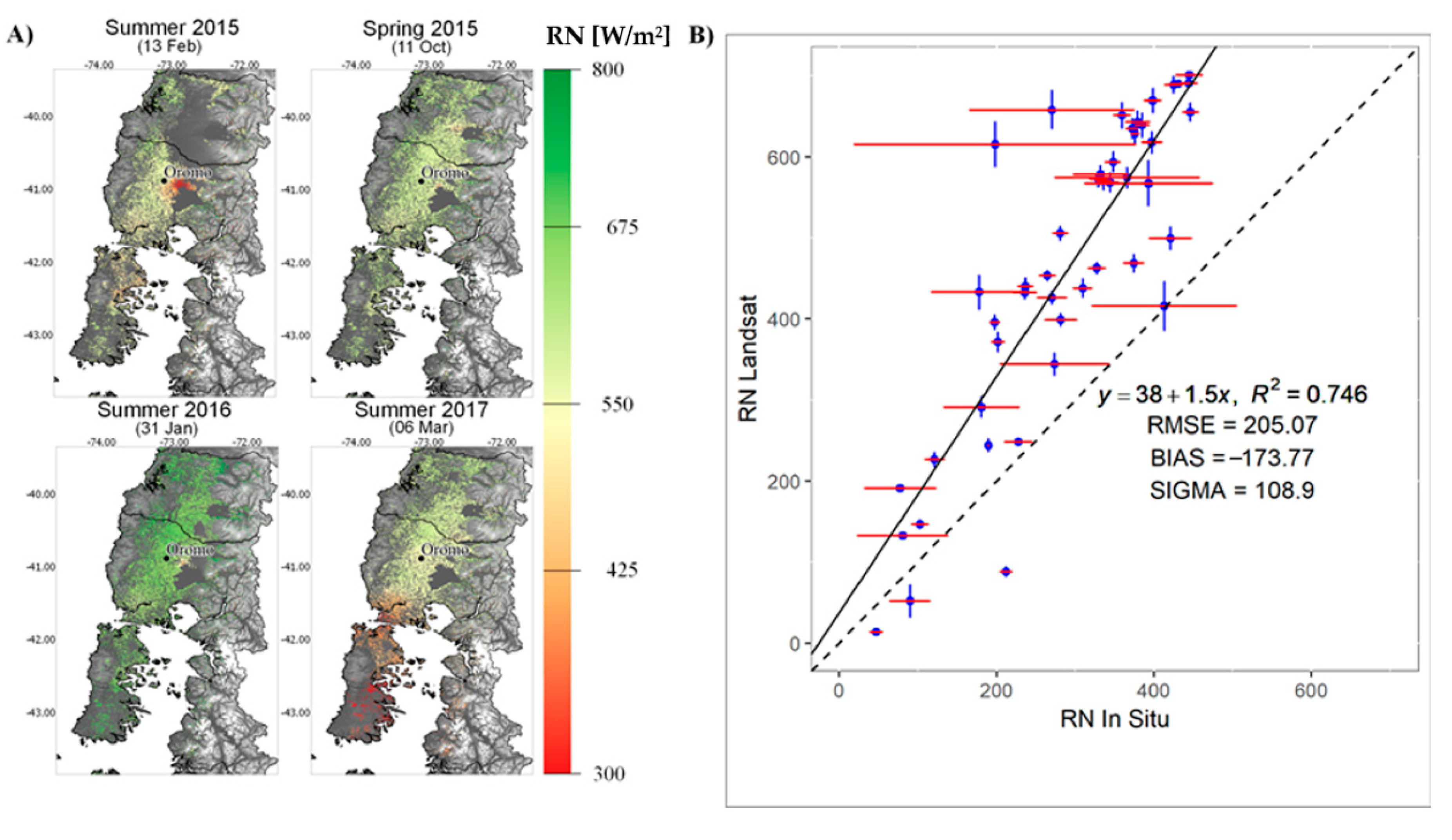
3.2. Net Radiation Estimates
3.3. Surface Energy Balance Models and Eapotranspiration Modelling
4. Results
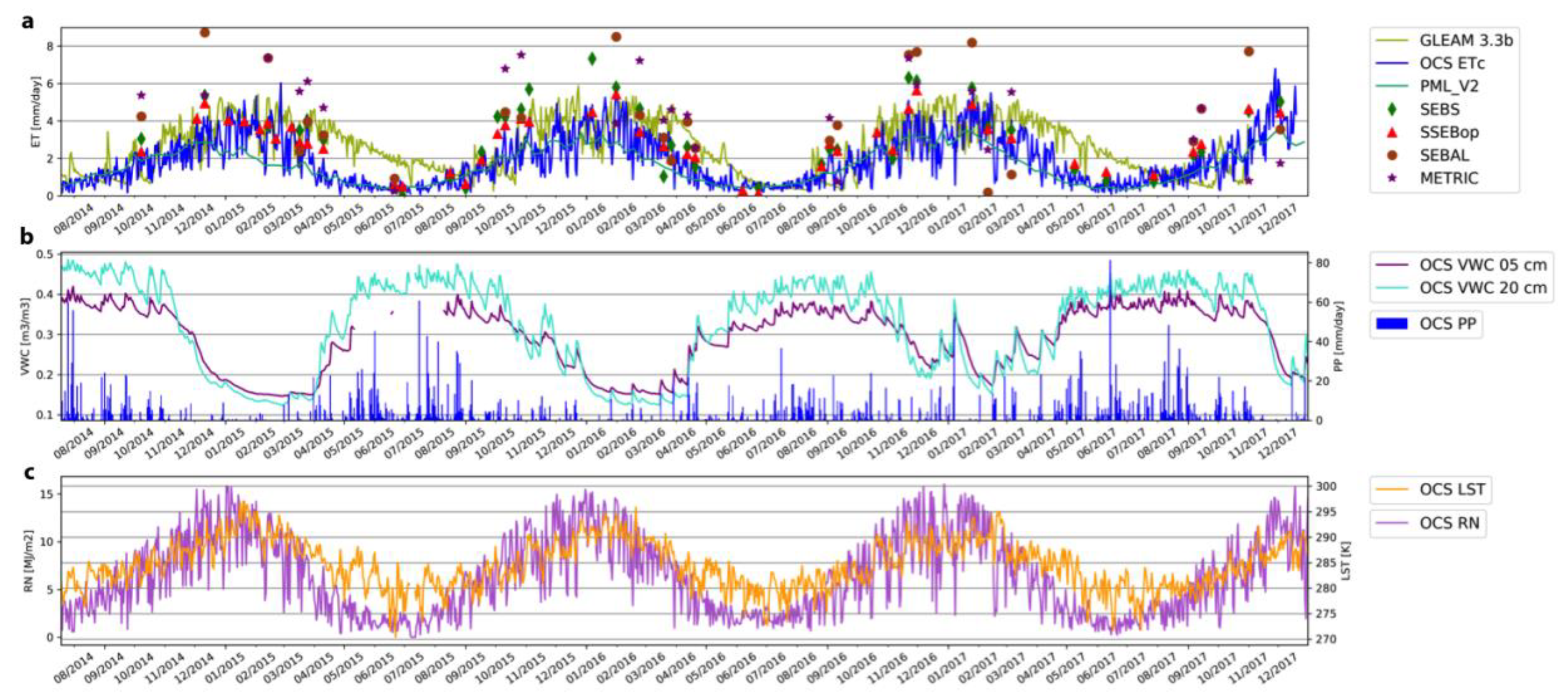
4.1. Estimated Surface and Meteorological Fields
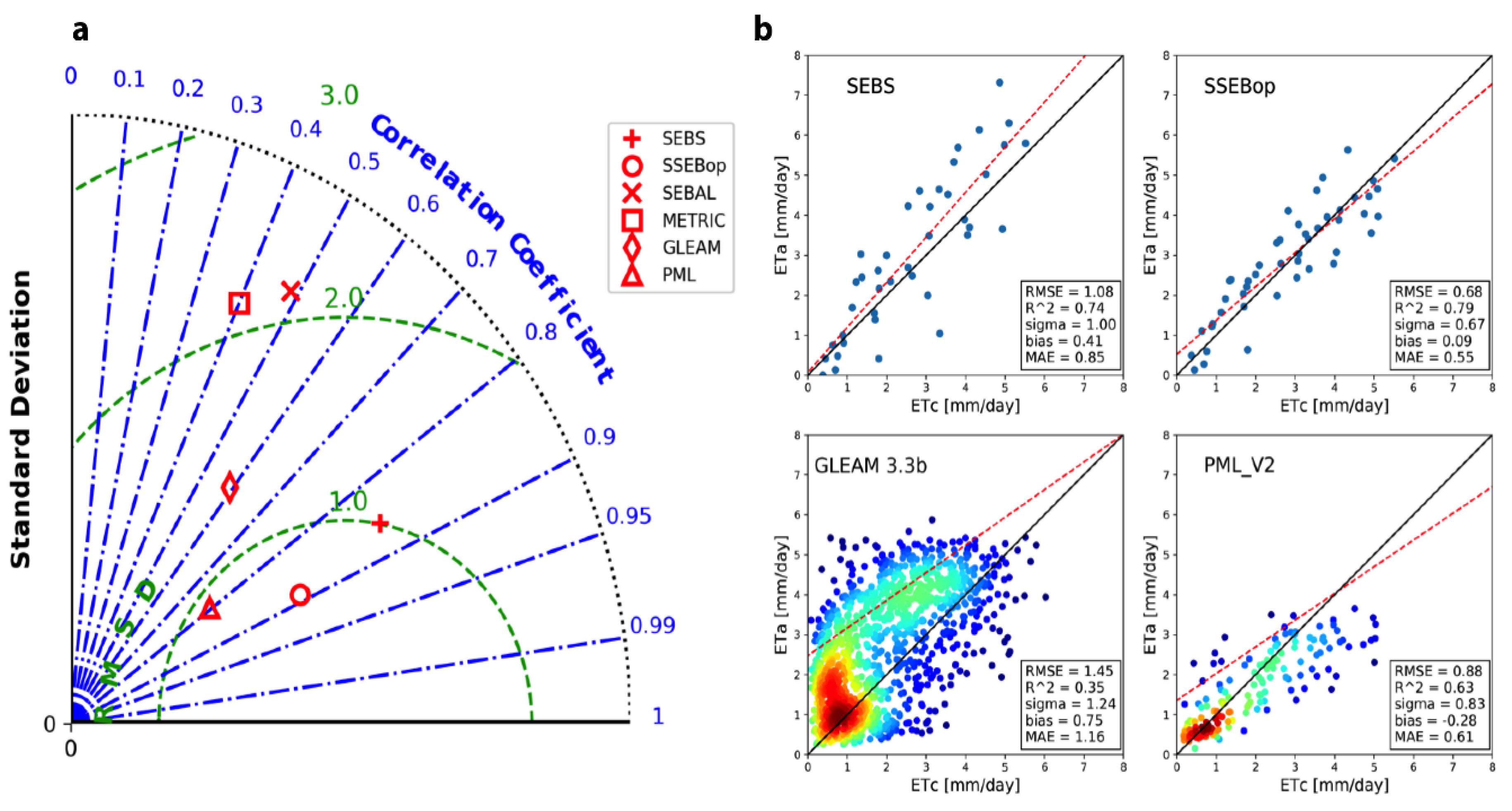
4.2. In-situ and Modeled Grassland Evapotranspiration
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nguyen, H.; Lucas, C.; Evans, A.; Timbal, B.; Hanson, L. Expansion of the Southern Hemisphere Hadley Cell in Response to Greenhouse Gas Forcing. J. Clim. 2015, 28, 8067–8077. [Google Scholar] [CrossRef]
- Boisier, J.P.; Rondanelli, R.; Garreaud, R.; Muñoz, F. Anthropogenic Contribution to the Southeast Pacific Precipitation Decline and Recent (2010–2015) Mega-Drought in Chile. Am. Geophys. Union 2016, 43, 1–9, Fall Meeting 2015, Abstract Id. H43E-1549. [Google Scholar] [CrossRef]
- Garreaud, R.D. Record-breaking climate anomalies lead to severe drought and environmental disruption in western Patagonia in 2016. Clim. Res. 2018, 74, 217–229. [Google Scholar] [CrossRef]
- Osborn, T.J.; Barichivich, J.; Harris, I.; van der Schrier, G.; Jones, P.D. Monitoring global drought using the self-calibrating Palmer Drought Severity Index [in “State of the Climate in 2017”]. Bull. Am. Meteorol. Soc. 2018, 99, S36–S37. [Google Scholar] [CrossRef]
- Barichivich, J.; Osborn, T.J.; Harris, I.; van der Schrier, G.; Jones, P.D. Monitoring global drought using the self-calibrating Palmer Drought Severity Index [in “State of the Climate in 2019”]. Bull. Am. Meteorol. Soc. 2020, 101, S59–S60. [Google Scholar] [CrossRef]
- Barichivich, J.; Osborn, T.J.; Harris, I.; van der Schrier, G.; Jones, P.D. Drought [in “State of the Climate in 2018”]. Bull. Am. Meteorol. Soc. 2019, 100, S39–S40. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, D.; Yu, L.; Wang, X.; Chen, Y.; Bai, Y.; Hernández, H.J.; Galleguillos, M.; Estades, C.; Biging, G.S.; et al. Detailed dynamic land cover mapping of Chile: Accuracy improvement by integrating multi-temporal data. Remote. Sens. Environ. 2016, 183, 170–185. [Google Scholar] [CrossRef]
- Flores, P.G. Sustainable Pasture Improvement in the South of Chile. Adv. Plants Agric. Res. 2017, 6, 1–3. [Google Scholar] [CrossRef]
- Di Bella, C.M.; Rebella, C.M.; Paruelo, J.M. Evapotranspiration estimates using NOAA AVHRR imagery in the Pampa region of Argentina. Int. J. Remote. Sens. 2010, 21, 791–797. [Google Scholar] [CrossRef]
- Nutini, F.; Boschetti, M.; Candiani, G.; Bocchi, S.; Brivio, P.A. Evaporative Fraction as an Indicator of Moisture Condition and Water Stress Status in Semi-Arid Rangeland Ecosystems. Remote. Sens. 2014, 6, 6300–6323. [Google Scholar] [CrossRef]
- Rost, S.; Gerten, D.; Bondeau, A.; Lucht, W.; Rohwer, J.; Schaphoff, S. Agricultural green and blue water consumption and its influence on the global water system. Water Resour. Res. 2008, 44, 1–17. [Google Scholar] [CrossRef]
- Seaquist, J.; Olsson, L.; Ardö, J. A remote sensing-based primary production model for grassland biomes. Ecol. Model. 2003, 169, 131–155. [Google Scholar] [CrossRef]
- Zonderland-Thomassen, M.; Lieffering, M.; Ledgard, S. Water footprint of beef cattle and sheep produced in New Zealand: Water scarcity and eutrophication impacts. J. Clean. Prod. 2014, 73, 253–262. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Ortega-Farías, S. Evaluation of single and dual crop coefficients over a drip-irrigated Merlot vineyard (Vitis vinifera L.) using combined measurements of sap flow sensors and an eddy covariance system. Aust. J. Grape Wine Res. 2013, 19, 249–260. [Google Scholar] [CrossRef]
- Sobrino, J.; Mattar, C.; Jímenez-Muñoz, J.C.; Franch, B.; Corbari, C. On the Synergy between Optical and TIR Observations for the Retrieval of Soil Moisture Content: Exploring Different Approaches. In Remote Sensing of Energy Fluxes and Soil Moisture Content; CRC Press: Boca Ratón, FL, USA, 2013; pp. 363–385. [Google Scholar]
- Uddin, J.; Hancock, N.; Smith, R.J.; Foley, J. Measurement of evapotranspiration during sprinkler irrigation using a precision energy budget (Bowen ratio, eddy covariance) methodology. Agric. Water Manag. 2013, 116, 89–100. [Google Scholar] [CrossRef]
- Yang, B.; Wen, X.; Sun, X. Irrigation depth far exceeds water uptake depth in an oasis cropland in the middle reaches of Heihe River Basin. Sci. Rep. 2015, 5, 15206. [Google Scholar] [CrossRef]
- Jia, L. Modeling Heat Exchanges at the Land-Atmosphere Interface Using Multi-Angular Thermal Infrared Measurements. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2004. [Google Scholar]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.-H.; Yan, G.; Zhang, X. A Review of Current Methodologies for Regional Evapotranspiration Estimation from Remotely Sensed Data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Norman, J.; Divakarla, M.; Goel, N. Algorithms for extracting information from remote thermal-IR observations of the earth’s surface. Remote. Sens. Environ. 1995, 51, 157–168. [Google Scholar] [CrossRef]
- Guan, H.; Wilson, J.L. A hybrid dual-source model for potential evaporation and transpiration partitioning. J. Hydrol. 2009, 377, 405–416. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: II. Recommended documentation. Agric. Water Manag. 2011, 98, 921–929. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.G.M.; Kramber, W.; Lorite, I.J.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.; Roerink, G.; Van Der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL). J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Hulley, G.; Hook, S.; Fisher, J.; Lee, C. ECOSTRESS, A NASA Earth-Ventures Instrument for studying links between the water cycle and plant health over the diurnal cycle. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS); Institute of Electrical and Electronics Engineers (IEEE), Fort Worth, TX, USA, 23–28 July 2017; pp. 5494–5496. [Google Scholar]
- Roy, D.P.; Wulder, M.; Loveland, T.R.; Woodcock, C.; Allen, R.; Anderson, M.; Helder, D.; Irons, J.; Johnson, D.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Q.; Batkhishig, O.; Ouyang, Z. Relationship between Evapotranspiration and Land Surface Temperature under Energy- and Water-Limited Conditions in Dry and Cold Climates. Adv. Meteorol. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Olivera-Guerra, L.; Mattar, C.; Merlin, O.; Durán-Alarcón, C.; Santamaría-Artigas, A.; Fuster, R. An operational method for the disaggregation of land surface temperature to estimate actual evapotranspiration in the arid region of Chile. ISPRS J. Photogramm. Remote. Sens. 2017, 128, 170–181. [Google Scholar] [CrossRef]
- Martens, B.; MirallesiD, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Miralles D, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Gan, R.; Zhang, Y.; Shi, H.; Yang, Y.; Eamus, D.; Cheng, L.; Chiew, F.H.; Yu, Q. Use of satellite leaf area index estimating evapotranspiration and gross assimilation for Australian ecosystems. Ecohydrology 2018, 11, e1974. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, D.; Gan, R.; Chiew, F.H.; McVicar, T.R.; Zhang, Q.; Yang, Y. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote. Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
- Sarricolea, P.; Herrera-Ossandon, M. Meseguer-Ruiz, Óliver Climatic regionalisation of continental Chile. J. Maps 2017, 13, 66–73. [Google Scholar] [CrossRef]
- Masek, J.; Vermote, E.; Saleous, N.; Wolfe, R.; Hall, F.; Huemmrich, K.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat Surface Reflectance Dataset for North America, 1990–2000. IEEE Geosci. Remote. Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote. Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote. Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Abbott, E.; Malakar, N.K.; Islam, T.; Abrams, M. The ASTER Global Emissivity Dataset (ASTER GED): Mapping Earth’s emissivity at 100 meter spatial scale. Geophys. Res. Lett. 2015, 42, 7966–7976. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote. Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—a new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote. Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Barsi, J.; Barker, J.; Schott, J. An Atmospheric Correction Parameter Calculator for a single thermal band earth-sensing instrument. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003. [Google Scholar] [CrossRef]
- Moletto-Lobos, I.; Mattar, C.; Jímenez-Muñoz, J.C.; Pérez, T. Impact of Atmosphere and emissivity data base in the validation of Land Surface Temperature over pastures. In Proceedings of the 5th International Symposium on Recent Advances in Quantitative Remote Sensing: RAQRS’V, Valencia, Spain, 18–22 September 2017. [Google Scholar]
- Mattar, C.; Santamaria-Artigas, A.E.; Durán-Alarcón, C.; Olivera-Guerra, L.; Fuster, R.; Borvarán, D. The LAB-Net Soil Moisture Network: Application to Thermal Remote Sensing and Surface Energy Balance. Data 2016, 1, 6. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skoković, D.; Mattar, C.; Cristobal, J. Land Surface Temperature Retrieval Methods from Landsat-8 Thermal Infrared Sensor Data. IEEE Geosci. Remote. Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Cristóbal, J.; Jiménez-Muñoz, J.C.; Prakash, A.; Mattar, C.; Skoković, D.; Sobrino, J.A. An Improved Single-Channel Method to Retrieve Land Surface Temperature from the Landsat-8 Thermal Band. Remote Sens. 2018, 10, 431. [Google Scholar] [CrossRef]
- Guillevic, P. Land Surface Temperature Product Validation Best Practice Protocol. 2018. [Google Scholar]
- Liang, S.; Shuey, C.J.; Russ, A.L.; Fang, H.; Chen, M.; Walthall, C.L.; Daughtry, C.S.; Hunt, R. Narrowband to broadband conversions of land surface albedo: II. Validation. Remote. Sens. Environ. 2003, 84, 25–41. [Google Scholar] [CrossRef]
- Mattar, C.; Franch, B.; Sobrino, J.A.; Corbari, C.; Muñoz, J.C.J.; Olivera-Guerra, L.; Skokovic, D.; Sória, G.; Oltra-Carriò, R.; Julien, Y.; et al. Impacts of the broadband albedo on actual evapotranspiration estimated by S-SEBI model over an agricultural area. Remote. Sens. Environ. 2014, 147, 23–42. [Google Scholar] [CrossRef]
- Bristow, K.L.; Campbell, G.S. On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agric. For. Meteorol. 1984, 31, 159–166. [Google Scholar] [CrossRef]
- Brutsaert, W. On a derivable formula for long-wave radiation from clear skies. Water Resour. Res. 1975, 11, 742–744. [Google Scholar] [CrossRef]
- Kustas, W.P.; Daughtry, C.S.; Van Oevelen, P.J. Analytical treatment of the relationships between soil heat flux/net radiation ratio and vegetation indices. Remote. Sens. Environ. 1993, 46, 319–330. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 24, 163–187. [Google Scholar]
- Sobrino, J.A.; Gómez, M.; Jimenez, J.C.; Olioso, A. Application of a simple algorithm to estimate daily evapotranspiration from NOAA–AVHRR images for the Iberian Peninsula. Remote. Sens. Environ. 2007, 110, 139–148. [Google Scholar] [CrossRef]
- Qiu, G.Y.; Yano, T.; Momii, K. An improved methodology to measure evaporation from bare soil based on comparison of surface temperature with a dry soil surface. J. Hydrol. 1998, 210, 93–105. [Google Scholar] [CrossRef]
- Allen, R.; Walter, I.; Elliott, R.; Howell, T.; Itenfisu, D.; Jensen, M.E. he ASCE standardized reference evapotranspiration equation: ASCE-EWRI Standardization of Reference Evapotranspiration Task Committe Report. 2005. [Google Scholar]
- Baldridge, A.M.; Hook, S.; Grove, C.; Rivera, G. The ASTER spectral library version 2.0. Remote. Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote. Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]
- Paul, G.; Gowda, P.H.; Prasad, P.V.; Howell, T.A.; Staggenborg, S.A.; Neale, C.M. Lysimetric evaluation of SEBAL using high resolution airborne imagery from BEAREX08. Adv. Water Resour. 2013, 59, 157–168. [Google Scholar] [CrossRef]
- Singh, R.K.; Senay, G.B. Comparison of Four Different Energy Balance Models for Estimating Evapotranspiration in the Midwestern United States. Water 2015, 8, 9. [Google Scholar] [CrossRef]
| 2014 | 2015 | 2016 | 2017 | Mean | |
|---|---|---|---|---|---|
| Evapotranspiration (mm) | |||||
| Spring | [222.8] | [227.8] | 238.5 [239.5] | 194.3 [242.8] | 216.4 [233.3] |
| Summer | [176.8] | 148.2 [170.8] | 189.2 [226.1] | 163.1 [254.9] | 166.8 [204.9] |
| Autumn | [71.2] | 59.7 [63.8] | 70.4 [75.9] | 61.7 [79.0] | 60.6 [69.4] |
| Winter | [71.9] | 27.7 [65.9] | 64.4 [71.4] | 52.6 [68.2] | 48.2 [72.5] |
| Annual | [542.8] | [528.4] | 562.2 [612.9] | 471.8 [635.9] | 517.0 [580.0] |
| Precipitation (mm) | |||||
| Spring | 130.8 | 150.6 | 231.6 | 228.8 | 185.5 |
| Summer | - | 46.7 | 81.7 | 222.8 | 117.1 |
| Autumn | - | 442.2 | 183.2 | 537.1 | 387.6 |
| Winter | 490.7 | 543.8 | 371.9 | 509.9 | 487.9 |
| Annual | 621.5 | 1183.3 | 868.4 | 1498.6 | 1178.0 |
| Soil moisture 7 cm (%) | |||||
| Spring | 32.2 | 29.8 | 31.1 | 32.4 | 31.3 |
| Summer | - | 14.3 | 13.9 | 22.6 | 16.9 |
| Autumn | - | 35.9 | 30.5 | 36.1 | 34.2 |
| Winter | 45.9 | 42.2 | 41.3 | 41.9 | 43.0 |
| Soil moisture 20 cm (%) | |||||
| Spring | 30.7 | 28.2 | 29.8 | 30.2 | 29.3 |
| Summer | - | 15.7 | 16.3 | 24.3 | 18.8 |
| Autumn | - | 28.6 | 27.9 | 34.1 | 30.3 |
| Winter | 38.2 | 35.6 | 35.5 | 37.1 | 36.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moletto-Lobos, I.; Mattar, C.; Barichivich, J. Performance of Satellite-Based Evapotranspiration Models in Temperate Pastures of Southern Chile. Water 2020, 12, 3587. https://doi.org/10.3390/w12123587
Moletto-Lobos I, Mattar C, Barichivich J. Performance of Satellite-Based Evapotranspiration Models in Temperate Pastures of Southern Chile. Water. 2020; 12(12):3587. https://doi.org/10.3390/w12123587
Chicago/Turabian StyleMoletto-Lobos, Italo, Cristian Mattar, and Jonathan Barichivich. 2020. "Performance of Satellite-Based Evapotranspiration Models in Temperate Pastures of Southern Chile" Water 12, no. 12: 3587. https://doi.org/10.3390/w12123587
APA StyleMoletto-Lobos, I., Mattar, C., & Barichivich, J. (2020). Performance of Satellite-Based Evapotranspiration Models in Temperate Pastures of Southern Chile. Water, 12(12), 3587. https://doi.org/10.3390/w12123587







