A Review of Tank Model and Its Applicability to Various Korean Catchment Conditions
Abstract
1. Introduction
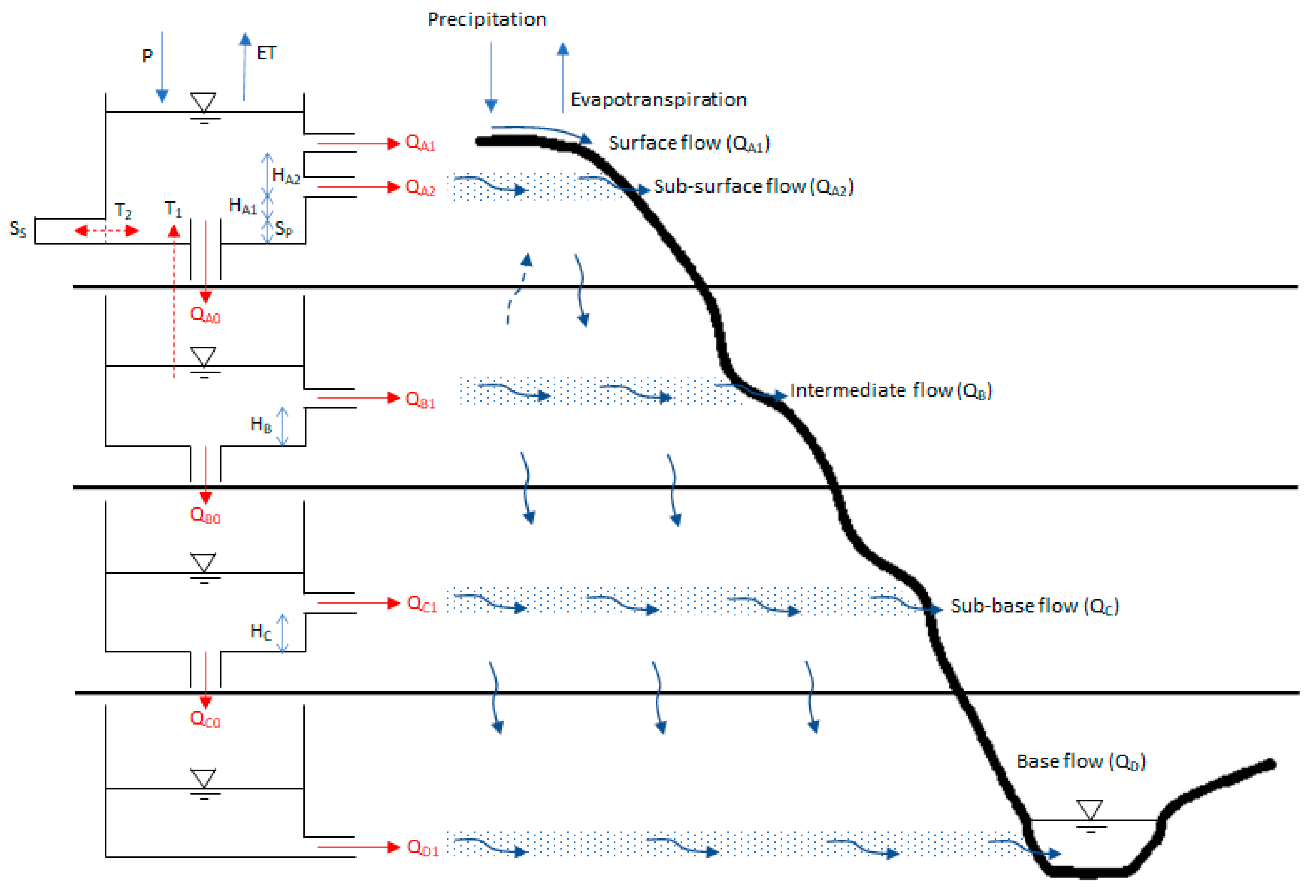
2. Tank Model
3. Model Uncertainty and Optimization Algorithms
3.1. Model Uncertainty Estimation
3.2. Dynamically Dimensioned Search (DDS)
- Define a maximum number of iterations, .
- Populate an initial set of parameters, .
- Calculate hydrologic performance and allocate the best performing set to and .
- Generate a random number for each parameter space and select all parameter sets for perturbation when their random numbers are bigger than , where is the current iteration.
- Generate by perturbate for the selected parameters from Step 4 with a standard normal random variable of as , where , , is the parameter determining the perturbation range and is the total number of the parameter sets selected in Step 4.
- and , if .
- Go to Step 4 until the predefined maximum iteration is reached.
3.3. Robust Parameter Estimation (ROPE)
- Select random data sets, .
- Measure their hydrological performances.
- Select best performing sets (10% of the initial sets), .
- Calculate the depths of every point in with respect to .
- Generate random parameter sets, such that the sets have higher depths with respect to .
- Replace with .
- Repeat Steps 2–6 until the performance from two samples are not significantly different or specified maximum iteration numbers are exceeded.
3.4. Shuffled Complex Evolution (SCE)
- Generate samples using a uniform probability distribution from users defined bounds.
- Sort performances of the samples in increasing order.
- Divide the samples into partitions with points in each partition in a way that the nth partition contains every ranked point, where .
- Evolve each complex based on the competitive complex evolution (CCE, [35]).
- Combine the evolved points into a single sample then repeat Steps 2–5 until convergence criteria are satisfied.
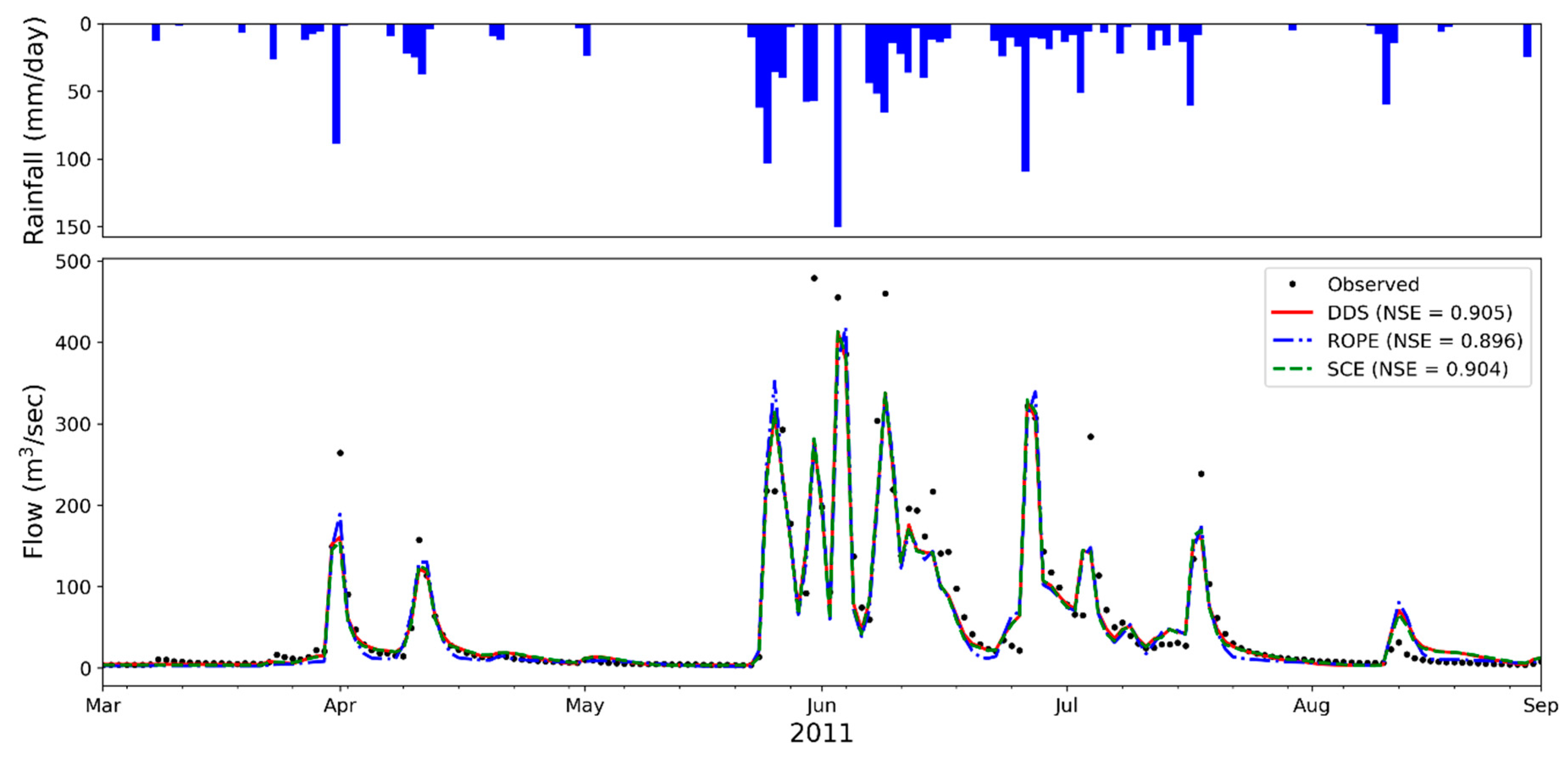
4. Application
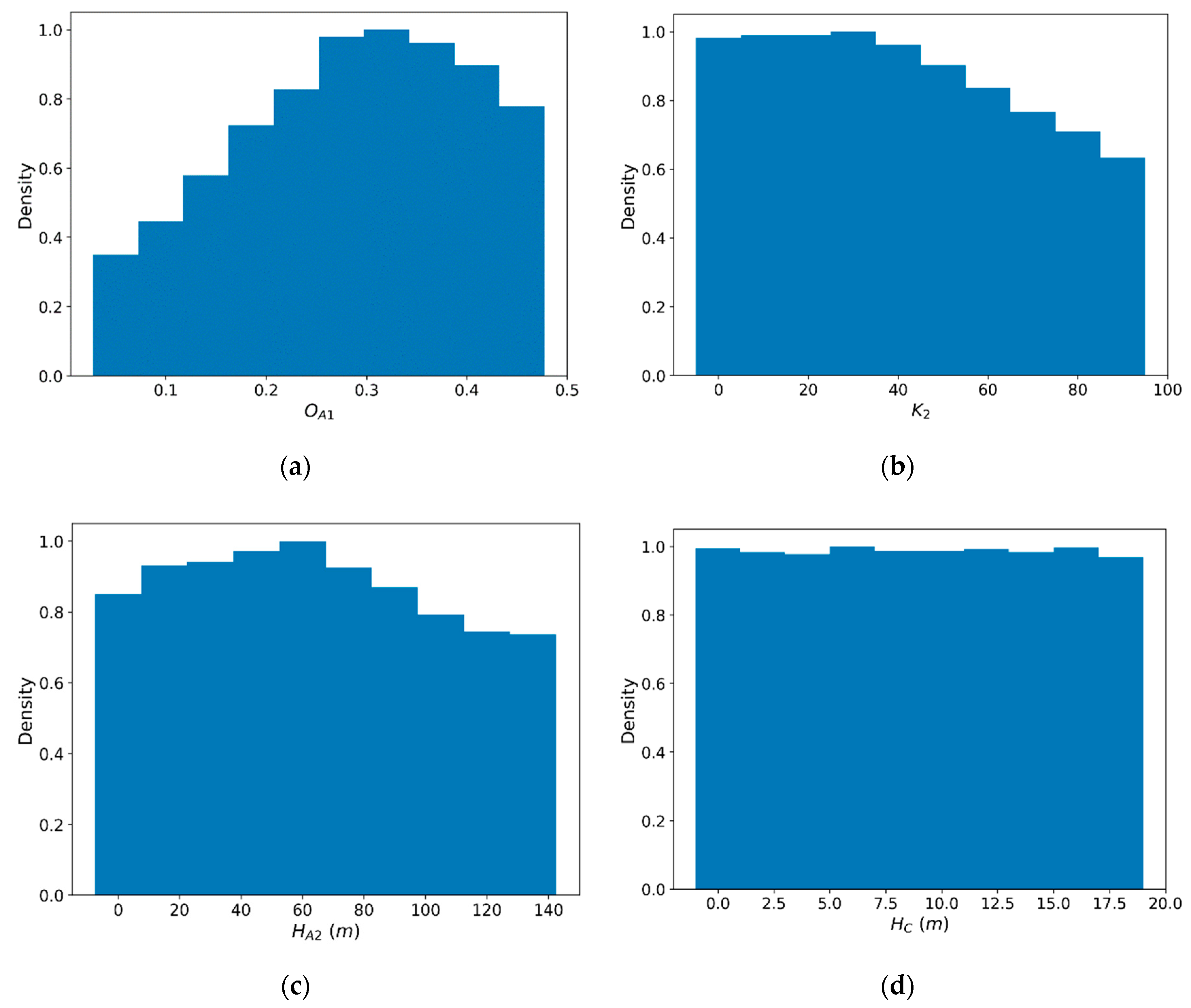
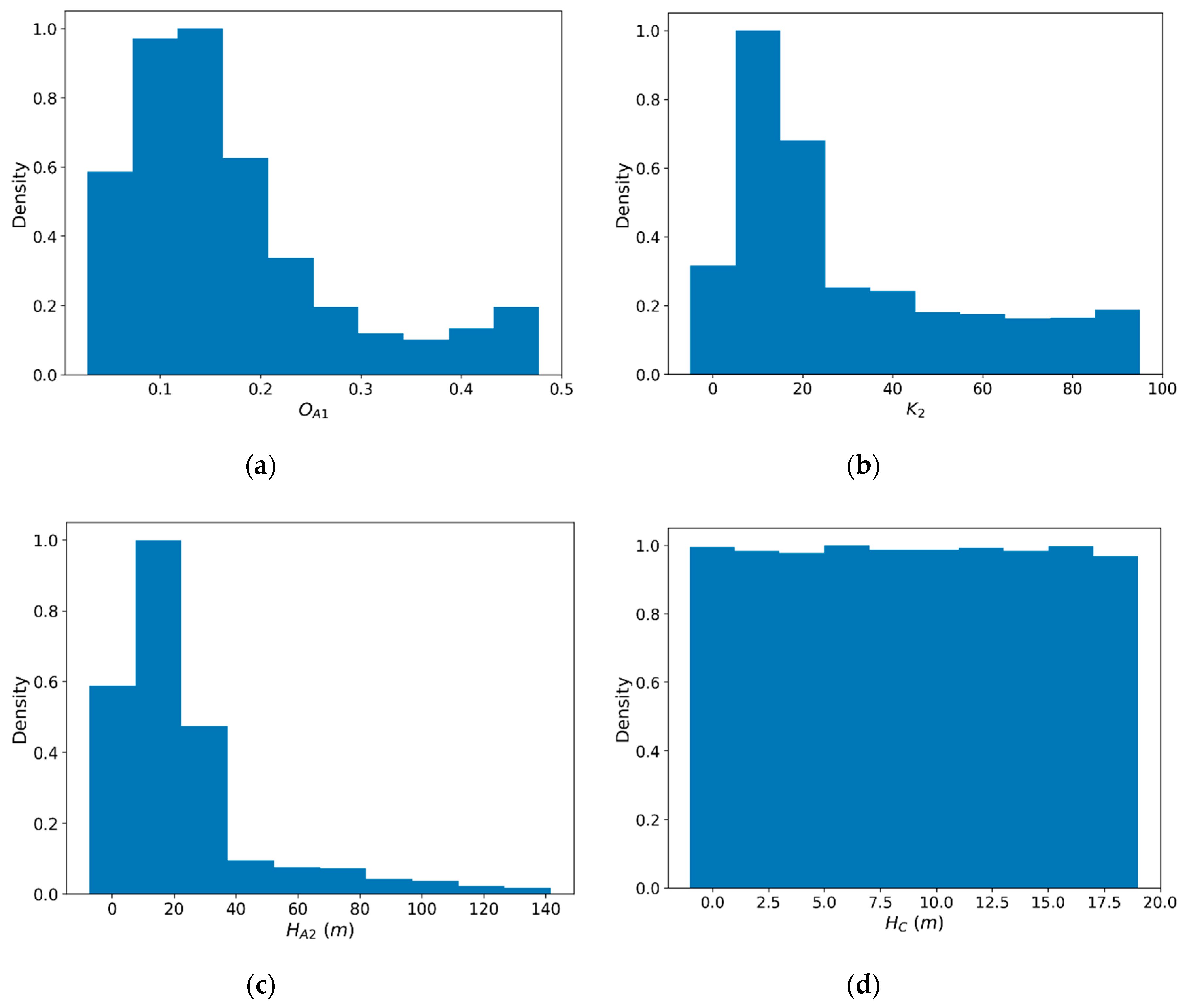
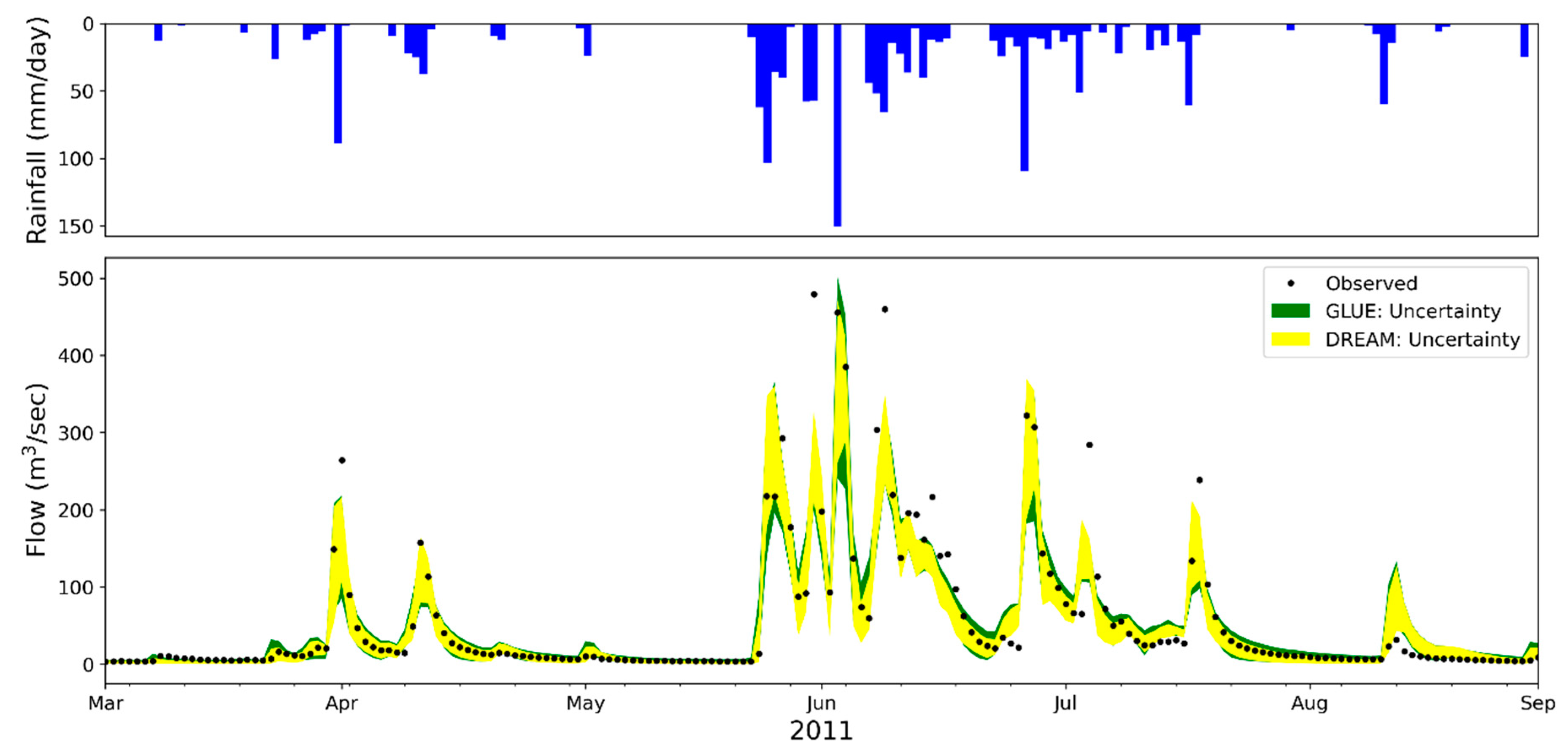
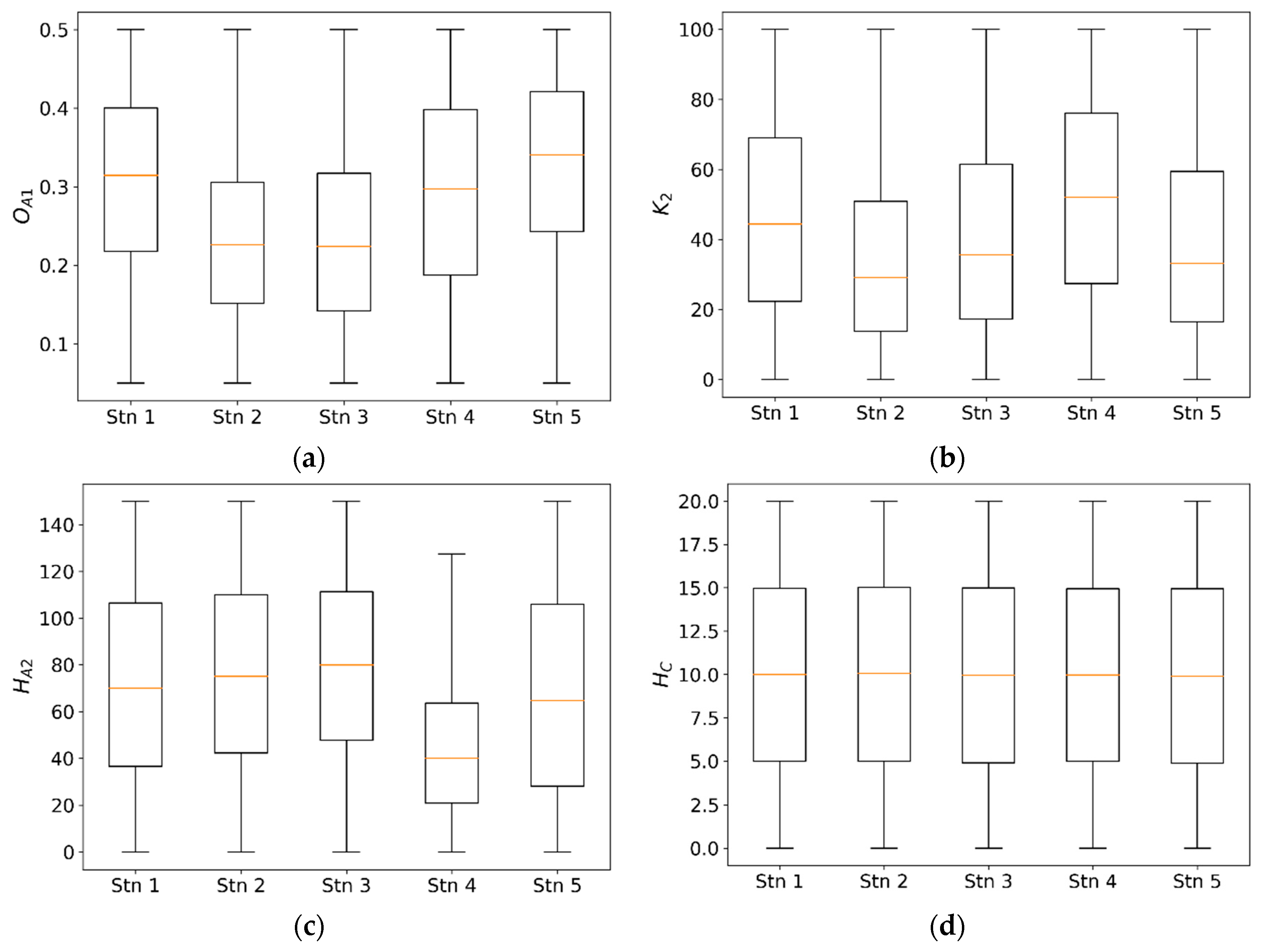
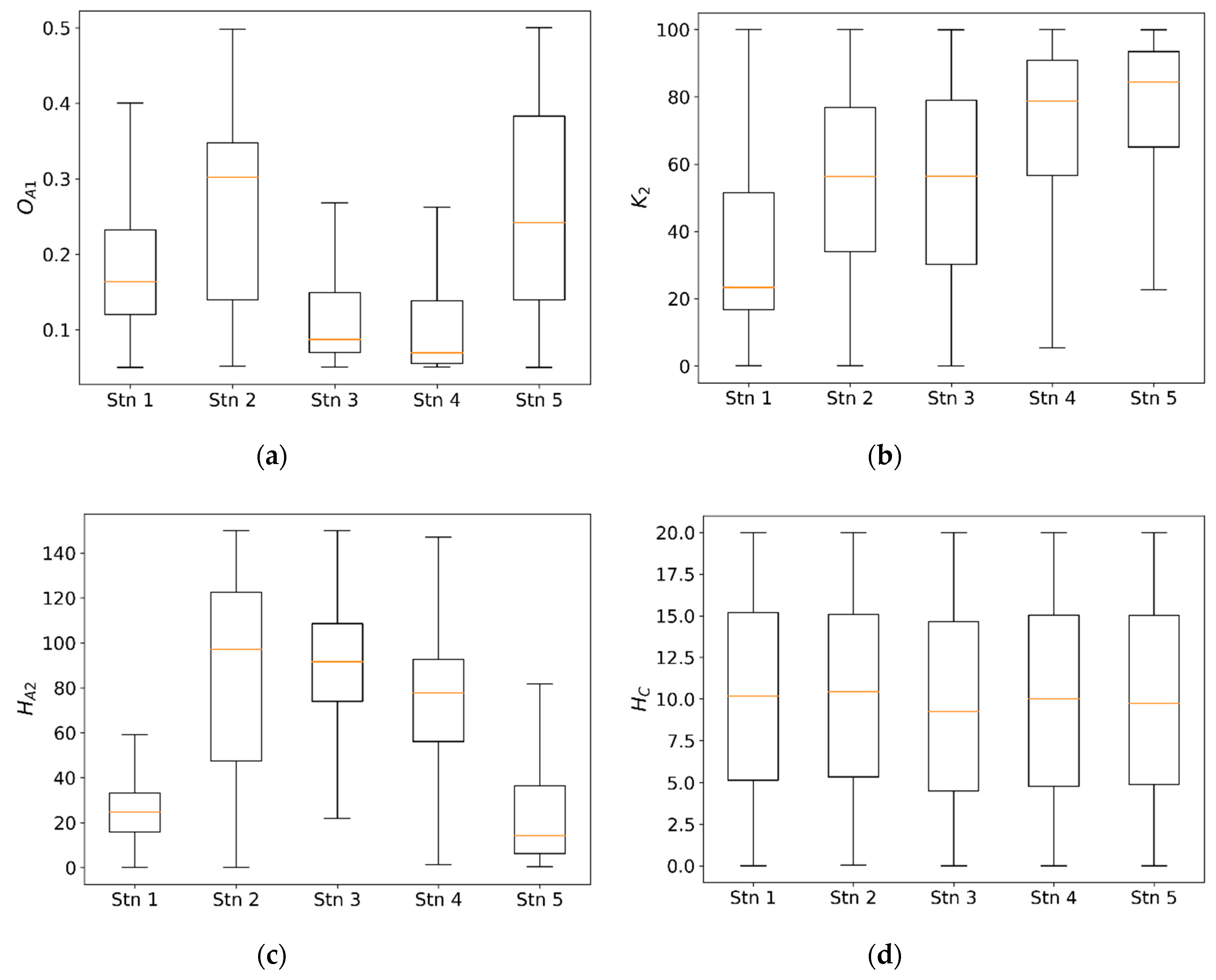
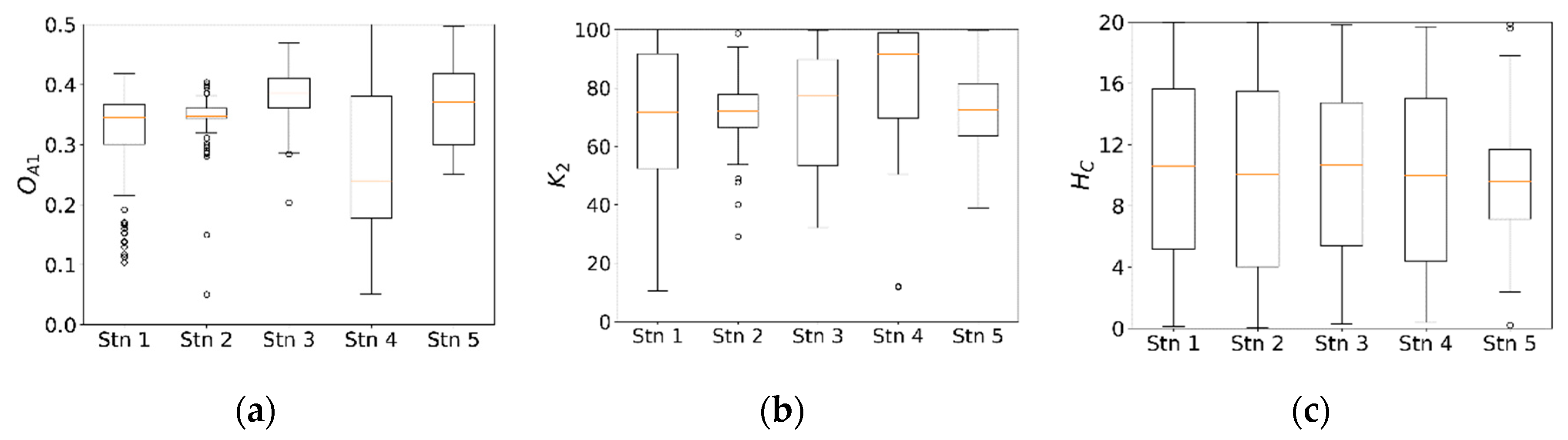
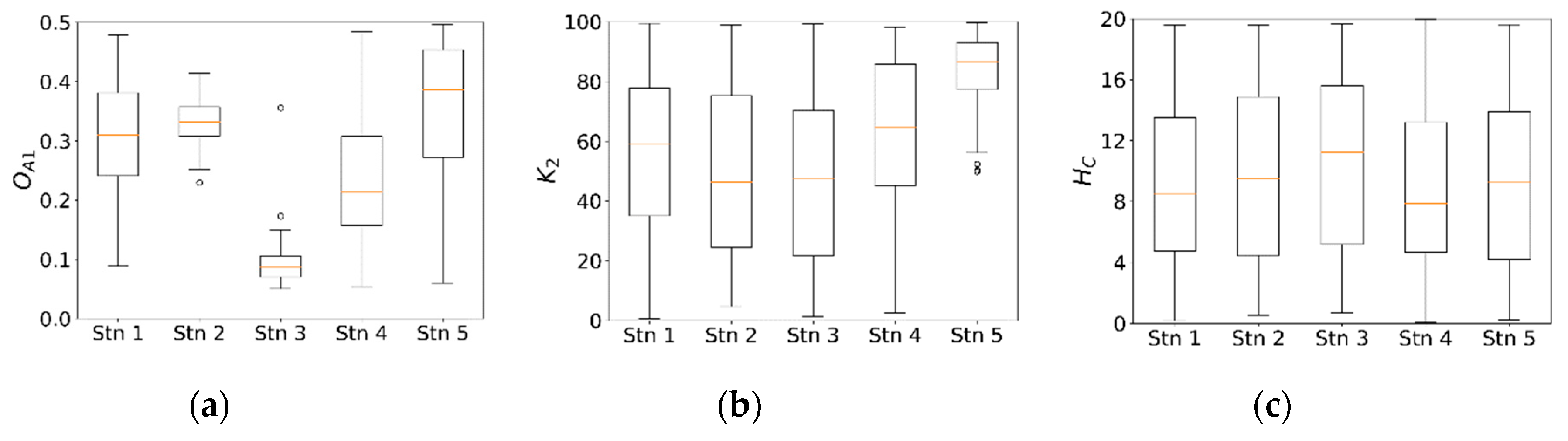
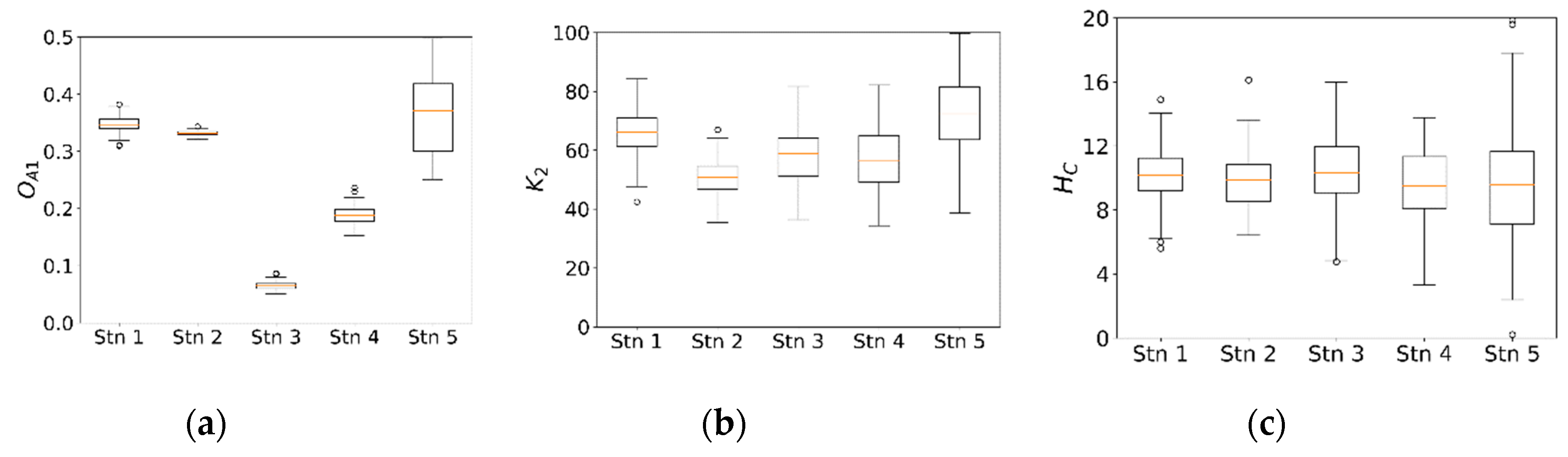
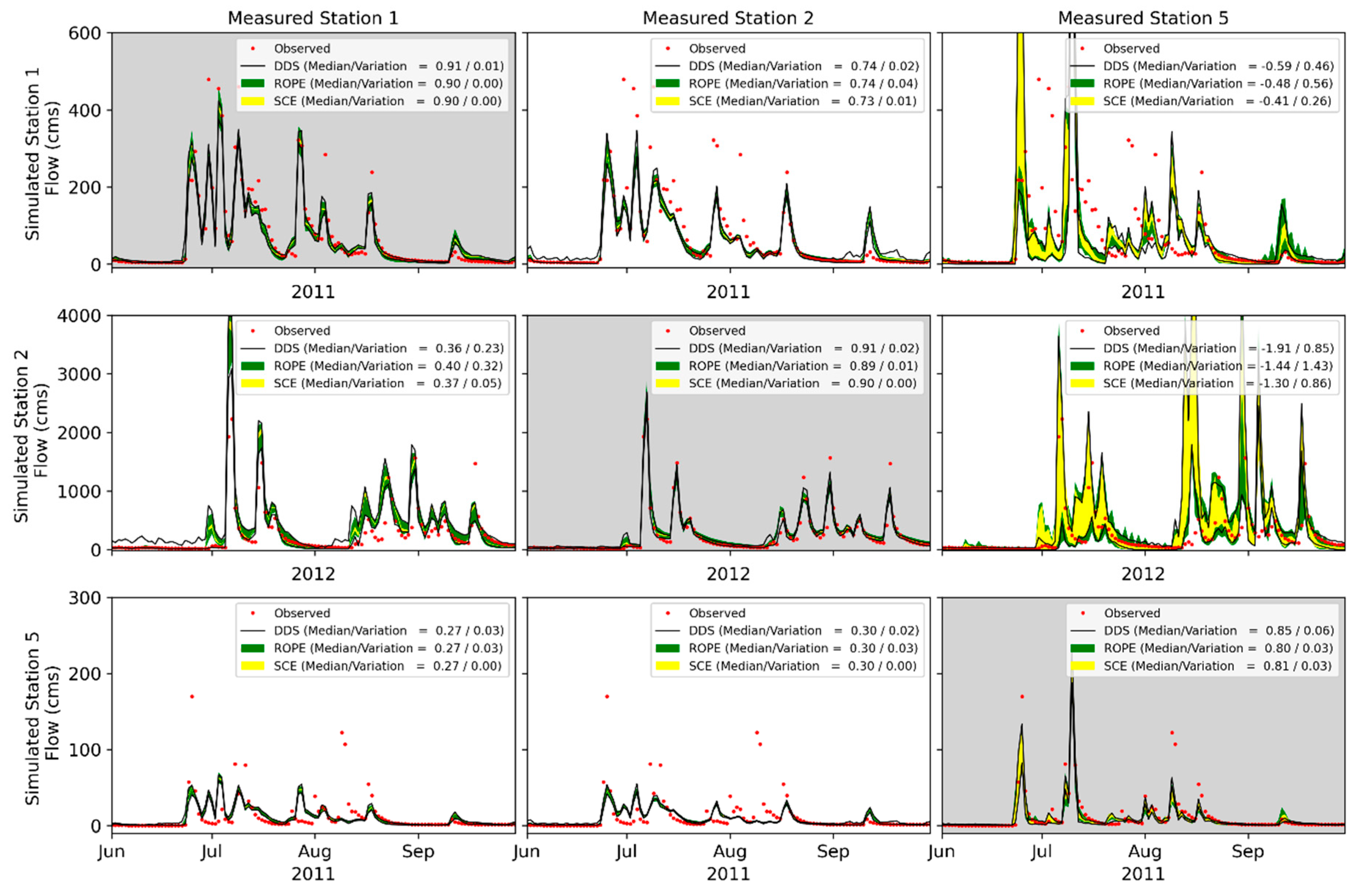
4.1. Parameter Sensitivity and Uncertainty
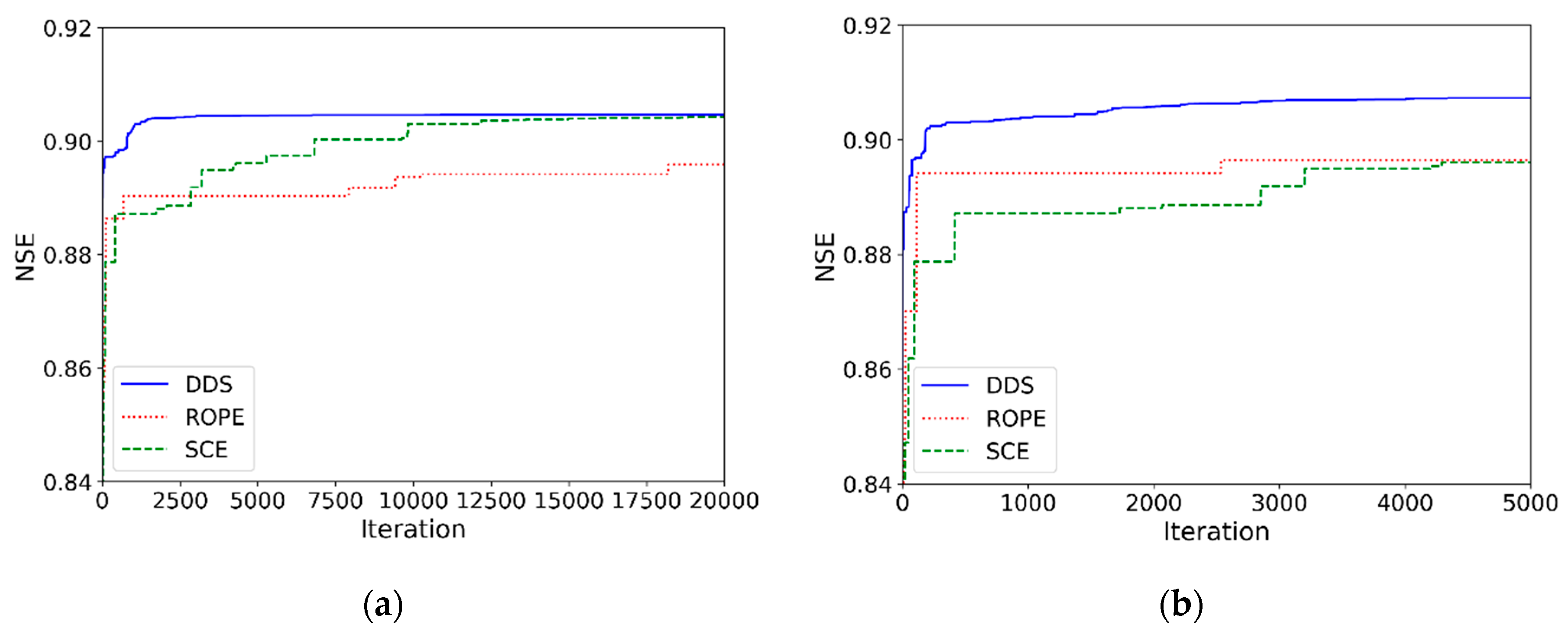
4.2. Comparison of the Optimization Algorithms
4.3. Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- MLIT. Long Term Water Resource Plan (2001-2020), 3rd ed.; Ministry of Land, Infrastructure and Transport (MLIT); Government of South Korea: Seoul, Korea, 2016. [Google Scholar]
- Sugawara, M.; Fuyuki, M. A Method of Revision of River Discharge by Means of a Rainfall Model. In A Collection of Research Papers about Forecasting Hydrologic Variables; The Geosphere Research Institute of Saitama University: Saitama, Japan, 1956; pp. 14–18. [Google Scholar]
- Yokoo, Y.; Kazama, S.; Sawamoto, M.; Nishimura, H. Regionalization of lumped water balance model parameters based on multiple regression. J. Hydrol. 2001, 246, 209–222. [Google Scholar] [CrossRef]
- Powell, M.J.D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar]
- Chen, R.-S.; Pi, L.-C.; Hsieh, C.-C. Application of parameter optimization method for calibrating tank model. J. Am. Water. Resour. Assoc. 2005, 41, 389–402. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Kim, T.; Jung, I.W.; Koo, B.Y.; Bae, D.H. Optimization of Tank model parameters using multi-objective genetic Algorithm (I): Methodology and model formulation. J. Korea Water Resour. Assoc. 2007, 40, 677–685. [Google Scholar] [CrossRef]
- Park, C.I.; Baek, C.W.; Jun, H.D.; Kim, J.H. Parameter estimation of Tank model by data interval and rainfall factors for dry season. J. Korean Soc Water Qual. 2006, 22, 856–864. [Google Scholar]
- Beven, K.J.; Binley, A.M. The future of distributed models: model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44, W00B09. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int. J. Nonlin. Sci. Num. 2009, 10, 273–290. [Google Scholar]
- Kuczera, G.; Renard, B.; Thyer, M.; Kavetski, D. There are no hydrological monsters, just models and observations with large uncertainties. Hydrolog. Sci. J. 2010, 55, 980–991. [Google Scholar] [CrossRef]
- Kang, S.U.; Lee, D.R.; Lee, S.H. A study on calibration of Tank model with soil moisture structure. J. Korea Water Resour. Assoc. 2004, 37, 133–144. [Google Scholar] [CrossRef]
- Lee, S.H.; Kang, S.U. A parameter regionalization study of a modified Tank model using characteristic factors of watersheds. J. Korean Soc. Civ. Eng. 2007, 27, 379–385. [Google Scholar]
- Kang, M.G.; Lee, J.H.; Park, K.W. Parameter regionalization of a Tank model for simulating runoffs from ungauged watersheds. J. Korea Water Resour. Assoc. 2013, 46, 519–530. [Google Scholar] [CrossRef][Green Version]
- Sugawara, M. Tank model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publishers: Berlin/Heidelberg, Germany, 1995; pp. 165–214. [Google Scholar]
- Stedinger, J.R.; Vogel, R.M.; Lee, S.U.; Batchelder, R. Appraisal of the generalized likelihood uncertainty estimation (GLUE) method. Water Resour. Res. 2008, 44, W00B06. [Google Scholar] [CrossRef]
- Choi, H.T.; Beven, K. Multi-period and multi-criteria model conditioning to reduce prediction uncertainty in an application of TOPMODEL within the GLUE framework. J. Hydrol. 2007, 332, 316–336. [Google Scholar]
- Houska, T.; Multsch, S.; Kraft, P.; Frede, H.-G.; Breuer, L. Monte Carlo-based calibration and uncertainty analysis of a coupled plant growth and hydrological model. Biogeosciences 2014, 11, 2069–2082. [Google Scholar] [CrossRef]
- Hellweger, F.L.; Lall, U. Modeling the effect of algal dynamics on arsenic speciation in Lake Biwa. Environ. Sci. Technol. 2004, 38, 6716–6723. [Google Scholar] [CrossRef]
- Smith, R.M.S.; Evans, D.J.; Wheater, H.S. Evaluation of two hybrid metric-conceptual models, for simulating phosphorus transfer from agricultural land in the river enborne, a lowland UK catchment. J. Hydrol. 2005, 304, 366–380. [Google Scholar] [CrossRef]
- Blasone, R.-S.; Vrugt, J.A.; Madsen, H.; Rosbjerg, D.; Robinson, B.A.; Zyvoloski, G.A. Generalized likelihood uncertainty estimation (GLUE) using adaptive Markov Chain Monte Carlo sampling. Adv. Water. Resour. 2008, 31, 630–648. [Google Scholar]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef]
- Houska, T.; Kraft, P.; Chamorro-Chavez, A.; Breuer, L. SPOTting Model Parameters Using a Ready-Made Python Package. PLoS ONE 2015, 10, e0145180. [Google Scholar] [CrossRef] [PubMed]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43, W01413. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optimiz. Theory App. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Jungnickel, D. The Greedy Algorithm. In Graphs, Networks and Algorithms. Algorithms and Computation in Mathematics; Springer: Berlin/Heidelberg, Germany, 1999; Volume 5. [Google Scholar]
- Bárdossy, A.; Singh, S.K. Robust estimation of hydrological model parameters. Hydrol. Earth Syst. Sci. 2008, 12, 1273–1283. [Google Scholar]
- Tukey, J. Mathematics and picturing data. Proc. Int. Ernation. Cong. Math. 1975, 2, 523–531. [Google Scholar]
- Bárdossy, A. Calibration of hydrological model parameters for ungauged catchments. Hydrol. Earth Syst. Sci. 2007, 11, 703–710. [Google Scholar]
- Serfling, R. Generalized quantile processes based on multivariate depth functions, with applications in nonparametric multivariate analysis. J. Multivar. Anal. 2002, 83, 232–247. [Google Scholar] [CrossRef]
- Cheng, A.Y.; Liu, R.Y.; Luxhøj, J.T. Monitoring multivariate aviation safety data by data depth: control charts and threshold systems. IIE Trans. 2002, 32, 861–872. [Google Scholar] [CrossRef]
- Liu, R.Y. Control charts for multivariate processes. J. Am. Stat. Assoc. 1995, 90, 1380–1387. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B.M.J. Depth and homogeneity in regional flood frequency analysis. Water Resour. Res. 2008, 44, W11422. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of rainfall-runoff models’ application of global optimization to the Sacramento soil moisture accounting model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Abudulla, F.A.; Lettenmaier, D.P. Development of regional parameter estimation equations for a macroscale hydrologic model. J. Hydrol. 1997, 197, 230–257. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and efficient algorithm for multiobjective optimization of hydrologic models. Water Resour. Res. 2003, 39, 1–19. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F.P. Continuous streamflow prediction in ungauged basins: The effects of equifinality and parameter set selection on uncertainty in regionalization approaches. Water Resour. Res. 2014, 50, 6135–6153. [Google Scholar] [CrossRef]
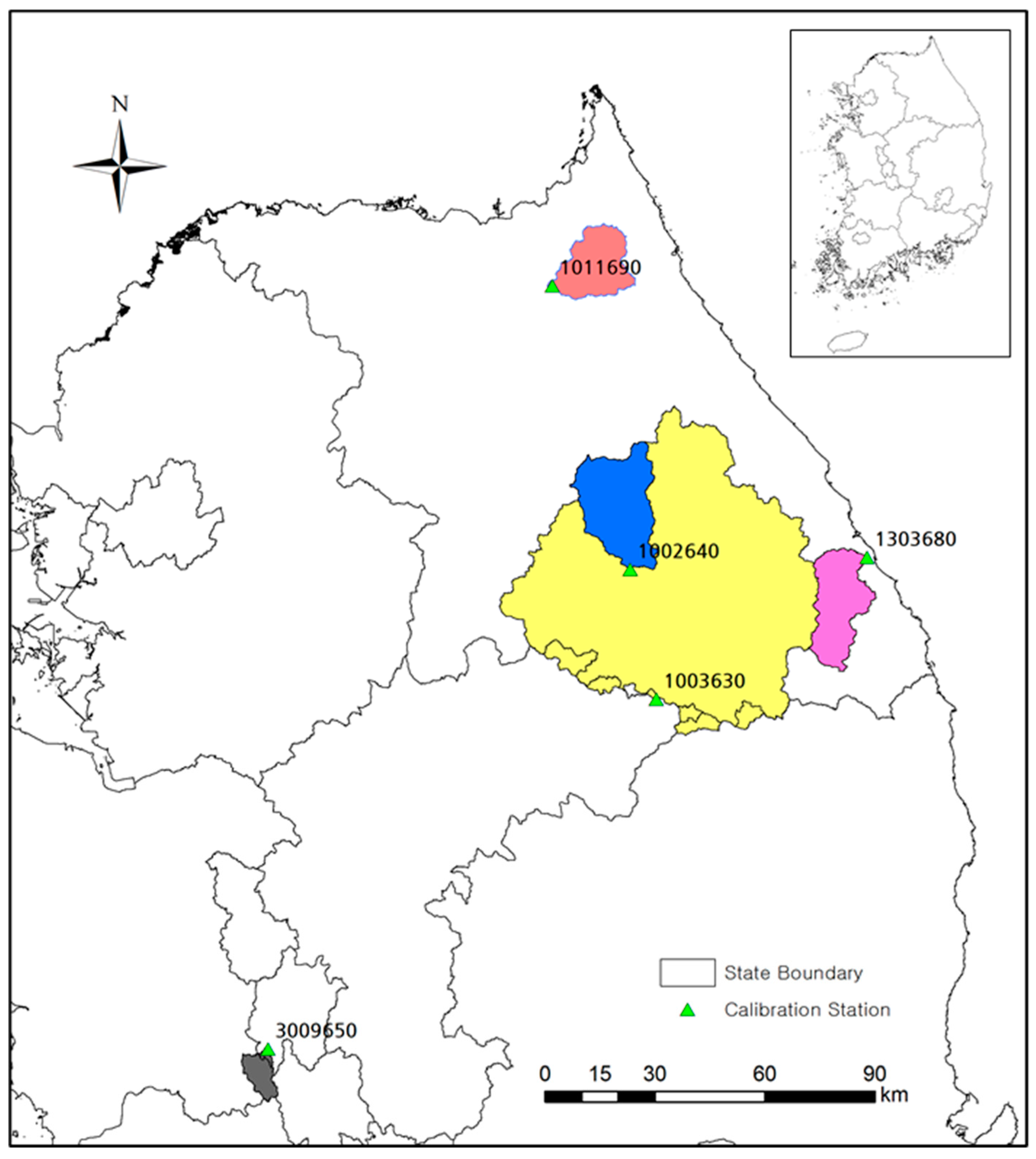

| Station No (Station Name) | Longitude/Latitude | Catchment Area (km2) | Average Slop (%) | Altitude Max/ SD (m) | Rainfall (mm/yr) | Calibration Year | Validation Year |
|---|---|---|---|---|---|---|---|
| 1002640 (Sangbangrim) | 128.42/ 37.43 | 527.9 | 47.9 | 1574.7/183.2 | 1336 | 2011 | 2012 |
| 1003630 (Osa Ri) | 128.51/ 37.10 | 4786.2 | 49.6 | 1574.6/238.8 | 1246 | 2012 | 2013 |
| 1011690 (Wolhak Ri) | 128.21/ 38.12 | 301.1 | 63.3 | 1701.5/262.0 | 1587 | 2011 | 2014 |
| 1303680 (Osipcheon Br.) | 129.23/ 37.70 | 371.7 | 58.1 | 1353.8/252.6 | 1249 | 2018 | 2012 |
| 3009650 (Youngchon Br.) | 127.32/ 36.25 | 83.4 | 44.2 | 872.0/126.6 | 1313 | 2011 | 2016 |
| Station | NSE | R2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DDS | ROPE | SCE | DDS | ROPE | SCE | DDS | ROPE | SCE | DDS | ROPE | SCE | |
| 1002640 | 0.90 | 0.90 | 0.90 | 0.5 | 2.1 | 0.8 | 0.92 | 0.90 | 0.92 | 9.1 | 9.4 | 9.1 |
| 1003630 | 0.91 | 0.89 | 0.90 | −0.2 | −15.4 | −0.3 | 0.91 | 0.89 | 0.90 | 35.1 | 44.0 | 36.7 |
| 1011690 | 0.78 | 0.82 | 0.82 | 0.7 | 0.8 | 0.8 | 0.79 | 0.87 | 0.86 | 7.6 | 8.3 | 8.0 |
| 1303680 | 0.82 | 0.77 | 0.81 | 5.7 | 6.2 | 5.7 | 0.85 | 0.83 | 0.85 | 8.8 | 9.6 | 9.1 |
| 3009650 | 0.85 | 0.80 | 0.82 | 1.3 | 1.9 | 1.2 | 0.87 | 0.83 | 0.86 | 2.5 | 3.1 | 2.7 |
| Algorithm | NSE | Station | ||||
|---|---|---|---|---|---|---|
| 1002640 | 1003630 | 1011690 | 1303680 | 3009650 | ||
| DDS | Median | 0.78 | 0.82 | 0.62 | 0.46 | 0.68 |
| 95%ile–5%ile | 0.08 | 0.07 | 0.10 | 0.51 | 0.25 | |
| ROPE | Median | 0.80 | 0.82 | 0.51 | 0.50 | 0.70 |
| 95%ile–5%ile | 0.09 | 0.07 | 0.10 | 0.42 | 0.29 | |
| SCE | Median | 0.79 | 0.81 | 0.53 | 0.66 | 0.77 |
| 95%ile–5%ile | 0.01 | 0.01 | 0.02 | 0.01 | 0.19 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.W.; Chegal, S.D.; Lee, S.O. A Review of Tank Model and Its Applicability to Various Korean Catchment Conditions. Water 2020, 12, 3588. https://doi.org/10.3390/w12123588
Lee JW, Chegal SD, Lee SO. A Review of Tank Model and Its Applicability to Various Korean Catchment Conditions. Water. 2020; 12(12):3588. https://doi.org/10.3390/w12123588
Chicago/Turabian StyleLee, Jong Wook, Sun Dong Chegal, and Seung Oh Lee. 2020. "A Review of Tank Model and Its Applicability to Various Korean Catchment Conditions" Water 12, no. 12: 3588. https://doi.org/10.3390/w12123588
APA StyleLee, J. W., Chegal, S. D., & Lee, S. O. (2020). A Review of Tank Model and Its Applicability to Various Korean Catchment Conditions. Water, 12(12), 3588. https://doi.org/10.3390/w12123588





