Evaluation of the Impact of Climate Change on Runoff Generation in an Andean Glacier Watershed
Abstract
1. Introduction
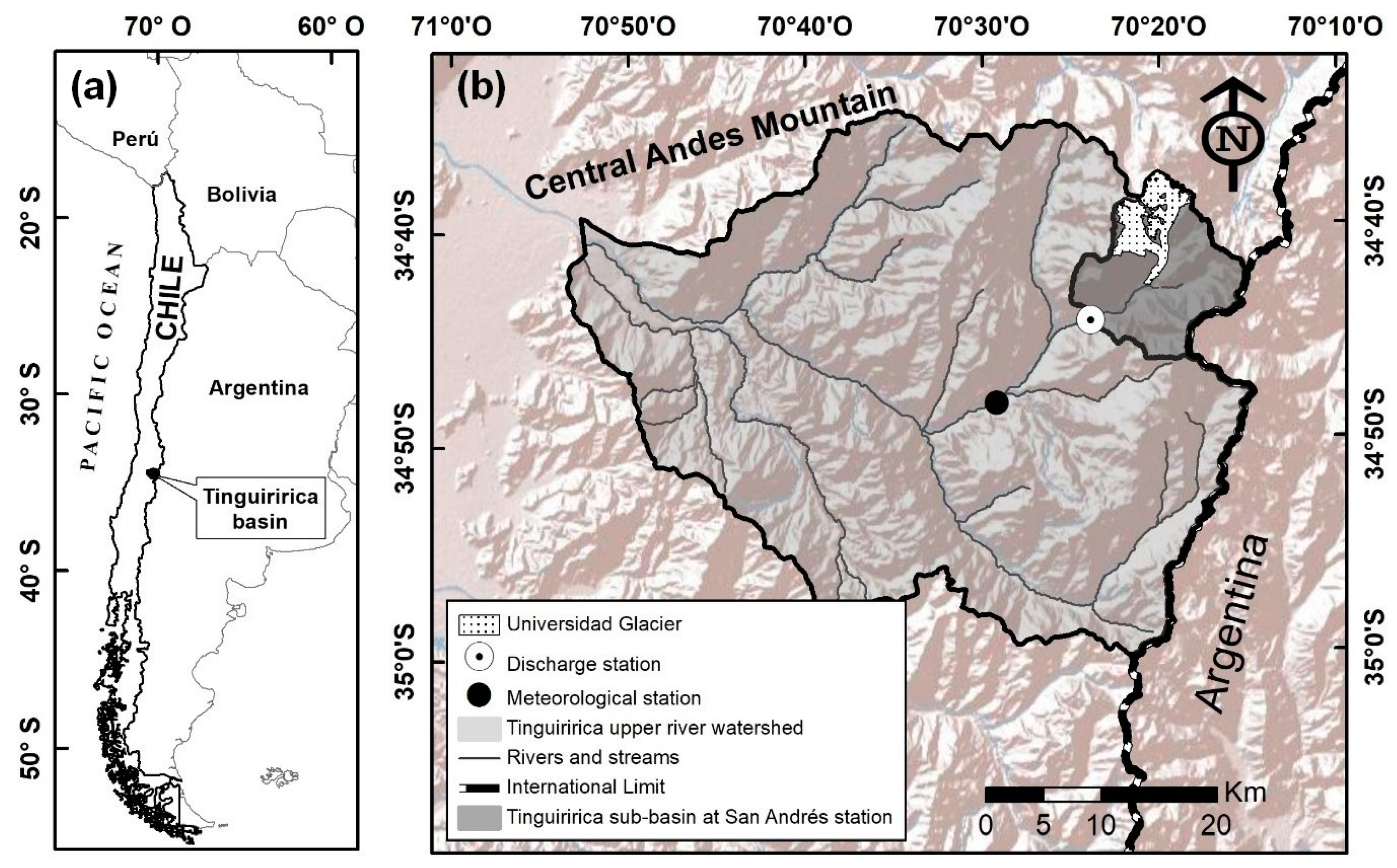
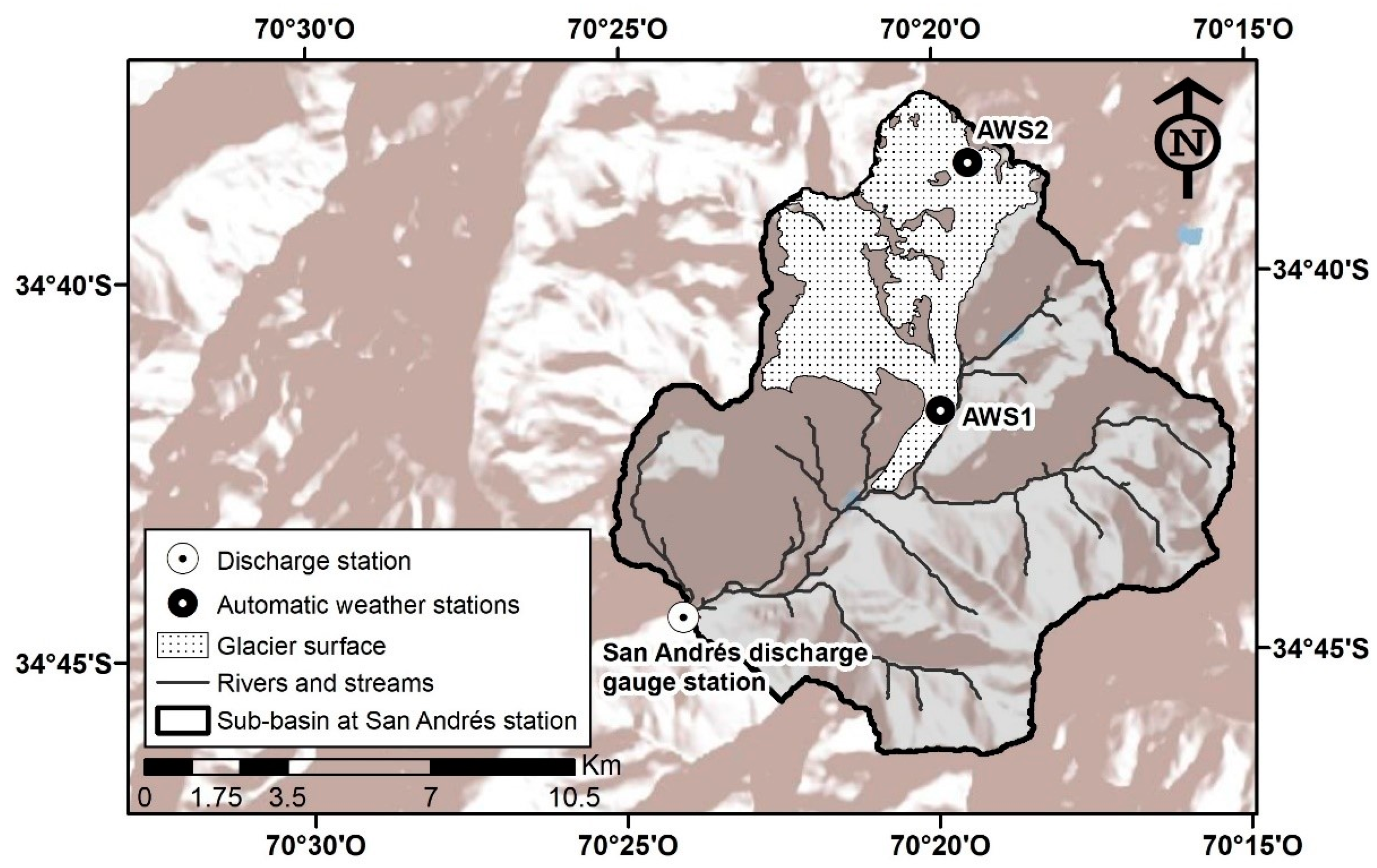
2. Study Area
3. Methods
3.1. Hydrological Model
3.1.1. Model Structure
3.1.2. Model Parameters
3.2. Model Effiency Indicators
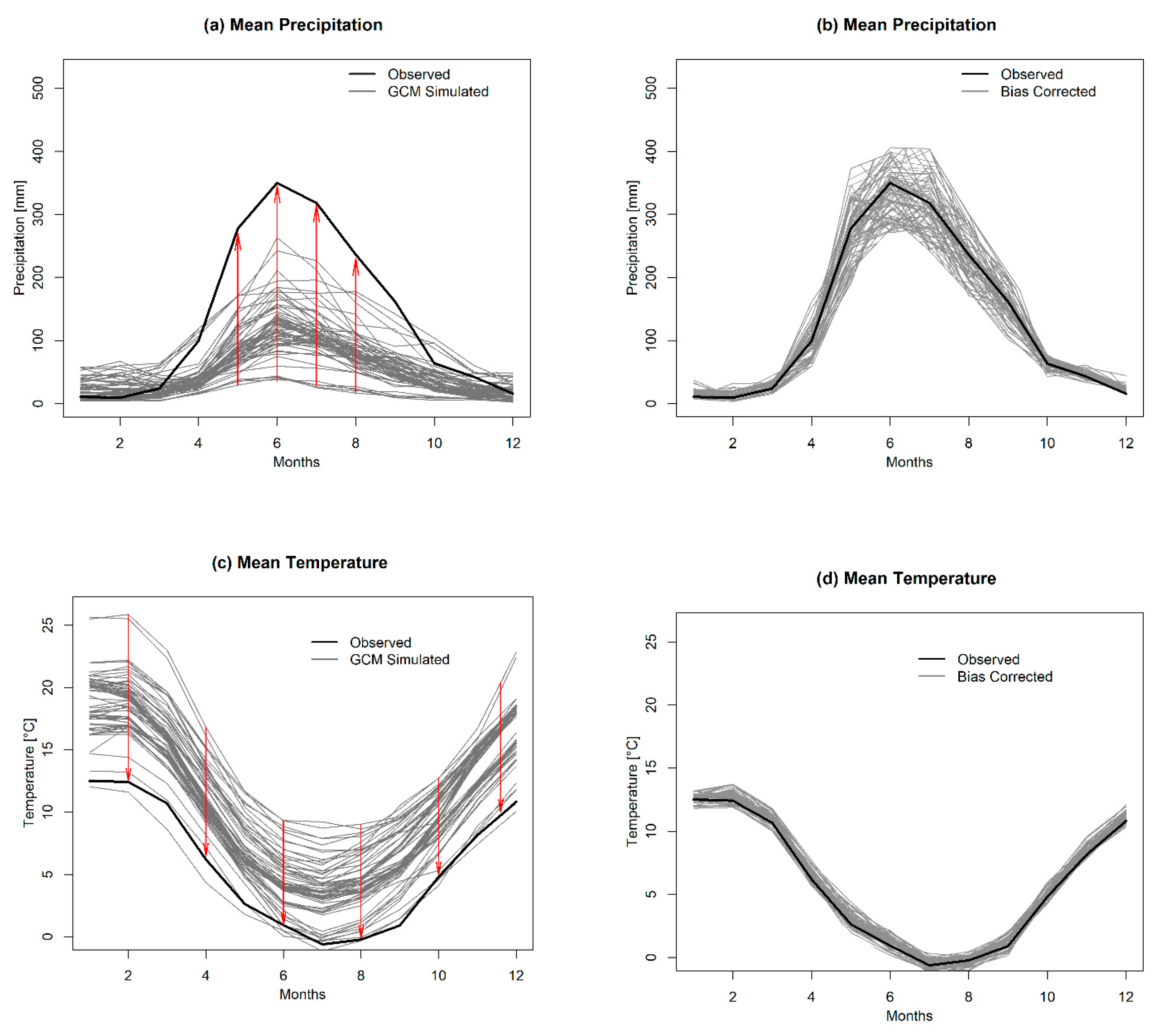
3.3. Climate Change Scenarios
Downscaling
3.4. Projections
4. Results
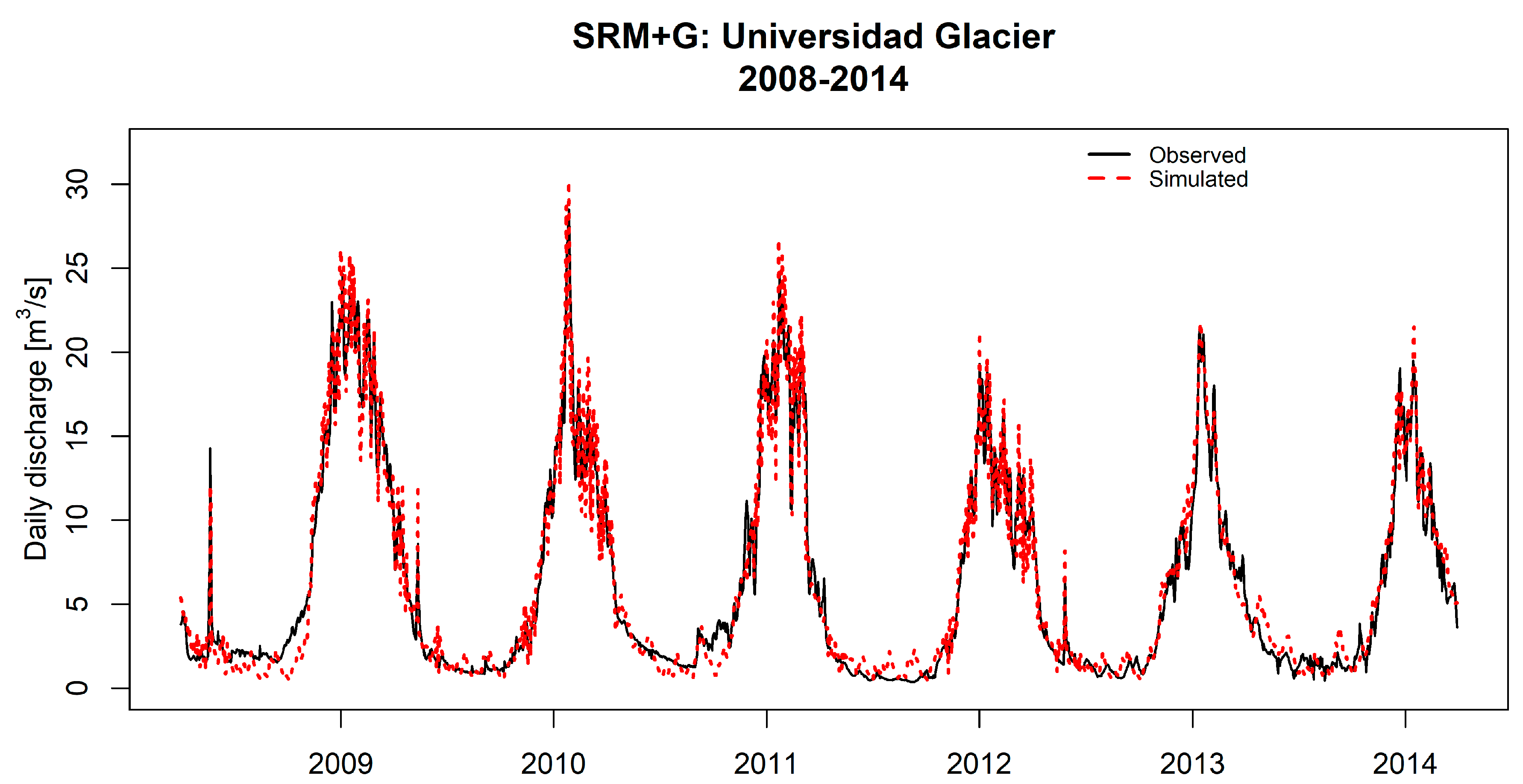
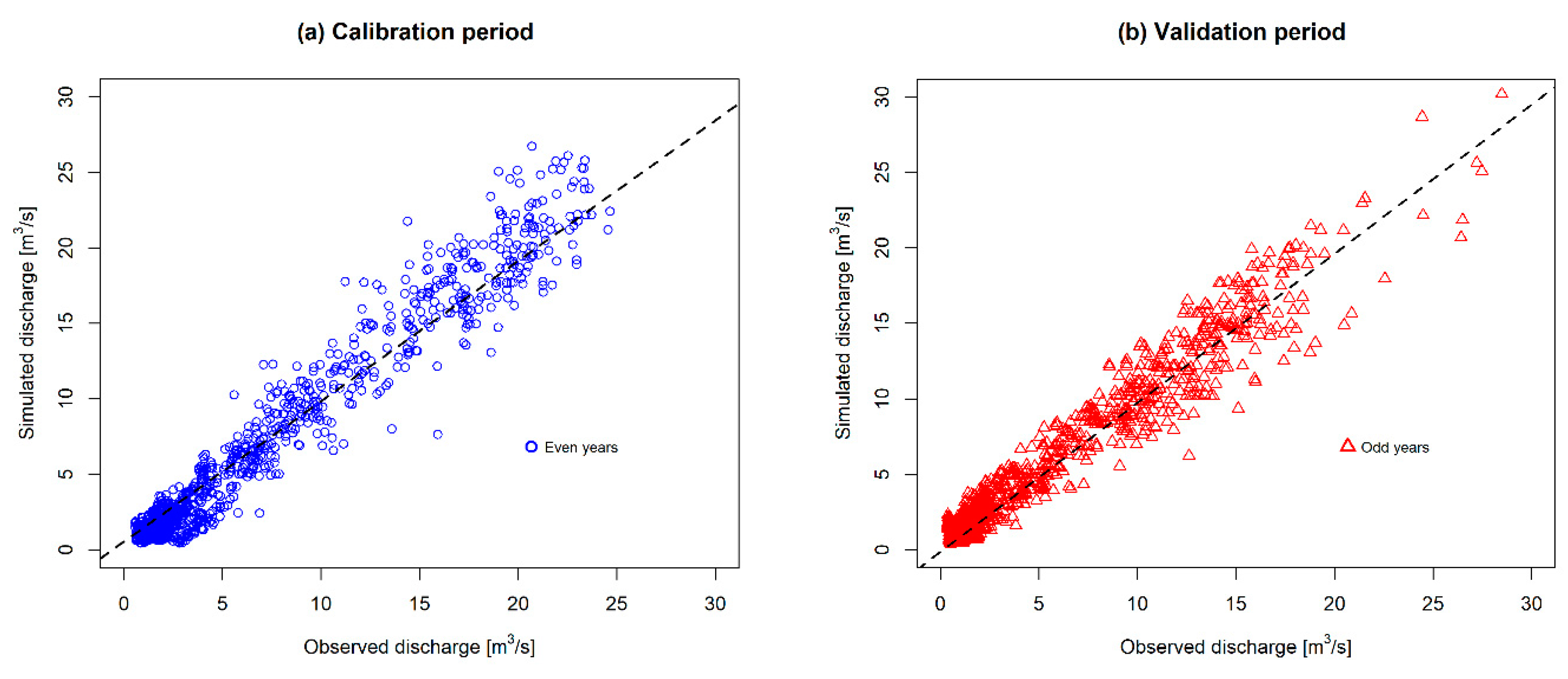
4.1. Hydrological Model
4.2. Climate Change
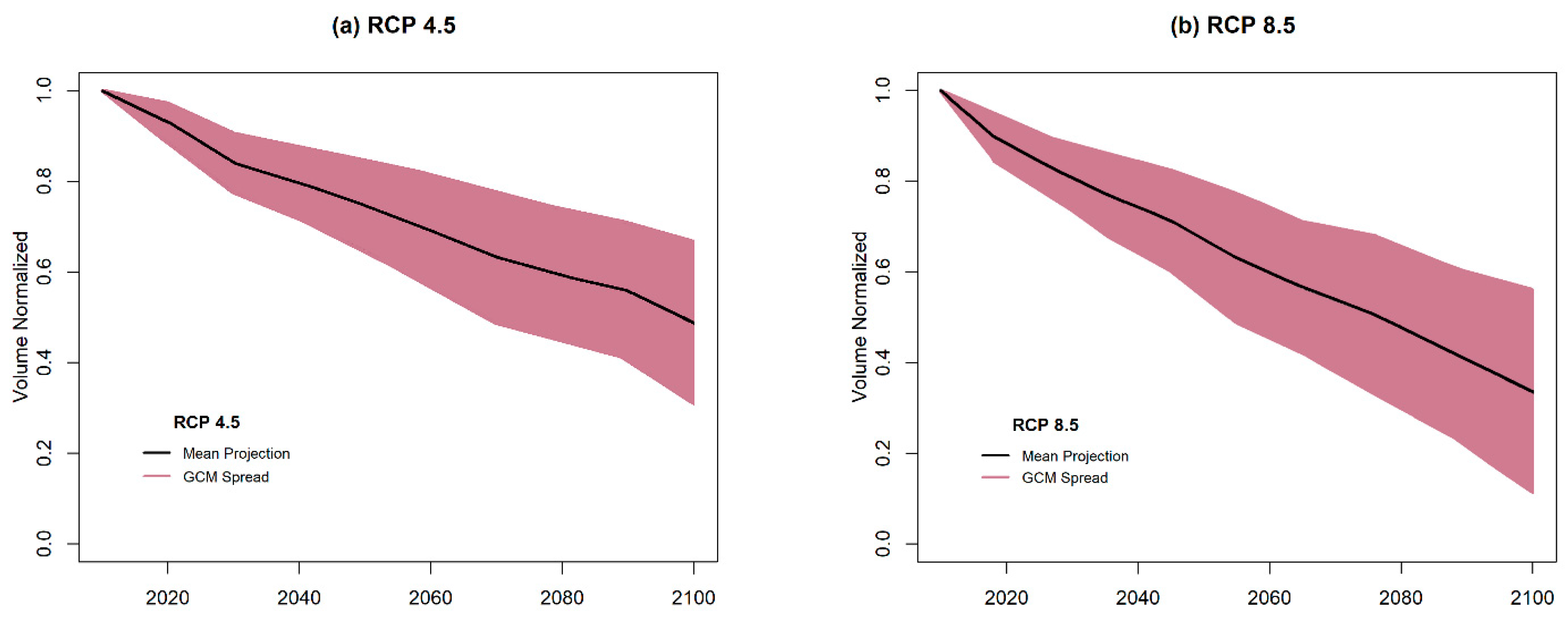
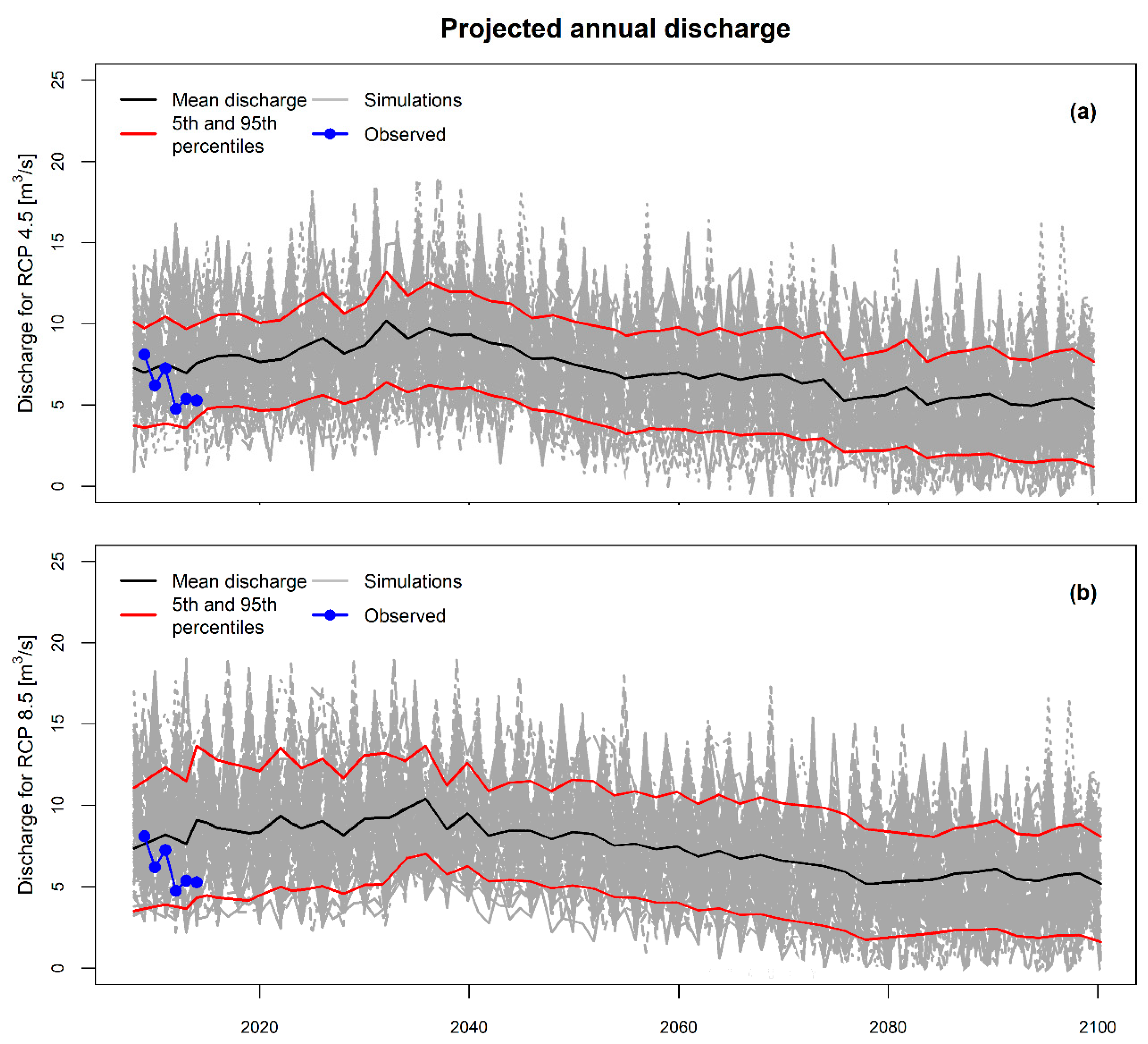
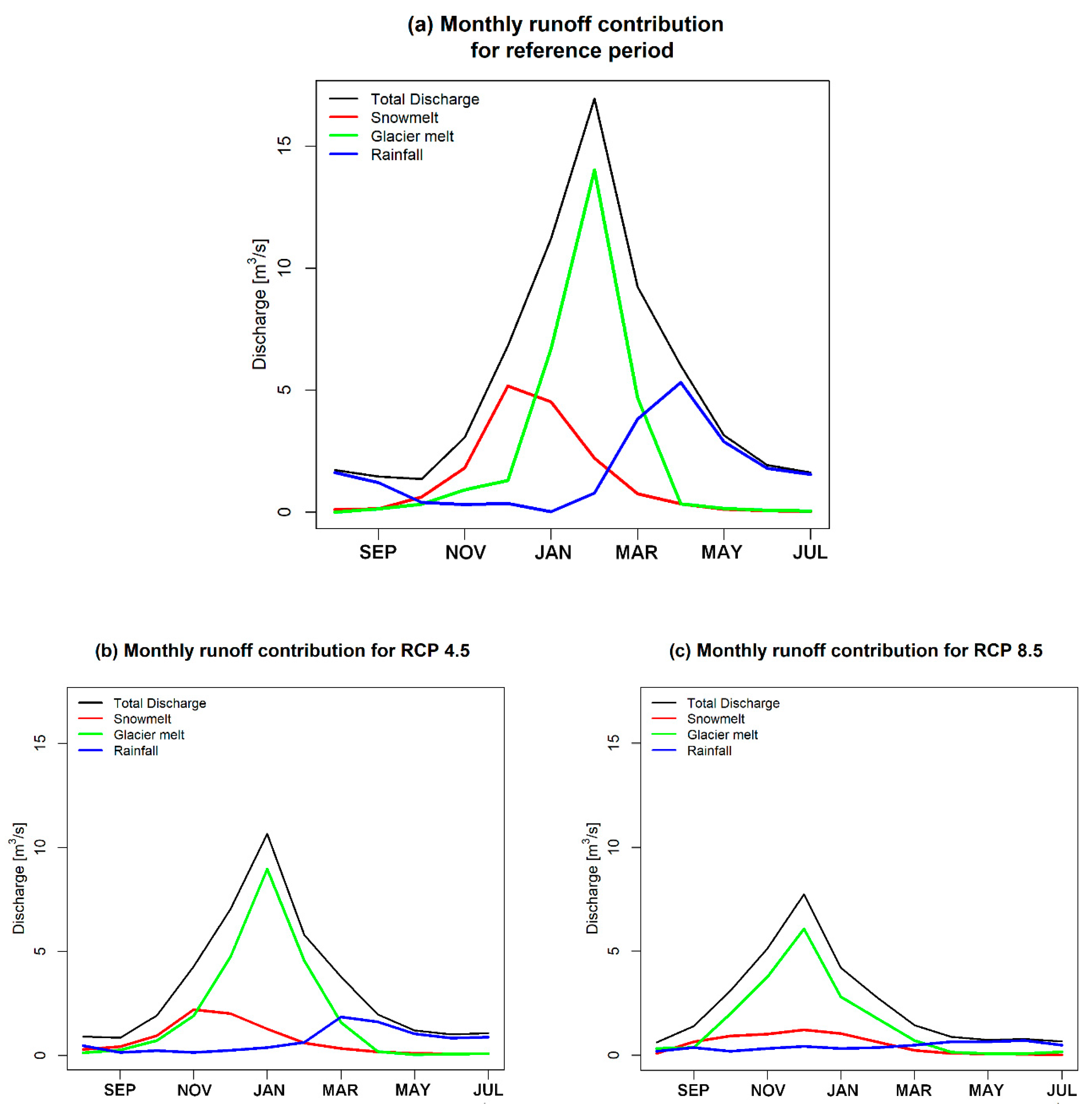
4.3. Projections
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Migliavacca, F.; Confortola, G.; Soncini, A.; Senese, A.; Diolaiuti, G.A.; Smiraglia, C.; Barcaza, G.; Bocchiola, D. Hydrology and potential climate changes in the Rio Maipo (Chile). Geogr. Fis. E Din. Quat. 2015, 32, 155–168. [Google Scholar]
- Huh, K.; Baraër, M.; Mark, B.; Ahn, Y. Evaluating Glacier Volume Changes since the Little Ice Age Maximum and Consequences for Stream Flow by Integrating Models of Glacier Flow and Hydrology in the Cordillera Blanca, Peruvian Andes. Water 2018, 10, 1732. [Google Scholar] [CrossRef]
- Huss, M.; Hock, R. Global-scale hydrological response to future glacier mass loss. Nat. Clim. Chang. 2018, 8, 135–140. [Google Scholar] [CrossRef]
- Ayala, A.; Pellicciotti, F.; MacDonell, S.; McPhee, J.; Vivero, S.; Campos, C.; Egli, P. Modelling the hydrological response of debris-free and debris-covered glaciers to present climatic conditions in the semiarid Andes of central Chile. Hydrol. Process. 2016, 30, 4036–4058. [Google Scholar] [CrossRef]
- Bown, F.; Rivera, A.; Acuña, C. Recent glacier variations at the Aconcagua basin, central Chilean Andes. Ann. Glaciol. 2008, 48, 43–48. [Google Scholar] [CrossRef]
- Gascoin, S.; Kinnard, C.; Ponce, R.; Lhermitte, S.; MacDonell, S.; Rabatel, A. Glacier contribution to streamflow in two headwaters of the Huasco River, Dry Andes of Chile. Cryosphere 2011, 5, 1099–1113. [Google Scholar] [CrossRef]
- Aitken, D.; Rivera, D.; Godoy-Faúndez, A.; Holzapfel, E. Water scarcity and the impact of the mining and agricultural sectors in Chile. Sustainability 2016, 8, 128. [Google Scholar] [CrossRef]
- Valdés-Pineda, R.; Pizarro, R.; García-Chevesich, P.; Valdés, J.B.; Olivares, C.; Vera, M.; Balocchi, F.; Pérez, F.; Vallejos, C.; Fuentes, R.; et al. Water governance in Chile: Availability, management and climate change. J. Hydrol. 2014, 519, 2538–2567. [Google Scholar] [CrossRef]
- Rössler, O.; Fischer, A.M.; Huebener, H.; Maraun, D.; Benestad, R.E.; Christodoulides, P.; Soares, P.M.M.; Cardoso, R.M.; Pagé, C.; Kanamaru, H.; et al. Challenges to link climate change data provision and user needs: Perspective from the COST-action VALUE. Int. J. Climatol. 2019, 39, 3704–3716. [Google Scholar] [CrossRef]
- IPCC. Fifth Assessment Report Synthesis Report: Climate Change; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2014; ISBN 978-92-9169-343-6. [Google Scholar]
- Araya-Osses, D.; Casanueva, A.; Román-Figueroa, C.; Uribe, J.M.; Paneque, M. Climate change projections of temperature and precipitation in Chile based on statistical downscaling. Clim. Dyn. 2020, 54, 4309–4330. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Ragettli, S.; Carenzo, M.; McPhee, J. Changes of glaciers in the Andes of Chile and priorities for future work. Sci. Total Environ. 2014, 493, 1197–1210. [Google Scholar] [CrossRef] [PubMed]
- Hayat, H.; Akbar, T.A.; Tahir, A.A.; Hassan, Q.K.; Dewan, A.; Irshad, M. Simulating Current and Future River-Flows in the Karakoram and Himalayan Regions of Pakistan Using Snowmelt-Runoff Model and RCP Scenarios. Water 2019, 11, 761. [Google Scholar] [CrossRef]
- Garreaud, R.D.; Boisier, J.P.; Rondanelli, R.; Montecinos, A.; Sepúlveda, H.H.; Veloso-Aguila, D. The Central Chile Mega Drought (2010–2018): A climate dynamics perspective. Int. J. Climatol. 2020, 40, 421–439. [Google Scholar] [CrossRef]
- Falvey, M.; Garreaud, R.D. Regional cooling in a warming world: Recent temperature trends in the southeast Pacific and along the west coast of subtropical South America (1979–2006). J. Geophys. Res. 2009, 114, D04102. [Google Scholar] [CrossRef]
- Carrasco, J.F.; Casassa, G.; Quintana, J. Changes of the 0 °C isotherm and the equilibrium line altitude in central Chile during the last quarter of the 20th century/Changements de l’isotherme 0 °C et de la ligne d’équilibre des neiges dans le Chili central durant le dernier quart du 20ème siècle. Hydrol. Sci. J. 2005, 50. [Google Scholar] [CrossRef]
- Kinnard, C.; Ginot, P.; Surazakov, A.; MacDonell, S.; Nicholson, L.; Patris, N.; Rabatel, A.; Rivera, A.; Squeo, F.A. Mass Balance and Climate History of a High-Altitude Glacier, Desert Andes of Chile. Front. Earth Sci. 2020, 8. [Google Scholar] [CrossRef]
- Le Quesne, C.; Acuña, C.; Boninsegna, J.A.; Rivera, A.; Barichivich, J. Long-term glacier variations in the Central Andes of Argentina and Chile, inferred from historical records and tree-ring reconstructed precipitation. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 334–344. [Google Scholar] [CrossRef]
- Masiokas, M.H.; Christie, D.A.; Le Quesne, C.; Pitte, P.; Ruiz, L.; Villalba, R.; Luckman, B.H.; Berthier, E.; Nussbaumer, S.U.; González-Reyes, Á.; et al. Reconstructing the annual mass balance of the Echaurren Norte glacier (Central Andes, 33.5° S) using local and regional hydroclimatic data. Cryosphere 2016, 10, 927–940. [Google Scholar] [CrossRef]
- Dussaillant, I.; Berthier, E.; Brun, F.; Masiokas, M.; Hugonnet, R.; Favier, V.; Rabatel, A.; Pitte, P.; Ruiz, L. Two decades of glacier mass loss along the Andes. Nat. Geosci. 2019, 12, 802–808. [Google Scholar] [CrossRef]
- Ragettli, S.; Immerzeel, W.W.; Pellicciotti, F. Contrasting climate change impact on river flows from high-altitude catchments in the Himalayan and Andes Mountains. Proc. Natl. Acad. Sci. USA 2016, 113, 9222–9227. [Google Scholar] [CrossRef]
- Gleick, P.H.; Palaniappan, M. Peak water limits to freshwater withdrawal and use. Proc. Natl. Acad. Sci. USA 2010, 107, 11155–11162. [Google Scholar] [CrossRef] [PubMed]
- Casassa, G.; López, P.; Pouyaud, B.; Escobar, F. Detection of changes in glacial run-off in alpine basins: Examples from North America, the Alps, central Asia and the Andes. Hydrol. Process. 2009, 23, 31–41. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Clark, M.P. HESS Opinions: The complementary merits of competing modelling philosophies in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3953–3973. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F.P. Continuous streamflow prediction in ungauged basins: The effects of equifinality and parameter set selection on uncertainty in regionalization approaches. Water Resour. Res. 2014, 50, 6135–6153. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Barnhart, B.L. SWAT hydrologic model parameter uncertainty and its implications for hydroclimatic projections in snowmelt-dependent watersheds. J. Hydrol. 2014, 519, 2081–2090. [Google Scholar] [CrossRef]
- Nemri, S.; Kinnard, C. Comparing calibration strategies of a conceptual snow hydrology model and their impact on model performance and parameter identifiability. J. Hydrol. 2020, 582, 124474. [Google Scholar] [CrossRef]
- Martinec, J.; Rango, A.; Roberts, R. Snowmelt runoff model (SRM) user’s manual. Agric. Exp. Stn. Spec. Rep. 2008, 100, 180. [Google Scholar] [CrossRef]
- Ismail, M.F.; Bogacki, W. Scenario approach for the seasonal forecast of Kharif flows from the Upper Indus Basin. Hydrol. Earth Syst. Sci. 2018, 22, 1391–1409. [Google Scholar] [CrossRef]
- Kinnard, C.; MacDonell, S.; Petlicki, M.; Mendoza Martinez, C.; Abermann, J.; Urrutia, R. Mass Balance and Meteorological Conditions at Universidad Glacier, Central Chile. In Andean Hydrology; CRC Press: Boca Raton, FL, USA, 2018; pp. 102–123. [Google Scholar]
- Bravo, C.; Loriaux, T.; Rivera, A.; Brock, B.W. Assessing glacier melt contribution to streamflow at Universidad Glacier, central Andes of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 3249–3266. [Google Scholar] [CrossRef]
- Podgórski, J.; Kinnard, C.; Pętlicki, M.; Urrutia, R. Performance Assessment of TanDEM-X DEM for Mountain Glacier Elevation Change Detection. Remote Sens. 2019, 11, 187. [Google Scholar] [CrossRef]
- EULA. Establecimiento de Red de Estaciones Nivo-Glaciales de Cordillera de la Región de O´Higgins y Desarrollo de un Modelo para la Gestión Integrada de los Recursos Hídricos de la Cuenca del Río Rapel; Universidad de Concepción: VI Región, Chile, 2017. [Google Scholar]
- Escobar, C. Aplicacion del Modelo “SRM 3-11” en Cuencas de los Andes Centrales. Segudas Jornadas de Hidráulica Francisco Javier Domínguez; Department of Hydrology, Ministry of Public Works: Santiago, Chile, 1992; pp. 283–295. [Google Scholar]
- Arsenault, R.; Brissette, F.; Martel, J.-L. The hazards of split-sample validation in hydrological model calibration. J. Hydrol. 2018, 566, 346–362. [Google Scholar] [CrossRef]
- Rango, A.; Martinec, J. Revisiting the Degree-Day Method for Snowmelt Computations. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 657–669. [Google Scholar] [CrossRef]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. Earth Environ. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Xie, S.; Du, J.; Zhou, X.; Zhang, X.; Feng, X.; Zheng, W.; Li, Z.; Xu, C.-Y. A progressive segmented optimization algorithm for calibrating time-variant parameters of the snowmelt runoff model (SRM). J. Hydrol. 2018, 566, 470–483. [Google Scholar] [CrossRef]
- Adnan, M.; Nabi, G.; Kang, S.; Zhang, G.; Adnan, R.M.; Anjum, M.N.; Iqbal, M.; Ali, A.F. Snowmelt Runoff Modelling under Projected Climate Change Patterns in the Gilgit River Basin of Northern Pakistan. Pol. J. Environ. Stud. 2017, 26, 525–542. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Ismail, M.F.; Bogacki, W.; Muhammad, N.; Bagacki, W. Degree Day Factor Models for Forecasting the Snowmelt Runoff for Naran Watershed. Sci. Int. 2015, 27, 1961–1969. [Google Scholar]
- Schneider, C.; Kilian, R.; Glaser, M. Energy balance in the ablation zone during the summer season at the Gran Campo Nevado Ice Cap in the Southern Andes. Glob. Planet. Chang. 2007, 59, 175–188. [Google Scholar] [CrossRef]
- Brock, B.W.; Burger, F.; Rivera, A.; Montecinos, A. A fifty year record of winter glacier melt events in southern Chile, 38°–42° S. Environ. Res. Lett. 2012, 7, 045403. [Google Scholar] [CrossRef]
- Fernández, A.; Mark, B.G. Modeling modern glacier response to climate changes along the Andes Cordillera: A multiscale review. J. Adv. Model. Earth Syst. 2016, 8, 467–495. [Google Scholar] [CrossRef]
- Pino Vargas, E.; Cornejo Navarretty, L.; Román Arce, C. Uso de Algoritmos Genéticos para la Calibración de un Modelo Hidrológico Precipitación Escorrentia en la Cuenca del Caplina. Cienc. Desarro. 2019, 18, 45–50. [Google Scholar] [CrossRef]
- Ragettli, S.; Cortés, G.; McPhee, J.; Pellicciotti, F. An evaluation of approaches for modelling hydrological processes in high-elevation, glacierized Andean watersheds. Hydrol. Process. 2014, 28, 5674–5695. [Google Scholar] [CrossRef]
- Dirección General de Aguas. Inventario Nacional de Glaciares; Dirección General de Aguas: Santiago, Chile, 2014. [Google Scholar]
- Arsenault, K.R.; Houser, P.R.; De Lannoy, G.J.M. Evaluation of the MODIS snow cover fraction product. Hydrol. Process. 2014, 28, 980–998. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. MODIS/Terra Snow Cover Daily L3 Global 500 m SIN Grid, Version 6. [NDSI]; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2016. [Google Scholar]
- Salomonson, V.V.; Appel, I. Development of the Aqua MODIS NDSI fractional snow cover algorithm and validation results. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1747–1756. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; De Roo, A. Hydrological evaluation of satellite-based rainfall estimates over the Volta and Baro-Akobo Basin. J. Hydrol. 2013, 499, 324–338. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Wise, M.; Calvin, K.; Thomson, A.; Clarke, L.; Bond-Lamberty, B.; Sands, R.; Smith, S.J.; Janetos, A.; Edmonds, J. Implications of Limiting CO2 Concentrations for Land Use and Energy. Science 2009, 324, 1183–1186. [Google Scholar] [CrossRef]
- Smith, S.J.; Wigley, T.M.L. Multi-Gas Forcing Stabilization with Minicam. Energy J. 2006, SI2006. [Google Scholar] [CrossRef]
- Riahi, K.; Rao, S.; Krey, V.; Cho, C.; Chirkov, V.; Fischer, G.; Kindermann, G.; Nakicenovic, N.; Rafaj, P. RCP 8.5—A scenario of comparatively high greenhouse gas emissions. Clim. Chang. 2011, 109, 33–57. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Regional Climate Models for Hydrological Impact Studies at the Catchment Scale: A Review of Recent Modeling Strategies. Geogr. Compass 2010, 4, 834–860. [Google Scholar] [CrossRef]
- Li, H.; Sheffield, J.; Wood, E.F. Bias correction of monthly precipitation and temperature fields from Intergovernmental Panel on Climate Change AR4 models using equidistant quantile matching. J. Geophys. Res. 2010, 115, D10101. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using quantile mapping—A comparison of methods. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 6185–6201. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Chen, J.; Ohmura, A. Estimation of Alpine glacier water resources and their change since the 1870s. Hydrol. Mt. Reg. 1990, 193, 127–135. [Google Scholar]
- Bahr, D.B.; Meier, M.F.; Peckham, S.D. The physical basis of glacier volume-area scaling. J. Geophys. Res. Solid Earth 1997, 102, 20355–20362. [Google Scholar] [CrossRef]
- Científicos, C.; De Aguas, D.G. Dirección General de Aguas. In Estimación de Volúmenes de Hielo Mediante Radio Eco Sondaje en Chile Central; General Water Authority: Santiago, Chile, 2012. [Google Scholar]
- Radić, V.; Hock, R. Modeling future glacier mass balance and volume changes using ERA-40 reanalysis and climate models: A sensitivity study at Storglaciären, Sweden. J. Geophys. Res. Earth Surf. 2006, 111. [Google Scholar] [CrossRef]
- Khadka, D.; Babel, M.S.; Shrestha, S.; Tripathi, N.K. Climate change impact on glacier and snow melt and runoff in Tamakoshi basin in the Hindu Kush Himalayan (HKH) region. J. Hydrol. 2014, 511, 49–60. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Parajuli, A.; Chand, M.B.; Kayastha, R.B.; Shea, J.M.; Mool, P.K. Modified temperature index model for estimating the melt water discharge from debris-covered Lirung Glacier, Nepal. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 409–414. [Google Scholar]
- Chand, M.B.; Kayastha, R.B.; Parajuli, A.; Mool, P.K. Seasonal variation of ice melting on varying layers of debris of Lirung Glacier, Langtang Valley, Nepal. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 21–26. [Google Scholar] [CrossRef]
- Braithwaite, R.J. Encyclopedia of snow, ice and glaciers. In Encyclopedia of Snow, Ice and Glaciers; Springer: Dordrecht, The Netherlands, 2011; pp. 186–190. [Google Scholar]
- Klein Tank, A.; Zwiers, F. Guidelines on Analysis of Extremes in a Changing Climate in Support of Informed Decisions for Adaptation; Climate Data and Monitoring, WCDMP-No. 72, WMO-TD No. 1500; World Meteorological Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Ragettli, S.; Pellicciotti, F.; Immerzeel, W. Contrasting response of glacierized catchments in the Central Himalaya and the Central Andes to climate change. In Proceedings of the EGU General Assembly, Vienna, Austria, 12–17 April 2015. [Google Scholar]
- Omani, N.; Srinivasan, R.; Karthikeyan, R.; Venkata Reddy, K.; Smith, P.K. Impacts of climate change on the glacier melt runoff from five river basins. Trans. ASABE 2016, 59, 829–848. [Google Scholar]
- Radić, V.; Hock, R. Regionally differentiated contribution of mountain glaciers and ice caps to future sea-level rise. Nat. Geosci. 2011, 4, 91–94. [Google Scholar] [CrossRef]
- Radić, V.; Bliss, A.; Beedlow, A.C.; Hock, R.; Miles, E.; Cogley, J.G. Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models. Clim. Dyn. 2014, 42, 37–58. [Google Scholar] [CrossRef]
- Aldunce, P.; Araya, D.; Sapiain, R.; Ramos, I.; Lillo, G.; Urquiza, A.; Garreaud, R. Local Perception of Drought Impacts in a Changing Climate: The Mega-Drought in Central Chile. Sustainability 2017, 9, 2053. [Google Scholar] [CrossRef]
- Penalba, O.C.; Rivera, J.A. Regional aspects of future precipitation and meteorological drought characteristics over Southern South America projected by a CMIP5 multi-model ensemble. Int. J. Climatol. 2016, 36, 974–986. [Google Scholar] [CrossRef]
- Carey, M.; Huggel, C.; Bury, J.; Portocarrero, C.; Haeberli, W. An integrated socio-environmental framework for glacier hazard management and climate change adaptation: Lessons from Lake 513, Cordillera Blanca, Peru. Clim. Chang. 2012, 112, 733–767. [Google Scholar] [CrossRef]
| Parameters | Symbol | Value | Units | Remarks |
|---|---|---|---|---|
| Runoff Coefficient-Rain | CR | 0.6 | - | Constant |
| Runoff Coefficient-Snow | CS | 0.8 | - | Constant |
| Runoff Coefficient-Glacier | CG | 0.7 | - | Constant |
| Degree-day Factor-Snow | ddf | 0.10–0.55 | cm °C−1 d−1 | November–March |
| Degree-day Factor-Glacier | aG | 0.80 | cm °C−1 d−1 | Constant |
| Recession Coefficient | x | 1.0248 | - | November–March |
| 0.9251 | - | April–October | ||
| y | 0.0892 | - | November–March | |
| 0.0180 | - | April–October | ||
| Temperature Lapse Rate | α | −6.8 | °C km−1 | Constant |
| GCM | Climate Modeling Center and Location | Ensemble | GCM | Climate Modeling Center and Location | Ensemble |
|---|---|---|---|---|---|
| ACCESS1 | Centre for Australian Weather and Climate Research, Australia | r1i1p1 | GFDL | NOAA Geophysical Fluid Dynamics Laboratory, USA | r1i1p1, r2i1p1, r3i1p1 |
| BNU-ESM | College of Global Change and Earth System Science, Beijing Normal University, China | r1i1p1 | GISS-E2 | NSA Goddard Institute for Space Studies, USA | r1i1p1, r2i1p1, r3i1p1, r4i1p1, r5i1p1 |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis, Canada | r1i1p1, r2i1p1, r3i1p1, r4i1p1, r5i1p1 | HadGEM2-AO | National Institute of Meteorological Research, Korea Meteorological Administration, Korea | r1i1p1, r2i1p1, r3i1p1 |
| CCSM4 | National Centre for Atmospheric Research, USA | r1i1p1, r2i1p1, r3i1p1, r4i1p1, r5i1p1, r6i1p1, r7i1p1, r8i1p1 | HadGEM2-CC | Met Office Hadley Centre, UK | r1i1p1, r2i1p1, r3i1p1, r4i1p1, r5i1p1 |
| CESM1 | Community Earth System Model Contributors | r1i1p1, r2i1p1, r3i1p1 | IPSL-CM5A | Institut Pierre Simon Laplace, France | r1i1p1, r2i1p1, r3i1p1, r4i1p1 |
| CMCC-CM | Centro Euro-Mediterrano per I Cambianmenti Climatici, Italy | r1i1p1, r2i1p1, r3i1p1, r4i1p1, r5i1p1 | MIROC-ESM | Japan Agency for Marine Earth Science and Technology, Atmosphere and Ocean Research Institute (The University of Tokyo), and National Institute for Environmental Studies, Japan | r1i1p1 |
| CSIRO-MK3 | Commonwealth Scientific and Industrial Research Organization in collaboration with Queensland Climate Change Centre of Excellence, Australia | r1i1p1, r2i1p1, r3i1p1, r4i1p1, r5i1p1, r6i1p1, r7i1p1, r8i1p1, r9i1p1, r10i1p1 | MPI-ESM | Max Planck Institute for Meteorology, Germany | r1i1p1, r2i1p1, r3i1p1 |
| EC-EARTH | EC-EARTH consortium, Europe | r2i1p1, r8i1p1, r9i1p1, r12i1p1 | MRI-CGCM3 | Meteorological Research Institute, Japan | r1i1p1, r2i1p1, r3i1p1, r4i1p1, r5i1p1 |
| FGOALS | LASG, Institute of Atmospheric Physics, Chinese Academy of Sciences and CESS, Tsinghua University, China | r1i1p1 | NorESM1 | Norwegian Climate Centre, Norway | r1i1p1, r2i1p1, r3i1p1 |
| Season | T_Factor | PP_Factor | CI |
|---|---|---|---|
| Summer | 38.375 | 5.586 | −47.032 |
| Autumn | −22.68 | −4.667 | 48.575 |
| Winter | −5.404 | 1.263 | 43.616 |
| Spring | 34.734 | 5.037 | −3.468 |
| Indicator | Values | |
|---|---|---|
| Calibration | Validation | |
| r2 | 0.93 | 0.90 |
| NSE | 0.92 | 0.88 |
| RMSE | 1.32 | 1.15 |
| KGE’ | 0.90 | 0.89 |
| Precipitation [mm] | ||||||
| Emission Scenario | 2050 | 2100 | ||||
| 5% | Mean | 95% | 5% | Mean | 95% | |
| RCP 4.5 | −7% | −16% | −25% | −12% | −24% | −35% |
| RCP 8.5 | −10% | −20% | −30% | −21% | −40% | −58% |
| Temperature [°C] | ||||||
| Emission Scenario | 2050 | 2100 | ||||
| 5% | Mean | 95% | 5% | Mean | 95% | |
| RCP 4.5 | 1.5 | 1.8 | 2.1 | 2.3 | 2.9 | 3.4 |
| RCP 8.5 | 2.3 | 2.9 | 3.4 | 3.2 | 3.9 | 4.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escanilla-Minchel, R.; Alcayaga, H.; Soto-Alvarez, M.; Kinnard, C.; Urrutia, R. Evaluation of the Impact of Climate Change on Runoff Generation in an Andean Glacier Watershed. Water 2020, 12, 3547. https://doi.org/10.3390/w12123547
Escanilla-Minchel R, Alcayaga H, Soto-Alvarez M, Kinnard C, Urrutia R. Evaluation of the Impact of Climate Change on Runoff Generation in an Andean Glacier Watershed. Water. 2020; 12(12):3547. https://doi.org/10.3390/w12123547
Chicago/Turabian StyleEscanilla-Minchel, Rossana, Hernán Alcayaga, Marco Soto-Alvarez, Christophe Kinnard, and Roberto Urrutia. 2020. "Evaluation of the Impact of Climate Change on Runoff Generation in an Andean Glacier Watershed" Water 12, no. 12: 3547. https://doi.org/10.3390/w12123547
APA StyleEscanilla-Minchel, R., Alcayaga, H., Soto-Alvarez, M., Kinnard, C., & Urrutia, R. (2020). Evaluation of the Impact of Climate Change on Runoff Generation in an Andean Glacier Watershed. Water, 12(12), 3547. https://doi.org/10.3390/w12123547






