1. Introduction
High-intensity rainfall, which frequently occurs in the U.S. Upper Midwest during the warm season (March–September), often causes flooding, with extensive socioeconomic impacts. In the U.S. alone, flooding caused nearly
$11 billion in damages and 126 fatalities in 2016, and surpassed
$60 billion in damages with again 126 fatalities during the tropically active 2017 [
1,
2]. Providing more accurate and timely streamflow forecasts to decision makers is important for mitigating some of the impacts caused by flooding. Operational streamflow forecasts typically are made using quantitative precipitation estimates (i.e., QPE) [
3,
4,
5], which are not available until the precipitation occurs, providing little lead time for emergency management. However, as quantitative precipitation forecasts (QPFs) become more skillful, they are increasingly being used in streamflow forecasting to add valuable lead time to flood guidance, especially for flash flooding [
6,
7,
8,
9].
Enhancements in technology and computing resources have improved the ability to predict convective precipitation; however, large uncertainties in forecasting the location, timing, and intensity of such rainfall remain [
9,
10,
11,
12]. Uncertainties related to QPFs are due in part to errors in simulating convective initiation [
11,
13,
14,
15], model parameterizations, and initialization data [
16,
17]. Upgrades to convection-allowing models, which have high enough resolution to explicitly resolve convection, such as the High-Resolution Rapid Refresh (HRRR) model, have improved biases for intense precipitation; however, more extreme rainfall rates (75
or greater) may still be underpredicted during the first 3 forecast hours [
18]. Because of these well-known difficulties in accurately depicting small-scale atmospheric processes, predictability of convective initiation beyond 1–2 h remains problematic [
19]. As a result, errors in the location of precipitation forecasts, or QPF spatial displacement errors, are also problematic. Both Duda and Gallus [
15] and Yan and Gallus [
12] found that QPF spatial displacement errors averaged ~100 km. Because hydrologic processes at the land surface are bound by topographic divides that define and separate watersheds, spatial displacement errors in QPFs can translate into a missed event or false alarm when used for streamflow forecasting. Displacement errors are commonly large enough to cause the heaviest QPF to entirely miss a small basin that receives high-intensity precipitation, while another basin is predicted to receive precipitation that never occurs, leading to forecast inaccuracies for multiple basins.
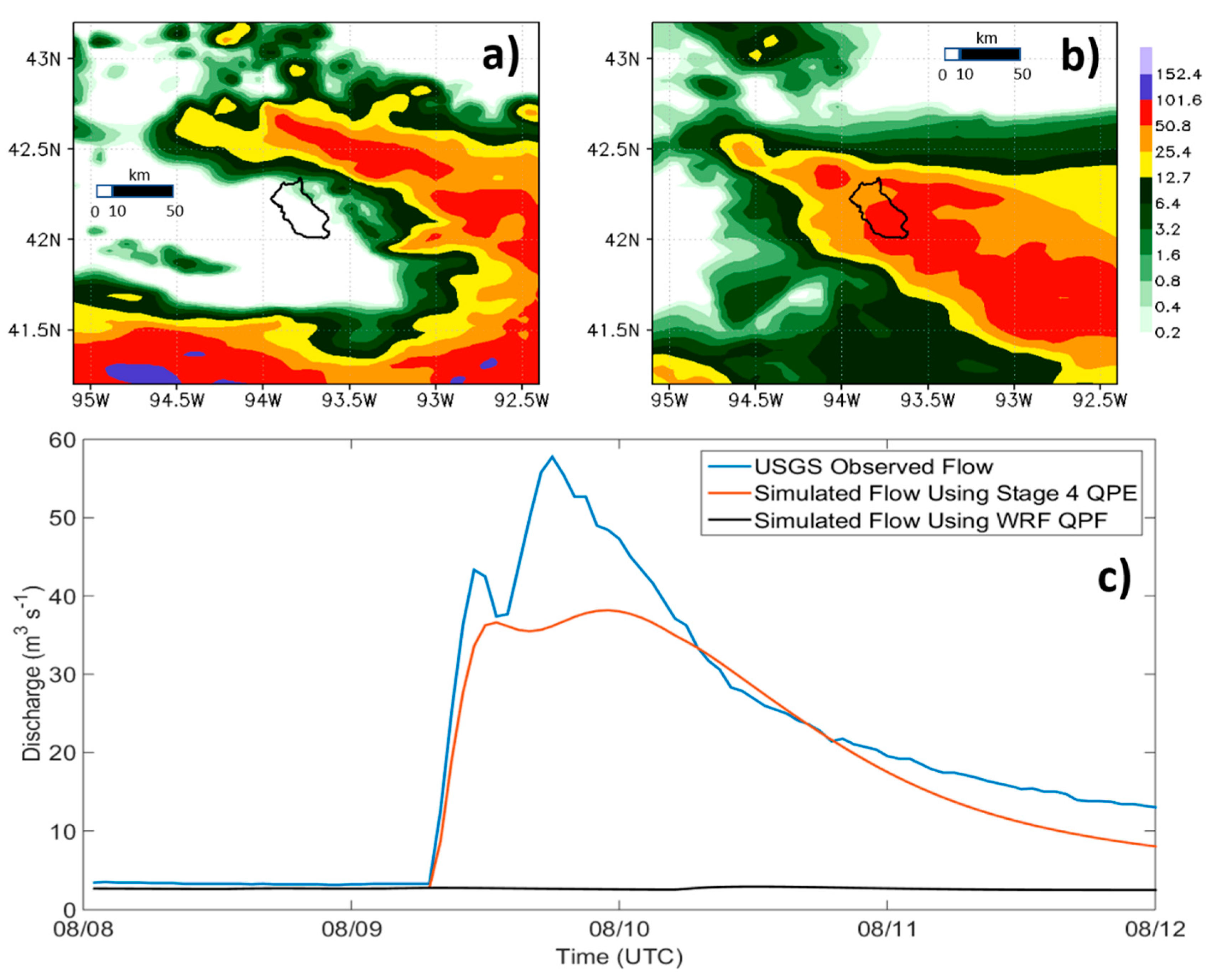
The impact of QPF displacement errors is illustrated for a high-intensity precipitation event that occurred over central Iowa on 9 August 2015 (
Figure 1). A streamflow forecast for the Squaw Creek watershed (depicted in
Figure 1a,b) was created for this event by running a hydrologic model for the basin using the predicted QPF in
Figure 1a. While the general orientation and magnitude of the QPF (
Figure 1a) matched the Stage IV precipitation (
Figure 1b) quite well, and the spatial errors were less than the averages found in the sample cases of Duda and Gallus [
15] and Yan and Gallus [
12], the location of the heaviest predicted rainfall was completely outside the boundaries of the Squaw Creek watershed. The resulting streamflow forecast (
Figure 1c, black line) predicted no streamflow response. However, because some of the heaviest precipitation occurred directly over the watershed, the observed discharge showed a rapid and significant streamflow response (
Figure 1c, blue line). The model run using the Stage IV observed precipitation as input suggests that the streamflow forecast would have predicted a reasonably accurate rise in streamflow had the QPF better matched the location of the observed precipitation (
Figure 1c, red line). This study focuses on an approach to account for QPF spatial displacement errors such as those illustrated in
Figure 1.
We take an ensemble forecasting approach because ensembles represent forecast uncertainty in both predicted precipitation [
20,
21,
22,
23,
24] and predicted streamflow [
25,
26,
27,
28,
29]. Ensemble QPFs are based on multiple combinations of model configurations or initial and lateral boundary conditions, whereas ensemble streamflow forecasts are most often based on multiple model forcings (precipitation and temperature). Further, our approach shifts the location of the QPF in a way that maintains information about the structure of the predicted precipitation system contained in the QPF. Others have explored the use of ensembles to address spatial displacement errors in QPFs, most commonly by using a neighborhood approach. For example, Clark et al. [
30] shuffled ensemble QPFs based on ranking randomly selected historical data for multiple neighboring observing stations. Schwartz et al. [
31] created precipitation threshold forecast probabilities by including all of the neighboring grid points within a given radius (e.g., r = 25 km) surrounding a forecast point. Meanwhile, Schaffer et al. [
32] considered all grid points of a square neighborhood centered on each grid point, along with a conversion of QPF to probability of precipitation based on hit rates in a training dataset, to produce mean probabilities of QPF thresholds from a ten-member ensemble. Although the Schwartz et al. [
31] and Schaffer et al. [
32] methods did address some of the spatial variability in QPFs among model runs, the approaches created probabilistic guidance at each grid point for a few specified thresholds. As such, the approaches did not directly address how the spatial errors would affect forecast precipitation patterns that in turn affect basin streamflow.
In the study presented here, forecasts from the High-Resolution Rapid Refresh Ensemble (HRRRE) [
33] are used to create a shifted QPF ensemble. The nine members of the HRRRE are shifted in eight directions and combined with the original nine members, and then input individually into the distributed Hydrologic Laboratory-Research Development Hydrologic Model (HL-RDHM) [
34,
35]. Major rainfall events in the North Central River Forecast Center (NCRFC) forecast region were monitored during the 2017 season, and those that produced flooding were used to select study basins. Six HRRRE QPFs from heavy rainfall events that occurred during the 2017 and 2018 warm seasons (March–September) were used to create streamflow forecasts for the selected basins, resulting in 46 ensemble streamflow forecasts. Ensemble streamflow forecasts were produced using the original nine HRRRE members and using two different degrees of spatial shifting. All resulting streamflow forecasts were evaluated for prediction of peak flow.
2. Materials and Methods
2.1. Selection of Events and Forecast Basins
The study sites consist of 17 forecast basins located in Iowa, Illinois, and Wisconsin (
Table 1); all within the NCRFC forecast area (
Figure 2). Basin sizes range from 445 to 1672
(
Table 1). Basins were selected based on the location of the heaviest observed precipitation that occurred on 11 June, 19 June, and 21 June in 2017. Selected basins ranged from those with minimal discharge response to those exceeding flood stage, and adjacent basins were chosen when possible. Basins that experienced no events were included in the analysis to determine if the shifted QPFs produced false alarms in watersheds that had minor or no response. Basins were also restricted to headwater locations to avoid introducing uncertainties associated with modeling the downstream routing of flow from one forecast point to the next. Initial testing of the 2017 events indicated that basin-specific calibration, which aims to optimize the model parameters for individual basins, was necessary to improve performance of the HL-RDHM model (see
Section 2.4). Due to this calibration requirement, no additional basins were added once the initial set was selected.
The selected events consist of four forecasts from the three high-intensity rainfall events in 2017 mentioned above, and two in 2018 that occurred near the same basins impacted by the 2017 events (
Table 2). Training thunderstorms, which produce prolonged intense rainfall over the same area, occurred over north-central Wisconsin during the afternoon and evening hours on 11 June 2017, leading to several flash flood warnings. On 19 July 2017, a persistent system with moderate to heavy rainfall tracked across Minnesota into west-central and southwestern Wisconsin during the afternoon hours, with a second system producing multiple rounds of intense precipitation over west-central and southwestern Wisconsin during the overnight hours, triggering multiple flash floods. The third flooding event began late on 21 July 2017, and continued into the early morning hours of 22 July, which was due to a nearly stationary line of intense precipitation that hovered over northeast Iowa, far southwest Wisconsin, and into north-central Illinois for roughly five hours. On 4 May 2018, a system with persistent and heavier precipitation occurred over northeast Iowa. This event followed two nights of moderate precipitation and caused rivers in northeast Iowa to flood. The final event occurred during the morning hours of 14 June 2018, when several training storms produced heavy precipitation over central Iowa.
2.2. Observed Data
Multi-sensor precipitation estimates (MPEs) [
36,
37] from January 2014 through June 2018 obtained from the NCRFC were used as observed precipitation. Although MPEs have been shown to have errors that are relatively larger for heavy convective precipitation, with an underestimate compared to gauges [
38], they have been used as ground truth in other studies focused on heavy warm season precipitation [
39]. MPEs are a near-real-time hourly gridded precipitation product with 4 km spatial resolution produced from algorithms that combine precipitation measurements from rain gauges, precipitation estimates from radar (standard and dual-polarization), and satellite products, with hourly quality control measures. Climatological potential evapotranspiration (PET) and air temperature data, also needed as hydrologic model forcings, were obtained from the NCRFC. Hourly observed discharge for the study basins was obtained from the United States Geological Survey (USGS) National Water Information System [
40].
2.3. Precipitation Forecasts
The HRRRE, which was established to advance the efforts of severe weather prediction [
41], consists of nine members with convection permitting 3 km horizontal grid spacing configured identical to HRRR v3 [
42,
43] but using a standard vertical coordinate instead of a hybrid coordinate. The hybrid vertical coordinate is terrain-following at the surface but reduces to a pressure coordinate at some point above the surface, whereas the standard vertical coordinate uses pressure throughout [
42]. Random perturbations to U and V winds, temperature, dry air mass in a column, and mixing ratio are added to boundary conditions to create each individual forecast member. Initialization times for the HRRRE forecasts during 2017 and 2018 were either 00, 12, 15, 18, or 21 UTC (
Table 2), and varied according to the needs of projects that the HRRRE supported (e.g., National Oceanic and Atmospheric Administration (NOAA) Spring Forecast Experiment [
33]). The HRRRE runs initialized at 00 UTC during 2017 provided hourly QPF output for 36 h, while all the simulations in 2018 were 36 h. However, HRRRE forecasts for the remaining initialization times in 2017 were only 18 h in duration. Therefore, to remain consistent across all cases examined, only the hourly QPF outputs from the first 18 h were used as input into the hydrologic model.
2.4. Hydrologic Model
The Hydrology Laboratory-Research Distributed Hydrologic Model (HL-RDHM) version 3.5.11 (NOAA, National Weather Service (NWS), Silver Spring, MD, USA) was used to produce the ensemble streamflow forecasts. HL-RDHM is a spatially gridded model with a 4 × 4 km horizontal resolution on the Hydrologic Rainfall Analysis Project (HRAP) grid [
34]. The HRRRE QPFs were re-gridded to match the nominal resolution of the model by using bilinear interpolation. Performance of the HL-RDHM in the study region has been previously documented [
44,
45], thus the model provided a useful testbed for the QPF shifting method.
The Sacramento Soil Moisture Accounting Heat Transfer model (SAC-HT) [
46,
47] and the kinematic hillslope and channel routing model options within HL-RDHM were used for this study. The SAC-HT is the conceptually based rainfall-runoff Sacramento Soil Moisture Accounting model [
48] that incorporates a physically based frozen ground model. SAC-HT utilizes a two-zone soil structure to simulate runoff, infiltration, and soil storage. Both the upper and lower soil zones consist of free and tension water storage. Free water storage represents the water drained due to gravitational forces and tension water storage represents the water that can only be depleted by evaporation or transpiration. The hillslope and channel routing model routes surface and subsurface runoff over conceptual hillslopes and channels using drainage density, surface slope, and hillslope roughness properties within grid cells [
49]. The model was run using a 1 h timestep.
Based on preliminary testing and previous experience with HL-RDHM [
44], we determined that the a priori SAC-HT parameter values required calibration to improve model performance for the study basins. Ten SAC-HT parameters (
Table 3) were optimized to hourly discharge observations for each study basin. Rather than calibrating individual parameter values for each grid within a basin, the HL-RDHM calibrates a single multiplier for each parameter. These basin-specific multipliers are then applied to the a priori parameter values to produce the calibrated values.
Following the current standard procedure for calibration with the HL-RDHM, automatic calibration was conducted using the Stepwise Line Search (SLS) [
50], which is a local search method that steps progressively through each parameter multiplier by decreasing the objective function [
35] value until it is minimized. The objective function,
, is defined as:
where
and
are the observed and simulated streamflows averaged over the time interval
,
is the standard deviation of the observed streamflow,
is the total number of time scales used, and
is the number of ordinates for time scale
. When a specific parameter multiplier value remains the same for three consecutive optimization loops, it is eliminated from successive loops. Minimum and maximum multipliers were set for each parameter to maintain the allowable parameter ranges as described in Spies et al. [
44]. Not all a priori parameter values fell within the range indicated in
Table 3. When these instances occurred, the parameter ranges were set to
of the a priori value. The routing parameters were not included in the calibration because the a priori values generally perform well [
44].
The hourly MPE data from the NCRFC began 1 January 2014; therefore, the automatic calibration was conducted from 1 January 2014 through 15 March 2017. The calibration period ended on 15 March 2017 to prevent overlap between the calibration and forecast periods. Due to the short three-year calibration period, an additional manual calibration was conducted to optimize simulated streamflow for the 2017 and 2018 seasons based on the latest antecedent conditions. The following five parameters have the greatest effect on simulated peak flow and baseflow and were the only ones included in the manual calibration: UZTWM, UZFWM, LZTWM, LZFSM, and LZFPM (see
Table 3 for acronym definitions). Adjusting the UZTWM, UZFWM, and LZTWM largely affect the peak flows, while adjusting the LZFSM and LZFPM generally affect the baseflows [
51]. The manual calibration period spanned 15 March 2017 through 31 July 2017, covering a majority of the 2017 forecast period. Because the focus of this study is on performance of ensemble QPFs rather than on calibration of the hydrologic model, using part of the forecast period for calibration was not expected to alter the conclusions. Parameters were adjusted one at a time based on a qualitative comparison between the simulated and observed streamflow. Which parameter was chosen for adjustment varied for each iteration depending on how much the previous parameter adjustment affected the simulated streamflow. The manual calibration for each watershed ended once the parameter adjustments failed to qualitatively improve the simulated streamflow, or after ten total iterations of adjustments were complete.
After the manual calibration was completed, the root mean square error was calculated for discharge simulations produced using the automatically calibrated and manually calibrated parameter sets for the 15 March–31 July 2017 period. If the manually calibrated parameter values resulted in an average root mean square error improvement of at least 15% compared to the automatically calibrated parameters, then the manually adjusted parameters were kept. Otherwise, the automatically calibrated parameters were used.
2.5. Ensemble Streamflow Predictions
Four types of streamflow forecasts were generated from the QPFs and evaluated for prediction of peak discharge:
A nine-member ensemble generated from the original nine HRRRE QPF members (“raw QPF”),
An 81-member ensemble generated by shifting the HRRRE members by 55.5 km (0.5° latitude)
An 81-member ensemble generated by shifting the HRRRE members by 111 km (1.0° latitude), and
The MPE-generated “perfect forecast”.
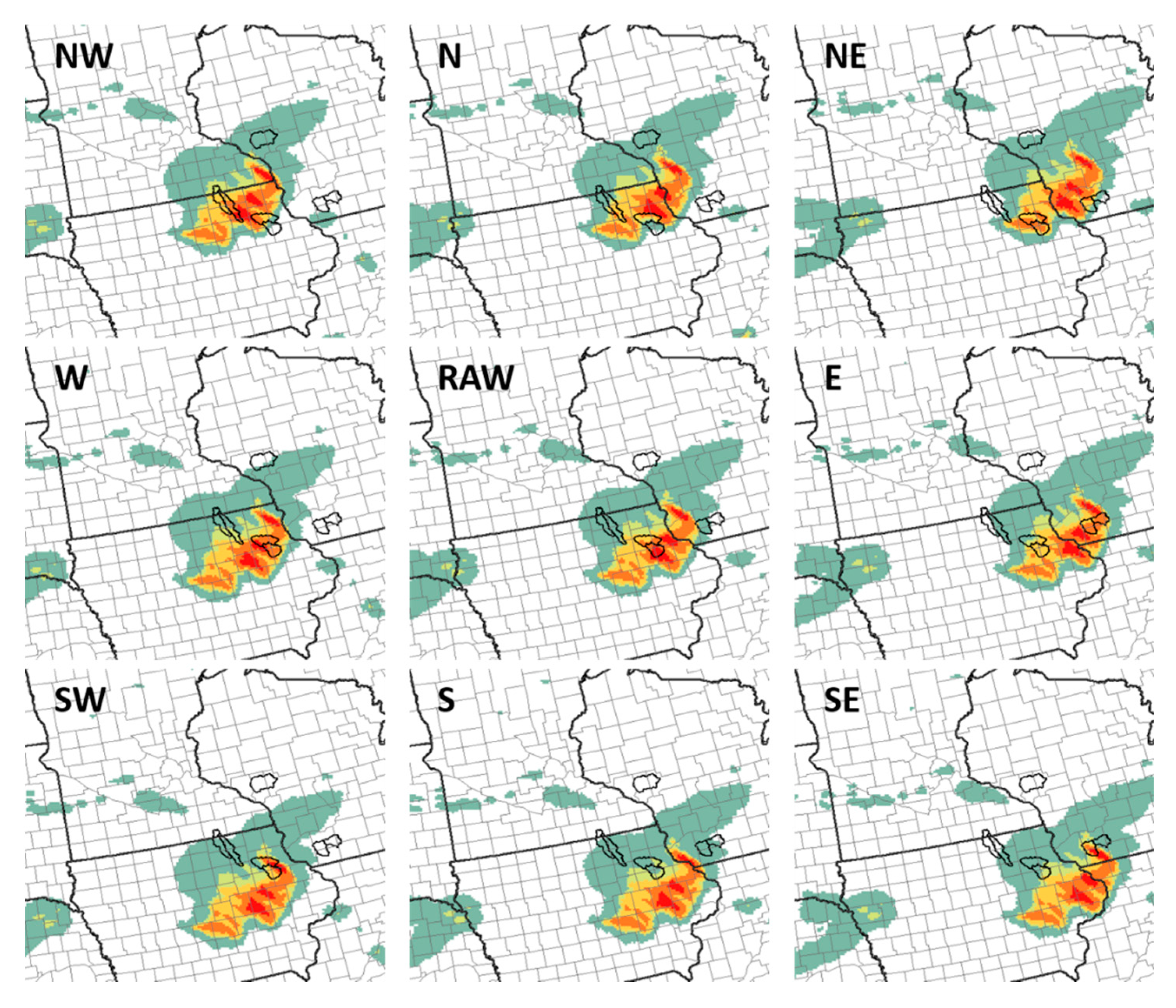
The 81-member precipitation ensemble created from the HRRRE consisted of the nine raw QPFs plus 72 members created by systematically shifting the original nine HRRRE members in the four cardinal directions (N, E, S, W) and four intermediate directions (NE, NW, SE, SW) (
Figure 3). The original nine members were maintained in the 81-member ensembles since it is possible for some cases that displacement errors would be very small, and the purpose of the technique is to try to better account for the full range of displacements common in QPFs. To explore a range of possible displacements and the impact of shifting on the hydrologic forecasts, shifts of both 55.5 and 111 km were examined. These values were in part chosen based on previous studies that found an average ~100 km displacement using different cases and model configurations [
12,
15,
52].
A four-month spin up period prior to the start of the forecast was used to initialize the HL-RDHM. Specifically, the MPE from the NCRFC was used to force the HL-RDHM up to the time of the HRRRE initialization, at which time the QPF was used for the following 18 h. After the 18 h QPF period ended, the HL-RDHM was run for an additional twelve hours without additional precipitation forcing to create a 30 h forecast period (18 h of QPF plus 12 additional hours with no precipitation). No precipitation was used in those additional 12 h since RFCs in the central United States (including the NCRFC) have found that errors are reduced with this assumption compared to using climatological values during the convectively active spring and summer (Tony Anderson, NOAA/NWS, 2020, personal communication), likely due to the high variability of convection-driven precipitation. In addition, for the warm season events in the present study, no rain typically occurred in the basin after the 18 h forecast period. Further, our method was intended to mimic an operational setting, in which forcings would not be known beyond the end of the QPF.
Due to structural and calibration errors, a hydrologic model inherently introduces uncertainty into the initial conditions and streamflow forecasts. Therefore, simulations under “perfect forcing” were performed by running the HL-RDHM with MPE for the forecast period (18 h) with zero precipitation input for the additional 12 h. This simulation is then considered a “perfect streamflow forecast” and is used to assess the ensemble forecast performance in light of other forecast system error, such as hydrologic model error.
2.6. Forecast Evaluation and Verification
Although the present study focuses on methods to account for spatial errors in QPFs, it is important to also understand if general errors exist in the magnitude of the rain events predicted, since large under- or over-estimates of amount would prevent accurate streamflow forecasts, even if the location is predicted perfectly. Thus, errors in predicted precipitation magnitude were evaluated by comparing the maximum MPE and HRRRE QPF values over the study area. For streamflow forecasting purposes, it is useful to consider the total depth of precipitation averaged across the entire watershed in addition to comparing the maximum precipitation values of a single grid point only. Using the average area of the study basins, a synthetic 28 × 28 km square watershed was created and then centered on the maximum MPE and the maximum QPF from each member for individual events. The spatial average QPF and MPE depths of the 18 h totals from these synthetic watersheds were compared to determine whether HRRRE members have a tendency to under- or over-predict the heaviest precipitation totals for each forecast.
Given the objective of improving forecasts of flood threat, the following four forecast categories were used to evaluate the predicted peak discharge from the streamflow forecasts: non-event, 50% action, action, and flooding (
Table 1). A non-event is when the peak discharge remains below the level corresponding to 50% of the action stage defined by NCRFC for individual watersheds. A 50% action event is when the peak discharge exceeds the level corresponding to 50% of the action stage. Because some of our basins are small, the rivers can rise quickly and there may not be enough time to perform necessary tasks to protect life and property if the tasks begin at the action stage, so the 50% action stage is used as another potentially useful threshold. Action and flooding events occur when the peak discharge exceeds the levels corresponding to the action and minor flood stages, respectively. Although timing errors could occur in the forecast due to the QPF shifting, QPF error, or hydrologic model errors, the evaluation focused on peak flow predictions and peak timing was not evaluated.
The forecasts were evaluated using several verification metrics (
Table 4). To measure the ability of the forecast system to create an ensemble that contains the observations within its bounds, the frequency of non-exceedance (FNE) is used, where:
with
where
is the upper bound of the ensemble, and N is the total number of forecasts. Because the focus of this analysis is on evaluating flood prediction, we use non-exceedance rather than considering the lower bound of the ensemble. In addition, by not evaluating the lower bound of the ensemble, we prevented the forecast from being penalized if the baseflow was modeled incorrectly leading up to the forecast (a possible initial condition error).
The 2 × 2 contingency table is used to define four possible outcomes for deterministic yes/no forecasts and discrete observations [
53]. Because this table requires dichotomous events, the categories were limited to flooding or non-flooding, with flooding meaning exceeding the minor flood stage, as defined previously. Thus, a hit (H) occurs when a flood is both forecasted and observed, a false alarm (FA) occurs when a flood is forecasted but not observed, a miss (M) occurs when a flood is observed but not forecasted, and a correct negative (CN) occurs when a flood is neither forecasted nor observed. Due to the large difference in size between the two ensembles (9 members vs. 81 members), only the maximum forecasted peak streamflow from each ensemble was used to determine whether shifting QPFs can improve the indication of a flood threat. Therefore, only one ensemble member had to reach flood level in order for a flood to be considered predicted, even though the probability of flooding in that case would be very low.
From the outcomes defined by the contingency table, four metrics are computed: probability of detection (POD), false alarm ratio (FAR), critical success index (CSI) [
54], and equitable threat score (ETS) [
55]. The POD is the ratio of hits to the total number of events observed H/(H + M). The FAR is the ratio of false alarms to the total number of events forecasted FA/(FA + H). While the FAR and POD provide valuable verification information, the CSI and ETS may be a better indicator of successful forecasts because they incorporate all of the events that were either forecasted or observed [
55]. CSI is the ratio of hits to all events forecasted or observed H/(H + FA + M). The ETS provides a metric that corrects for the number of hits that would be expected by a chance forecast (H − chance forecast)/(H + FA + M − chance forecast), where the chance forecast [(H + FA) × (H + M)/N] is the events forecasted multiplied by the events observed divided by the total number of forecasts (N). POD, FAR, and CSI all result in scores ranging from 0 to 1 and ETS scores range from −1/3 to 1. Perfect scores for ETS, POD, and CSI are 1, while 0 is a perfect score for FAR (
Table 4).
The ranked probability score (RPS) is a squared error score that measure the performance of the probabilistic forecasts across multiple forecast/observation categories [
53]. RPS is sensitive to distance between the cumulative forecast streamflow probabilities and the observed streamflow. The forecast cumulative distribution (
) is:
where
is the relative frequency of the forecasted peaks, and
is the number of forecast categories [
53]. In this case, four forecast categories were used, as described earlier in this subsection. The observation
only occurs in one of the categories, which is given a value of 1, and the remaining categories are given a value of 0. The cumulative distributions of the observation is [
53]:
The RPS for a single forecast is the sum of the squared differences of the cumulative distributions:
RPS for a group of forecasts is the average of the RPSs calculated from all the forecasts. A perfect forecast would result in an RPS value of 0 and occurs when all of the probability of occurrence falls in the same category as the observation.
3. Results and Discussion
Of the 46 streamflow forecasts analyzed, 23 had an observed peak that exceeded at least the 50% action stage. Of the 23 with peaks above the 50% action stage, 15 exceeded the flood stage, with seven of the floods occurring during the period covered by the forecast initialized at 21 UTC on 21 July 2017 (
Table 2). No flooding occurred in the study basins investigated for the forecast initialized at 12 UTC on 11 June 2017, though there were two basins where peak streamflow exceeded the 50% action stage. Of the remaining four events for which forecasts were made (
Table 2), peaks exceeding the flood stage occurred in two basins.
To understand the role that QPF magnitude errors might play in the results, the HRRRE QPF maxima and observed MPE maxima from the system of interest were compared for each forecast period. Overall, the HRRRE QPF maxima were typically less than the MPE maximum. Since Wooten and Boyles [
38] found that MPE in general underestimates heavy rainfall, it is very likely the HRRRE is not intense enough with its QPF maxima. Three of the six HRRRE forecasts produced QPF maxima greater than the observed MPE maximum; however, only one member of the nine from each of these three forecasts produced a QPF maximum greater than the MPE maximum. For the synthetic basin, the number of forecasts where QPF maxima for at least one member exceeded the MPE increased to five out of six. Although there were more forecasts that produced greater maximum QPF depths, only one or two members exceeded the MPE maximum for four of those five forecasts. The one exception was the event initialized at 00 UTC on 4 May 2018, in which seven of the nine members produced QPF depths that exceeded the MPE. These results indicate that the HRRRE has an overall low bias in the heaviest precipitation.
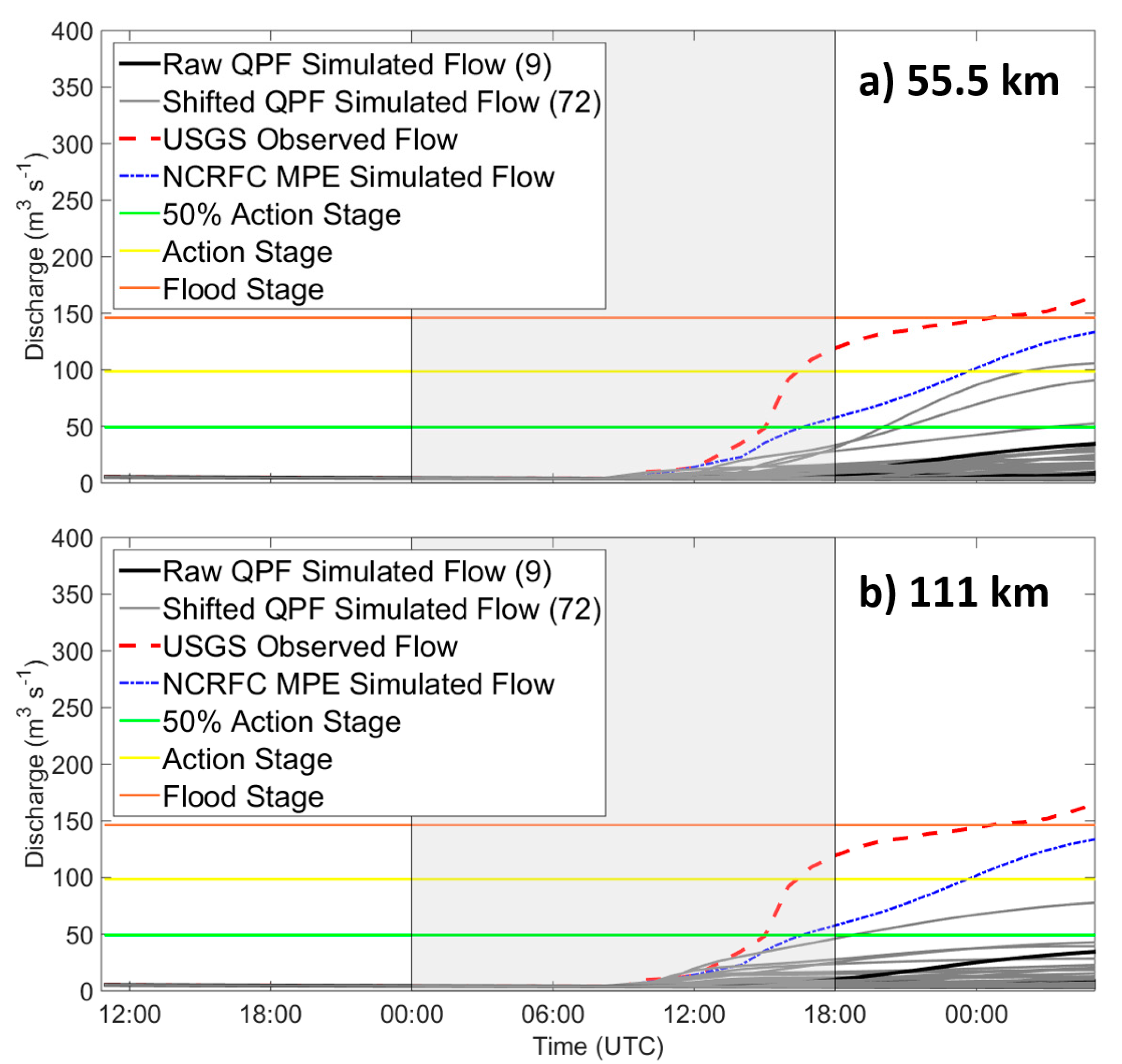
In many cases, as might be expected, shifting the QPFs resulted in an increased ensemble spread compared to the raw streamflow forecast: this occurred for both the 55.5 and 111 km shifts (example shown in
Figure 4). As a result, the FNE of the peak discharge forecasts increased, with the 111 km shift producing the highest FNE (
Table 5). The POD also improved from 0.33 when using the raw QPFs to 0.60 when using the 55.5 km shifted QPFs and 0.80 when using the 111 km shifted QPFs (
Table 5). While the POD improved for the shifted ensemble, the shifting also produced worse FAR scores: the FAR was 0.29 for the raw ensemble, 0.44 for the 55.5 km shifted ensemble, and 0.45 for the 111 km shifted ensemble. Thus, compared to the raw ensemble, the shifting improved the POD but not the FAR. When considering the POD and FAR simultaneously through the CSI and ETS, the higher CSI and ETS indicate that the two shifted QPF ensemble have greater ability to predict a flood compared to the raw QPFs.
Recall that only one ensemble member had to reach the flood level in order for the forecast to be labeled as a forecast of flood. Given such a low probability threshold, it is likely that the shifted ensembles would more often predict floods because they have more members, and therefore, more chances to reach the flood threshold. More frequent forecasts for floods would explain the higher FARs of the shifted forecasts. Typically, forecasters would examine the skill of different probability thresholds for a climatological set of cases and would use the threshold that had provided the greatest skill as the criteria for issuing a flood forecast. A higher threshold would yield lower POD and FAR values and should mitigate the higher FAR value present for the shifted ensemble.
The “perfect” streamflow forecasts, which were made using MPE as hydrologic model input, produced a POD of 0.73, which is lower than the perfect score of 1. This POD, along with the FAR of 0, suggest that the perfect forecasts sometimes failed to produce a large enough discharge. These results indicate that there are errors in the streamflow model and/or the observations that are also limiting forecast skill.
The RPS for the peak discharge forecasts using the raw QPF ensemble was 0.75 (
Table 5). Shifting the QPFs by 55.5 km resulted in a forecast with a nearly equal RPS of 0.74; however, shifting the QPFs by 111 km resulted in a worsening of RPS to 0.82. While the shifted QPF ensembles typically increased the streamflow, ensemble spread and produced greater peak magnitudes compared to the raw QPF ensembles (
Figure 4), usually just one or two of the shifted QPF members resulted in greater peaks. The majority of shifts resulted in little to no precipitation occurring in the basin, and thus, many streamflow ensemble members that predicted low discharge. The reason that only one or two shifted QPF members exceeded the peaks produced by the raw QPF member is because, in most cases, only a few of the shifts resulted in heavy rain being placed directly into the basin boundaries. This is in part caused by the small basin and precipitation footprint sizes resulting in the shifted heavy rain forecasts to “miss” the basin. The shifting produced forecasts with high probabilities in the lowest discharge categories and only a slight increase in probability for flood categories, ultimately negatively affecting the RPS metric for the larger ensemble. For example, when a flood occurred and the raw QPF ensemble produced just one member that exceeded the flood stage, the probability of exceedance would be 11.1% (1 member exceeding the flood stage out of 9 members). If shifting the QPFs increased the number of members that exceeded the flood stage to three (e.g.,
Figure 4a), the probability of exceedance would actually decrease to 3.7% (three members exceeding the flood stage out of 81 members), despite having more members indicating that a flood may occur. As a result, the RPS for the shifted QPF ensemble (0.93) would be worse than that for the raw QPF ensemble (0.79) in this example. For larger-scale precipitation events, it is likely that the RPS would not be as negatively affected as more of the shifts may result in precipitation falling within a basin boundary.
Given the finding that the systematic shifting likely moves a heavy rain into a small basin in at most only one of the eight QPF shifts, a preliminary analysis was performed to determine if spatial displacement errors in HRRRE members could be accounted for in a more informed way. It is possible that weighting the ensemble members based on the climatological likelihood of spatial displacement errors could improve the probability forecasts. As an initial test of this concept, the direction of displacement errors for the HRRRE forecasting system was determined for 28 cases occurring over the study region in 2017 and 2018. The analysis considered error in the location of the centroid of the storm system (forecasted compared to observed), for events that had at least one inch (25.4 mm) of accumulated precipitation. For 17 of the 28 simulations, a statistically significant (p < 0.05) bias existed in the meridional direction, and the same was true in 22 of the 28 simulations for the zonal direction. Of the 17 simulations with a meridional bias, eight had a northern bias and nine had a southern bias, resulting in no real preference in either direction. In contrast, a westward bias was present in the zonal direction among 16 of the 22 simulations, while the remaining six were displaced to the east. Given this finding, the discharge ensembles produced from the shifted QPFs were weighted such that more weight was given to those shifted in the eastward directions. Each eastern shift was assigned a probability of 0.036, the NE, SE, and raw QPFs were all assigned a probability of 0.012, and the N, NW, W, SW, and S shifts were assigned a probability of 0.007. Recalculating RPS with the new member weighting scheme yielded an RPS value of 0.70 for the 55.5 km shift and 0.78 for the 111 km shift, both slight improvements over the RPS from the forecast using equally weighted members. These results suggest that a better understanding of the climatology of the displacement errors in QPFs could be used to build an informed weighting scheme and improve the skill of the shifted streamflow ensemble predictions. While the HRRRE had a westward bias of precipitation within the study region, different models may have different directional biases and forecast system-specific weighting schemes may be required.
In one of the six HRRRE forecast cases studied, an additional source of error was noted that affects verification and further shows the challenges facing flood forecasting. The 14 June 2018 high-intensity rainfall event caused flash flooding in both the streets of Ames, IA, and in the two river basins that affect the city—the Squaw Creek and South Skunk River. While the observed streamflow of both basins exceeded the flood stage, none of the ensemble members forecasted a flood to occur in either basin (
Figure 5, Squaw Creek shown). In addition, the “perfect” streamflow forecast using MPE did not produce a flood during the forecast period. To explore why the “perfect” forecast failed, rainfall measurements from the Community Collaborative Rain, Hail and Snow Network (CoCoRAHS) [
56] were examined for the event. The maximum CoCoRAHS observation reported was 178.8 mm of precipitation, which exceeded the maximum MPE of 121.2 mm, with several additional reports exceeding 101.6 mm. Therefore, these CoCoRAHS reports suggest that the MPE might not have reflected the ground truth for this event. Furthermore, none of the HRRRE members showed QPF amounts as heavy as the maximum CoCoRAHS report.
Although assessing the errors in the timing of the peak discharge was not a focus of this study, the topic warrants a brief mention. The impact of the QPF shifting on the timing of the peak will likely vary by case. In
Figure 4a, nearly all QPF-driven discharge simulations show a significant lag in the timing of the hydrograph rise and peak. In
Figure 4b, a single shifted QPF produces an improved peak timing, although it is the only one to overestimate the magnitude. All other QPF-driven simulations shown in
Figure 4b show a significant lag in peak streamflow, with no improvement due to the shifting. The simulation produced with the observed precipitation has a lag similar to the shifted QPF, thus error in the timing of the peak may be due to the hydrologic model itself. Future work is needed to better understand the combined effects of errors in precipitation timing, precipitation intensity/magnitude, and the hydrologic model.
4. Conclusions
We examined a flood forecasting method that accounts for spatial displacement errors in QPFs by shifting the location of meteorological ensemble members prior to their input to a hydrologic model. QPFs from the 9-member HRRRE ensemble and the HL-RDHM hydrological prediction model were used to test the approach. Forty-six ensemble streamflow forecasts were created for five high-intensity rainfall events covering six forecast periods occurring in the Upper Midwest US during 2017 and 2018. An 81-member ensemble streamflow prediction was created by shifting each HRRRE member in eight directions (both 55.5 and 111 km shifts were tested) and compared to the streamflow forecasts created using the original raw HRRRE members.
We conclude that accounting for displacement errors by shifting ensemble member QPF to create a larger ensemble improves the ability of a probabilistic streamflow forecasting system to identify potential flooding events. This finding was indicated by the improved FNE, POD, ETS, and CSI metrics for the shifted ensembles, as compared to metrics from the ensembles using QPFs from the original nine HRRRE members alone. While shifting QPFs to create an ensemble streamflow forecast did improve the ability to predict a flooding event, the 81-member ensemble did not provide large probabilities of flooding when a flood occurred. These results raise the question: Keeping in mind that using QPFs was intended to improve lead time, does the early indication that a flood could occur in a basin provide useful information despite the relatively low forecast probability given for such events, thus justifying the effort of generating the larger ensemble? This type of improved prediction capability may be helpful to forecasters and forecast users who are interested in dichotomous information (i.e., flood and no flood), for example.
Differences in some forecast verification metrics, such as RPS and ETS, were small when the shifted streamflow ensemble members were given equal weight; however, we also conclude that adjusting member weights using additional information, such as the QPF climatology of displacement errors, can improve the shifted ensemble. Accounting for the westward bias of the HRRRE precipitation slightly improved the probabilistic forecasts, suggesting that a solid understanding of QPF displacement is needed to create a well-informed ensemble weighting technique or a more selective approach to shifting the QPF members. Additional bias correction methods may improve the probabilistic forecasts even further. Machine learning techniques could be applied to determine the most beneficial distance for members to be shifted. Additionally, weighting schemes could be devised in real-time to better reflect the observed displacement as the precipitation event is evolving. Although this latter approach would somewhat reduce the available lead-time of the forecast information compared to the technique presented in this paper, the lead-time would still be larger than for forecasts that rely on quantitative precipitation estimates.