Evaluation of the Performance of Different Methods for Estimating Evaporation over a Highland Open Freshwater Lake in Mountainous Area
Abstract
:1. Introduction
2. Materials and Methods
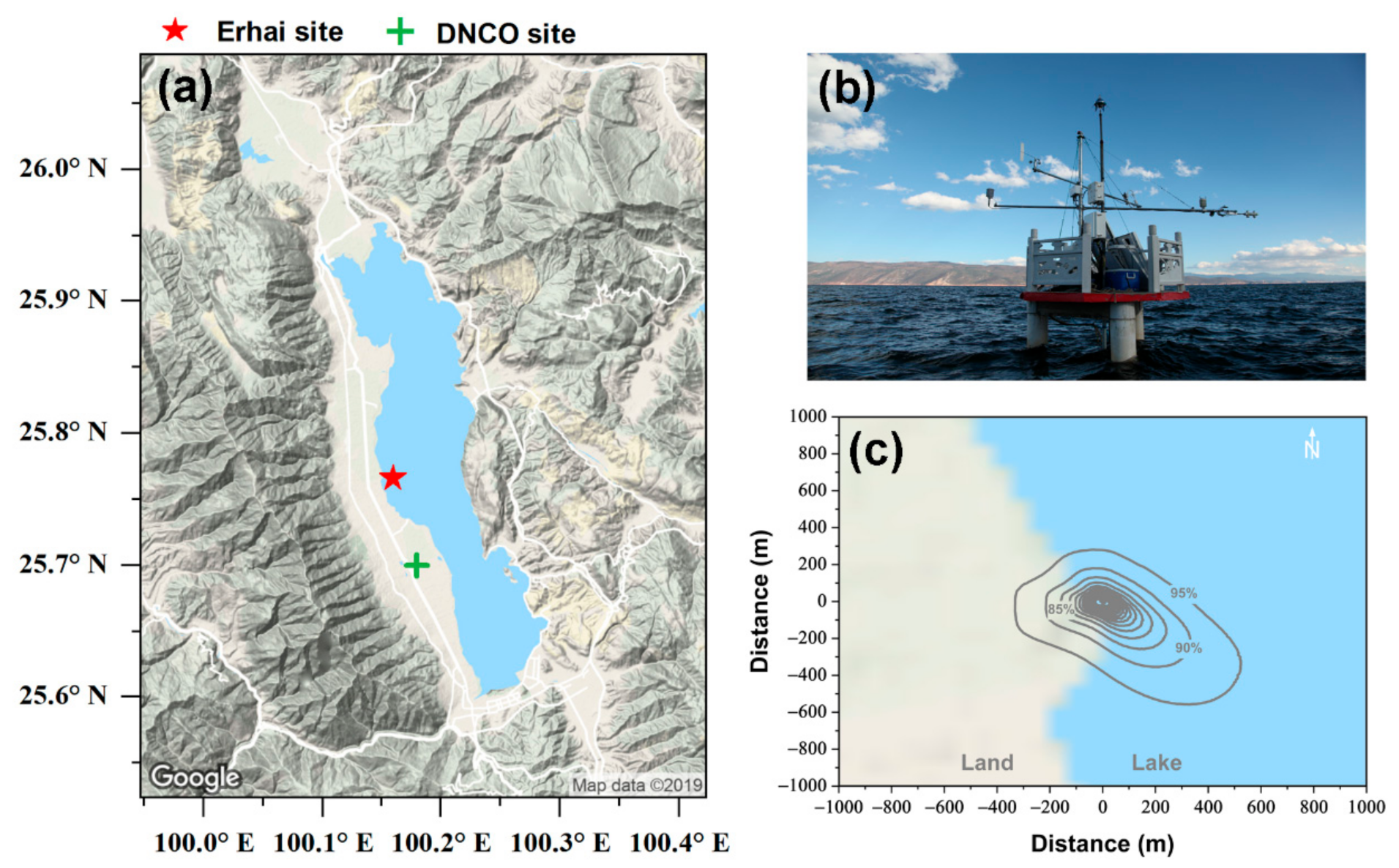
2.1. Observation Site and Instruments
2.2. EC Data PostProcessing
2.3. Introduction of Evaporation Methods
2.3.1. Combination Methods
2.3.2. Solar Radiation-Based Methods
2.3.3. Dalton-Based Methods
2.4. Calibration of Evaporation Methods
2.5. Evaluation Criteria of Evaporation Methods
2.6. Assessment of Relative Contribution
3. Results and Discussions
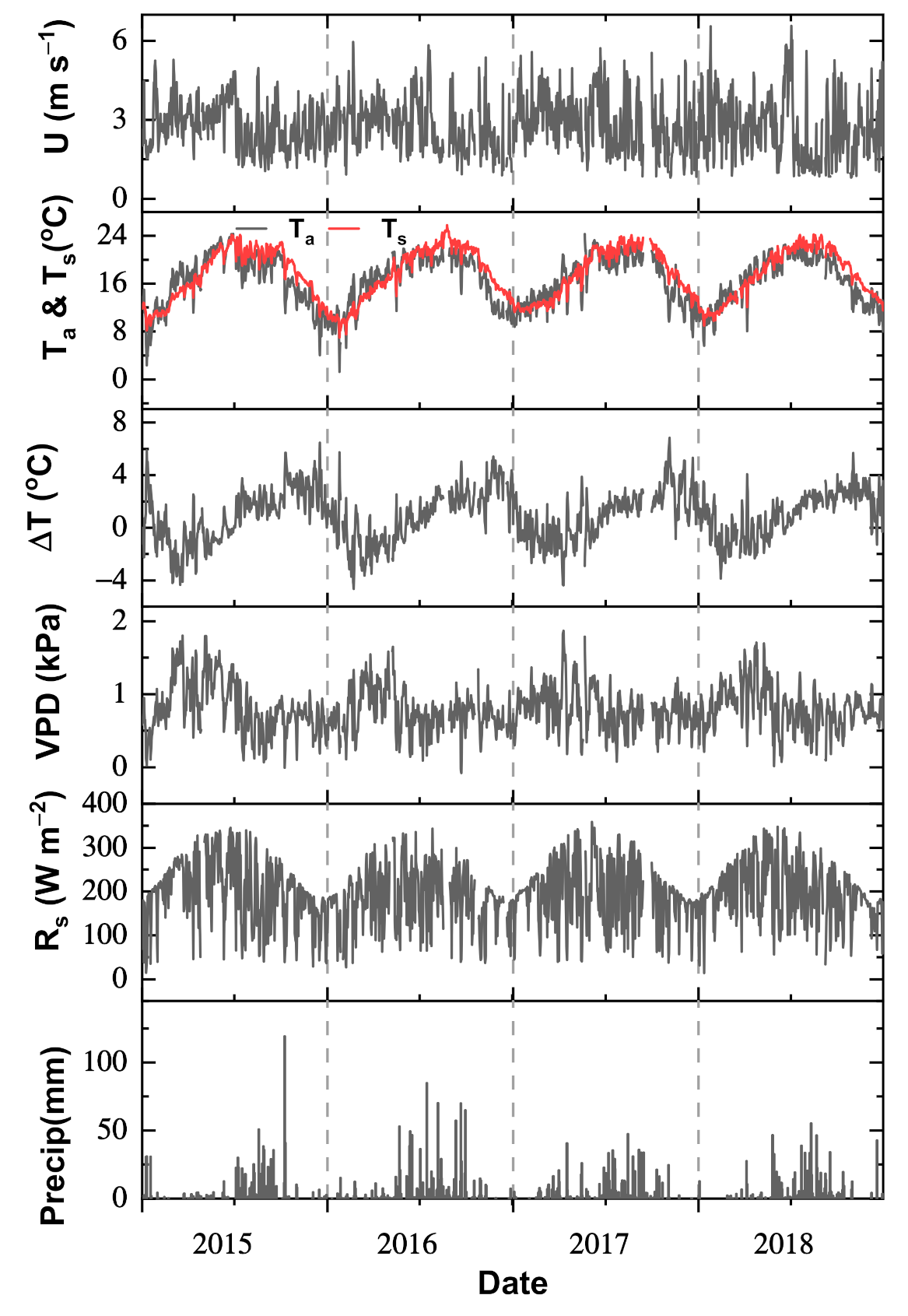
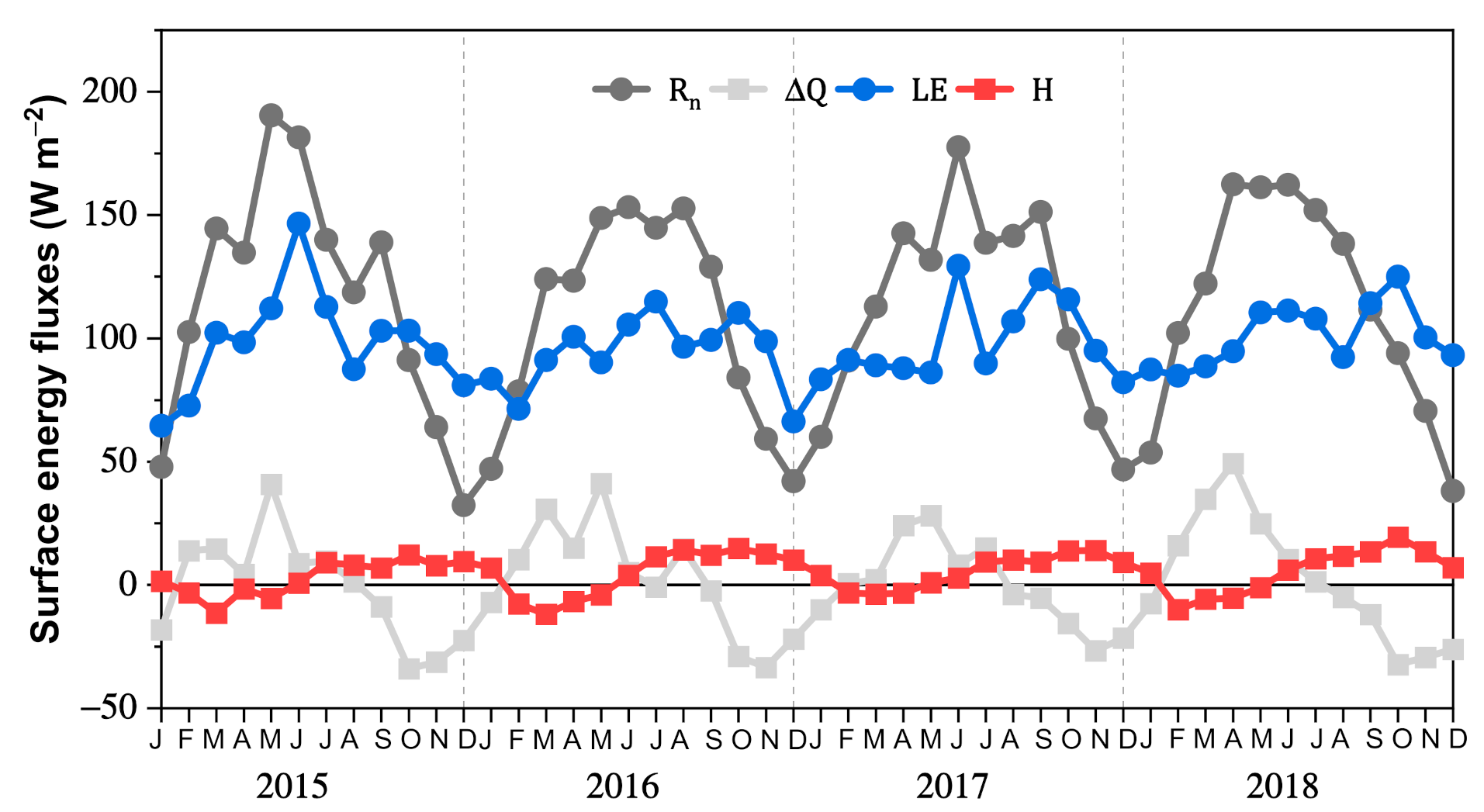
3.1. Meteorological Conditions and Surface Energy Budget
3.2. Evaluation of Evaporation Methods at Different Timescales
3.2.1. Evaluation of Combination Methods
3.2.2. Evaluation of Solar Radiation-Based Methods
3.2.3. Evaluation of Dalton-based Methods
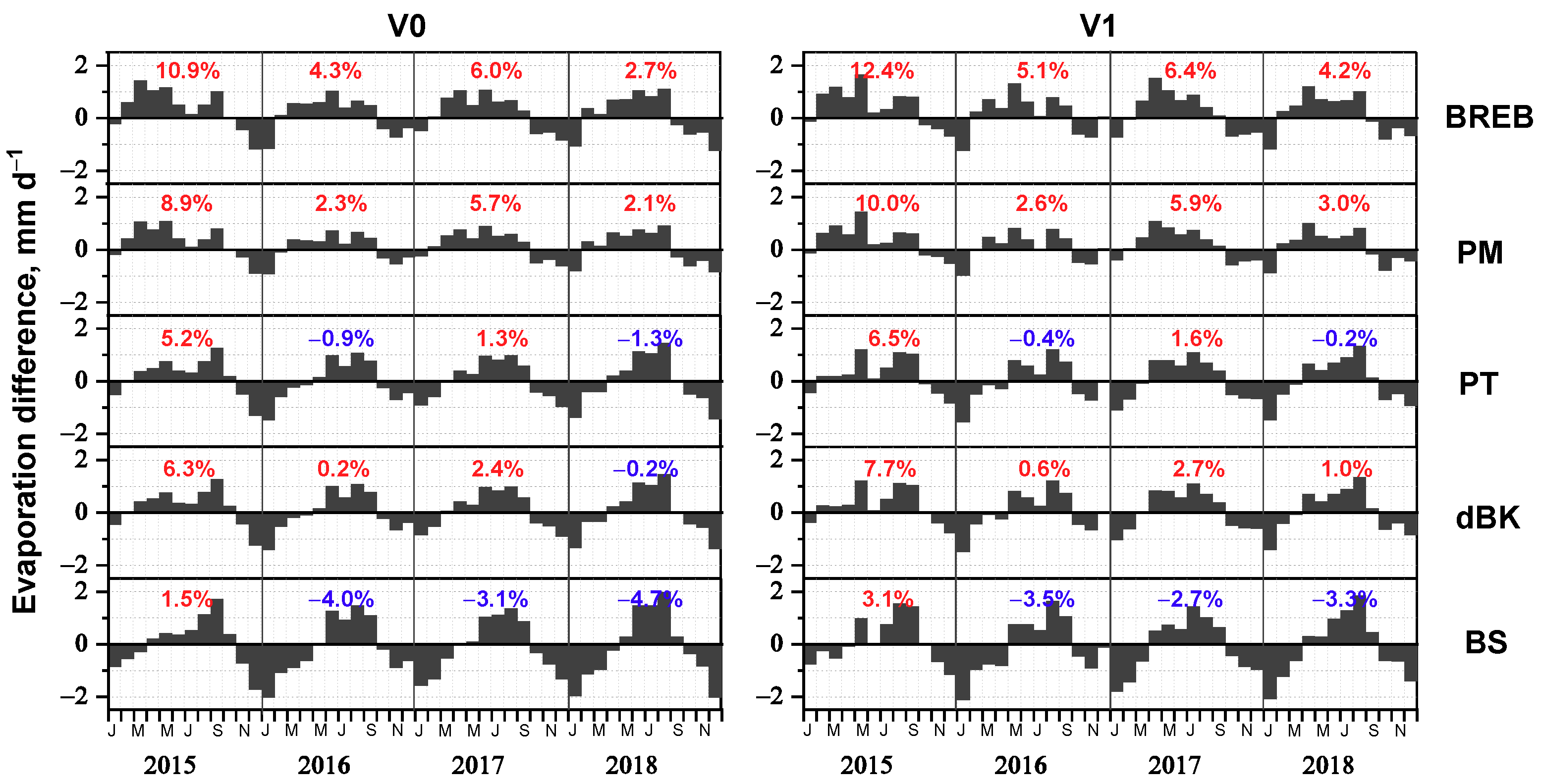
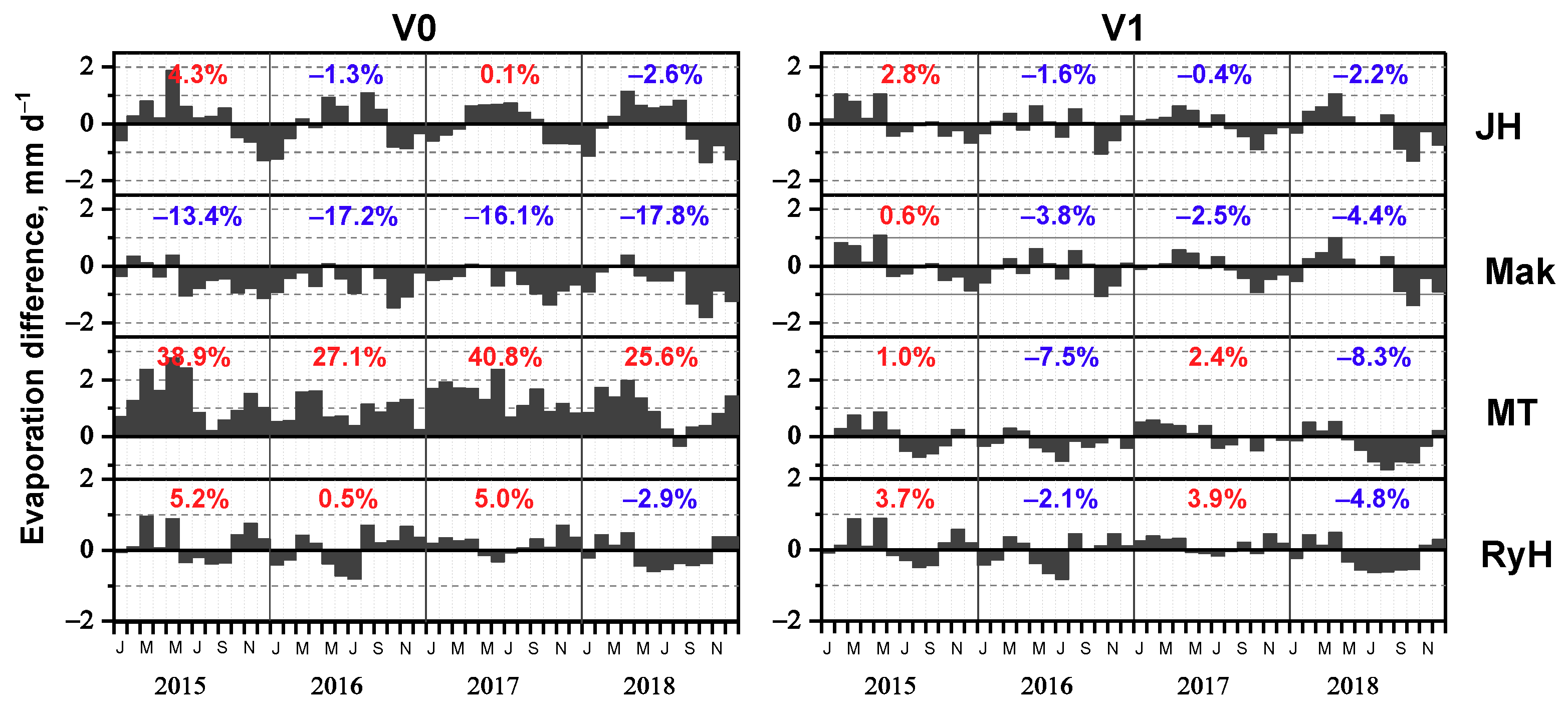
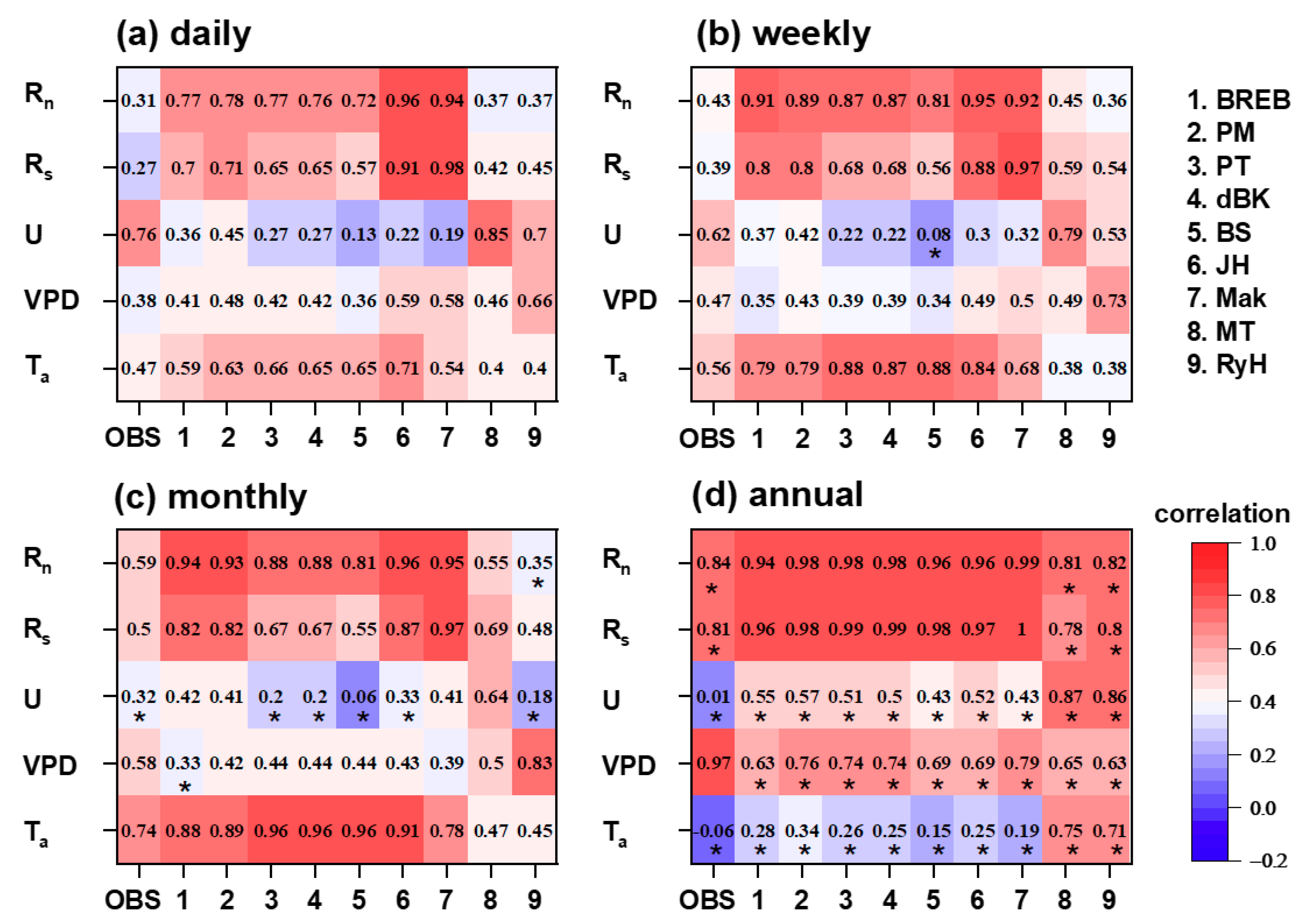
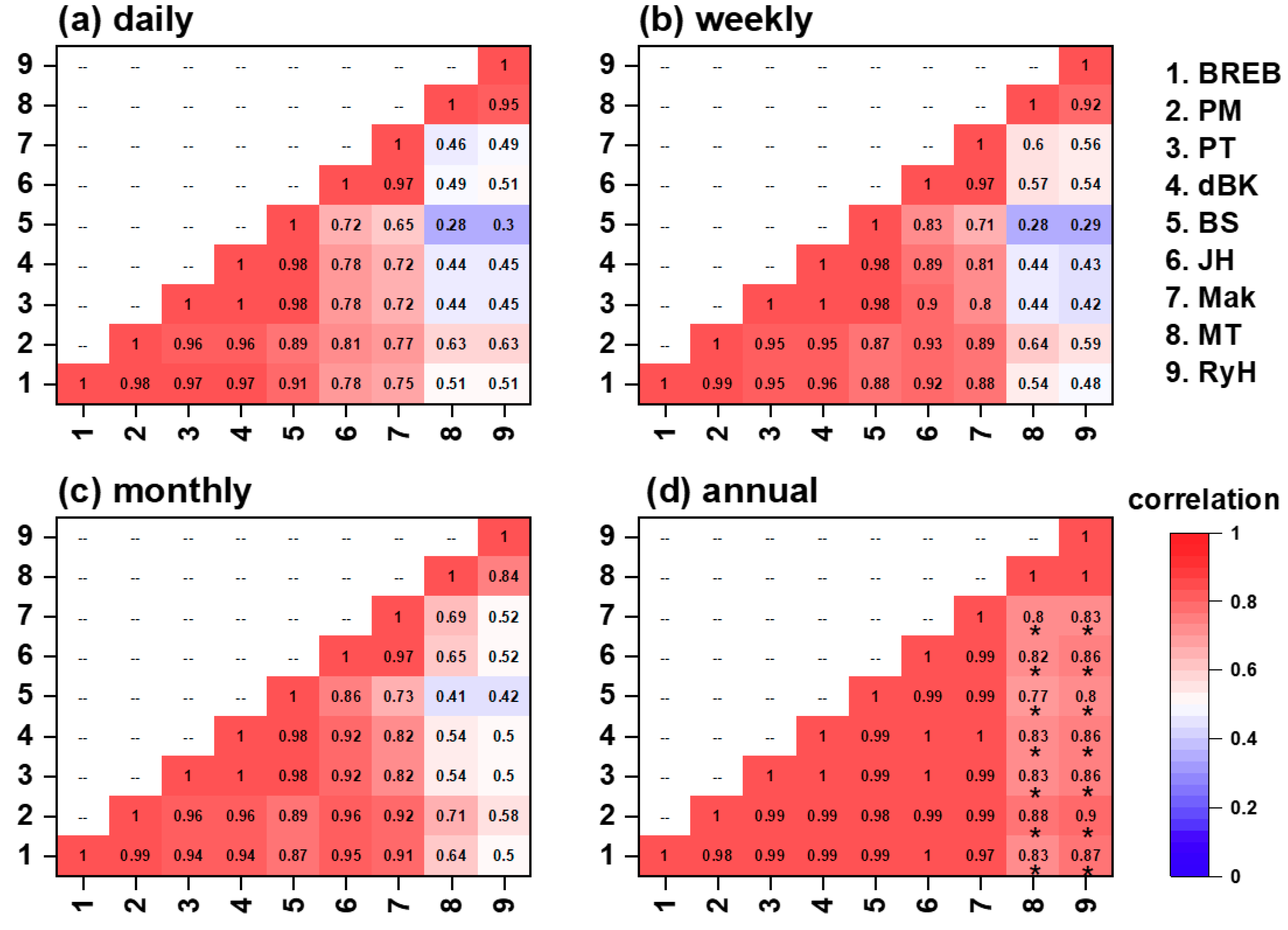
3.3. Inter-Comparisons between Evaporation Methods at Different Timescales
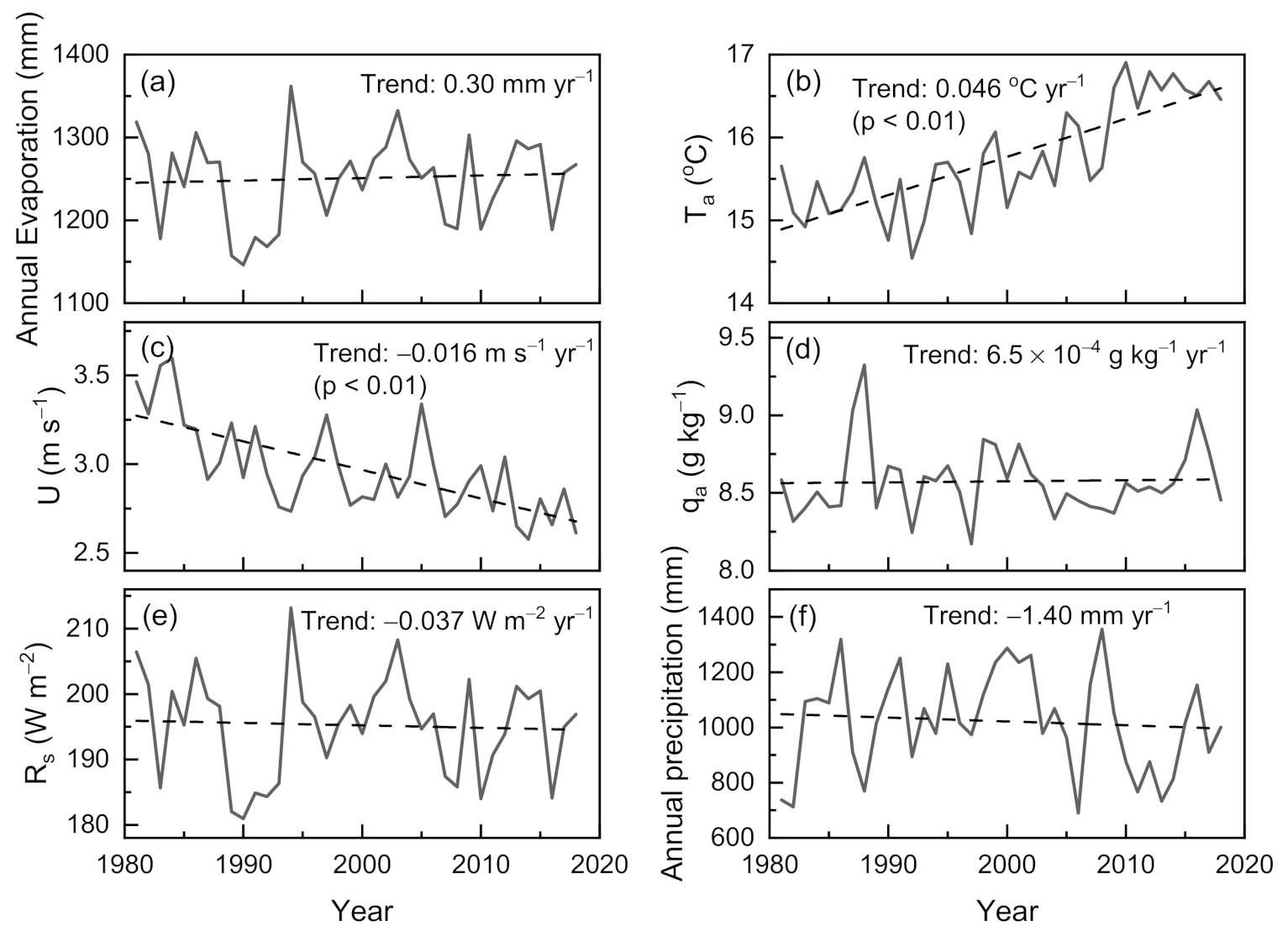
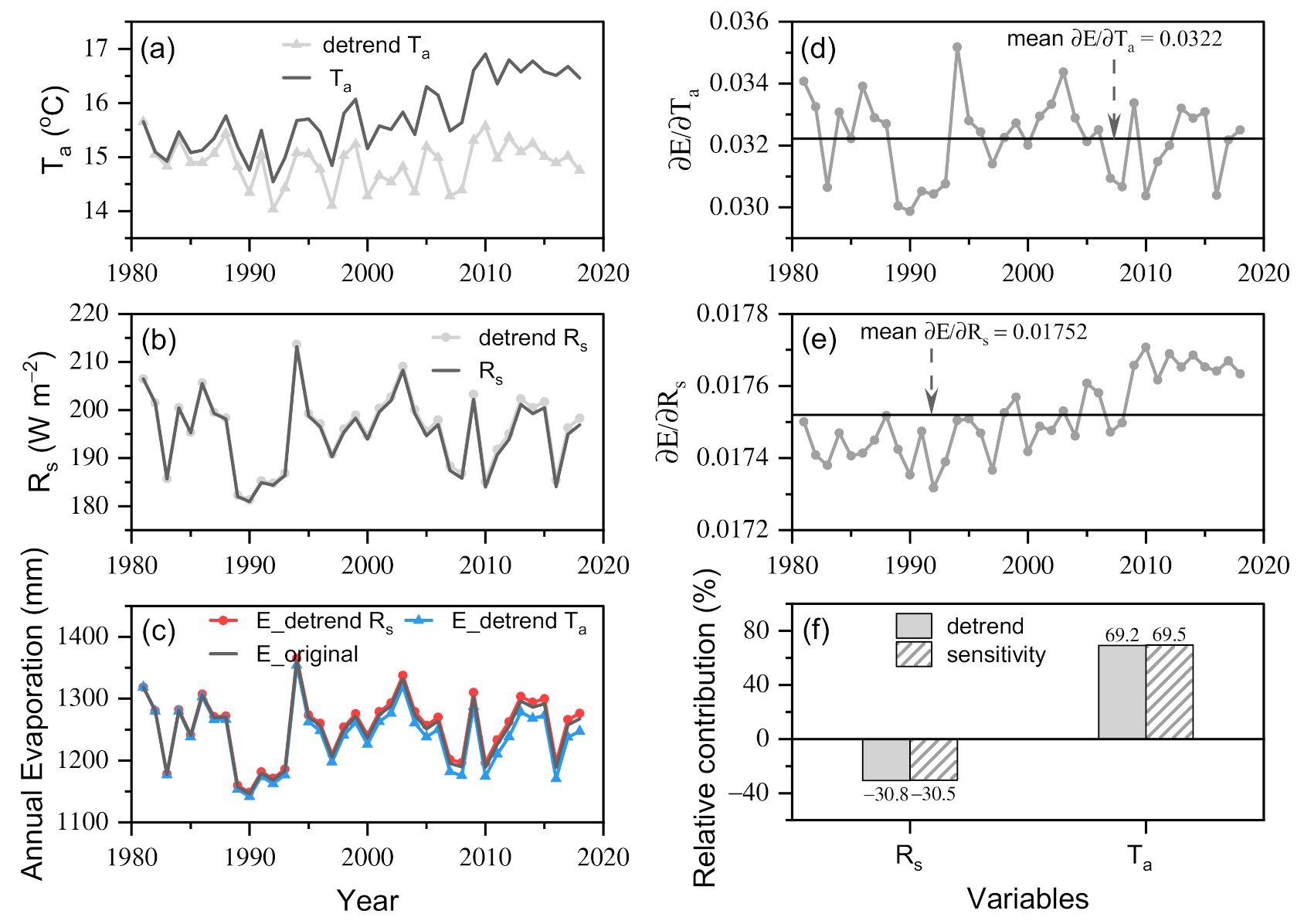
3.4. Estimation of Long-Term Lake Evaporation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gianniou, S.K.; Antonopoulos, V.Z. Evaporation and energy budget in Lake Vegoritis, Greece. J. Hydrol. 2007, 345, 212–223. [Google Scholar] [CrossRef]
- Oki, T. Global Hydrological Cycles and World Water Resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koutsoyiannis, D. Revisiting the global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M.; et al. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42, 10773. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Yu, Z.; Luo, Y.; Zhou, X.; Shang, C. Spatial-Temporal Variation of Lake Surface Water Temperature and Its Driving Factors in Yunnan-Guizhou Plateau. Water Resour. Res. 2019, 55, 4688–4703. [Google Scholar] [CrossRef]
- Sharma, S.; Blagrave, K.; Magnuson, J.J.; O’Reilly, C.M.; Oliver, S.; Batt, R.D.; Magee, M.R.; Straile, D.; Weyhenmeyer, G.A.; Winslow, L.A.; et al. Widespread loss of lake ice around the Northern Hemisphere in a warming world. Nat. Clim. Chang. 2019, 9, 227–231. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Wang, W.; Lee, X.; Xiao, W.; Liu, S.; Schultz, N.M.; Wang, Y.; Zhang, M.; Zhao, L. Global lake evaporation accelerated by changes in surface energy allocation in a warmer climate. Nat. Geosci. 2018, 11, 410–414. [Google Scholar] [CrossRef]
- Long, Z.; Perrie, W.; Gyakum, J.; Caya, D.; Laprise, R. Northern Lake Impacts on Local Seasonal Climate. J. Hydrometeorol. 2007, 8, 881–896. [Google Scholar] [CrossRef] [Green Version]
- Friedrich, K.; Grossman, R.L.; Huntington, J.; Blanken, P.D.; Lenters, J.D.; Holman, K.D.; Gochis, D.; Livneh, B.; Prairie, J.; Skeie, E.; et al. Reservoir Evaporation in the Western United States: Current Science, Challenges, and Future Needs. Bull. Am. Meteorol. Soc. 2018, 99, 167–187. [Google Scholar] [CrossRef]
- Xiao, K.; Griffis, T.J.; Baker, J.M.; Bolstad, P.V.; Erickson, M.D.; Lee, X.; Wood, J.D.; Hu, C.; Nieber, J.L. Evaporation from a temperate closed-basin lake and its impact on present, past, and future water level. J. Hydrol. 2018, 561, 59–75. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef] [Green Version]
- Sene, K.; Gash, J.; McNeil, D. Evaporation from a tropical lake: Comparison of theory with direct measurements. J. Hydrol. 1991, 127, 193–217. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Liu, S.; Jiang, H.; Sheng, L.; Williams, Q.L. Eddy covariance measurements of surface energy budget and evaporation in a cool season over southern open water in Mississippi. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Nordbo, A.; Launiainen, S.; Mammarella, I.; Leppäranta, M.; Huotari, J.; Ojala, A.; Vesala, T. Long-term energy flux measurements and energy balance over a small boreal lake using eddy covariance technique. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Shao, C.; Chen, J.; Stepien, C.A.; Chu, H.; Ouyang, Z.; Bridgeman, T.B.; Czajkowski, K.P.; Becker, R.H.; John, R. Diurnal to annual changes in latent, sensible heat, and CO2 fluxes over a Laurentian Great Lake: A case study in Western Lake Erie. J. Geophys. Res. Biogeosciences 2015, 120, 1587–1604. [Google Scholar] [CrossRef]
- Philippe, C.; Ma, Y.-J.; Huang, Y.-M.; Hu, X.; Wu, X.-C.; Wang, P.; Li, G.-Y.; Zhang, S.-Y.; Wu, H.-W.; Jiang, Z.-Y.; et al. Evaporation and surface energy budget over the largest high-altitude saline lake on the Qinghai-Tibet Plateau. J. Geophys. Res. Atmos. 2016, 121, 10470. [Google Scholar] [CrossRef]
- Bowen, I.S. The Ratio of Heat Losses by Conduction and by Evaporation from any Water Surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef] [Green Version]
- Lenters, J.D.; Kratz, T.K.; Bowser, C.J. Effects of climate variability on lake evaporation: Results from a long-term energy budget study of Sparkling Lake, northern Wisconsin (USA). J. Hydrol. 2005, 308, 168–195. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. In Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character; The Royal Society: London, UK, 1948; Volume 193, pp. 120–145. [Google Scholar]
- Harbeck, G.E. A Practical Field Technique for Measuring Reservoir Evaporation Utilizing Mass-Transfer Theory; U.S. Government Publishing Office: Washington, DC, USA, 1962; pp. 101–105.
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History, and Application, 1st ed.; Kluwer Academic: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Xu, C.Y.; Singh, V.P. Evaluation and generalization of radiation-based methods for calculating evaporation. Hydrol. Process. 2000, 14, 339–349. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Singh, V.P. Evaluation and generalization of temperature-based methods for calculating evaporation. Hydrol. Process. 2001, 15, 305–319. [Google Scholar] [CrossRef] [Green Version]
- Rosenberry, D.O.; Winter, T.C.; Buso, D.; Likens, G.E. Comparison of 15 evaporation methods applied to a small mountain lake in the northeastern USA. J. Hydrol. 2007, 340, 149–166. [Google Scholar] [CrossRef]
- Finch, J.; Calver, A. Methods for the Quantification of Evaporation from Lakes; World Meteorological Organization’s Commission for Hydrology: Oxfordshire, UK, 2008. [Google Scholar]
- Duan, Z.; Bastiaanssen, W.G.M. Evaluation of three energy balance-based evaporation models for estimating monthly evaporation for five lakes using derived heat storage changes from a hysteresis model. Environ. Res. Lett. 2017, 12, 024005. [Google Scholar] [CrossRef] [Green Version]
- Singh, V.P.; Xu, C.Y. Evaluation and generalization of 13 mass-transfer equations for determining free water evaporation. Hydrol. Process. 1997, 11, 311–323. [Google Scholar] [CrossRef]
- Elsawwaf, M.; Willems, P.; Pagano, A.; Berlamont, J. Evaporation estimates from Nasser Lake, Egypt, based on three floating station data and Bowen ratio energy budget. Theor. Appl. Clim. 2009, 100, 439–465. [Google Scholar] [CrossRef] [Green Version]
- Majidi, M.; Alizadeh, A.; Farid, A.; Vazifedoust, M. Estimating Evaporation from Lakes and Reservoirs under Limited Data Condition in a Semi-Arid Region. Water Resour. Manag. 2015, 29, 3711–3733. [Google Scholar] [CrossRef]
- Wang, W.; Xiao, W.; Cao, C.; Gao, Z.; Hu, Z.; Liu, S.; Shen, S.; Wang, L.; Xiao, Q.; Xu, J.; et al. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. J. Hydrol. 2014, 511, 811–824. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Ma, W.; Su, B.; Dong, X. Evaluation of ten methods for estimating evaporation in a small high-elevation lake on the Tibetan Plateau. Theor. Appl. Clim. 2018, 136, 1033–1045. [Google Scholar] [CrossRef]
- McGloin, R.; McGowan, H.; McJannet, D.; Burn, S. Modelling sub-daily latent heat fluxes from a small reservoir. J. Hydrol. 2014, 519, 2301–2311. [Google Scholar] [CrossRef] [Green Version]
- Metzger, J.; Nied, M.; Corsmeier, U.; Kleffmann, J.; Kottmeier, C. Dead Sea evaporation by eddy covariance measurements vs. aerodynamic, energy budget, Priestley–Taylor, and Penman estimates. Hydrol. Earth Syst. Sci. 2018, 22, 1135–1155. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Liu, H.; Xu, L.; Liu, Y.; Wang, L. The monsoon effect on energy and carbon exchange processes over a highland lake in the southwest of China. Atmos. Chem. Phys. 2018, 18, 15087–15104. [Google Scholar] [CrossRef] [Green Version]
- Xu, A.; Li, J. An Overview of the Integrated Meteorological Observations in Complex Terrain Region at Dali National Climate Observatory, China. Atmosphere 2020, 11, 279. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Liu, H.; Liu, Y.; Wang, L.; Xu, L.J.; Sun, J.H.; Xu, A.L. Factors controlling evaporation and the CO2 flux over an open water lake in southwest of China on multiple temporal scales. Int. J. Clim. 2018, 38, 4723–4739. [Google Scholar] [CrossRef]
- Feng, J.W.; Liu, H.; Sun, J.H.; Wang, L. The surface energy budget and interannual variation of the annual total evaporation over a highland lake in Southwest China. Theor. Appl. Clim. 2015, 126, 303–312. [Google Scholar] [CrossRef]
- Liu, H.; Feng, J.; Sun, J.; Wang, L.; Xu, A. Eddy covariance measurements of water vapor and CO2 fluxes above the Erhai Lake. Sci. China Earth Sci. 2014, 58, 317–328. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement, 1st ed.; Oxford University Press: Oxford, UK, 1994; p. 289. [Google Scholar]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of Flux Measurements for Density Effects Due to Heat and Water-Vapor Transfer. Q. J. Roy. Meteor. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Documentation and instruction manual of the eddy-covariance software package324 TK3. Abt. Mikrometeorol. 2004, 46. Available online: https://core.ac.uk/download/pdf/33806389.pdf (accessed on 11 November 2020).
- Kormann, R.; Meixner, F.X. An Analytical Footprint Model for Non-Neutral Stratification. Boundary-Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. Assessment of Surface Heat-Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Keijman, J.Q. The Priestley-Taylor Evaporation Model Applied to a Large, Shallow Lake in the Netherlands. J. Appl. Meteorol. 1979, 18, 898–903. [Google Scholar] [CrossRef] [Green Version]
- Hicks, B.B.; Hess, G.D. On the Bowen Ratio and Surface Temperature at Sea. J. Phys. Oceanogr. 1977, 7, 141–145. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W.; Stricker, H. An advection-aridity approach to estimate actual regional evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. Proc. Am. Soc. Civil Eng. 1963, 89, 15–41. [Google Scholar]
- Makkink, G.F. Testing the Penman Formula by Means of Lysimeters. J. Instit. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Harbeck, G.E. Water-Loss Investigations: Lake Mead studies; U.S. Government Publishing Office: Washington, DC, USA, 1958; p. 100.
- Ryan, P.J.; Harleman, D.R.F. An Analytical and Experimental Study of Transient Cooling Pond Behavior. In Parsons Laboratory for Water Resources and Hydrodynamics; Ralph, M., Ed.; Massachusetts Institute of Technology: Cambridge, UK, 1973. [Google Scholar]
- Duan, Z.; Bastiaanssen, W. A new empirical procedure for estimating intra-annual heat storage changes in lakes and reservoirs: Review and analysis of 22 lakes. Remote Sens. Environ. 2015, 156, 143–156. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Zhang, L.; Zhang, Q.; Gan, R.; Li, X. Attribution of Evapotranspiration Changes in Humid Regions of China from 1982 to 2016. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, X.; Liu, C.; Dai, X.; Zhu, R. Assessing contributions to panevaporation trends in Haihe River Basin, China. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Momii, K.; Ito, Y. Heat budget estimates for Lake Ikeda, Japan. J. Hydrol. 2008, 361, 362–370. [Google Scholar] [CrossRef]
- Blanken, P.D.; Spence, C.; Hedstrom, N.; Lenters, J.D. Evaporation from Lake Superior: 1. Physical controls and processes. J. Great Lakes Res. 2011, 37, 707–716. [Google Scholar] [CrossRef]
- Shao, C.; Chen, J.; Chu, H.; Stepien, C.A.; Ouyang, Z. Intra-Annual and Interannual Dynamics of Evaporation Over Western Lake Erie. Earth Space Sci. 2020, 7, 001091. [Google Scholar] [CrossRef]
- Finch, J.W.; Hall, R.L. Estimation of Open Water Evaporation; Environment Agency: Bristol, UK, 2001.
- Liu, H.; Zhang, Q.; Dowler, G. Environmental Controls on the Surface Energy Budget over a Large Southern Inland Water in the United States: An Analysis of One-Year Eddy Covariance Flux Data. J. Hydrometeorol. 2012, 13, 1893–1910. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, A.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef] [Green Version]
- Gan, G.; Liu, Y. Heat Storage Effect on Evaporation Estimates of China’s Largest Freshwater Lake. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
- Giadrossich, F.; Niedda, M.; Cohen, D.; Pirastru, M.I. Evaporation in a Mediterranean environment by energy budget and Penman methods, Lake Baratz, Sardinia, Italy. Hydrol. Earth Syst. Sci. 2015, 19, 2451–2468. [Google Scholar] [CrossRef] [Green Version]
- Mauder, M.; Foken, T.; Cuxart, J. Surface-Energy-Balance Closure over Land: A Review. Boundary-Layer Meteorol. 2020, 177, 395–426. [Google Scholar] [CrossRef]
- Pérez, A.; Lagos, O.; Lillo-Saavedra, M.; Souto, C.; Paredes, J.; Arumi, J. Mountain Lake Evaporation: A Comparative Study between Hourly Estimations Models and In Situ Measurements. Water 2020, 12, 2648. [Google Scholar] [CrossRef]
- Gan, G.; Liu, Y.; Pan, X.; Zhao, X.; Li, M.; Wang, S. Seasonal and Diurnal Variations in the Priestley–Taylor Coefficient for a Large Ephemeral Lake. Water 2020, 12, 849. [Google Scholar] [CrossRef] [Green Version]
- Jansen, F.A.; Teuling, A. Evaporation from a large lowland reservoir—(Dis)agreement between evaporation models from hourly to decadal timescales. Hydrol. Earth Syst. Sci. 2020, 24, 1055–1072. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, A.H.; Hondzo, M.; Stefan, H.G. A Test of Several Evaporation Equations for Water Temperature Simulations in Lakes. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 1023–1028. [Google Scholar] [CrossRef]
- Liefert, D.T.; Shuman, B.N.; Parsekian, A.D.; Mercer, J.J. Why Are Some Rocky Mountain Lakes Ephemeral? Water Resour. Res. 2018, 54, 5245–5263. [Google Scholar] [CrossRef]
- Abtew, W. Evaporation Estimation for Lake Okeechobee in South Florida. J. Irrig. Drain. Eng. 2001, 127, 140–147. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Y.; Wang, W.; Liu, S.; Piao, M.; Xiao, W.; Lee, X. Trends in evaporation of a large subtropical lake. Theor. Appl. Clim. 2017, 129, 159–170. [Google Scholar] [CrossRef]
- Althoff, D.; Rodrigues, L.N.; da Silva, D.D. Evaluating Evaporation Methods for Estimating Small Reservoir Water Surface Evaporation in the Brazilian Savannah. Water 2019, 11, 1942. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.J.; Wang, Y.P.; Li, Q.H. Evaporation variation from Erhai Lake and its controls under climatic warming. J. Meteorol. Environ. 2010, 26, 32–35. [Google Scholar]
- Zhao, G.; Gao, H. Estimating reservoir evaporation losses for the United States: Fusing remote sensing and modeling approaches. Remote. Sens. Environ. 2019, 226, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.J.; Wang, Y.P.; Li, Q.H. Climatic Characteristics over Erhai Lake Basin in the Late 50 Years and the Impact on Water Resources of Erhai Lake. Meteor Mon. 2013, 39, 436–442. [Google Scholar]
- Tao, S.; Zhang, H.; Feng, Y.; Zhu, J.; Cai, Q.; Xiong, X.; Ma, S.; Fang, L.; Fang, W.; Tian, D.; et al. Changes in China’s water resources in the early 21st century. Front. Ecol. Environ. 2020, 18, 188–193. [Google Scholar] [CrossRef]
- Ding, W.R. A Study on the Characteristics of Climate Change around the Erhai Area, China. Res. Environ. Yangtze Basin 2016, 25, 599–605. [Google Scholar]
| Methods | V0 | V1 | |
|---|---|---|---|
| Combination methods | BREB | is calculated from measured water temperature profiles. | is derived from the hysteresis function of Rn where a, b, and c are empirical constants and determined by the measurement data |
| PM | |||
| PT | |||
| dBK | |||
| BS | |||
| Solar radiation-based methods | JH | Default setting in Section 2.3 | |
| Mak | |||
| Dalton-based methods | MT | , Von-Karman constant (0.4, dimensionless) Air density (kg m−3) Measurement height (5 m); Momentum roughness length (0.001 m); | |
| RyH | |||
| R | RMSE (mm d−1) | MAE (mm d−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1d | 7d | Monthly | 1d | 7d | Monthly | 1d | 7d | Monthly | ||
| BREB | 0.53 | 0.70 | 0.83 | 1.63 | 1.02 | 0.74 | 1.30 | 0.85 | 0.65 | |
| PM | 0.62 | 0.76 | 0.88 | 1.31 | 0.82 | 0.58 | 1.03 | 0.68 | 0.51 | |
| PT | 0.53 | 0.72 | 0.87 | 1.58 | 1.00 | 0.72 | 1.22 | 0.81 | 0.61 | |
| dBK | 0.52 | 0.71 | 0.87 | 1.58 | 1.01 | 0.74 | 1.23 | 0.82 | 0.63 | |
| V0 | BS | 0.43 | 0.65 | 0.82 | 1.97 | 1.32 | 1.02 | 1.54 | 1.08 | 0.88 |
| JH | 0.55 | 0.74 | 0.85 | 1.65 | 1.05 | 0.74 | 1.28 | 0.83 | 0.64 | |
| Mak | 0.48 | 0.70 | 0.78 | 1.50 | 0.97 | 0.74 | 1.13 | 0.74 | 0.61 | |
| MT | 0.85 | 0.81 | 0.73 | 1.77 | 1.47 | 1.31 | 1.44 | 1.22 | 1.16 | |
| RyH | 0.82 | 0.80 | 0.74 | 0.79 | 0.56 | 0.44 | 0.61 | 0.45 | 0.38 | |
| BREB | 0.50 | 0.66 | 0.79 | 1.59 | 1.02 | 0.76 | 1.27 | 0.86 | 0.66 | |
| PM | 0.61 | 0.75 | 0.85 | 1.31 | 0.83 | 0.59 | 1.04 | 0.69 | 0.51 | |
| PT | 0.50 | 0.70 | 0.84 | 1.61 | 1.02 | 0.74 | 1.28 | 0.83 | 0.63 | |
| dBK | 0.49 | 0.69 | 0.84 | 1.61 | 1.03 | 0.76 | 1.28 | 0.84 | 0.64 | |
| V1 | BS | 0.38 | 0.59 | 0.78 | 2.02 | 1.36 | 1.07 | 1.62 | 1.11 | 0.91 |
| JH | 0.45 | 0.67 | 0.74 | 1.51 | 0.86 | 0.53 | 1.18 | 0.70 | 0.42 | |
| Mak | 0.48 | 0.70 | 0.78 | 1.50 | 0.87 | 0.54 | 1.17 | 0.70 | 0.43 | |
| MT | 0.86 | 0.82 | 0.76 | 0.82 | 0.61 | 0.48 | 0.64 | 0.50 | 0.40 | |
| RyH | 0.84 | 0.82 | 0.77 | 0.76 | 0.53 | 0.40 | 0.58 | 0.43 | 0.34 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Liu, H.; Du, Q.; Xu, L.; Liu, Y. Evaluation of the Performance of Different Methods for Estimating Evaporation over a Highland Open Freshwater Lake in Mountainous Area. Water 2020, 12, 3491. https://doi.org/10.3390/w12123491
Meng X, Liu H, Du Q, Xu L, Liu Y. Evaluation of the Performance of Different Methods for Estimating Evaporation over a Highland Open Freshwater Lake in Mountainous Area. Water. 2020; 12(12):3491. https://doi.org/10.3390/w12123491
Chicago/Turabian StyleMeng, Xiaoni, Huizhi Liu, Qun Du, Lujun Xu, and Yang Liu. 2020. "Evaluation of the Performance of Different Methods for Estimating Evaporation over a Highland Open Freshwater Lake in Mountainous Area" Water 12, no. 12: 3491. https://doi.org/10.3390/w12123491
APA StyleMeng, X., Liu, H., Du, Q., Xu, L., & Liu, Y. (2020). Evaluation of the Performance of Different Methods for Estimating Evaporation over a Highland Open Freshwater Lake in Mountainous Area. Water, 12(12), 3491. https://doi.org/10.3390/w12123491






