Case Study: Reconstruction of Runoff Series of Hydrological Stations in the Nakdong River, Korea
Abstract
:1. Introduction
2. Methods
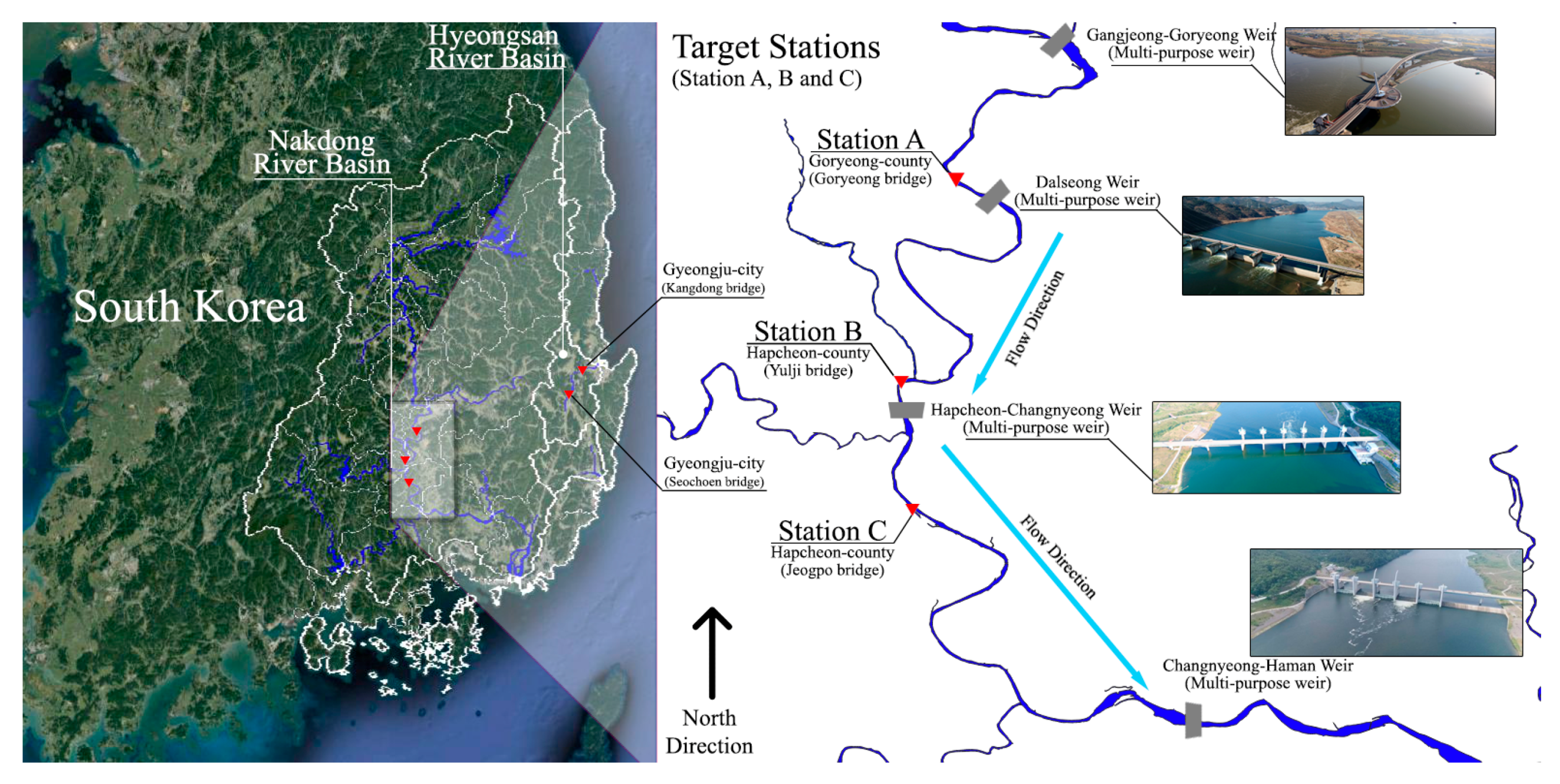
2.1. Study Material
2.2. Variational Mode Decomposition (VMD)
2.3. Artificial Neural Network (ANN)
3. Application and Discussion
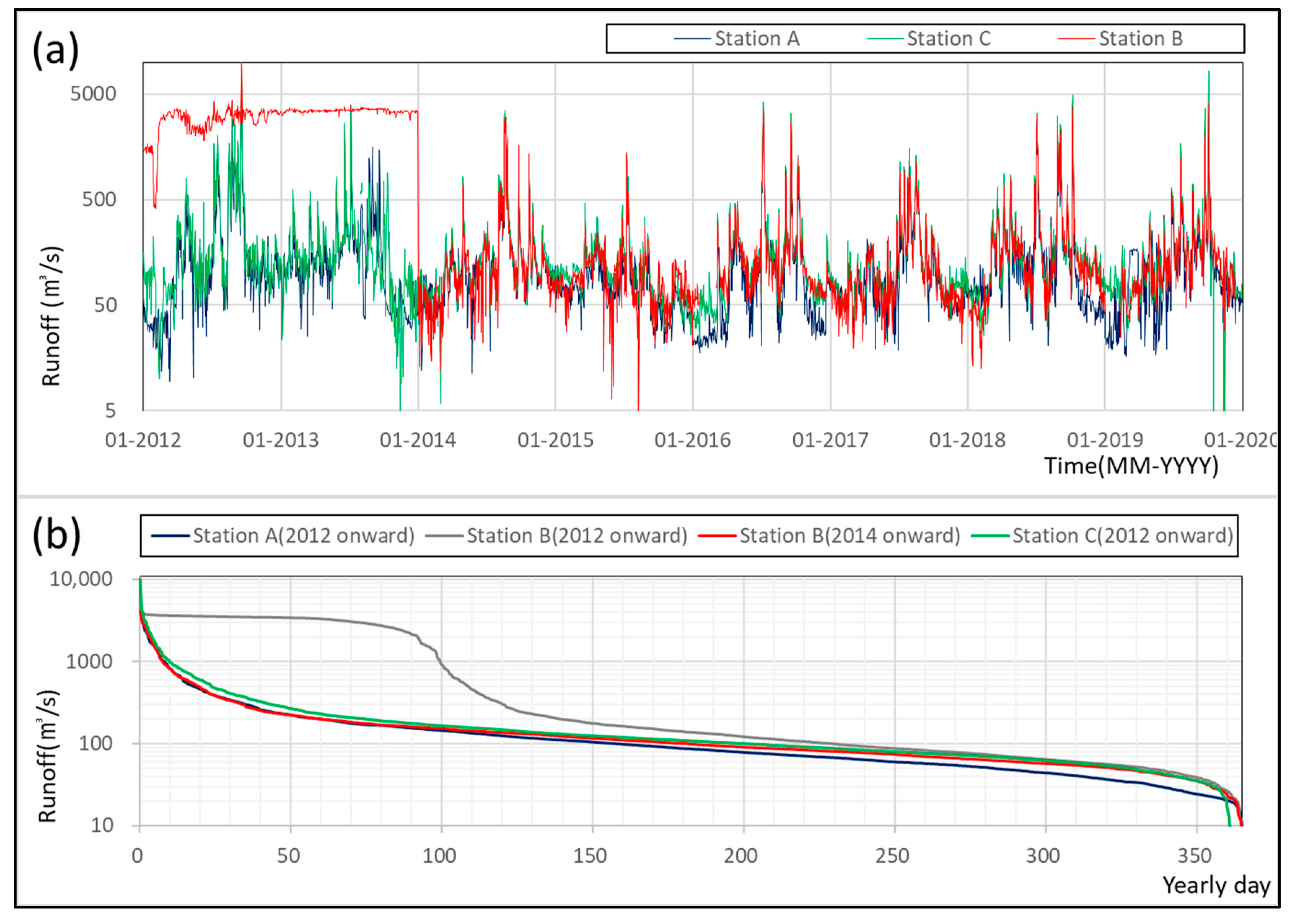
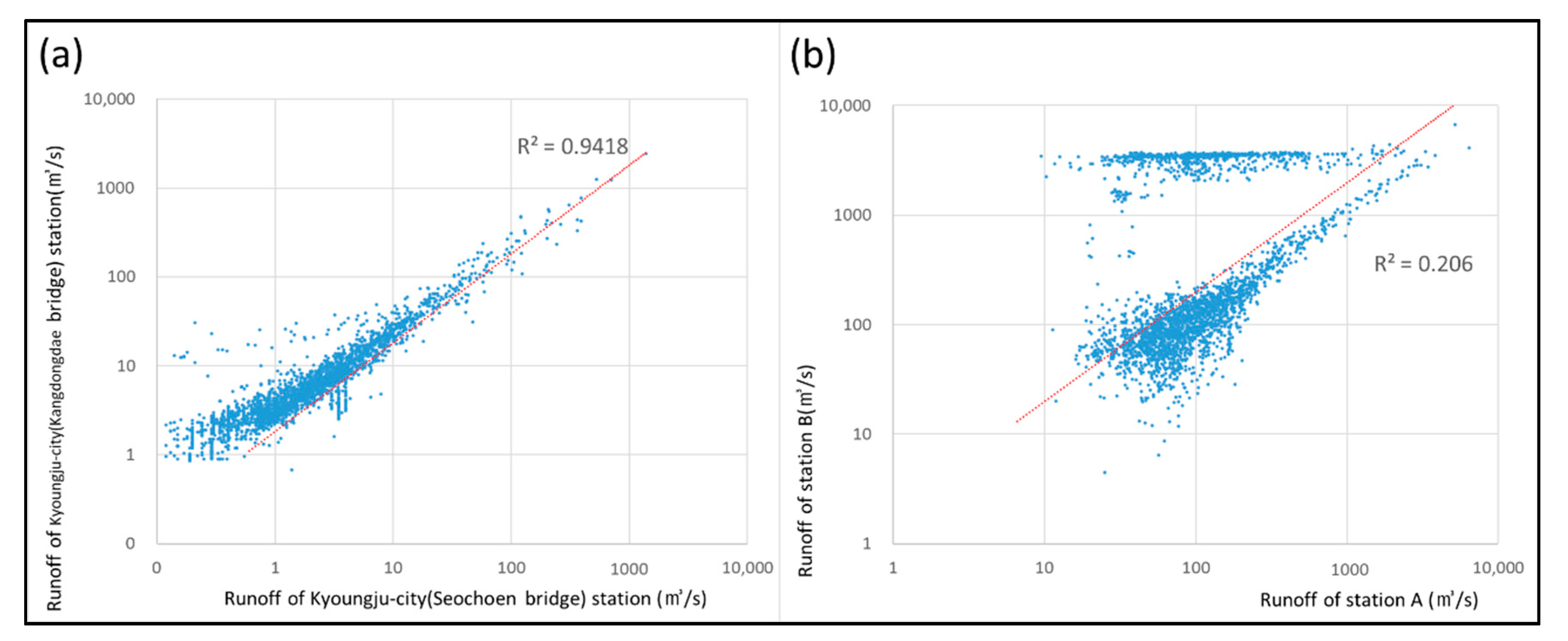
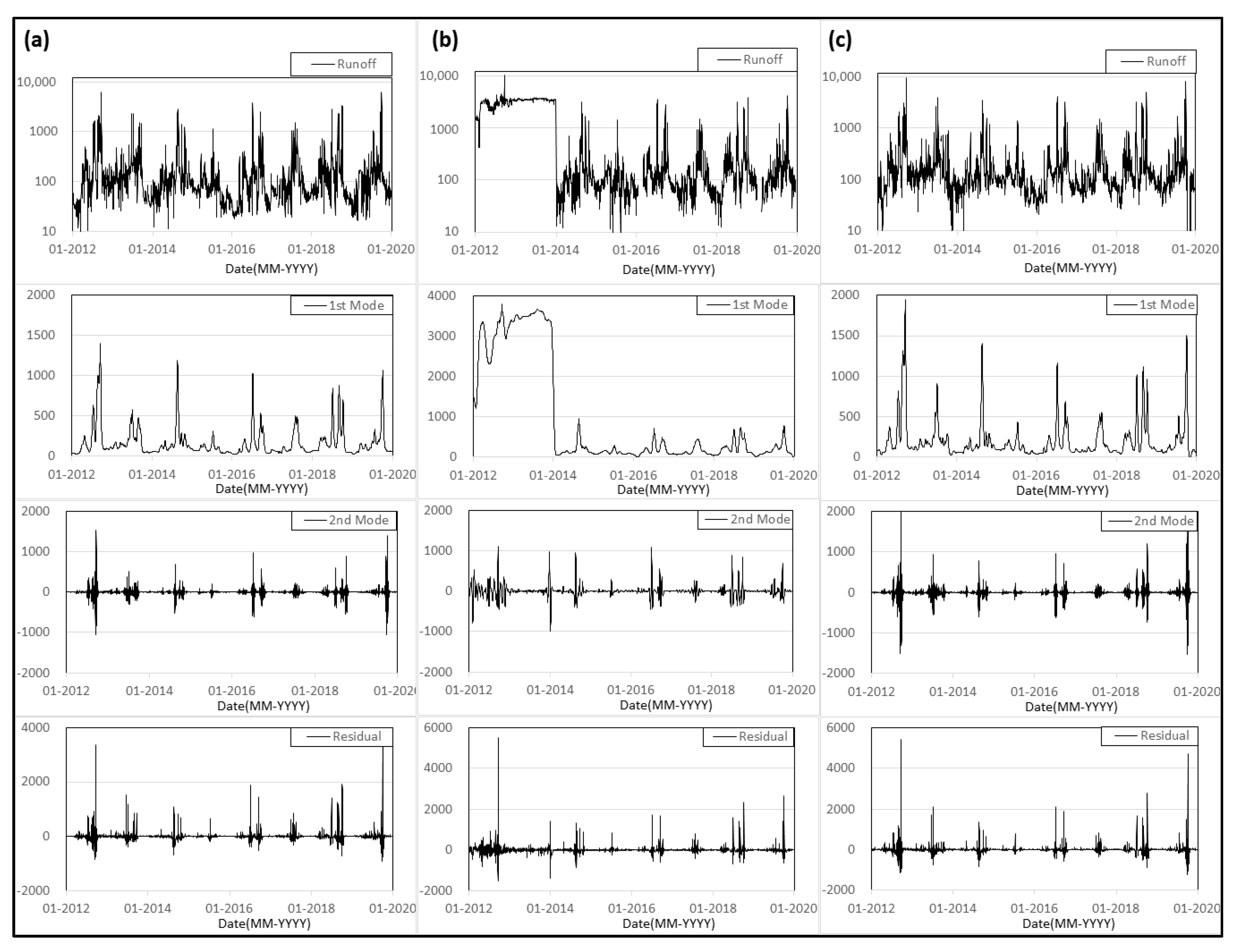
3.1. Runoff Series Characteristics and Its Decomposition
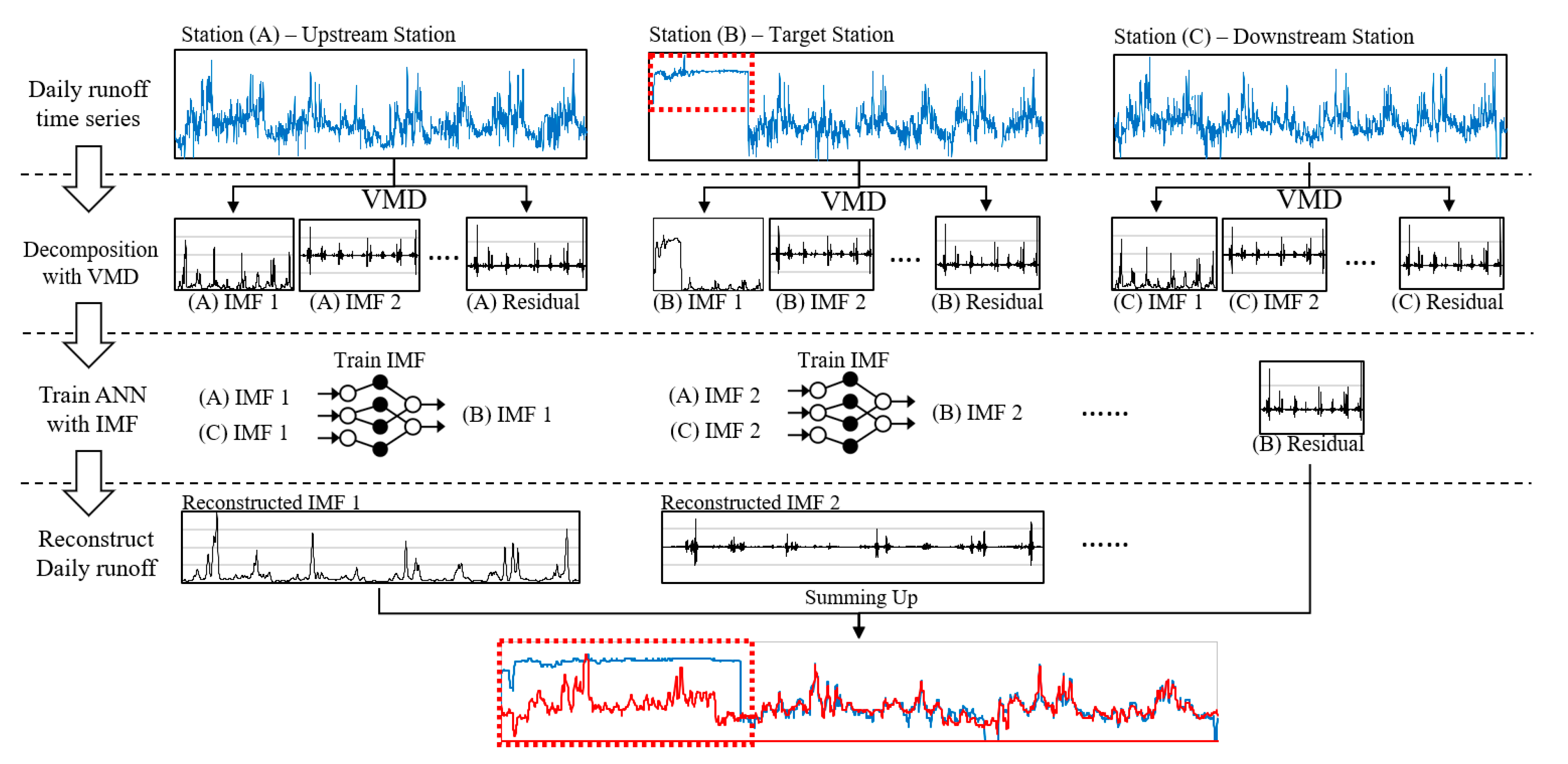
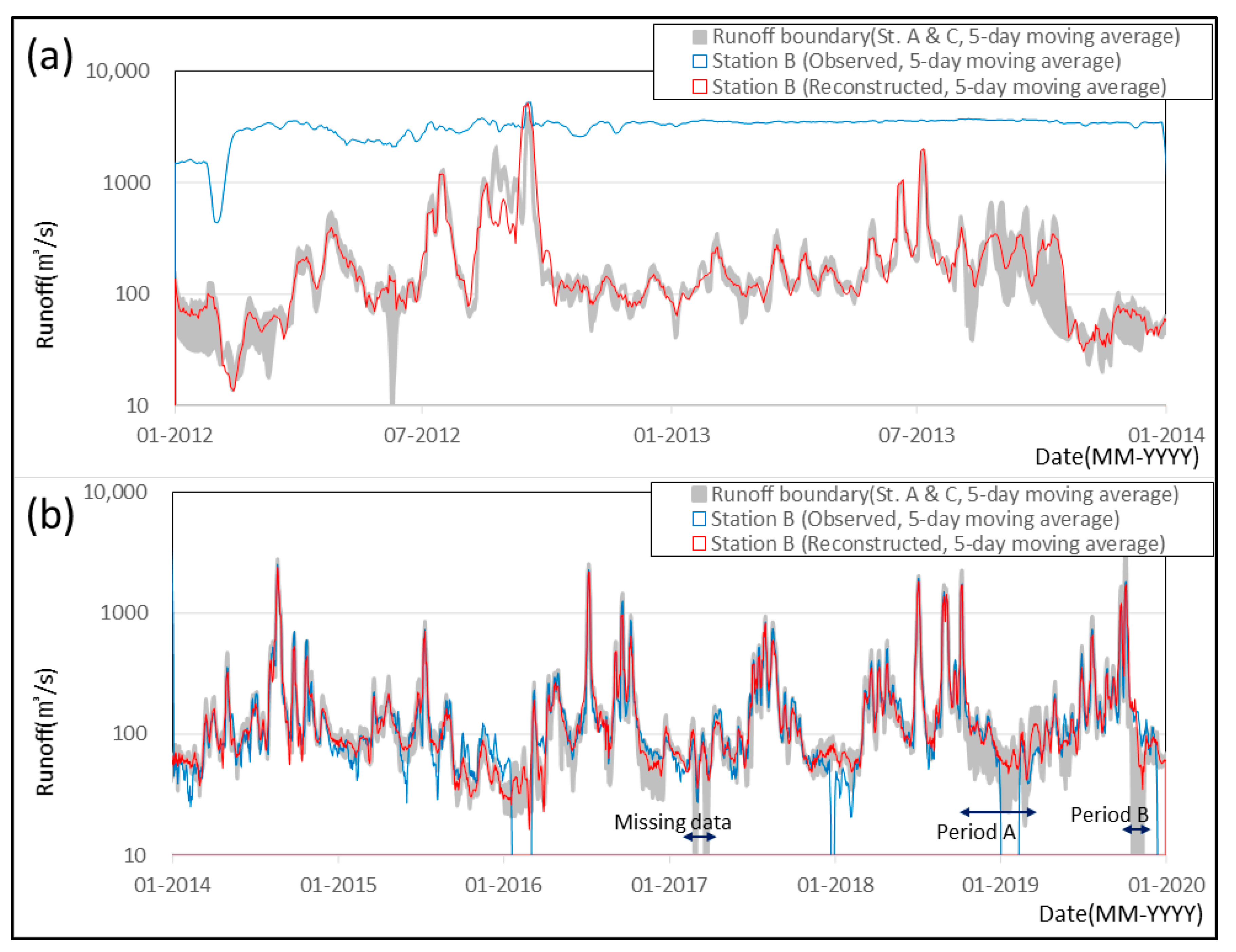
3.2. Establishment of Reconstruction Model
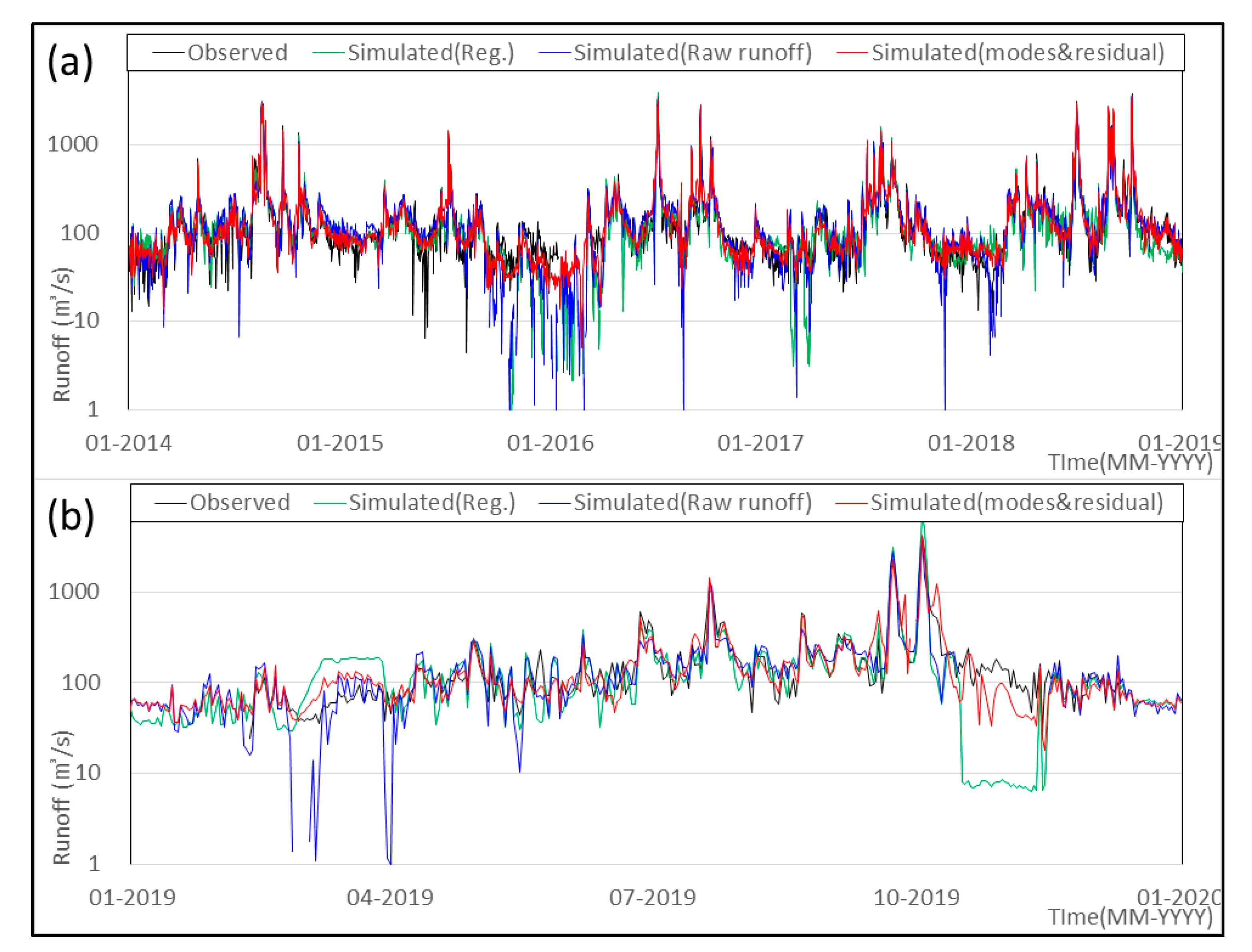
3.3. Reconstruction Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miyamura, E.; Nakajima, Y.; Yoshimura, A. Full-scale Commercialized Microwave Doppler Current Meter-Fixed Doppler Current Meter & RYUKAN. New Era River Disch. Meas. 2012, 3, 55–60. [Google Scholar]
- Stoppa, A.; Hess, U. Design and use of weather derivatives in agricultural policies: The case of rainfall index insurance in Morocco. In Proceedings of the International Conference Agricultural Policy Reform and the WTO: Where Are We Heading, Citeseer, Italy, 23–26 June 2003. [Google Scholar]
- Yamaguchi, T.; Niizato, K. Flood Discharge Observation Using Radio Current Meter. Doboku Gakkai Ronbunshu 1994, 497, 41–50. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Won, N.I.; Noh, J.; Park, W.C. Development of high-performance microwave water surface current meter for general use to extend the applicable velocity range of microwave water surface current meter on river discharge measurements. J. Korea Water Resour. Assoc. 2015, 48, 613–623. [Google Scholar]
- Zhao, Z.; Zhang, Y.; Mi, H.; Zhou, Y.; Zhang, Y. Experimental Research of a Water-Source Heat Pump Water Heater System. Energies 2018, 11, 1205. [Google Scholar] [CrossRef] [Green Version]
- Costa, J.E.; Spicer, K.R.; Cheng, R.T.; Haeni, F.P.; Melcher, N.B.; Thurman, E.M.; Plant, W.J.; Keller, W.C. measuring stream discharge by non-contact methods: A Proof-of-Concept Experiment. Geophys. Res. Lett. 2000, 27, 553–556. [Google Scholar] [CrossRef]
- Costa, J.E.; Cheng, R.T.; Haeni, F.P.; Melcher, N.; Spicer, K.R.; Hayes, E.; Plant, W.; Hayes, K.; Teague, C.; Barrick, D. Use of radars to monitor stream discharge by noncontact methods. Water Resour. Res. 2006, 42, 42. [Google Scholar] [CrossRef]
- Foster, G.R.; Huggins, L.F.; Meyer, L.D. A Laboratory Study of Rill Hydraulics: I. Velocity Relationships. Trans. ASAE 1984, 27, 790–796. [Google Scholar] [CrossRef]
- Govers, G. Relationship between discharge, velocity and flow area for rills eroding loose, non-layered materials. Earth Surf. Process. Landf. 1992, 17, 515–528. [Google Scholar] [CrossRef]
- Lei, T.; Nearing, M. Flume experiments for determining rill hydraulic characteristic erosion and rill patterns. J. Hydraul. Eng. 2000, 11, 49–54. [Google Scholar]
- Yu, K.; Kim, S.; Yoo, B.; Bae, I. A test of a far infrared camera for development of new surface image velocimeter for day and night measurement. J. Korea Water Resour. Assoc. 2015, 48, 659–672. [Google Scholar]
- Raffel, M.; Willert, C.; Wereley, S.; Kompenhans, J. Particle image velocimetry. In Experimental Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 10, pp. 978–981. [Google Scholar]
- Daly, C.; Gibson, W.; Doggett, M.; Smith, J.; Taylor, G. A probabilistic-spatial approach to the quality control of climate observations. In Proceedings of the 14th AMS Conference on Applied Climatology, American Meteorological Society, Seattle, WA, USA, 13 January 2004. [Google Scholar]
- Kundzewicz, Z.; Robson, A. Detecting Trend and Other Changes in Hydrological Data; World Meteorological Organization: Geneva, Switzerland, 2000. [Google Scholar]
- Sciuto, G.; Bonaccorso, B.; Cancelliere, A.; Rossi, G. Probabilistic quality control of daily temperature data. Int. J. Clim. 2013, 33, 1211–1227. [Google Scholar] [CrossRef] [Green Version]
- World Meteorological Organization. Manual on Stream Gauging; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 1980. [Google Scholar]
- Gunston, H. Field Hydrology in Tropical Countries: A Practical Introduction; Intermediate Technology Publications: Rugby, UK, 1998. [Google Scholar]
- Gray, B.; Toucher, M. Rain Gauge Accuracy at a High-Altitude Meteorological Station in Cathedral Peak. J. Hydrol. Eng. 2019, 24, 04018064. [Google Scholar] [CrossRef]
- Lewis, E.; Quinn, N.; Blenkinsop, S.; Fowler, H.J.; Freer, J.; Tanguy, M.; Hitt, O.; Coxon, G.; Bates, P.; Woods, R. A rule based quality control method for hourly rainfall data and a 1 km resolution gridded hourly rainfall dataset for Great Britain: CEH-GEAR1hr. J. Hydrol. 2018, 564, 930–943. [Google Scholar] [CrossRef]
- Cressman, G.P. An Operation Objective Analysis System. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Barnes, S.L. A Technique for Maximizing Details in Numerical Weather Map Analysis. J. Appl. Meteorol. 1964, 3, 396–409. [Google Scholar] [CrossRef] [Green Version]
- Banhatti, A.G.; Deka, P.C. Performance Evaluation of Artificial Neural Network Model using Data Preprocessing in Non-Stationary Hydrologic Time Series. Int. J. Artif. Intell. Syst. Mach. Learn. 2012, 4, 223–229. [Google Scholar]
- Nourani, V.; Komasi, M.; Mano, A. A Multivariate ANN-Wavelet Approach for Rainfall–Runoff Modeling. Water Resour. Manag. 2009, 23, 2877–2894. [Google Scholar] [CrossRef]
- Kozma, R.; Kitamura, M.; Sakuma, M.; Yokoyama, Y. Anomaly detection by neural network models and statistical time series analysis. In Proceedings of the 1994 IEEE International Conference on Neural Networks, Orlando, FL, USA, USA, 28 June–2 July 1994; pp. 3207–3210. [Google Scholar]
- Sciuto, G.; Bonaccorso, B.; Cancelliere, A.; Rossi, G. Quality control of daily rainfall data with neural networks. J. Hydrol. 2009, 364, 13–22. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lee, M.K.; Moon, S.H.; Yoon, Y.; Kim, Y.H.; Moon, B.R. Detecting anomalies in meteorological data using support vector regression. Adv. Meteorol. 2018, 2018, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Asefa, T.; Kemblowski, M.; McKee, M.; Khalil, A. Multi-time scale stream flow predictions: The support vector machines approach. J. Hydrol. 2006, 318, 7–16. [Google Scholar] [CrossRef]
- Lin, J.Y.; Cheng, C.T.; Chau, K.W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Georgievskii, V.Y.; Grek, E.A.; Grek, E.N.; Lobanova, A.G.; Molchanova, T.G. Spatiotemporal Changes in Extreme Runoff Characteristics for the Volga Basin Rivers. Russ. Meteorol. Hydrol. 2018, 43, 633–638. [Google Scholar] [CrossRef]
- Langhammer, J.; Česák, J. Applicability of a Nu-Support Vector Regression Model for the Completion of Missing Data in Hydrological Time Series. Water 2016, 8, 560. [Google Scholar] [CrossRef] [Green Version]
- Tencaliec, P.; Favre, A.C.; Prieur, C.; Mathevet, T. Reconstruction of missing daily streamflow data using dynamic regression models. Water Resour. Res. 2015, 51, 9447–9463. [Google Scholar] [CrossRef] [Green Version]
- Coulibaly, P.; Evora, N.D. Comparison of neural network methods for infilling missing daily weather records. J. Hydrol. 2007, 341, 27–41. [Google Scholar] [CrossRef]
- Kim, J.W.; Pachepsky, Y.A. Reconstructing missing daily precipitation data using regression trees and artificial neural networks for SWAT streamflow simulation. J. Hydrol. 2010, 394, 305–314. [Google Scholar] [CrossRef]
- Dastorani, M.T.; Moghadamnia, A.; Piri, J.; Rico-Ramirez, M. Application of ANN and ANFIS models for reconstructing missing flow data. Environ. Monit. Assess. 2010, 166, 421–434. [Google Scholar] [CrossRef]
- Jeffrey, S.J.; Carter, J.O.; Moodie, K.B.; Beswick, A.R. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ. Model. Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.; Chandramouli, V. Improved weighting methods, deterministic and stochastic data-driven models for estimation of missing precipitation records. J. Hydrol. 2005, 312, 191–206. [Google Scholar] [CrossRef]
- Zuo, G.; Luo, J.; Wang, N.; Lian, Y.; He, X. Two-stage Variational Mode Decomposition and Support Vector Regression for Streamflow Forecasting. Hydrol. Earth Syst. Sci. 2020, 24, 5491–5518. [Google Scholar] [CrossRef]
- He, X.; Luo, J.; Zuo, G.; Xie, J. Daily Runoff Forecasting Using a Hybrid Model Based on Variational Mode Decomposition and Deep Neural Networks. Water Resour. Manag. 2019, 33, 1571–1590. [Google Scholar] [CrossRef]
- Xie, T.; Zhang, G.; Hou, J.; Xie, J.; Lv, M.; Liu, F. Hybrid forecasting model for non-stationary daily runoff series: A case study in the Han River Basin, China. J. Hydrol. 2019, 577, 123915. [Google Scholar] [CrossRef]
- Ministry of Land, Transport and Maritime Affairs. Basic Plan for the Nakdong River Development and Management; Ministry of Land, Transport and Maritime Affairs: Sejong, Korea, 2009. [Google Scholar]
- Morlock, S.E.; Nguyen, H.T.; Ross, J.H. Feasibility of Acoustic Doppler Velocity Meters for the Production of Discharge Records from US Geological Survey Streamflow-Gaging Stations; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2002. [Google Scholar]
- Ministry of Land, Transport and Maritime Affairs. Masterplan for the Four Major Rivers Project; Ministry of Land, Transport and Maritime Affairs: Sejong, Korea, 2009. [Google Scholar]
- Ministry of Environment. Water Resources Management Information System. Available online: http://www.wamis.go.kr (accessed on 6 June 2020).
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal. Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Royal Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. In IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing; NSIP-03; IEEE: Piscataway, NJ, USA, 2003; pp. 8–11. [Google Scholar]
- Liu, W.; Cao, S.; Chen, Y. Applications of variational mode decomposition in seismic time-frequency analysis. Geophysics 2016, 81, 365–378. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Herrera, R.H.; Han, J.; van der Baan, M. Applications of the synchrosqueezing transform in seismic time-frequency analysis. Geophysics 2014, 79, V55–V64. [Google Scholar] [CrossRef]
- Schürmann, J. Pattern Classification: A Unified View of Statistical and Neural Approaches; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Soltane, M.; Ismail, M.; Rashid, Z.A.A. Artificial Neural Networks (ANN) approach to PPG signal classification. Int. J. Comput. Inf. Sci. 2004, 2, 58–65. [Google Scholar]
- Dase, R.K.; Pawar, D.D. Application of Artificial Neural Network for stock market predictions: A review of literature. Int. J. Mach. Intell. 2010, 2, 14–17. [Google Scholar]
- George, J.; Mary, L.; Riyas, K.S. Vehicle detection and classification from acoustic signal using ANN and KNN. In Proceedings of the 2013 International Conference on Control Communication and Computing (ICCC), Thiruvananthapuram, India, 13–15 December 2013; pp. 436–439. [Google Scholar]
- Anuradha, B.; Reddy, V.V. ANN for classification of cardiac arrhythmias. ARPN J. Eng. Appl. Sci. 2008, 3, 1–6. [Google Scholar]
- French, J. The time traveller’s. CAPM. Investig. Anal. J. 2017, 46, 81–96. [Google Scholar] [CrossRef]
- Kihoro, J.; Otieno, R.O.; Wafula, C. Seasonal time series forecasting: A comparative study of ARIMA and ANN models. Afr. J. Sci. Technol. 2004, 5. [Google Scholar] [CrossRef] [Green Version]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [Green Version]
- Kwak, J.; Kim, S.; Kim, G.; Singh, V.P.; Hong, S.; Kim, H.S. Scrub typhus incidence modeling with meteorological factors in South Korea. Int. J. Environ. Res. Public Health 2015, 12, 7254–7273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Battiti, R. Accelerated backpropagation learning: Two optimization methods. Complex. Syst. 1989, 3, 331–342. [Google Scholar]
- Water, K. Handbook of Multi-Purpose Weir Management; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Cincinnati, OH, USA, 2019. [Google Scholar]
- Manesh, S.S.; Ahani, H.; Rezaeian-Zadeh, M. ANN-based mapping of monthly reference crop evapotranspiration by using altitude, latitude and longitude data in Fars province, Iran. Environ. Dev. Sustain. 2014, 16, 103–122. [Google Scholar] [CrossRef]
- Shafie-khah, M.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K. Price forecasting of day-ahead electricity markets using a hybrid forecast method. Energy Convers. Manag. 2011, 52, 2165–2169. [Google Scholar] [CrossRef]
- Laio, F.; Porporato, A.; Ridolfi, L.; Tamea, S. Detecting nonlinearity in time series driven by non-Gaussian noise: The case of river flows. Nonlinear Process. Geophys. 2004, 11, 463–470. [Google Scholar] [CrossRef] [Green Version]
- Modarres, R.; Ouarda, T.B. Modeling rainfall–runoff relationship using multivariate GARCH model. J. Hydrol. 2013, 499, 1–18. [Google Scholar] [CrossRef]
- Wang, W.; Vrijling, J.K.; Gelder, P.H.V.; Ma, J. Testing for nonlinearity of streamflow processes at different timescales. J. Hydrol. 2006, 322, 247–268. [Google Scholar] [CrossRef]
- Xu, J.; Li, W.; Ji, M.; Lu, F.; Dong, S. A comprehensive approach to characterization of the nonlinearity of runoff in the headwaters of the Tarim River, western China. Hydrol. Process. 2009, 24, 136–146. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Ministry of Land, Transport and Maritime Affairs. A Construction of Quality Control System for National Hydrological Data; Ministry of Land, Transport and Maritime Affairs: Sejong, Korea, 2011. [Google Scholar]
- Pearson, E.S.; Hartley, H.O. Biometrika Tables for Statisticians 2; Cambridge University Press: Cambridge, UK, 1972. [Google Scholar]
| Station | Before the Project (Until 2012) | After the Project (2012 Onward) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Runoff at Quantile (m3/s) | Standard Deviation | Kurtosis Coefficient | Runoff at Quantile (m3/s) | Standard Deviation | Kurtosis Coefficient | |||||
| 0.75 | 0.5 | 0.25 | 0.75 | 0.5 | 0.25 | |||||
| Station A | 132.0 | 53.6 | 23.5 | 602.0 | 70.1 | 152.1 | 85.3 | 52.5 | 343.0 | 110.9 |
| Station B | 140.8 | 70.0 | 48.6 | 355.7 | 58.4 | 155.5 | 94.3 | 61.1 | 309.1 | 57.1 |
| Station C | 181.7 | 85.9 | 53.3 | 819.7 | 89.3 | 174.5 | 107.4 | 71.7 | 447.9 | 144.9 |
| Evaluation Criteria | Training Period (2014~2018) | Validation Period (2019) | ||
|---|---|---|---|---|
| R2 | RMSE (m3/s) | R2 | RMSE (m3/s) | |
| ANN with Raw | 0.93 | 59.3 | 0.84 | 127.3 |
| ANN with VMD | 0.93 | 80.3 | 0.91 | 99.3 |
| Multiple Regression | 0.88 | 116.7 | 0.81 | 219.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, J.; Lee, J.; Jung, J.; Kim, H.S. Case Study: Reconstruction of Runoff Series of Hydrological Stations in the Nakdong River, Korea. Water 2020, 12, 3461. https://doi.org/10.3390/w12123461
Kwak J, Lee J, Jung J, Kim HS. Case Study: Reconstruction of Runoff Series of Hydrological Stations in the Nakdong River, Korea. Water. 2020; 12(12):3461. https://doi.org/10.3390/w12123461
Chicago/Turabian StyleKwak, Jaewon, Jongso Lee, Jaewon Jung, and Hung Soo Kim. 2020. "Case Study: Reconstruction of Runoff Series of Hydrological Stations in the Nakdong River, Korea" Water 12, no. 12: 3461. https://doi.org/10.3390/w12123461
APA StyleKwak, J., Lee, J., Jung, J., & Kim, H. S. (2020). Case Study: Reconstruction of Runoff Series of Hydrological Stations in the Nakdong River, Korea. Water, 12(12), 3461. https://doi.org/10.3390/w12123461






