A Study on Water and Salt Transport, and Balance Analysis in Sand Dune–Wasteland–Lake Systems of Hetao Oases, Upper Reaches of the Yellow River Basin
Abstract
:1. Introduction
2. Materials and Methods
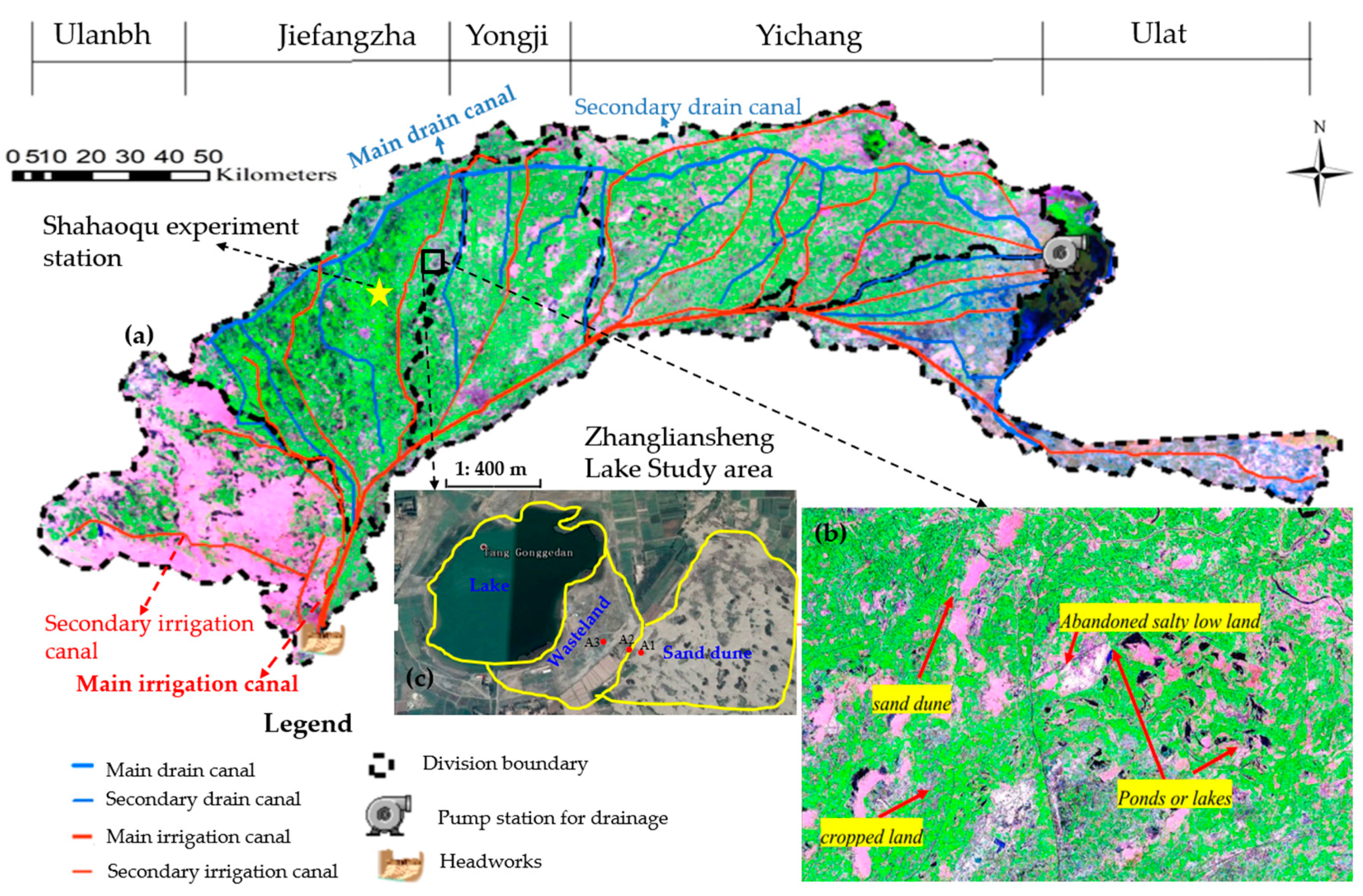
2.1. Study Area
2.2. Experiment Design
2.3. Test Items
2.3.1. Soil Physical Properties of Study Area
2.3.2. Soil Data
2.3.3. Water-Sample Data
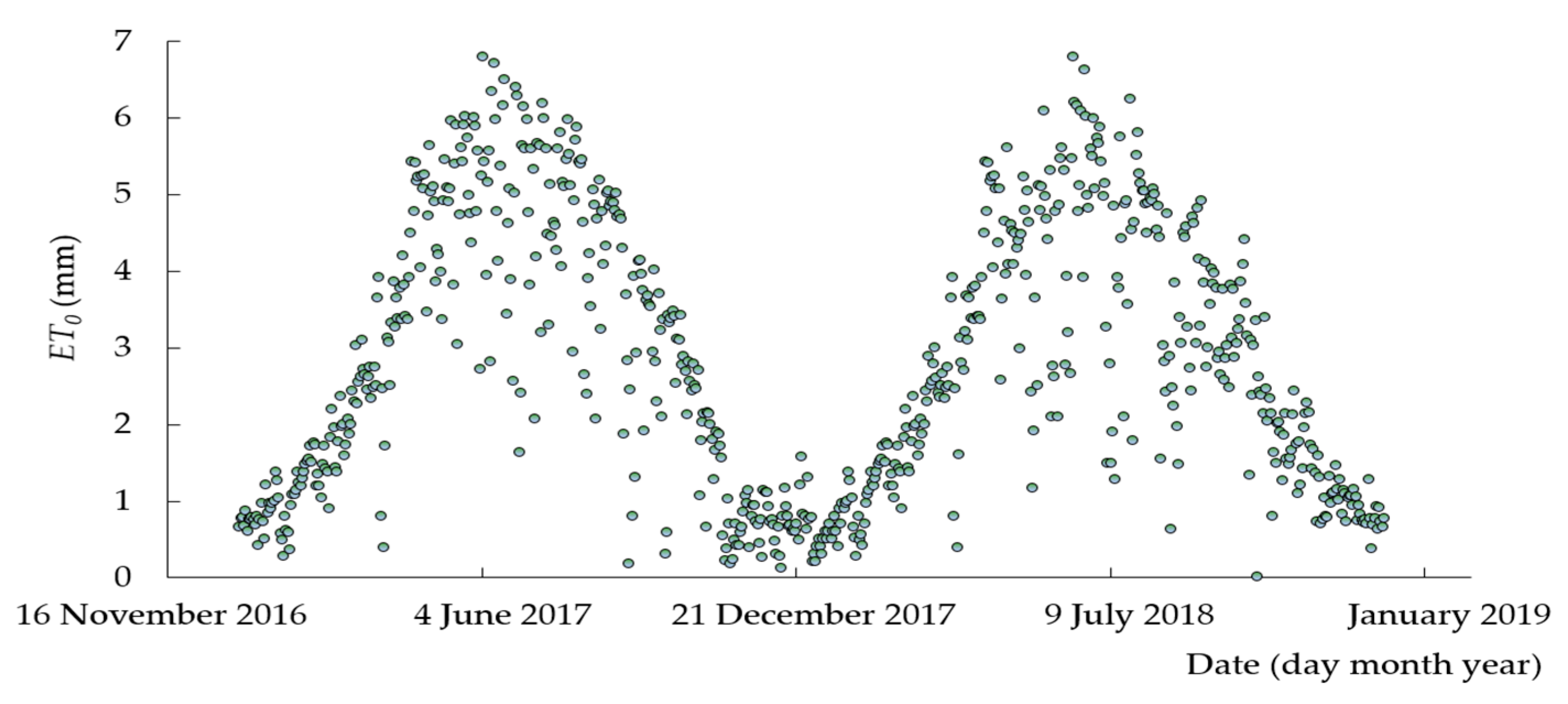
2.3.4. Meteorological Data
2.4. Study Method
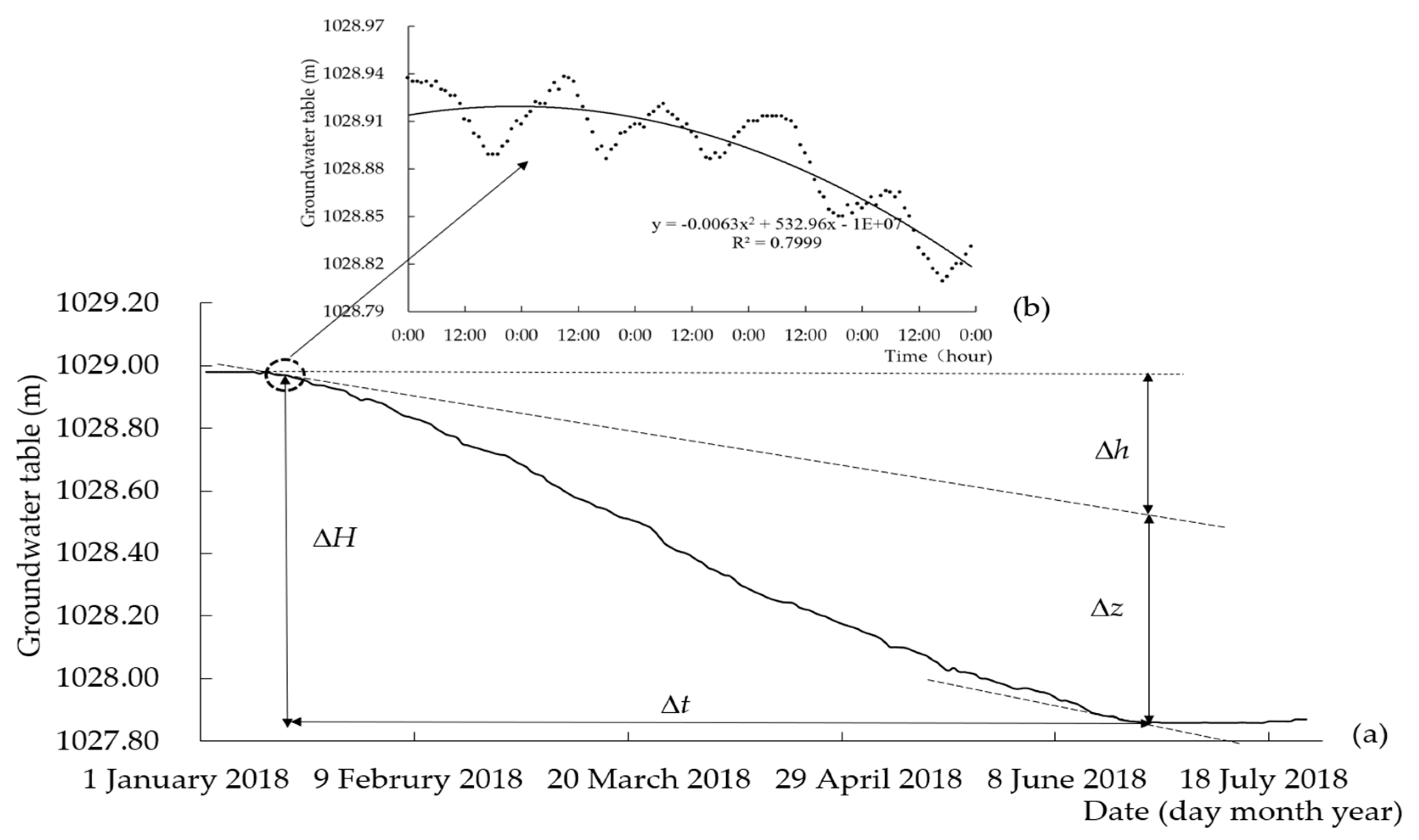
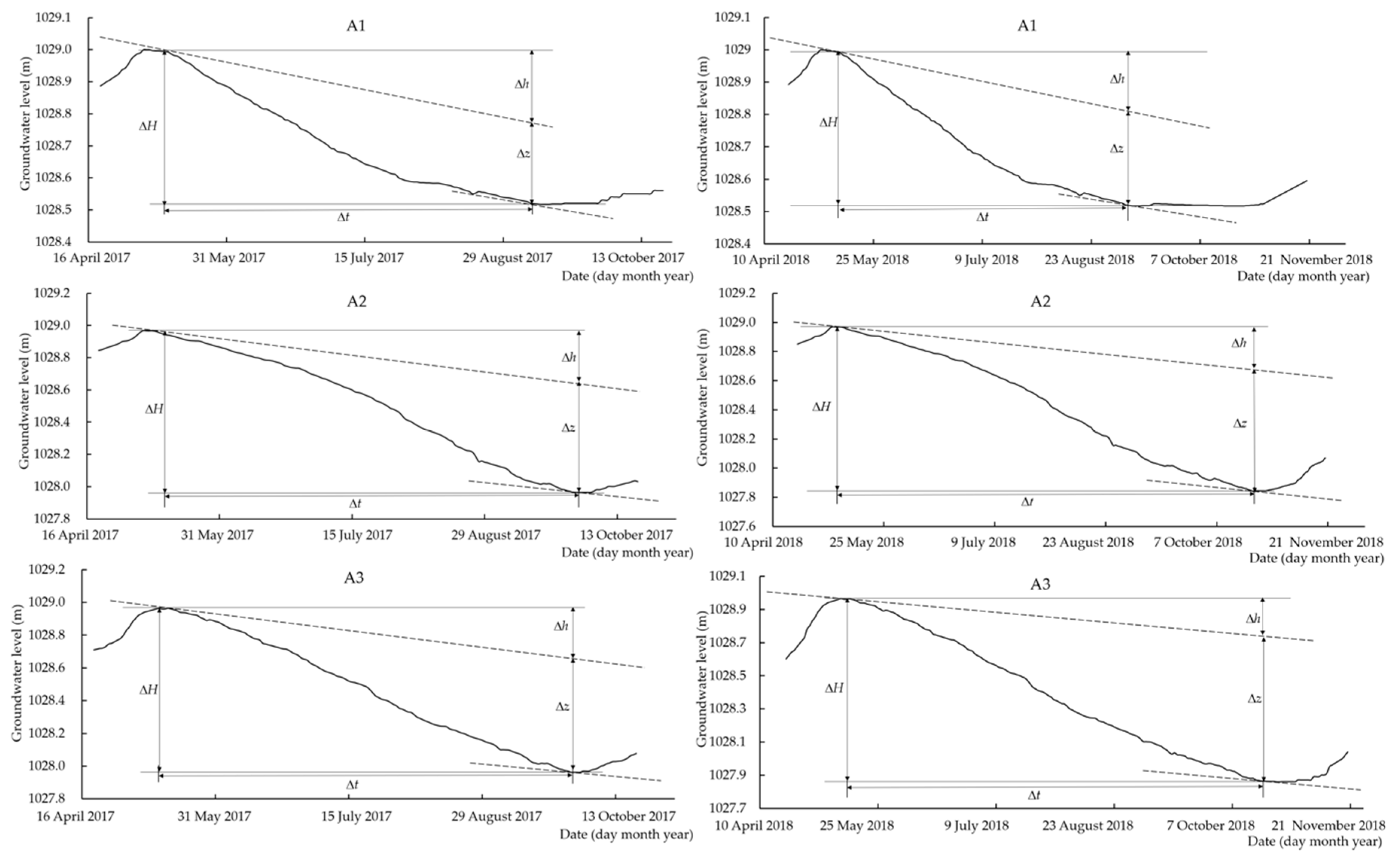
2.4.1. Water-Table-Fluctuation Method
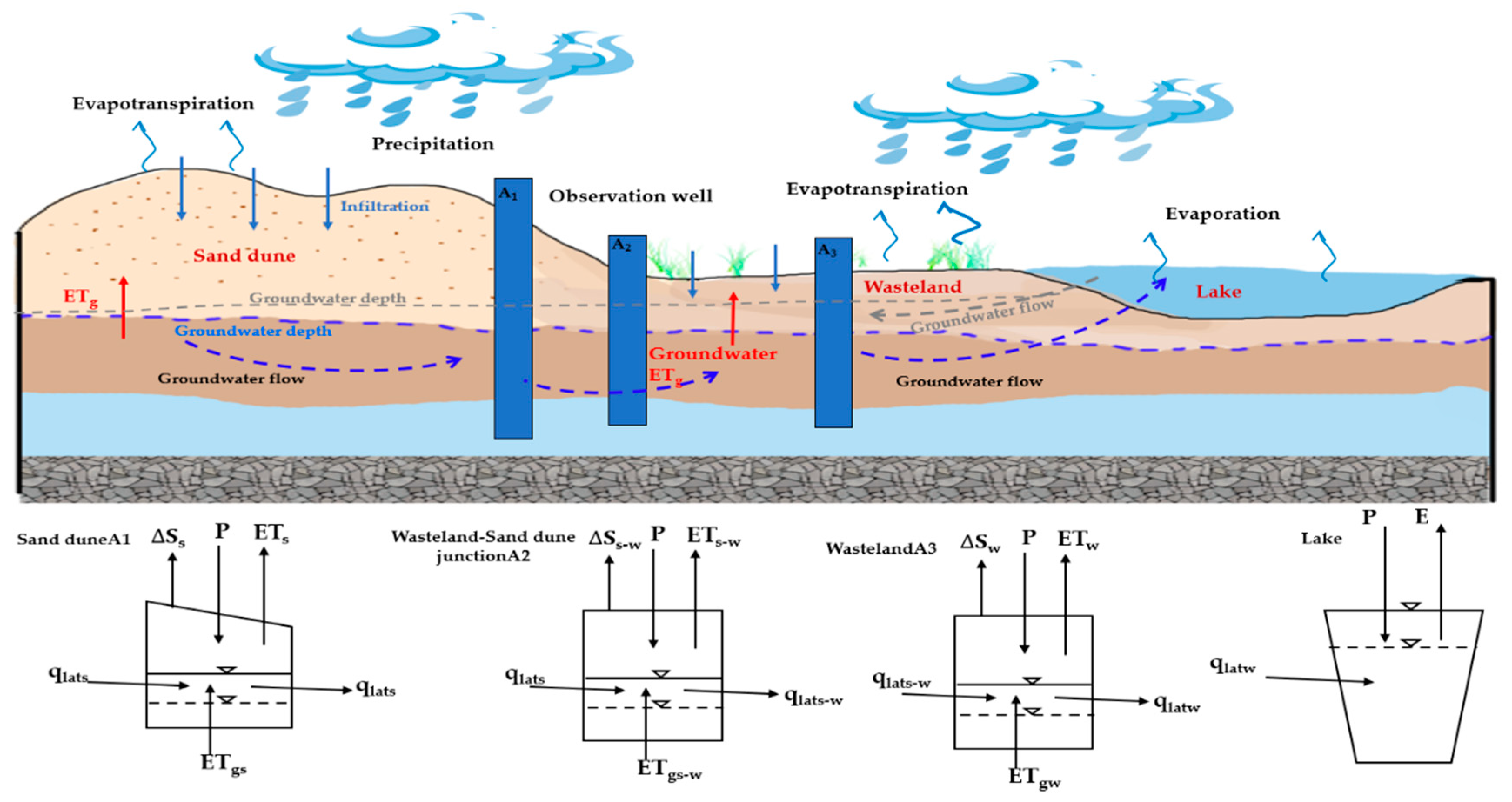
2.4.2. Water-Balance Model
2.4.3. Groundwater Salt-Transport Model in Sand Dune–Wasteland–Lake System
Horizontal Groundwater Salt-Transport Model
Vertical Groundwater Salt-Transport Model
2.4.4. Soil Salt-Storage Equation
3. Results
3.1. Groundwater Dynamics in Sand Dune–Wasteland–Lake System
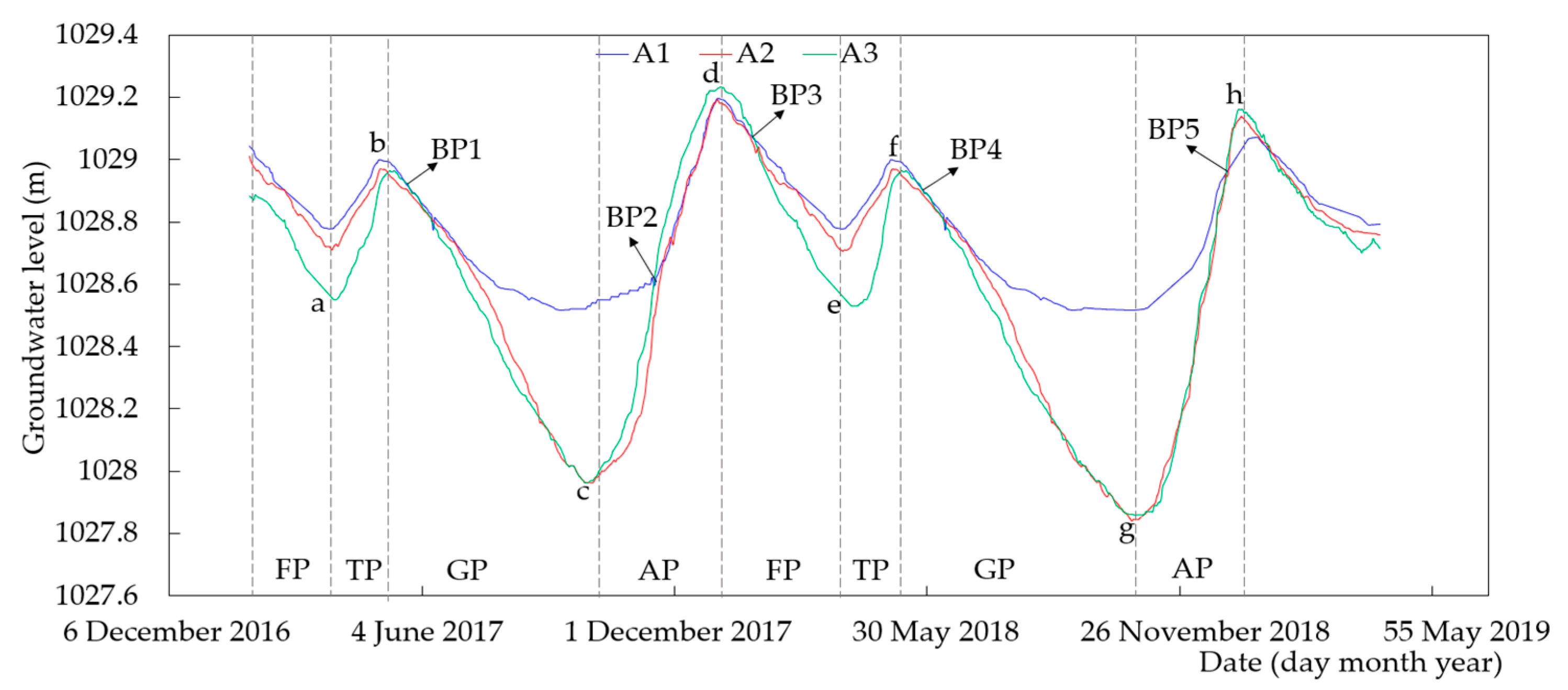
3.1.1. Groundwater-Level Fluctuation in Different Periods
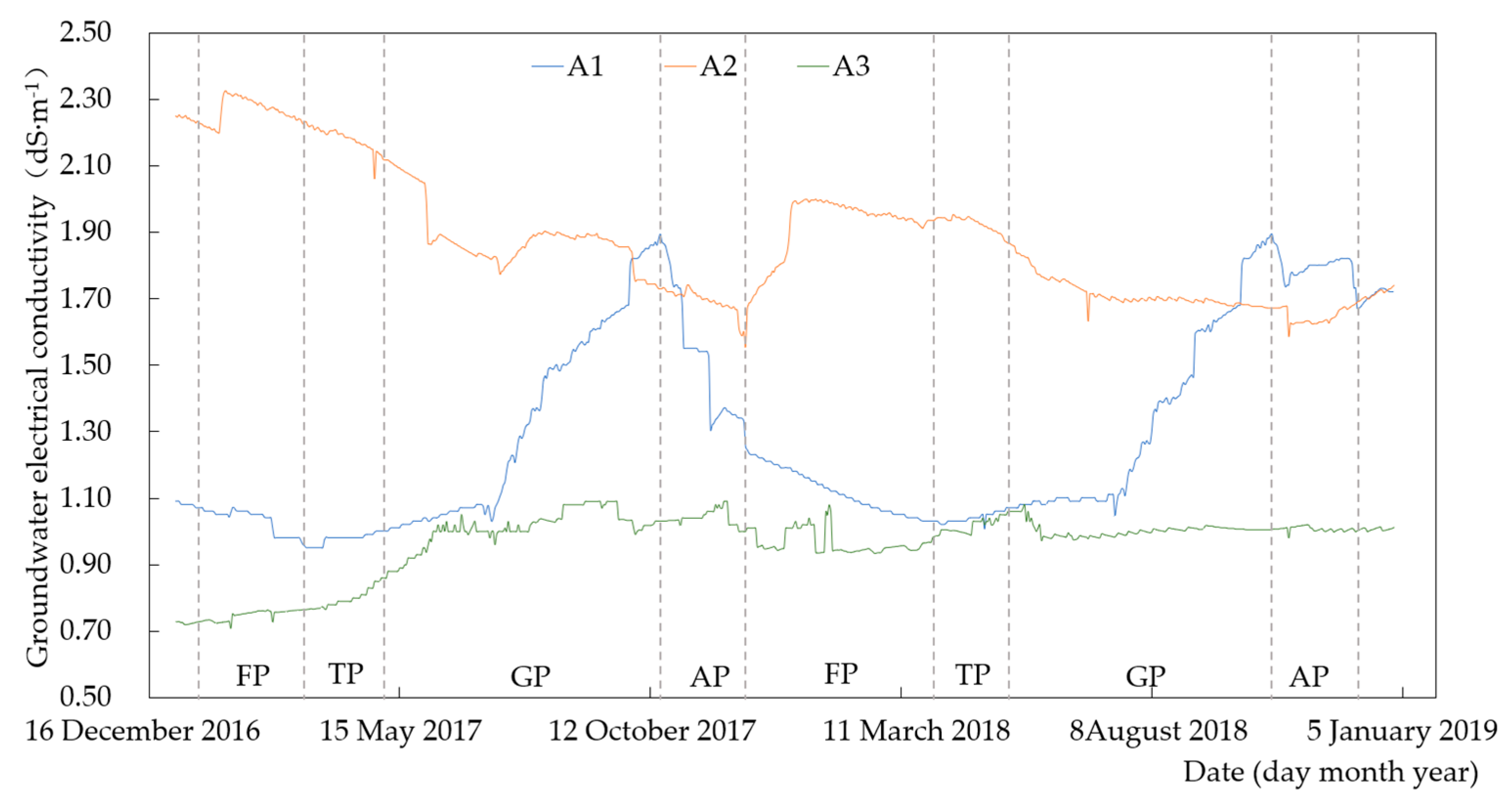
3.1.2. Groundwater Transport Direction
3.2. Water-Balance Estimation
3.2.1. Estimation of Specific Yield and Storage Changes of Unsaturated Zone and Groundwater
3.2.2. Estimation of ETg and −∇qlat
3.2.3. Evapotranspiration Estimations
3.3. Salt-Balance Calculation
3.3.1. Groundwater EC Dynamics in 2017 and 2018
3.3.2. Estimation of Vertical Salt Transport of Groundwater
3.3.3. Estimation of Horizontal Salt Transport of Groundwater
3.3.4. Estimation of Soil Salt Storage
4. Discussion
5. Conclusions
- (1)
- The groundwater transport direction in the sand dune–wasteland–lake system changed during different periods. The dynamics of groundwater EC were affected by the groundwater transport path.
- (2)
- During the growth period in 2017 and 2018, sand-dune water consumption was 1.95 times that of the wasteland–sand dune junction and 1.88 times that of the wasteland. Average ET values of the sand dunes, wasteland–sand dune junction, and wasteland were 42%, 37%, and 31%, respectively, of the ET0. Lake water loss was 761.25–869.05 mm. If there was no water supply, the lake would dry up.
- (3)
- During the growth period, the vertical salt transport of groundwater at the sand-dune site was 1.13 times that at the wasteland–sand dune junction site and 1.82 times that at the wasteland site. Of sand-dune groundwater salt, 54% was accumulated in the groundwater of the wasteland–sand dune junction. Of the groundwater salt of the wasteland–sand dune junction, 53% was accumulated in wasteland groundwater, and the remaining 47% was accumulated in lake. Salt storage of the 1 m soil layer of sand dunes was 85% that of the wasteland–sand dune junction and 82% that of the wasteland.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, M.Y.; Liu, T.X.; Duan, L.M. The Scale Effect of Double-Ring Infiltration and Soil Infiltration Zoning in a Semi-Arid Steppe. Water 2019, 11, 1457. [Google Scholar] [CrossRef] [Green Version]
- Han, P.F.; Wang, X.S.; Wang, J. Using large-aperture scintilla meter to estimate lake-water evaporation and heat fluxes in the Badain Jaran Desert, China. Water 2019, 11, 2575. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.S.; Zhou, Y. Investigating the mysteries of groundwater in the Badain Jaran Desert, China. Hydrogeol. J. 2018, 26, 1639–1655. [Google Scholar] [CrossRef]
- Yue, D.P.; Zhao, J.B.; Ma, Y.D. Relationship between landform development and lake water recharge in the Badain Jaran Desert, China. Water 2019, 11, 1999. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.K.; Liu, J.; Wang, X.S. Analysis of groundwater-lake interaction by distributed temperature sensing in Badain Jaran Desert, Northwest China. Hydrol. Process. 2015, 30, 1330–1341. [Google Scholar] [CrossRef]
- Gong, Y.P.; Wang, X.S.; Zhou, Y.X. Groundwater contributions in water-salt balances of the lakes in the Badain Jaran Desert, China. J. Arid Land 2016, 8, 694–706. [Google Scholar] [CrossRef] [Green Version]
- Hou, L.Z.; Wang, X.S.; Hu, B.X. Experimental and numerical investigations of soil water balance at the hinterland of the Badain Jaran Desert for groundwater recharge estimation. J. Hydrol. 2016, 540, 386–396. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, X.S.; Han, P.F. Depth-dependent seasonal variation of soil water in a thick vadose zone in the Badain Jaran Desert, China. Water 2018, 10, 1719. [Google Scholar] [CrossRef] [Green Version]
- Ren, D.; Xu, X.; Huang, G. Analyzing the role of shallow groundwater systems in the water use of different land-use types in arid irrigated regions. Water 2018, 10, 634. [Google Scholar] [CrossRef] [Green Version]
- Cui, G.; Lu, Y.; Zheng, C.; Liu, Z. Relationship between soil salinization and groundwater hydration in yaoba oasis, northwest China. Water 2019, 11, 175. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lu, S.; Gao, Y. Numerical simulation of circulation and boundary layer characteristics in oasis on different scales. Plateau Meteorol. 2004, 23, 177–183. [Google Scholar]
- Chen, X.; Song, J.; Wang, W. Spatial variability of specific yield and vertical hydraulic conductivity in a highly permeable alluvial aquifer. Hydrology 2010, 388, 379–388. [Google Scholar] [CrossRef]
- Wen, J.; Su, Z.; Zhang, T. New evidence for the links between the local water cycle and the underground wet sand layer of a mega-dune in the Badain Jaran Desert, China. J. Arid Land 2014, 6, 371–377. [Google Scholar] [CrossRef]
- Wang, G.S.; Shi, H.B.; Li, X.Y. Analysis of water and salt transportation and balance during cultivated land, waste land and lake system in Hetao Irrigation Area. J. Hydraul. Eng. 2019, 50, 1518–1528. (In Chinese) [Google Scholar]
- Tai, Y.Y.; Huang, Y.; Du, X.Q. Application of water-table fluctuation method for evaluation of groundwater recharge in arid region-an example of Nalingguole River Alluvial-proluvial Fan in Qaidum Basin. Sci. Technol. Eng. 2014, 14, 123–130. [Google Scholar]
- Wang, P.; Grinevsky, S.O.; Pozdniakov, S.P. Application of the water table fluctuation method for estimating evapotranspiration at two phreatophyte-dominated sites under hyper-arid environments. J. Hydrol. 2014, 519, 2289–2300. [Google Scholar] [CrossRef]
- Yue, W.; Wang, T.; Franz, T.E. Spatiotemporal patterns of water table fluctuations and evapotranspiration induced by riparian vegetation in a semiarid area. Water Resour. Res. 2016, 52, 1948–1960. [Google Scholar] [CrossRef] [Green Version]
- Cheng, D.; Li, Y.; Chen, X. Estimation of groundwater evapotranspiration using diurnal water table fluctuations in the Mu Us Desert, northern China. Hydrology 2013, 490, 106–113. [Google Scholar] [CrossRef]
- Ren, D.Y.; Xu, X.; Huang, G.H. Irrigation water use in typical irrigation and drainage system of Hetao Irrigation District. Trans. Csae 2019, 35, 98–105. (In Chinese) [Google Scholar]
- Yue, W.F.; Yang, J.Z.; Tong, J.X. Transfer and balance of water and salt in irrigation district of arid region. J. Hydraul. Eng. 2008, 39, 623–626. (In Chinese) [Google Scholar]
- Mao, W.; Yang, J.Z.; Zhu, Y. Loosely coupled SaltMod for simulating groundwater and salt dynamics under well-canal conjunctive irrigation in semi-arid areas. Agric. Water Manag. 2017, 192, 209–220. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, L.S.; Yang, J.Z. Coupling methology and application of a fully integrated model for contaminant transport in the subsurface system. J. Hydrol. 2013, 501, 56–72. [Google Scholar] [CrossRef]
- Ceng, J.F.; Liu, X.; Li, J.H. Dynamic analysis of water and salt in cropland-saline alkali land-sand dunes-lake area based on SWAP model. J. Agric. Resour. Environ. 2018, 35, 540–549. (In Chinese) [Google Scholar]
- Ren, D.; Wei, B.; Xu, X. Analyzing spatiotemporal characteristics of soil salinity in arid irrigated agro-ecosystems using integrated approaches. Geoderma 2019, 356, 113935. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.; Zhan, H. Integration of SWAP and MODFLOW-2000 for modeling groundwater dynamics in shallow water table areas. J. Hydrol. 2012, 412–413, 170–181. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.; Qu, Z.; Pereira, L.S. Assessing the groundwater dynamics and impacts of water saving in the Hetao irrigation district, yellow river basin. Agric. Water Manag. 2010, 98, 301–313. [Google Scholar] [CrossRef]
- Bameng Survey. Researches on the Water Resources and Salinization Control System Management Model in Hetao Irrigation District of Inner Mongolia; Bameng Hydrology and Water Resources Survey Teams of Inner Mongolia: Hohhot, China, 1994. (In Chinese) [Google Scholar]
- Ren, D.; Xu, X.; Hao, Y. Modeling and assessing field irrigation water use in a canal system of Hetao, upper Yellow River basin: Application to maize, sunflower and watermelon. J. Hydrol. 2016, 532, 122–139. [Google Scholar] [CrossRef]
- Wu, J.W.; Vincent, B.; Yang, J.Z.; Bouarfa, S.; Vidal, A. Remote sensing monitoring of changes in soil salinity: A case study in Inner Mongolia, China. Sensors 2008, 8, 7035–7049. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Pozdniakov, S. A statistical approach to estimating evapotranspiration from diurnal groundwater level fluctuations. Water Resour. Res. 2014, 50, 2276–2292. [Google Scholar] [CrossRef]
- Healy, R.; Cook, P. Using groundwater levels to estimate recharge. J. Hydrogeol. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Nimmo, J.; Horowitz, C.; Mitchell, L. Discrete-storm water-table fluctuation method to estimate episodic recharge. Groundwater 2015, 53, 282–292. [Google Scholar] [CrossRef]
- Sophocleous, M. Combining the soil water balance and water-level fluctuation methods to estimate natural groundwater recharge-practical aspects. J. Hydrol. 1991, 124, 229–241. [Google Scholar] [CrossRef]
- Varni, M.; Comas, R.; Weinzettel, P. Application of the water table fluctuation method to characterize groundwater recharge in the Pampa plain, Argentina. Hydrol. Sci. J. 2013, 58, 1445–1455. [Google Scholar] [CrossRef] [Green Version]
- Weeks, E.; Sorey, M. Use of Finite-Difference Arrays of Observation Wells to Estimate Evapotranspiration from Ground Water in the Arkansas River Valley; US Geological Survey Water Supply Paper 2029-C; U.S. Government Printing Office: Lakewood, CO, USA, 1973. [CrossRef]
- Healy, R. Estimating Groundwater Recharge; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Lautz, L. Estimating groundwater evapotranspiration rates using diurnal water-table fluctuations in a semi-arid riparian zone. J. Hydrogeol. 2008, 16, 483–497. [Google Scholar] [CrossRef]
- Crosbie, R.S.; Binning, P.; Kalma, J.D. A time series approach to inferring groundwater recharge using the water table fluctuation method. Water Resour. Res. 2005, 41, W01008. [Google Scholar] [CrossRef]
- Tong, W.J. Study on Salt Tolerance of Crops and Cropping System Optimization in Hetao Irrigation District; China Agricultural University: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Zhao, Y.G.; Li, Y.Y.; Wang, J. Buried straw layer plus plastic mulching reduces soil salinity and increases sunflower yield in saline soils. Soil Tillage Res. 2016, 155, 363–370. [Google Scholar] [CrossRef]
- Peng, Z.Y.; Huang, J.S.; Wu, J.W. Salt movement of seasonal freezing-thawing soil under autumn irrigation condition. Trans. Csae 2012, 28, 77–81. [Google Scholar]
- Zhang, W.Z.; Zhang, Y.F. Soil specific yield and free void rate. Irrig. Drain. 1983, 2, 1–16. [Google Scholar]
- Cai, M.J. Study on sand specific yield. Groundwater 1986, 3, 10–14. [Google Scholar]
- Krogulec, E. Evaluating the risk of groundwater drought in groundwater-dependent ecosystems in the central part of the Vistula River Valley, Poland. Eco-Hydrol. Hydrobiol. 2018, 18, 82–91. [Google Scholar] [CrossRef]
- Si, J.H.; Feng, Q.; Zhang, X.Y. Growing season evapotranspiration from Tamarix ramosissima stands under extreme arid conditions in northwest China. Environ. Geol. 2005, 48, 861–870. [Google Scholar] [CrossRef]
- Krogulec, E. Hydrogeological study of groundwater-dependent ecosystems-an overview of selected methods. Eco-Hydrol. Hydrobiol. 2016, 16, 185–193. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.H.; Qu, Z.Y. Using MODFLOW and GIS to assess changes in groundwater dynamics in response to water saving measures in irrigation districts of the upper Yellow River basin. Water Resour. Manag. 2011, 25, 2035–2059. [Google Scholar] [CrossRef]


| Sample | Soil Layer (cm) | Soil Physical Properties | van Genuchten Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| <0.02 mm (%) | 0.02–0.5 mm (%) | >0.5 mm (%) | Bulk Density (g cm−3) | Saturated Hydraulic Conductivity (cm d−1) | θr (cm3·cm−3) | θs (cm3·cm−3) | α (cm−1) | n | ||
| A1 | 200 | 0.518 | 7.494 | 91.691 | 1.762 | 257.59 | 0.043 | 0.308 | 0.0385 | 2.825 |
| A2 | 200 | 3.16 | 45.28 | 51.56 | 1.66 | 22.56 | 0.027 | 0.309 | 0.0341 | 1.132 |
| A3 | 200 | 5.612 | 80.064 | 14.324 | 1.678 | 18.34 | 0.031 | 0.369 | 0.0127 | 1.853 |
| Year | 10 April | 30 April | 20 May | 10 June | 30 June | 20 July | 10 August | 30 August | 20 September | 1 October |
|---|---|---|---|---|---|---|---|---|---|---|
| 2017 | 2.30 | 2.50 | 3.19 | 2.70 | 2.80 | 3.50 | 2.20 | 2.20 | 2.30 | 2.50 |
| 2018 | 2.10 | 2.54 | 3.40 | 2.57 | 2.72 | 3.33 | 3.04 | 3.21 | 3.13 | 3.22 |
| Time | Turning Point | Observation Points | ||
|---|---|---|---|---|
| A1 (m) | A2 (m) | A3 (m) | ||
| 31 March 2017 | a | 1028.778 | 1028.714 | 1028.56 |
| 6 May 2017 | b | 1029 | 1028.968 | 1028.93 |
| 29 September 2017 | c | 1028.521 | 1027.963 | 1027.963 |
| 1 January 2018 | d | 1029.198 | 1029.191 | 1029.228 |
| 3 March 2018 | e | 1028.778 | 1028.705 | 1028.56 |
| 5 May 2018 | f | 1029 | 1028.968 | 1028.93 |
| 27 October 2018 | g | 1028.517 | 1027.845 | 1027.86 |
| 8 January 2019 | h | 1029.73 | 1029.137 | 1029.16 |
| Balance Point | Date | Groundwater Level (m) |
|---|---|---|
| BP1 | 23 May 2017 | 1028.927 |
| BP2 | 16 November 2017 | 1028.6 |
| BP3 | 26 January 2018 | 1029.07 |
| BP4 | 28 May 2018 | 1028.894 |
| BP5 | 23 December 2018 | 1028.94 |
| Date | Observation Point | ΔH (m) | Δh (m) | Δz (m) | Δt (d) | Sy | −∇qlat (mm d−1) | ETg (mm d−1) | ΔS (mm) | P (mm) | ET (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| b–c | A1 | 0.48 | 0.22 | 0.26 | 126.00 | 0.26 | 0.45 | 0.54 | 124.80 | 53.4 | 246.24 |
| A2 | 1.01 | 0.31 | 0.70 | 146.00 | 0.06 | 0.13 | 0.29 | 60.60 | 53.4 | 203.68 | |
| A3 | 0.97 | 0.27 | 0.70 | 146.00 | 0.07 | 0.12 | 0.31 | 63.05 | 53.4 | 163 | |
| f–g | A1 | 0.48 | 0.19 | 0.29 | 124.00 | 0.26 | 0.40 | 0.61 | 124.80 | 113.4 | 313.6 |
| A2 | 1.12 | 0.28 | 0.84 | 175.00 | 0.06 | 0.10 | 0.29 | 67.20 | 113.4 | 283.92 | |
| A3 | 1.07 | 0.19 | 0.88 | 176.00 | 0.07 | 0.07 | 0.33 | 69.55 | 113.4 | 244.7 |
| Year | Precipitation (mm) | Transport Recharge (mm) | Water Evaporation (mm) | ΔW (mm) |
|---|---|---|---|---|
| 2017 | 53.4 | 17.55 | 940 | −869.05 |
| 2018 | 113.4 | 12.35 | 887 | −761.25 |
| Date | Observation Point | N (d) | ETg (mm d−1) | TDS (g L−1) | Salinity (kg hm−2) |
|---|---|---|---|---|---|
| b–c | A1 | 126 | 0.54 | 0.88 | 598.75 |
| A2 | 146 | 0.29 | 1.31 | 554.65 | |
| A3 | 146 | 0.31 | 0.70 | 316.82 | |
| f–g | A1 | 124 | 0.61 | 0.93 | 703.45 |
| A2 | 175 | 0.29 | 1.19 | 603.93 | |
| A3 | 176 | 0.33 | 0.69 | 400.75 |
| Date | Transport Direction | N (d) | −∇qlat (mm d−1) | TDS (g L−1) | L (kg hm−2) | ΔL (kg hm−2) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| b–c | A1→A2 | 126 | qlats | 0.45 | 0.88 | Ls→s–w | 498.96 | ΔLs–w | 250.32 | ||
| A2→A3 | 146 | qlats–w | 0.13 | 1.31 | Ls–w→w | 248.64 | ΔLw | 126.00 | |||
| A3→Lake | 146 | qlatw | 0.12 | 0.70 | Lw→l | 122.64 | |||||
| f–g | A1→A2 | 124 | qlats | 0.40 | 0.93 | Ls→s–w | 461.28 | ΔLs–w | 253.03 | ||
| A2→A3 | 175 | qlats–w | 0.10 | 1.19 | Ls–w→w | 208.25 | ΔLw | 123.24 | |||
| A3→Lake | 176 | qlatw | 0.07 | 0.69 | Lw→l | 85.01 | |||||
| Soil Layers (cm) | 10 April | 30 April | 20 May | 10 June | 30 June | 20 July | 10 August | 30 August | 20 September | 1 October |
|---|---|---|---|---|---|---|---|---|---|---|
| 0–20 | 678 | 678 | 678 | 744 | 877 | 877 | 1075 | 1009 | 1142 | 1333 |
| 20–40 | 2003 | 2136 | 2401 | 2467 | 2600 | 2666 | 3064 | 3594 | 4389 | 4522 |
| 40–60 | 3594 | 3925 | 3859 | 4190 | 4190 | 4323 | 4456 | 4721 | 5251 | 5450 |
| 60–80 | 3992 | 4124 | 4787 | 5649 | 6643 | 7438 | 8432 | 9426 | 9559 | 8764 |
| 80–100 | 5383 | 5781 | 5781 | 7107 | 8432 | 9360 | 9625 | 11,746 | 13,734 | 15,723 |
| Sum | 15,650 | 16,644 | 17,506 | 20,157 | 22,742 | 24,664 | 26,652 | 30,496 | 34,075 | 35,790 |
| Soil Layers (cm) | 10 April | 30 April | 20 May | 10 June | 30 June | 20 July | 10 August | 30 August | 20 September | 1 October |
|---|---|---|---|---|---|---|---|---|---|---|
| 0–20 | 1975 | 1796 | 1647 | 1475 | 1143 | 1197 | 1280 | 1327 | 1202 | 2629 |
| 20–40 | 26,537 | 27,706 | 28,553 | 31,895 | 33,046 | 33,832 | 32,866 | 35,807 | 35,684 | 35,663 |
| 40–60 | 1014 | 1264 | 1264 | 1236 | 1389 | 1606 | 1264 | 1702 | 1639 | 2077 |
| 60–80 | 3077 | 3577 | 4713 | 4367 | 3825 | 4640 | 4890 | 5828 | 6015 | 6109 |
| 80–100 | 12,501 | 12,514 | 13,063 | 14,689 | 17,353 | 19,348 | 19,114 | 21,672 | 21,955 | 22,325 |
| Sum | 45,105 | 46,857 | 49,241 | 53,662 | 56,756 | 60,623 | 59,414 | 66,335 | 66,496 | 68,804 |
| Soil Layers (cm) | 10 April | 30 April | 20 May | 10 June | 30 June | 20 July | 10 August | 30 August | 20 September | 1 October |
|---|---|---|---|---|---|---|---|---|---|---|
| 0–20 | 9573 | 11,774 | 12,403 | 13,032 | 14,290 | 16,805 | 17,434 | 17,811 | 18,063 | 18,503 |
| 20–40 | 8064 | 10,076 | 9636 | 11,714 | 13,035 | 15,579 | 14,570 | 16,554 | 17,413 | 17,308 |
| 40–60 | 17,874 | 18,928 | 20,010 | 19,761 | 19,950 | 21,836 | 23,849 | 24,037 | 24,729 | 24,729 |
| 60–80 | 19,258 | 20,410 | 20,874 | 20,975 | 21,333 | 21,459 | 21,689 | 22,562 | 22,591 | 22,842 |
| 80–100 | 24,079 | 21,231 | 18,705 | 20,712 | 20,594 | 19,698 | 18,548 | 19,918 | 19,200 | 19,950 |
| Sum | 78,848 | 82,419 | 81,628 | 86,194 | 89,201 | 95,377 | 96,090 | 100,882 | 101,996 | 103,332 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Shi, H.; Li, X.; Yan, J.; Miao, Q.; Li, Z.; Akae, T. A Study on Water and Salt Transport, and Balance Analysis in Sand Dune–Wasteland–Lake Systems of Hetao Oases, Upper Reaches of the Yellow River Basin. Water 2020, 12, 3454. https://doi.org/10.3390/w12123454
Wang G, Shi H, Li X, Yan J, Miao Q, Li Z, Akae T. A Study on Water and Salt Transport, and Balance Analysis in Sand Dune–Wasteland–Lake Systems of Hetao Oases, Upper Reaches of the Yellow River Basin. Water. 2020; 12(12):3454. https://doi.org/10.3390/w12123454
Chicago/Turabian StyleWang, Guoshuai, Haibin Shi, Xianyue Li, Jianwen Yan, Qingfeng Miao, Zhen Li, and Takeo Akae. 2020. "A Study on Water and Salt Transport, and Balance Analysis in Sand Dune–Wasteland–Lake Systems of Hetao Oases, Upper Reaches of the Yellow River Basin" Water 12, no. 12: 3454. https://doi.org/10.3390/w12123454
APA StyleWang, G., Shi, H., Li, X., Yan, J., Miao, Q., Li, Z., & Akae, T. (2020). A Study on Water and Salt Transport, and Balance Analysis in Sand Dune–Wasteland–Lake Systems of Hetao Oases, Upper Reaches of the Yellow River Basin. Water, 12(12), 3454. https://doi.org/10.3390/w12123454







