Developing Pseudo Continuous Pedotransfer Functions for International Soils Measured with the Evaporation Method and the HYPROP System: I. The Soil Water Retention Curve
Abstract
:1. Introduction
2. Materials and Methods
2.1. Soil Data Sets
2.2. ANN PC-PTFs Development
2.3. Modeling Scenarios
2.4. Model Evaluation
2.5. Domain of the Pedotransfer Functions
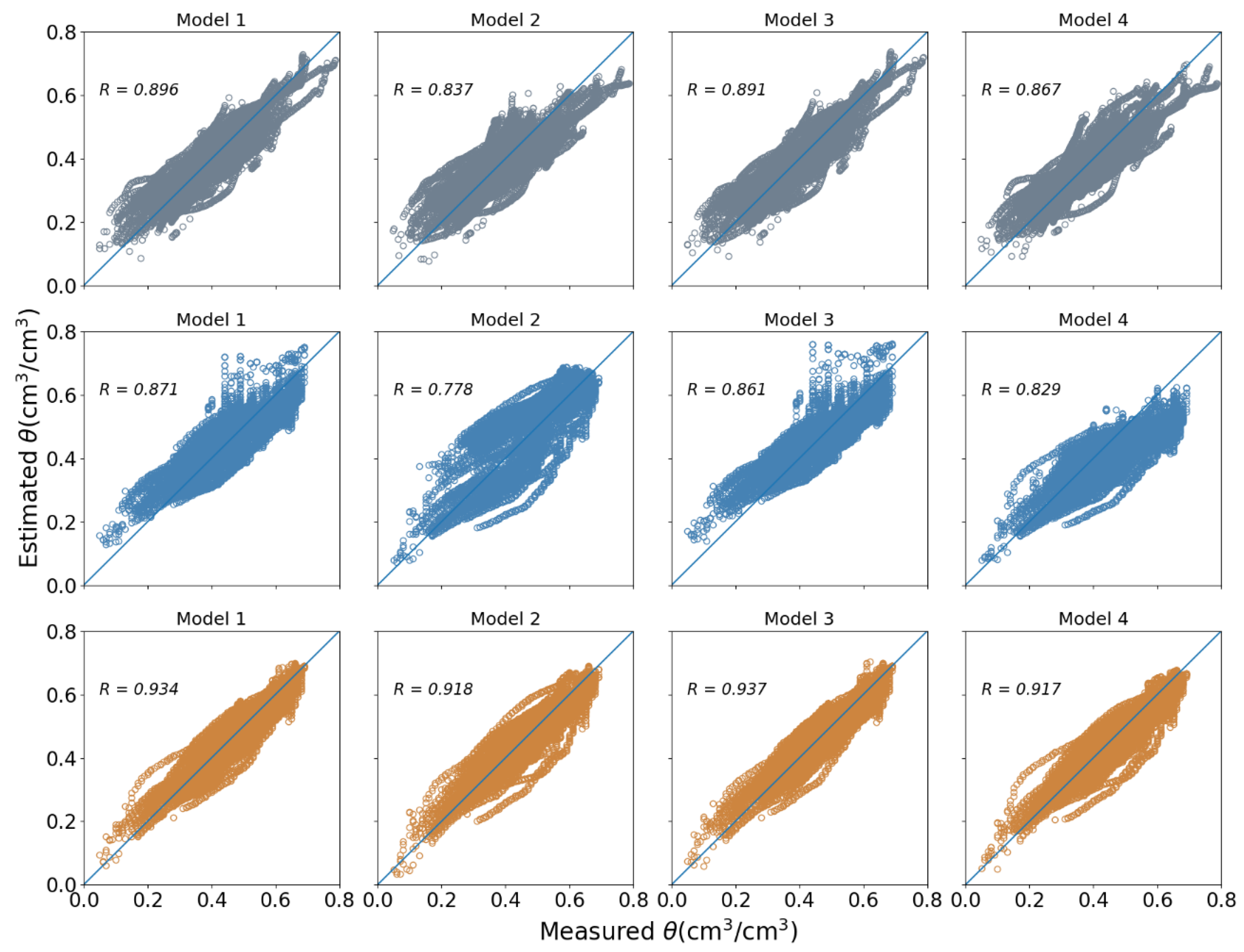
3. Results
3.1. Importance of the Input Predictors
3.2. Performance across Soil Textures
3.3. Performance at the Wet, Intermediate and Dry Parts of the SWRC
4. Discussion
4.1. Accuracy and Reliability of the Developed PTFs
4.2. Importance of Input Variables
4.3. Performance across Textural Classes and Tension Ranges
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vereecken, H.; Weynants, M.; Javaux, M.; Pachepsky, Y.; Schaap, M.G.; van Genuchten, M.T. Using Pedotransfer Functions to Estimate the van Genuchten–Mualem Soil Hydraulic Properties: A Review. Vadose Zone J. 2010, 9, 795. [Google Scholar] [CrossRef]
- Githinji, L.J.M.; Dane, J.H.; Walker, R.H. Water-use patterns of tall fescue and hybrid bluegrass cultivars subjected to ET-based irrigation scheduling. Irrig. Sci. 2009, 27, 377–391. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892. [Google Scholar] [CrossRef] [Green Version]
- Prevedello, C.L.; Armindo, R.A. Generalization of the Green-Ampt Theory for Horizontal Infiltration into Homogeneous Soils. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Gallipoli, D.; Gens, A.; Sharma, R.; Vaunat, J. An elasto-plastic model for unsaturated soil incorporating the effects of suction and degree of saturation on mechanical behaviour. Geotechnique 2003, 53, 123–135. [Google Scholar] [CrossRef]
- Ghaffaripour, O.; Esgandani, G.A.; Khoshghalb, A.; Shahbodaghkhan, B. Fully coupled elastoplastic hydro-mechanical analysis of unsaturated porous media using a meshfree method. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1919–1955. [Google Scholar] [CrossRef]
- Gupta, S.C.; Larson, W.E. Estimating Soil Water Retention Characteristics From Particle Size Distribution, Organic Matter Percent, and Bulk Density. Water Resour. Res. 1979, 15, 1633–1635. [Google Scholar] [CrossRef]
- Haghverdi, A.; Cornelis, W.M.; Ghahraman, B. A pseudo-continuous neural network approach for developing water retention pedotransfer functions with limited data. J. Hydrol. 2012, 442–443, 46–54. [Google Scholar] [CrossRef]
- Pachepsky, Y.A.; Timlin, D.; Varallyay, G. Artificial Neural Networks to Estimate Soil Water Retention from Easily Measurable Data. Soil Sci. Soc. Am. J. 1996, 60, 727–733. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Saxtonn, K.E. Estimation of Soil Water Properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Børgesen, C.D.; Schaap, M.G. Point and parameter pedotransfer functions for water retention predictions for Danish soils. Geoderma 2005, 127, 154–167. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.S.; Durner, W. Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: II. Evaluation of Parametric Pedotransfer Functions against Direct Fits. Water 2020, 12, 896. [Google Scholar] [CrossRef] [Green Version]
- Minasny, B.; McBratney, A.B.; Bristow, K.L. Comparison of different approaches to the development of pedotransfer functions for water-retention curves. Geoderma 1999, 93, 225–253. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; van Genuchten, M.T. Using Texture and Other Soil Properties to Predict the Unsaturated Soil Hydraulic Functions. Soil Sci. Soc. Am. J. 1988, 52, 1762–1770. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Weighted recalibration of the Rosetta pedotransfer model with improved estimates of hydraulic parameter distributions and summary statistics (Rosetta3). J. Hydrol. 2017, 547, 39–53. [Google Scholar] [CrossRef] [Green Version]
- Minasny, B.; McBratney, A.B. The Neuro-m Method for Fitting Neural Network Parametric Pedotransfer Functions. Soil Sci. Soc. Am. J. 2002, 66, 352–361. [Google Scholar] [CrossRef] [Green Version]
- Haghverdi, A.; Öztürk, H.S.; Cornelis, W.M. Revisiting the pseudo continuous pedotransfer function concept: Impact of data quality and data mining method. Geoderma 2014, 226–227, 31–38. [Google Scholar] [CrossRef]
- Haghverdi, A.; Leib, B.G.; Washington-Allen, R.A.; Ayers, P.D.; Buschermohle, M.J. High-resolution prediction of soil available water content within the crop root zone. J. Hydrol. 2015, 530, 167–179. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.S.; Durner, W. Measurement and estimation of the soil water retention curve using the evaporation method and the pseudo continuous pedotransfer function. J. Hydrol. 2018, 563, 251–259. [Google Scholar] [CrossRef]
- Nguyen, P.M.; Haghverdi, A.; de Pue, J.; Botula, Y.D.; Le, K.V.; Waegeman, W.; Cornelis, W.M. Comparison of statistical regression and data-mining techniques in estimating soil water retention of tropical delta soils. Biosyst. Eng. 2017, 153, 12–27. [Google Scholar] [CrossRef]
- Schindler, U.; Durner, W.; von Unold, G.; Mueller, L.; Wieland, R. The evaporation method: Extending the measurement range of soil hydraulic properties using the air-entry pressure of the ceramic cup. J. Plant Nutr. Soil Sci. 2010, 173, 563–572. [Google Scholar] [CrossRef]
- Schindler, U.; Durner, W.; von Unold, G.; Müller, L. Evaporation Method for Measuring Unsaturated Hydraulic Properties of Soils: Extending the Measurement Range. Soil Sci. Soc. Am. J. 2010, 74, 1071. [Google Scholar] [CrossRef]
- Schelle, H.; Heise, L.; Jänicke, K.; Durner, W. Water retention characteristics of soils over the whole moisture range: A comparison of laboratory methods. Eur. J. Soil Sci. 2013, 64, 814–821. [Google Scholar] [CrossRef]
- Schindler, U.; Müller, L. Soil hydraulic functions of international soils measured with the Extended Evaporation Method (EEM) and the HYPROP device. Open Data J. Agric. Res. 2017, 3, 10–16. [Google Scholar] [CrossRef] [Green Version]
- Patil, N.G.; Singh, S.K. Pedotransfer Functions for Estimating Soil Hydraulic Properties: A Review. Pedosphere 2016, 26, 417–430. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Pachepsky, A.; Rawls, J. Pedotransfer functions: Bridging the gap between available basic soil data and missing soil hydraulic characteristics. J. Hydrol. 2001, 251, 123–150. [Google Scholar] [CrossRef]
- Schindler, U. Ein Schnellverfahren zur Messung der Wasserleitfähigkeit im teilgesättigten Boden an Stechzylinderproben. Arch. Acker Pflanzenbau Bodenkd. 1980, 24, 1–7. [Google Scholar]
- Schindler, U.; Mueller, L.; von Unold, G.; Durner, W.; Fank, J. Emerging Measurement Methods for Soil Hydrological Studies. In Novel Methods for Monitoring and Managing Land and Water Resources in Siberia; Springer: Berlin/Heidelberg, Germany, 2016; pp. 345–363. ISBN 978-3-319-24407-5. [Google Scholar]
- Jackson, M.L. Soil Chemical Analysis: Advanced Course; UW-Madison Libraries Parallel Press: Madison, WI, USA, 2005; ISBN 1893311473. [Google Scholar]
- Gee, G.W.; Bauder, J.W. Particle-size analysis. In Methods of Soil Analysis. Part 1, 2nd ed.; Agron. Monogr. 9; Klute, A., Ed.; ASA and SSSA: Madison, WI, USA, 1986; pp. 383–411. [Google Scholar] [CrossRef]
- Haghverdi, A.; Najarchi, M.; Öztürk, H.S.; Durner, W. Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: I. Direct Model Fit Using the Extended Evaporation and Dewpoint Methods. Water 2020, 12, 900. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Indust. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; ISBN 0387848584. [Google Scholar]
- Al Majou, H.; Bruand, A.; Duval, O.; Le Bas, C.; Vautier, A. Prediction of soil water retention properties after stratification by combining texture, bulk density and the type of horizon. Soil Use Manag. 2008, 24, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Tranter, G.; McBratney, A.B.; Minasny, B. Using distance metrics to determine the appropriate domain of pedotransfer function predictions. Geoderma 2009, 149, 421–425. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; van Zomeren, B.C. Unmasking multivariate outliers and leverage points. J. Am. Stat. Assoc. 1990, 85, 633–639. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Schaap, M.G. Data mining and exploration techniques. In Development of Pedotransfer Functions in Soil Hydrology; Elsevier: Amsterdam, The Netherlands, 2004; Volume 30, ISBN 0166-2481. [Google Scholar]
- Moreira De Melo, T.; Pedrollo, O.C. Artificial neural networks for estimating soil water retention curve using fitted and measured data. Appl. Environ. Soil Sci. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Nemes, A.; Schaap, M.G.; Wösten, J.H.M. Functional Evaluation of Pedotransfer Functions Derived from Different Scales of Data Collection. Soil Sci. Soc. Am. J. 2003, 67, 1093. [Google Scholar] [CrossRef]
- McBratney, A.B.; Minasny, B.; Cattle, S.R.; Vervoort, R.W. From pedotransfer functions to soil inference systems. Geoderma 2002, 109, 41–73. [Google Scholar] [CrossRef]
- Nemes, A.; Rawls, W.J.; Pachepsky, Y.A. Use of the Nonparametric Nearest Neighbor Approach to Estimate Soil Hydraulic Properties. Soil Sci. Soc. Am. J. 2006, 70, 327. [Google Scholar] [CrossRef]
- Schaap, M.G.; Nemes, A.; van Genuchten, M.T. Comparison of Models for Indirect Estimation of Water Retention and Available Water in Surface Soils. Vadose Zone J. 2004, 3, 1455–1463. [Google Scholar] [CrossRef]
- Patil, N.G.; Tiwary, P.; Pal, D.K.; Bhattacharyya, T.; Sarkar, D.; Mandal, C.; Mandal, D.K.; Chandran, P.; Ray, S.K.; Prasad, J.; et al. Soil water retention characteristics of black soils of india and pedotransfer functions using different approaches. J. Irrig. Drain. Eng. 2013, 139, 313–324. [Google Scholar] [CrossRef]
- Zacharias, S.; Wessolek, G. Excluding Organic Matter Content from Pedotransfer Predictors of Soil Water Retention. Soil Sci. Soc. Am. J. 2007, 71, 43–50. [Google Scholar] [CrossRef]
- Børgesen, C.D.; Iversen, B.V.; Jacobsen, O.H.; Schaap, M.G. Pedotransfer functions estimating soil hydraulic properties using different soil parameters. Hydrol. Process. 2008, 22, 1630–1639. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Limited effect of organic matter on soil available water capacity. Eur. J. Soil Sci. 2018, 69, 39–47. [Google Scholar] [CrossRef] [Green Version]
- Khlosi, M.; Cornelis, W.M.; Douaik, A.; van Genuchten, M.T.; Gabriels, D. Performance Evaluation of Models That Describe the Soil Water Retention Curve between Saturation and Oven Dryness. Vadose Zone J. 2008, 7, 87. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Neural Network Analysis for Hierarchical Prediction of Soil Hydraulic Properties. Soil Sci. Soc. Am. J. 1998, 62, 847. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Using neural networks to predict soil water retention and soil hydraulic conductivity. Soil Tillage Res. 1998, 47, 37–42. [Google Scholar] [CrossRef]
- Cornelis, W.M.; Ronsyn, J.; Van Meirvenne, M.; Hartmann, R. Evaluation of Pedotransfer Functions for Predicting the Soil Moisture Retention Curve. Soil Sci. Soc. Am. J. 2001, 65, 638–648. [Google Scholar] [CrossRef]
- Twarakavi, N.K.C.; Šimůnek, J.; Schaap, M.G. Development of Pedotransfer Functions for Estimation of Soil Hydraulic Parameters using Support Vector Machines. Soil Sci. Soc. Am. J. 2009, 73, 1443–1452. [Google Scholar] [CrossRef] [Green Version]
- Nemes, A.; Schaap, M.; Leij, F..; Wösten, J.H. Description of the unsaturated soil hydraulic database UNSODA version 2.0. J. Hydrol. 2001, 251, 151–162. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of European soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
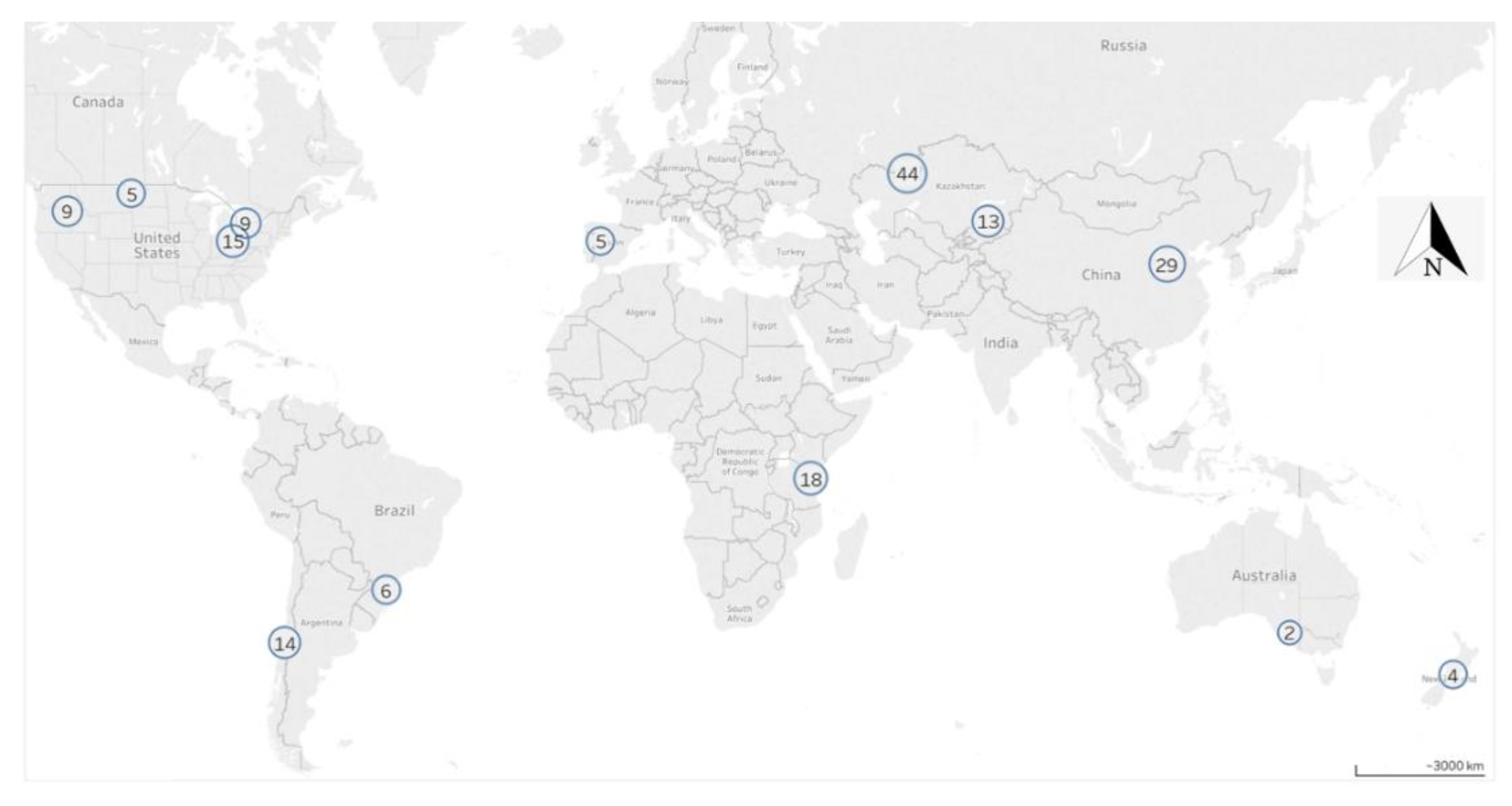
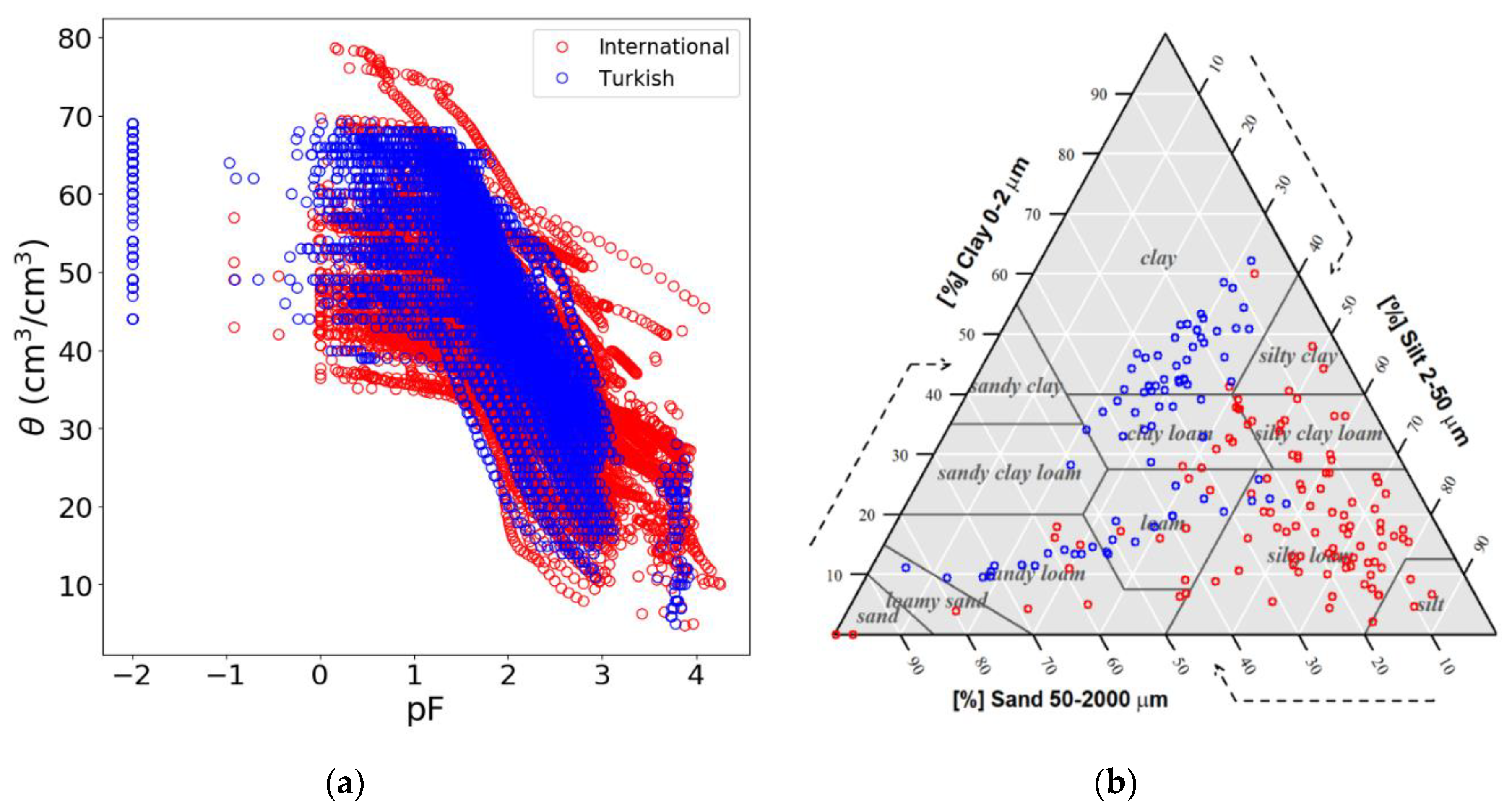
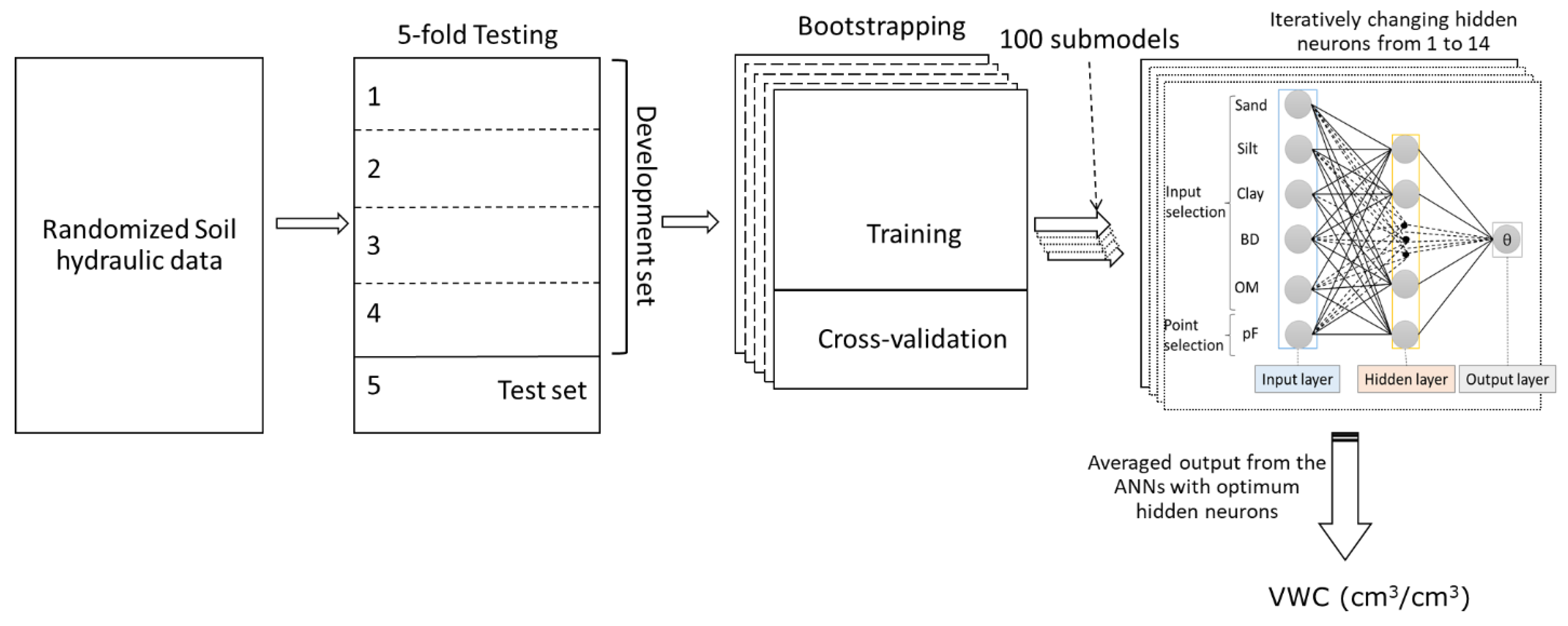
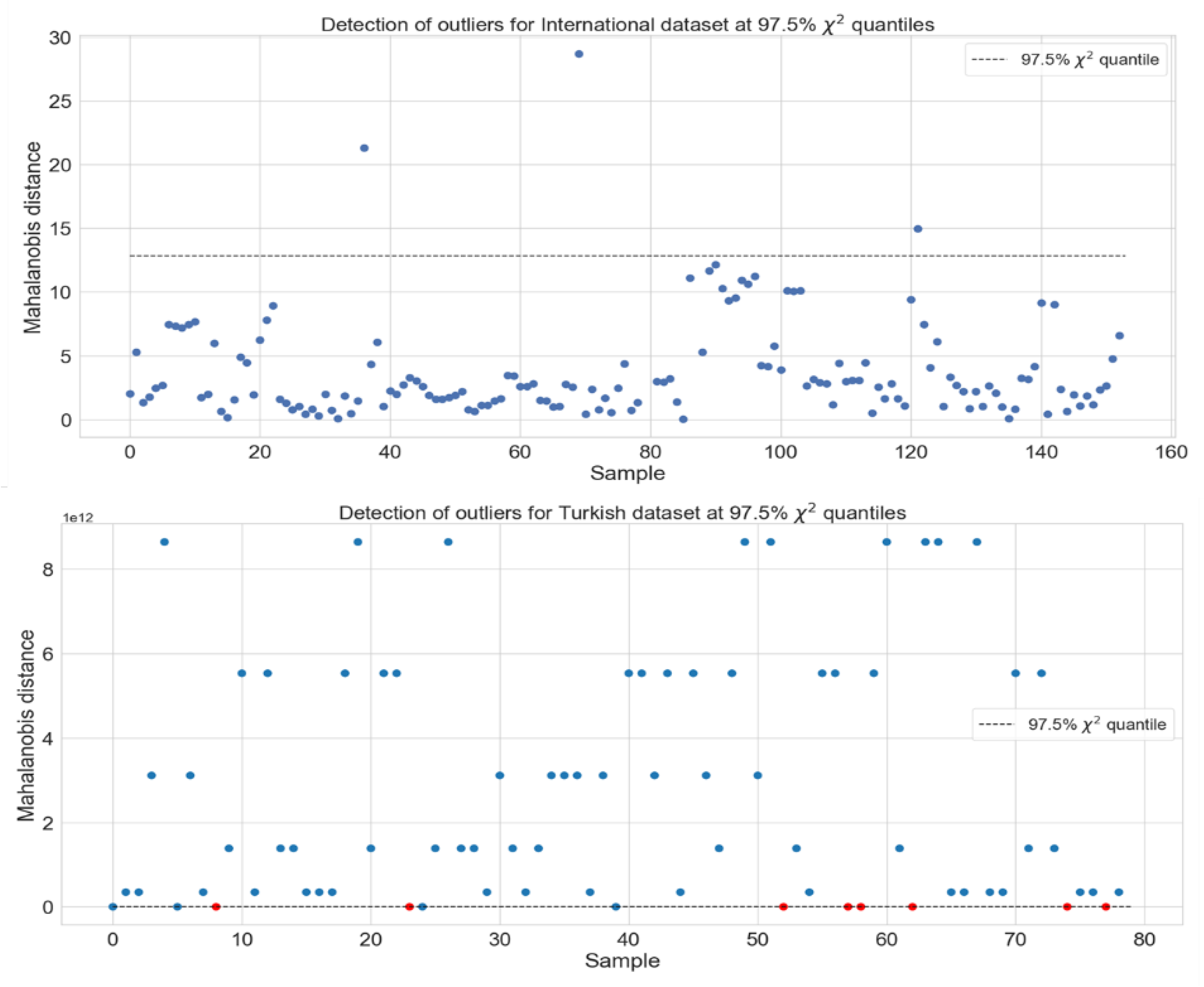
| Attribute | International Data Set | Turkish Dataset | ||||
|---|---|---|---|---|---|---|
| Mean | Range | SD | Mean | Range | SD | |
| Clay (%) | 19.9 | 0.0–60.0 | 12.4 | 34.1 | 9.4–62.2 | 15.0 |
| Silt (%) | 56.7 | 0.2–86.8 | 17.2 | 30.7 | 5.2–57.6 | 8.7 |
| Sand (%) | 23.5 | 3.9–99.8 | 17.4 | 35.3 | 6.0–84.0 | 17.4 |
| Bulk density (g cm−3) | 1.33 | 0.55–1.69 | 0.23 | 0.98 | 0.69–1.33 | 0.14 |
| Organic matter content (%) | 3.0 | 0.00–12.0 | 2.5 | 1.2 | 0.0–3.1 | 0.6 |
| Model | Input Attributes |
|---|---|
| 1 | SSC, BD, SOM, pF |
| 2 | SSC, pF |
| 3 | SSC, BD, pF |
| 4 | SSC, SOM, pF |
| Training & Test: I | Training: I; Validation: T | Training: I + T; Test: T | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | RMSE | MAE | MBE | R | RMSE | MAE | MBE | R | RMSE | MAE | MBE | R |
| 1 | 0.046 | 0.035 | 0.002 | 0.896 | 0.061 | 0.051 | −0.003 | 0.871 | 0.044 | 0.035 | −0.002 | 0.934 |
| 2 | 0.056 | 0.045 | 0.001 | 0.837 | 0.081 | 0.066 | 0.010 | 0.778 | 0.049 | 0.039 | −0.006 | 0.918 |
| 3 | 0.047 | 0.036 | 0.001 | 0.891 | 0.064 | 0.053 | 0.001 | 0.861 | 0.043 | 0.035 | −0.002 | 0.937 |
| 4 | 0.051 | 0.040 | 0.000 | 0.867 | 0.092 | 0.078 | −0.060 | 0.829 | 0.050 | 0.040 | −0.012 | 0.917 |
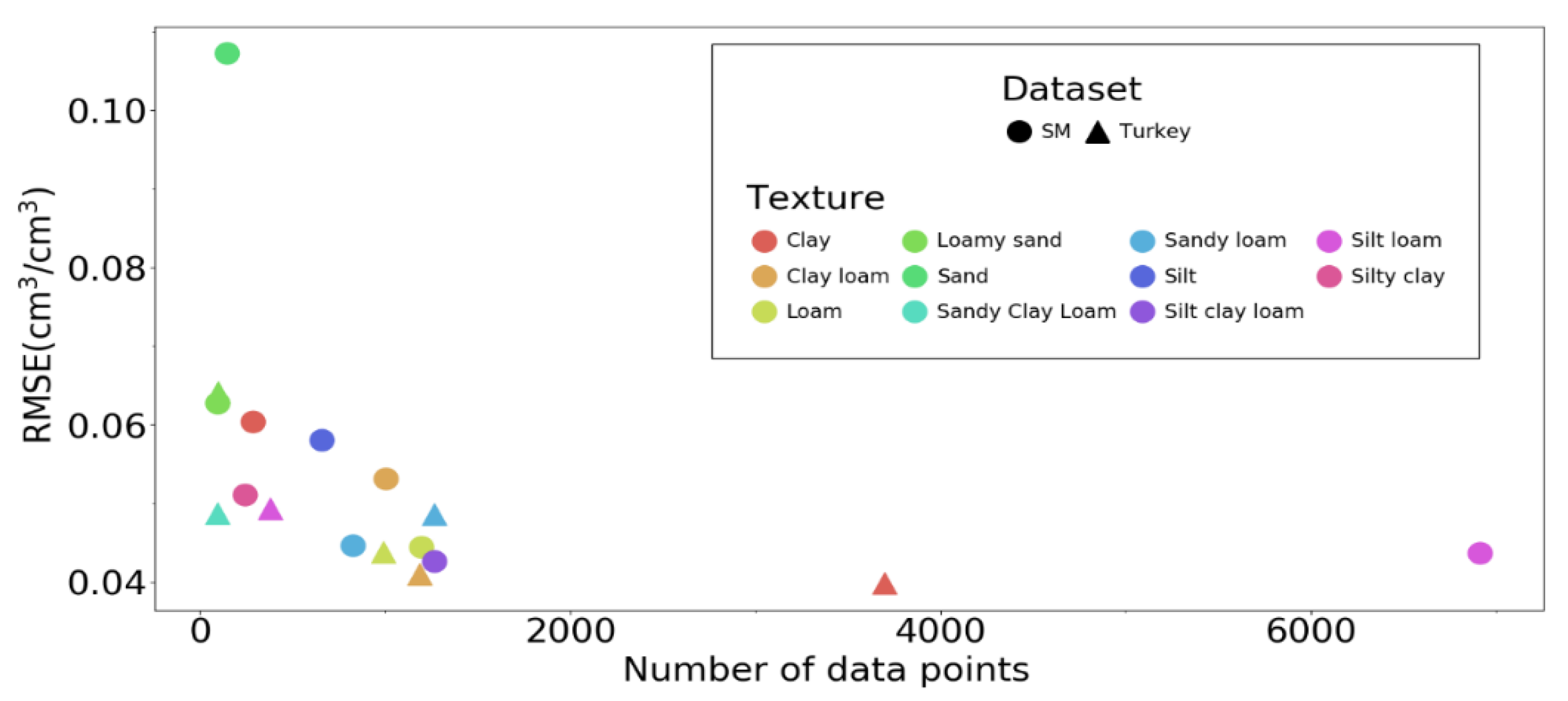
| Silt Loam | Loam | Silty Clay Loam | Clay Loam | Sandy Loam | |
|---|---|---|---|---|---|
| RMSE | 0.043 | 0.042 | 0.04 | 0.052 | 0.043 |
| MAE | 0.034 | 0.033 | 0.028 | 0.038 | 0.033 |
| MBE | 0.002 | 0.004 | 0.016 | −0.016 | 0.009 |
| R | 0.888 | 0.935 | 0.824 | 0.926 | 0.882 |
| Training: International | Training: International + Turkish | |||||||
|---|---|---|---|---|---|---|---|---|
| C | SL | CL | L | C | SL | CL | L | |
| RMSE | 0.060 | 0.069 | 0.052 | 0.060 | 0.039 | 0.047 | 0.044 | 0.042 |
| MAE | 0.052 | 0.055 | 0.042 | 0.048 | 0.032 | 0.037 | 0.035 | 0.034 |
| MBE | −0.006 | 0.032 | −0.019 | −0.009 | −0.001 | 0.001 | −0.001 | −0.004 |
| R | 0.879 | 0.813 | 0.905 | 0.820 | 0.938 | 0.895 | 0.910 | 0.907 |
| Training and Test: I | Training: I; Validation: T | Training: I + T; Test: T | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Wet | Mid | Dry | Wet | Mid | Dry | Wet | Mid | Dry | |
| RMSE | 0.041 | 0.050 | 0.043 | 0.061 | 0.062 | 0.066 | 0.041 | 0.049 | 0.037 |
| MAE | 0.031 | 0.039 | 0.034 | 0.050 | 0.052 | 0.059 | 0.032 | 0.039 | 0.028 |
| MBE | −0.001 | 0.007 | −0.008 | −0.018 | 0.021 | 0.058 | −0.003 | 0.000 | 0.015 |
| R | 0.868 | 0.733 | 0.790 | 0.713 | 0.661 | 0.902 | 0.866 | 0.778 | 0.883 |
| Study | Method | Modeling Approach | Inputs | Origin, no. Samples/Datapoints | RMSE (cm3 cm−3) | |
|---|---|---|---|---|---|---|
| Test | Validation | |||||
| Haghverdi et al. (2012) [8] | Iranian data from pressure plate and Australian data set using various equilibrium-based methods | NN | SSC | (Traing and Test- 122 soil samples from Iran) (772 soil samples for training from Australia, Validation- Iran) | 0.029 | 0.037 |
| SSC, BD | - | 0.028 | 0.037 | |||
| SSC, OC | - | 0.028 | 0.036 | |||
| SSC, BD, OC | - | 0.027 | 0.036 | |||
| Haghverdi et al. (2014) [18] | sandbox/pressure plate | NN | SSC, BD, SOM | Turkey, 135 soil samples x 8 SWR points | 0.047 | - |
| Belgium, (69 soil samples x 8 to 10 SWR points) | 0.040 | - | ||||
| SVM | SSC, BD, SOM | Turkey | 0.054 | |||
| Belgium | 0.069 | |||||
| de Melo and Pedrollo (2015) [39] | different equilibrium-based methods (Pressure based, hanging water, tensiometer, and sand-box) | NN | SSC, particle density, total porosity, BD | UNSODA, (137 soil samples for training and 51 for validation) | 0.088 | |
| Nguyen et al. (2017) [21] | sand-boxes and pressure chambers | NN | SSC, BD, OC | Vietnamese Mekong Delta, (1280 data points for training, 232 validation) | 0.044 | 0.052 |
| MLR | - | 0.056 | 0.066 | |||
| SVM | - | 0.036 | 0.068 | |||
| k-NN | - | 0.056 | 0.050 | |||
| Haghverdi et al. (2018) [20] | evaporation | NN | SSC | Turkey, (81 soil samples) | 0.129 | |
| SSC, BD | - | 0.080 | ||||
| SSC, SOM | - | 0.159 | ||||
| SSC, SA | - | 0.107 | ||||
| SSC, SA, BD, SOM | - | 0.061 | ||||
| SSC, BD, OM, SA, IWC | - | 0.033 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.; Haghverdi, A.; Öztürk, H.S.; Durner, W. Developing Pseudo Continuous Pedotransfer Functions for International Soils Measured with the Evaporation Method and the HYPROP System: I. The Soil Water Retention Curve. Water 2020, 12, 3425. https://doi.org/10.3390/w12123425
Singh A, Haghverdi A, Öztürk HS, Durner W. Developing Pseudo Continuous Pedotransfer Functions for International Soils Measured with the Evaporation Method and the HYPROP System: I. The Soil Water Retention Curve. Water. 2020; 12(12):3425. https://doi.org/10.3390/w12123425
Chicago/Turabian StyleSingh, Amninder, Amir Haghverdi, Hasan Sabri Öztürk, and Wolfgang Durner. 2020. "Developing Pseudo Continuous Pedotransfer Functions for International Soils Measured with the Evaporation Method and the HYPROP System: I. The Soil Water Retention Curve" Water 12, no. 12: 3425. https://doi.org/10.3390/w12123425
APA StyleSingh, A., Haghverdi, A., Öztürk, H. S., & Durner, W. (2020). Developing Pseudo Continuous Pedotransfer Functions for International Soils Measured with the Evaporation Method and the HYPROP System: I. The Soil Water Retention Curve. Water, 12(12), 3425. https://doi.org/10.3390/w12123425





