Using Budyko-Type Equations for Separating the Impacts of Climate and Vegetation Change on Runoff in the Source Area of the Yellow River
Abstract
:1. Introduction
2. Study Area and Data
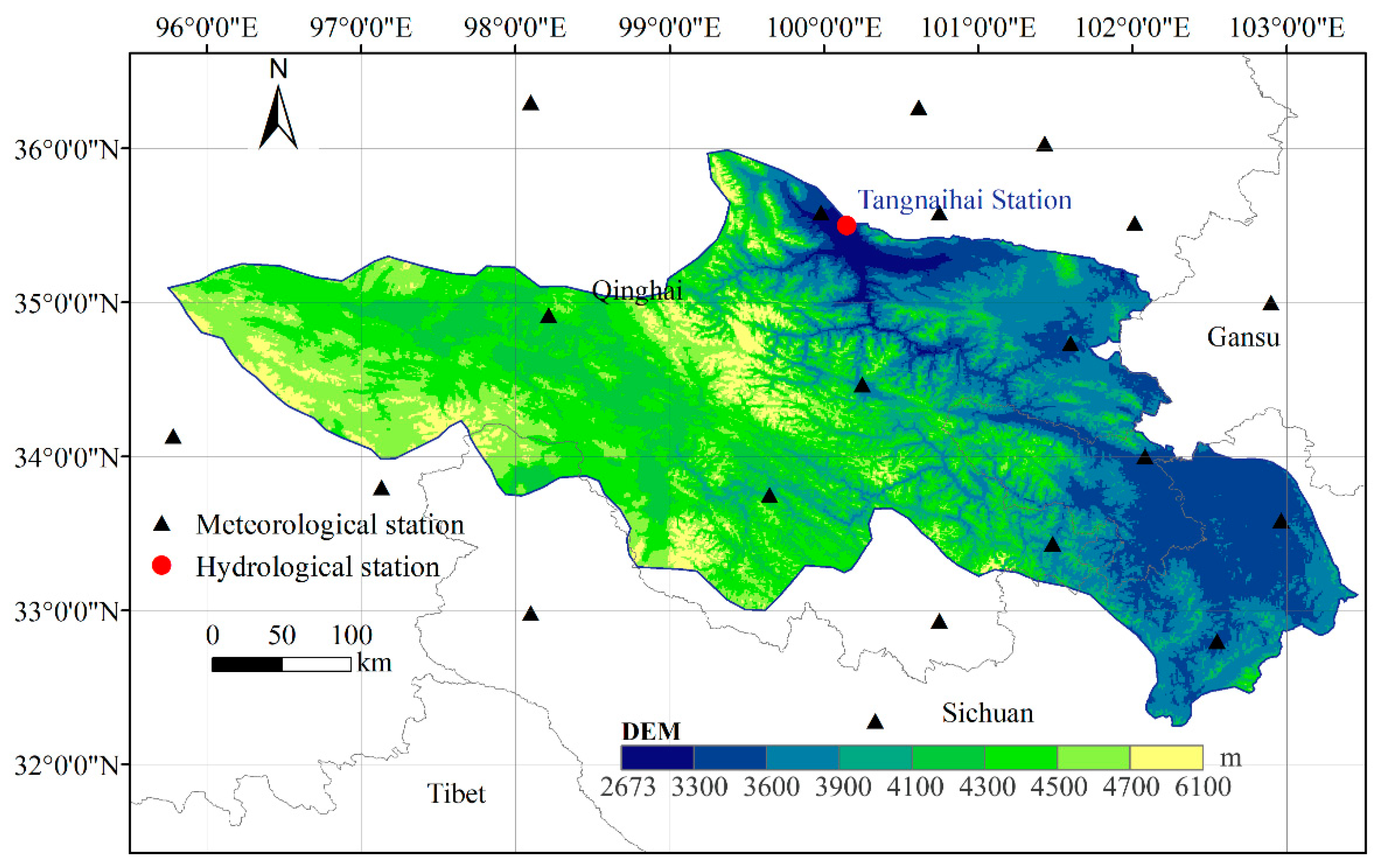
2.1. Study Area
2.2. Data Sources
3. Research Methods
3.1. Trend Analysis (Slope)
3.2. Mutation Analysis
3.3. Budyko Hypothesis
4. Results and Discussion
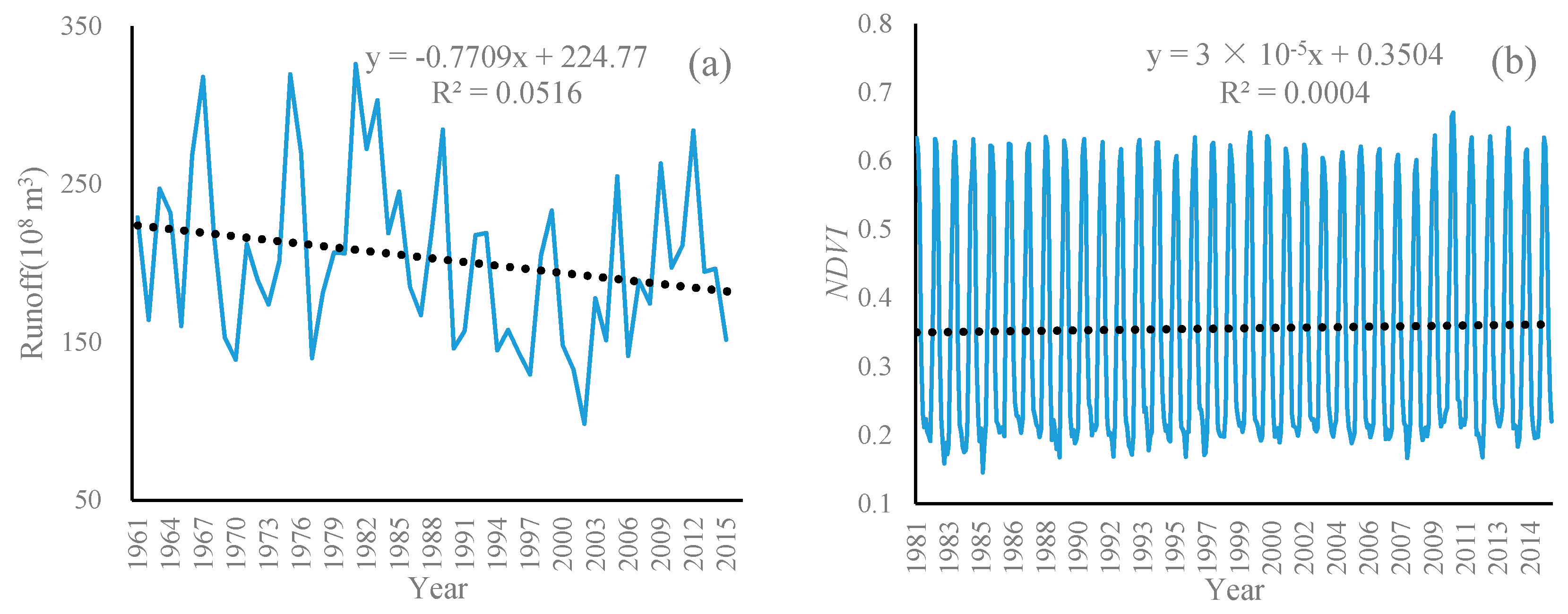
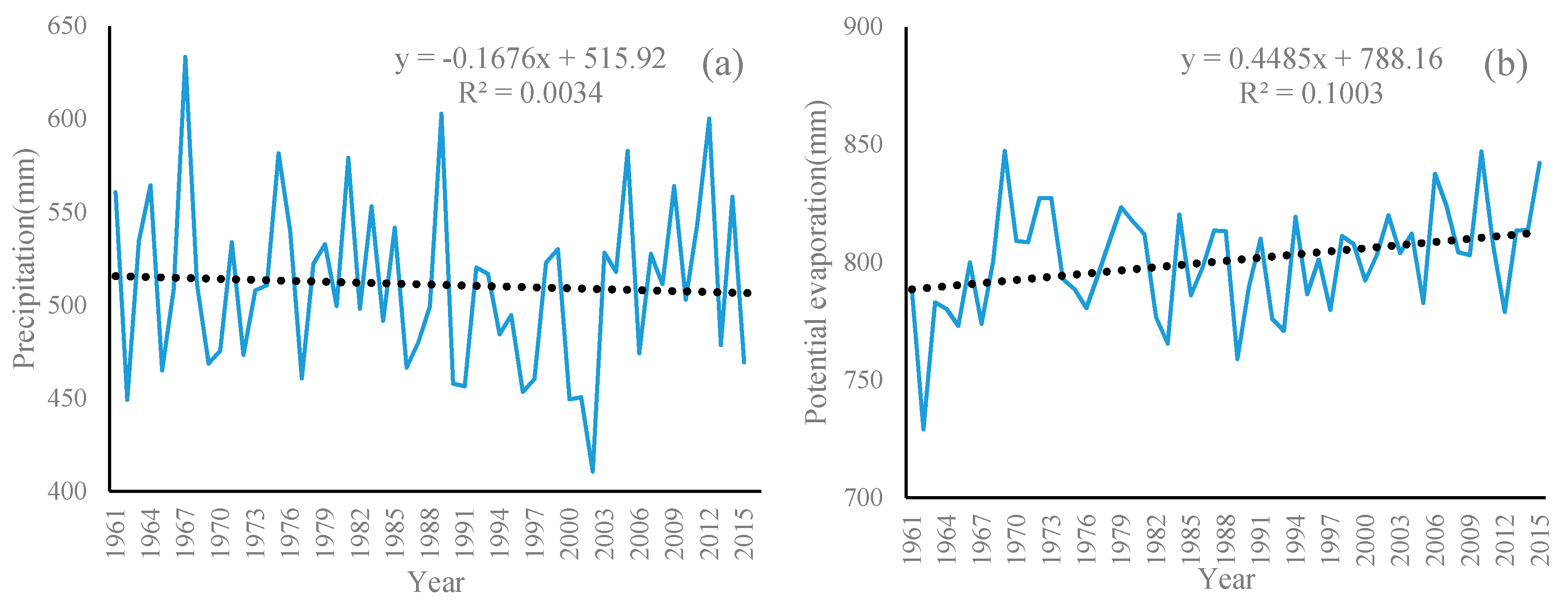
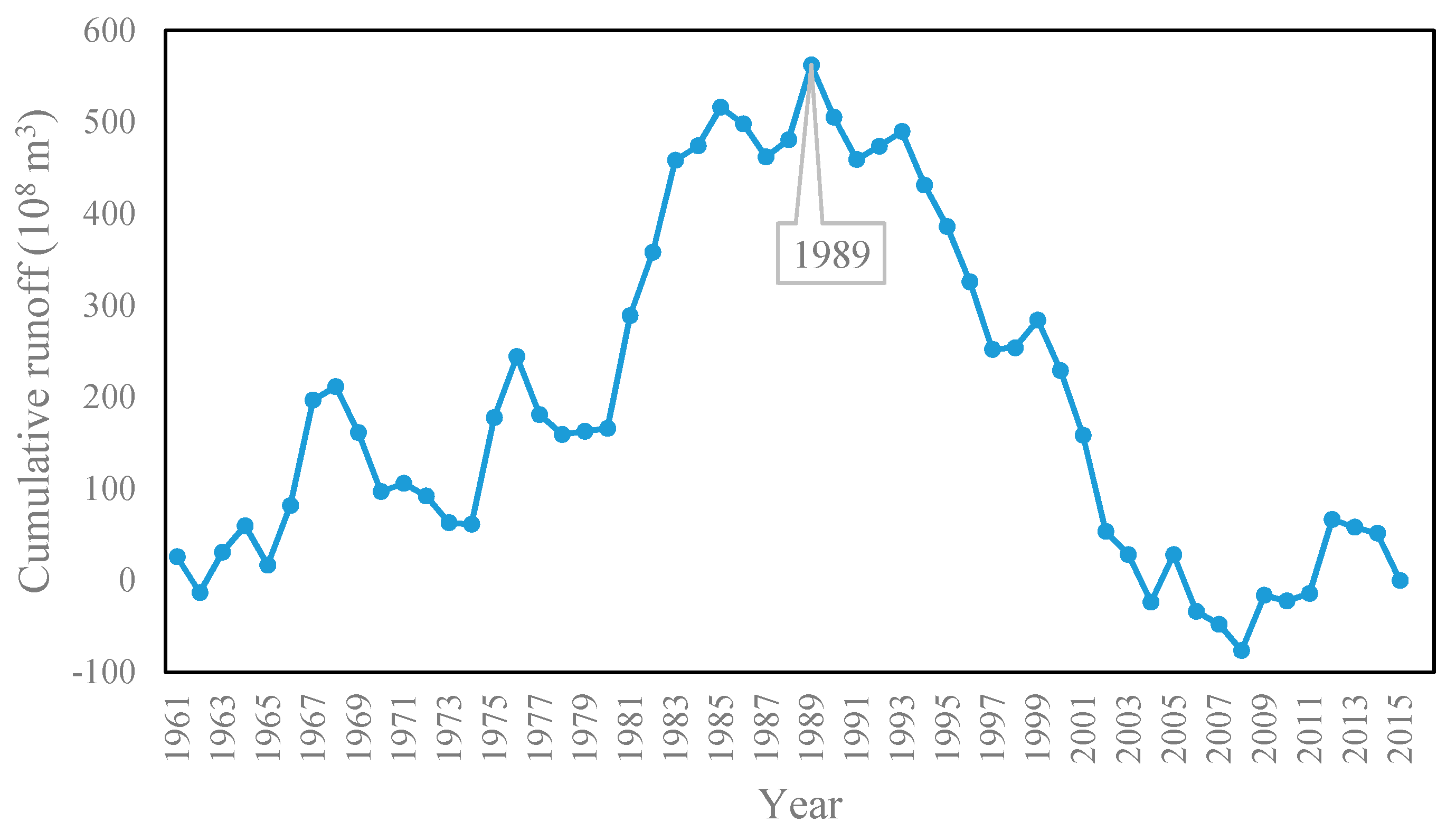
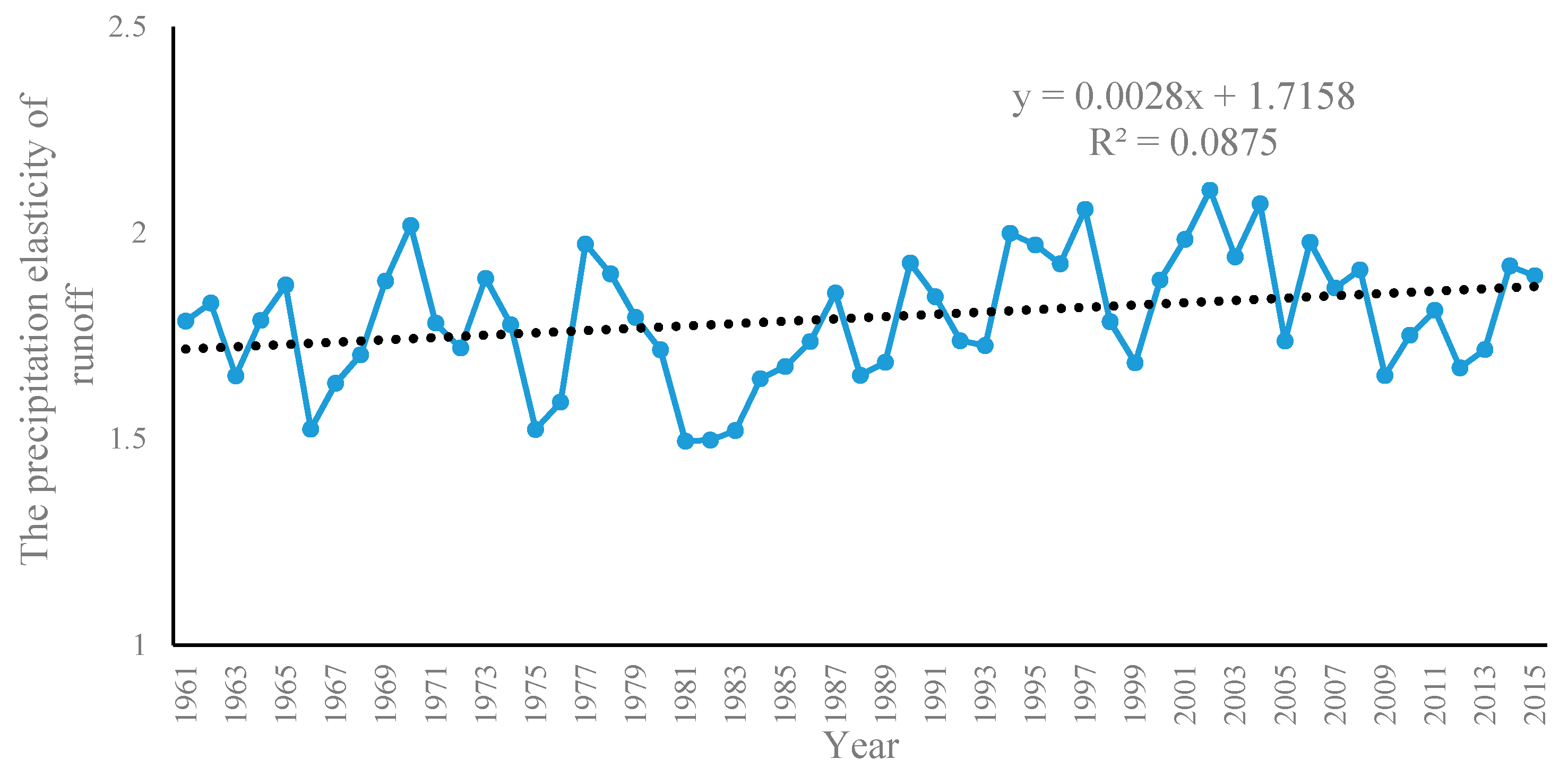
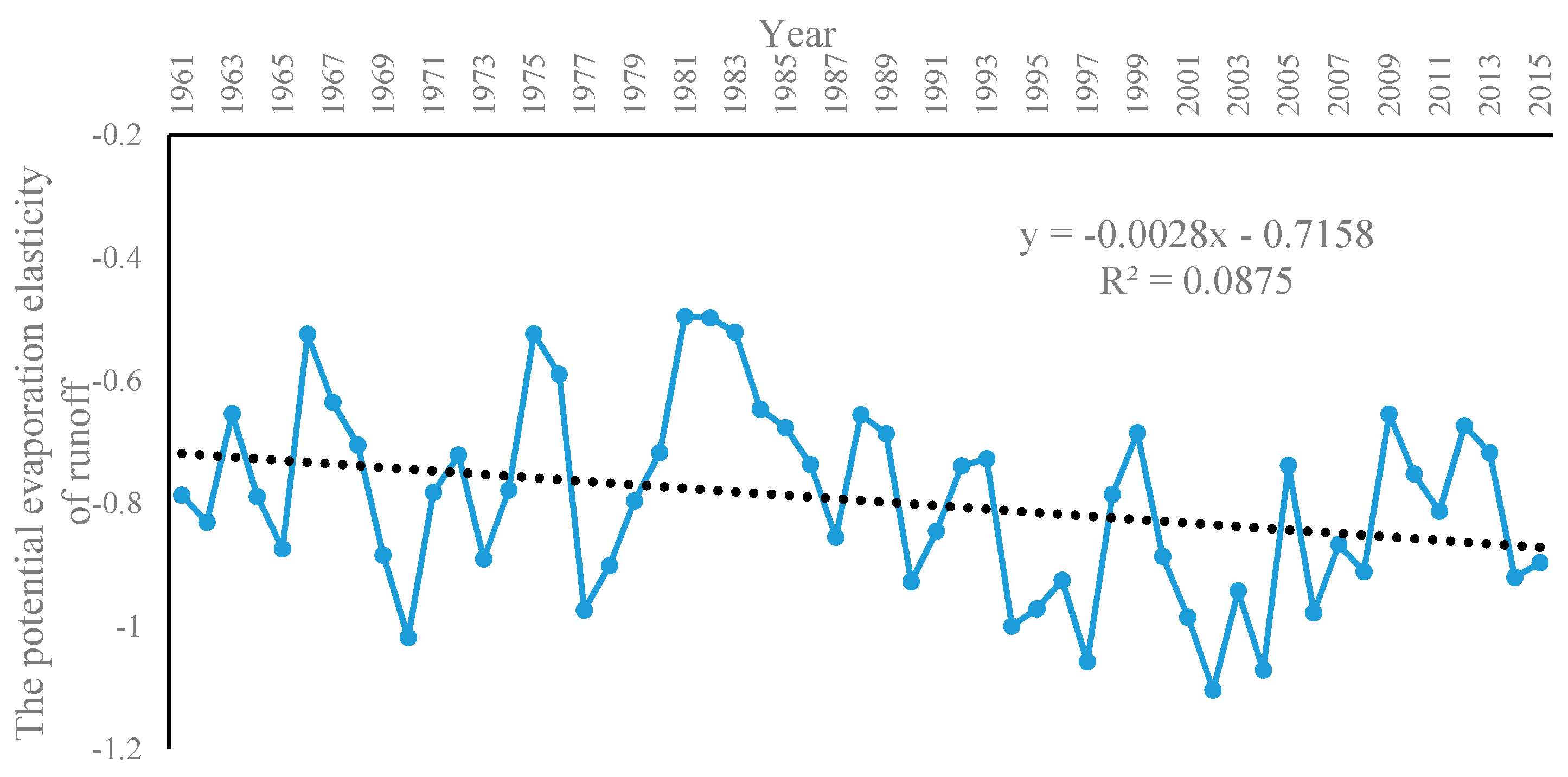
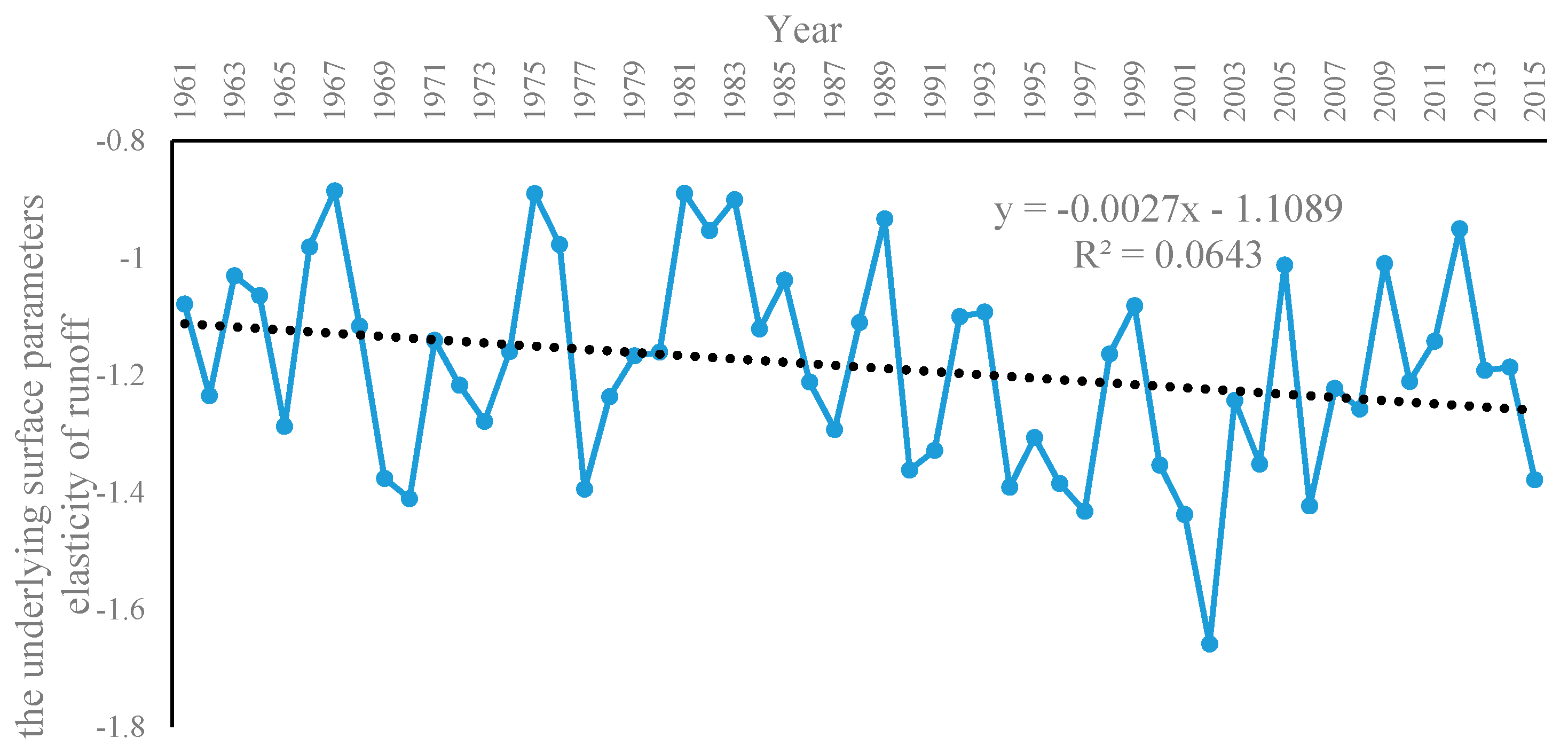
4.1. Trends of Runoff, NDVI, and Climate Change
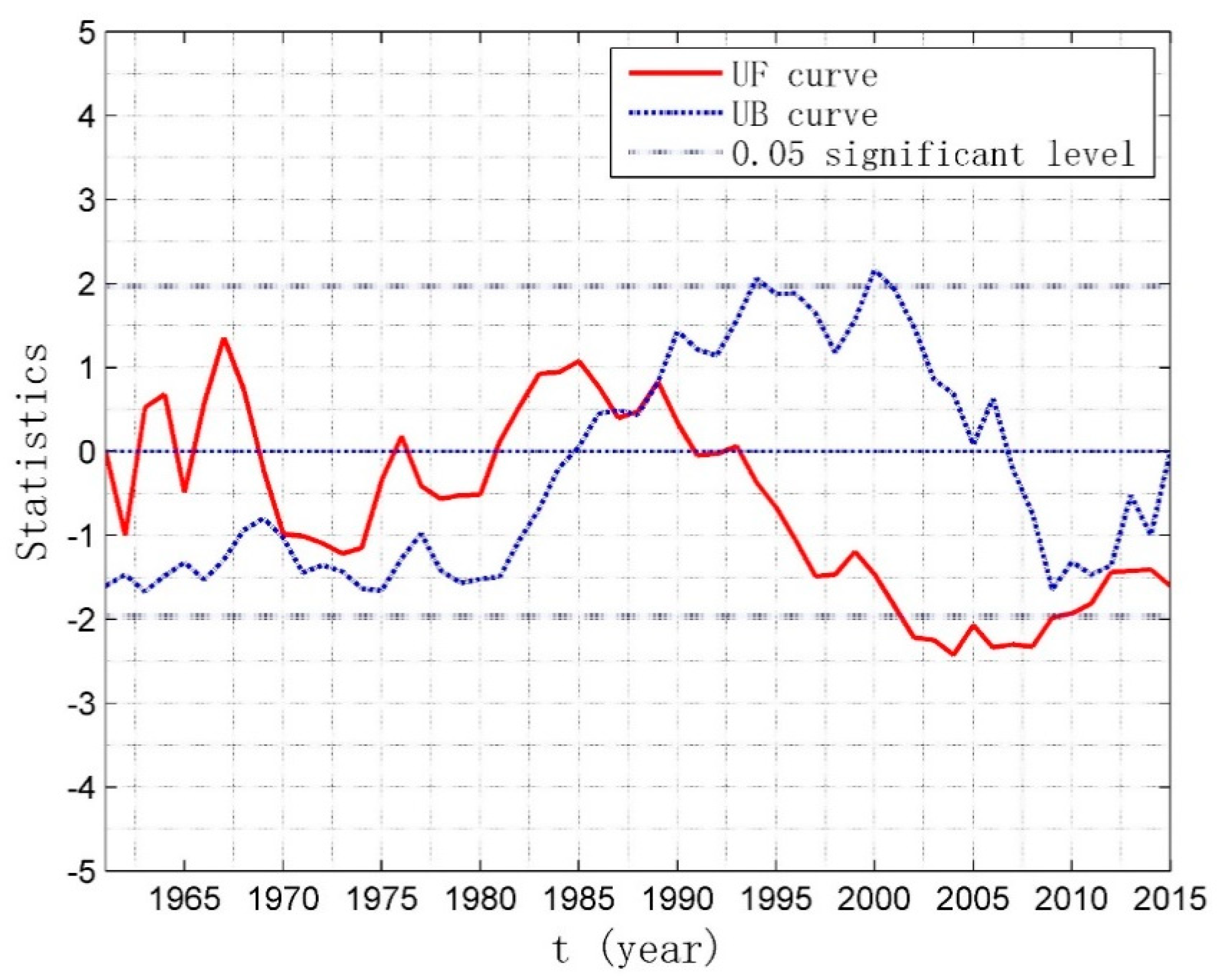
4.2. Abrupt Changes of Runoff
4.3. Assessment of the Contribution Rates of Climate Change and Human Activities to Runoff Change
- (1)
- There were NDVI remote sensing image data from June 1981 to December 1989 in T1 period (1961–1989), so we established the multiple linear regression relationship between NDVI and climatic factors (precipitation and potential evaporation) from July 1981 to December 1989.
- (2)
- Due to a lack of NDVI values in the period from January 1961 to June 1981, we further assumed that the multiple linear regression relationship in the period from June 1981 to December 1989 was the same as the period from January 1961 to June 1981. NDVI values for the period from January 1961 to June 1981 were calculated based on precipitation and potential evaporation in the corresponding periods.
- (3)
- We calculated the mean value of measured NDVI () in T1 period (1961–1989), the mean value of measured NDVI () in T2 period (1990–2015), and the mean value of NDVI under climate change () in the T2 period (1990–2015) according to the multiple linear regression function.
- (4)
- We calculated the contribution rates of climate change and human activities to NDVI changes using formula (26)–(29) (Table 1).
4.4. Discussions
- (1)
- Uncertainties of meteorological station observation data
- (2)
- Uncertainties in the division of base period and change period
- (3)
- Uncertainties caused by using NDVI to characterize land type change
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jia, Y.; Wang, H.; Peng, H. A review on international development trend in the fileld of hydrology and water resources. J. China Inst. Resour. Hydropower Res. 2009, 7, 241–248. (In Chinese) [Google Scholar]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flow regimes at the global scale. J. Hydrol. 2013, 486, 351–364. [Google Scholar] [CrossRef]
- Van Vliet, M.T.H.; Franssen, W.H.P.; Yearsley, J.R.; Ludwig, F.; Haddeland, I.; Lettenmaier, D.P.; Kabat, P. Global river runoff and water temperature under climate change. Glob. Environ. Chang. 2013, 23, 450–464. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Vörösmarty, C.J. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Shen, H.; Dai, S.; Xiao, J.; Shi, X. Response of runoff to climate change and its future tendency in the source region of Yellow River. J. Geogr. Sci. 2012, 22, 431–440. [Google Scholar] [CrossRef]
- Li, H.; Shi, C.; Zhang, Y.; Ning, T.; Sun, P.; Liu, X.; Ma, X.; Liu, W.; Collins, A.L. Using the Budyko hypothesis for detecting and attributing changes in runoff to climate and vegetation change in the soft sandstone area of the middle Yellow River basin, China. Sci. Total Environ. 2020, 703, 135588. [Google Scholar] [CrossRef]
- Caracciolo, D.; Pumo, D.; Viola, F. Budyko’s Based Method for Annual Runoff Characterization across Different Climatic Areas: An Application to United States. Water Resour. Manag. 2018, 32, 3189–3202. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, Q.; Cheng, L.; Xia, J. A Budyko-based framework for quantifying the impacts of aridity index and other factors on annual runoff. J. Hydrol. 2019, 579, 124224. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y.; Leng, G. Quantifying the Relative Contribution of Climate and Human Impacts on Runoff Change Based on the Budyko Hypothesis and SVM Model. Water Resour. Manag. 2016, 30, 2377–2390. [Google Scholar] [CrossRef]
- Liang, W.; Bai, D.; Wang, F.; Wang, F.; Fu, B.; Yan, J.; Wang, S.; Yang, Y.; Long, D.; Feng, M. Quantifying the impacts of climate change and ecological restoration on streamflow changes based on a Budyko hydrological model in China’s Loess Plateau. Water Resour. Res. 2015, 51, 6500–6519. [Google Scholar] [CrossRef]
- Shen, Q.; Cong, Z.; Lei, H. Evaluating the impact of climate and underlying surface change on runoff within the Budyko framework: A study across 224 catchments in China. J. Hydrol. 2017, 554, 251–262. [Google Scholar] [CrossRef]
- Wang, T.; Yang, H.; Yang, D.; Qin, Y.; Wang, Y. Quantifying the streamflow response to frozen ground degradation in the source region of the Yellow River within the Budyko framework. J. Hydrol. 2018, 558, 301–313. [Google Scholar] [CrossRef]
- Zhang, D.; Cong, Z.; Ni, G.; Yang, D.; Hu, S. Effects of snow ratio on annual runoff within the Budyko framework. Hydrol. Earth Syst. Sci. 2015, 12, 939–973. [Google Scholar] [CrossRef]
- Xu, X.; Yang, D.; Yang, H.; Lei, H. Attribution analysis based on the Budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Q.; Singh, V.P.; Shi, P. Contribution of multiple climatic variables and human activities to streamflow changes across China. J. Hydrol. 2017, 545, 145–162. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Wang, Y.; Guo, A.; Li, Z.; Li, Y.; Guo, Z. Assessment on impacts of climate change and human activities on runoff in source region of the Yellow River. J. Xi’an Univ. Technol. 2018, 34, 205–210. (In Chinese) [Google Scholar]
- Zheng, Y.; Huang, Y.; Zhou, S.; Wang, K.; Wang, G. Effect partition of climate and catchment changes on runoff variation at the headwater region of the Yellow River based on the Budyko complementary relationship. Sci. Total Environ. 2018, 643, 1166–1177. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Z.; Xu, J.; Yan, B.; Hong, X. Research on the attribution identification of source runoff variation in the Yellow River Source Region based on water and energy balance model. IOP. Conf. Ser. Earth Environ. Sci. 2019, 344, 012122. [Google Scholar] [CrossRef]
- Shang, F.; Wang, K.; Huang, Y.; Wei, J. Variation Characteristics of Runoff and the Quantitative Separation Based on Budyko Hypothesis in the Three-River Headwaters Region. J. Tongji Univ. (Nat. Sci.) 2020, 48, 305–316. (In Chinese) [Google Scholar]
- Yang, Y.; Guo, L.; Huang, Q.; Li, D. Temporal and spatial variation of land cover change in the source regions of the Yangtze and Yellow Rivers. Ecol. Sci. 2013, 32, 098–103. (In Chinese) [Google Scholar]
- Lu, H.; Shi, J. Reconstruction and analysis of temporal and spatial variations in surface soil moisture in China using remote sensing. Chin. Sci. Bull. 2012, 57, 1412–1422. (In Chinese) [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Chen, X.; Li, Y.; Liao, J.; Ye, Y.; Zhang, H.; Huang, N.; Kuang, Y. China’s 19-year city-level carbon emissions of energy consumptions, driving forces and regionalized mitigation guidelines. Renew. Sustain. Energy Rev. 2014, 35, 231–243. [Google Scholar] [CrossRef]
- Wang, H.; Ji, G.; Xia, J. Analysis of Regional Differences in Energy-Related PM2.5 Emissions in China: Influencing Factors and Mitigation Countermeasures. Sustainability 2019, 11, 1409. [Google Scholar] [CrossRef] [Green Version]
- Xia, H.; Wang, H.; Ji, G. Regional Inequality and Influencing Factors of Primary PM Emissions in the Yangtze River Delta, China. Sustainability 2019, 11, 2269. [Google Scholar] [CrossRef] [Green Version]
- He, B.; Miao, C.; Shi, W. Trend, abrupt change, and periodicity of streamflow in the mainstream of Yellow River. Environ. Monit. Assess. 2013, 185, 6187–6199. [Google Scholar] [CrossRef]
- Jia, F.; Li, X.; Sun, C.; Sun, H. Characteristics of runoff variation in the Huangyang River basin from 1951 to 2016. J. Liaoning Norm. Univ. (Nat. Sci. Ed.) 2019, 42, 262–267. (In Chinese) [Google Scholar]
- Song, X.; Mu, X.; Gao, P.; Wang, S.; Wang, F. Trends of Runoff Variation from 1900 to 2005 at Harbin Station of Songhua River. J. Nat. Resour. 2009, 24, 1803–1809. (In Chinese) [Google Scholar]
- Wang, S.; Yan, M.; Yan, Y.; Shi, C.; He, L. Contributions of climate change and human activities to the changes in runoff increment in different sections of the Yellow River. Quat. Int. 2012, 282, 66–77. [Google Scholar] [CrossRef]
- Wang, S.; Yan, Y.; Yan, M.; Zhao, X. Quantitative estimation of the impact of precipitation and human activities on runoff change of the Huangfuchuan River basin. J. Geogr. Sci. 2012, 22, 906–918. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Ran, L.; Su, T. Climatic and anthropogenic impacts on runoff change in the Songhua River basin over the last 56 years (1955–2010), Northeastern China. Catena 2015, 127, 258–269. [Google Scholar] [CrossRef]
- Yan, X.; Bao, Z.; Zhang, J.; Wang, G.; He, R.; Liu, C. Quantifying contributions of climate change and local human activities to runoff decline in the upper reaches of the Luanhe River basin. J. Hydro. Environ. Res. 2020, 28, 67–74. [Google Scholar] [CrossRef]
- Yang, M.; Sang, Y.; Wang, Z.; Liu, C. Variation of rainfall-runoff relationship and the driving factors identification in the Chaohe River. Geogr. Res. 2014, 33, 1658–1667. (In Chinese) [Google Scholar]
- Zhang, L.; Zhao, G.; Mu, X.; Gaol, P.; Sun, W. Attribution of runoff variation in the Wei River basin based on the Budyko hypothesis. Acta Ecol. Sin. 2018, 38, 7607–7617. (In Chinese) [Google Scholar]
- Al-Safi, H.I.J.; Kazemi, H.; Sarukkalige, P.R. Comparative study of conceptual versus distributed hydrologic modelling to evaluate the impact of climate change on future runoff in unregulated catchments. J. Water Clim. Chang. 2020, 11, 341–366. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Xu, J.; Lin, Y.; Zhou, M. Attribution of Runoff Variation in the Headwaters of the Yangtze River Based on the Budyko Hypothesis. Int. J. Environ. Res. Public Health 2019, 16, 2506. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Miao, C.; Wang, Y.; Duan, Q.; Zhang, X. Contribution analysis of the long-term changes in seasonal runoff on the Loess Plateau, China, using eight Budyko-based methods. J. Hydrol. 2017, 545, 263–275. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Wang, D.; Liu, P.; Guo, S.; Xu, C. Separating the impacts of climate change and human activities on runoff using the Budyko-type equations with time-varying parameters. J. Hydrol. 2015, 522, 326–338. [Google Scholar] [CrossRef]
- Choudhury, B.J. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water- energy balance equation. Water Resour. Res. 2008, 44, W03410. [Google Scholar] [CrossRef]
- Li, J.; Peng, S.; Li, Z. Detecting and attributing vegetation changes on China’s Loess Plateau. Agric. For. Meteorol. 2017, 247, 260–270. [Google Scholar] [CrossRef]
- Gao, J.; Jiao, K.; Wu, S. Investigating the spatially heterogeneous relationships between climate factors and NDVI in China during 1982 to 2013. J. Geogr. Sci. 2019, 29, 1597–1609. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Zuo, L.; Gao, J.; Jiang, Y.; Zhang, Y.; Ma, S.; Zou, Y.; Wu, S. Revealing the Fingerprint of Climate Change in Interannual NDVI Variability among Biomes in Inner Mongolia, China. Remote Sens. 2020, 12, 1332. [Google Scholar] [CrossRef] [Green Version]
| T1 | T2 | Fitting Equation | ||||||
|---|---|---|---|---|---|---|---|---|
| 1961–1989 | 1990–2015 | NDVI = 3.069 × 10−3 P + 8.875× 10−4 ET0 + 0.1588 (R2 = 0.79) | 0.0282 | 0.3289 | 0.3466 | 0.3571 | 62.79 | 37.21 |
| Hydrological Station | Period | ET0/mm | R/mm | P/mm | R/P | ET0/P | |
|---|---|---|---|---|---|---|---|
| Tangnaihai | T1 | 796.54 | 180.39 | 518.92 | 1.13 | 0.35 | 1.54 |
| T2 | 805.38 | 148.85 | 502.66 | 1.26 | 0.30 | 1.60 |
| εP | εET0 | εω | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.77 | −0.77 | −1.16 | −31.54 | −16.26 | 8.84 | 0.13 | −9.36 | −1.41 | −13.32 | −7.89 | 75.33 | 24.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, D.; Lai, Z.; Ji, G. Using Budyko-Type Equations for Separating the Impacts of Climate and Vegetation Change on Runoff in the Source Area of the Yellow River. Water 2020, 12, 3418. https://doi.org/10.3390/w12123418
Yan D, Lai Z, Ji G. Using Budyko-Type Equations for Separating the Impacts of Climate and Vegetation Change on Runoff in the Source Area of the Yellow River. Water. 2020; 12(12):3418. https://doi.org/10.3390/w12123418
Chicago/Turabian StyleYan, Dan, Zhizhu Lai, and Guangxing Ji. 2020. "Using Budyko-Type Equations for Separating the Impacts of Climate and Vegetation Change on Runoff in the Source Area of the Yellow River" Water 12, no. 12: 3418. https://doi.org/10.3390/w12123418
APA StyleYan, D., Lai, Z., & Ji, G. (2020). Using Budyko-Type Equations for Separating the Impacts of Climate and Vegetation Change on Runoff in the Source Area of the Yellow River. Water, 12(12), 3418. https://doi.org/10.3390/w12123418





