A Numerical Simulation of Membrane Distillation Treatment of Mine Drainage by Computational Fluid Dynamics
Abstract
:1. Introduction
2. Theory
2.1. Governing Theory
2.2. Mass Transfer
2.3. Heat Transfer
- (1)
- Heat flows from the main body of the feed liquid through the thermal boundary layer to the surface of the membrane by natural convectionwhere is the local heat transfer coefficient of the feed liquid; is the main body temperature of the feed liquid; is the membrane surface temperature on the feed side.where hf is the local heat transfer coefficient;
- (2)
- Heat passes through the membrane in two ways: latent heat of vaporization and heat conduction:
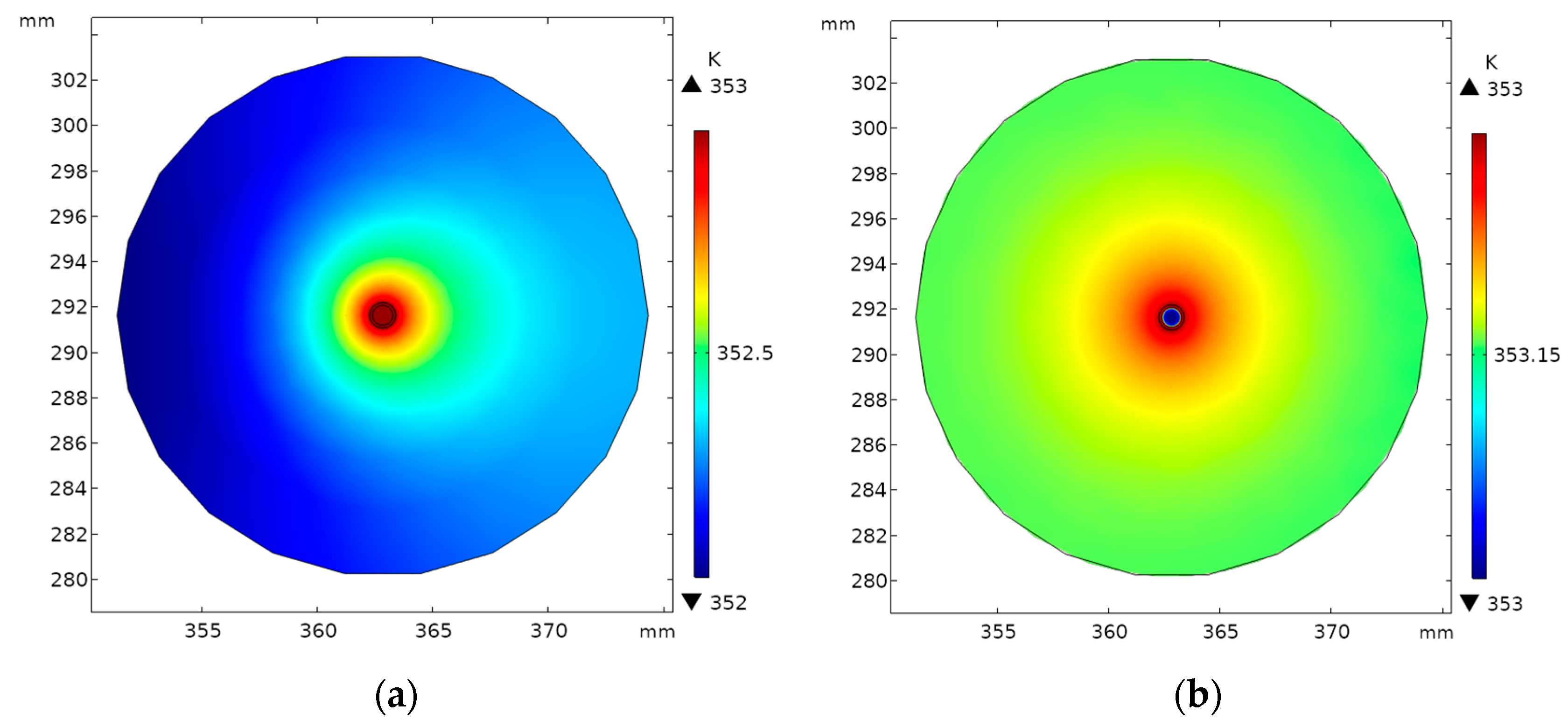
3. CFD Model Formation
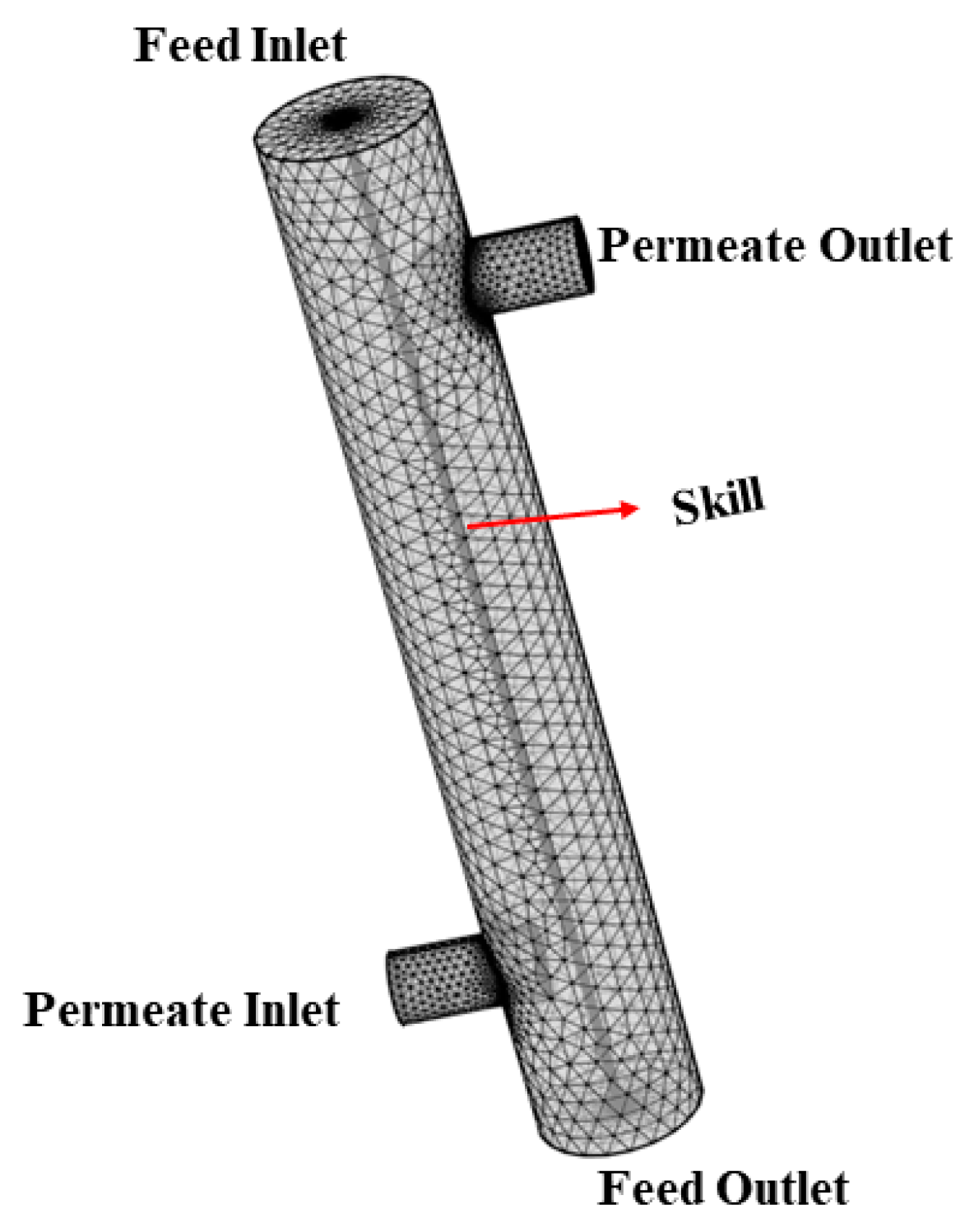
3.1. Geometry and Mesh
- (1)
- Steady-state operation;
- (2)
- Both the feed side and the permeate side are incompressible flow, laminar flow model;
- (3)
- The membrane has a 100% rejection rate of the feed liquid, and the removal rate of the precipitate from the membrane surface is ignored;
- (4)
- No chemical reaction;
- (5)
- No heat loss to the open environment.
3.2. Boundary Conditions
3.3. Design of CFD Simulation
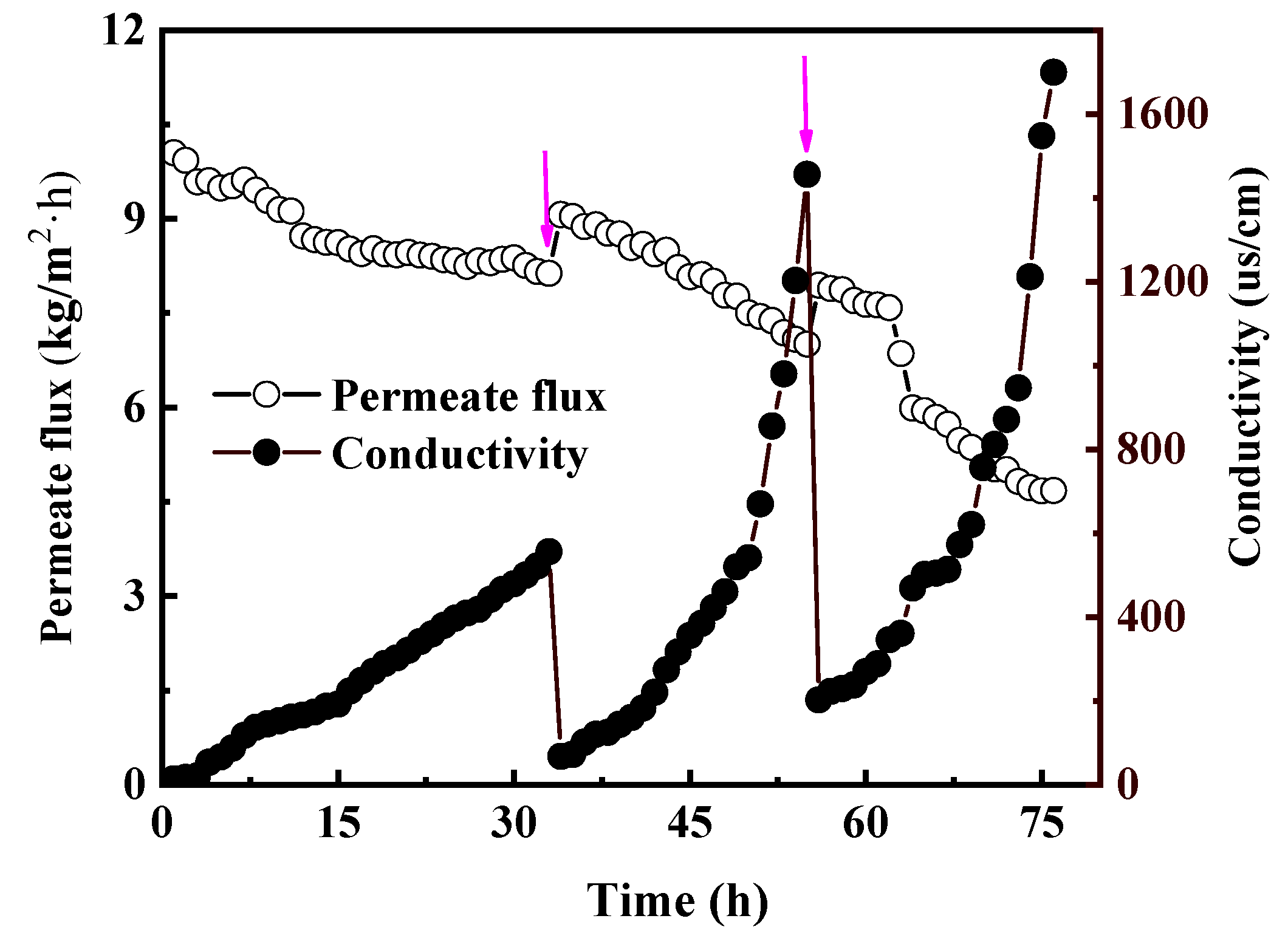
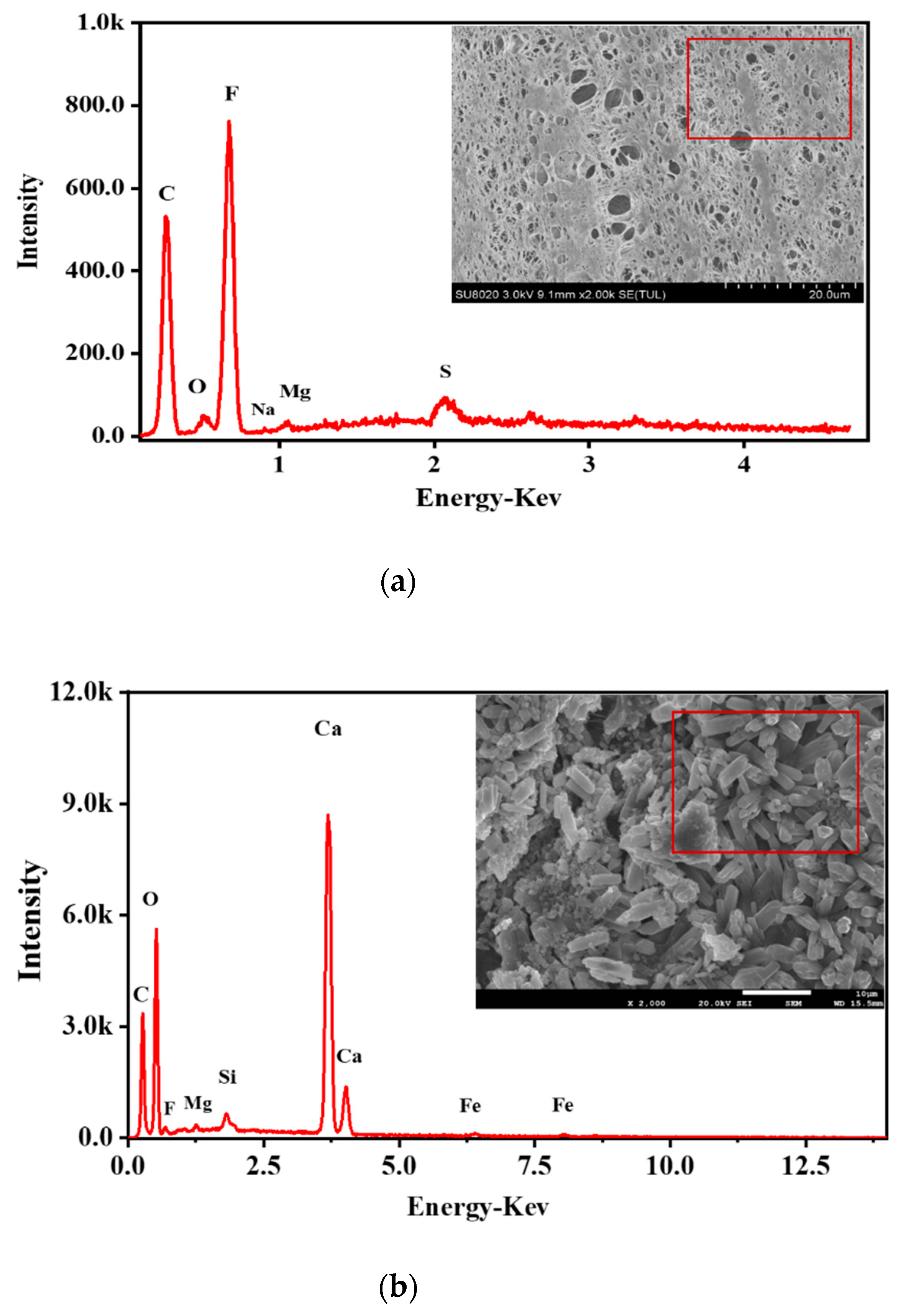
4. Experiment Method
5. Results and Discussion
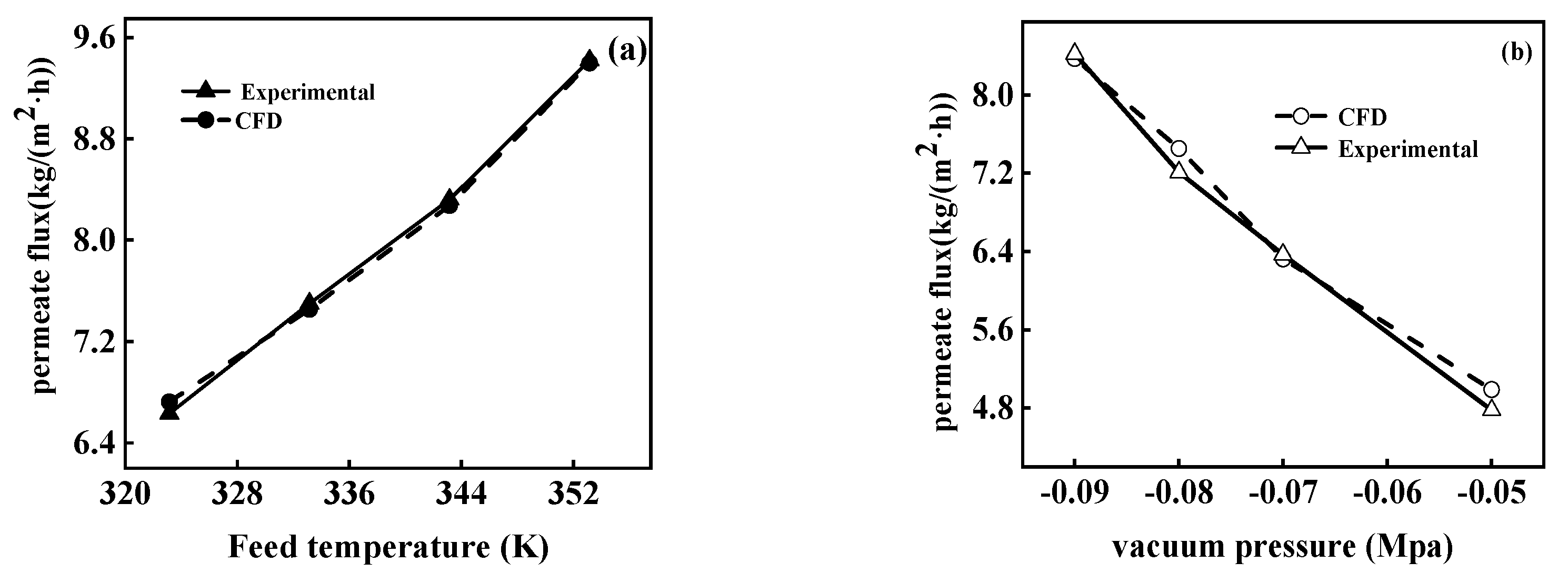
5.1. Model Validation
5.2. Mass Transfer in VMD
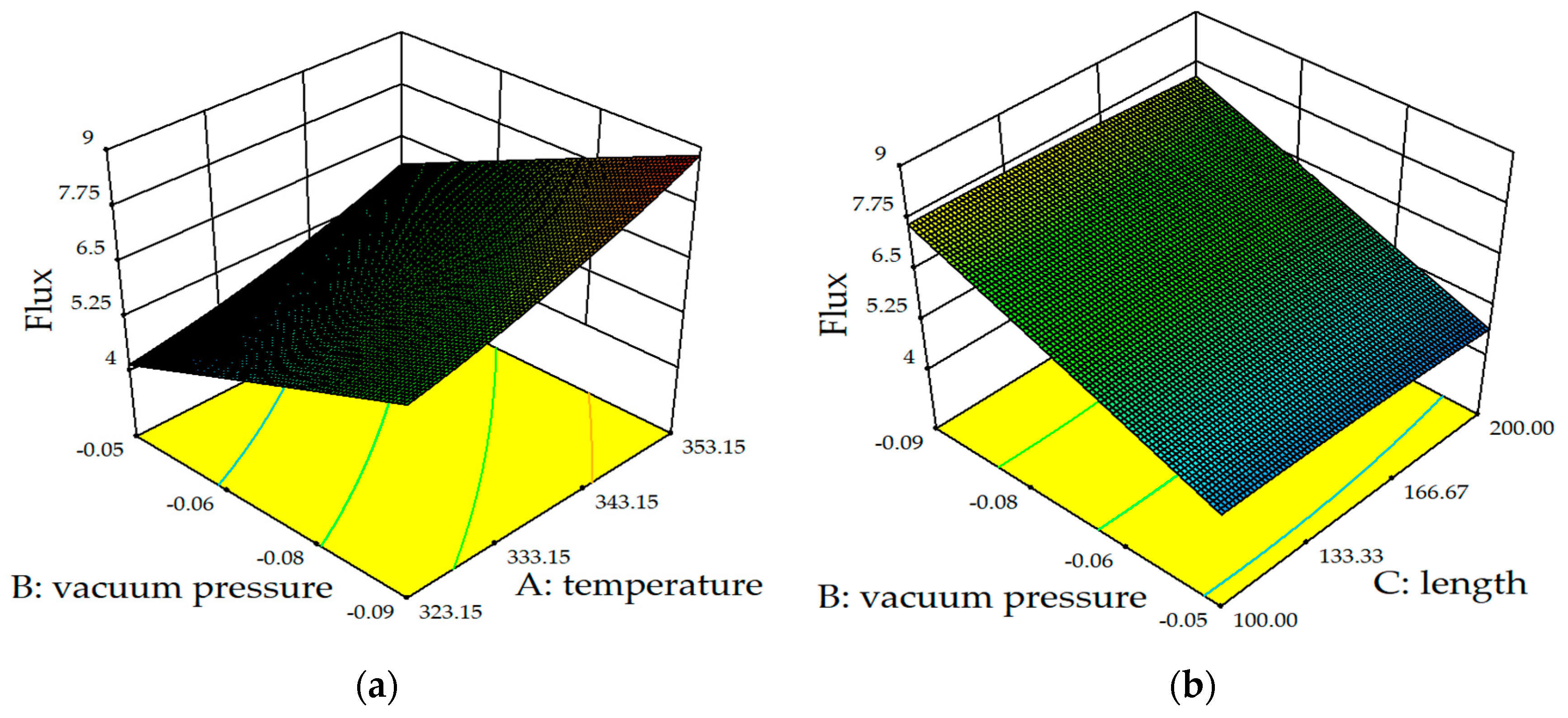
5.2.1. Effect of Membrane Parameters on Flux
5.2.2. Effect of Operational Factors on Flux
5.2.3. CPC
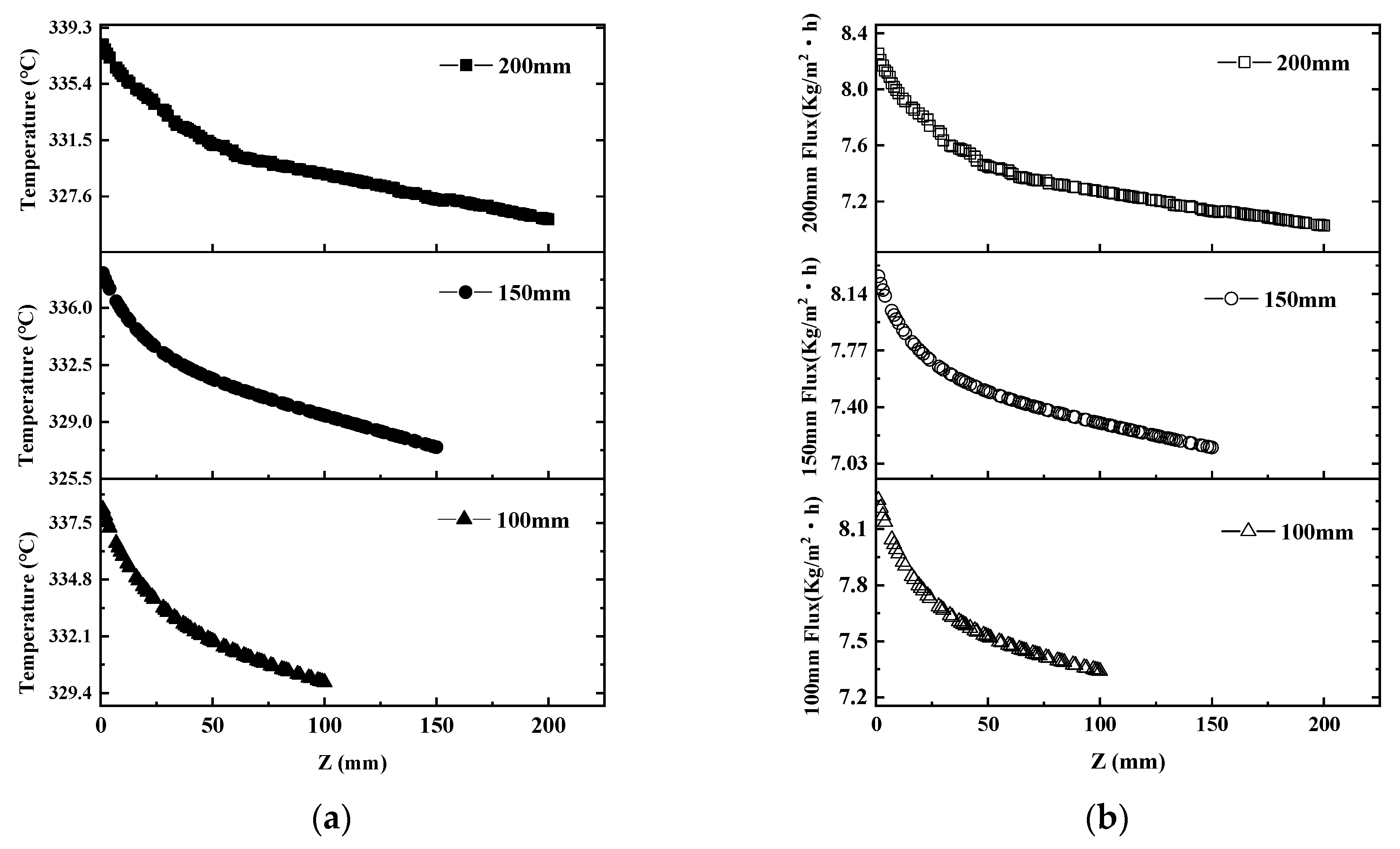
5.3. Heat Transfer in VMD
5.3.1. Effects of Membrane Characteristics on Heat Transfer
5.3.2. Effect of Operational Factors on Heat Transfer
5.3.3. TPC
6. Conclusions
- (1)
- In addition to the membrane length, the two operating conditions were positively correlated with permeate flux. With the increase in feed temperature/vacuum pressure, the permeate flux was raised;
- (2)
- The results of RSM showed that the impact on the permeate flux was: vacuum pressure > feed temperature > membrane length > feed-temperature–membrane length;
- (3)
- The heat transfer efficiency can be improved by increasing vacuum pressure and feed temperature, but the effects of them were different. The vacuum pressure affected the permeate flux, and thus changes the heat transfer efficiency. However, the feed temperature can provide heat for the evaporation of water vapor through convective heat transfer, which plays a certain role in heat transfer efficiency;
- (4)
- The influence on heat transfer efficiency was: vacuum pressure > feed temperature > film length > feed temperature;
- (5)
- TPC also has a significant effect on MD heat transfer. The temperature of the feed liquid is negatively correlated with TPC. There was a negative correlation between temperature and TPC. TPC decreased with the increase in feed temperature.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Cp | Heat capacity (KJ/(Kg·K)) |
| Df,b | Diffusion coefficient (m/s) |
| d | Hydraulic diameter (m) |
| hf | Local heat transfer coefficient (W/(m2·K)) |
| Latent heat of vaporization of water (J/ kg) | |
| J | Membrane flux (kg/(m2·h)) |
| K | Heat conductivity (W/(m·K)) |
| KB | Boltzmann constant |
| KM | Membrane distillation coefficient (W/(m·K)) |
| Kn | Knudsen Number |
| M | Molecular mass (kg /mol) |
| P | Average pressure (pa) |
| Pf,m | Vapor pressure at feed membrane interface |
| Pvacuum | Vacuum pressure (pa) |
| Psv | Water vapor pressure (pa) |
| Q | Heat flux (W/m2) |
| R | Gas universal constant (J/(mol·K)) |
| Re | Reynolds number |
| r | Average pore size (m) |
| rw | Activity coefficient of water |
| S | Membrane area(m2) |
| Sc | Schmidt number |
| Sh | Energy source term (J/(m3·s)) |
| Sm | Mass source term (Kg/(m3·s)) |
| Sv | Momentum source term (N/m3) |
| T | Temperature (K) |
| u | Velocity of feed (m/s) |
| xs | Molar fraction of sodium chloride |
| Greek symbols | |
| Porosity (%) | |
| Mean free path of water molecule (m) | |
| Collision diameter(m) | |
| Membrane thickness (m) | |
| Tortuosity | |
| Thermal efficiency (%) | |
| Viscosity (Pa·S) | |
| Subscript | |
| f,b | Feed bulk |
| f,m | Membrane surface on the feed side feed |
| p | Permeate |
| P,m | Membrane surface on the permeate side |
| Abbreviations | |
| CFD | Computational fluid dynamics |
| MD | Membrane distillation |
| VMD | Vacuum membrane distillation |
| TPC | Temperature polarization coefficient |
References
- Dazhao, G.; Yong, Z.; Zhiguo, C. Technical progress of water resource protection and utilization by coal mining in China. Coal Sci. Technol. 2016, 44, 1–7. [Google Scholar]
- Ministry of Water Resources People’s Republic of China. China Water Resources Bulletin; Ministry of Water Resources People’s Republic of China: Beijing, China, 2018.
- Binbin, J.; Xiaolong, H.; Qiang, G.; Xinjie, L. Research on underground classification treatment technology of highly mineralized mine water in Lingxin Coal Mine. Coal Eng. 2018, 50, 83–85. [Google Scholar]
- Andrjesdottir, O.; Ong, C.L.; Nabavi, M.; Paredes, S.; Khalil, A.S.G.; Michel, B.; Poulikakos, D. An experimentally optimized model for heat and mass transfer in direct contact membrane distillation. Int. J. Heat Mass Transf. 2013, 66, 855–867. [Google Scholar] [CrossRef]
- Khayet, M. Membranes and theoretical modeling of membrane distillation: A review. Adv. Colloid Interface. 2011, 164, 56–88. [Google Scholar] [CrossRef] [PubMed]
- Fuqin, L.; Guifeng, Z.; Yunhao, Z. Research on Zero Drainage Process of Highly Mineralized Mine Water. Coal Sci. Technol. 2018, 46, 81–86. [Google Scholar]
- Abu-Zeid, M.A.E.-R.; Zhang, Y.; Dong, H.; Zhang, L.; Chen, H.-L.; Hou, L. A comprehensive review of vacuum membrane distillation technique. Desalination 2015, 356, 1–14. [Google Scholar] [CrossRef]
- El-Zanati, E.; El-Khatib, K.M. Integrated membrane—Based desalination system. Desalination 2007, 205, 15–25. [Google Scholar] [CrossRef]
- Drioli, E.; Ali, A.; Macedonio, F. Membrane distillation: Recent developments and perspectives. Desalination 2015, 356, 56–84. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C.J. Heat and mass transfer in membrane distillation. J. Membr. Sci. 1987, 33, 299–313. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Li, H.; Yi, F.; Li, X.; Pavlenko, A.N.; Gao, X. Numerical simulation for falling film flow characteristics of refrigerant on the smooth and structured surfaces. J. Eng. Thermophys. Rus. 2018, 27, 1–19. [Google Scholar] [CrossRef]
- Long, R.; Kuang, Z.; Liu, Z.; Liu, W. Ionic thermal up-diffusion in nanofluidic salinity gradient energy harvesting. Nat. Sci. Rev. 2019, 6. [Google Scholar] [CrossRef]
- Tang, N.; Zhang, H.; Wang, W. Computational fluid dynamics numerical simulation of vacuum membrane distillation for aqueous NaCl solution. Desalination 2011, 274, 120–129. [Google Scholar] [CrossRef]
- Shokrollahi, M.; Rezakazemi, M.; Younas, M. Producing water from saline streams using membrane distillation: Modeling and optimization using CFD and design expert. Int. J. Energy Res. 2020, 44. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.; Han, L.; Li, B. Simulation of heat and mass transfer with cross-flow hollow fiber vacuum membrane distillation: The influence of fiber arrangement. Chem. Eng. Res. Des. 2017, 119, 12–22. [Google Scholar] [CrossRef]
- Parakala, S.; Moulik, S.; Sridhar, S. Effective separation of methylene blue dye from aqueous solutions by integration of micellar enhanced ultrafiltration with vacuum membrane distillation. Chem. Eng. Res. Des. 2019, 375. [Google Scholar] [CrossRef]
- Ho, C.-D.; Huang, C.-H.; Tsai, F.-C.; Chen, W.-T. Performance improvement on distillate flux of countercurrent-flow direct contact membrane distillation systems. Desalination 2014, 338, 26–32. [Google Scholar] [CrossRef]
- Kuang, Z.; Long, R.; Liu, Z.; Liu, W. Analysis of temperature and concentration polarizations for performance improvement in direct contact membrane distillation. Int. J. Heat Mass Transf. 2019, 145, 118724. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Ji, S.; Wang, S. Numerical simulation of 3d hollow-fiber vacuum membrane distillation by computational fluid dynamics. Chem. Eng. Sci. 2019, 152, 172–185. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Yu, H.; Yang, X.; Wang, R.; Fan, A.G. Numerical simulation of heat and mass transfer in direct membrane distillation in a hollow fiber module with laminar flow. J. Membr. Sci. 2011, 384, 107–116. [Google Scholar] [CrossRef]
- Julian, H.; Lian, B.; Li, H.; Liu, X.; Wang, Y.; Leslie, G.; Chen, V. Numerical study of CaCo3 scaling in submerged vacuum membrane distillation and crystallization (VMDC). J. Membr. Sci. 2018, 559, 87–97. [Google Scholar] [CrossRef]
- Martnez, L.; Florido-Daz, F.J.; Hernández, A.; Prádanos, P. Characterisation of three hydrophobic porous membranes used in membrane distillation modelling and evaluation of their water vapour permeabilities. J. Membr. Sci. 2002, 203, 15–27. [Google Scholar] [CrossRef]
- El-Bourawi, M.S.; Ding, Z.; Ma, R.; Khayet, M. A framework for better understanding membrane distillation separation process. J. Membr. Sci. 2006, 285, 24–29. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G. Effect of pore size distribution and air flux on mass transport in direct contact membrane distillation. J. Membr. Sci. 2003, 215, 75–85. [Google Scholar] [CrossRef]
- Yang, Y.; Rana, D.; Matsuura, T.; Lan, C.Q. The heat and mass transfer of vacuum membrane distillation: Effect of active layer morphology with and without support material. Sep. Purif. Technol. 2016, 164, 56–62. [Google Scholar] [CrossRef]
- Bandini, S.; Sarti, G.C. Heat and mass transport resistances in vacuum membrane distillation per drop. AIChE J. 1999, 45, 1422–1433. [Google Scholar] [CrossRef]
- Bandini, S.; Gostoli, C.; Sarti, G.C. Separation efficiency in vacuum membrane distillation. J. Membr. Sci. 1992, 73, 217–229. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Duke, M.; Hoang, M.; Xie, Z.; Groth, A.; Tun, C.; Gray, S. Modelling of vacuum membrane distillation. J. Membr. Sci. 2013, 434, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Sherwood, T.K.; Pigford, R.L.; Wilke, C.R. Mass Transfer; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Ibrahim, S.S.; Alsalhy, Q.F. Modeling and simulation for direct contact membrane distillation in hollow fiber modules. AIChE J. 2013, 59, 589–603. [Google Scholar] [CrossRef]
- Ameen, N.A.M.; Ibrahim, S.S.; Alsalhy, Q.F.; Figoli, A. Highly Saline Water Desalination Using Direct Contact Membrane Distillation (DCMD): Experimental and Simulation Study. Water 2020, 12, 1–24. [Google Scholar] [CrossRef]
- Lian, B.; Wang, Y.; Le-Clech, P.; Chen, V.; Leslie, G. A numerical approach to module module design for crossflow vacuum membrane distillation systems. J. Membr. Sci. 2016, 510, 489–496. [Google Scholar] [CrossRef]
- Bandini, S.; Sarti, G.C. Concentration of must through vacuum membrane distillation. Desalination 2002, 149, 253–259. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, L.; Ma, R. Study on the effect of flow maldistribution on the performance of the hollow fiber modules used in membrane distillation. J. Membr. Sci. 2003, 215, 11–23. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, F.; Luo, G.; Dai, Y. Effect of Random packing on shell-side flow and mass transfer in hollow fiber module described by normal distribution function. J. Membr. Sci. 2003, 216, 81–93. [Google Scholar] [CrossRef]
- Taamneh, Y.; Bataineh, K. Improving the performance of direct contact membrane distillation utilizing spacer-filled channel. Desalination 2017, 408, 25–35. [Google Scholar] [CrossRef]
- Singh, S.; Chakraborty, J.P.; Mondal, M.K. Optimization of process parameters for torrefaction of Acacia nilotica using response surface methodology and character istics of torrefied biomass as upgraded fuel. Energy 2019, 186, 115865. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Guo, H.; Zhang, W.; Xu, K.; Li, B. Mass transfer in hollow fiber vacuum membrane distillation process based on membrane structure. J. Membr. Sci. 2017, 532, 115–123. [Google Scholar] [CrossRef]
- Baghel, R.; Kalla, S.; Upadhyaya, S.; Chaurasia, S.P.; Singh, K. Cfd modeling of vacuum membrane distillation for removal of naphthol blue black dye from aqueous solution using COMSOL multiphysics. Chem. Eng. Res. Des. 2020, 158. [Google Scholar] [CrossRef]
- Lovineh, S.G.; Asghari, M.; Rajaei, B. Numerical simulation and theoretical study on simultaneous effects of operating parameters in vacuum membrane distillation. Desalination 2013, 314. [Google Scholar] [CrossRef]






| Expression | ||
|---|---|---|
| (4) | ||
| (5) | ||
| (6) | ||
| Characteristics | PVDF |
|---|---|
| Inner diameter (mm) | 0.849 |
| Outer diameter (mm) | 1.139 |
| Thickness (mm) | 0.186 |
| Contact angle (°) | 106.5 |
| Effective membrane surface area (m2) | 0.1066 |
| Thermal conductivity (Wm−1K−1) | 0.2 |
| Conditons | Value |
|---|---|
| Feed temperature (k) | 323.15 to 353.15 K |
| Permeate Temperature (K) | 303.15 |
| Feed solution concentration (Kg/L) | 0.3 |
| Feed inlet rate (L/min) | 1.5 |
| Permeate inlet rate (L/min) | 1.5 |
| Permeate pressure (MPa) | −0.05 to −0.09 |
| Variables | Levels | ||
|---|---|---|---|
| Lower (−1) | Central (0) | Upper (+1) | |
| Feed temperature (K) | 323.15 | 33.15 | 353.15 |
| Vacuum pressure (Mpa) | −0.05 | −0.07 | −0.09 |
| Membrane length (mm) | 100 | 150 | 200 |
| Source | Sum of Squares | Df | Mean Square | F Value | p-Value | Distinctiveness |
|---|---|---|---|---|---|---|
| Model | 23.17 | 9 | 2.57 | 371.26 | <0.0001 | ** |
| A-feed temperature | 7.29 | 1 | 7.29 | 1051.25 | <0.0001 | ** |
| B-vacuum pressure | 15.57 | 1 | 15.57 | 2245.10 | <0.0001 | ** |
| C-length | 0.067 | 1 | 0.067 | 9.68 | 0.0171 | * |
| AC | 0.053 | 1 | 0.053 | 7.60 | 0.0282 | * |
| A2 | 0.16 | 1 | 0.16 | 23.54 | 0.0019 | ** |
| Residual | 0.049 | 1 | 6.935 × 10−3 | |||
| Lack of Fit | 3.512 × 10−3 | 3 | 1.171 × 10−3 | 0.10 | 0.9535 | |
| Pure Error | 0.045 | 4 | 0.011 | |||
| Cor Total | 23.22 | 16 |
| Source | Sum of Squares | Df | Mean Square | F Value | p-Value | Distinctiveness |
|---|---|---|---|---|---|---|
| Model | 0.053 | 6 | 8.764 × 10−3 | 8.69 | 0.0017 | ** |
| A-feed temperature | 9.143 × 10−3 | 1 | 9.143 × 10−3 | 9.07 | 0.0131 | * |
| B-vacuum pressure | 0.027 | 1 | 0.027 | 27.15 | 0.0004 | ** |
| AC | 0.013 | 1 | 0.013 | 13.10 | 0.0047 | * |
| Residual | 0.010 | 1 | 1.008 × 10−3 | |||
| Lack of Fit | 7.434 × 10−3 | 6 | 1.239 × 10−3 | 1.87 | 0.2833 | |
| Pure Error | 2.649 × 10−3 | 4 | 6.622 × 10−4 | |||
| Cor Total | 0.063 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.; Lv, J.; Li, Z.; Bian, W.; Li, J.; Liu, S. A Numerical Simulation of Membrane Distillation Treatment of Mine Drainage by Computational Fluid Dynamics. Water 2020, 12, 3403. https://doi.org/10.3390/w12123403
Qi J, Lv J, Li Z, Bian W, Li J, Liu S. A Numerical Simulation of Membrane Distillation Treatment of Mine Drainage by Computational Fluid Dynamics. Water. 2020; 12(12):3403. https://doi.org/10.3390/w12123403
Chicago/Turabian StyleQi, Ji, Jiafeng Lv, Zhen Li, Wei Bian, Jingfeng Li, and Shuqin Liu. 2020. "A Numerical Simulation of Membrane Distillation Treatment of Mine Drainage by Computational Fluid Dynamics" Water 12, no. 12: 3403. https://doi.org/10.3390/w12123403
APA StyleQi, J., Lv, J., Li, Z., Bian, W., Li, J., & Liu, S. (2020). A Numerical Simulation of Membrane Distillation Treatment of Mine Drainage by Computational Fluid Dynamics. Water, 12(12), 3403. https://doi.org/10.3390/w12123403




