Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach
Abstract
1. Introduction
2. Materials and Methods
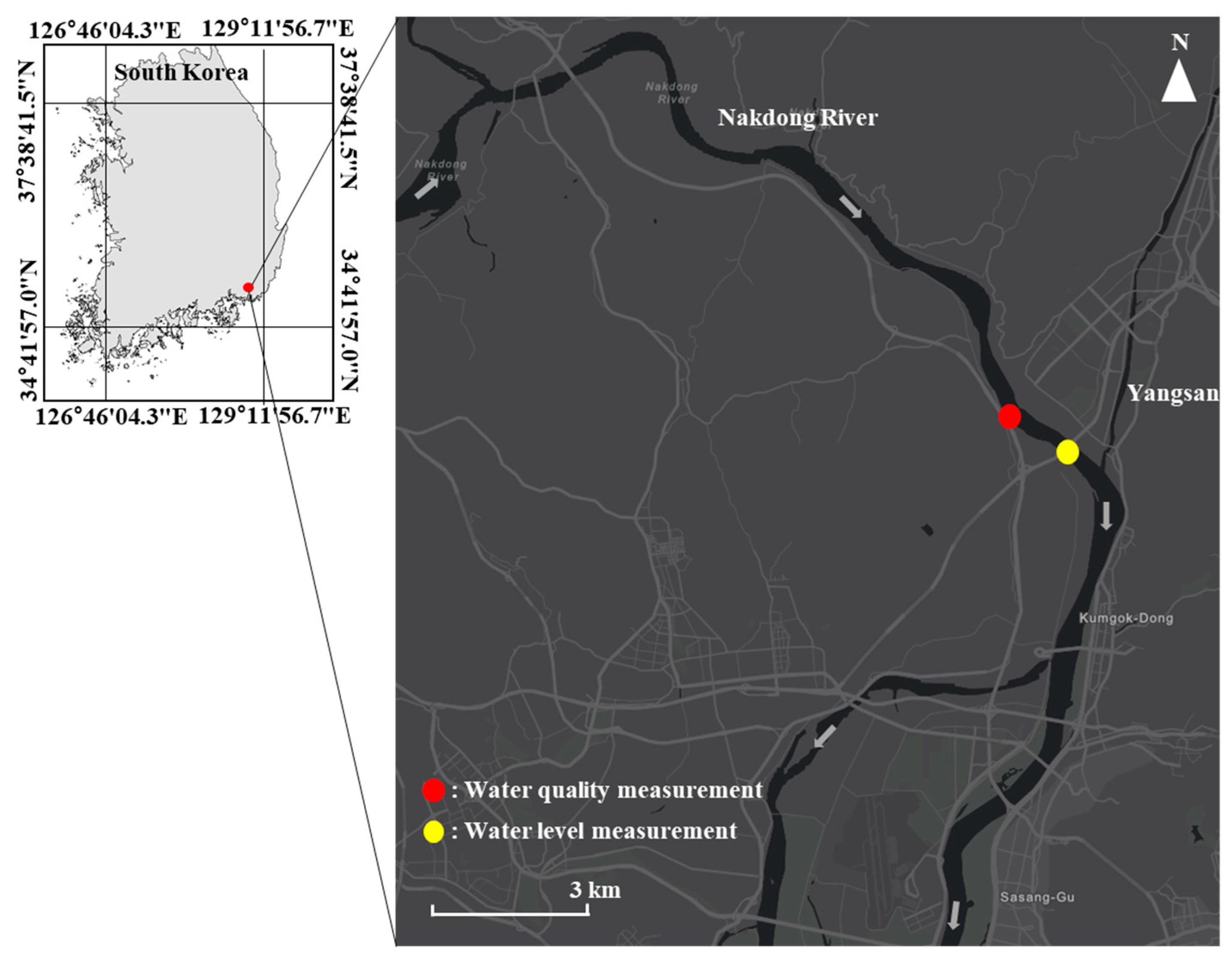
2.1. Study Area and Data Acquisition
2.2. Water Level and Quality Simulation
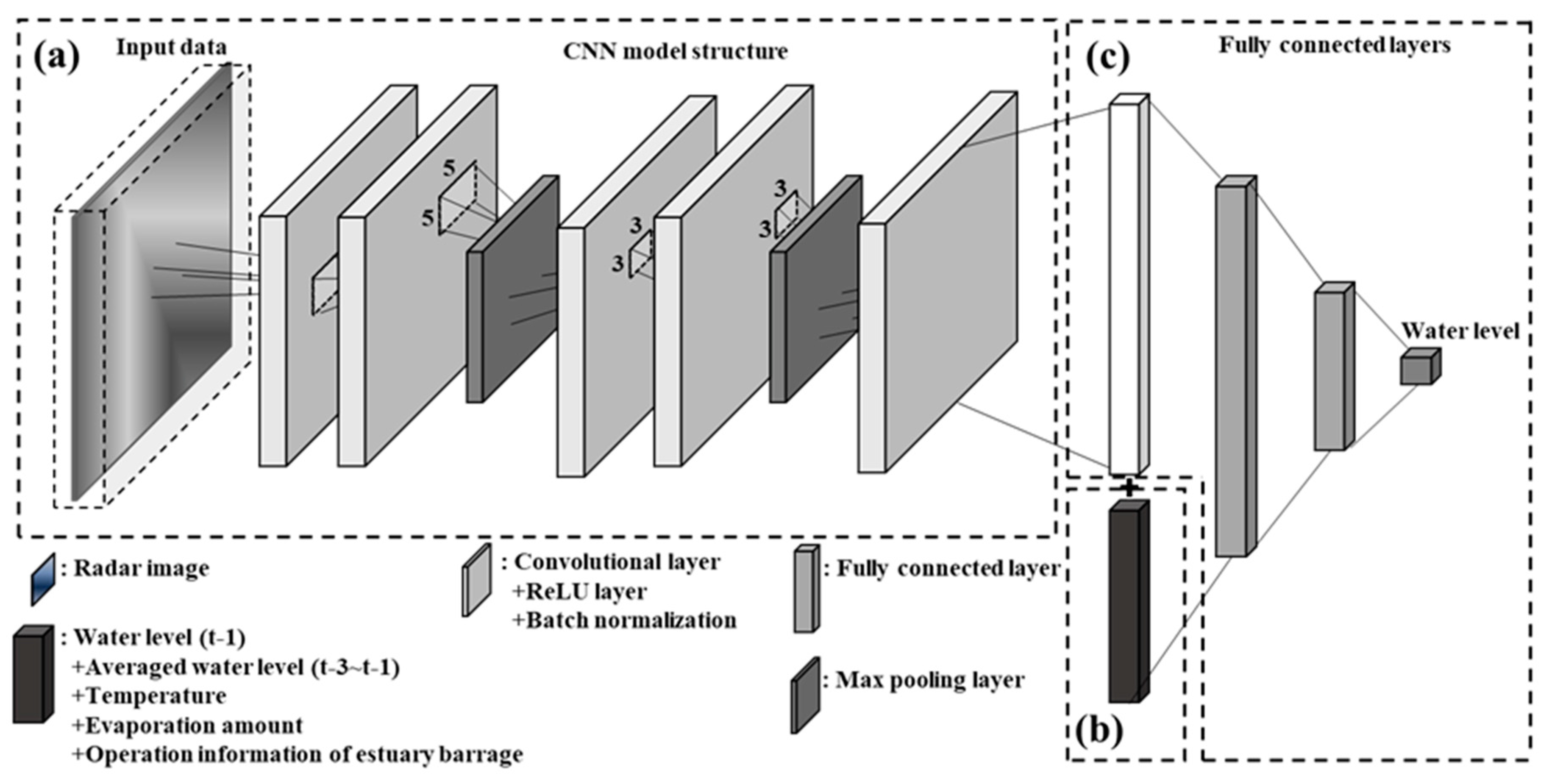
2.3. Convolutional Neural Network (CNN)
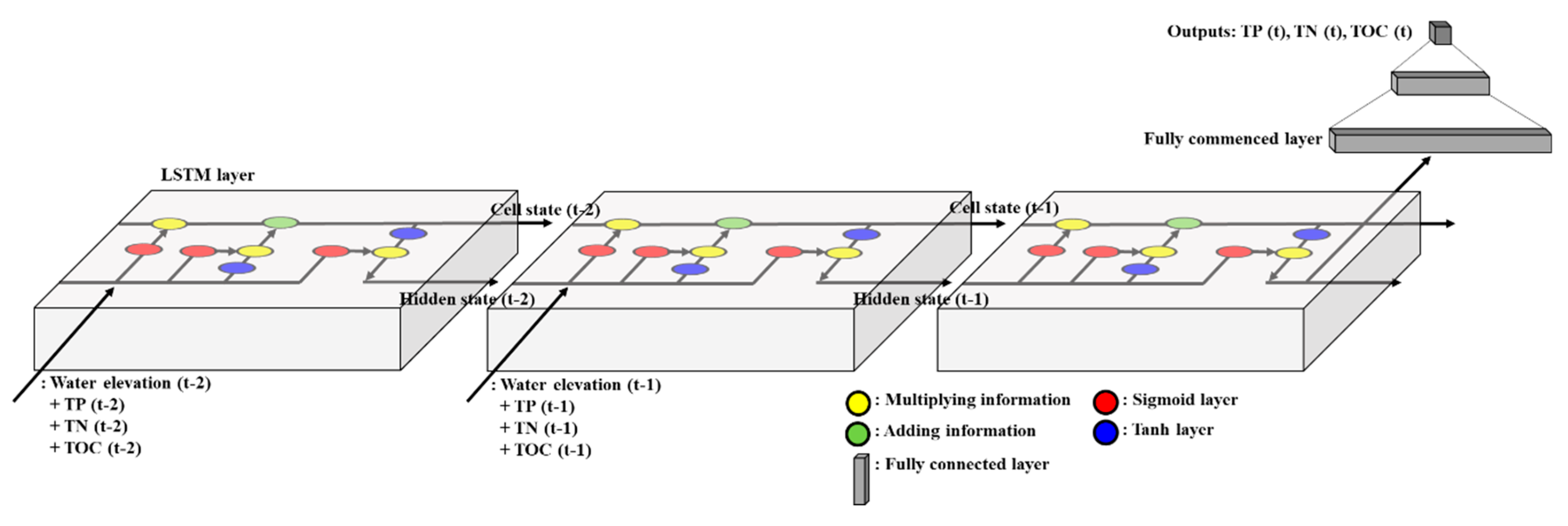
2.4. Long Short-Term Memory (LSTM)
2.5. Performance Evaluation
3. Results and Discussion
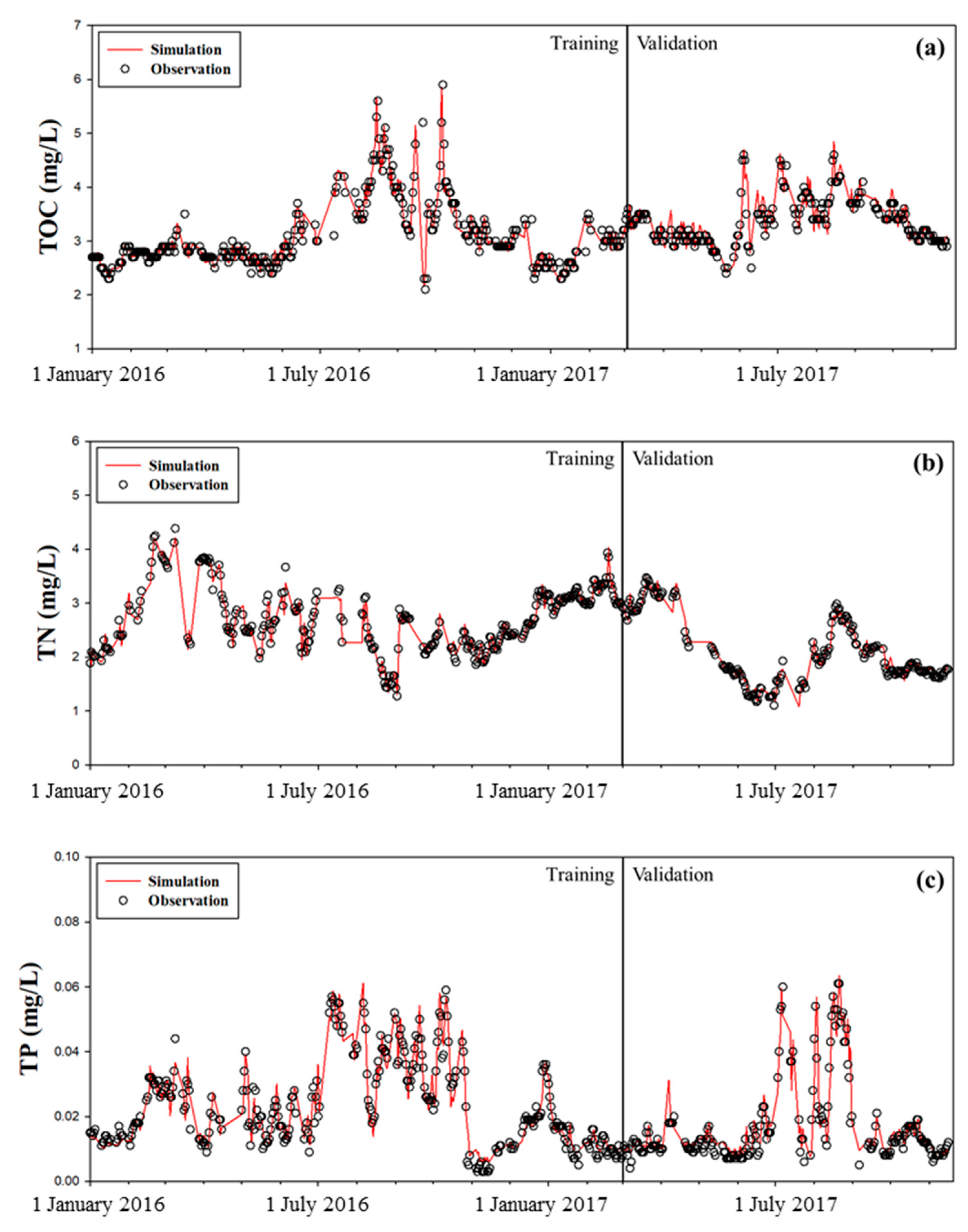
3.1. Monitoring of Water Level and Water Quality
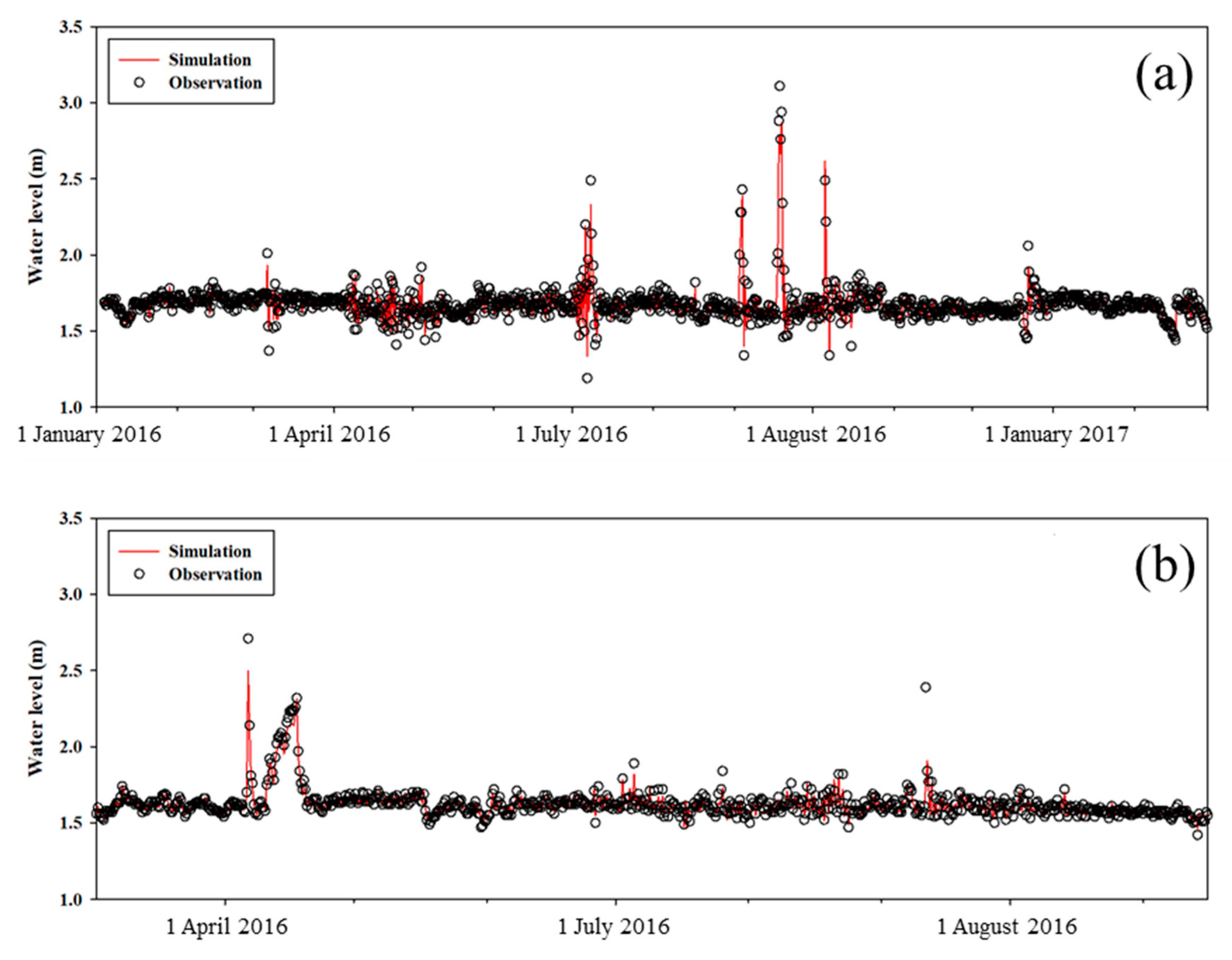
3.2. Water Level Simulation
3.3. Water Quality Simulation
4. Conclusions and Future Work
- (1)
- The water level from the CNN model produced the NSE value of 0.933 that can be regarded as acceptable model performance. The water levels increased in the rainy season, while those were low in the dry season.
- (2)
- For all of the pollutants, the NSE values of the LSTM model for the training and validation periods were above 0.75 which is within the “very good” performance range. The LSTM model in this study well represented the different temporal variations of each pollutant type.
- (3)
- The TOC and TP concentrations had similar temporal variations in that the concentrations of the pollutants were highly fluctuated in the rainy season, while TN increased in the spring season.
Author Contributions
Funding
Conflicts of Interest
References
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. Asabe 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Huber, W.C. Storm Water Management Model (SWMM) Bibliography; Environmental Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cininnnati, OH, USA, 1985.
- Baek, S.; Ligaray, M.; Pyo, J.; Park, J.P.; Kang, J.H.; Pachepsky, Y.; Chun, J.A.; Cho, K.H. A novel water quality module of the SWMM model for assessing Low Impact Development (LID) in urban watersheds. J. Hydrol. 2020, 586, 124886. [Google Scholar] [CrossRef]
- Ahmed, A.N.; Othman, F.B.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Hossain, M.S.; Ehteram, M. Machine learning methods for better water quality prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Almalaq, A.; Zhang, J.J. Deep learning application: Load forecasting in big data of smart grids. In Deep Learning: Algorithms and Applications; Pedryca, W., Chen, S.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 103–128. [Google Scholar]
- Liu, P.; Wang, J.; Sangaiah, A.K.; Xie, Y.; Yin, X. Analysis and prediction of water quality using LSTM deep neural networks in IoT environment. Sustainability 2019, 11, 2058. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, Y.; Zhao, Y.; Xie, M.; Zhong, J.; Tu, Z.; Liu, J. A water quality prediction method based on the deep LSTM network considering correlation in smart mariculture. Sensors 2019, 19, 1420. [Google Scholar] [CrossRef] [PubMed]
- Barzegar, R.; Aalami, M.T.; Adamowsk, J. Short-term water quality variable prediction using a hybrid CNN-LSTM deep learning model. Stoch. Environ. Res. Risk. Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- K-Water. Dam Operation Practice Manual; K-Water: Daejeon, Korea, 2013. (In Korean) [Google Scholar]
- Nakdong River Environmental Management Office. Water Quality Conservation Strategies for the Greater Nakdong River Region, ’93–97 Implementation Status and Evaluation; Nakdong River Environmental Management Office: Changwon, Korea, 1998. [Google Scholar]
- Seo, M.; Lee, H.; Kim, Y. Relationship between Coliform Bacteria and Water Quality Factors at Weir Stations in the Nakdong River, South Korea. Water 2019, 11, 1171. [Google Scholar] [CrossRef]
- Kim, S.; Park, S.; Kim, H. Waste Load Allocation Study for a Large River System; Korea Environment Institute: Seoul, Korea, 1998. (In Korean) [Google Scholar]
- Park, S.S.; Lee, Y.S. A water quality modeling study of the Nakdong River, Korea. Ecol. Model. G 2002, 152, 65–75. [Google Scholar] [CrossRef]
- WAMIS. Available online: http://www.wamis.go/kr/ (accessed on 9 October 2020).
- Xudong, H.; Xiao, Z.; Jinyuan, X.; Linna, W.; Wei, X. Cross-Lingual Non-Ferrous Metals Related News Recognition Method Based on CNN with A Limited Bi-Lingual Dictionary. Comput. Mater. Contin. 2019, 58, 379–389. [Google Scholar]
- Jin, W.; Yongsong, Z.; Lei, P.; Lei, W.; Osama, A.; Amr, T. Research on Crack Opening Prediction of Concrete Dam based on Recurrent Neural Network. J. Internet Technol. 2020, 21, 1161–1170. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Yatian, S.; Yan, L.; Jun, S.; Wenke, D.; Xianjin, S.; Lei, Z.; Xiajiong, S.; Jing, H. Hashtag Recommendation Using LSTM Networks with Self-Attention. Comput. Mater. Continua 2019, 61, 1261–1269. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- Ciresan, D.C.; Meier, U.; Masci, J.; Gambardella, L.M.; Schmidhuber, J. Flexible, high performance convolutional neural networks for image classification. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, Manno-Lugano, Switzerland, 16–22 July 2011; pp. 1237–1242. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Dumoulin, V.; Visin, F. A guide to convolution arithmetic for deep learning. arXiv 2016, arXiv:1603.07285. [Google Scholar]
- Acharya, U.R.; Fujita, H.; Lih, O.S.; Hagiwara, Y.; Tan, J.H.; Adam, M. Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network. Inf. Sci. 2017, 405, 81–90. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Nagi, J.; Ducatelle, F.; Di Caro, G.A.; Cireşan, D.; Meier, U.; Giusti, A.; Nagi, F.; Schmidhuber, J.; Gambardella, L.M. Max-pooling convolutional neural networks for vision-based hand gesture recognition. In Proceedings of the 2011 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Manno-Lugano, Switzerland, 16–18 November 2011; pp. 342–347. [Google Scholar]
- Wu, J.N. Compression of fully-connected layer in neural network by kronecker product. In Proceedings of the 2016 Eighth International Conference on Advanced Computational Intelligence (ICACI), Chiang Mai, Thailand, 14–16 February 2016; pp. 173–179. [Google Scholar]
- Srivastava, H.M.; Gaboury, S.; Ghanim, F. A unified class of analytic functions involving a generalization of the Srivastava–Attiya operator. Appl. Math. Comput. 2015, 251, 35–45. [Google Scholar] [CrossRef]
- Heinermann, J.; Kramer, O. Machine learning ensembles for wind power prediction. Renew. Energy 2016, 89, 671–679. [Google Scholar] [CrossRef]
- Robert, C. Machine Learning, a Probabilistic Perspective; Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Salehinejad, H.; Sankar, S.; Barfett, J.; Colak, E.; Valaee, S. Recent advances in recurrent neural networks. arXiv 2017, arXiv:1801.01078. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Wang, H.J.; Liang, X.M.; Jiang, P.H.; Wang, J.; Wu, S.K.; Wang, H.Z. TN: TP ratio and planktivorous fish do not affect nutrient-chlorophyll relationships in shallow lakes. Freshw. Biol. 2008, 53, 935–944. [Google Scholar] [CrossRef]
- Guildford, S.J.; Hecky, R.E. Total nitrogen, total phosphorus, and nutrient limitation in lakes and oceans: Is there a common relationship? Limnol. Oceanogr. 2000, 45, 1213–1223. [Google Scholar] [CrossRef]
- Park, Y.; Cho, K.H.; Park, J.; Cha, S.M.; Kim, J.H. Development of early-warning protocol for predicting chlorophyll-a concentration using machine learning models in freshwater and estuarine reservoirs, Korea. Sci. Total Environ. 2015, 502, 31–41. [Google Scholar] [CrossRef] [PubMed]
- Reed, G.F.; Lynn, F.; Meade, B.D. Use of coefficient of variation in assessing variability of quantitative assays. Clin. Diagn. Lab. Immunol. 2002, 9, 1235–1239. [Google Scholar] [CrossRef] [PubMed]
- Abdi, H. Coefficient of variation. Encycl. Res. Des. 2010, 1, 169–171. [Google Scholar]
- Krvavica, N.; Rubinić, J. Evaluation of Design Storms and Critical Rainfall Durations for Flood Prediction in Partially Urbanized Catchments. Water 2020, 12, 2044. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Bustami, R.; Bessaih, N.; Bong, C.; Suhaili, S. Artificial Neural Network for Precipitation and Water Level Predictions of Bedup River. Iaeng Int. J. Comput. Sci. 2007, 34, 228–233. [Google Scholar]
- Panda, R.K.; Pramanik, N.; Bala, B. Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model. Comput. Geosci. 2010, 36, 735–745. [Google Scholar] [CrossRef]
- Lee, L.; Lawrence, D.; Price, M. Analysis of water-level response to rainfall and implications for recharge pathways in the Chalk aquifer, SE England. J. Hydrol. 2006, 330, 604–620. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Fitch, P.; Thorburn, P.J. Predicting the Trend of Dissolved Oxygen Based on the kPCA-RNN Model. Water 2020, 12, 585. [Google Scholar] [CrossRef]
- Choubin, B.; Darabi, H.; Rahmati, O.; Sajedi-Hosseini, F.; Kløve, B. River suspended sediment modelling using the CART model: A comparative study of machine learning techniques. Sci. Total Environ. 2018, 615, 272–281. [Google Scholar] [CrossRef]
- Parks, S.J.; Baker, L.A. Sources and transport of organic carbon in an Arizona river-reservoir system. Water Res. 1997, 31, 1751–1759. [Google Scholar] [CrossRef]
- Alamdari, N.; Sample, D.J.; Steinberg, P.; Ross, A.C.; Easton, Z.M. Assessing the effects of climate change on water quantity and quality in an urban watershed using a calibrated stormwater model. Water 2017, 9, 464. [Google Scholar] [CrossRef]
- Schrumpf, M.; Zech, W.; Lehmann, J.; Lyaruu, H.V. TOC, TON, TOS and TOP in rainfall, throughfall, litter percolate and soil solution of a montane rainforest succession at Mt. Kilimanjaro, Tanzania. Biogeochemistry 2006, 78, 361–387. [Google Scholar] [CrossRef]
- Park, M.; Choi, Y.S.; Shin, H.J.; Song, I.; Yoon, C.G.; Choi, J.D.; Yu, S.J. A comparison study of runoff characteristics of non-point source pollution from three watersheds in South Korea. Water 2019, 11, 966. [Google Scholar] [CrossRef]
- Cao, P.; Lu, C.C.; Yu, Z. Historical nitrogen fertilizer use in agricultural ecosystems of the contiguous United States during 1850–2015: Application rate, timing, and fertilizer types. Earth Syst. Sci. Data 2018, 10, 969–984. [Google Scholar] [CrossRef]
- Kim, J.G.; Chung, E.S.; Seo, S.; Kim, M.J.; Chang, Y.S.; Chung, B.C. Effect of nitrogen fertilizer level and mixture of small grain and forage rape on productivity and quality of spring at South Region in Korea. J. Korean Soc. Grasl. Forage Sci. 2005, 25, 143–150. (In Korean) [Google Scholar]
- RDA. Available online: http://www.rda.go.kr/foreign/ten/ (accessed on 9 October 2020).
- Karlen, D.L.; Dinnes, D.L.; Jaynes, D.B.; Hurburgh, C.R.; Cambardella, C.A.; Colvin, T.S.; Rippke, G.R. Corn response to late-spring nitrogen management in the Walnut Creek watershed. Agron. J. 2005, 97, 1054–1061. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
| Periods | Descriptive Statistics | Water Level (m) | TN (mg/L) | TP (mg/L) | TOC (mg/L) | |
|---|---|---|---|---|---|---|
| Total | Min | 1.19 | 1.104 | 0.003 | 2.100 | |
| Max | 3.11 | 4.383 | 0.061 | 5.900 | ||
| Mean | 1.65 | 2.465 | 0.021 | 3.202 | ||
| Median | 1.64 | 1.917 | 0.011 | 3.100 | ||
| Quantile | Q2 (25%) | 1.60 | 2.410 | 0.016 | 2.800 | |
| Q3 (75%) | 1.69 | 3.002 | 0.028 | 3.500 | ||
| Standard deviation | 0.12 | 0.666 | 0.013 | 0.577 | ||
| CoV | 0.07 | 0.270 | 0.646 | 0.180 | ||
| Training | Min | 1.19 | 1.274 | 0.003 | 2.100 | |
| Max | 3.11 | 4.383 | 0.059 | 5.900 | ||
| Mean | 1.68 | 2.706 | 0.023 | 3.100 | ||
| Median | 1.67 | 2.660 | 0.020 | 2.900 | ||
| Quantile | Q2 (25%) | 1.63 | 2.252 | 0.013 | 2.700 | |
| Q3 (75%) | 1.71 | 3.096 | 0.031 | 3.300 | ||
| Standard deviation | 0.11 | 0.589 | 0.013 | 0.636 | ||
| CoV | 0.07 | 0.218 | 0.564 | 0.205 | ||
| Validation | Min | 1.36 | 1.104 | 0.004 | 2.400 | |
| Max | 2.71 | 3.473 | 0.061 | 4.600 | ||
| Mean | 1.62 | 2.105 | 0.017 | 3.366 | ||
| Median | 1.61 | 1.866 | 0.012 | 3.300 | ||
| Quantile | Q2 (25%) | 1.57 | 1.681 | 0.009 | 3.100 | |
| Q3 (75%) | 1.64 | 2.671 | 0.017 | 3.600 | ||
| Standard deviation | 0.11 | 0.610 | 0.013 | 0.417 | ||
| CoV | 0.07 | 0.290 | 0.762 | 0.124 | ||
| Periods | Index | Water Level (m) | TN (mg/L) | TP (mg/L) | TOC (mg/L) |
|---|---|---|---|---|---|
| Training | R2 | 0.934 | 0.950 | 0.92 | 0.860 |
| MSE | 0.001 | 0.017 | 1.37 × 10−5 | 0.055 | |
| NSE | 0.926 | 0.951 | 0.921 | 0.864 | |
| Validation | R2 | 0.923 | 0.970 | 0.87 | 0.793 |
| MSE | 0.001 | 0.010 | 2.08 × 10−5 | 0.041 | |
| NSE | 0.933 | 0.987 | 0.899 | 0.832 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, S.-S.; Pyo, J.; Chun, J.A. Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach. Water 2020, 12, 3399. https://doi.org/10.3390/w12123399
Baek S-S, Pyo J, Chun JA. Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach. Water. 2020; 12(12):3399. https://doi.org/10.3390/w12123399
Chicago/Turabian StyleBaek, Sang-Soo, Jongcheol Pyo, and Jong Ahn Chun. 2020. "Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach" Water 12, no. 12: 3399. https://doi.org/10.3390/w12123399
APA StyleBaek, S.-S., Pyo, J., & Chun, J. A. (2020). Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach. Water, 12(12), 3399. https://doi.org/10.3390/w12123399






