Wave Run-Up on Mortar-Grouted Riprap Revetments
Abstract
1. Introduction
1.1. Motivation
1.2. Wave Run-Up
- they are the most widely used models for design purposes
- they are easy to use and comprehensible
- full-scale hydraulic model tests on MGRRs have been conducted, thus, the number of experiments is not suited for machine learning techniques
- we test the ability of different parameters for describing wave run-up for different roughnesses, porosities, and permeabilities, as these parameters vary considerably for MGRRs.
- To analyze the wave run-up process in the presence of partially or fully mortar-grouted riprap
- To determine the appropriate influence factors in the framework of the EurOtop equations
2. Materials and Methods
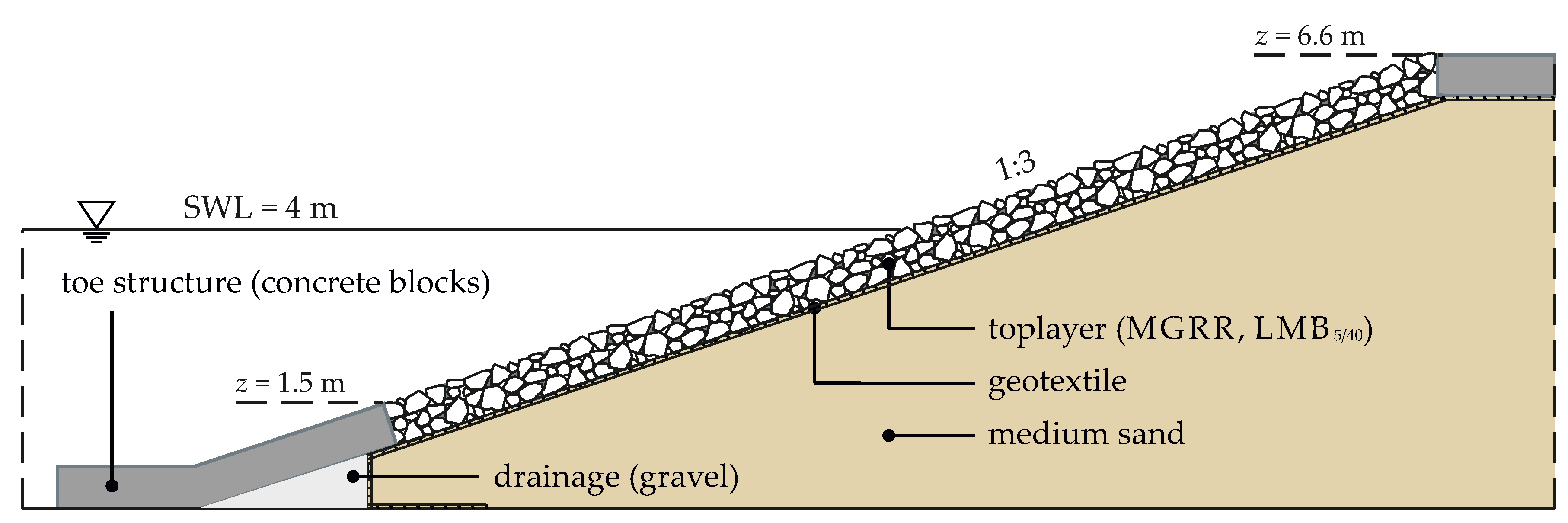
2.1. Revetment Configurations
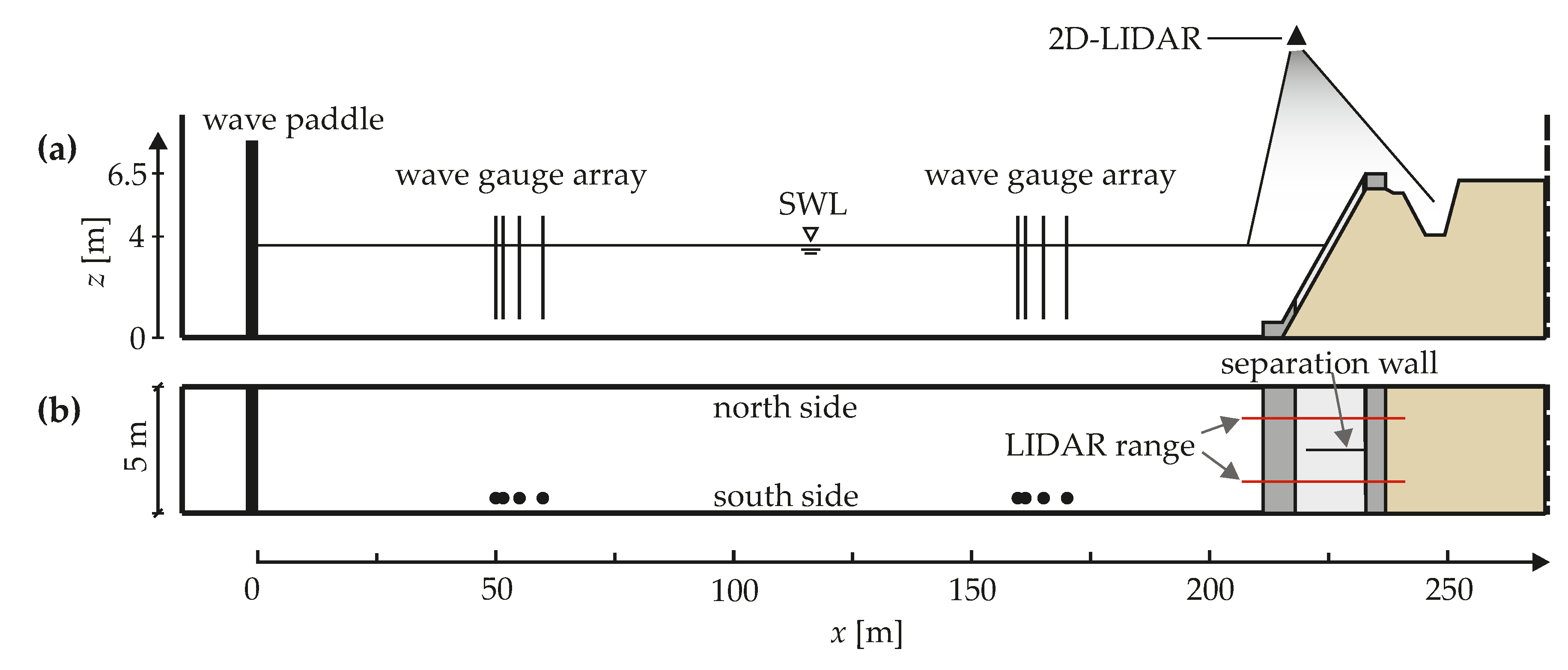
2.2. Instrumentation
2.3. Experimental Program
2.4. Detection of the Wave Run-Up Height
2.5. Error Evaluation of Different Equations and Parameters
3. Results
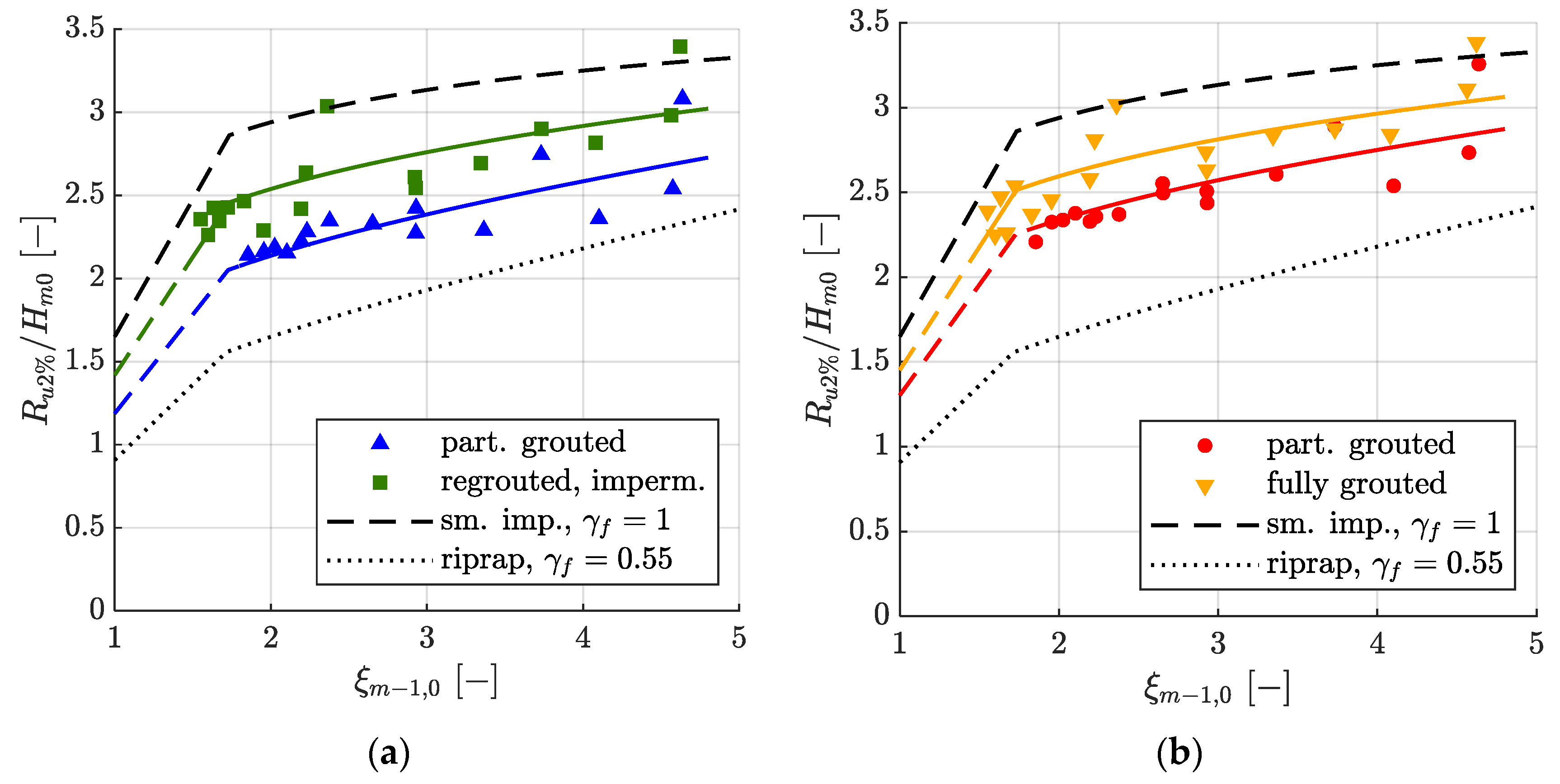
3.1. Relative Wave Run-Up Height as a Function of Surf Similarity Parameter ξm−1,0
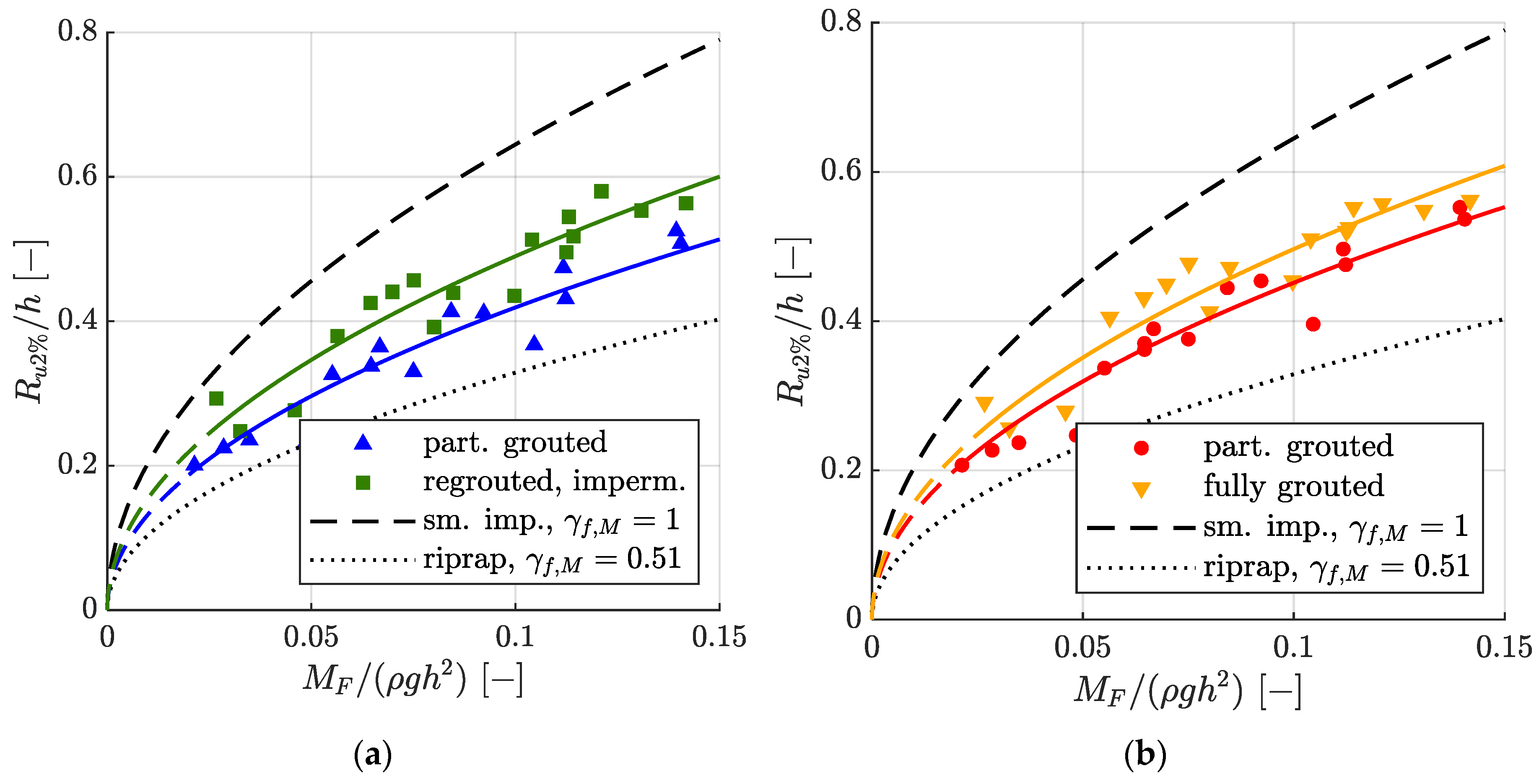
3.2. Relative Wave Run-Up Height as a Function of the Momentum Flux Parameter MF
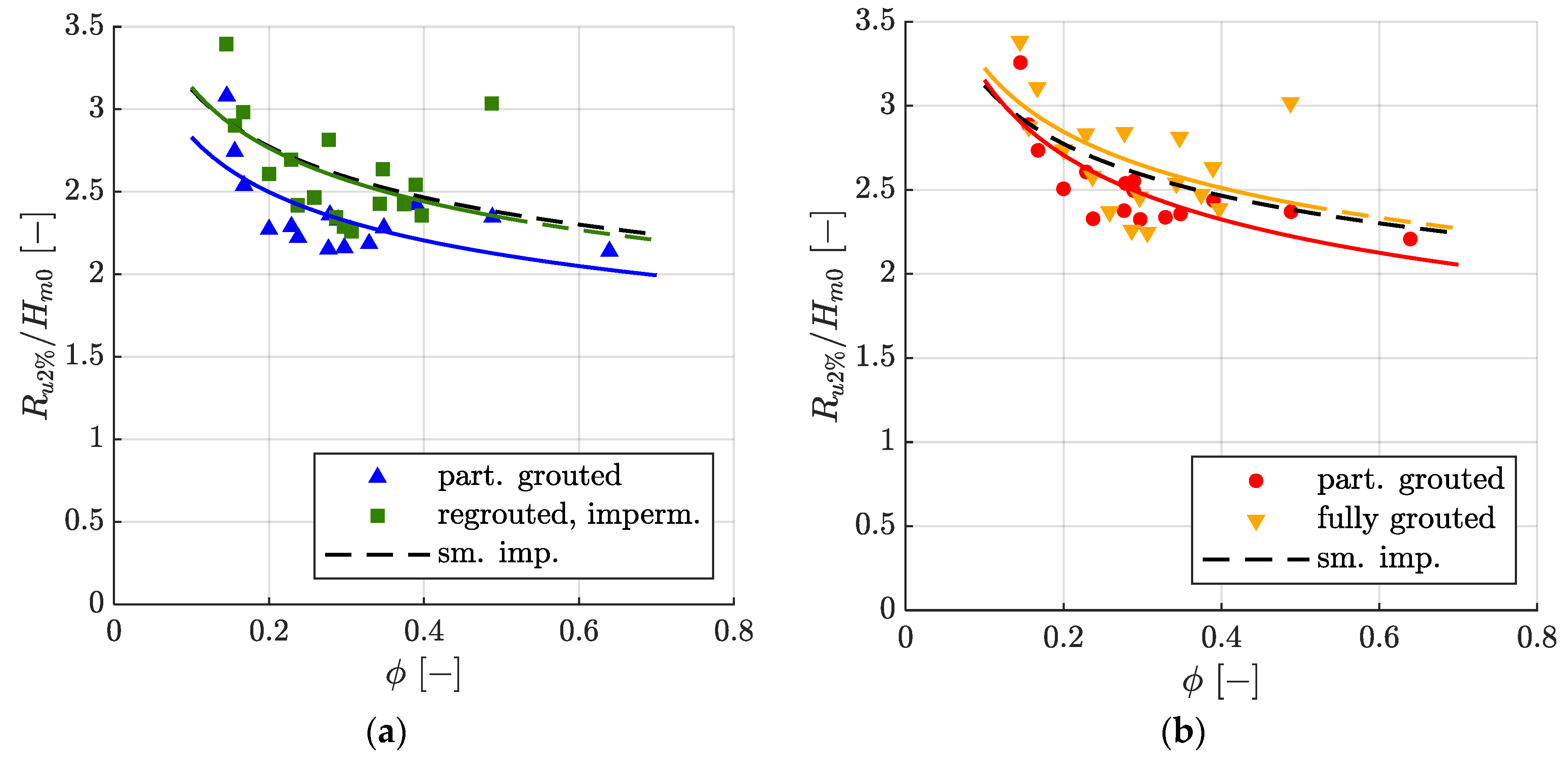
3.3. Relative Wave Run-Up Height as a Function of the Modified Surf Similarity Parameter ϕ
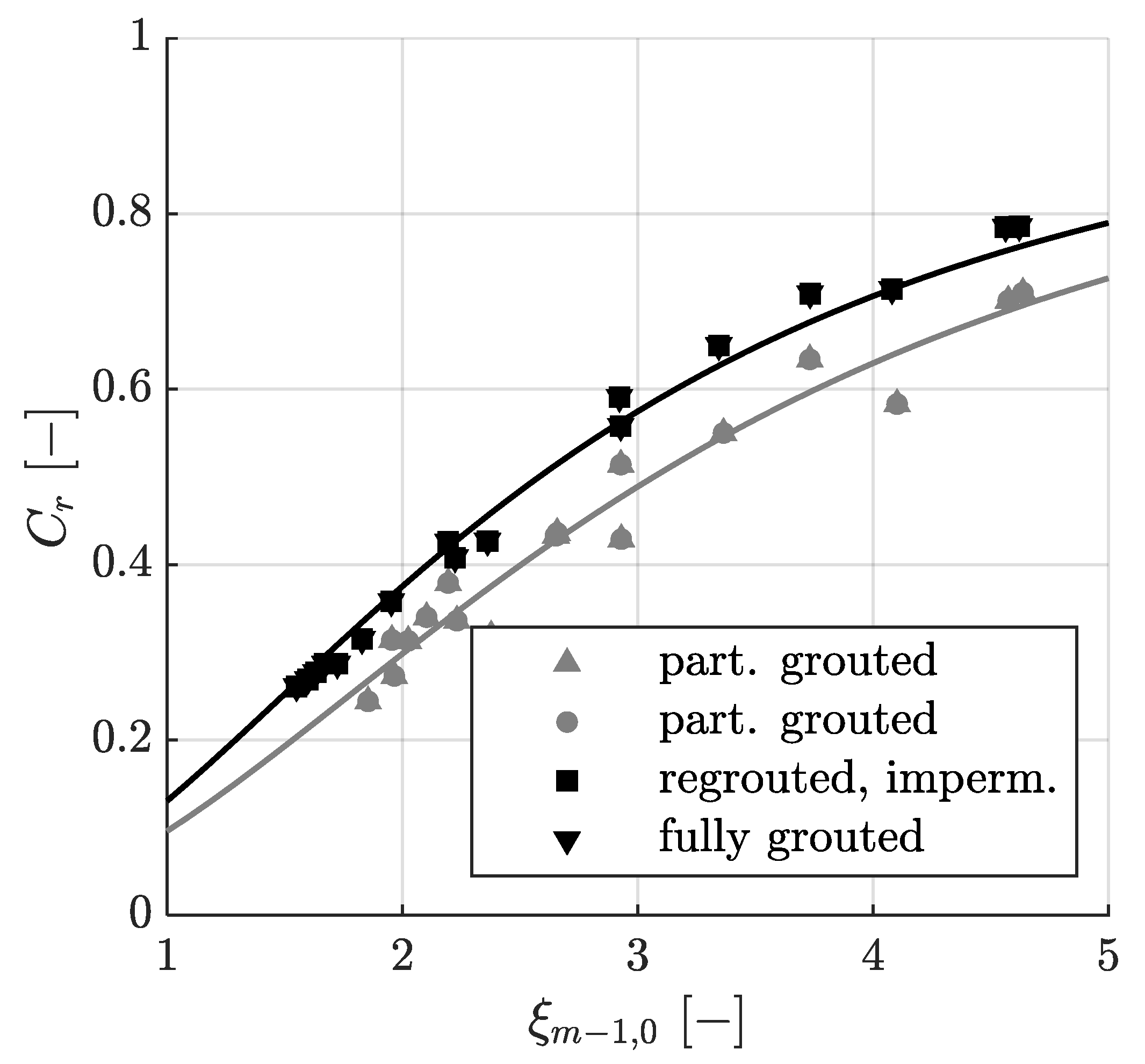
3.4. Relative Wave Run-Up Height as a Function of the Reflection Coefficient Cr
4. Discussion
4.1. 2D-LIDAR Measurements
4.2. Comparison of Models and Corresponding Parameters
4.3. Further Discussion
5. Conclusions
- The wave run-up heights on MGRRs are generally lower than for smooth impermeable revetments and higher than for non-grouted riprap revetments. Partially grouted MGRRs, due to their roughness, porosity, and permeability, reduce wave run-up heights from 21% to 28%, and fully grouted MGRRs, due to their roughness, reduce wave run-up heights from 12% to 14% compared to smooth impermeable revetments.
- Influence factors for the state-of-the-art design guideline EurOtop have been determined for four widely used revetment configurations, which can now be used for design purposes.
- For the results acquired in the model tests, wave run-up for all MGRR configurations is best described by the state-of-the-art EurOtop equation, which describes wave run-up as a function of the surf similarity parameter ξm−1,0. The model of Hughes [27], which describes wave run-up as a function of the momentum flux parameter MF, also gives very good results. Models describing wave run-up as a function of the modified surf similarity parameter ϕ or the reflection coefficient Cr give poorer results for MGRRs.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Configuration Nr. | Hm0 [m] | Tm−1,0 [s] | Tp [s] | Lm−1,0 [m] | Ru2% [m] | Ru2%/Hm0 [-] | Ru2%/h [-] | ξm−1,0 [-] | MF/(ρgh2) [-] | Φ [-] | Cr [-] | Hm0/Lp [-] | tan(α)/(Hm0/h) [-] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.375 | 2.73 | 3.01 | 11.60 | 0.80 | 2.14 | 0.201 | 1.85 | 0.021 | 0.639 | 0.24 | 0.027 | 3.56 |
| 1 | 0.389 | 6.14 | 7.08 | 58.92 | 0.92 | 2.36 | 0.230 | 4.10 | 0.048 | 0.279 | 0.58 | 0.005 | 3.43 |
| 1 | 0.383 | 3.53 | 4.01 | 19.48 | 0.90 | 2.35 | 0.225 | 2.38 | 0.028 | 0.488 | 0.32 | 0.015 | 3.48 |
| 1 | 0.577 | 6.14 | 6.58 | 58.78 | 1.32 | 2.29 | 0.330 | 3.36 | 0.075 | 0.229 | 0.55 | 0.009 | 2.31 |
| 1 | 0.759 | 6.13 | 6.85 | 58.57 | 1.72 | 2.27 | 0.431 | 2.93 | 0.112 | 0.200 | 0.51 | 0.010 | 1.76 |
| 1 | 0.765 | 7.84 | 9.24 | 95.87 | 2.10 | 2.74 | 0.525 | 3.73 | 0.139 | 0.156 | 0.63 | 0.006 | 1.74 |
| 1 | 0.389 | 4.39 | 4.89 | 30.06 | 0.94 | 2.42 | 0.236 | 2.93 | 0.035 | 0.390 | 0.43 | 0.010 | 3.43 |
| 1 | 0.579 | 8.36 | 10.10 | 109.07 | 1.47 | 2.54 | 0.367 | 4.57 | 0.105 | 0.168 | 0.70 | 0.004 | 2.30 |
| 1 | 0.659 | 9.04 | 12.18 | 127.54 | 2.03 | 3.08 | 0.508 | 4.64 | 0.141 | 0.145 | 0.71 | 0.003 | 2.02 |
| 1 | 0.667 | 3.97 | 4.27 | 24.61 | 1.46 | 2.19 | 0.364 | 2.02 | 0.067 | 0.329 | 0.31 | 0.023 | 2.00 |
| 1 | 0.764 | 4.41 | 5.08 | 30.41 | 1.65 | 2.15 | 0.411 | 2.10 | 0.092 | 0.277 | 0.34 | 0.019 | 1.75 |
| 1 | 0.853 | 4.87 | 5.30 | 36.97 | 1.90 | 2.22 | 0.474 | 2.19 | 0.112 | 0.237 | 0.38 | 0.019 | 1.56 |
| 1 | 0.765 | 4.11 | 4.44 | 26.32 | 1.65 | 2.16 | 0.413 | 1.96 | 0.084 | 0.297 | 0.31 | 0.025 | 1.74 |
| 1 | 0.580 | 4.85 | 5.36 | 36.68 | 1.35 | 2.33 | 0.338 | 2.65 | 0.065 | 0.289 | 0.43 | 0.013 | 2.30 |
| 1 | 0.572 | 4.05 | 4.47 | 25.63 | 1.30 | 2.28 | 0.326 | 2.23 | 0.055 | 0.348 | 0.34 | 0.018 | 2.33 |
| 1 | 0.580 | 4.85 | 5.36 | 36.76 | 1.35 | 2.33 | 0.338 | 2.65 | 0.065 | 0.289 | 0.43 | 0.013 | 2.30 |
| 2 | 0.375 | 2.73 | 3.01 | 11.60 | 0.83 | 2.21 | 0.207 | 1.85 | 0.021 | 0.639 | 0.24 | 0.027 | 3.56 |
| 2 | 0.389 | 6.14 | 7.08 | 58.92 | 0.99 | 2.54 | 0.247 | 4.10 | 0.048 | 0.279 | 0.58 | 0.005 | 3.43 |
| 2 | 0.383 | 3.53 | 4.01 | 19.48 | 0.91 | 2.37 | 0.227 | 2.38 | 0.028 | 0.488 | 0.32 | 0.015 | 3.48 |
| 2 | 0.577 | 6.14 | 6.58 | 58.78 | 1.50 | 2.61 | 0.376 | 3.36 | 0.075 | 0.229 | 0.55 | 0.009 | 2.31 |
| 2 | 0.759 | 6.13 | 6.85 | 58.57 | 1.90 | 2.51 | 0.476 | 2.93 | 0.112 | 0.200 | 0.51 | 0.010 | 1.76 |
| 2 | 0.765 | 7.84 | 9.24 | 95.87 | 2.21 | 2.89 | 0.552 | 3.73 | 0.139 | 0.156 | 0.63 | 0.006 | 1.74 |
| 2 | 0.389 | 4.39 | 4.89 | 30.06 | 0.95 | 2.44 | 0.237 | 2.93 | 0.035 | 0.390 | 0.43 | 0.010 | 3.43 |
| 2 | 0.579 | 8.36 | 10.10 | 109.07 | 1.58 | 2.74 | 0.396 | 4.57 | 0.105 | 0.168 | 0.70 | 0.004 | 2.30 |
| 2 | 0.659 | 9.04 | 12.18 | 127.54 | 2.15 | 3.26 | 0.537 | 4.64 | 0.141 | 0.145 | 0.71 | 0.003 | 2.02 |
| 2 | 0.667 | 3.97 | 4.27 | 24.61 | 1.56 | 2.34 | 0.390 | 2.02 | 0.067 | 0.329 | 0.31 | 0.023 | 2.00 |
| 2 | 0.764 | 4.41 | 5.08 | 30.41 | 1.82 | 2.38 | 0.454 | 2.10 | 0.092 | 0.277 | 0.34 | 0.019 | 1.75 |
| 2 | 0.853 | 4.87 | 5.30 | 36.97 | 1.99 | 2.33 | 0.497 | 2.19 | 0.112 | 0.237 | 0.38 | 0.019 | 1.56 |
| 2 | 0.765 | 4.11 | 4.44 | 26.32 | 1.78 | 2.32 | 0.445 | 1.96 | 0.084 | 0.297 | 0.31 | 0.025 | 1.74 |
| 2 | 0.580 | 4.85 | 5.36 | 36.68 | 1.48 | 2.55 | 0.370 | 2.65 | 0.065 | 0.289 | 0.43 | 0.013 | 2.30 |
| 2 | 0.572 | 4.05 | 4.47 | 25.63 | 1.35 | 2.36 | 0.337 | 2.23 | 0.055 | 0.348 | 0.34 | 0.018 | 2.33 |
| 2 | 0.580 | 4.85 | 5.36 | 36.76 | 1.45 | 2.50 | 0.362 | 2.65 | 0.065 | 0.289 | 0.43 | 0.013 | 2.30 |
| Configuration Nr. | Hm0 [m] | Tm−1,0 [s] | Tp [s] | Lm−1,0 [m] | Ru2% [m] | Ru2%/Hm0 [-] | Ru2%/h [-] | ξm−1,0 [-] | MF/(ρgh2) [-] | Φ [-] | Cr [-] | Hm0/Lp [-] | tan(α)/(Hm0/h) [-] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 0.768 | 4.11 | 4.44 | 26.36 | 1.76 | 2.29 | 0.439 | 1.95 | 0.085 | 0.296 | 0.36 | 0.025 | 1.74 |
| 3 | 0.856 | 4.87 | 5.43 | 37.08 | 2.07 | 2.42 | 0.518 | 2.19 | 0.114 | 0.237 | 0.43 | 0.019 | 1.56 |
| 3 | 0.760 | 6.12 | 6.85 | 58.42 | 1.98 | 2.61 | 0.496 | 2.92 | 0.112 | 0.200 | 0.59 | 0.010 | 1.75 |
| 3 | 0.386 | 3.52 | 3.68 | 19.38 | 1.17 | 3.04 | 0.293 | 2.36 | 0.027 | 0.488 | 0.43 | 0.018 | 3.45 |
| 3 | 0.390 | 4.39 | 4.53 | 30.09 | 0.99 | 2.54 | 0.248 | 2.93 | 0.033 | 0.389 | 0.56 | 0.012 | 3.42 |
| 3 | 0.582 | 6.13 | 7.06 | 58.59 | 1.57 | 2.69 | 0.392 | 3.34 | 0.080 | 0.228 | 0.65 | 0.007 | 2.29 |
| 3 | 0.763 | 7.83 | 8.47 | 95.67 | 2.21 | 2.90 | 0.553 | 3.73 | 0.131 | 0.156 | 0.71 | 0.007 | 1.75 |
| 3 | 0.664 | 9.04 | 12.18 | 127.65 | 2.25 | 3.40 | 0.564 | 4.62 | 0.142 | 0.145 | 0.79 | 0.003 | 2.01 |
| 3 | 0.393 | 6.14 | 6.57 | 58.90 | 1.11 | 2.82 | 0.277 | 4.08 | 0.046 | 0.277 | 0.71 | 0.006 | 3.39 |
| 3 | 0.576 | 4.05 | 4.55 | 25.63 | 1.52 | 2.64 | 0.380 | 2.22 | 0.056 | 0.347 | 0.41 | 0.018 | 2.31 |
| 3 | 0.584 | 8.37 | 9.36 | 109.46 | 1.74 | 2.98 | 0.435 | 4.56 | 0.100 | 0.167 | 0.79 | 0.004 | 2.28 |
| 3 | 0.752 | 3.59 | 3.90 | 20.10 | 1.83 | 2.43 | 0.457 | 1.72 | 0.075 | 0.343 | 0.29 | 0.032 | 1.77 |
| 3 | 0.727 | 3.34 | 3.79 | 17.45 | 1.76 | 2.43 | 0.441 | 1.63 | 0.070 | 0.374 | 0.28 | 0.033 | 1.83 |
| 3 | 0.941 | 4.26 | 4.77 | 28.31 | 2.32 | 2.47 | 0.580 | 1.83 | 0.121 | 0.258 | 0.32 | 0.027 | 1.42 |
| 3 | 0.929 | 3.87 | 4.42 | 23.32 | 2.18 | 2.35 | 0.545 | 1.67 | 0.113 | 0.286 | 0.29 | 0.030 | 1.44 |
| 3 | 0.908 | 3.66 | 4.10 | 20.87 | 2.05 | 2.26 | 0.513 | 1.60 | 0.104 | 0.306 | 0.27 | 0.035 | 1.47 |
| 3 | 0.722 | 3.16 | 3.43 | 15.61 | 1.70 | 2.36 | 0.426 | 1.55 | 0.064 | 0.397 | 0.26 | 0.039 | 1.85 |
| 4 | 0.768 | 4.11 | 4.44 | 26.36 | 1.89 | 2.46 | 0.472 | 1.95 | 0.085 | 0.296 | 0.36 | 0.025 | 1.74 |
| 4 | 0.856 | 4.87 | 5.43 | 37.08 | 2.21 | 2.58 | 0.552 | 2.19 | 0.114 | 0.237 | 0.43 | 0.019 | 1.56 |
| 4 | 0.760 | 6.12 | 6.85 | 58.42 | 2.08 | 2.74 | 0.520 | 2.92 | 0.112 | 0.200 | 0.59 | 0.010 | 1.75 |
| 4 | 0.386 | 3.52 | 3.68 | 19.38 | 1.17 | 3.02 | 0.291 | 2.36 | 0.027 | 0.488 | 0.43 | 0.018 | 3.45 |
| 4 | 0.390 | 4.39 | 4.53 | 30.09 | 1.03 | 2.63 | 0.257 | 2.93 | 0.033 | 0.389 | 0.56 | 0.012 | 3.42 |
| 4 | 0.582 | 6.13 | 7.06 | 58.59 | 1.65 | 2.83 | 0.412 | 3.34 | 0.080 | 0.228 | 0.65 | 0.007 | 2.29 |
| 4 | 0.763 | 7.83 | 8.47 | 95.67 | 2.19 | 2.88 | 0.548 | 3.73 | 0.131 | 0.156 | 0.71 | 0.007 | 1.75 |
| 4 | 0.664 | 9.04 | 12.18 | 127.65 | 2.25 | 3.38 | 0.562 | 4.62 | 0.142 | 0.145 | 0.79 | 0.003 | 2.01 |
| 4 | 0.393 | 6.14 | 6.57 | 58.90 | 1.12 | 2.84 | 0.279 | 4.08 | 0.046 | 0.277 | 0.71 | 0.006 | 3.39 |
| 4 | 0.576 | 4.05 | 4.55 | 25.63 | 1.62 | 2.81 | 0.405 | 2.22 | 0.056 | 0.347 | 0.41 | 0.018 | 2.31 |
| 4 | 0.584 | 8.37 | 9.36 | 109.46 | 1.82 | 3.11 | 0.454 | 4.56 | 0.100 | 0.167 | 0.79 | 0.004 | 2.28 |
| 4 | 0.752 | 3.59 | 3.90 | 20.10 | 1.91 | 2.54 | 0.477 | 1.72 | 0.075 | 0.343 | 0.29 | 0.032 | 1.77 |
| 4 | 0.727 | 3.34 | 3.79 | 17.45 | 1.80 | 2.47 | 0.450 | 1.63 | 0.070 | 0.374 | 0.28 | 0.033 | 1.83 |
| 4 | 0.941 | 4.26 | 4.77 | 28.31 | 2.23 | 2.37 | 0.557 | 1.83 | 0.121 | 0.258 | 0.32 | 0.027 | 1.42 |
| 4 | 0.929 | 3.87 | 4.42 | 23.32 | 2.10 | 2.26 | 0.525 | 1.67 | 0.113 | 0.286 | 0.29 | 0.030 | 1.44 |
| 4 | 0.908 | 3.66 | 4.10 | 20.87 | 2.04 | 2.25 | 0.510 | 1.60 | 0.104 | 0.306 | 0.27 | 0.035 | 1.47 |
| 4 | 0.722 | 3.16 | 3.43 | 15.61 | 1.73 | 2.39 | 0.431 | 1.55 | 0.064 | 0.397 | 0.26 | 0.039 | 1.85 |
References
- Pilarczyk, K.W. Other Design Considerations. In Dikes and Revetments: Design, Maintanance and Safety Assessment; Pilarczyk, K.W., Ed.; Rijkswaterstaat, DWW: Delft, The Netherlands, 1998; pp. 407–428. ISBN 9054104554. [Google Scholar]
- Schoonees, T.; Gijón Mancheño, A.; Scheres, B.; Bouma, T.J.; Silva, R.; Schlurmann, T.; Schüttrumpf, H. Hard Structures for Coastal Protection, Towards Greener Designs. Estuaries Coasts 2019, 42, 1709–1729. [Google Scholar] [CrossRef]
- Rupprecht, F.; Möller, I.; Paul, M.; Kudella, M.; Spencer, T.; van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; et al. Vegetation-Wave Interactions in Salt Marshes under Storm Surge Conditions. Ecol. Eng. 2017, 100, 301–315. [Google Scholar] [CrossRef]
- Anderson, M.E.; Smith, J.M. Wave Attenuation by Flexible, Idealized Salt Marsh Vegetation. Coast. Eng. 2014, 83, 82–92. [Google Scholar] [CrossRef]
- Burcharth, H.F.; Lykke Andersen, T.; Lara, J.L. Upgrade of Coastal Defence Structures against Increased Loadings Caused by Climate Change: A First Methodological Approach. Coast. Eng. 2014, 87, 112–121. [Google Scholar] [CrossRef]
- Ahrens, J.P. Reef Type Breakwaters. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; pp. 2648–2662. [Google Scholar] [CrossRef]
- Seabrook, S.R.; Hall, K.R. Wave Transmission at Submerged Rubblemound Breakwaters. In Proceedings of the 26th International Conference on Coastal Engineering, Copenhagen, Denmark, 22–26 June 1998; pp. 2000–2013. [Google Scholar] [CrossRef]
- EurOtop. Manual on Wave Overtopping of Sea Defences and Related Structures. An Overtopping Manual Largely Based on European Research, but for Worldwide Application, Second Edition. 2018. Available online: http://www.overtopping-manual.com/assets/downloads/EurOtop_II_2018_Final_version.pdf (accessed on 19 October 2020).
- CIRIA. The International Levee Handbook (C731); CIRIA: London, UK, 2013; ISBN 978-0-86017-734-0. [Google Scholar]
- German Institute for Standardization. Armourstone—Part 1: Specification; Beuth Verlag GmbH: Berlin, Germany, 2002. [Google Scholar]
- Losada, M.A.; Giménez-Curto, L.A. Flow Characteristics on Rough, Permeable Slopes under Wave Action. Coast. Eng. 1981, 4, 187–206. [Google Scholar] [CrossRef]
- Van der Meer, J.W. Wave Run-Up and Overtopping. In Dikes and Revetments: Design, Maintanance and Safety Assessment; Pilarczyk, K.W., Ed.; Rijkswaterstaat, DWW: Delft, The Netherlands, 1998; pp. 145–159. ISBN 9054104554. [Google Scholar]
- Alcerreca-Huerta, J.C. Process-Based Modelling of Waves Interacting with Porous Bonded Revetments and Their Sand Foundation. Ph.D. Thesis, Technische Universität Carolo-Wilhelmina, Braunschweig, Germany, 2014. [Google Scholar]
- Hammeken Arana, A. Wave Run-Up on Beaches and Coastal Structures. Ph.D. Thesis, University College London, London, UK, 2017. [Google Scholar]
- Elbisy, M.S. Estimation of Regular Wave Run-Up on Slopes of Perforated Coastal Structures Constructed on Sloping Beaches. Ocean Eng. 2015, 109, 60–71. [Google Scholar] [CrossRef]
- Passarella, M.; Goldstein, E.B.; de Muro, S.; Coco, G. The Use of Genetic Programming to Develop a Predictor of Swash Excursion on Sandy Beaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 599–611. [Google Scholar] [CrossRef]
- Power, H.E.; Gharabaghi, B.; Bonakdari, H.; Robertson, B.; Atkinson, A.L.; Baldock, T.E. Prediction of Wave Runup on Beaches Using Gene-Expression Programming and Empirical Relationships. Coast. Eng. 2019, 144, 47–61. [Google Scholar] [CrossRef]
- Erdik, T.; Savci, M.E.; Şen, Z. Artificial Neural Networks for Predicting Maximum Wave Runup on Rubble Mound Structures. Expert Syst. Appl. 2009, 36, 6403–6408. [Google Scholar] [CrossRef]
- Bonakdar, L.; Etemad-Shahidi, A. Predicting Wave Run-Up on Rubble-Mound Structures Using M5 Model Tree. Ocean Eng. 2011, 38, 111–118. [Google Scholar] [CrossRef][Green Version]
- Abolfathi, S.; Yeganeh-Bakhtiary, A.; Hamze-Ziabari, S.M.; Borzooei, S. Wave Runup Prediction Using M5′ Model Tree Algorithm. Ocean Eng. 2016, 112, 76–81. [Google Scholar] [CrossRef]
- Hunt, I.A. Design of Seawalls and Breakwaters. J. Waterw. Harb. Div. 1959, 85, 123–152. [Google Scholar]
- Oumeraci, H.; Staal, T.; Pförtner, S.; Ludwigs, G. Hydraulic Performance, Wave Loading and Response of PBA Revetments and Their Foundations. Eur. J. Environ. Civ. Eng. 2012, 16, 953–980. [Google Scholar] [CrossRef]
- Schimmels, S.; Vousdoukas, M.; Wziatek, D.; Becker, K.; Gier, F.; Oumeraci, H. Wave Run-Up Observations on Revetments with Different Porosities. In Proceedings of the 33rd Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012. [Google Scholar] [CrossRef]
- Allsop, N.W.H.; Franco, R.; Hawkes, P.J. Wave Run-Up on Steep Slopes—A Literature Review; Report No SR 1; Hydraulics Research Wallingford: Wallingford, Oxfordshire, UK, 1985. [Google Scholar]
- Technical Advisory Committee on Flood Defences. Technical Report Wave Run-up and Wave Overtopping at Dikes; Rijkswaterstaat, DWW: Delft, The Netherlands, 2002. [Google Scholar]
- Kerpen, N. Wave-Induced Responses of Stepped Revetments. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität, Hannover, Germany, 2017. [Google Scholar]
- Hughes, S.A. Estimating Irregular Wave Runup on Rough, Impermeable Slopes; Coastal and Hydraulics Engineering Technical Note ERDC/CHL CHETN-III-70; U.S. Army Engineer Research and Development Center Environmental Laboratory: Vicksburg, MS, USA, 2005. [Google Scholar]
- Capel, A. Wave Run-Up and Overtopping Reduction by Block Revetments with Enhanced Roughness. Coast. Eng. 2015, 104, 76–92. [Google Scholar] [CrossRef]
- Schüttrumpf, H. Wellenüberlaufströmung Bei Seedeichen: Experimentelle und Theoretische Untersuchungen. Ph.D. Thesis, Universität Carolo-Wilhelmina, Braunschweig, Germany, 2001. [Google Scholar]
- Ahrens, J.P.; Heimbaugh, M.S. Approximate Upper Limit of Irregular Wave Runup on Riprap; Technical Report CERC-88-5; Coastal Engineering Research Center: Vicksburg, MS, USA, 1988. [Google Scholar]
- Hughes, S.A. Estimation of Wave Run-Up on Smooth, Impermeable Slopes Using the Wave Momentum Flux Parameter. Coast. Eng. 2004, 51, 1085–1104. [Google Scholar] [CrossRef]
- Muttray, M.O.; Oumeraci, H.; ten Oever, E. Wave Reflection and Wave Run-Up at Rubble Mound Breakwaters. In Proceedings of the 30th Conference on Coastal Engineering, San Diego, CA, USA, 3–8 September 2006; Smith, J.M., Ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2006; pp. 4313–4324. [Google Scholar]
- Van der Meer, J.W.; Stam, C.-J.M. Wave Runup on Smooth and Rock Slopes of Coastal Structures. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 534–550. [Google Scholar] [CrossRef]
- Calabrese, M.; Buccino, M.; Ciardulli, F.; Di Pace, P.; Tomasicchio, R.; Vicinanza, D. Wave Run-Up and Reflection at Rubble Mound Breakwaters With Ecopode Armor Layer. Int. Conf. Coastal. Eng. 2011, 1. [Google Scholar] [CrossRef]
- Muttray, M.O. Wellenbewegung an und in einem geschütteten Wellenbrecher: Laborexperimente im Großmaßstab und theoretische Untersuchungen. Ph.D. Thesis, Technische Universität Carolo-Wilhelmina, Braunschweig, Germany, 2000. [Google Scholar]
- Oumeraci, H. More Than 20 Years of Experience Using the Large Wave Flume (GWK): Selected Research Projects. In Die Küste Heide; Holstein: Boyens, Germany, 2010; pp. 179–239. [Google Scholar]
- Gier, F.; Schüttrumpf, H.; Mönnich, J.; van der Meer, J.; Kudella, M.; Rubin, H. Stability of Interlocked Pattern Placed Block Revetments. In Proceedings of the Coastal Engineering Conference, Santander, Spain, 1–6 July 2012; Volume 1, p. 46. [Google Scholar] [CrossRef]
- Kreyenschulte, M. Wellen-Bauwerks-Interaktion Bei Mörtelvergossenen Schüttsteindeckwerken. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2020. [Google Scholar]
- Federal Waterways Engineering and Research Institute. Use of Cementitious and Bituminous Materials for Grouting Armourstone on Waterways (Anwendung von hydraulisch gebundenen Stoffen zum Verguss von Wasserbausteinen an Wasserstraßen, MAV); Federal Waterways Engineering and Research Institute: Karlsruhe, Germany, 2017. [Google Scholar]
- Monnet, W.; Dartsch, B.; Wehefritz, K. Colcrete-Beton im Wasserbau; Beton-Verlag: Düsseldorf, Germany, 1980; ISBN 3-7640-0134-8. [Google Scholar]
- Leichtweiß-Institut für Wasserbau. L~Davis: Manual for the Data Analysis and Visualization Software of the Leichtweiss Institute; Leichtweiß-Institut für Wasserbau: Braunschweig, Germany, 2007. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. The Measurement of Incident and Reflected Spectra Using a Least Square Method. In Proceedings of the 17th International Conference on Coastal Engineering (ICCE), Sydney, Australia, 23–28 March 1980; pp. 154–172. [Google Scholar]
- SICK. Laser Measurement Systems of the LMS5xx Product Family. 2020. Available online: www.sick.com (accessed on 19 October 2020).
- Howe, D. Bed Shear Stress under Wave Runup on Steep Slopes. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 2016. [Google Scholar]
- Blenkinsopp, C.E.; Mole, M.A.; Turner, I.L.; Peirson, W.L. Measurements of the Time-Varying Free-Surface Profile across the Swash Zone Obtained Using an Industrial LIDAR. Coast. Eng. 2010, 57, 1059–1065. [Google Scholar] [CrossRef]
- Blenkinsopp, C.E.; Turner, I.L.; Allis, M.J.; Peirson, W.L.; Garden, L.E. Application of LiDAR Technology for Measurement of Time-Varying Free-Surface Profiles in a Laboratory Wave Flume. Coast. Eng. 2012, 68, 1–5. [Google Scholar] [CrossRef]
- Hofland, B.; Diamantidou, E.; van Steeg, P.; Meys, P. Wave Runup and Wave Overtopping Measurements Using a Laser Scanner. Coast. Eng. 2015, 106, 20–29. [Google Scholar] [CrossRef]
- Seelig, W.N.; Ahrens, J.P. Estimation of Wave Reflection and Energy Dissipation Coefficients for Beaches, Revetments, and Breakwaters; Report No. TP-81-1; US Army Corps of Engineers, Coastal Engineering Research Center: Fort Belvoir, VA, USA, 1981. [Google Scholar]



| Type of Revetment | Influence Factor γf | Equation Nr. in This Work | Revetment Characteristics | Reference | ||
|---|---|---|---|---|---|---|
| Rough | Porous | Permeable | ||||
| Grass | 0.9–1.0 | (2) | (x) | [8] | ||
| Polyurethane bonded gravel | ≈0.75 | mod. (2) | (x) | x | x | [22,23] |
| Basalt | 0.9 | (2) | (x) | (x) | (x) | [8] |
| Stepped revetments | 0.4–0.9 | (4) | x | [26] | ||
| Two layers of rock | 0.55 | (2) | x | x | x | [8] |
| Two layers of rock | 0.51 | (10) | x | x | x | [27] |
| Pattern placed revetments with enhanced roughness | 0.65–0.85 | (4) | x | (x) | (x) | [28] |
| Partially Grouted | Fully Grouted | |||
|---|---|---|---|---|
| Section | North | South | North | South |
| Configuration Nr. | 1 | 2 | 3 | 4 |
| Top layer thickness t [m] | 0.6 | 0.4 | 0.6 | 0.4 |
| Amount of mortar vg [l/m2] | 80 | 80 | 80+100 | 180 |
| Estimated porosity n before grouting [-] | 0.45 | 0.45 | 0.45 | 0.45 |
| Porosity n after grouting [-] | 0.32 | 0.25 | 0.16 | 0 |
| Pore volume Vp after grouting [l/m2] | 190 | 100 | 90 | 0 |
| Partially Grouted | Fully Grouted | ||||||
|---|---|---|---|---|---|---|---|
| Section | North | South | North | South | |||
| Equation | Nr. | 1 (▲) | 2 (●) | 3 (■) | 4 (▼) | ||
| (2) | γf | 0.72 | 0.79 | 0.86 | 0.88 | ||
| bias | −0.02 | 0 | 0 | 0 | |||
| RMSE | 0.09 | 0.08 | 0.11 | 0.10 | |||
| SI | 6.27 | 5.51 | 6.00 | 5.56 | |||
| (10) | γf,M | 0.65 | 0.70 | 0.76 | 0.77 | ||
| bias | 0.01 | 0.02 | 0.01 | 0 | |||
| RMSE | 0.11 | 0.11 | 0.13 | 0.12 | |||
| SI | 7.86 | 7.38 | 7.22 | 6.68 | |||
| (11) | a | 1.87 | 1.90 | 2.07 | 2.13 | ||
| b | −0.18 | −0.22 | −0.18 | −0.18 | |||
| bias | 0.01 | 0.02 | 0.03 | 0.05 | |||
| RMSE | 0.12 | 0.10 | 0.16 | 0.19 | |||
| SI | 8.17 | 6.84 | 9.26 | 10.29 | |||
| (12) | a [-] | 1.63 | 1.73 | 1.77 | 1.81 | ||
| bias | 0 | −0.01 | −0.01 | 0 | |||
| RMSE | 0.09 | 0.07 | 0.11 | 0.10 | |||
| SI | 6.11 | 4.72 | 6.37 | 5.68 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kreyenschulte, M.; Schürenkamp, D.; Bratz, B.; Schüttrumpf, H.; Goseberg, N. Wave Run-Up on Mortar-Grouted Riprap Revetments. Water 2020, 12, 3396. https://doi.org/10.3390/w12123396
Kreyenschulte M, Schürenkamp D, Bratz B, Schüttrumpf H, Goseberg N. Wave Run-Up on Mortar-Grouted Riprap Revetments. Water. 2020; 12(12):3396. https://doi.org/10.3390/w12123396
Chicago/Turabian StyleKreyenschulte, Moritz, David Schürenkamp, Benedikt Bratz, Holger Schüttrumpf, and Nils Goseberg. 2020. "Wave Run-Up on Mortar-Grouted Riprap Revetments" Water 12, no. 12: 3396. https://doi.org/10.3390/w12123396
APA StyleKreyenschulte, M., Schürenkamp, D., Bratz, B., Schüttrumpf, H., & Goseberg, N. (2020). Wave Run-Up on Mortar-Grouted Riprap Revetments. Water, 12(12), 3396. https://doi.org/10.3390/w12123396







