Measurement and Modelling of Moisture Distribution and Water Binding Energy of Dredged Sludge
Abstract
:1. Introduction
2. Water Binding Energy Calculation Model
3. Materials and Methods
3.1. Sample Preparation and Characterization
3.2. LF-NMR Analysis
3.3. TG-DTA Analysis
4. Results and Discussion
4.1. Water Distribution in Dredged Sludge Detected by LF-NMR
4.2. Model Analysis
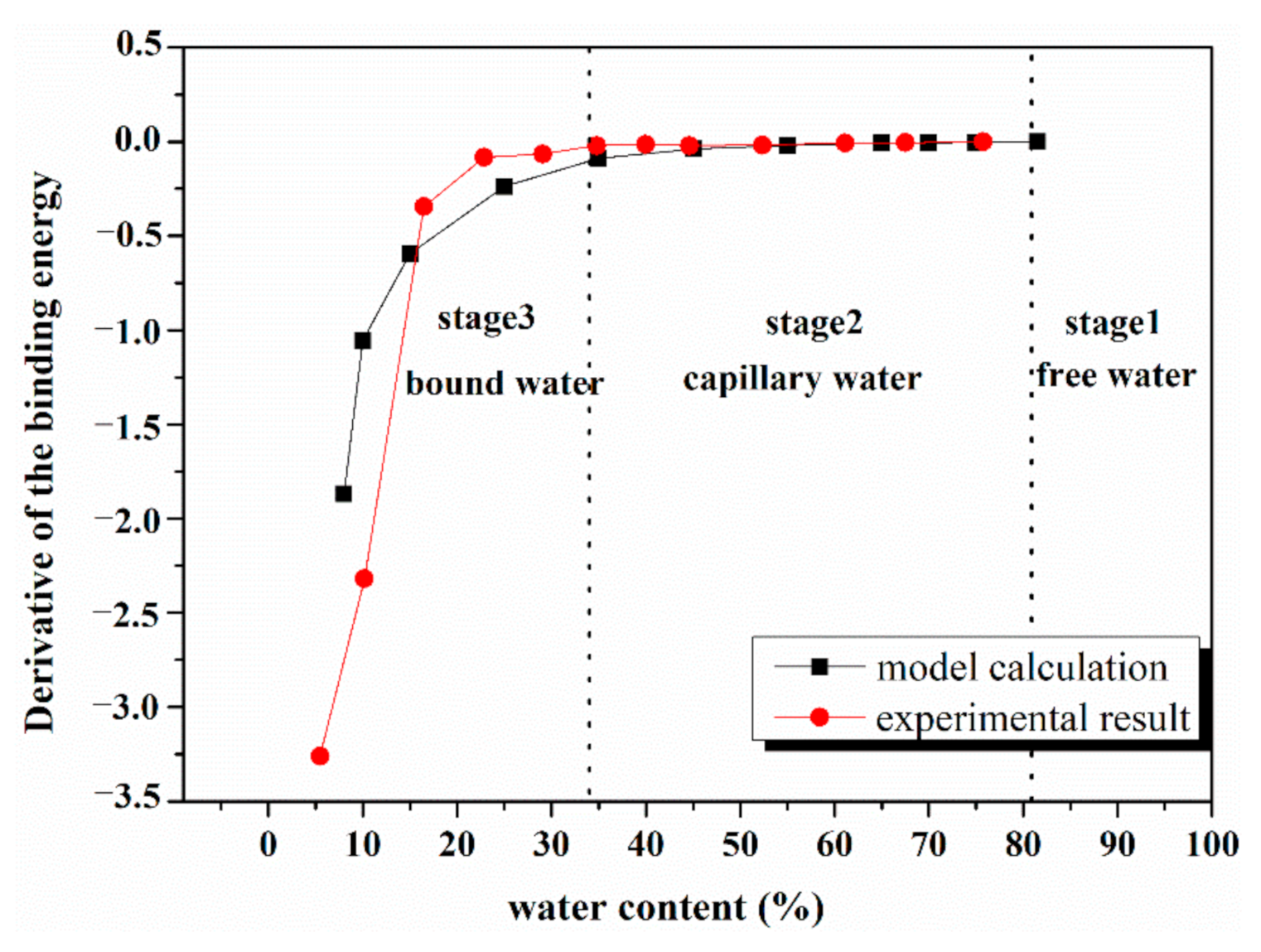
4.3. Comparison of Model Calculation and Experimental Result
4.4. Gradient of Energy Consumption Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amar, M.; Benzerzour, M.; Kleib, J.; Abriak, N.-E. From dredged sediment to supplementary cementitious material: Characterization, treatment, and reuse. Int. J. Sediment Res. 2021, 36, 92–109. [Google Scholar] [CrossRef]
- Oh, H.; Lee, J.; Banthia, N.; Talukdar, S. An Experimental Study of the Physicochemical Properties of a Cement Matrix Containing Dredged Materials. Mater. Sci. Appl. 2011, 2, 847–857. [Google Scholar] [CrossRef] [Green Version]
- Bhairappanavar, S.; Liu, R.; Coffman, R. Beneficial Uses of Dredged Material in Green Infrastructure and Living Architecture to Improve Resilience of Lake Erie. Infrastructures 2018, 3, 42. [Google Scholar] [CrossRef] [Green Version]
- Tri, D.Q.; Kandasamy, J.; Don, N.C. Quantitative Assessment of the Environmental Impacts of Dredging and Dumping Activities at Sea. Appl. Sci. 2019, 9, 1703. [Google Scholar] [CrossRef] [Green Version]
- Zonta, R.; Cassin, D.; Pini, R.; Dominik, J. Substantial Decrease in Contaminant Concentrations in the Sediments of the Venice (Italy) Canal Network in the Last Two Decades—Implications for Sediment Management. Water 2020, 12, 1965. [Google Scholar] [CrossRef]
- Cappuyns, V.; Deweirt, V.; Rousseau, S. Dredged sediments as a resource for brick production: Possibilities and barriers from a consumers’ perspective. Waste Manag. 2015, 38, 372–380. [Google Scholar] [CrossRef]
- Bagarani, M.; De Vincenzo, A.; Ievoli, C.; Molino, B. The Reuse of Sediments Dredged from Artificial Reservoirs for Beach Nourishment: Technical and Economic Feasibility. Sustainability 2020, 12, 6820. [Google Scholar] [CrossRef]
- Molino, B.; Bufalo, G.; De Vincenzo, A.; Ambrosone, L. Semiempirical Model for Assessing Dewatering Process by Flocculation of Dredged Sludge in an Artificial Reservoir. Appl. Sci. 2020, 10, 3051. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, W.; Gao, H.; Wang, D. Comprehensive assessment of flocculation conditioning of dredged sediment using organic polymers: Dredged sediment dewaterability and release of pollutants. Sci. Total Environ. 2020, 739, 139884. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Fu, H.; Cai, Y.; Hu, X.; Lou, X.; Jin, Y.; Hai, J.; Ni, J.; Zou, J. Vacuum preloading combined with multiple-flocculant treatment for dredged fill improvement. Eng. Geol. 2019, 259, 105194. [Google Scholar] [CrossRef]
- Pan, L.; Xing, J.; Luo, X.; Li, Y.; Sun, D.; Zhai, Y.; Yang, K.; Chen, Z. Influence of Electron Beam Irradiation on the Moisture and Properties of Freshly Harvested and Sun-Dried Rice. Foods 2020, 9, 1139. [Google Scholar] [CrossRef]
- Zhao, C.; Zheng, H.; Feng, L.; Wang, Y.; Liu, Y.; Liu, B.; Djibrine, B.Z. Improvement of Sludge Dewaterability by Ultrasound-Initiated Cationic Polyacrylamide with Microblock Structure: The Role of Surface-Active Monomers. Materials 2017, 10, 282. [Google Scholar] [CrossRef]
- Mao, H.; Chi, Y.; Wang, F.; Mao, F.; Liang, F.; Lu, S.; Cen, K. Effect of Ultrasonic Pre-treatment on Dewaterability and Moisture Distribution in Sewage Sludge. Waste Biomass Valoriz. 2018, 9, 247–253. [Google Scholar] [CrossRef]
- Jin, Y.; Zheng, X.; Chi, Y.; Ni, M. Rapid, Accurate Measurement of the Oil and Water Contents of Oil Sludge Using Low-Field NMR. Ind. Eng. Chem. Res. 2013, 52, 2228–2233. [Google Scholar] [CrossRef]
- Zheng, X.; Jin, Y.; Chi, Y.; Ni, M. Simultaneous Determination of Water and Oil in Oil Sludge by Low-Field 1H NMR Relaxometry and Chemometrics. Energy Fuels 2013, 27, 5787–5792. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D.R. Modified Spin-Echo Method for Measuring Nuclear Relaxation Times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef] [Green Version]
- Yao, W.; She, A.; Yang, P. 1H-NMR relaxation and state evolvement of evaporable water in cement pastes. J. Chin. Ceram. Soc. 2009, 37, 1. [Google Scholar]
- Karr, C. Analytical Methods for Coal and Coal Products: Volume II; Academic press: Cambridge, MA, USA, 2013; Volume 2. [Google Scholar]
- Chen, G.W.; Hung, W.T.; Chang, I.L.; Lee, S.F.; Lee, D.J. Continuous Classification of Moisture Content in Waste Activated Sludges. J. Environ. Eng. 1997, 123, 253–258. [Google Scholar] [CrossRef]
- Slimanou, H.; Bouguermouh, K.; Bouzidi, N. Synthesis of geopolymers based on dredged sediment in calcined and uncalcined states. Mater. Lett. 2019, 251, 188–191. [Google Scholar] [CrossRef]
- Li, Y.; Yang, F.; Miao, S.; Wang, D.; Li, Z.; Yuan, X.; Yuan, L.; Liu, Q. Achieved deep-dewatering of dredged sediments by Fe(II) activating persulfate pretreatment: Filtrating performance and mechanistic insights. Chem. Eng. J. 2021, 405, 126847. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, Q.; Long, X.-E.; Li, Z.-L.; Liu, D.-X.; Ye, D.-H.; He, C.-Q.; Liu, X.-Y.; Väänänen, K.; Chen, X. Anthropogenic activities drive the microbial community and its function in urban river sediment. J. Soils Sediments 2015, 16, 716–725. [Google Scholar] [CrossRef]
- Huang, P.L. A Review of: “Modern Drying Technology, Second Enhanced Edition Editors: Yongkang Pan, Xizhong Wang and Xiangdong Liu”. Dry. Technol. 2007, 25, 2057–2058. [Google Scholar] [CrossRef]
- Yariv, S.; Cross, H. Physical Chemistry of Surfaces. Geochem. Colloid Syst. 1979, 150, 93–155. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.N.; De Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria; Pearson Education: Hoboken, NJ, USA, 1998. [Google Scholar]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B.; Mayer, M.G. Molecular Theory of Gases and Liquids; Wiley: New York, NY, USA, 1964; Volume 165. [Google Scholar]
- Ansari, R.; Kazemi, E. Detailed investigation on single water molecule entering carbon nanotubes. Appl. Math. Mech. 2012, 33, 1287–1300. [Google Scholar] [CrossRef]
- Lin, D.T.W.; Chen, C.-K. A molecular dynamics simulation of TIP4P and Lennard-Jones water in nanochannel. Acta Mech. 2004, 173, 181–194. [Google Scholar] [CrossRef]
- Da Silva, L.B. Structural and dynamical properties of water confined in carbon nanotubes. J. Nanostruct. Chem. 2014, 4, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Fort, T.; Putnam, F. The interaction of gases with solid surfaces. J. Colloid Interface Sci. 1976, 57, 190–191. [Google Scholar] [CrossRef]
- Mao, H.; Wang, F.; Mao, F.; Chi, Y.; Lu, S.; Cen, K. Measurement of water content and moisture distribution in sludge by1H nuclear magnetic resonance spectroscopy. Dry. Technol. 2016, 34, 267–274. [Google Scholar] [CrossRef]
- Ahunbay, M.G. Monte Carlo simulation of water adsorption in hydrophobic MFI zeolites with hydrophilic sites. Langmuir 2011, 27, 4986–4993. [Google Scholar] [CrossRef]
- Prost, R.; Koutit, T.; Benchara, A.; Huard, E. State and location of water adsorbed on clay minerals: Consequences of the hydration and swelling-shrinkage phenomena. Clays Clay Min. 1998, 46, 117–131. [Google Scholar] [CrossRef]
- Steele, W.A. The physical interaction of gases with crystalline solids: I. Gas-solid energies and properties of isolated adsorbed atoms. Surf. Sci. 1973, 36, 317–352. [Google Scholar] [CrossRef]
- Smith, L.S.; Lee, L.L. The Lennard-Jones 9:3 adsorptive system I: The Percus–Yevick and hypernetted chain theories and their modifications. J. Chem. Phys. 1979, 71, 4085. [Google Scholar] [CrossRef]
- Huang, Q.; Zhou, G.; Yu, B.; Wang, S.; Chi, Y.; Yan, J. Quantitative model for predicting the desorption energy of water contained in lignite. Fuel 2015, 157, 202–207. [Google Scholar] [CrossRef]
- Bushuev, Y.G.; Sastre, G. Atomistic Simulation of Water Intrusion—Extrusion in ITQ-4 (IFR) and ZSM-22 (TON): The Role of Silanol Defects. J. Phys. Chem. C 2011, 115, 21942–21953. [Google Scholar] [CrossRef]
- Fitts, T.G.; Brown, K. Stress-induced smectite dehydration: Ramifications for patterns of freshening and fluid expulsion in the N. Barbados accretionary wedge. Earth Planet. Sci. Lett. 1999, 172, 179–197. [Google Scholar] [CrossRef]
- Allardice, D.; Evans, D. The-brown coal/water system: Part 2. Water sorption isotherms on bed-moist Yallourn brown coal. Fuel 1971, 50, 236–253. [Google Scholar] [CrossRef]
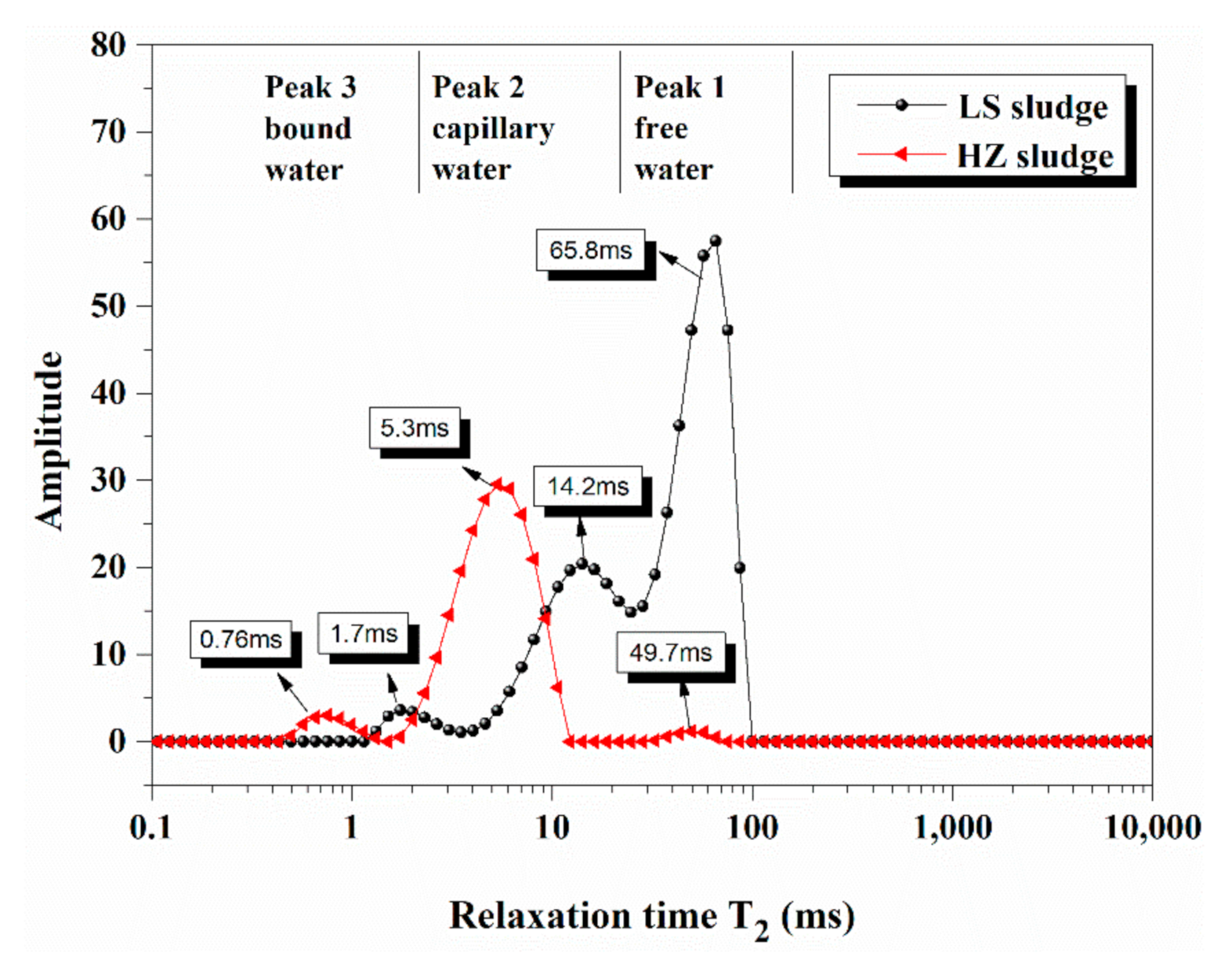
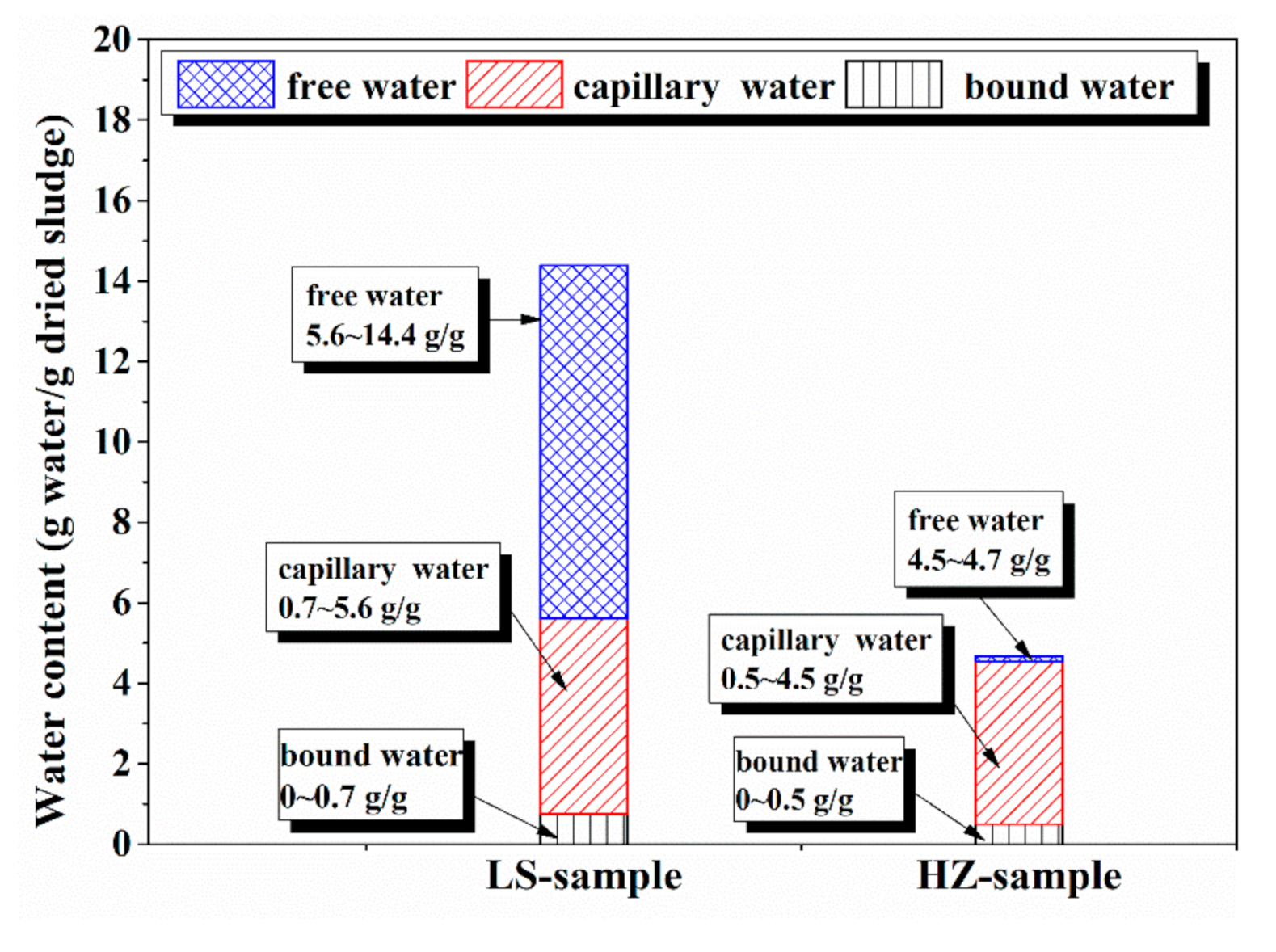
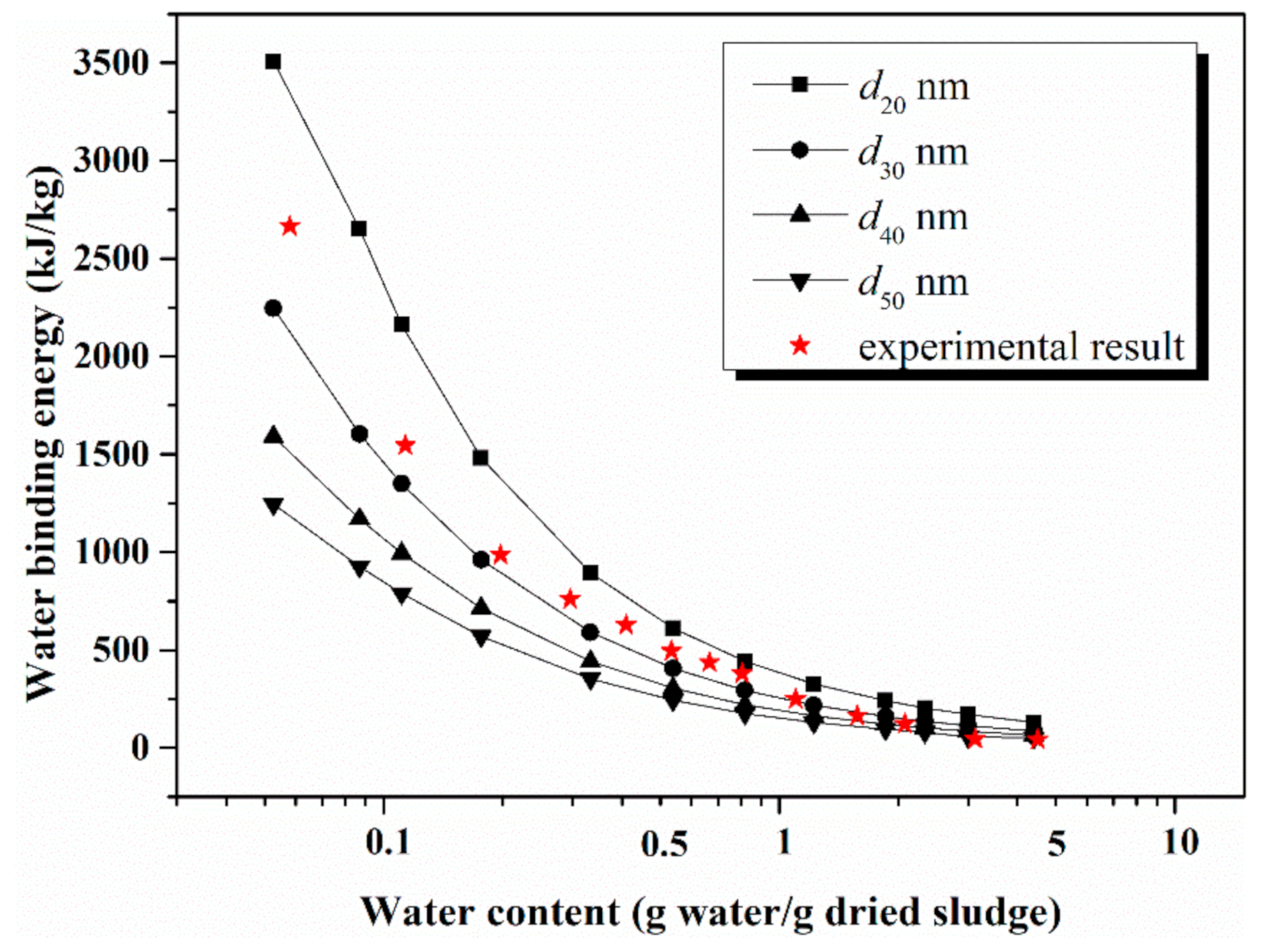
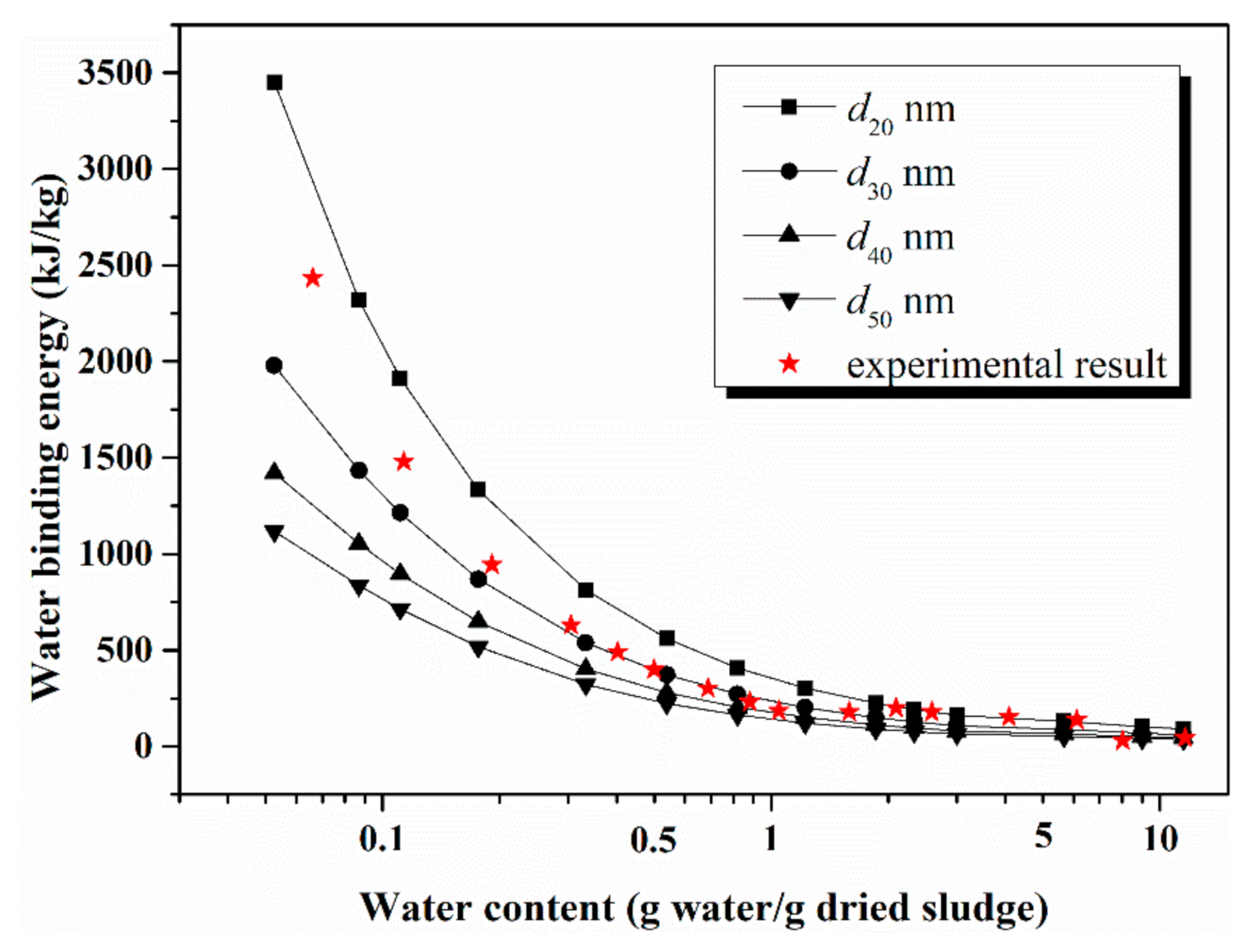
| Density g/cm3 | Specific Surface Area m2/g | Particle Size Distribution nm | |
|---|---|---|---|
| HZ sample | 1.42 | 32.5 | 25~130 |
| LS sample | 1.58 | 25.4 | 18~85 |
| Free Water % | Capillary Water % | Bound Water % | |
|---|---|---|---|
| HZ sample | 82.0~82.4% | 33.6~82.0 | 0~33.6% |
| LS sample | 84.9~93.5% | 43.3~84.9 | 0~43.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, F.; Zhao, Y.; Zhang, Y.; Chen, Z.; Yin, L. Measurement and Modelling of Moisture Distribution and Water Binding Energy of Dredged Sludge. Water 2020, 12, 3395. https://doi.org/10.3390/w12123395
Mao F, Zhao Y, Zhang Y, Chen Z, Yin L. Measurement and Modelling of Moisture Distribution and Water Binding Energy of Dredged Sludge. Water. 2020; 12(12):3395. https://doi.org/10.3390/w12123395
Chicago/Turabian StyleMao, Feiyan, Yingjie Zhao, Yiping Zhang, Zhou Chen, and Lu Yin. 2020. "Measurement and Modelling of Moisture Distribution and Water Binding Energy of Dredged Sludge" Water 12, no. 12: 3395. https://doi.org/10.3390/w12123395
APA StyleMao, F., Zhao, Y., Zhang, Y., Chen, Z., & Yin, L. (2020). Measurement and Modelling of Moisture Distribution and Water Binding Energy of Dredged Sludge. Water, 12(12), 3395. https://doi.org/10.3390/w12123395






