Isoscape of δ18O in Precipitation of the Qinghai-Tibet Plateau: Assessment and Improvement
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Isotope Observation Data
2.2. Global Precipitation Isoscape
2.3. Meteorological and Elevation Data
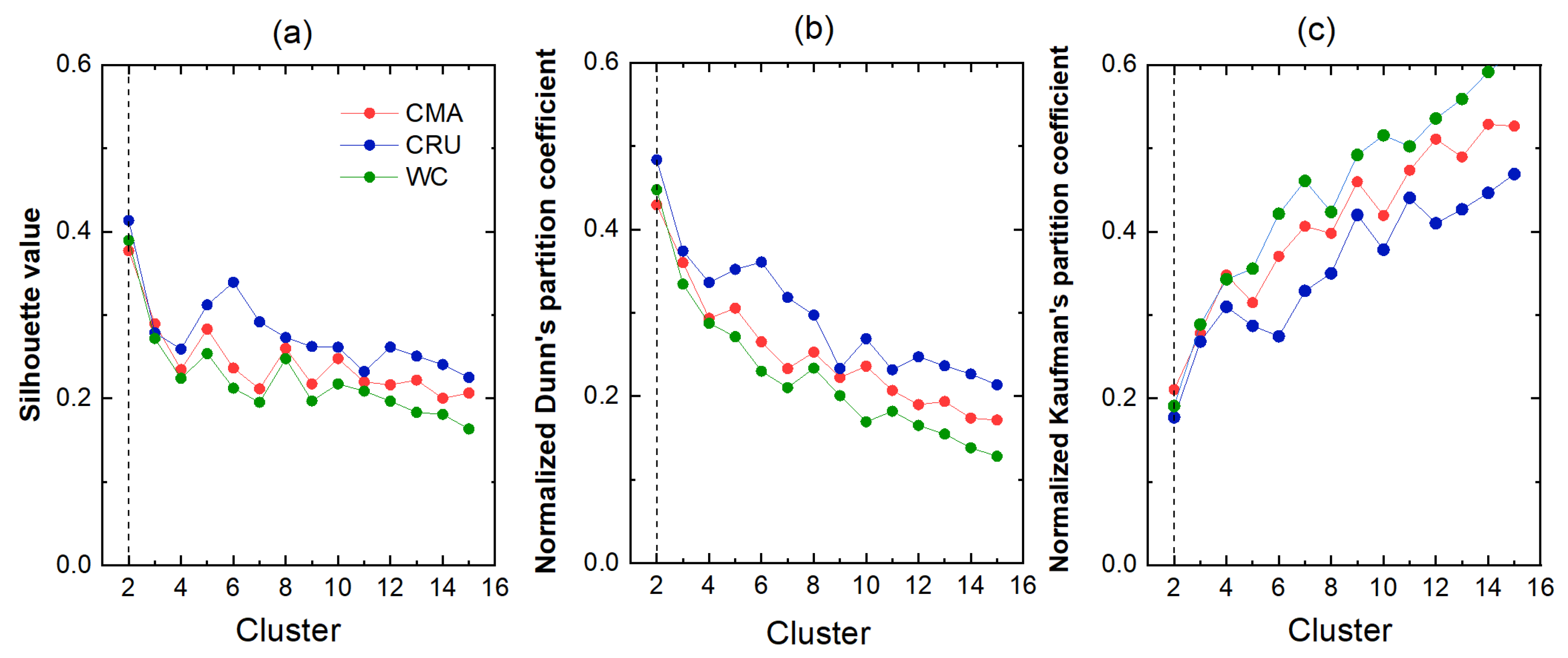
2.4. Fuzzy Clustering
2.5. Assessment Method
3. Results and Analysis
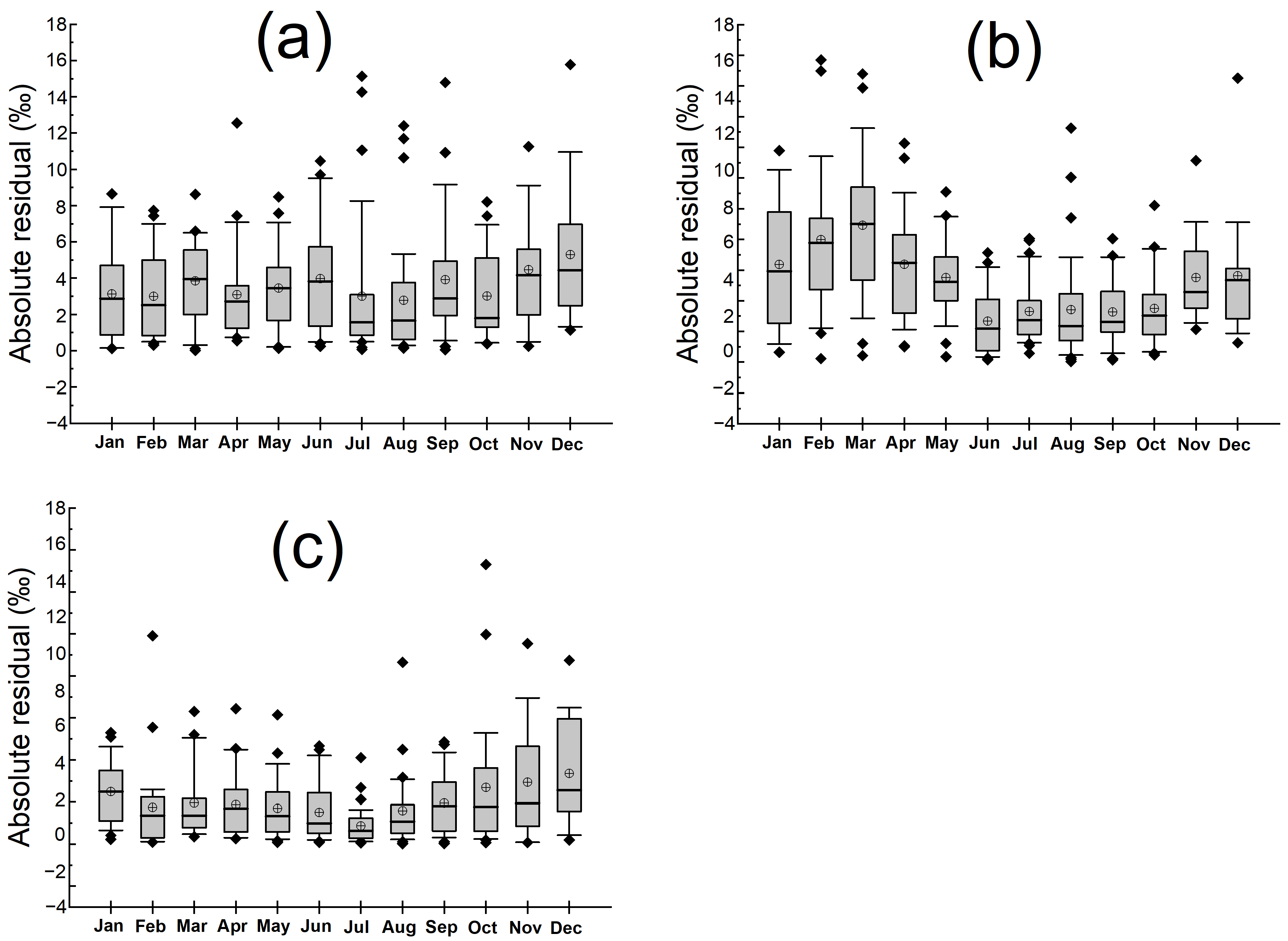
3.1. Assessment of Previous Global Products in the QTP
3.2. Isoscape Established Using a Regionalized Clustering
3.2.1. Climate Clustering
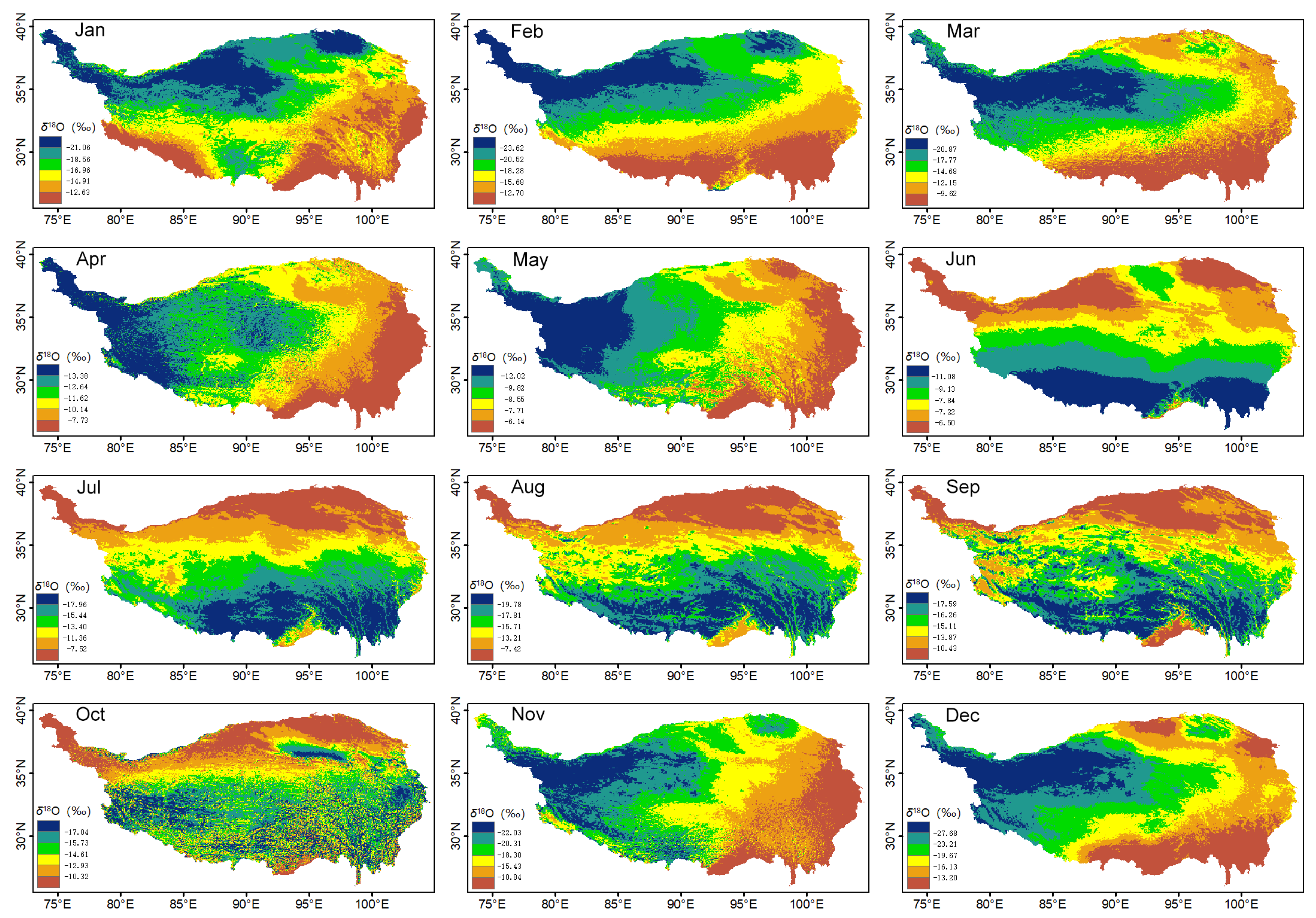
3.2.2. Establishing the Isoscape
3.2.3. Comparison with the OIPC and RCWIP
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bowen, G.J.; Cai, Z.; Fiorella, R.P.; Putman, A.L. Isotopes in the water cycle: Regional-to global-scale patterns and applications. Annu. Rev. Earth. Planet. Sci. 2019, 47, 453–479. [Google Scholar] [CrossRef] [Green Version]
- Jasechko, S. Global isotope hydrogeology―Review. Rev. Geophys. 2019, 57, 835–965. [Google Scholar] [CrossRef]
- Bowen, G.J. Isoscapes: Spatial pattern in isotopic biogeochemistry. Annu. Rev. Earth. Planet. Sci. 2010, 38, 161–187. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Zhang, M.; Bowen, G.J.; Liu, X.; Du, M.; Chen, F.; Qiu, X.; Wang, L.; Che, Y.; Zhao, G. Water source signatures in the spatial and seasonal isotope variation of Chinese tap waters. Water Resour. Res. 2018, 54, 9131–9143. [Google Scholar] [CrossRef]
- Hollins, S.E.; Hughes, C.E.; Crawford, J.; Cendón, D.I.; Meredith, K.T. Rainfall isotope variations over the Australian continent–implications for hydrology and isoscape applications. Sci. Total Environ. 2018, 645, 630–645. [Google Scholar] [CrossRef] [PubMed]
- Allen, S.T.; Kirchner, J.W.; Goldsmith, G.R. Predicting spatial patterns in precipitation isotope (δ2H and δ18O) seasonality using sinusoidal isoscapes. Geophys. Res. Let. 2018, 45, 4859–4868. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Wang, S. A review of precipitation isotope studies in China: Basic pattern and hydrological process. J. Geogr. Sci. 2016, 26, 921–938. [Google Scholar] [CrossRef]
- Bowen, G.J.; Wilkinson, B. Spatial distribution of δ18O in meteoric precipitation. Geology 2002, 30, 315–318. [Google Scholar] [CrossRef]
- Peng, P.; Zhang, X.J.; Chen, J. Bias correcting isotope-equipped GCMs outputs to build precipitation oxygen isoscape for eastern China. J. Hydrol. 2020, 589, 125153. [Google Scholar] [CrossRef]
- Vander Zanden, H.B.; Nelson, D.M.; Wunder, M.B.; Conkling, T.J.; Katzner, T. Application of isoscapes to determine geographic origin of terrestrial wildlife for conservation and management. Biol. Conserv. 2018, 228, 268–280. [Google Scholar] [CrossRef]
- Bowen, G.J.; Wassenaar, L.I.; Hobson, K.A. Global application of stable hydrogen and oxygen isotopes to wildlife forensics. Oecologia 2005, 143, 337–348. [Google Scholar] [CrossRef]
- Terzer, S.; Wassenaar, L.I.; Araguás-Araguás, L.J.; Aggarwal, P.K. Global isoscapes for δ18O and δ2H in precipitation: Improved prediction using regionalized climatic regression models. Hydrol. Earth Syst. Sci. 2013, 17, 4713–4728. [Google Scholar] [CrossRef]
- IAEA/WMO. Global network of isotopes in precipitation. the GNIP Database. 2020. Available online: http://www.iaea.org/water (accessed on 1 January 2020).
- Lisowska-Gaczorek, A.; Cienkosz-Stepańczak, B.; Szostek, K. Oxygen stable isotopes variation in water precipitation in Poland–anthropological applications. Anthropol. Rev. 2017, 80, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Tian, Q.; Fang, X.; Wang, M. Sedimentary n-alkanes record of precipitation D/H ratios in arid regions of the Tibetan Plateau. Chinese Sci. Bull. 2017, 62, 700–710. (In Chinese) [Google Scholar]
- Yao, T.; Masson-Delmotte, V.; Gao, J.; Yu, W.; Yang, X.; Risi, C.; Sturm, C.; Werner, M.; Zhao, H.; He, Y.; et al. A review of climatic controls on δ18O in precipitation over the Tibetan Plateau: Observations and simulations. Rev. Geophys. 2013, 51, 525–548. [Google Scholar] [CrossRef]
- Sun, C.; Chen, Y.; Li, J.; Chen, W.; Li, X. Stable isotope variations in precipitation in the northwesternmost Tibetan Plateau related to various meteorological controlling factors. Atmos. Res. 2019, 227, 66–78. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Zhang, J.; Li, J.; Liu, J.; Tian, L.; Fu, C. Stable isotopes of atmospheric water vapour and precipitation in the northeast Qinghai-Tibetan Plateau. Hydrol. Process. 2019, 33, 2997–3009. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Guo, Y.; Ma, N.; Dai, D.; Song, H.; Qu, D.; Gao, H. Controls of stable isotopes in precipitation on the central Tibetan Plateau: A seasonal perspective. Quatern. Int. 2019, 513, 66–79. [Google Scholar] [CrossRef]
- Ren, W.; Yao, T.; Xie, S.; He, Y. Controls on the stable isotopes in precipitation and surface waters across the southeastern Tibetan Plateau. J. Hydrol. 2017, 545, 276–287. [Google Scholar] [CrossRef]
- Gao, J.; Masson-Delmotte, V.; Yao, T.; Tian, L.; Risi, C.; Hoffmann, G. Precipitation water stable isotopes in the south Tibetan Plateau: Observations and modeling. J. Clim. 2011, 24, 3161–3178. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Gao, J.; Yao, T.; Ding, Y.; Xin, R. Spatial distribution of stable isotope in precipitation upon the Tibetan Plateau analyzed with various interpolation methods. J. Glaciol. Geocryol. 2015, 37, 351–359. (In Chinese) [Google Scholar]
- Xu, X.; Zhao, T.; Lu, C.; Guo, Y.; Chen, B.; Liu, R.; Li, Y.; Shi, X. An important mechanism sustaining the atmospheric “water tower” over the Tibetan Plateau. Atmos. Chem. Phys. 2014, 14, 11287–11295. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, B.; Zheng, D. Datasets of the boundary and area of the Tibetan Plateau. Glob. Chang. Res. Data Publ. Repos. 2014. [Google Scholar] [CrossRef]
- Ren, M.; Bao, H. Natural Regions of China and Their Exploitation; The Commercial Press: Beijing, China, 1992; pp. 1–483. (In Chinese) [Google Scholar]
- Zhang, C.; Tang, Q.; Chen, D. Recent changes in the moisture source of precipitation over the Tibetan Plateau. J. Clim. 2017, 30, 1807–1819. [Google Scholar] [CrossRef]
- Li, Z.; Yao, T.; Tian, L.; Xu, B.; Wu, G. Variations of δ18O in precipitation from the Muztagata Glacier, East Pamirs. Sci. China Ser. D 2006, 49, 36–42. [Google Scholar] [CrossRef]
- Zhao, L.; Yin, L.; Xiao, H.; Cheng, G.; Zhou, M.; Yang, Y.; Li, C.; Zhou, J. Isotopic evidence for the moisture origin and composition of surface runoff in the headwaters of the Heihe River basin. Chinese Sci. Bull. 2011, 56, 406–415. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Song, X.; Yuan, G.; Sun, X.; Yang, L. Stable isotopic compositions of precipitation in China. Tellus B 2014, 66, 22567. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Li, X.; Jiang, Z.; Li, J.; Zheng, X.; Zhao, D. Variations in water use for achnatherum splendens in Lake Qinghai Watershed, based on δD and δ18O. Acta Ecol. Sinica 2015, 35, 8174–8183. (In Chinese) [Google Scholar]
- Gui, J.; Li, Z.; Feng, Q.; Wei, W.; Li, Y.; Lü, Y.; Yuan, R.; Zhang, B. Space-time characteristics and environmental significance of the stable isotopes in precipitation in the Gulang River basin. Environ. Sci. 2019, 40, 149–156. (In Chinese) [Google Scholar]
- Zhu, J.; Chen, H.; Gong, G. Hydrogen and oxygen isotopic compositions of precipitation and its water vapor sources in Eastern Qaidam Basin. Environ. Sci. 2015, 36, 2784–2790. (In Chinese) [Google Scholar]
- Sun, C.; Shen, Y.; Chen, Y.; Chen, W.; Liu, W.; Zhang, Y. Quantitative evaluation of the rainfall influence on streamflow in an inland mountainous river basin within Central Asia. Hydrol. Sci. J. 2018, 63, 17–30. [Google Scholar] [CrossRef]
- Ren, W.; Yao, T.; Yang, X.; Joswiak, D.R. Implications of variations in δ18O and δD in precipitation at Madoi in the eastern Tibetan Plateau. Quatern. Int. 2013, 313, 56–61. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Q.; Yun, H. Characteristic analysis of stable isotope variation in precipitation and rivers in Beilu river permafrost region. Adv. Water Sci. 2013, 24, 978–985. (In Chinese) [Google Scholar]
- Cui, J.; Tian, L.; Biggs, T.W.; Wen, R. Deuterium-excess determination of evaporation to inflow ratios of an alpine lake: Implications for water balance and modeling. Hydrol. Process. 2017, 31, 1034–1046. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, J.; Xu, Y. Establishment and assessment of the grid precipitation datasets in China for the past 50 years. J. Meteorol. Sci. 2014, 34, 414–420. (In Chinese) [Google Scholar]
- New, M.; Lister, D.; Hulme, M.; Makin, I. A high-resolution data set of surface climate over global land areas. Clim. Res. 2002, 21, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: New York, NY, USA, 1990; pp. 1–342. [Google Scholar]
- Wu, C.F.J. Jackknife, bootstrap and other resampling methods in regression analysis. Ann. Stat. 1986, 14, 1261–1295. [Google Scholar] [CrossRef]
- Gao, J.; Masson-Delmotte, V.; Risi, C.; He, Y.; Yao, T. What controls precipitation δ18O in the southern Tibetan Plateau at seasonal and intra-seasonal scales? A case study at Lhasa and Nyalam. Tellus B 2013, 65, 21043. [Google Scholar] [CrossRef]
- Gao, J.; He, Y.; Masson-Delmotte, V.; Yao, T. ENSO effects on annual variations of summer precipitation stable isotopes in Lhasa, southern Tibetan Plateau. J. Clim. 2018, 31, 1173–1182. [Google Scholar] [CrossRef]
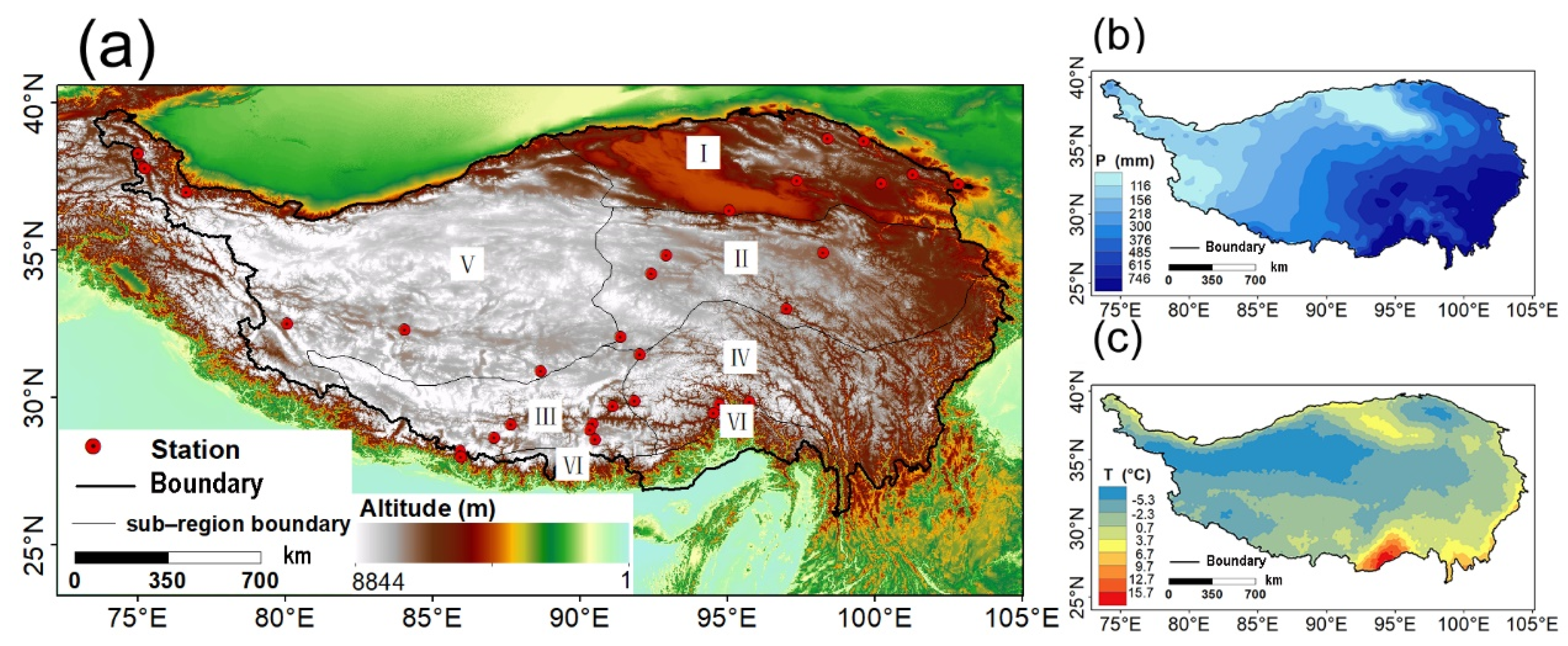

| Station | Longitude (°E) | Latitude (°N) | Altitude (m) | P (mm) 1 | T (℃) 1 | Water Vapor Regime 2 | Sub-Region 3 | n4 | Data Source |
|---|---|---|---|---|---|---|---|---|---|
| Tuole | 98.42 | 38.80 | 3367 | 473 | −5.35 | the westerly domain | Qaidam | 7 | [27] |
| Yeniugou | 99.63 | 38.70 | 3320 | 434 | −0.55 | the westerly domain | Qaidam | 9 | [28] |
| Haibei | 101.31 | 37.56 | 3280 | 592 | −0.89 | the westerly domain | Qaidam | 12 | [29] |
| Delhi | 97.37 | 37.37 | 2981 | 223 | −0.29 | the westerly domain | Qaidam | 12 | [16] |
| Gangca | 100.22 | 37.29 | 3260 | 411 | −0.31 | the westerly domain | Qaidam | 6 | [30] |
| Tianzhu | 102.85 | 37.25 | 2700 | 439 | 3.37 | the westerly domain | Qaidam | 10 | [31] |
| Golmud | 95.09 | 36.35 | 2889 | 63 | 3.01 | the westerly domain | Qaidam | 3 | [32] |
| Muztag | 75.02 | 38.28 | 4430 | 150 | −0.84 | the westerly domain | Kunlun-Ngari-North Tibet | 5 | [28] |
| Tizinafu | 75.20 | 37.83 | 3058 | 96 | 0.10 | the westerly domain | Kunlun-Ngari-North Tibet | 4 | [33] |
| Taxkorgen | 75.27 | 37.77 | 3100 | 96 | 0.10 | the westerly domain | Kunlun-Ngari-North Tibet | 12 | [16] |
| Xihexiu | 76.68 | 36.98 | 2960 | 119 | −2.90 | the westerly domain | Kunlun-Ngari-North Tibet | 10 | [17] |
| Shiquanhe | 80.08 | 32.50 | 4278 | 169 | −2.18 | the transition domain | Kunlun-Ngari-North Tibet | 10 | [16] |
| Gaize | 84.07 | 32.30 | 4430 | 133 | −1.81 | the transition domain | Kunlun-Ngari-North Tibet | 12 | [16] |
| Xainza | 88.70 | 30.90 | 4770 | 330 | −1.25 | the transition domain | Kunlun-Ngari-North Tibet | 12 | [19] |
| Madoi | 98.26 | 34.92 | 4300 | 370 | −3.69 | the transition domain | Eastern Qinghai-Tibet | 11 | [34] |
| Beiluhe | 92.94 | 34.83 | 4642 | 315 | −4.81 | the transition domain | Eastern Qinghai-Tibet | 10 | [35] |
| Tuotuohe | 92.43 | 34.22 | 4533 | 323 | −4.51 | the transition domain | Eastern Qinghai-Tibet | 12 | [16] |
| Yushu | 97.02 | 33.02 | 3682 | 656 | −2.48 | the transition domain | Eastern Qinghai-Tibet | 12 | [16] |
| Cona | 91.40 | 32.07 | 4623 | 453 | −2.06 | the transition domain | Eastern Qinghai-Tibet | 9 | [36] |
| Lhasa | 91.13 | 29.70 | 3649 | 426 | 1.62 | the monsoon domain | South Tibet | 12 | [16] |
| Nagqu | 92.07 | 31.48 | 4508 | 514 | −1.95 | the monsoon domain | South Tibet | 12 | [16] |
| Baidi | 90.43 | 29.12 | 4430 | 358 | 0.25 | the monsoon domain | South Tibet | 11 | [16] |
| Larzi | 87.68 | 29.08 | 4000 | 336 | 0.69 | the monsoon domain | South Tibet | 4 | [16] |
| Wengguo | 90.35 | 28.90 | 4500 | 361 | −0.43 | the monsoon domain | South Tibet | 7 | [16] |
| Dingri | 87.12 | 28.65 | 4330 | 302 | −0.26 | the monsoon domain | South Tibet | 8 | [16] |
| Dui | 90.53 | 28.58 | 5030 | 389 | −0.30 | the monsoon domain | South Tibet | 10 | [16] |
| Nyalam | 85.97 | 28.18 | 3810 | 396 | −1.70 | the monsoon domain | South Tibet | 12 | [16] |
| Zhangmu | 85.98 | 27.98 | 2239 | 407 | −1.64 | the monsoon domain | South Tibet | 4 | [16] |
| Yangcun | 91.88 | 29.88 | 3500 | 522 | 0.14 | the monsoon domain | Western Sichuan-Southeast Tibet | 8 | [16] |
| Bomi | 95.77 | 29.87 | 2737 | 553 | 3.12 | the monsoon domain | Western Sichuan-Southeast Tibet | 11 | [16] |
| Lulang | 94.73 | 29.77 | 3327 | 611 | 4.41 | the monsoon domain | Western Sichuan-Southeast Tibet | 11 | [16] |
| Nuxia | 94.57 | 29.47 | 2780 | 599 | 7.18 | the monsoon domain | Western Sichuan-Southeast Tibet | 8 | [16] |
| CMA | CRU | WC | |
|---|---|---|---|
| Spatial Resolution | 30′ × 30′ | 10′ × 10′ | 10′ × 10′ |
| Period | 1981–2010 | 1961–1990 | 1970–2000 |
| Variable 1 | P, T | P, T | P, T, V |
| Reference | [37] | [38] | [39] |
| URL | http://data.cma.cn/ | https://crudata.uea.ac.uk/cru/data/hrg/ | http://worldclim.org |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Wang, S.; Zhang, M.; Argiriou, A.A.; Guo, R.; Song, Y.; Zhu, X. Isoscape of δ18O in Precipitation of the Qinghai-Tibet Plateau: Assessment and Improvement. Water 2020, 12, 3392. https://doi.org/10.3390/w12123392
Shi Y, Wang S, Zhang M, Argiriou AA, Guo R, Song Y, Zhu X. Isoscape of δ18O in Precipitation of the Qinghai-Tibet Plateau: Assessment and Improvement. Water. 2020; 12(12):3392. https://doi.org/10.3390/w12123392
Chicago/Turabian StyleShi, Yudong, Shengjie Wang, Mingjun Zhang, Athanassios A. Argiriou, Rong Guo, Yang Song, and Xiaofan Zhu. 2020. "Isoscape of δ18O in Precipitation of the Qinghai-Tibet Plateau: Assessment and Improvement" Water 12, no. 12: 3392. https://doi.org/10.3390/w12123392
APA StyleShi, Y., Wang, S., Zhang, M., Argiriou, A. A., Guo, R., Song, Y., & Zhu, X. (2020). Isoscape of δ18O in Precipitation of the Qinghai-Tibet Plateau: Assessment and Improvement. Water, 12(12), 3392. https://doi.org/10.3390/w12123392








