Analysis of Spatiotemporal Variability of Corn Yields Using Empirical Orthogonal Functions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. EOF Analysis
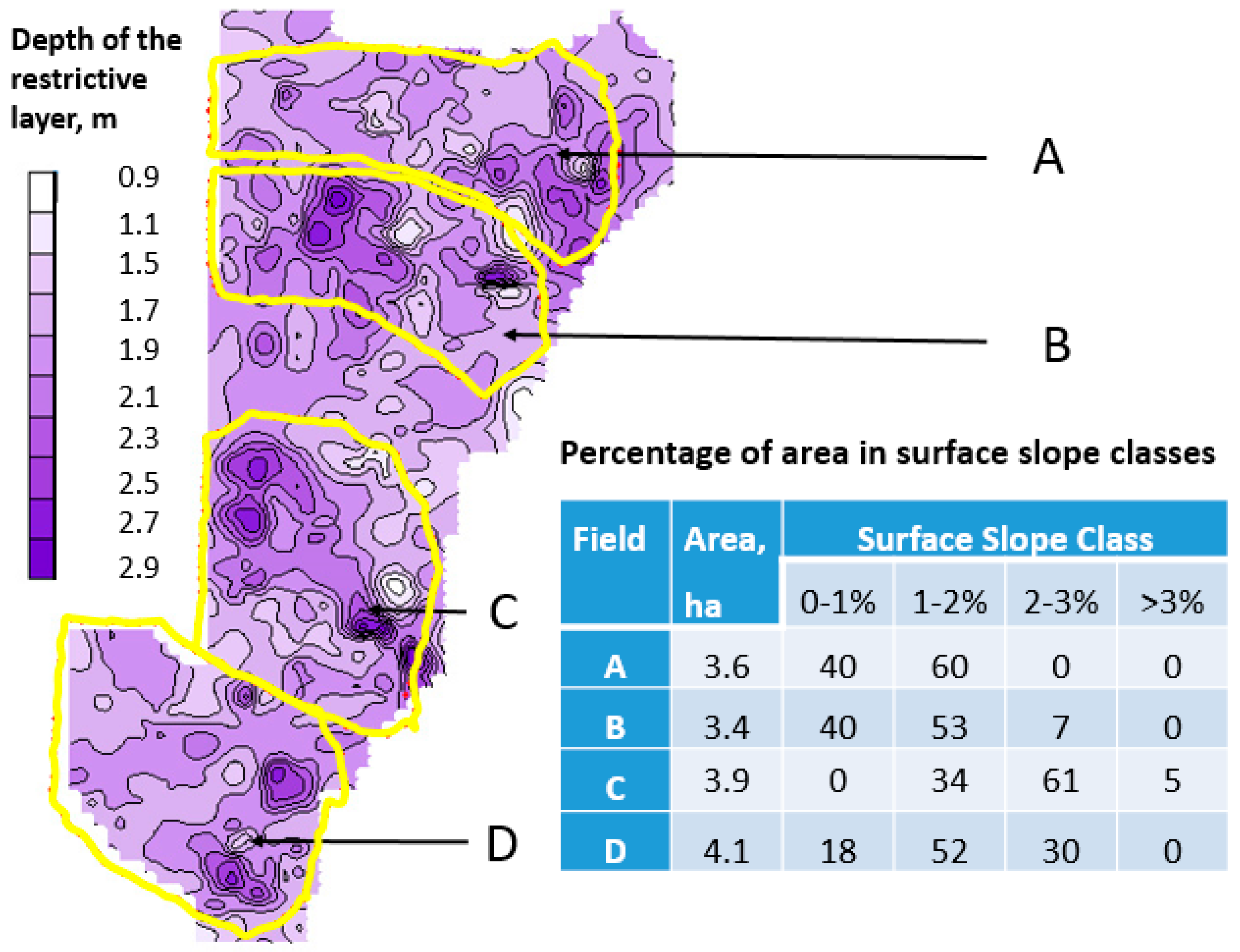
2.3. The Restrictive Layer Topography and Subsurface Flow Pathways
3. Results
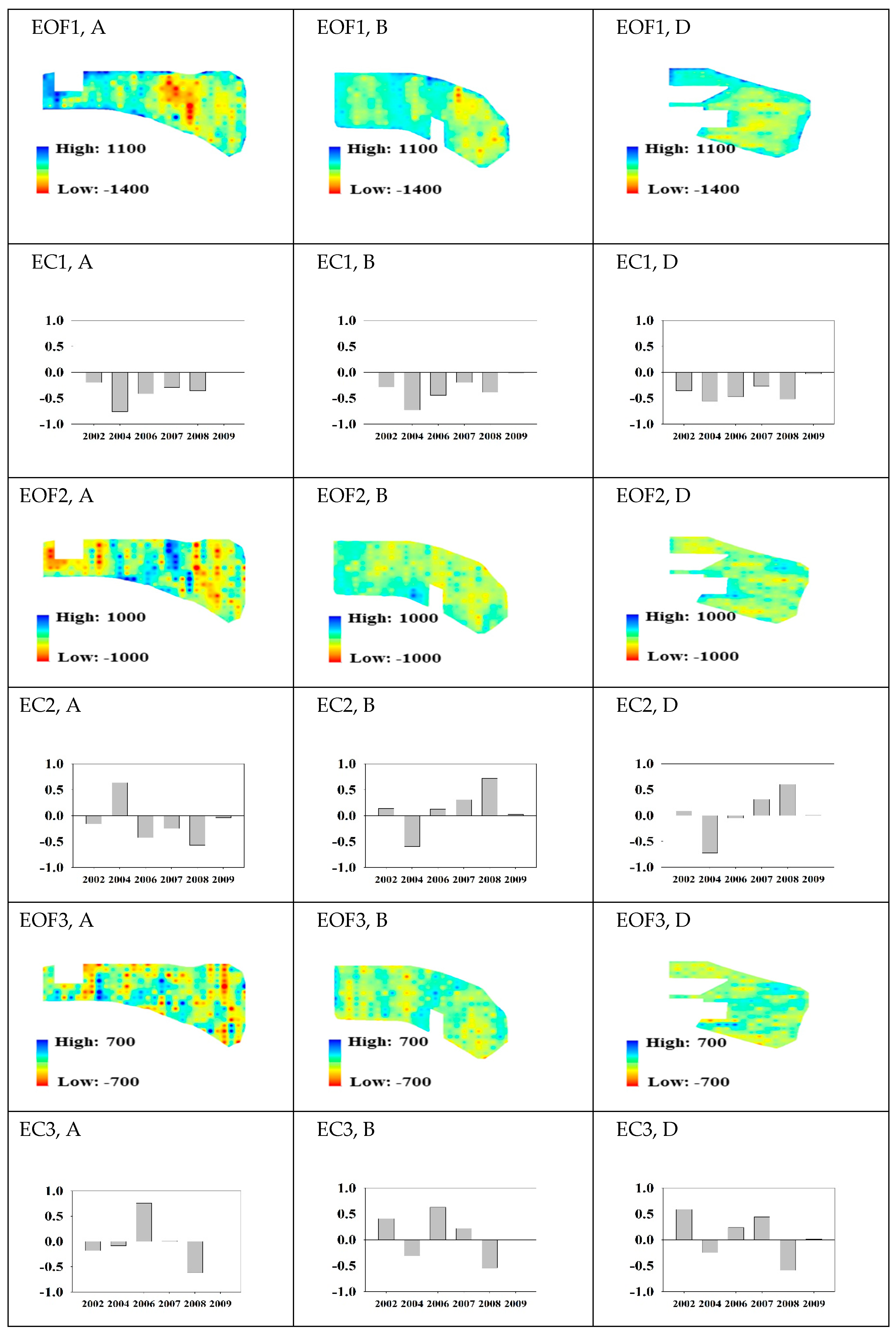
3.1. EOF Analysis
3.2. Subsurface Flow Pathways and EOFs
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Daughtry, C.S.T.; Gish, T.J.; Dulaney, W.P.; Walthall, C.L.; Kung, K.J.; McCarty, G.W.; Angier, J.T.; Buss, P. Surface and subsurface nitrate flow pathways on a field scale. Sci. World J. 2001, 1, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Nawar, S.; Corstanje, R.; Halcro, G.; Mulla, D.; Mouazen, A.M. Delineation of soil management zones for variable-rate fertilization: A review. Adv. Agron. 2017, 143, 175–245. [Google Scholar]
- Reyes, J.; Wendroth, O.; Matocha, C.; Zhu, J. Delineating Site-Specific Management Zones and Evaluating Soil Water Temporal Dynamics in a Farmer’s Field in Kentucky. Vadose Zone J. 2019, 18, 1. [Google Scholar] [CrossRef]
- Whetton, R.; Zhao, Y.; Mouazen, A.M. Quantifying individual and collective influences of soil properties on crop yield. Soil Res. 2018, 56, 19–27. [Google Scholar] [CrossRef] [Green Version]
- Kahlown, M.A.; Ashraf, M. Effect of shallow groundwater table on crop water requirements and crop yields. Agric. Water Manag. 2005, 76, 24–35. [Google Scholar] [CrossRef]
- Zipper, S.C.; Soylu, M.E.; Booth, E.G.; Loheide, S.P. Untangling the effects of shallow groundwater and soil texture as drivers of subfeld-scale yield variability. Water Resour. Res. 2015, 51, 6338–6358. [Google Scholar] [CrossRef] [Green Version]
- Yoder, R.E.; Freeland, R.S.; Ammons, J.T.; Leonard, L.L. Mapping agricultural fields with GPR and EMI to identify offsite movement of agrochemicals. J. Appl.Geophys. 2001, 47, 251–259. [Google Scholar] [CrossRef]
- Gish, T.J.; Dulaney, W.P.; Kung, K.J.; Daughtry, C.S.T.; Doolittle, J.A.; Miller, P.T. Evaluating use of ground penetrating radar for identifying subsurface flow pathways. Soil Sci. Soc. Am. J. 2002, 66, 1620–1629. [Google Scholar] [CrossRef] [Green Version]
- Tromp-van Meerveld, H.J.; McDonnell, J.J. Threshold relations in subsurface stormflow: 2. The fill and spill hypothesis. Water Resour. Res. 2006, 42, 2. [Google Scholar] [CrossRef] [Green Version]
- Vereecken, H.; Pachepsky, Y.; Simmer, C.; Rihani, J.; Kunoth, A.; Korres, W.; Shao, Y. On the role of patterns in understanding the functioning of soil-vegetation-atmosphere systems. J. Hydrol. 2016, 542, 63–86. [Google Scholar] [CrossRef]
- Navarra, A.; Simoncini, V. A Guide to Empirical Orthogonal Functions for Climate Data Analysis; Springer Science & Business Media: New York, MY, USA, 2010; pp. 39–67. [Google Scholar]
- Martinson, D.G. Quantitative Methods of Data Analysis for the Physical Sciences and Engineering; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Cantelaube, P.; Terres, J.; Doblas-Reyes, F.J. Influence of climate variability on european agriculture—Analysis of winter wheat production. Clim. Res. 2004, 27, 135–144. [Google Scholar] [CrossRef]
- Rodríguez-Puebla, C.; Ayuso, S.M.; Frías, M.D.; García-Casado, L.A. Effects of climate variation on winter cereal production in Spain. Clim. Res. 2007, 34, 223–232. [Google Scholar] [CrossRef] [Green Version]
- Chun, J.A.; Kim, S.; Lee, W.; Oh, S.M.; Lee, H. Assessment of multimodel ensemble seasonal hindcasts for satellite-based rice yield prediction. J. Agric. Meteorol. 2016, 72, 107–115. [Google Scholar] [CrossRef] [Green Version]
- Cordero, E.; Longchamps, L.; Khosla, R.; Sacco, D. Spatial management strategies for nitrogen in maize production based on soil and crop data. Sci. Total Environ. 2019, 697, 133854. [Google Scholar] [CrossRef] [PubMed]
- Gish, T.J.; Dulaney, W.P.; Daughtry, C.S.T.; Kung, K.J.S. Influence of preferential flow on surface runoff fluxes. In Proceedings of the ASAE International Symposium of Preferential Flow, Honolulu, HI, USA, 3–5 January 2001; pp. 205–209. [Google Scholar]
- Gish, T.J.; Daughtry, C.S.T.; Russ, A.; McKee, L.; Prueger, J. Improved nitrogen management utilizing ground-penetrating radar: A nine-year investigation. In Proceedings of the 4th Interagency Conference on Research in the Watersheds, Fairbanks, AK, USA, 26–30 September 2011; pp. 94–99. [Google Scholar]
- Gish, T.J.; Walthall, C.L.; Daughtry, C.S.T.; Kung, K.S. Landscape and field processes: Using soil moisture and spatial yield patterns to identify subsurface flow pathways. J. Environ. Qual. 2005, 34, 274–286. [Google Scholar] [CrossRef] [PubMed]
- Gish, T.J.; Dulaney, W.P.; Daughtry, C.S.T.; Kung, K.-J.S. Influence of Preferential Flow on Surface Runoff Fluxes. 2008. Available online: https://hrsl.ba.ars.usda.gov/ope3/poster01.htm (accessed on 13 October 2020).
- Meisinger, J.J.; Bandel, V.A.; Angel, J.S.; O’Keefe, B.E.; Reynolds, C.M. Presidedress soil nitrate test evaluation in Maryland. Soil Sci. Soc. Am. J. 1992, 56, 1527–1532. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer Series in Statistics: New York, NY, USA, 2002. [Google Scholar]
- Korres, W.; Koyama, C.N.; Fiener, P.; Schneider, K. Analysis of surface soil moisture patterns in agricultural landscapes using Empirical Orthogonal Functions. Hydrol. Earth Syst. Sci. 2010, 14, 751–764. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://github.com/marchtaylor/sinkr (accessed on 7 July 2020).
- R Core Team. R: The R Project for Statistical Computing. 2019. Available online: http://www.R-project.org/ (accessed on 7 July 2020).
- Morgan, B.J.; Daughtry, C.S.; Russ, A.L.; Dulaney, W.P.; Gish, T.J.; Pachepsky, Y.A. Effect of shallow subsurface flow pathway networks on corn yield spatial variation under different weather and nutrient management. Int. Agrophys. 2019, 33, 271–276. [Google Scholar] [CrossRef]
- Yanan, T.; Emteryd, O.; Dianqing, L.; Grip, H. Effect of organic manure and chemical fertilizer on nitrogen uptake and nitrate leaching in a Eum-orthic anthrosols profile. Nutr. Cycl. AgroecoSyst. 1997, 48, 225–229. [Google Scholar] [CrossRef]
- Miller, J.J.; Beasley, B.W.; Hazendonk, P.; Drury, C.F.; Chanasyk, D.S. Influence of long-term application of feedlot manure amendments on water repellency of a clay loam soil. J. Environ. Qual. 2017, 46, 667–675. [Google Scholar] [CrossRef]
- Voelkner, A.; Diercks, C.; Horn, R. Compared impact of compost and digestate on priming effect and hydrophobicity of soils depending on textural composition. Die Bodenkult. J. Land Manag. Food Environ. 2019, 70, 47–57. [Google Scholar] [CrossRef] [Green Version]
- Wanniarachchi, D.; Cheema, M.; Thomas, R.; Kavanagh, V.; Galagedara, L. Impact of Soil Amendments on the Hydraulic Conductivity of Boreal Agricultural Podzols. Agriculture 2019, 9, 133. [Google Scholar] [CrossRef] [Green Version]
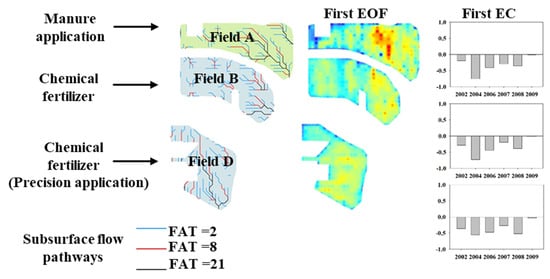
 field A,
field A,  field B,
field B,  field D.
field D.
 field A,
field A,  field B,
field B, 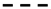 field D.
field D.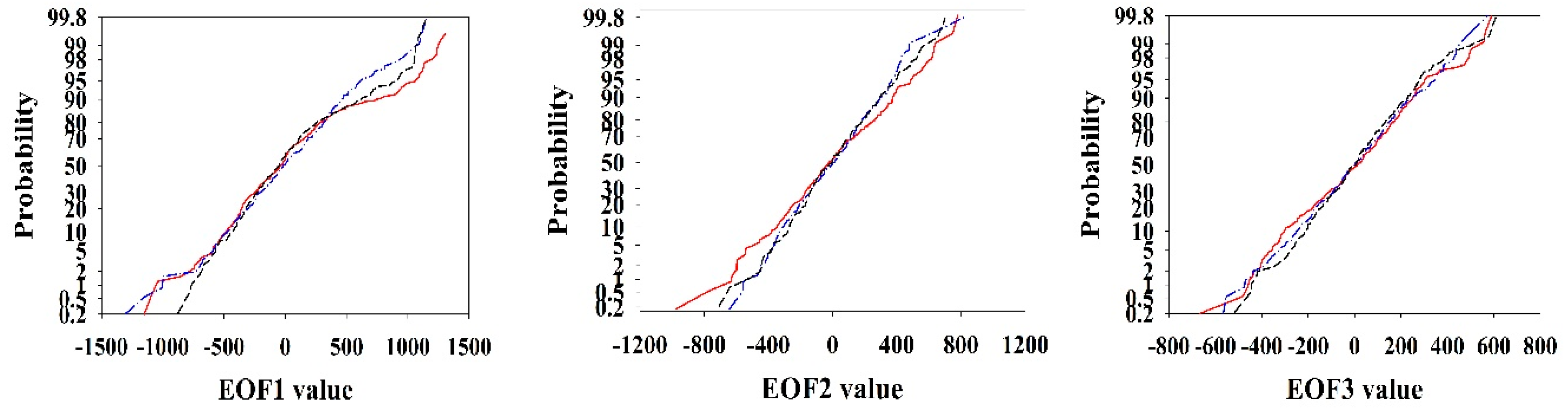
 , 5–10 m
, 5–10 m  , and 10–15 m
, and 10–15 m  around the potential subsurface flow pathways derived with three flow accumulation threshold (FAT) values at fields A, B, and D.
around the potential subsurface flow pathways derived with three flow accumulation threshold (FAT) values at fields A, B, and D.
 , 5–10 m
, 5–10 m  , and 10–15 m
, and 10–15 m  around the potential subsurface flow pathways derived with three flow accumulation threshold (FAT) values at fields A, B, and D.
around the potential subsurface flow pathways derived with three flow accumulation threshold (FAT) values at fields A, B, and D.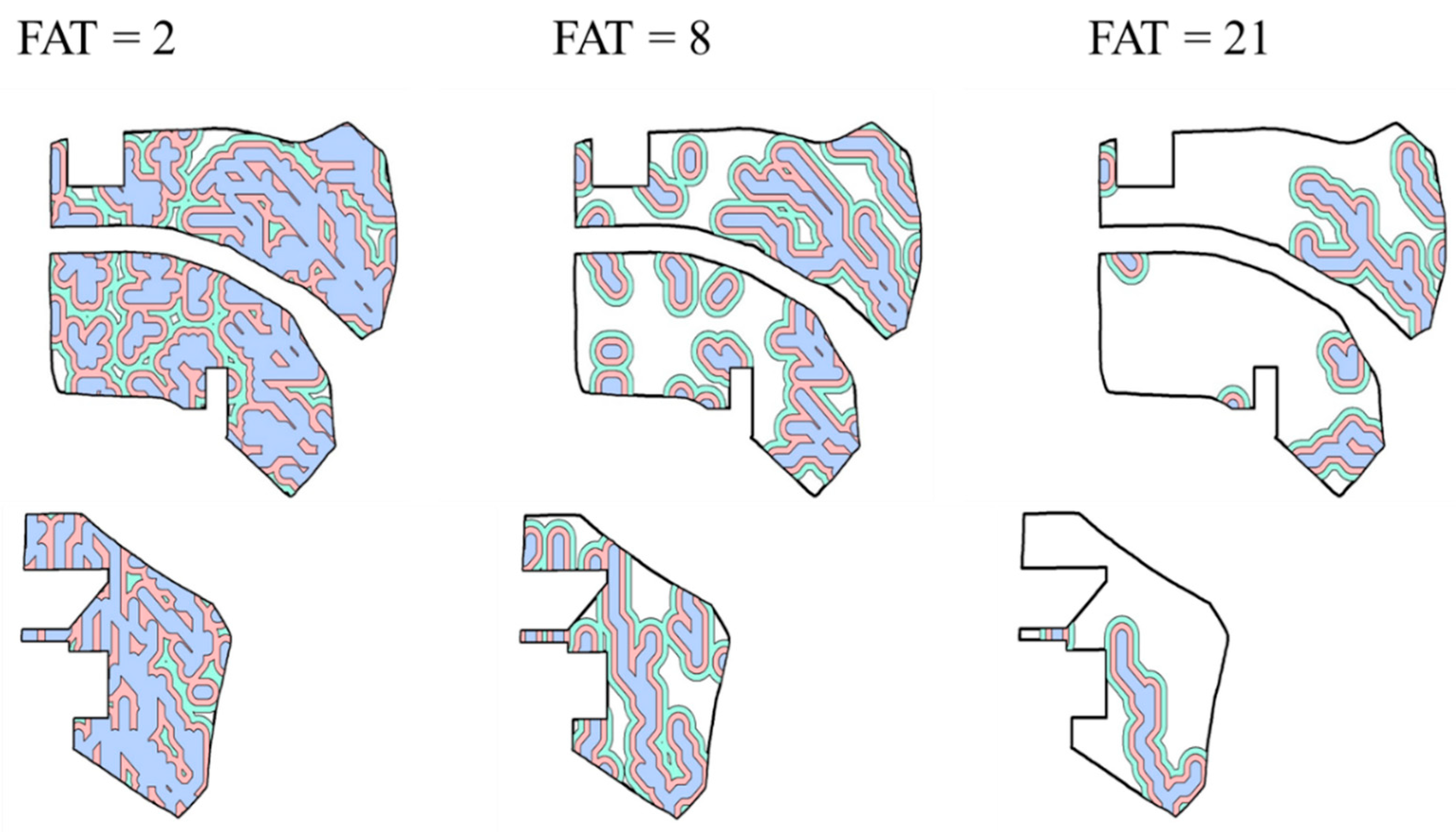
 0 to 5 m buffer,
0 to 5 m buffer,  5 to 10 m buffer,
5 to 10 m buffer,  10 to 15 m buffer.
10 to 15 m buffer.
 0 to 5 m buffer,
0 to 5 m buffer,  5 to 10 m buffer,
5 to 10 m buffer,  10 to 15 m buffer.
10 to 15 m buffer.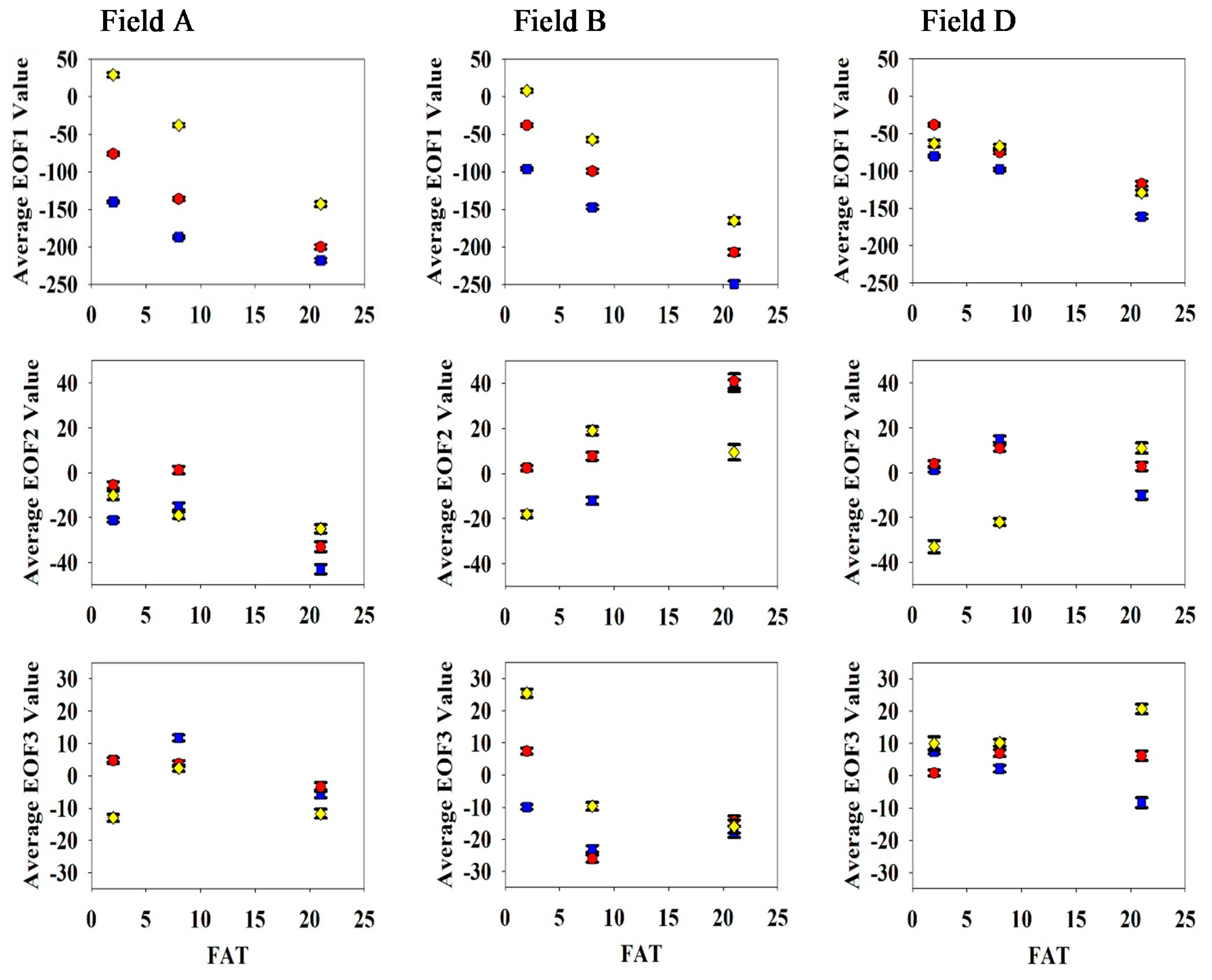
| Year | Planting Date | Total N Applied, kg N ha−1 | Cumulative Precipitation, mm | Corn Grain Yield, kg ha−1 | ||||
|---|---|---|---|---|---|---|---|---|
| Field A | Field B | Field D | Field A | Field B | Field D | |||
| 2002 | 17 April | 73 | 103 | 80 | 275 | 4796 | 5259 | 6153 |
| 2004 | 18 May | 154 | 172 | 109 | 402 | 7775 | 7508 | 6346 |
| 2006 | 29 April | 161 | 164 | 121 | 388 | 8783 | 7710 | 7474 |
| 2007 | 5 May | 161 | 164 | 121 | 188 | 4578 | 3428 | 3571 |
| 2008 | 28 June | 161 | 164 | 121 | 287 | 8571 | 7763 | 7359 |
| 2009 | 4 July | 117 | 164 | 121 | 382 | 6166 | 6013 | 6105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Daughtry, C.; Russ, A.; Pedrera-Parrilla, A.; Pachepsky, Y. Analysis of Spatiotemporal Variability of Corn Yields Using Empirical Orthogonal Functions. Water 2020, 12, 3339. https://doi.org/10.3390/w12123339
Kim S, Daughtry C, Russ A, Pedrera-Parrilla A, Pachepsky Y. Analysis of Spatiotemporal Variability of Corn Yields Using Empirical Orthogonal Functions. Water. 2020; 12(12):3339. https://doi.org/10.3390/w12123339
Chicago/Turabian StyleKim, Seongyun, Craig Daughtry, Andrew Russ, Aura Pedrera-Parrilla, and Yakov Pachepsky. 2020. "Analysis of Spatiotemporal Variability of Corn Yields Using Empirical Orthogonal Functions" Water 12, no. 12: 3339. https://doi.org/10.3390/w12123339
APA StyleKim, S., Daughtry, C., Russ, A., Pedrera-Parrilla, A., & Pachepsky, Y. (2020). Analysis of Spatiotemporal Variability of Corn Yields Using Empirical Orthogonal Functions. Water, 12(12), 3339. https://doi.org/10.3390/w12123339