1. Introduction
Groundwater has been one of the most important natural resources, which have many dimensions for being evaluated in society such as residential, agricultural, and industrial water supply [
1]. In recent decades, a large quantity of research has been developed for studying the groundwater and surface water interaction [
2,
3,
4].
Modelling groundwater has significant challenges, and it involves a large number of variables in its analysis such as clogging, design, optimisation, feasibility, water quality, geotechnical processes, groundwater management, recovery efficiency, saltwater intrusion, and residence time [
5]. This research is focused on one area of the groundwater management that is the interaction between surface water and groundwater.
MODFLOW (United States Geological Survey, Reston, VA, USA) is a hydrologic model that simulates and makes predictions of groundwater conditions and groundwater surface-water interactions [
6]. During the development of MODFLOW, many packages have been built to satisfy and model some scenarios. The principal challenge of modelling the interaction with the river–aquifer or the flow in the unsaturated zone would be the higher numerical instability, the high costs of modelling, and the computational efficiency. Moreover, it is crucial to understand that the groundwater velocity beneath and in the vicinity of a riverbed is essential when applying the model to estimate the river-aquifer interaction accurately [
7].
There has been an interesting amount of research studies developed during the last years related to improving the estimation and knowledge of the fluxes between the river and the aquifer. Some of these methodologies are described below.
Zeng [
8] suggests a new HYDRUS package for MODFLOW, which is a quasi-3D method that is simulating the regional unsaturated–saturated flow, reducing the complexity of the problem. His latest package is an improvement from previous HYDRUS packages [
9]. The approximation consists of a switching strategy applied in the Richard equation [
10]. According to Zeng [
8], with this methodology, the cost and the time of simulation is reduced. On the one hand, the package proposed by Zeng [
8] is efficient, and it satisfies many of the proposed challenges in the unsaturated flow produces by the interaction of the surface water and groundwater. On the other, it would have some limitations when it is applied at the most significant scale. Another package and methodology using MODFLOW were proposed to model the interaction between surface water and groundwater, which, according to the research, could be applied regionally. This methodology is proposed by Taie [
11], in a study case in Gharehsoo River Basin (GRB) in Iran. The method includes the use of the Soil and Water Assessment Tool (SWAT) as the surface hydrological model, which works in conjunction with the Modular Three-Dimensional Finite-Difference Groundwater Flow (MODFLOW-NWT). One advantage of the Newton–Raphson technique is that it can resolve unconfined flows problems in MODFLOW [
11]. Taie and Koch argue that previous researchers have focused only on the exchange fluxes between both systems in a permanent flow regime. At the same time, they propose to apply this in a seasonal and intermittent river system. Their results were interesting, and it demonstrates that the combination of a SWAT-MODFLOW-NWT model gives more accurate results than the MODFLOW-NWT by itself. However, in contrast with the Zeng [
8], the spatial and temporal resolution applied to the models in this research is higher.
In order to show new strategies to optimise the computational cost, Foglia [
12] offers an exciting procedure in a case study located in Scott Valley in California. This research presents an example of environmental goals at the Scott River, which must keep a specific ecologic flow because it is an important salmon spawning habitat. So, it was necessary to make a model for estimating the fluxes between the surface water and the groundwater. This study analysed two packages of MODFLOW to represent the river. The first package is the MODFLOW-RIV, which uses a uniform, constant stream water depth. It would not be able to capture in detail the spatial and temporal changes in streamflow dynamics; thus, the cost of producing and running it is lower.
In contrast, the second package used was the MODFLOW-SFR. It is a Streamflow Routing Package; in other words, it is a package that can reproduce the dynamic behaviour in the river caused by seasonal changes (summer–winter). Nevertheless, this model requires a high economic and computational cost.
The research presented by Foglia [
12] showed that there would not be a big difference in the boundary balance. However, it showed that the “exchange of water between surface water and groundwater was about three times larger in MODFLOW-RIV than MODFLOW-SFR”. The interesting aspect of the Foglia [
12] approach is that he showed MODFLOW packages included by default in MODFLOW for the development of the integrated model of surface water and groundwater and not external packages in contrast to the previous authors, who integrated external tools to MODFLOW.
According to Cardenas [
13], since the mid-1990s, necessary studies have been carried out about the hyporheic flux. However, one of the first completed investigations of hyporheic exchange using the MODFLOW code was by Storey [
14]. The research looked for a multiresolution groundwater flow model. Nevertheless, the water exchange in the hyporheic zone is still treated insufficiently accurately [
15]. Other studies that involved the roles of exchange flow in the hyporheic zone regarding nutrient transport, organic matter, and biogeochemical processing in rivers have been carried out [
16]. In the same line, other researchers paired a MODFLOW model with MT3D (United States Geological Survey, Reston, VA, USA) to simulate hyporheic zones transport around debris dams and meander along a semi-arid stream [
12].
Groundwater modelling has evolved quickly in the last years, moving from early two-dimensional steady-state homogeneous or layer cake models to dynamic three-dimensional models capable of simulating highly heterogeneous formations and complex phenomena [
17]. This evolution has required an improvement in computational technology and the quantity and quality of data [
18]. It is for that reason that our groundwater modelling will use MODFLOW [
19] through FloPy. The FloPy package consists of a set of Python scripts to run MODFLOW, MT3D, SEAWAT (United States Geological Survey, Reston, VA, USA), and other MODFLOW-related groundwater programs [
20]. On one hand, this tool has the complexity in that it does not have a graphic interface, and all the pre- and post-processing must be done by coding. Implementation of the numeric approach through algorithms in Python will make the model more accessible.
Many of the models for groundwater modelling, such as MODFLOW, use the finite-difference method to solve the groundwater flow equation. Depending on the problem, it can give a very accurate approach. However, there are some models that require a fine-grid discretisation to obtain a better resolution and to get the correct answer to the problem. Unfortunately, this process is typically in line with a high computational cost [
21].
This paper uses the Biebrza River to develop the research about the river and aquifer interaction. During the last years, there has been an increasing interest in the study in the identification of water exchange areas in the hyporheic zone for ecological purposes [
16]. The Biebrza River is located in the north-eastern corner of Poland, in the Podlaskie Voivodship, around 230 km northeast of Warsaw [
22]. This river shows many particular aspects that make it an ideal course of water to analyse.
For instance, the Biebrza River is one of the few natural systems located in Europe that has had little intervention [
23]. It is one of the reasons that this area is of high importance, and it is unique. This catchment has the presence of shallow groundwater tables, which is required for the continuance of groundwater-dependent wetlands and their environment [
22]. Often, the vegetation depends on the quality, quantity, and the process of river discharge and groundwater–surface water interaction [
22,
24].
The interaction between the stream and the aquifer is generally assessed by assuming vertical water seepage into the streambed, causing water flux. The current work will evaluate the interaction between the river and aquifer in a condition where the river is very narrow, and there is an essential component that most of the model does not take in consideration: the bank flux. This document will present a new analytical model—the Analytical Hyporheic Flux model (AHF). The model allows estimating the seepage at river banks through a riverbed using a simplified geometry [
25].
The AHF model is based in the hyporheic zone, which is a region where surface and ground waters mix within the bed and banks of a river [
16]. The hyporheic zone exists as an interface between surface and ground waters, in near-stream sediments. The hyporheic zone could act in centimeters to meters [
26].
Although the flux though the hyporheic zone conceptually is quite complex to estimate, the interactions can be simulated using numerical groundwater flow models. The reason is that the hyporheic flow is nested within the local groundwater flow system. Then, an arrangement on boundary conditions within the model can be implemented [
26].
The AHF model allows calculating the amount of water exchange in the hyporheic zone, including both vertical water seepage through the streambed and seepage through riverbanks. The analytical model assumes a simplified rectangular geometry of the river bed cross-section [
25].
The methodology implemented in this research allows implementing the lateral contribution on the banks of a river through the AHF model, which is applied in a real case using a groundwater modelling tool in three dimensions as MODFLOW. The implementation of the AHF model is done through the recharge package, which is a Neumann boundary condition type. Then, in order to represent it as a Cauchy boundary condition type for a river, we used an iterative algorithm that allows defining the AHF fluxes through seepage in MODFLOW.
This research is a contribution to a better understanding of the fluxes between the river and the aquifer. Moreover, it presents a strategy of modelling applying FloPy for the implementation of an analytical scheme. This document addresses its advantages, disadvantages, and limitations.
2. Material and Methods
2.1. Study Area
The Biebrza River is the second-longest effluent of the Narew River, and it is located in the Biebrza National Park (Europe, Poland). The following area is also famous and meaningful for being the most significant wetland territory in Central and Western Europe. The Biebrza river has a basin area of 7092 km
2 (7067 km
2) (53°13′02″ N 22°25′52″ E) and a length of 164 km [
27]. The study area is located in the upper part of the Biebrza river Catchment.
This location has interesting characteristics that make it suitable for current research, such as a natural lowland river, low dynamic river due to the low flow velocities, undisturbed river bed due to the ban on mowing and dredging since 1992, diversity of riverine and riparian ecosystems, and several research activities conducted in the area aiming at ecohydrology.
The Biebrza Valley belongs to the Suwalsko–Podlaskie and Podlaskie hydrogeological region. The river in the upper basin tends to drain at the subsurface level [
28]. “The valley of the Biebrza River is formed by eroded channel cutting off loamy–sandy sediments and filled to a depth of 30 to 40 m with sandy formations of moderate permeability” [
29].
The catchment presents a mean discharge in the Lower Basin almost seven times the discharge of the Upper Basin (respectively, 30.6 m
3 s
–1 and 4.61 m
3 s
–1) [
30]. It is quite probable that the peatland flow does not have direct contact with mineral/alluvial aquifer. In hydrogeological terms, the riverbed is muddy and has an uncompacted bottom. In addition, there is the presence of Reed peat on the banks along the whole 6 km stretch of the meandering river [
31]. It is interesting to notice that during the last glaciation, “the Valley served as an ice-marginal valley to glacial waters, whereas after climate warming, the peat formation processes took place there” [
28]. The study area is dominated principally by arable land and meadow and in minor quantity covered by forest. Peat is the dominant type of bog. The Upper Biebrza is constructed with peat deposits with a thickness of 3–6 m. The basin is distinguished by extensive sand dunes surrounded by peat bogs, which formed as a result of Aeolian processes. Large swampy areas are cover by birches, spruce, and a large proportion of boreal species. The study area has small urban areas represented basically in small villages and small cottages and communities dedicated to agriculture.
The climate has sub-boreal elements. It is influenced by local conditions such as landform and vast wetlands. It is characterised by long winters, a short prevernal season, and a very short growing season [
22]. The Biebrza River is one of the few natural systems located in Europe that has had little intervention [
23]. The place is the habitat of valuable river marshes and peatlands “including highly threatened plant and animal species” [
22]. The maximum precipitation registered in the zone during the interest period was 24.3 mm day
−1, with an average of 0.97 mm day
−1. Between 6 September 2018 and 25 June 2019, there are 293 days, of which 106 days had precipitation [
32].
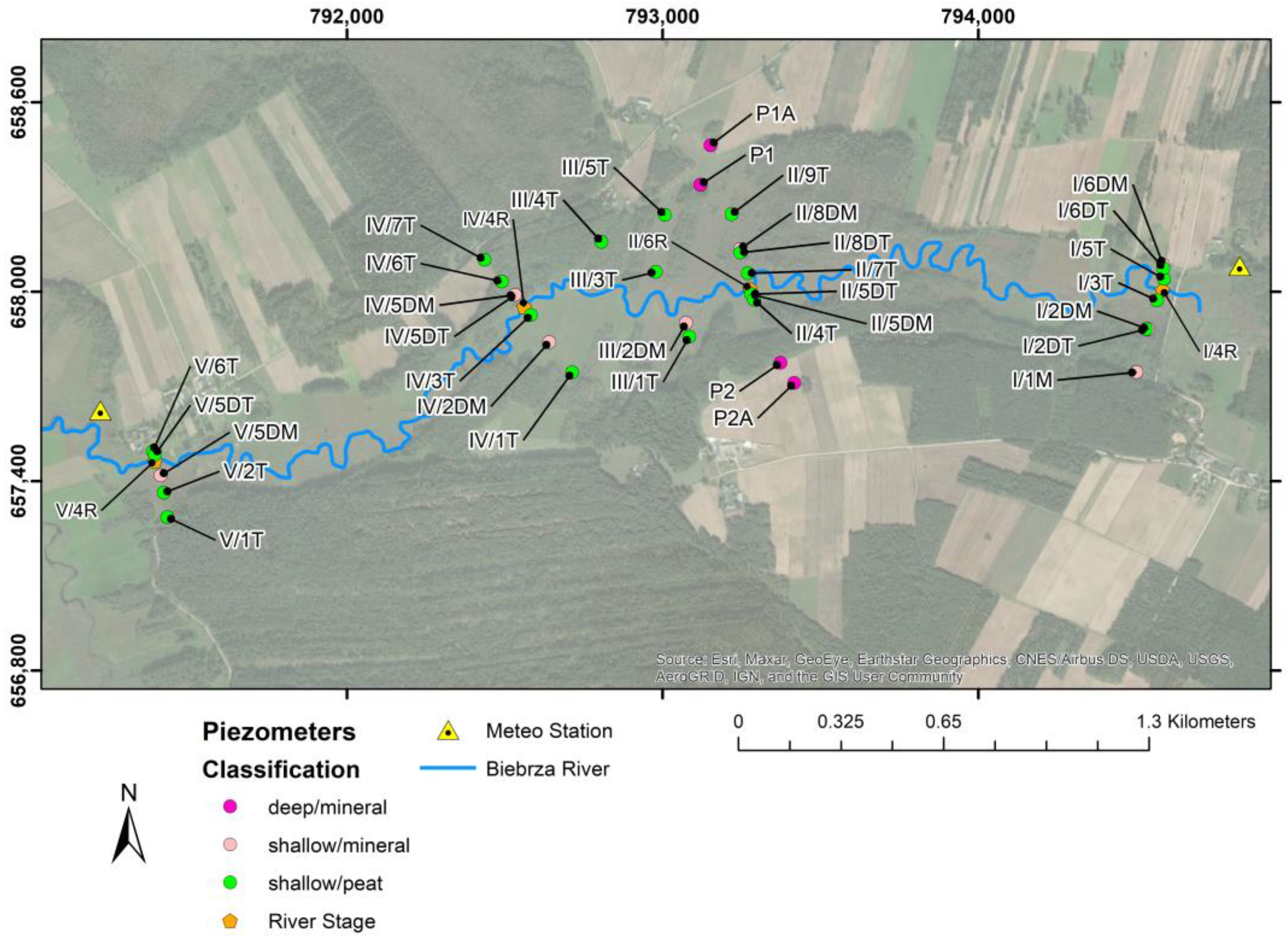
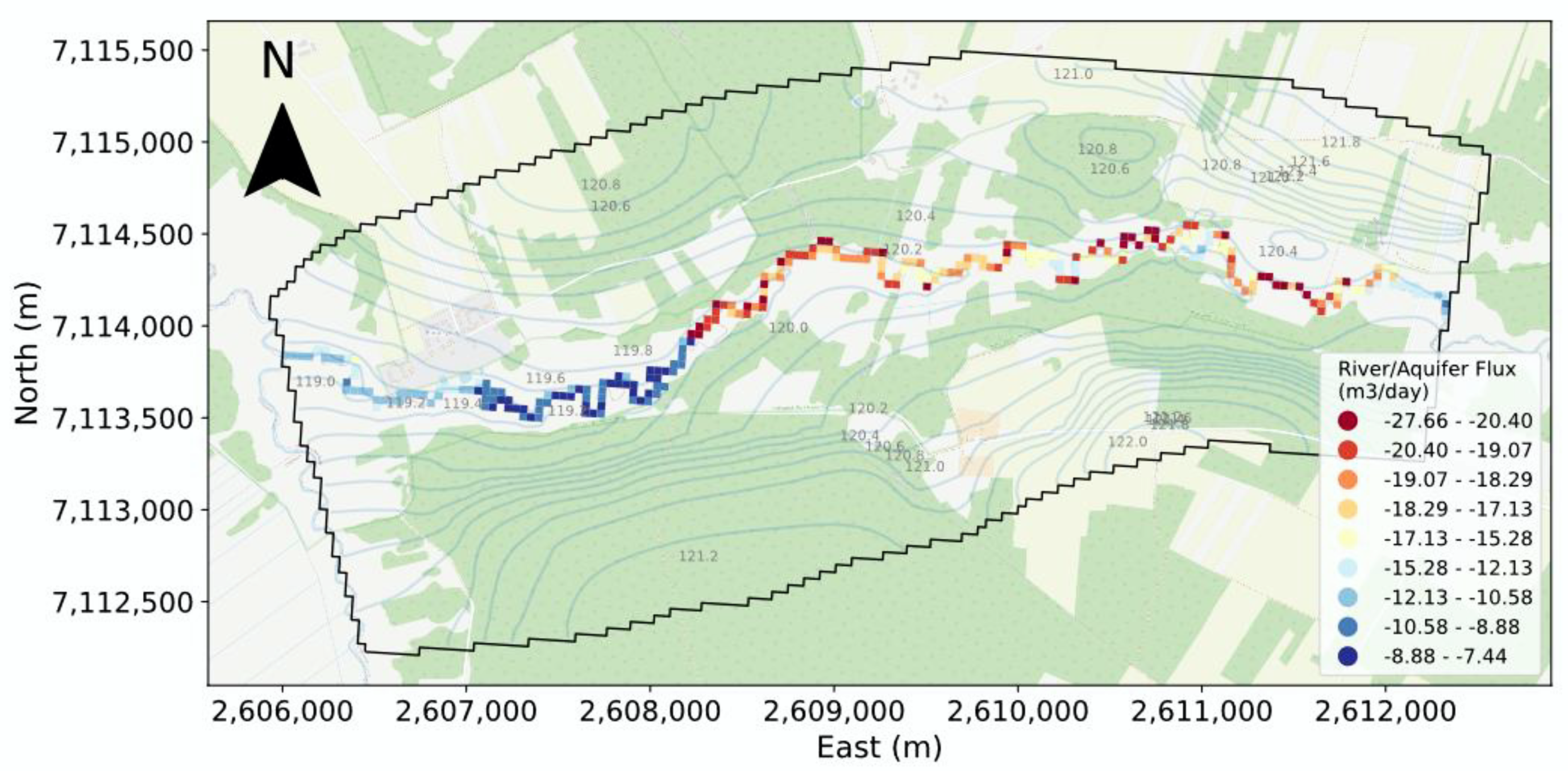
The monitoring network takes into consideration 35 piezometers (22 shallows/peat, 9 shallows/mineral, and 4 deep/mineral) (
Figure 1). In addition, there are 2 barologgers for the atmospheric pressure correction and two meteorology stations. The measurements are done every 3 h for groundwater and river water level (stage) and every 0.5 h for meteorology station. The water river levels are measured through four piezometers located along the river.
2.2. AHF Model
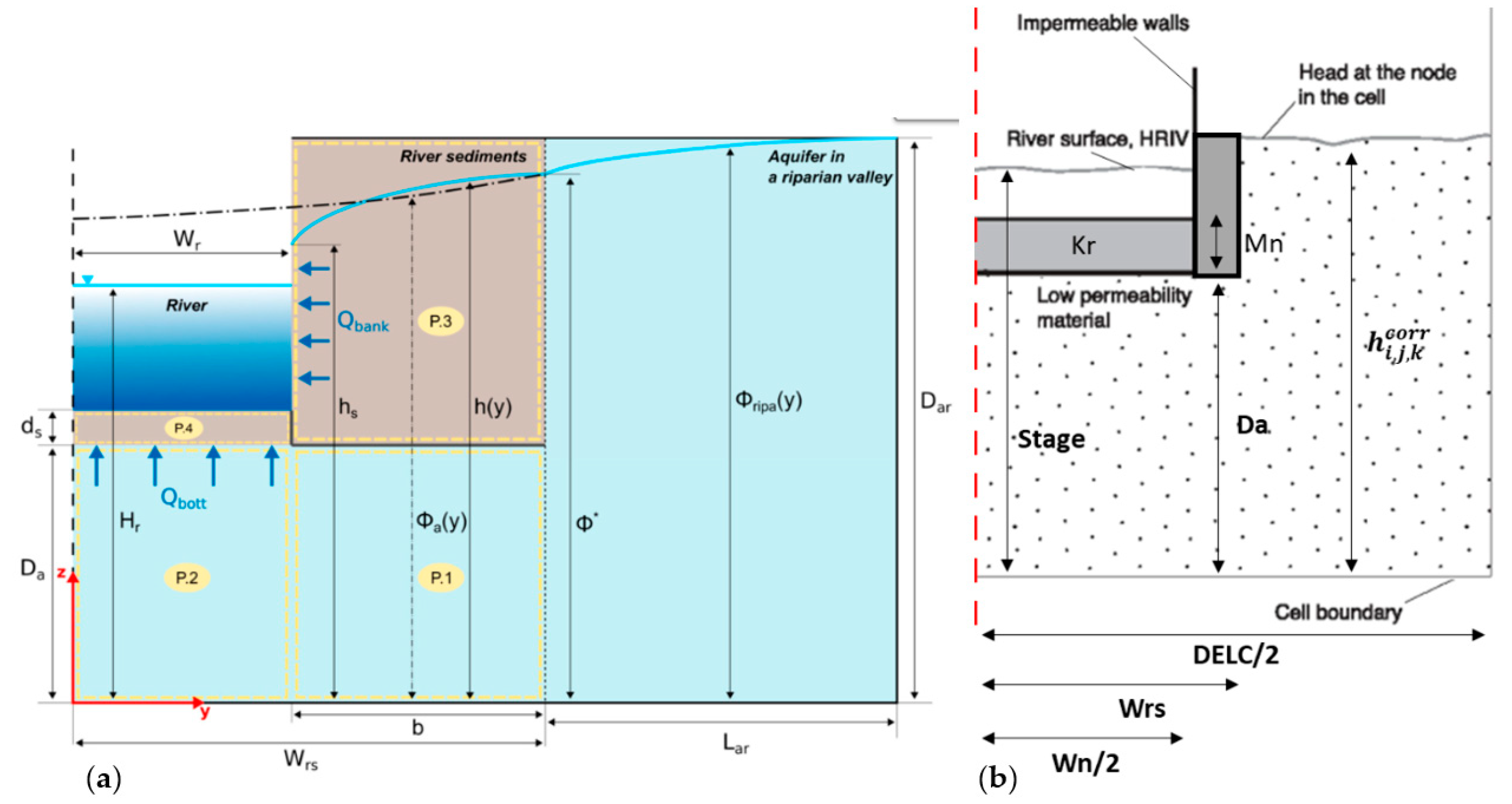
The approach suggested by Nawalany et al. [
25] adds a lateral term in the interaction between river and aquifer called the recharge/discharge bank.
Figure 2 shows the adaptation of the equation of Nawalany et al. [
25] to the MODFLOW scheme.
This approach implemented in MODFLOW takes into consideration the river as a seepage boundary condition with the package RECHARGE. The variable is the height of the water table defined in MODFLOW cell location (i,j). This is represented in the AHF scheme as . The subindexes i and j give the spatial position of the cell, and k is the iteration number. The piezometric head in the aquifer next to the riverbed in the MODFLOW scheme MODFLOW cell location (i,j) iteration k is represented in the AHF model as .
The flow in subdomain P.1 is confined and described by the Laplace equation:
for y ∈ [Wr, Wrs], z ∈ [0, Da] where
is the hydraulic conductivity of the aquifer under river sediments, i.e., in P.1 and P.2 (LT
−1).
is the thickness of the aquifer beneath river sediments cell location (
i,
j) (L),
is the half-width of the river (L), and
is the half-width of river sediments (L). Applying the assumptions of Nawalany et al. [
25] in this domain, it is possible to establish the relationships described in Equations (1) and (2), where
.
On the other side, the flow in subdomain P.2, i.e., in the part of the aquifer under the river bottom sediments of P.4, is also described by the Laplace equation for y ∈ [0, Wr], z ∈ [0, Da]. Nawalany et al. [
25] determined Equations (3) and (4).
With this set of equations, Nawalany et al. [
25,
33] estimated the recharge/discharge on the bottom and the bank of the river where
is the length of the reach.
Additionally, from Darcy law, it is possible to estimate the flow from P2 to P4 (Equations (3) and (5))
, where
is the thickness of river sediments under the river bottom (L) and
is the hydraulic conductivity of river sediments (LT
−1). This relationship allows estimating an expression for
.
To resolve the equation system (Equations (6), (7), and (9)), and then to estimate the
, we applied the Newton iterative method as suggested by Nawalany et al. [
25], where there is N+1 values of
, which is calculated using the Newton iteration method
.
is the number indicating the finite approximation for an infinite series (it can be increased to assure a divergence of the approximation). Then, considering
, the forward solution applying the Newton method is represented by
where
.
Finally, equilibrating Equation (1) with Equations (2) and (3) with Equation (4) determines the equation system that allows obtaining
and
and calculating the bottom flux.
The notation meaning of the equation system is shown below.
2.3. Implementation of Biebrza River Groundwater Model Using River Package (RIV)
The first step has the objective of implementing a groundwater model capable of representing the behaviour of the Biebrza River groundwater system through the utilisation of the river package (RIV). The numerical model is designed to operate in the transient mode and determine vertical groundwater–surface water exchange in the hyporheic zone. The work suggests a conceptual approach to outline the process of the groundwater–surface exchange, under the weight of the hydrogeological characteristics, location of piezometers, and terrain of the Valley.
The groundwater model is performed in several stages: fieldwork, information gathering, set up of conceptual and numerical models, and calibration. The model is constructed for the part of the Biebrza River between Rogożyn and Rogożynek villages. This model is described in detail by Diaz [
32].
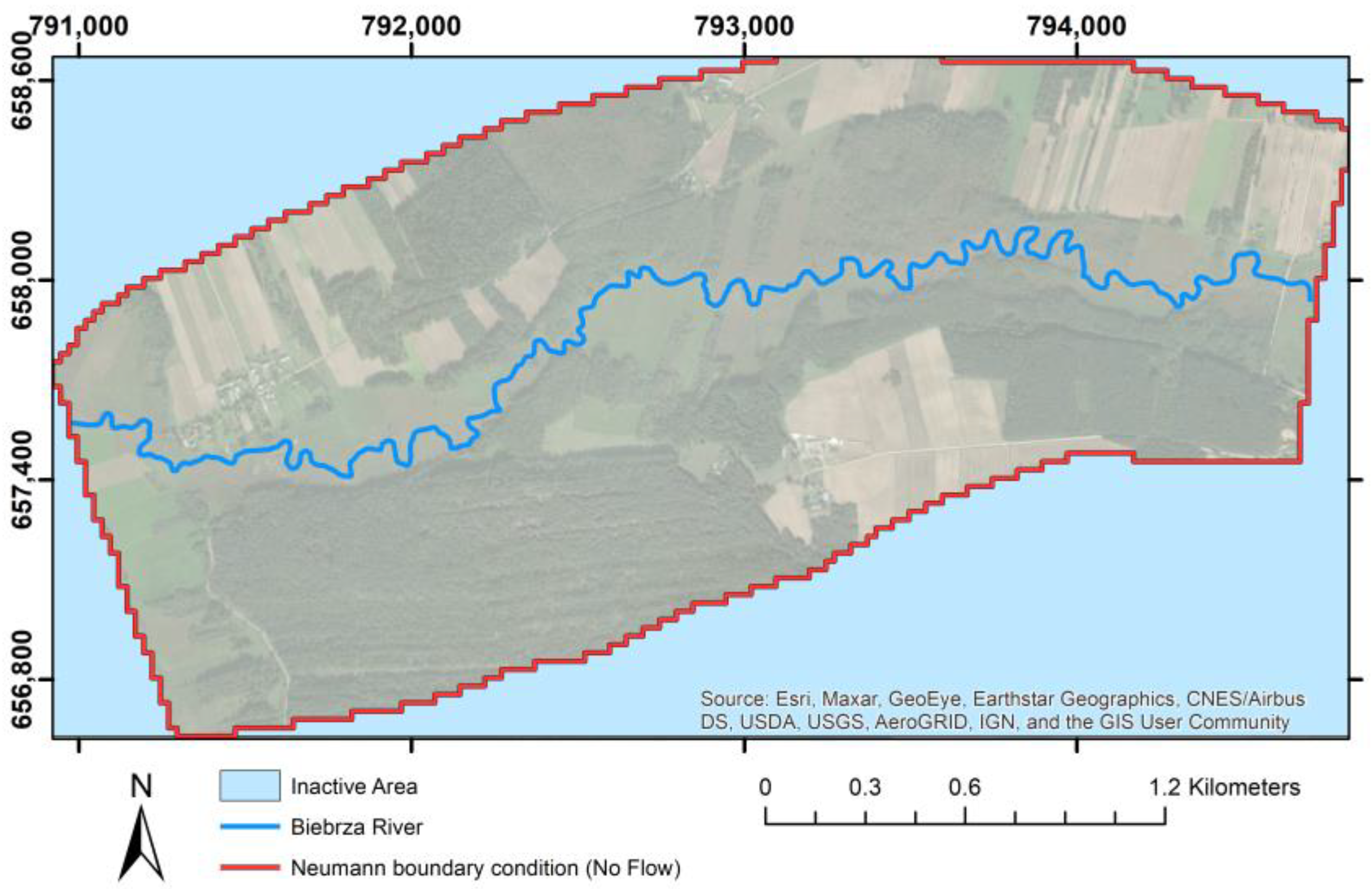
A Neumann boundary condition is considered around the model, which is assumed as no flow. After analysing the conceptual model, it was found that the water to the model is led by subsurface runoff from the upland. The amount of this runoff was a parameter calibrated in the model and was expressed by appropriately adjusting the amount of recharge. During the model sensitivity analysis, no significant impact of the assumption on the model boundary of the no-flow boundary condition on the behavior of the river was found. In addition, as the river is interacting directly with the aquifer along the modelling area, it is feasible to assume that flows coming from the east and west in a plane perpendicular to the river are depreciable. Therefore, the boundary of no flow is defined (condition type 2) (
Figure 3).
The recharge over the model is distributed in zones according to the friction of precipitation. These zones are characterised by the topography, slope, soil type, and land use. Additionally, the recharge calculated is a rate between 0.5 and 0.7 of the precipitation, depending on the zone.
The numerical model also has an evapotranspiration component principally in the peat soil of the first layer. The precipitation and evaporation data are taken with a daily frequency from the meteorological stations located in the study area as input for the transient model.
A Robin or Cauchy boundary condition is typically applied along the river on the groundwater flow domain. It is a function that represents a linear combination of the normal component of specific discharge and the piezometric head. Therefore, the Biebrza River is defined as condition type 3 (
Figure 3).
The numerical model was built in MODFLOW 2005 in finite difference, with a regular grid of 25 per 25 m. It runs in transient flow considering 293 stress periods with a time step of 1 day. The full simulations are from September 6th, 2018 to September 25th, 2019. The model is calibrated manually for this period.
The model takes into consideration two layers. The first layer represents the peat soil mainly, while the second layer is characterised principally by the sand. Both materials are representative of the physical composition of the study zone.
2.4. Implementation of AHF Model Using Seepage Package in Biebrza River Model
The integration of the AHF model with the Biebrza River model built in MODFLOW is done through the seepage package under an iterative methodology implemented in Python through FloPy.
FloPy is a tool that allows creating the MODFLOW packages in a Python environment. The fact that FloPy is developed in Python helps the implementation of the analytical AHF model.
The algorithm implemented has the objective of finding a stable solution of the water table on the river cell after a certain number of iterations. The algorithm was developed in detail by Diaz [
32], and it is summarised in four stages described below.
It is essential to understand that the AHF model is implemented through the recharge package in FloPy, which is a Neumann boundary condition. However, these results are expected, as the river package (RIV) must be a Cauchy boundary condition. Then, the iterative process of the AHF model allows generating the Neumann boundary condition through the recharge package.
The algorithm has the objective of establishing from a known river height the flux rate value , estimating iteratively the river cells height aquifer , which must satisfy the convergency in the algorithm.
Stage 1: The MODFLOW model was created with a Seepage Package instead of the river package. This package replaces the definition of the river on the model. The model finds a solution for the iteration 0 considering as an initial head H0; after the first iteration “m”, the initial head changes in each time step, and it is the solution of the previous time step. During this stage, the flux over the river is calculated through the AHF model shown in Equation (19).
The recharge package, as is shown in Equation (18), calculates the seepage flux applied to the model at horizontal cell location (
i,
j) as a fluid volume per unit time (L
3T
−1) where
is the rate flux applicable to the map area
of the cell (LT
−1). Then, the AHF model fluxes will be implemented through the
as a seepage. It is shown in Equation (19).
Stage 2: This stage compares the result obtained with the previous one if it is lower than an epsilon value, while the model breaks and saves the solution as an initial condition for the next time step. Contrary, if the difference value is higher, then the amount of the recharge flux will be recalculated, adding the bank and bottom flux. Then, the iterative algorithm starts.
Stage 3: This stage takes the corrected value of and it replaces the averaged piezometric head in the riparian aquifer along the river. The iterative process starts, and the model run “k” times until it obtains where “k” represents the current state of the model, and “k−1” means the value of the previous state (during the same stress period). It is important to mention that in each “k” iteration, the model does a correction of over the river, but it does not over the initial condition (the initial state only changes in the “m” iterations, which represents the iteration over each time step).
Stage 4: This stage involves the unsteady state principally—in this case, after each iteration “k” when the convergence of the AHF model is done. The results of the water head are recorded, and these are used as an initial condition during the next time step “m”. This process is repeated for all of the stress periods of the model.
3. Results
The implementation of the algorithm shows consistent results. However, this methodology has some restrictions produced by instability in the first iterations. These instabilities produce dry and flood cells breaking the algorithm for the small thickness of the layer and low hydraulic conductivities. This methodology has some limitations for being used in a complex model; for one, the problem of dry and wet cells is corrected. If the thickness of the riverbed increases, the results have better convergence with respect to the dry cells.
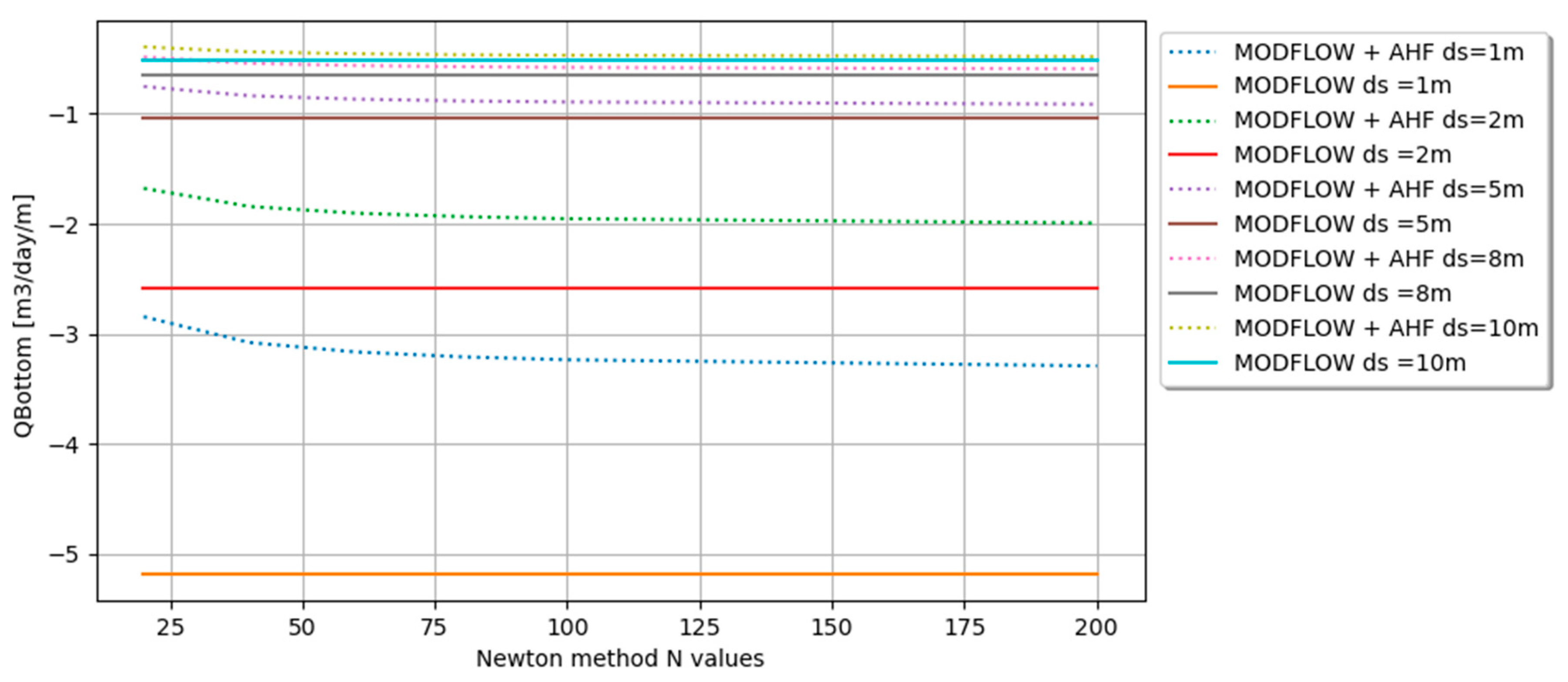
The AHF model was sensitised for one cell taking into consideration reasonable Biebrza River values, as shown in
Table 1.
Afterwards, this sensitivity analysis considers different values of
and different values of N (a number indicating finite approximation for the infinite series Newton method). The results presented in
Figure 4 show that
produces significative changes at the bottom flow. As the value of
increases, the AHF model tends to be closer to the MODFLOW approximation using the river package (RIV). An important remark is that the value of
remains constant in this sensitivity analysis and only the value of
is changed. The objective here is to identify the influence of the riverbed thickness in the flux exchange.
Another relevant aspect is that as the value of N increases, the approximation starts to converge (
Figure 4).
The computational cost associated increases as the value of N rises. The exponential increment of the simulation time regarding the N newton value can be considerable. For example, the Biebrza River model has a stream that contains 270 cells. The iterations of the AHF model are around 7, and it is a transient model with 293 stress periods; the total time of simulation could increase to 1.4 to 35 days (the model runs in a machine with the following technical specifications: Processor: Intel Core i7-4710HQ CPU @ 2.5 GHz and RAM: 16 GB).
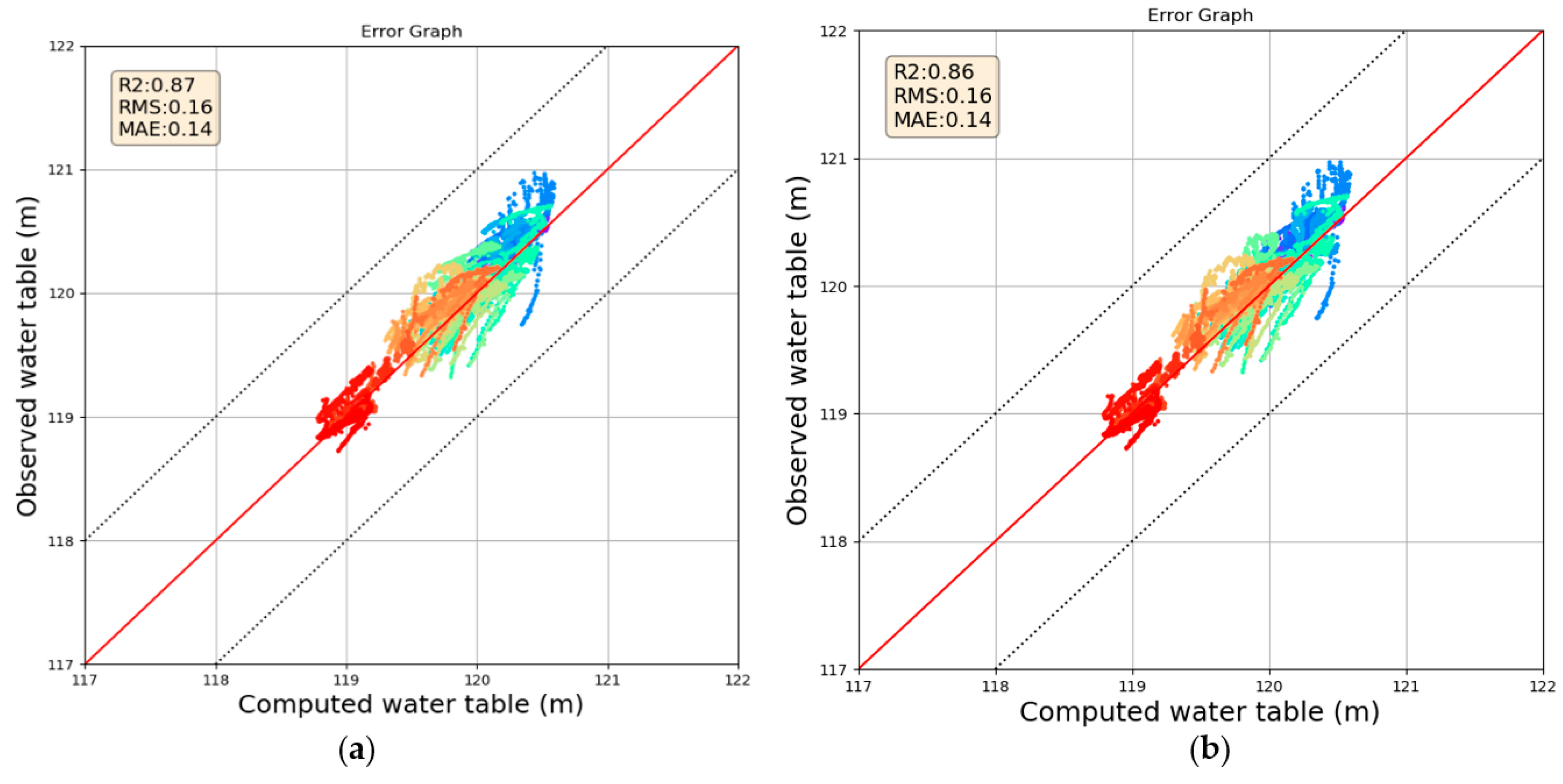
The model applying the MODFLOW+AHF does not show a clear improvement of the results regarding observation heads in the piezometers. There is a slight improvement in some piezometers and a diminishing of the accuracy in others. The MODFLOW + AHF model was not recalibrated; then, the same hydraulic properties as those in the MODFLOW model remain.
Regarding the calibration, both models (MODFLOW and MODFLOW+AHF) show statistics results of Root Mean Square values in a range between 0.08 and 0.37 m. While for the Mean Absolute Error, the range is between 0.06 and 0.35 m. These values are very acceptable, considering an error value less than 1 m for each measure, as shown in
Figure 5.
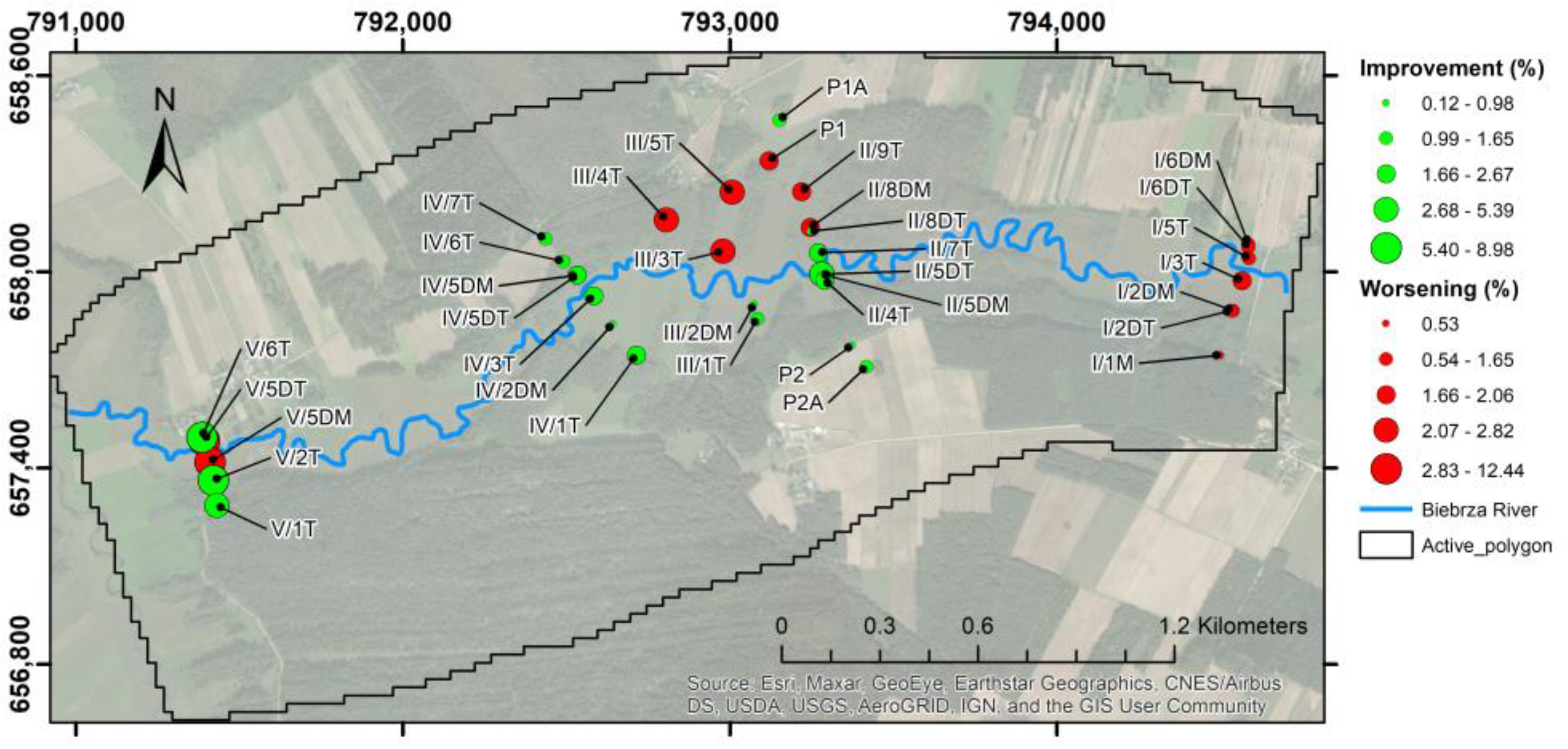
The piezometers, which have shown improvement in the calibration of their water head, are shown in
Figure 6. It shows in red and green the evaluation of the percentage variation of the error, which have improved or not. Green means that the result improved, while red means that the result has not improved. Twenty of the piezometers have improved, while thirteen of them have shown a slight worsening. The piezometers with the highest amelioration are located south of the river and in the central part of the modelling area. Nevertheless, the improvement is low: between 0.1 and 9%.
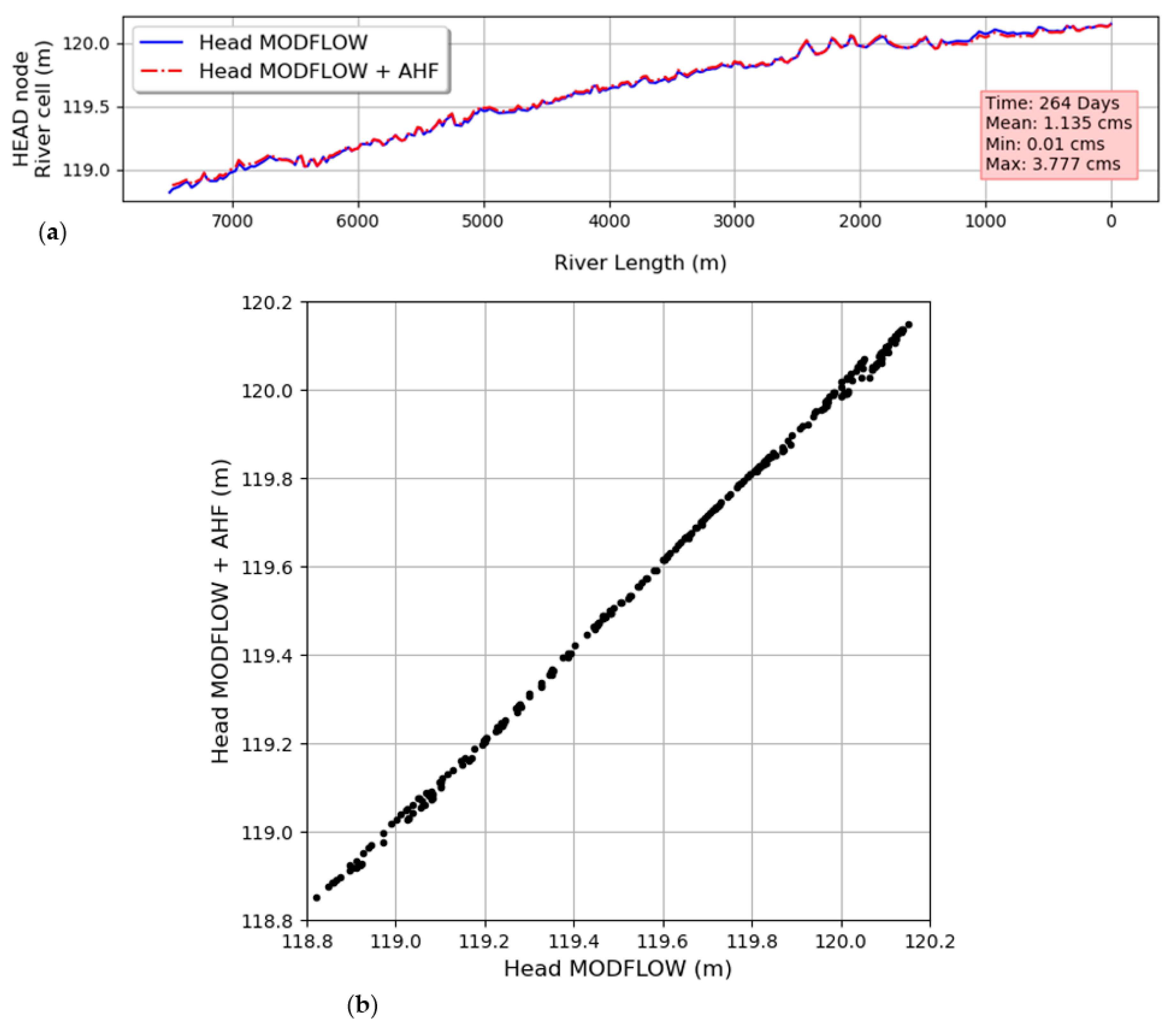
According to
Figure 7, the maximum difference between the head calculated by MODFLOW versus the head calculated by MODFLOW + AHF is 3.8 cm, considering all the simulation periods. The difference is found on day 264 (27/05/2019).
Figure 7 also shows that the highest discrepancies between both models appear principally upstream and downstream of the river.
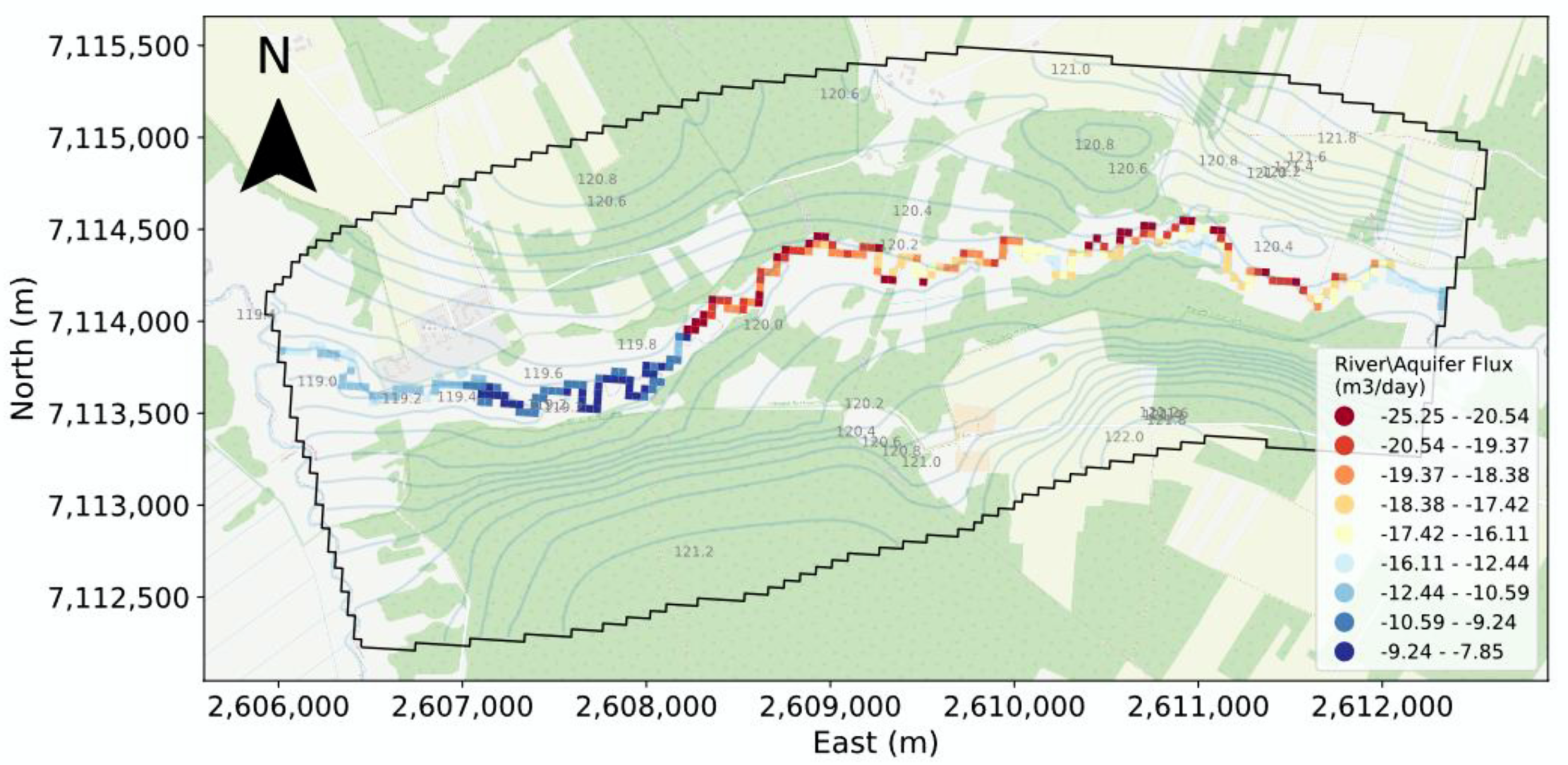
According to
Figure 8, during this period, the river flux for both models did not show a significant discrepancy. Indeed, the results indicate just a slight difference in the extreme values of discharge, but the same behavior remains.
Regarding the contours,
Figure 8 shows that for the stress periods where the difference of the head is highest between MODFLOW and the MODFLOW + AHF scenario, the contour lines tend to have very similar behavior for both models. Then, the results of AHF model show that it seems to not affect the water heads of the MODFLOW model.
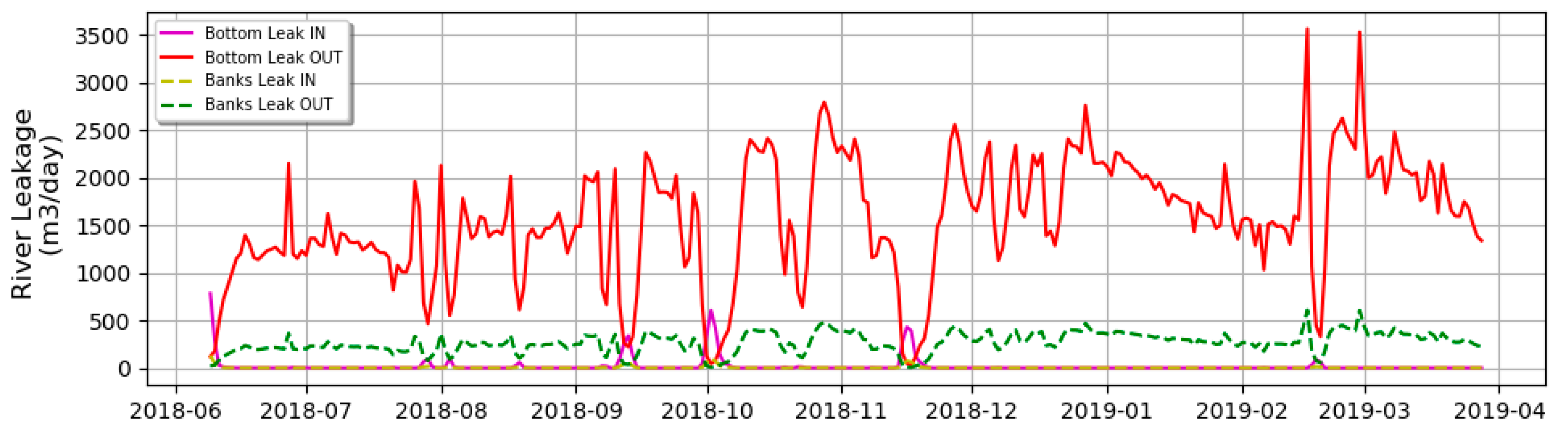
The results of the average budget of the MODFLOW + AHF are shown in
Table 2. The results show that in general terms, there are no significant differences between the MODFLOW model and MODFLOW + AHF model. However, there is a very slightly decrease of the “river leakage out” regarding the MODFLOW model.
It is important to have in mind that the river package (RIV) takes into account just the bottom flux. Then, according to the results, the implementation of the AHF model generates a river leakage comparable to the model without AHF in total terms. Moreover, there is a reduction of the bottom flux implementing AHF regarding that calculated without AHF.
Figure 9 shows the variation of the river leakage flow during the simulation. It shows that the leakage flux that discharges to the river from the bottom is even one order of magnitude higher than the flux from the banks of the river. In comparison, the recharge from the river moves in the same order of magnitude for the banks and the bottom.
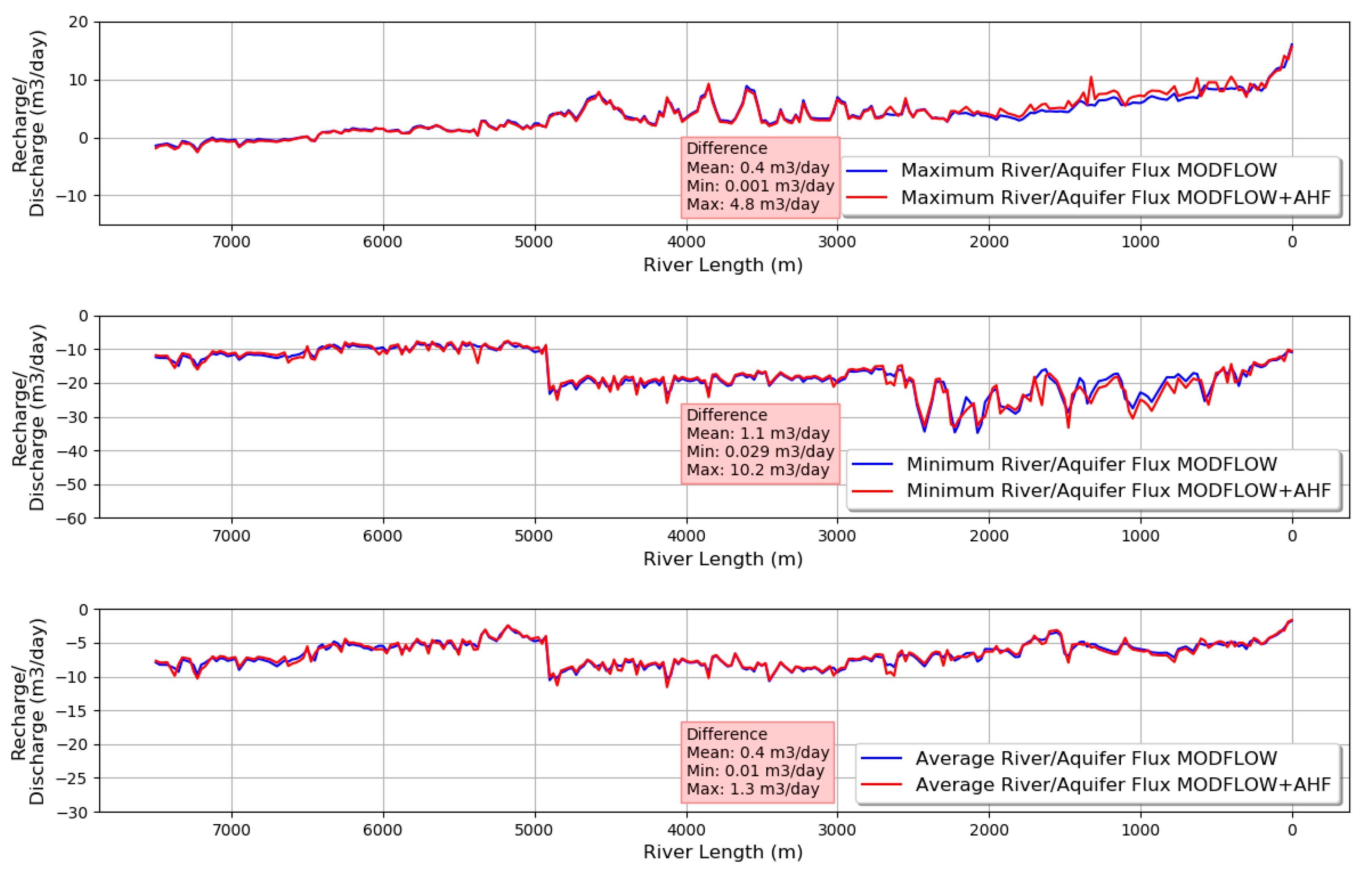
Figure 10 shows that in general terms, the MODFLOW model and the MODFLOW coupled with the AHF model have very close results for extreme values.
It is important to have the notation clearly explained in previous sections to understand
Figure 10. According to this, when the graph shows “negative values of recharge” (to the aquifer), this is equivalent to “positive value of discharge” (to the river). Therefore, when the author mentions the
minimum recharge (to the aquifer) in negative values, it means there is a
maximum discharge (to the river) in positive values.
The results show that the maximum river flux is positive in almost whole the section, which means that there is a recharge from the river to the aquifer during the simulation (
Figure 10). However, from the same figure, it is possible to see that for the last kilometer at the west part of the river, the maximum river flux is negative. It means that in this part of the river, there is always gaining river.
A similar result is obtained if it is compared to the minimum river flux, where there is a discharge from the aquifer to the river, and it is gaining along the river. In this case, the first 5000 m in the MODFLOW model has the highest values of discharge; however, after the 5000 m, this behavior changes, and the aquifer reduces its release to the river (
Figure 10). In terms of the average recharge/discharge, both models have a gaining behavior, which oscillated between −2 and −15 m
3 day
−1.
Figure 10 shows comparatively both models. Regarding the maximum river flux, the difference can reach 4.8 m
3 day
−1, while for the minimum river flux where the river is recharging, the aquifer the magnitude is even higher, reaching 10.5 m
3 day
−1.
Then, for extreme and average values, there are no significant differences between the MODFLOW model and the MODFLOW+AHF model. However, suppose a detailed analysis of each river cell is considered for each time. In that case, it is possible to distinguish that there are relevant variations in terms of the river/aquifer flux.
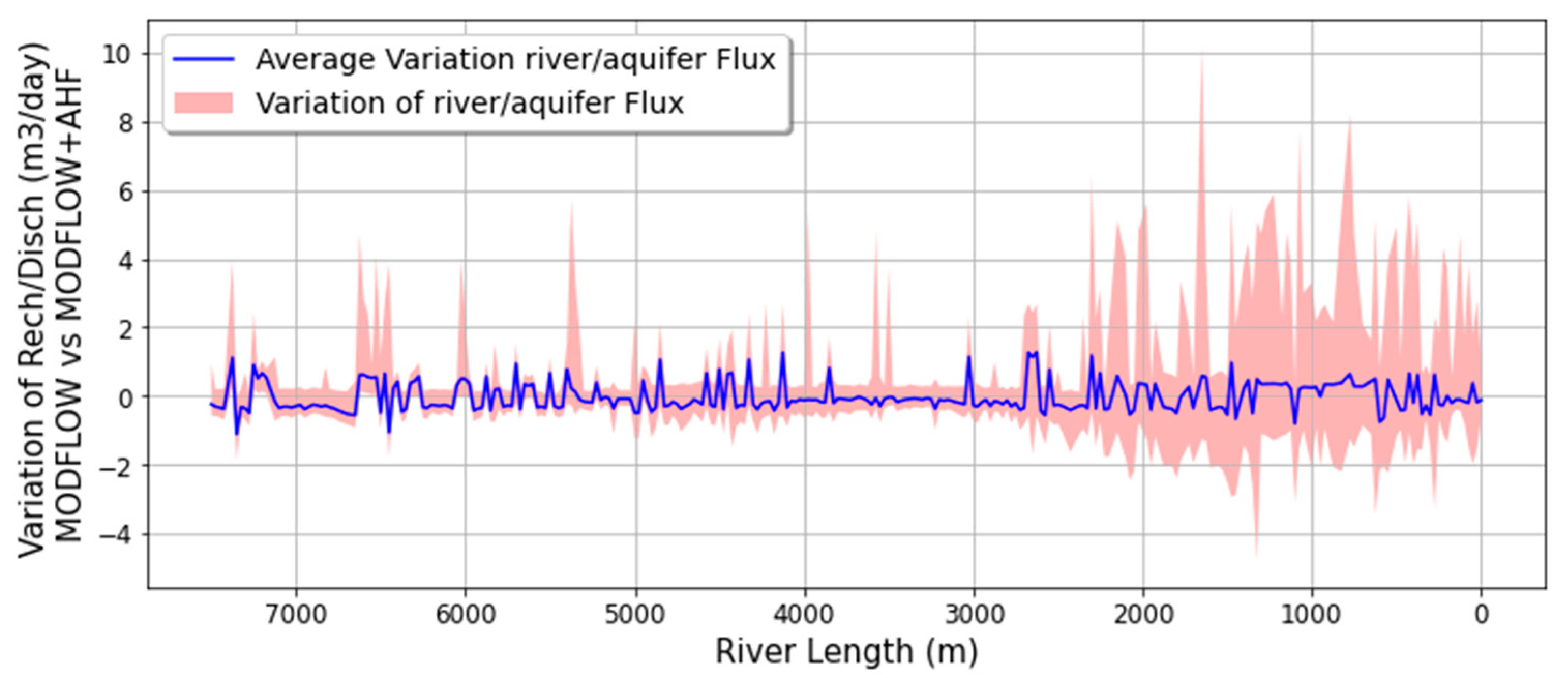
Figure 11 gives a more detailed representation of each cell of the river. This figure shows the maximum differences of the river/aquifer flux for each river cell between the MODFLOW and the MODFLOW+AHF model during the whole simulation.
According to this analysis, the average variation of the river/aquifer flux oscillates around 0. However, there are some periods where the difference of the river/aquifer flux between MODFLOW and MODFLOW+AHF model can reach even the 10 m3 day−1 per cell. Therefore, even when on average, the MODFLOW and the MODFLOW+AHF model seems to be very similar, this analysis demonstrates some critical differences for some stress periods simulation.
Additionally, geometrically, the lowest thickness of the peat layer () is located in the first 2000 m of the river. Therefore, it explains that there are more dramatic fluctuations in the difference between the river/aquifer flux of both models.
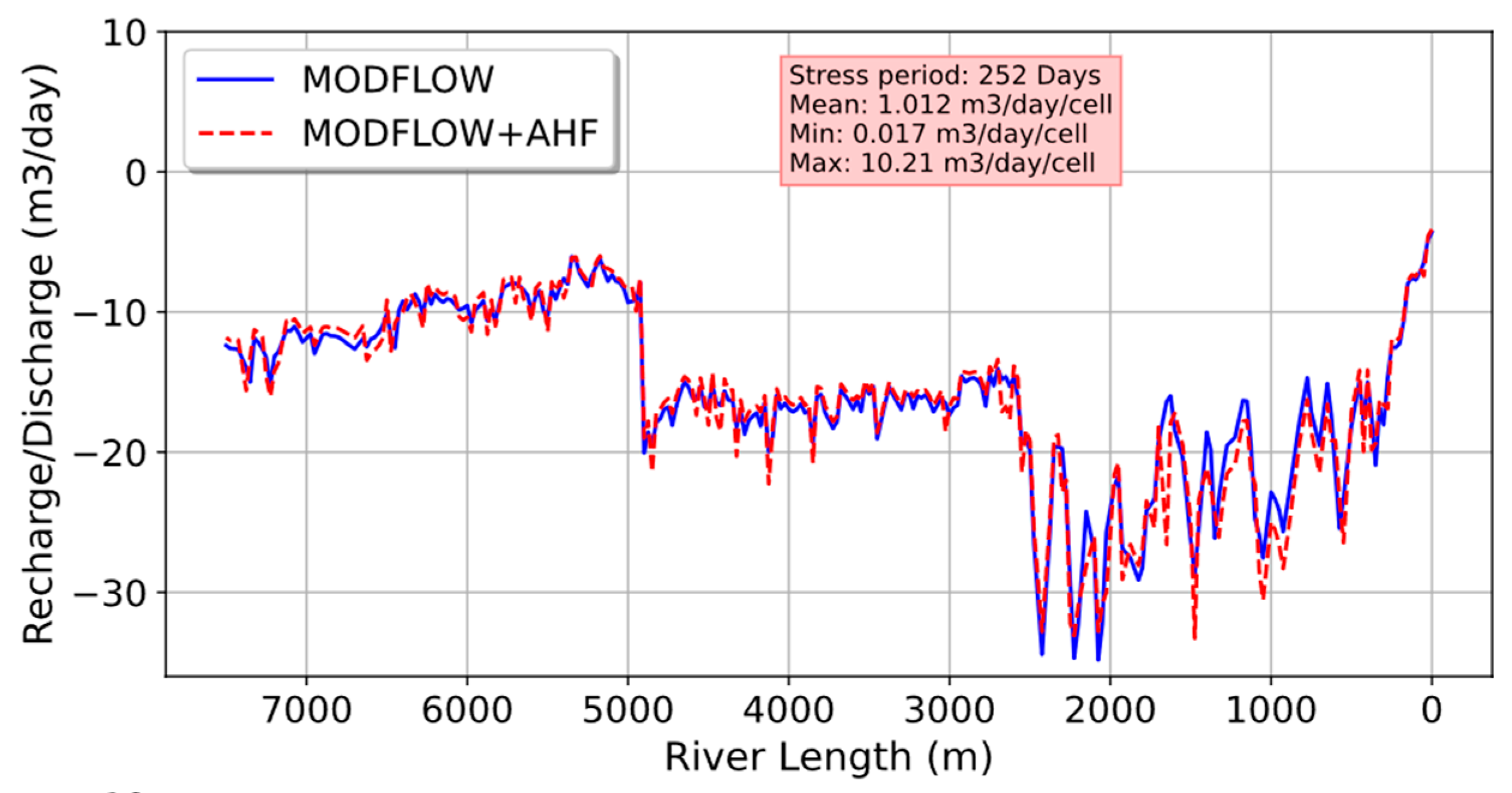
The stress period on day 264 (15/05/2019) is where the difference of river flux between MODFLOW and the AHF model is the highest, reaching 10.2 m
3 day
−1 of variance (
Figure 12).
4. Discussion and Recommendation
The implementation of the seepage package instead of the river package (RIV) shows some limitations of the algorithm related to the hydraulic properties and the geometry. These parameters can affect the convergence of the model directly, producing faster convergence or even a total divergence of the model, and the results showed that the model with the native river package (RIV) could converge normally, but applying the algorithm, it can be unstable. These instabilities produce dry and flood cells breaking the algorithm.
The simplified model in steady state is done in MODFLOW, where the Analytical Hyporheic Flux model is represented numerically by the iterative algorithm through the seepage package, which presented significant challenges and interesting conclusions. One was the sensitivity of the model to the thickness of the riverbed sediments. This parameter affects the value of the bottom recharge/discharge. If the thickness of the riverbed sediments is low, the flux through the bottom will increase. This growth of the flux is exponential, and then after a certain value of thickness, the MODFLOW model can get dry or over wet, breaking the algorithm. Therefore, the MODFLOW + AHF has convergency problems for high bottom discharge produced by the geometry of the riverbed. Thus, will increasing the values of the thickness fix the convergence problem? The answer is yes, partially. However, since the thickness is high, the bottom flux will be low and unrealistic in terms of the objective of the AHF model. Therefore, the parametrisation of the geometry will affect the implementation of this methodology in MODFLOW. The author suggests that the thickness of the riverbed sediments must be over 10 m and the width of the riverbed over 400 m. Unfortunately, some realistic scenarios values of this thickness and width lower than this cannot be simulated in MODFLOW at least not applying the algorithm suggested in this paper.
The Biebrza River model in transient mode run in MODFLOW was calibrated using the river package (RIV). The calibration was completed successfully, and the statistics obtained after this process shows an acceptable accuracy of the model. Values obtained for recharge and discharge between the river and aquifer are smaller than that presented by Anibas [
22]. For meandering parts, the results of the modelling of the river–groundwater exchange are similar to those presented by Anibas [
22]. There are higher exchange fluxes at the convex banks of meanders and lower exchange fluxes in the concave banks, since the flow lines are diverging.
The Biebrza River model coupled with the analytical hyporheic flux (AHF) in transient mode brings interesting conclusions regarding the relationship of the riverbed sediments and its geometry.
By one side, the transient regime involved a significant challenge in the implementation of the model for many stress periods. The research concludes that it can be performed, joining several models of one stress period, which must be connected with the inputs, outputs, boundaries, and initial conditions.
On the other side, the application of this methodology in a real case brings important conclusions about the computational cost concerned to obtain accurate results. The computational cost has two important aspects. Firstly, the solution of the aquifer head on the river cell must be obtained iteratively in each period. Secondly, the infinite series of Newton method ensures the convergence and accuracy of the approximation. This research concludes that the simulation time rises exponentially in order to obtain an accurate solution for the Newton method (the simulation time can take hours, days, or months in a simple model as the Biebrza river). Therefore, when it is applied to the AHF model, the selection of the Newton method approximation size has to be sensitised in order to obtain accurate results with a reasonable computational cost.
Additionally, the implementation of the AHF model brings other conclusions. On one side, there are no substantial changes regarding the water heads. Moreover, the averages and extreme values of the river/aquifer flux remained similar for both models (MODFLOW and MODFLOW+AHF). On the other side, a detailed analysis of the river/aquifer flux per cell and stress period shows differences, especially in zones where there is a steeper topography gradient and lower thickness of the riverbed.
The AHF model can be implemented successfully through FloPy in MODFLOW to resolve scenarios of river and aquifer interaction in streams with specific geometries, where the depth is dimensionally higher than the width, showing promising results that are more accurate in the interaction between the river and the aquifer. Moreover, it adds an important value to the groundwater and surface water interaction modelling, considering that MODFLOW just estimates this interaction in a simplified way through the Darcy law flux in one direction.
Additionally, this methodology allows dividing the fluxes coming from the bottom and the banks of the river for the adopted simplified model of the rectangular river bed (for artificial channels rather than for rivers with complex natural channel geometry). These results undertake an innovative strategy to face projects where the lateral and bottom flux must be identified separately.