Spatiotemporal Evolution of Evapotranspiration in China after 1998
Abstract
1. Introduction
2. Data and Methods
2.1. Study Area and Data
2.2. Methods
3. Results and Discussion
3.1. Spatial-Temporal Distribution and Trend of Evapotranspiration in China
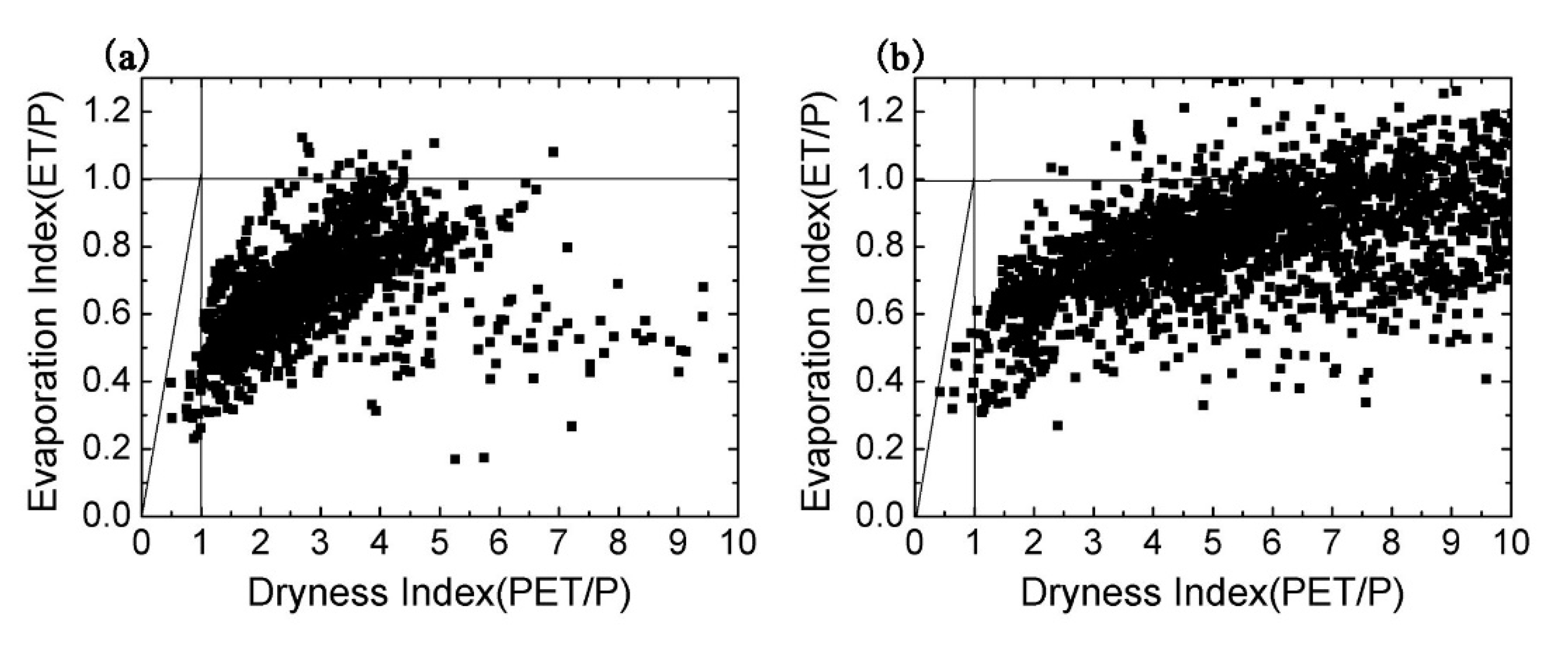
3.2. Regional Division in China
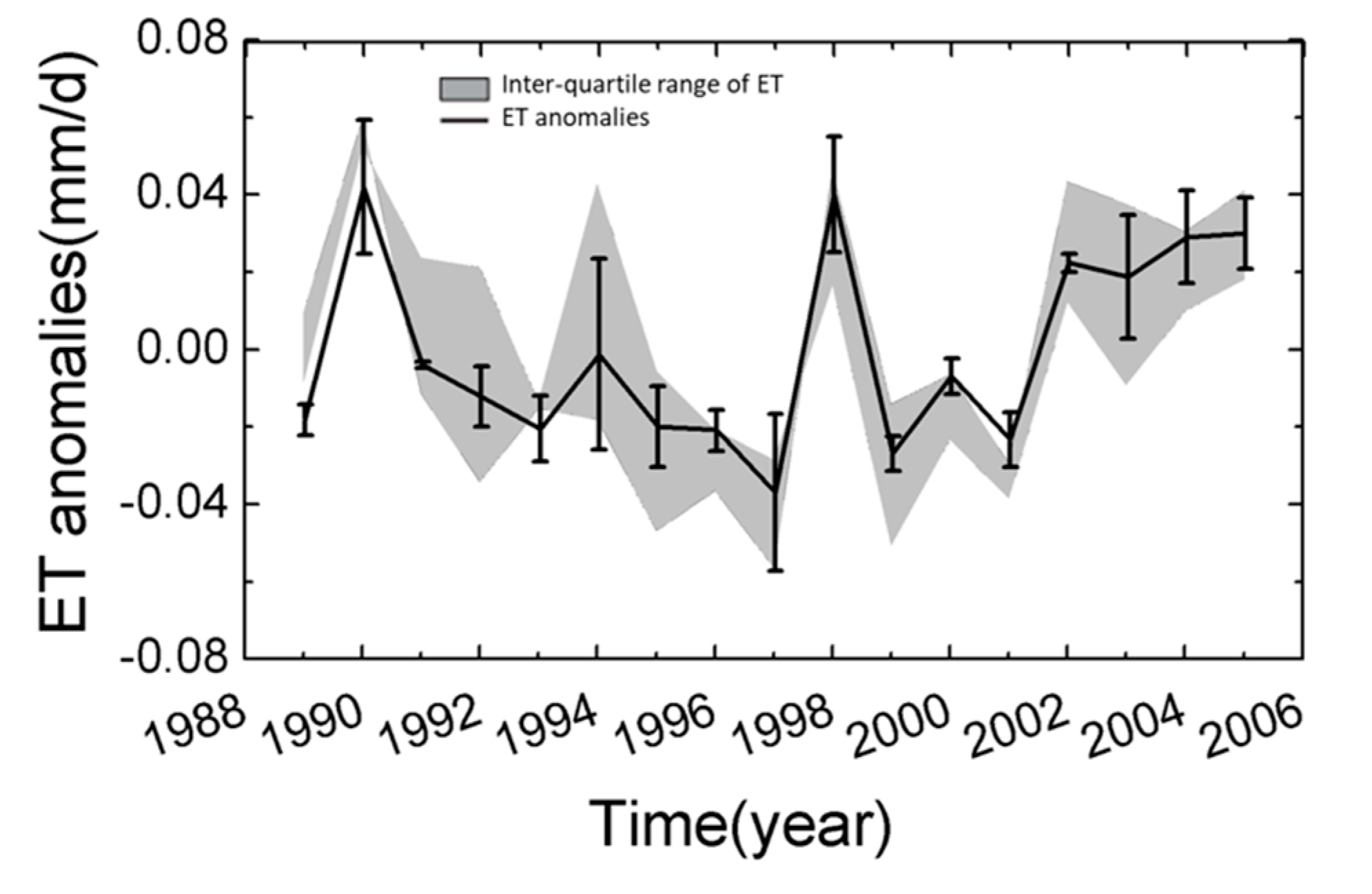
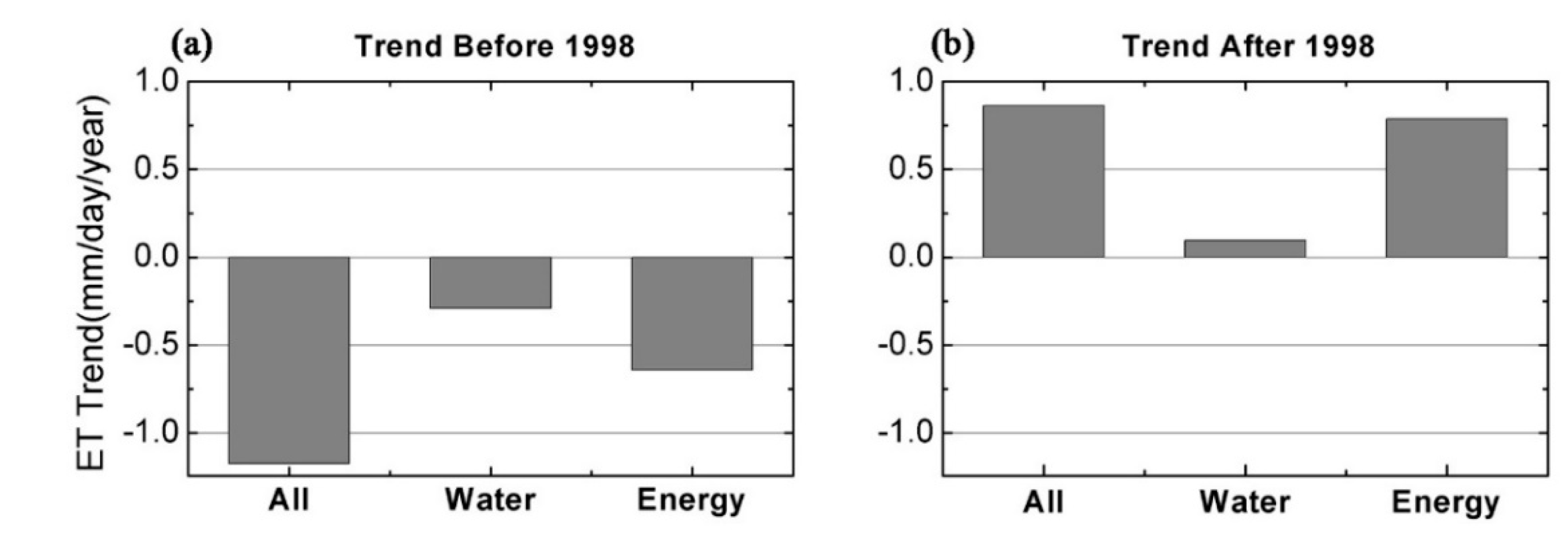
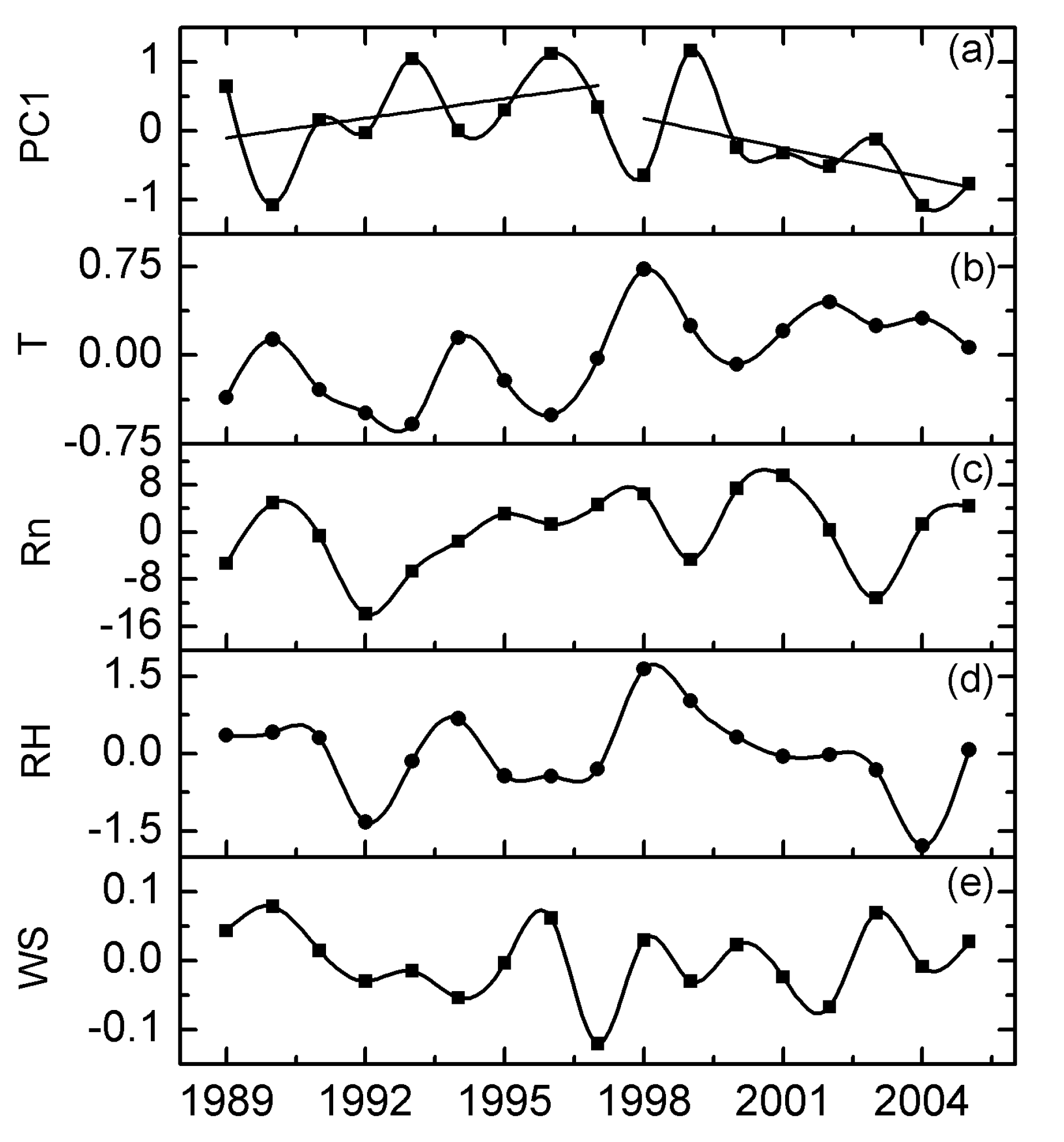
3.3. Evolution and Attribution of ET in Different Regions of China
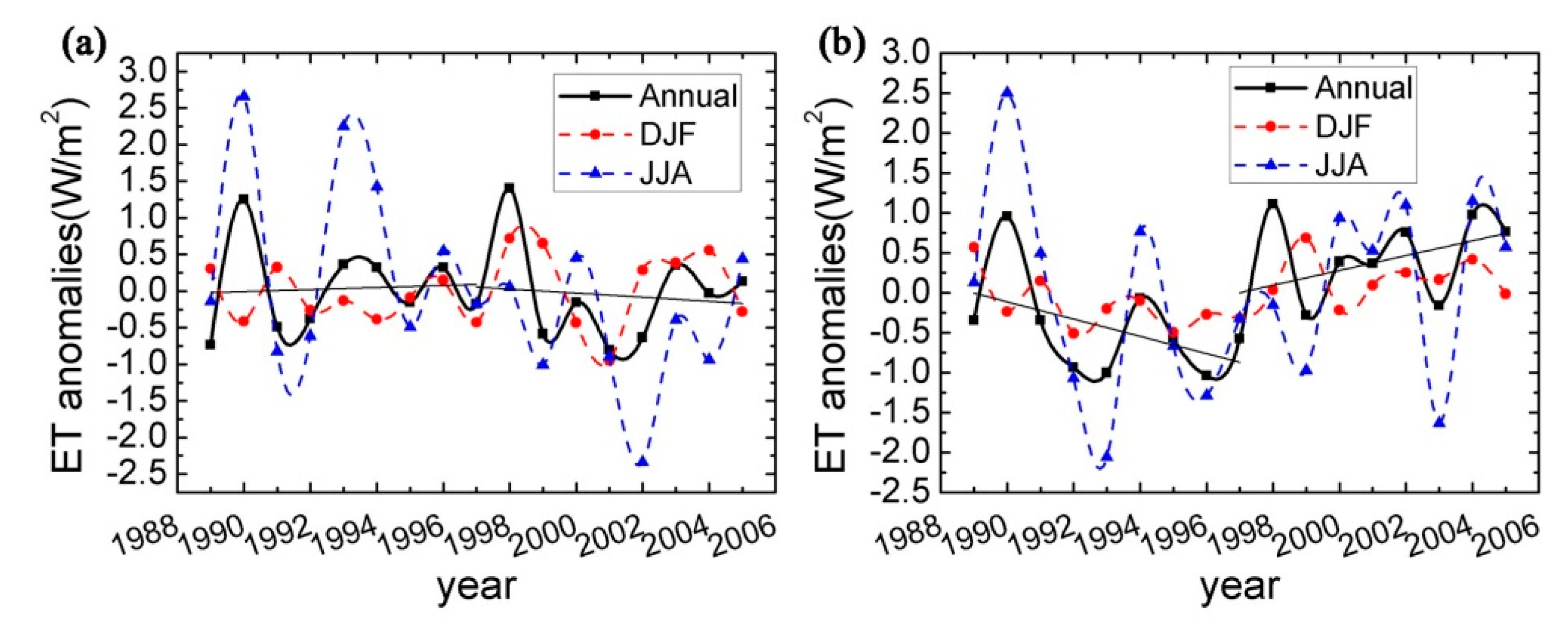
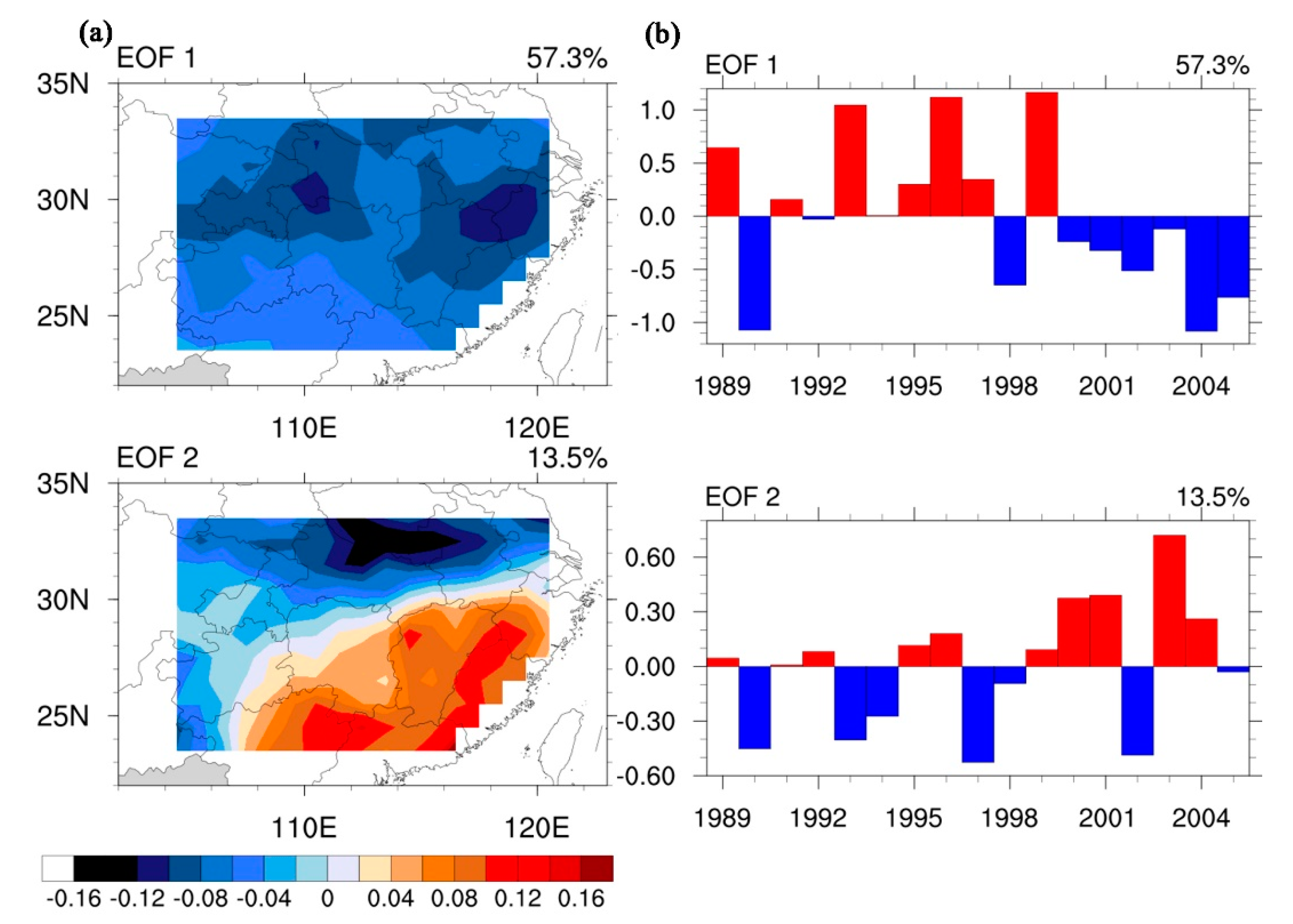
3.4. Dominant Modes of Evapotranspiration in the Energy-Control Region
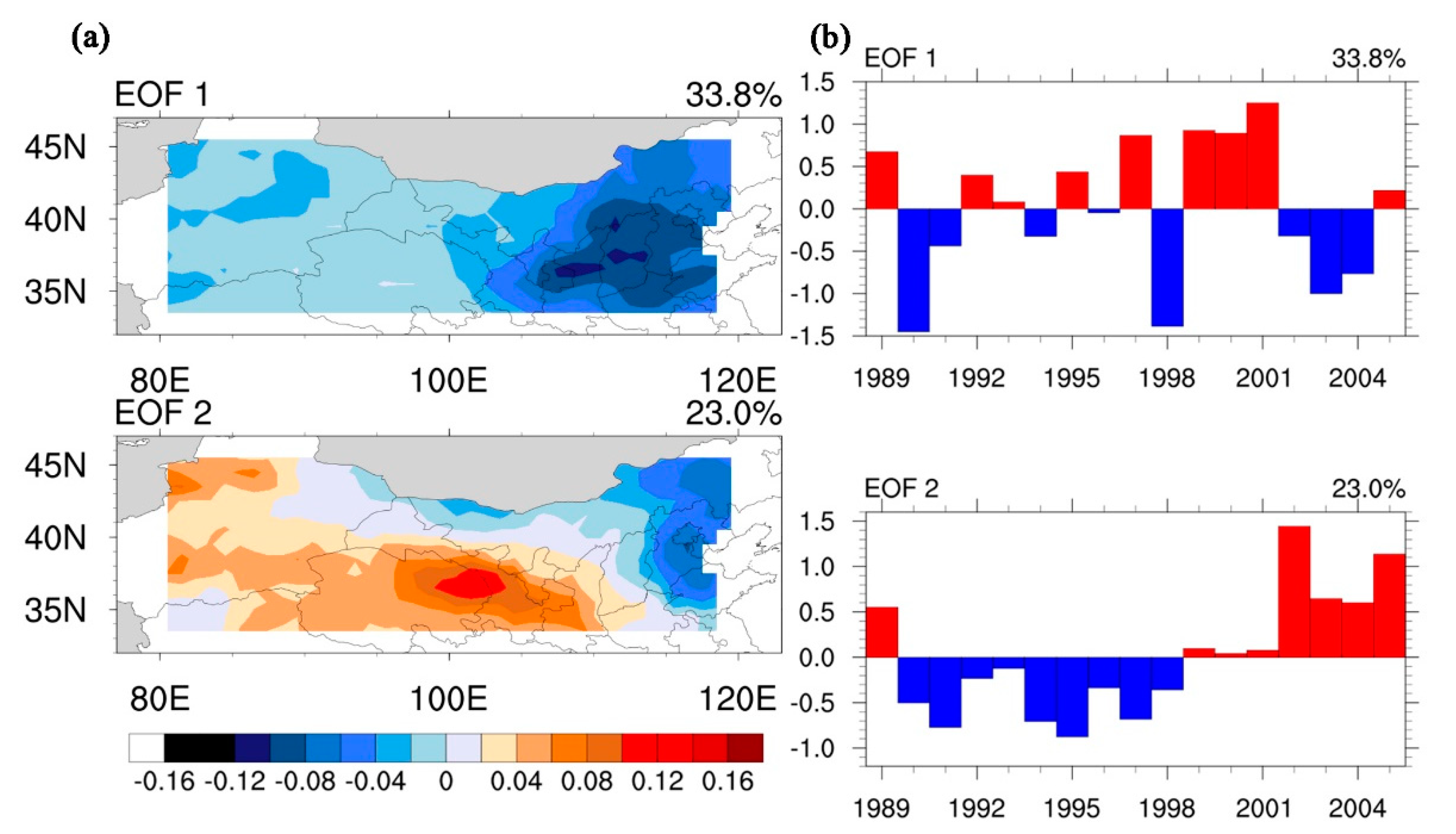
3.5. Dominant Modes of Evapotranspiration in the Water-Control Region
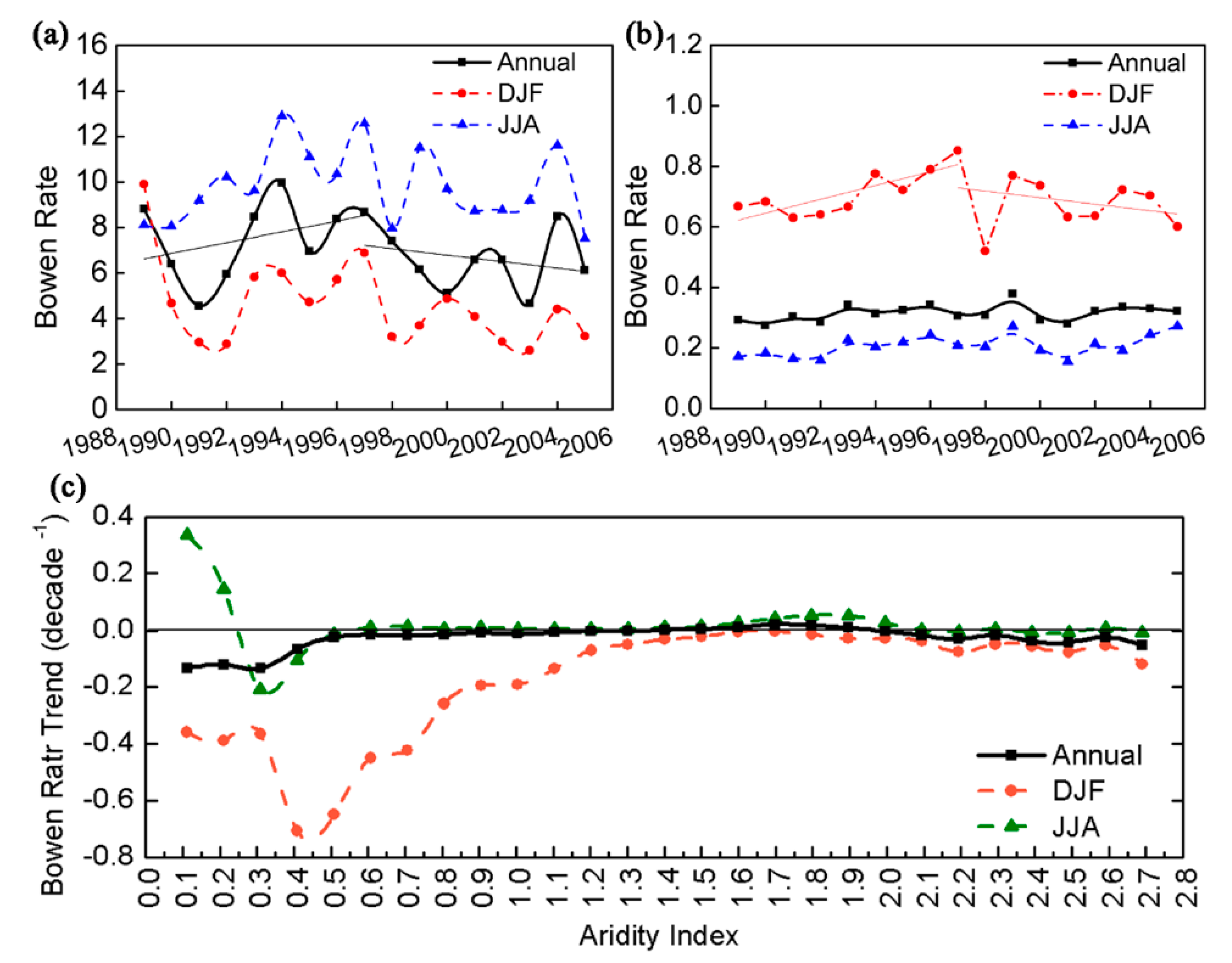
3.6. The Difference in Surface Energy Partition
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Vautard, R.; Yiou, P.; D’Andrea, F.; de Noblet, N.; Viovy, N.; Cassou, C.; Polcher, J.; Ciais, P.; Kageyama, M.; Fan, Y. Summertime European heat and drought waves induced by wintertime Mediterranean rainfall deficit. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Wang, K.C.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Luthi, D.; Litschi, M.; Schar, C. Land-atmosphere coupling and climate change in Europe. Nature 2006, 443, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Novick, K.A.; Ficklin, D.L.; Stoy, P.C.; Williams, C.A.; Bohrer, G.; Oishi, A.C.; Papuga, S.A.; Blanken, P.D.; Noormets, A.; Sulman, B.N.; et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Chang. 2016, 6, 1023–1027. [Google Scholar] [CrossRef]
- Berg, A.; Findell, K.; Lintner, B.; Giannini, A.; Seneviratne, S.I.; van den Hurk, B.; Lorenz, R.; Pitman, A.; Hagemann, S.; Meier, A.; et al. Land-atmosphere feedbacks amplify aridity increase over land under global warming. Nat. Clim. Chang. 2016, 6, 869–874. [Google Scholar] [CrossRef]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.A.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global changes in drought conditions under different levels of warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- Feng, T.C.; Su, T.; Ji, F.; Zhi, R.; Han, Z.X. Temporal characteristics of actual evapotranspiration over China under global warming. J. Geophys. Res. Atmos. 2018, 123, 5845–5858. [Google Scholar] [CrossRef]
- Yang, Z.S.; Zhang, Q.; Hao, X.C.; Yue, P. Changes in evapotranspiration over global semiarid regions 1984–2013. J. Geophys. Res. Atmos. 2019, 124, 2946–2963. [Google Scholar] [CrossRef]
- Yao, T.C.; Lu, H.W.; Feng, W.; Yu, Q. Evaporation abrupt changes in the Qinghai-Tibet Plateau during the last half-century. Sci Rep.UK 2019, 9. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2007: The Scientific Basis; Forth Assessment Report; Cambridge University Press: New York, NY, USA, 2007; 996p. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. B Am. Meteorol. Soc. 2003, 84, 1205–1217. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. B Am. Meteorol. Soc. 2009, 90, 311–323. [Google Scholar] [CrossRef]
- Roderick, M.L.; Hobbins, M.T.; Farquhar, G.D.J.G.C. Pan evaporation trends and the terrestrial water balance. II. Energy Balance Interpret 2009, 3, 761–780. [Google Scholar]
- Zheng, C.L.; Wang, Q. Spatiotemporal pattern of the global sensitivity of the reference evapotranspiration to climatic variables in recent five decades over China. Stoch. Env. Res. Risk A 2015, 29, 1937–1947. [Google Scholar] [CrossRef]
- Sun, S.L.; Chen, H.S.; Wang, G.J.; Li, J.J.; Mu, M.Y.; Yan, G.X.; Xu, B.; Huang, J.; Wang, J.; Zhang, F.M.; et al. Shift in potential evapotranspiration and its implications for dryness/wetness over Southwest China. J. Geophys. Res. Atmos. 2016, 121, 9342–9355. [Google Scholar] [CrossRef]
- Yang, D.W.; Sun, F.B.; Liu, Z.T.; Cong, Z.T.; Lei, Z.D. Interpreting the complementary relationship in non-humid environments based on the Budyko and Penman hypotheses. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.C.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef]
- Roderick, M.L.; Rotstayn, L.D.; Farquhar, G.D.; Hobbins, M.T. On the attribution of changing pan evaporation. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Van Heerwaarden, C.C.; de Arellano, J.V.G.; Teuling, A.J. Land-atmosphere coupling explains the link between pan evaporation and actual evapotranspiration trends in a changing climate. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Azorin-Molina, C.; Vicente-Serrano, S.M.; Sanchez-Lorenzo, A.; McVicar, T.R.; Moran-Tejeda, E.; Revuelto, J.; El Kenawy, A.; Martin-Hernandez, N.; Tomas-Burguera, M. Atmospheric evaporative demand observations, estimates and driving factors in Spain (1961–2011). J. Hydrol. 2015, 523, 262–277. [Google Scholar] [CrossRef]
- Wang, Z.L.; Xie, P.W.; Lai, C.G.; Chen, X.H.; Wu, X.S.; Zeng, Z.Y.; Li, J. Spatiotemporal variability of reference evapotranspiration and contributing climatic factors in China during 1961–2013. J. Hydrol. 2017, 544, 97–108. [Google Scholar] [CrossRef]
- Liu, T.G.; Li, L.G.; Lai, J.B.; Liu, C.; Zhuang, W.H. Reference evapotranspiration change and its sensitivity to climate variables in southwest China. Theor. Appl. Climatol. 2016, 125, 499–508. [Google Scholar] [CrossRef]
- Sun, S.L.; Chen, H.S.; Ju, W.M.; Wang, G.J.; Sun, G.; Huang, J.; Ma, H.D.; Gao, C.J.; Hua, W.J.; Yan, G.X. On the coupling between precipitation and potential evapotranspiration: Contributions to decadal drought anomalies in the Southwest China. Clim. Dynam 2017, 48, 3779–3797. [Google Scholar] [CrossRef]
- Cong, Z.T.; Yang, D.W.; Ni, G.H. Does evaporation paradox exist in China? Hydrol. Earth Syst. Sci. 2009, 13, 357–366. [Google Scholar] [CrossRef]
- Sorensson, A.A.; Ruscica, R.C. Intercomparison and uncertainty assessment of nine evapotranspiration estimates over South America. Water Resour. Res. 2018, 54, 2891–2908. [Google Scholar] [CrossRef]
- Jamshidi, S.; Zand-parsa, S.; Pakparvar, M.; Niyogi, D. Evaluation of evapotranspiration over a semiarid region using multiresolution data sources. J. Hydrometeorol. 2019, 20, 947–964. [Google Scholar] [CrossRef]
- Liu, B.H.; Xu, M.; Henderson, M.; Gong, W.G. A spatial analysis of pan evaporation trends in China, 1955–2000. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liu, C.M.; Tang, Y.H.; Yang, Y.H. Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Li, X.Y.; He, Y.; Zeng, Z.Z.; Lian, X.; Wang, X.H.; Du, M.Y.; Jia, G.S.; Li, Y.N.; Ma, Y.M.; Tang, Y.H.; et al. Spatiotemporal pattern of terrestrial evapotranspiration in China during the past thirty years. Agric. Forest Meteorol. 2018, 259, 131–140. [Google Scholar] [CrossRef]
- Xu, S.Q.; Yu, Z.B.; Yang, C.G.; Ji, X.B.; Zhang, K. Trends in evapotranspiration and their responses to climate change and vegetation greening over the upper reaches of the Yellow River Basin. Agric. Forest Meteorol. 2018, 263, 118–129. [Google Scholar] [CrossRef]
- Su, T.; Feng, T.C.; Feng, G.L. Evaporation variability under climate warming in five reanalyses and its association with pan evaporation over China. J. Geophys. Res. Atmos. 2015, 120, 8080–8098. [Google Scholar] [CrossRef]
- Wang, L.Y.; Yuan, X.; Xie, Z.H.; Wu, P.L.; Li, Y.H. Increasing flash droughts over China during the recent global warming hiatus. Sci. Rep. UK 2016, 6, 30571. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.D.; Zhou, T.J. Why was the arid and semiarid northwest China getting wetter in the recent decades? J. Geophys. Res. Atmos. 2017, 122, 9060–9075. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II reanalysis (R-2). B Am. Meteorol. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.; Poli, P.; Brugge, R.; Fielding, K.; Fuentes, M.; Kallberg, P.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-Interim Archive, Version 2.0; ERA report series. 1. Technical Report; ECMWF: Reading, UK, 2011; p. 23. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Confguration and performance of the data assimilation system. Q. J. R Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Mueller, B.; Seneviratne, S.I.; Jimenez, C.; Corti, T.; Hirschi, M.; Balsamo, G.; Ciais, P.; Dirmeyer, P.; Fisher, J.B.; Guo, Z.; et al. Evaluation of global observations-based evapotranspiration datasets and IPCC AR4 simulations. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Mueller, B.; Hirschi, M.; Jimenez, C.; Ciais, P.; Dirmeyer, P.A.; Dolman, A.J.; Fisher, J.B.; Jung, M.; Ludwig, F.; Maignan, F.; et al. Benchmark products for land evapotranspiration: LandFlux-EVAL multi-data set synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 3707–3720. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Jimenez, C.; Kummerow, C.; McCabe, M.; Rossow, W.; Wood, E.F.; Hirschi, M.; Mueller, B.; Teuling, A.J. GEWEX-iLEAPS LandFlux/LandFlux-EVAL Mini-Workshop. GEWEX Newsl. 2011, 21, 2. [Google Scholar]
- Seneviratne, S.I.; Jimenez, C.; Kummerow, C.; McCabe, M.; Rossow, W.; Wood, E.F.; Hirschi, M.; Mueller, B.; Teuling, A.J. GEWEX-iLEAPS LandFlux/LandFlux-EVAL Mini-Workshop. ILEAPS Newsl. 2011, 11, 48–50. [Google Scholar]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 33, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.J. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Wang, W.; Chen, X.; Shi, P.; van Gelder, P.H.A.J.M. Detecting changes in extreme precipitation and extreme streamflow in the Dongjiang River Basin in southern China. Hydrol. Earth Syst. Sci. 2008, 12, 207–221. [Google Scholar] [CrossRef]
- Wilcox, R.R. Fundamentals of Modern Statistical Methods: Substantially Improving Power and Accuracy; Springer: Berlin/Heidelberg, Germany, 2010; pp. 207–210. [Google Scholar]
- Wei, F.J. Modern Climatic Statistical Diagnosis and Prediction Technology; Meteorological Press: Beijing, China, 2007; Volume 63, p. 117. [Google Scholar]
- Ndehedehe, C.; Awange, J.; Agutu, N.; Kuhn, M.; Heck, B. Understanding changes in terrestrial water storage over West Africa between 2002 and 2014. Adv. Water Resour. 2016, 88, 211–230. [Google Scholar] [CrossRef]
- Feng, S.; Fu, Q. Expansion of global drylands under a warming climate. Atmos. Chem. Phys. 2013, 13, 10081–10094. [Google Scholar] [CrossRef]
- United Nations Environment Programme (UNEP). World Atlas of Desertification; Edward Arnold: Sevenoaks, UK, 1992; p. 69. [Google Scholar]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Lewis, J.M. The story behind the Bowen ratio. B Am. Meteorol. Soc. 1995, 76, 2433–2443. [Google Scholar] [CrossRef]
- Han, B.; Lu, S.H.; Li, R.Q.; Wang, X.; Zhao, L.; Zhao, C.L.; Wang, D.Y.; Meng, X.H. Global land surface climate analysis based on the calculation of a modified bowen ratio. Adv. Atmos. Sci. 2017, 34, 663–678. [Google Scholar] [CrossRef]
- Budyko, M.I. (Ed.) Climate and Life; Academic Press: San Diego, CA, USA, 1974; pp. 321–330. [Google Scholar]
- Wang, K.; Liang, S. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture. J. Hydrometeorol. 2008, 9, 712–727. [Google Scholar] [CrossRef]
- Wang, K.C.; Dickinson, R.E.; Wild, M.; Liang, S.L. Evidence for decadal variation in global terrestrial evapotranspiration between 1982 and 2002: 1. Model development. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Wang, K.C.; Dickinson, R.E.; Wild, M.; Liang, S.L. Evidence for decadal variation in global terrestrial evapotranspiration between 1982 and 2002: 2. Results. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Roderick, M.L.; Michael, T.H.; Farquhar, G.D. Pan evaporation trends and the terrestrial water balance. I. Principles and observations. Geog. Compass 2009, 3, 746–760. [Google Scholar] [CrossRef]
- Han, J.Y.; Du, H.B.; Wu, Z.F.; He, H.S. Changes in extreme precipitation over dry and wet regions of china during 1961–2014. J. Geophys. Res. Atmos. 2019, 124, 5847–5859. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.Q.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.K.; Wen, X.F.; Sun, X.M.; Wang, H.M. Interannual variation of the bowen ratio in a subtropical coniferous plantation in Southeast China, 2003–2012. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.P.; Yu, H.P.; Guan, X.D.; Wang, G.Y.; Guo, R.X. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166. [Google Scholar] [CrossRef]
- Greve, P.; Orlowsky, B.; Mueller, B.; Sheffield, J.; Reichstein, M.; Seneviratne, S.I. Global assessment of trends in wetting and drying over land. Nat. Geosci. 2014, 7, 716–721. [Google Scholar] [CrossRef]
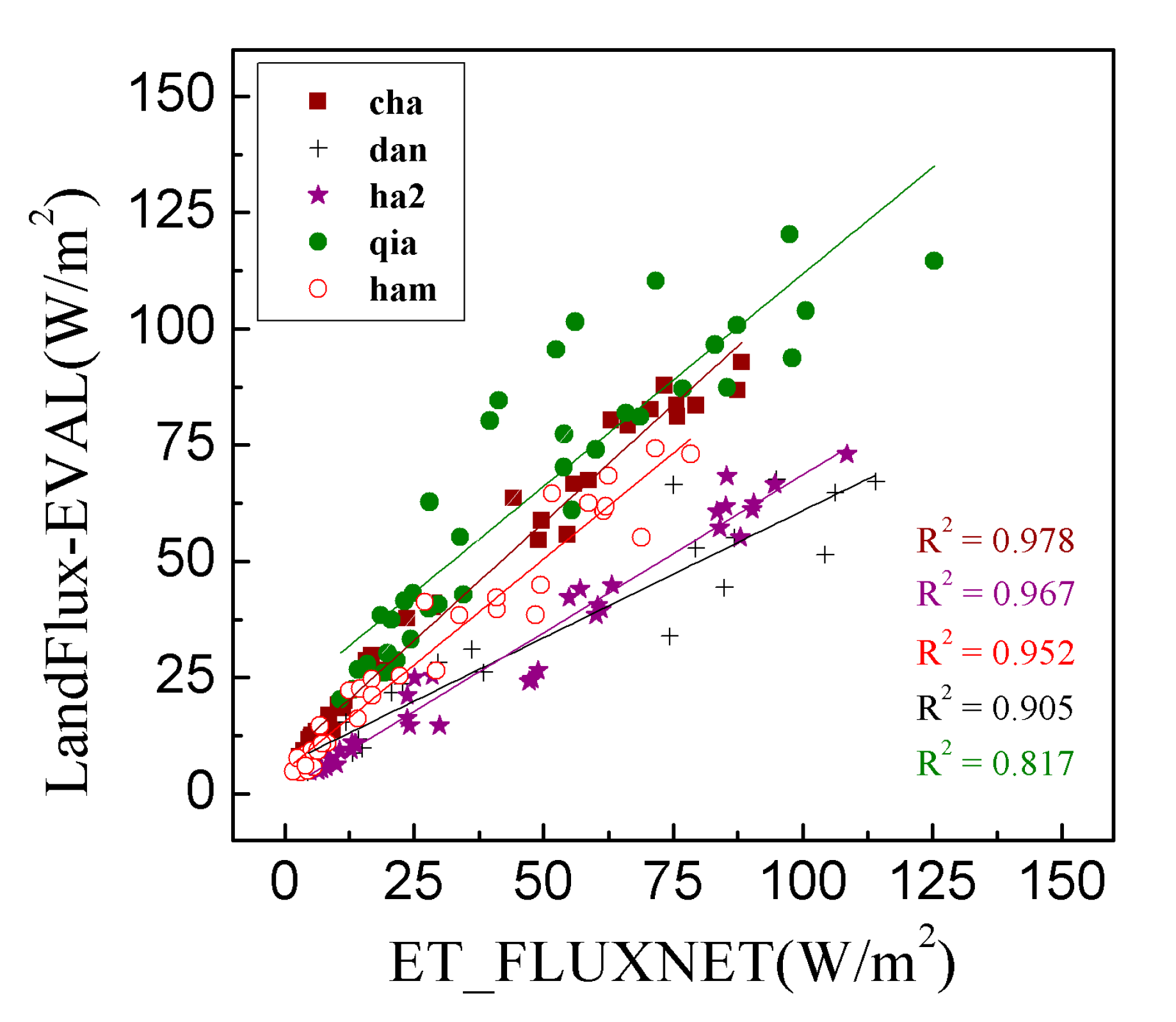
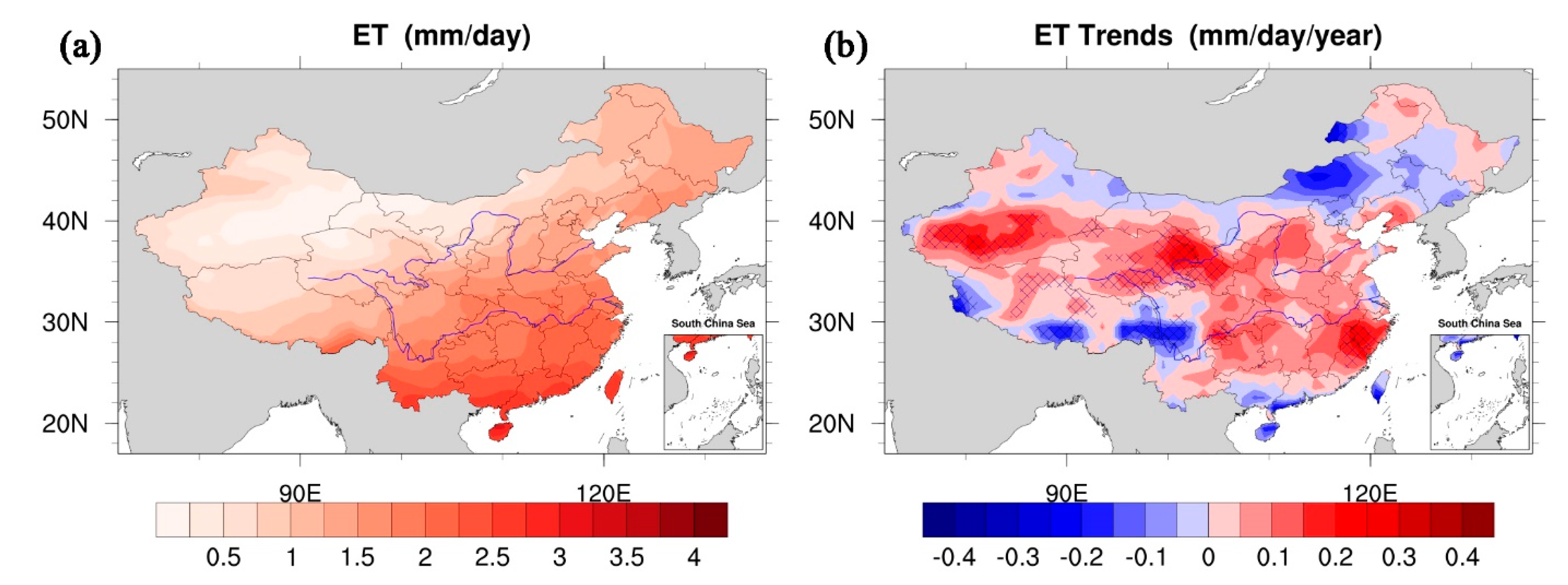
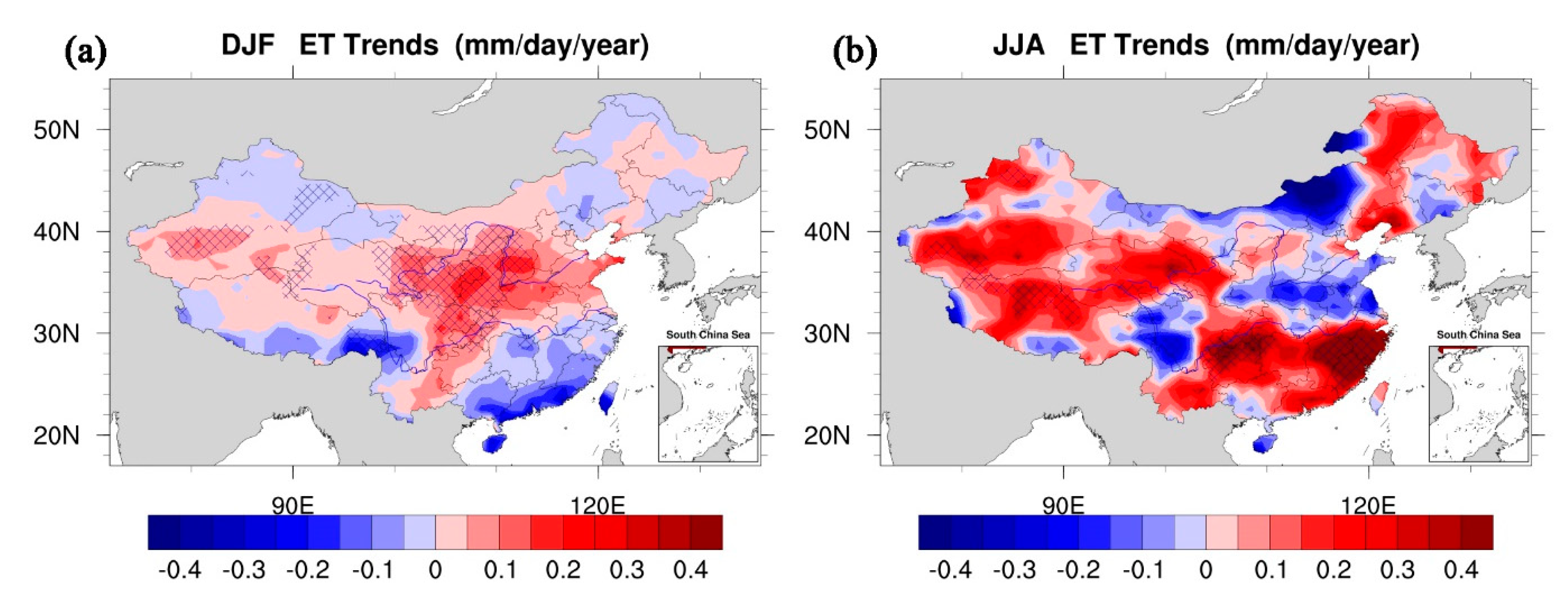
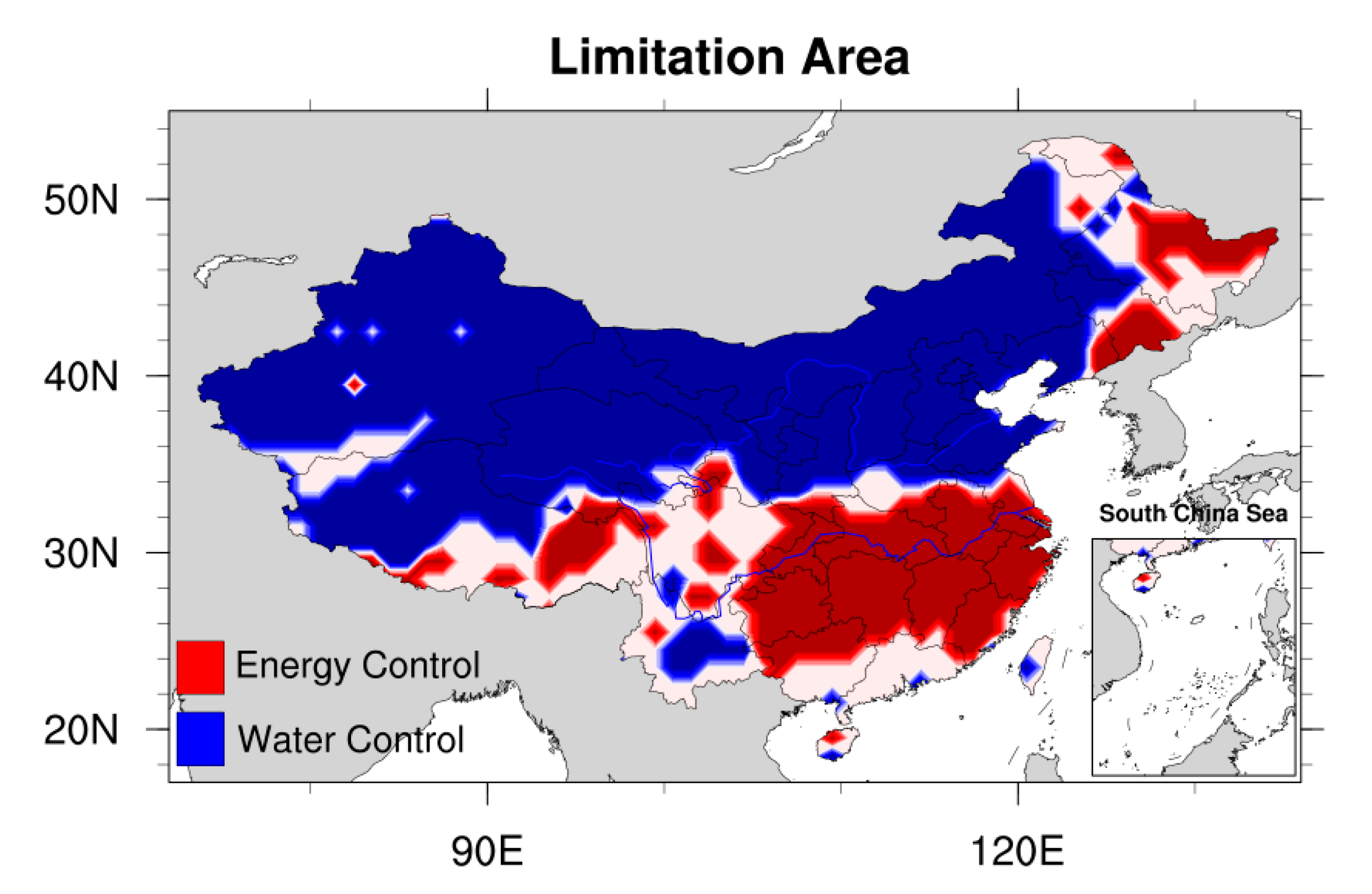
| Datasets | Variables | Time Scale | Resolution |
|---|---|---|---|
| LandFlux-EVAL | Evapotranspiration | 1989–2005 (Monthly) | 1 × 1° |
| FLUXNET | Sensible heat flux, Latent heat flux | 2003–2005 (Monthly) | Site |
| CRU | Temperature, Precipitation, Potential evaporation | 1989–2005 (Monthly) | 0.5 × 0.5° |
| NCEP/DOE Reanalysis 2 | Soil moisture, Relative humidity | 1989–2005 (Monthly) | 1 × 1° |
| ERA-Interim | Net radiation, Wind speed, Sensible heat flux, Latent heat flux | 1989–2005 (Monthly) | 1 × 1° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Liang, J.; Cao, X.; Zhang, Z.; Zhang, L. Spatiotemporal Evolution of Evapotranspiration in China after 1998. Water 2020, 12, 3250. https://doi.org/10.3390/w12113250
Guo Q, Liang J, Cao X, Zhang Z, Zhang L. Spatiotemporal Evolution of Evapotranspiration in China after 1998. Water. 2020; 12(11):3250. https://doi.org/10.3390/w12113250
Chicago/Turabian StyleGuo, Qi, Jiening Liang, Xianjie Cao, Zhida Zhang, and Lei Zhang. 2020. "Spatiotemporal Evolution of Evapotranspiration in China after 1998" Water 12, no. 11: 3250. https://doi.org/10.3390/w12113250
APA StyleGuo, Q., Liang, J., Cao, X., Zhang, Z., & Zhang, L. (2020). Spatiotemporal Evolution of Evapotranspiration in China after 1998. Water, 12(11), 3250. https://doi.org/10.3390/w12113250






