Evaluation of TMPA Satellite Precipitation in Driving VIC Hydrological Model over the Upper Yangtze River Basin
Abstract
1. Introduction
2. Materials and Methods
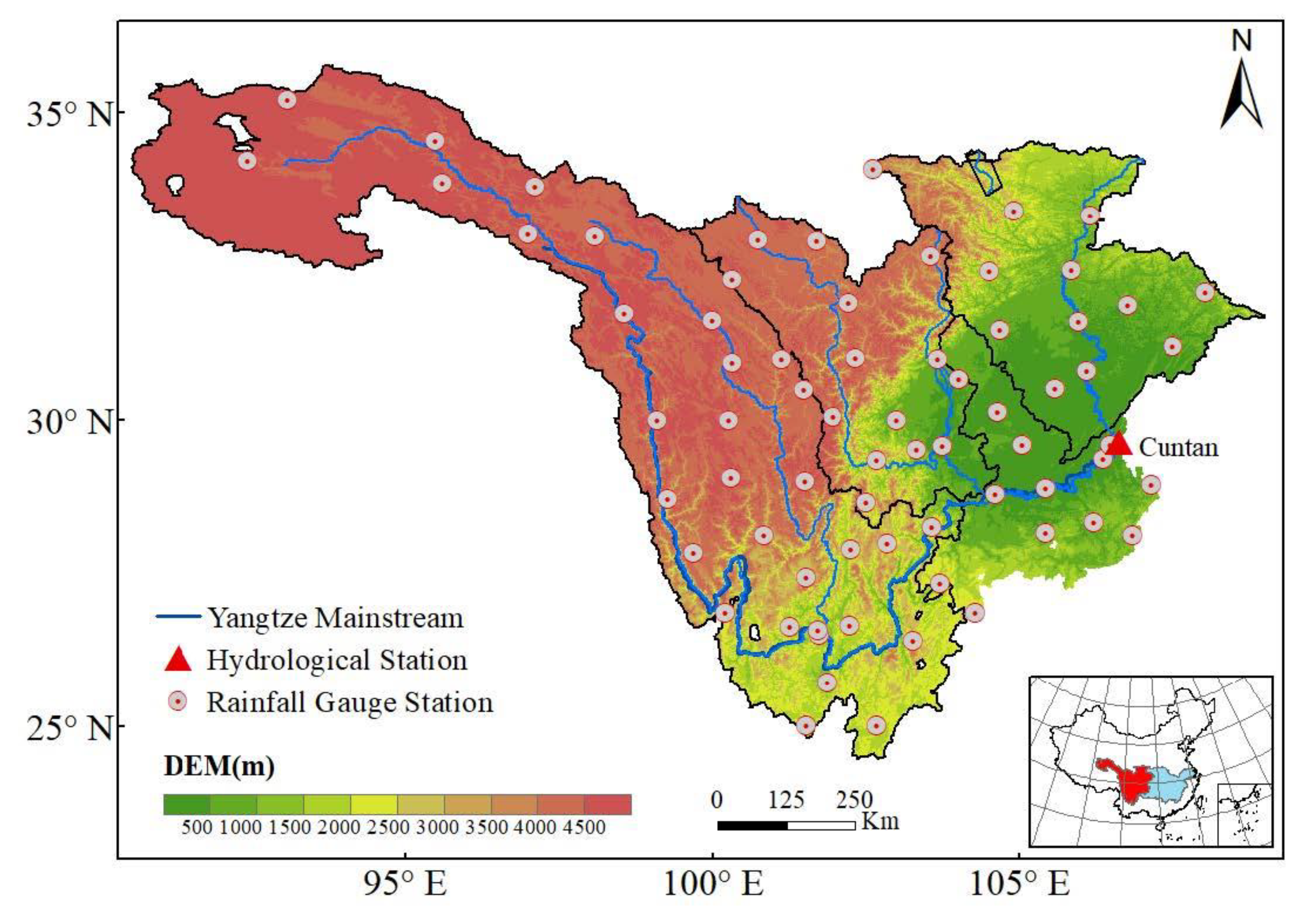
2.1. Study Area
2.2. Data
2.3. Hydrological Model
2.4. Statistical Method
3. Results
3.1. Evaluation of the TMPA Precipitation Products
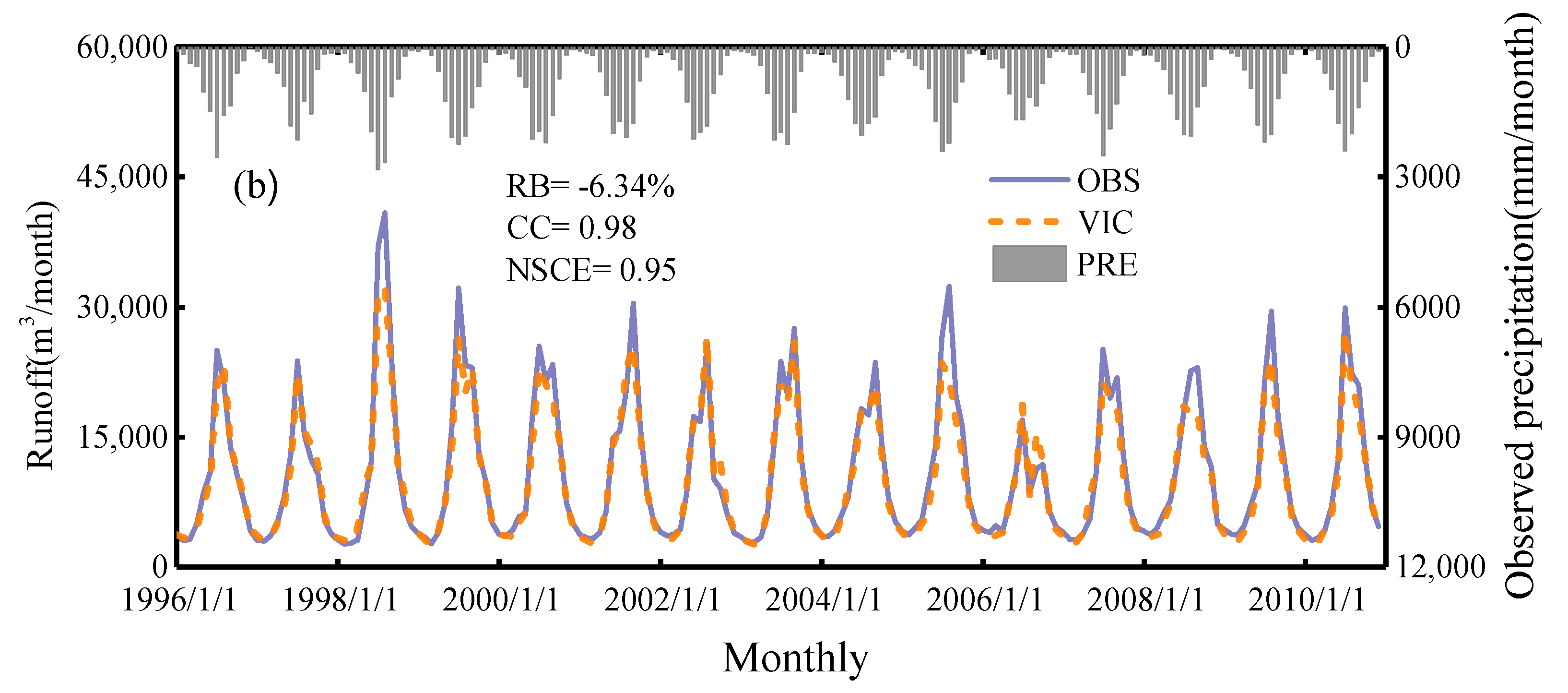
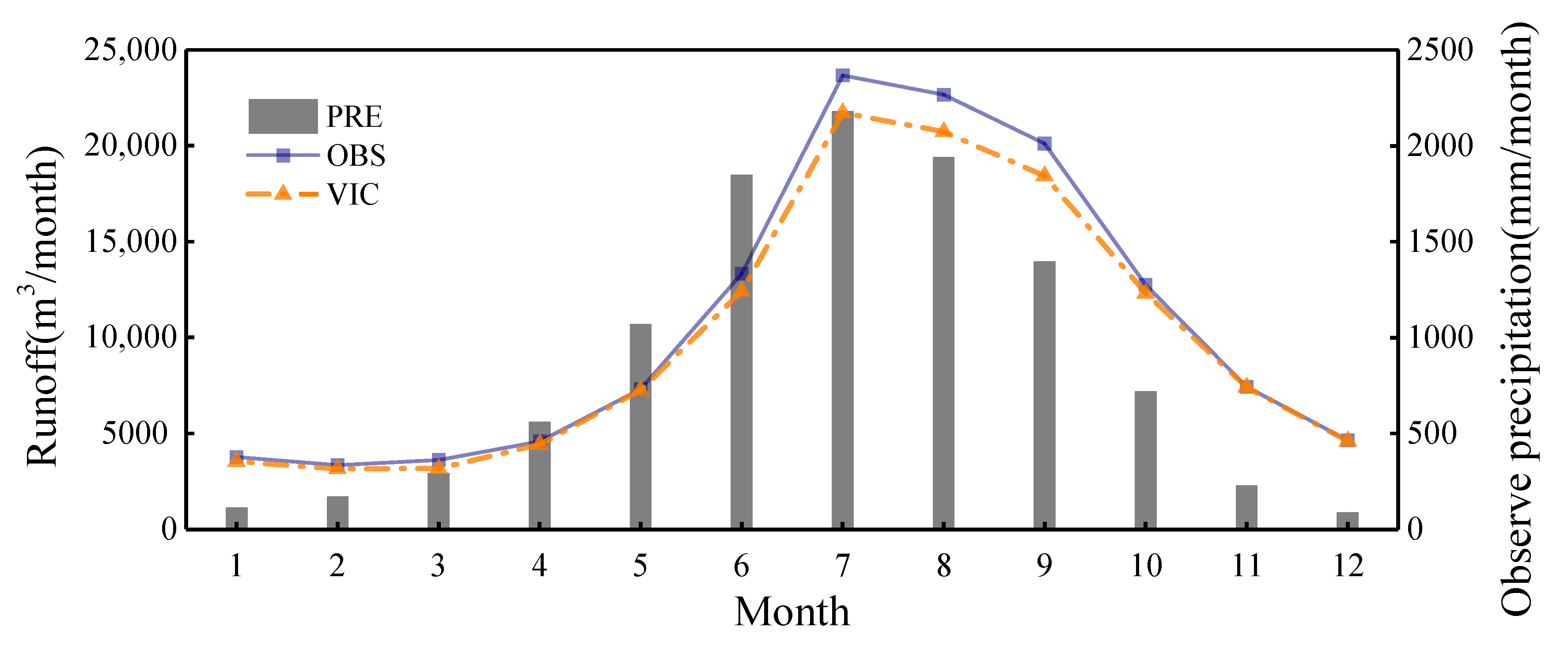
3.2. Hydrologic Model Calibration
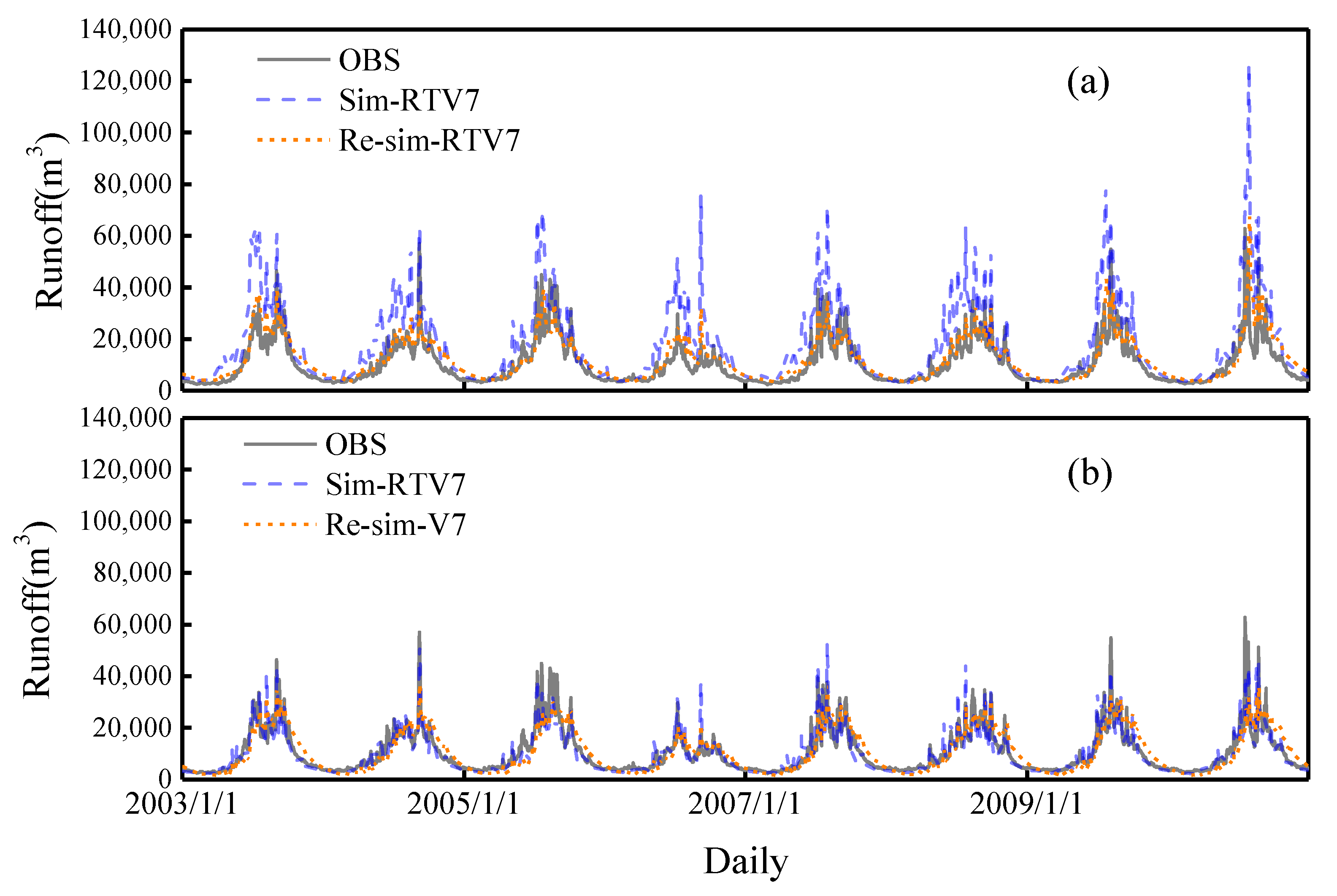
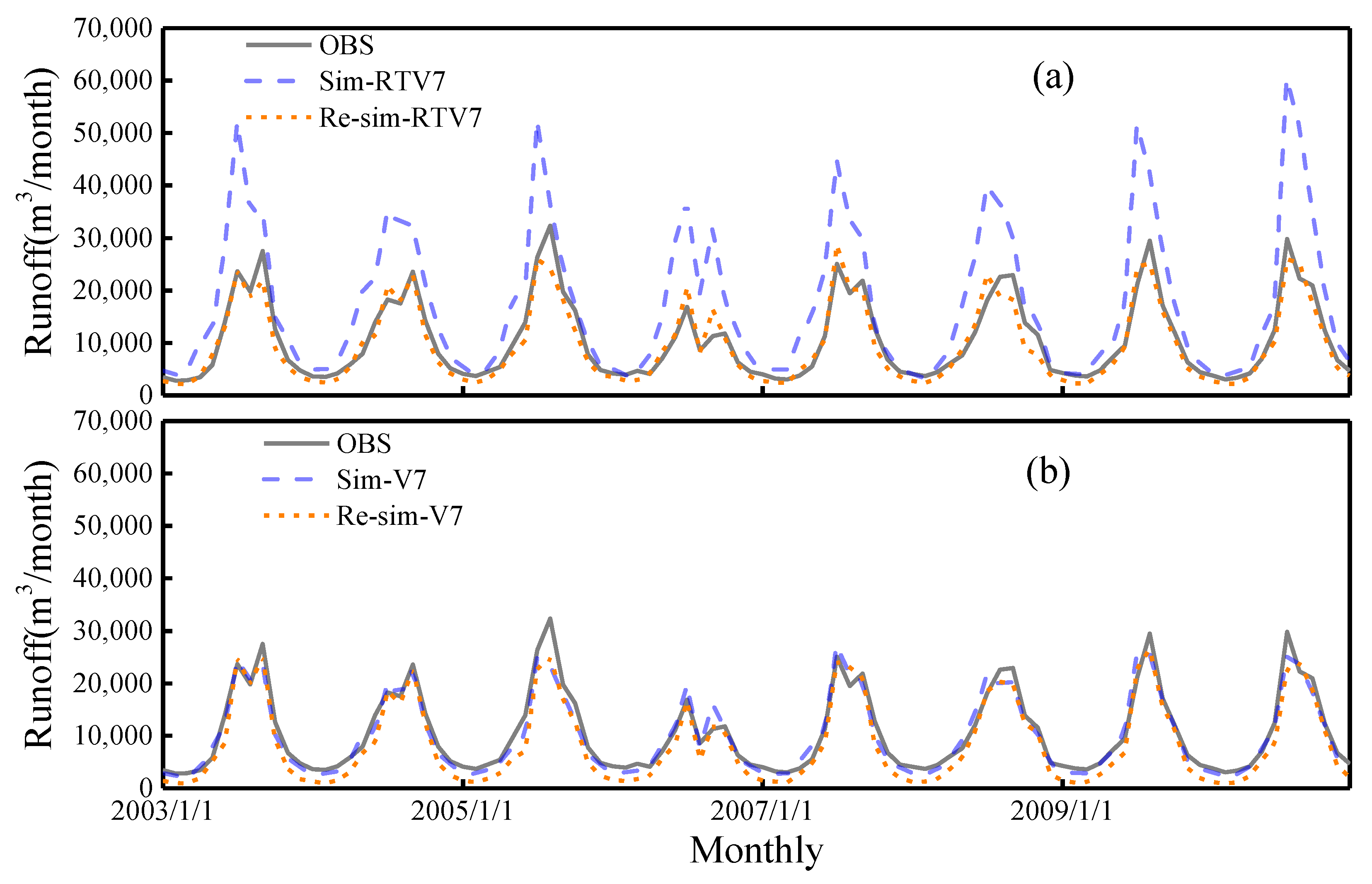
3.3. Hydrologic Model Simulation
4. Discussion
5. Conclusions
- (1)
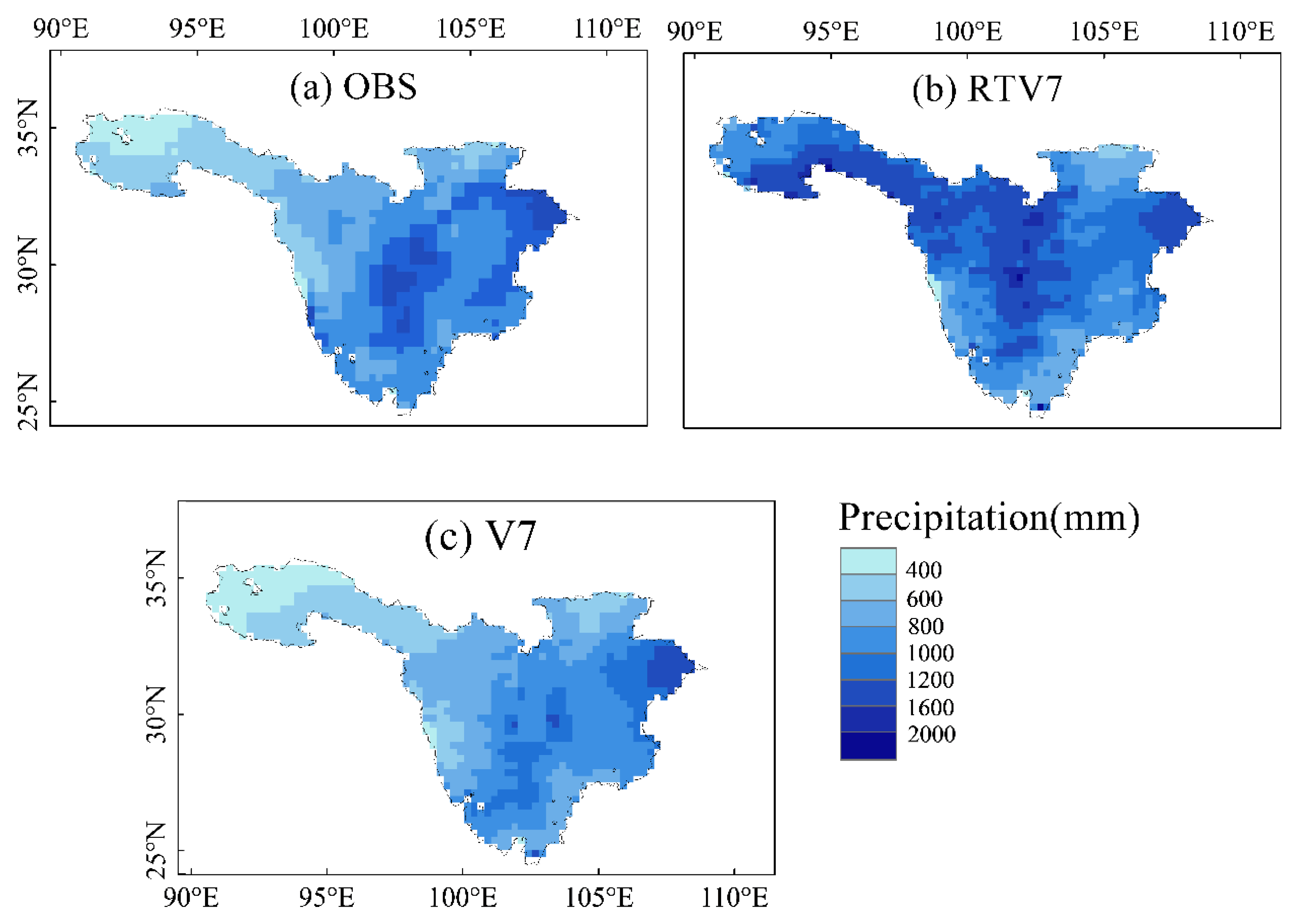
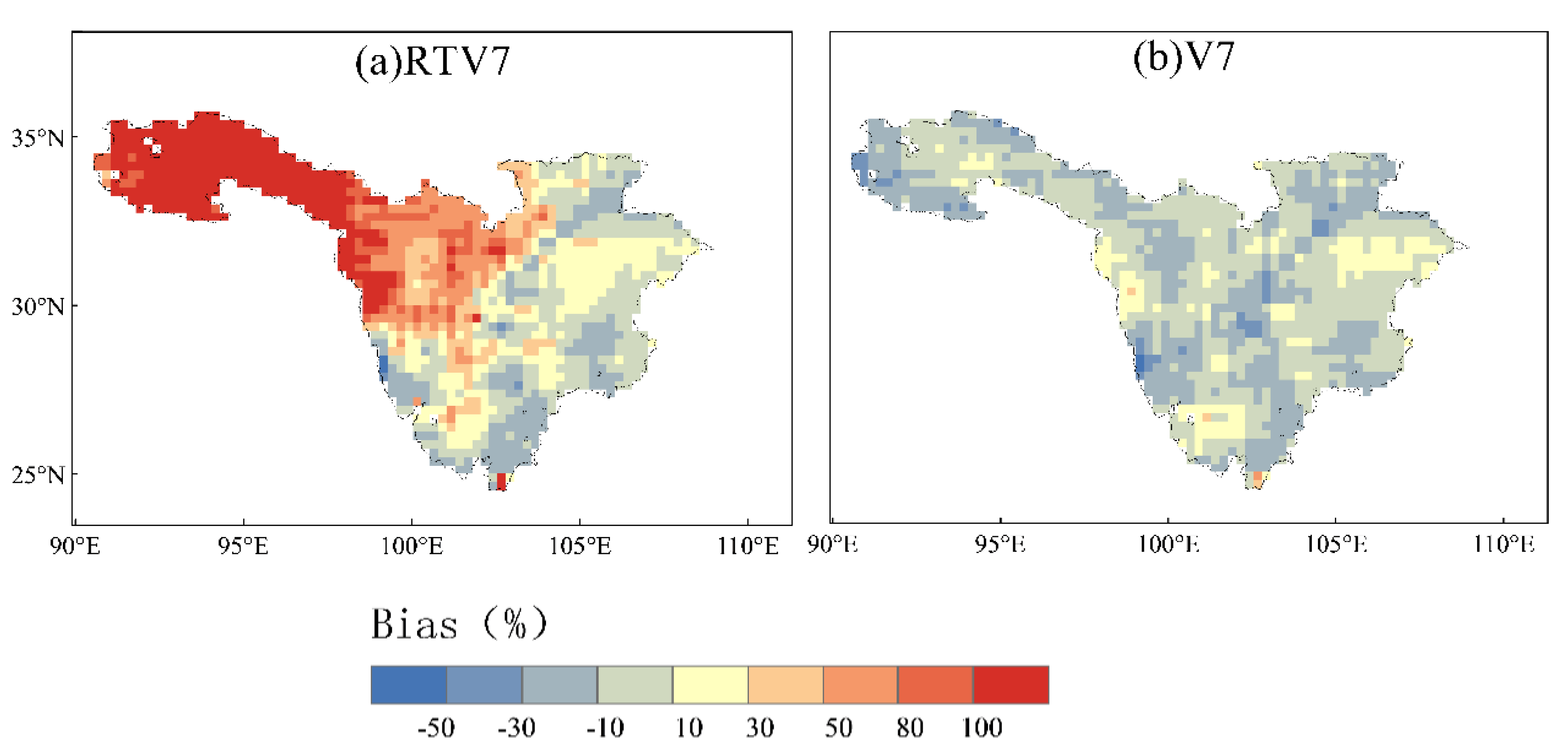
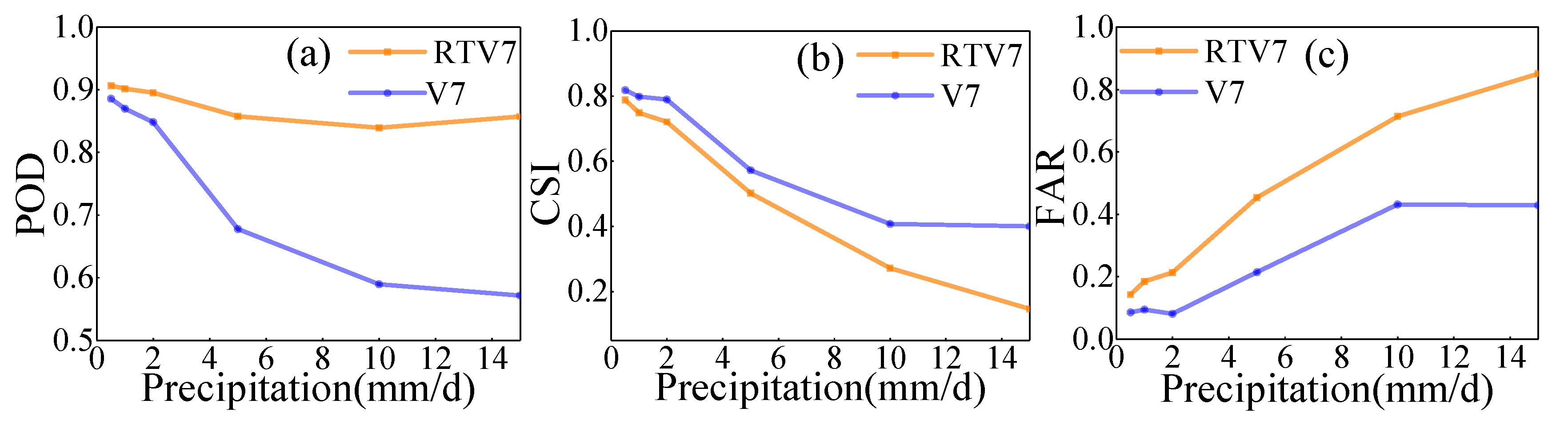
- The spatiotemporal comparisons of precipitation over the upper Yangtze River basin suggest that 3B42V7 had a reliable performance in the precipitation estimation. Although 3B42V7 (RB = −6.24%, RMSE = 1.10 mm/day and CC = 0.92) slightly underestimated precipitation, 3B42RTV7 (RB = −34.68%, RMSE = 2.2 mm/day and CC = 0.84) significantly overestimated precipitation at the daily time scale. 3B42V7 well captured the distribution of precipitation but underestimated almost 66% of parts of the entire study area. 3B42RTV7 overestimated more than 75% of parts of the entire study area, especially in the northwestern parts of the Jinshajiang River basin. Besides, 3B42RTV7 was more sensitive to precipitation events (POD > 0.7), while 3B42V7 showed better ability and accuracy in slight precipitation events detection (precipitation < 4 mm/day, POD > 0.7). Overall, the good performances of the 3B42RTV7/V7 precipitation products suggest that they are feasible for runoff simulation.
- (2)
- The VIC hydrological model has good adaptability in hydrological simulation in the upper reaches of the Yangtze River. The simulated runoff using the VIC hydrological model has a good correlation with the gauged runoff at daily/monthly time scales using the gauged precipitation for parameter calibration. The NSCE value was as high as 0.85, the RB was −6.36% and the CC value was 0.93 at daily scales, while the NSCE and CC rose to 0.95 and 0.98 at monthly scales, respectively. The VIC model simulation results indicated that it was reliable in runoff simulation over the upper Yangtze River basin. When using 3B42RTV7/V7 as the input data, the 3B42V7-driven runoff simulation agreed well with the gauged runoff, where the CC was 0.90, the RB was −5.78 and the NSCE was 0.79 at the daily scale. Although the 3B42RTV7-driven runoff simulation had a good correlation with the gauged runoff (CC = 0.85/daily, 0.93/monthly), it over-simulated the gauged runoff with a significant bias (RB = 66.58%/daily, 66.61%/monthly), and the NSCE was −0.92/daily and −0.81/monthly.
- (3)
- The accuracy of the 3B42RTV7-driven runoff simulation (daily/monthly) had been improved by using the hydrological calibration parameters obtained from 3B42RTV7 compared with parameters obtained from the gauged precipitation. The NSCE rose from −0.92 to 0.71, the RB decreased from 66.58% to 14.38% and the CC rose from 0.85 to 0.87 at daily time scales. However, the performance of the 3B42V7-driven runoff simulation (daily/monthly) was not improved in the same operation accordingly. In particular, the negative RB increased from −5.78% to −19.17% and from −5.75 to −20.90 at daily and monthly time scales, respectively. The outcomes of this work suggest that it might be better to calibrate the parameters using satellite data in hydrological simulations, especially for unadjusted satellite data. It also provides a reference for the application of satellite data to hydrological simulations in other river basins of the world, especially in regions lacking gauged data.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duan, Z.; Bastiaanssen, W.G.M. First results from Version 7 TRMM 3B43 precipitation product in combination with a new downscaling-calibration procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Y.; Zhao, C.; Jiang, H. Impact of precipitation with different intensity on PM2.5 over typical regions of China. Atmosphere 2020, 11, 906. [Google Scholar] [CrossRef]
- Marzano, F.S.; Cimini, D.; Montopoli, M. Investigating precipitation microphysics using ground-based microwave remote sensors and disdrometer data. Atmos. Res. 2010, 97, 583–600. [Google Scholar] [CrossRef]
- Bohnenstengel, S.I.; Schlünzen, K.H.; Beyrich, F. Representativity of in situ precipitation measurements—A case study for the LITFASS area in North-Eastern Germany. J. Hydrol. 2011, 400, 387–395. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, C.; Wang, Y.; Ma, Z. Spatiotemporal variations of precipitation in china using surface gauge observations from 1961 to 2016. Atmosphere 2020, 11, 303. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R. GIS-based spatial precipitation estimation: A comparison of geostatistical approaches. J. Am. Water Resour. 2009, 45, 894. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, C.; Su, Y.; Ma, Z.; Li, J.; Letu, H.; Yang, Y.; Fan, H. Distinct impacts of light and heavy precipitation on PM2.5 mass concentration in Beijing. Earth Space Sci. 2019, 6, 1915–1925. [Google Scholar] [CrossRef]
- Zhao, C.; Garrett, T.J. Ground-based remote sensing of precipitation in the Arctic. J. Geophys. Res. Atmos. 2008, 113, D14204. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Xu, C. Suitability of the TRMM satellite rainfalls in driving a distributed hydrological model for water balance computations in Xinjiang catchment, Poyang lake basin. J. Hydrol. 2012, 426–427, 28–38. [Google Scholar] [CrossRef]
- Arkin, P.A.; Ardanuy, P.E. Estimating climatic-scale precipitation from space: A review. J. Clim. 1989, 2, 1229–1238. [Google Scholar] [CrossRef]
- Zhao, C.; Lin, Y.; Wu, F.; Wang, Y.; Li, Z.; Rosenfeld, D.; Wang, Y. Enlarging rainfall area of tropical cyclones by atmospheric aerosols. Geophys. Res. Lett. 2018, 45, 8604–8611. [Google Scholar] [CrossRef]
- Nair, S.; Srinivasan, G.; Nemani, R. Evaluation of multi-satellite TRMM derived rainfall estimates over a western state of India. J. Meteorol. Soc. Jpn. 2009, 87, 927–939. [Google Scholar] [CrossRef]
- Vrieling, A.; Sterk, G.; de Jong, S.M. Satellite-based estimation of rainfall erosivity for Africa. J. Hydrol. 2010, 395, 235–241. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, P.; Liang, L.; Zhang, S. Evaluation of precipitation from CMORPH, GPCP-2, TRMM 3B43, GPCC, and ITPCAS with ground-based measurements in the Qinling-Daba Mountains, China. PLoS ONE 2017, 12, e185147. [Google Scholar] [CrossRef] [PubMed]
- Mehran, A.; AghaKouchak, A. Capabilities of satellite precipitation datasets to estimate heavy precipitation rates at different temporal accumulations. Hydrol. Process 2014, 28, 2262–2270. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Grover Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Naumann, G.; Barbosa, P.; Carrao, H.; Singleton, A.; Vogt, J. Monitoring drought conditions and their uncertainties in Africa using TRMM data. J. Appl. Meteorol. Clim. 2012, 51, 1867–1874. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Y.; Huang, Y.; Li, Y.; Hou, C.; Shi, X. Evaluation and hydrological application of satellite-based precipitation datasets in driving hydrological models over the Huifa river basin in Northeast China. Atmos. Res. 2018, 207, 28–41. [Google Scholar] [CrossRef]
- Habib, E.; Henschke, A.; Adler, R.F. Evaluation of TMPA satellite-based research and real-time rainfall estimates during six tropical-related heavy rainfall events over Louisiana, USA. Atmos. Res. 2009, 94, 373–388. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Huang, Y.; Chen, X.; Chen, S.; Duan, Z. Hydrologic evaluation of TRMM and GPM IMERG Satellite-based Precipitation in a Humid Basin of China. Remote Sens. 2019, 11, 431. [Google Scholar] [CrossRef]
- Krishnaswamy, J. Remote Sensing-Based Rainfall Estimates in Data-Scarce Himalaya: Performance Assessment of TRMM_3B42v7, TRMM_3B42RT v7 & GPM_3IMERGHH v03 Using Ground Rainfall and Stream Hydrographs in Sikkim Himalaya, India; In Proceedings of the Fall Meeting 2016; American Geophysical Union: San Francisco, CA, USA, 2016. [Google Scholar]
- Tang, G.; Li, Z.; Xue, X.; Hu, Q.; Yong, B.; Hong, Y. A study of substitutability of TRMM remote sensing precipitation for gauge-based observation in Ganjiang River basin. Adv. Water Sci. 2015, 26, 340–346. [Google Scholar]
- Hao, Z.; Tong, K.; Liu, X.; Zhang, L. Capability of TMPA products to simulate streamflow in upper Yellow and Yangtze River basins on Tibetan Plateau. Water Sci. Eng. 2014, 7, 237–249. [Google Scholar]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and hydrological comparisons between TRMM and GPM level-3 products over a Mid-latitude Basin: Is day-1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2015, 17, 121–137. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Xie, P. Integrated Multi-Satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG); In Proceedings of the Satellite Precipitation Measurement; Springer: Cham, Germany, 2020; pp. 343–353. [Google Scholar]
- Islam, M.; Uyeda, H. Use of TRMM in determining the climatic characteristics of rainfall over Bangladesh. Remote Sens. Environ. 2007, 108, 264–276. [Google Scholar] [CrossRef]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based Multi-satellite Precipitation Analysis over the Wangchu Basin of Bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Zhaochen, L.; Meixue, Y.; Xuejia, W.; Lizhen, C. The GPM and TRMM satellite-based precipitation products applied in the source regions of the Yellow River. J. Glaciol. Geocryol. 2020, 42, 575–586. [Google Scholar]
- Tan, M.; Duan, Z. Assessment of GPM and TRMM Precipitation Products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176–177, 121–133. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Hao, Z. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Hughes, D.A.; Andersson, L.; Wilk, J.; Savenije, H.H.G. Regional calibration of the Pitman model for the Okavango River. J. Hydrol. 2006, 331, 30–42. [Google Scholar] [CrossRef]
- Su, F.; Hong, Y.; Lettenmaier, D.P. Evaluation of TRMM Multisatellite Precipitation Analysis (TMPA) and its utility in hydrologic prediction in the La Plata Basin. J. Hydrometeorol. 2008, 9, 622–640. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Using SWAT to model streamflow in two river basins with ground and satellite precipitation data1. J. Am. Water Resour. 2009, 45, 253–271. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Hong, Y.; Yong, B.; Yang, X.; Yuan, F.; Ma, M. Comprehensive evaluation of multi-satellite precipitation products with a dense rain gauge network and optimally merging their simulated hydrological flows using the Bayesian model averaging method. J. Hydrol. 2012, 452–453, 213–225. [Google Scholar] [CrossRef]
- Wang, B.; Jin, S. Study on the feasibility of rainfall measuring productsbase on satellite remote sensing in the source region of Yellow River. J. Qinghai Univ. 2020, 38, 78–85. [Google Scholar]
- Adler, R.F.; Wang, J.; Gu, G.; Huffman, G.J. A ten-year tropical rainfall climatology based on a composite of TRMM products. J. Meteorol. Soc. Jpn. 2009, 87A, 281–293. [Google Scholar] [CrossRef]
- Fengying, Z.; Zengxin, Z.; Jiaxi, T.; Richao, H.; Kong, R.; Bin, Z.; Zhu, M.; Wang, Y.; Chen, X. Forest NPP simulation in the Yangtze River Basin and its response to climate change. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2020, 1–7. [Google Scholar]
- Long, D.; Yang, Y.; Wada, Y.; Hong, Y.; Liang, W.; Chen, Y.; Yong, B.; Hou, A.; Wei, J.; Chen, L. Deriving scaling factors using a global hydrological model to restore GRACE total water storage changes for China’s Yangtze River Basin. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Guan, Y.; Zhang, X.; Zheng, F.; Wang, B. Trends and variability of daily temperature extremes during 1960–2012 in the Yangtze River Basin, China. Glob. Planet. Chang. 2015, 124, 79–94. [Google Scholar] [CrossRef]
- Li, Q.; Liu, X.; Zhang, J. Changing trends of acid rain types in the Yangtze River Delta region. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2020, 1–8. [Google Scholar]
- Kummerow, C.; Simpson, J.; Thiele, O.; Barnes, W.; Chang, A.T.C.; Stocker, E.; Adler, R.F.; Hou, A.; Kakar, R.; Wentz, F.; et al. The status of the Tropical Rainfall Measuring Mission (TRMM) after two years in orbit. J. Appl. Meteorol. 2000, 39, 1965–1982. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J.; et al. Similarity and difference of the two successive V6 and V7 TRMM multisatellite precipitation analysis performance over China. J. Geophys. Res. Atmos. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Franchini, M.; Pacciani, M. Comparative analysis of several conceptual rainfall-runoff models. J. Hydrol. 1991, 122, 161–219. [Google Scholar] [CrossRef]
- Liang, X.; Wood, E.F.; Lettenmaier, D.P. Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification. Glob. Planet. Chang. 1996, 13, 195–206. [Google Scholar] [CrossRef]
- Xu, L. A Two-Layer Variable Infiltration Capacity Land Surface Representation for General Circulation Models. Ph.D. Thesis, University of Washington, Washington, DC, USA, 1 May 1994. [Google Scholar]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- El Kenawy, A.M.; Lopez-Moreno, J.I.; McCabe, M.F.; Vicente-Serrano, S.M. Evaluation of the TMPA-3B42 precipitation product using a high-density rain gauge network over complex terrain in northeastern Iberia. Glob. Planet. Chang. 2015, 133, 188–200. [Google Scholar] [CrossRef]
- Omranian, E.; Sharif, H.O. Evaluation of the Global Precipitation Measurement (GPM) satellite rainfall products over the lower Colorado River Basin, Texas. J. Am. Water. Resour. 2018, 54, 882–898. [Google Scholar] [CrossRef]
- Chang, J.; Zhang, Z.; Tian, J.; Chen, X.; Chen, Y. Spatio-temporal characteristics of grassland water use efficiency and its response to climate change in northwest China. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2020, 44, 119–125. [Google Scholar]
- Xie, Z.; Yuan, F.; Duan, Q.; Zheng, J.; Liang, M.; Chen, F. Regional parameter estimation of the VIC land surface model: Methodology and application to river basins in China. J. Hydrometeorol. 2007, 8, 447–468. [Google Scholar] [CrossRef]
- Su, F.G.; Adam, J.C.; Bowling, L.C.; Lettenmaier, D.P. Streamflow simulations of the terrestrial Arctic domain. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Chen, C.; Yu, Z.; Li, L.; Yang, C. Adaptability evaluation of TRMM satellite rainfall and its application in the Dongjiang River Basin. Procedia Environ. Sci. 2011, 10, 396–402. [Google Scholar] [CrossRef]
- Yong, B.; Ren, L.; Hong, Y.; Wang, J.; Gourley, J.J.; Jiang, S.; Chen, X.; Wang, W. Hydrologic evaluation of Multisatellite Precipitation Analysis standard precipitation products in basins beyond its inclined latitude band: A case study in Laohahe basin, China. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D. A global map of uncertainties in satellite-based precipitation measurements. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Bai, A.J.; Liu, C.H.; Liu, X.D. Diurnal variation of summer rainfall over the Tibetan Plateau and its neighboring regions revealed by TRMM Multi-satellite Precipitation Analysis. Chin. J. Geophys. 2008, 51, 518–529. [Google Scholar] [CrossRef]
- Ward, E.; Buytaert, W.; Peaver, L.; Wheater, H. Evaluation of precipitation products over complex mountainous terrain: A water resources perspective. Adv. Water Resour. 2011, 34, 1222–1231. [Google Scholar] [CrossRef]
- Narayanan, M.S.; Shah, S.; Kishtawal, C.M.; Sathiyamoorthy, V.; Rajeevan, M.; Kriplani, R.H. Validation of TRMM merge daily rainfall with IMD raingauge analysis over Indian Land Mass. Tech. Rep. 2005, 87, 927–939. [Google Scholar]
- Chen, Y.; Ebert, E.E.; Walsh, K.J.E.; Davidson, N.E. Evaluation of TRMM 3B42 precipitation estimates of tropical cyclone rainfall using PACRAIN data. J. Geophys. Res. Atmos. 2013, 118, 2184–2196. [Google Scholar] [CrossRef]
- Huang, Y.H.; Zhang, Z.X.; Fei, M.Z.; Jin, Q. Hydrological evaluation of the TMPA multisatellite precipitation estimates over the Gangjiang basin. Resour. Environ. Yangtze Basin 2016, 10, 1618–1625. [Google Scholar]
- Nijssen, B.; Lettenmaier, D.P. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res. 2004, 109, D2103. [Google Scholar] [CrossRef]



| Precipitation Product | Daily | Monthly | ||||
|---|---|---|---|---|---|---|
| RB (%) | RMSE (mm) | CC | RB (%) | RMSE (mm) | CC | |
| TMPA 3B42RTV7 | 34.68 | 2.2 | 0.84 | 34.71 | 1108.3 | 0.97 |
| TMPA 3B42V7 | −6.24 | 1.1 | 0.92 | −6.21 | 196.2 | 0.99 |
| Parameters | Definition | Value Range | Calibration Value | ||
|---|---|---|---|---|---|
| OBS | 3B42RTV7 | 3B42V7 | |||
| B | Variable infiltration curve parameter (binfilt) | 0–0.4 | 0.4 | 0.1872 | 0.4 |
| Ws | Fraction of maximum soil moisture where a non-linear base flow occurs | 0–1.0 | 0.2008 | 0.6004 | 0.2008 |
| Ds | Fraction of Dsmax where a non-linear base flow begins | 0–1.0 | 0.01 | 0.001 | 1 |
| Dsmax | Maximum velocity of the baseflow (mm/day) | 0–30 | 6.008 | 4.009 | 12.006 |
| d1 | Thickness of each soil moisture layer (m) | 0.1–2.0 | 0.01 | 0.01 | 0.01 |
| d2 | 0.1 | 0.6067 | 0.1 | ||
| d3 | 1.24 | 2 | 1.8733 | ||
| Simulated Runoff | Driven by the Precipitation | Hydrological Parameters |
|---|---|---|
| RRTV7_RTV7 | 3B42RTV7 | 3B42RTV7 |
| RRTV7_OBS | 3B42RTV7 | Gauged |
| RV7_V7 | 3B42V7 | 3B42V7 |
| RV7_OBS | 3B42V7 | Gauged |
| Hydrological Parameters | Driven by the Precipitation | Daily | Monthly | ||||
|---|---|---|---|---|---|---|---|
| RB (%) | CC | NSCE | RB (%) | CC | NSCE | ||
| Gauged | 3B42RTV7 | 66.58 | 0.85 | −0.92 | 66.61 | 0.93 | −0.81 |
| 3B42RTV7 | 3B42RTV7 | 14.38 | 0.87 | 0.71 | 14.41 | 0.95 | 0.86 |
| Gauged | 3B42V7 | −5.78 | 0.90 | 0.79 | −5.75 | 0.97 | 0.94 |
| 3B42V7 | 3B42V7 | −19.17 | 0.87 | 0.73 | −20.90 | 0.97 | 0.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Huang, Y.; Zhang, Z.; Kong, R.; Tian, J.; Zhou, Y.; Chen, S.; Duan, Z. Evaluation of TMPA Satellite Precipitation in Driving VIC Hydrological Model over the Upper Yangtze River Basin. Water 2020, 12, 3230. https://doi.org/10.3390/w12113230
Zhu B, Huang Y, Zhang Z, Kong R, Tian J, Zhou Y, Chen S, Duan Z. Evaluation of TMPA Satellite Precipitation in Driving VIC Hydrological Model over the Upper Yangtze River Basin. Water. 2020; 12(11):3230. https://doi.org/10.3390/w12113230
Chicago/Turabian StyleZhu, Bin, Yuhan Huang, Zengxin Zhang, Rui Kong, Jiaxi Tian, Yichen Zhou, Sheng Chen, and Zheng Duan. 2020. "Evaluation of TMPA Satellite Precipitation in Driving VIC Hydrological Model over the Upper Yangtze River Basin" Water 12, no. 11: 3230. https://doi.org/10.3390/w12113230
APA StyleZhu, B., Huang, Y., Zhang, Z., Kong, R., Tian, J., Zhou, Y., Chen, S., & Duan, Z. (2020). Evaluation of TMPA Satellite Precipitation in Driving VIC Hydrological Model over the Upper Yangtze River Basin. Water, 12(11), 3230. https://doi.org/10.3390/w12113230







