Return Level Analysis of the Hanumante River Using Structured Expert Judgment: A Reconstruction of Historical Water Levels
Abstract
1. Introduction
2. Materials and Methods
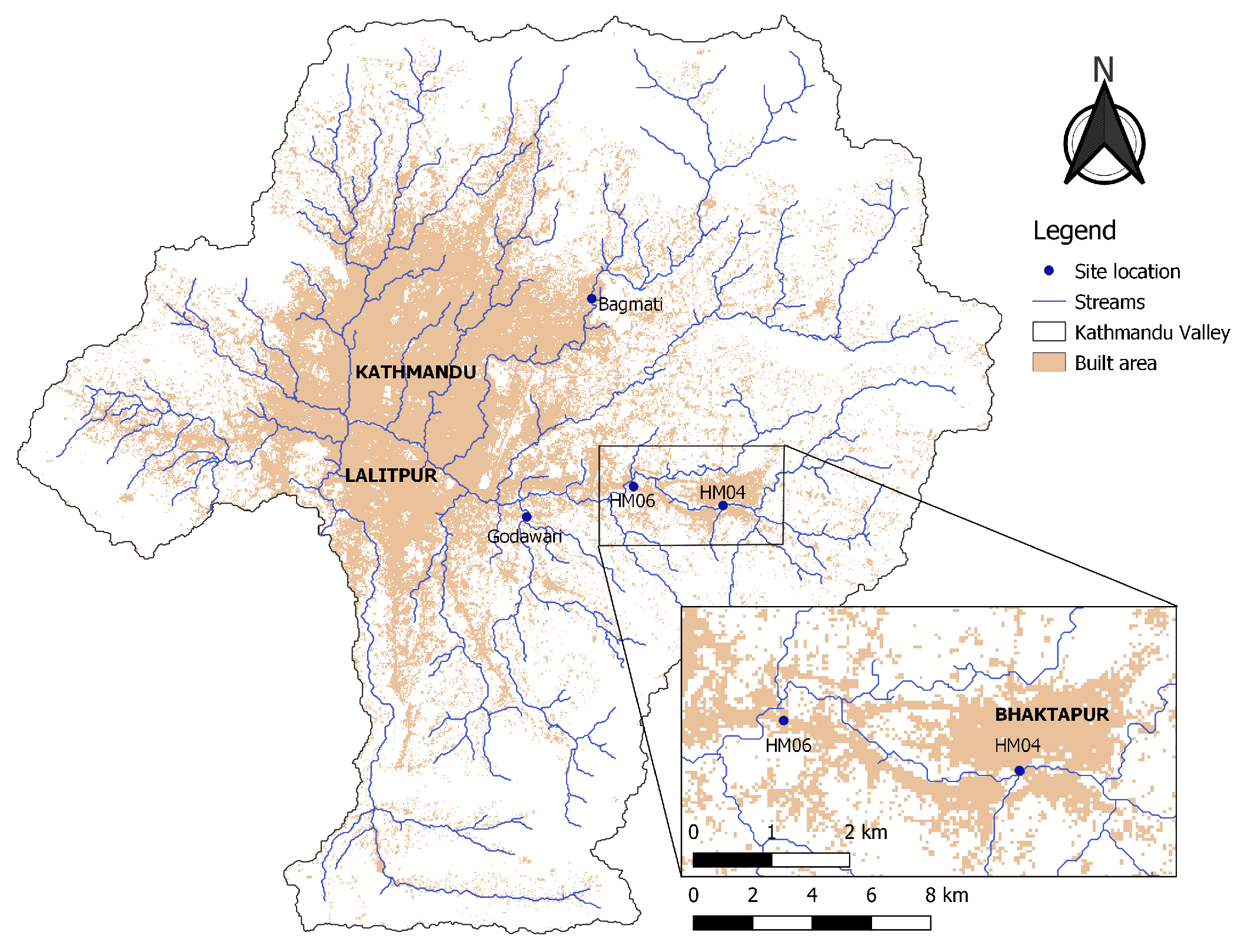
2.1. Study Area
2.2. Structured Expert Judgment
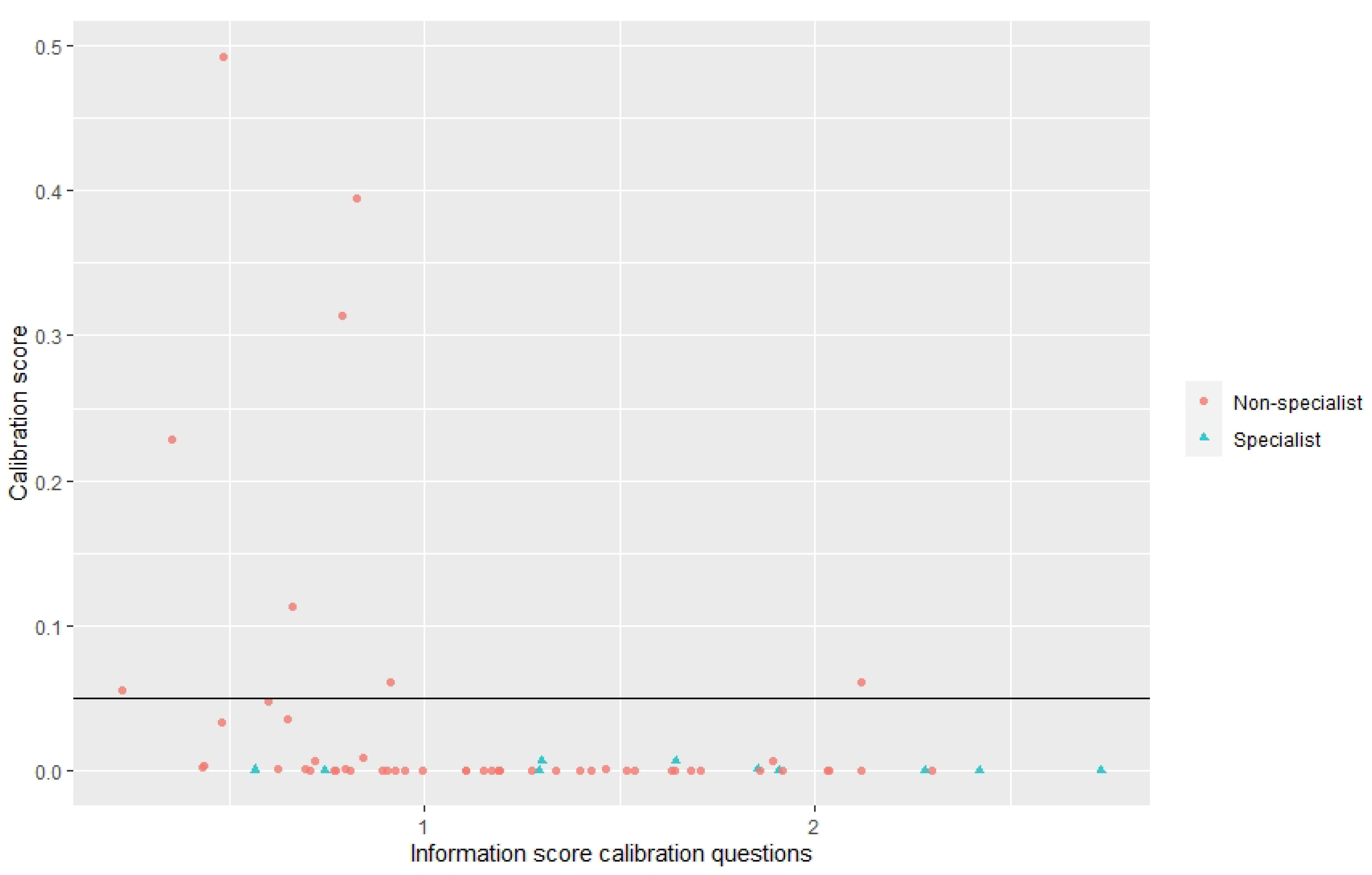
2.2.1. Evaluating Experts’ Assessments
2.2.2. Aggregating Experts’ Assessments
2.2.3. Expert Selection & Questionnaires
2.2.4. Calibration Questions & Target Questions
2.2.5. Software
2.3. Return Levels
- 0 Gumbel (Type I for maxima)
- 0 Fréchet (Type II for maxima)
- 0 Reverse Weibull (Type III for maxima)
3. Results
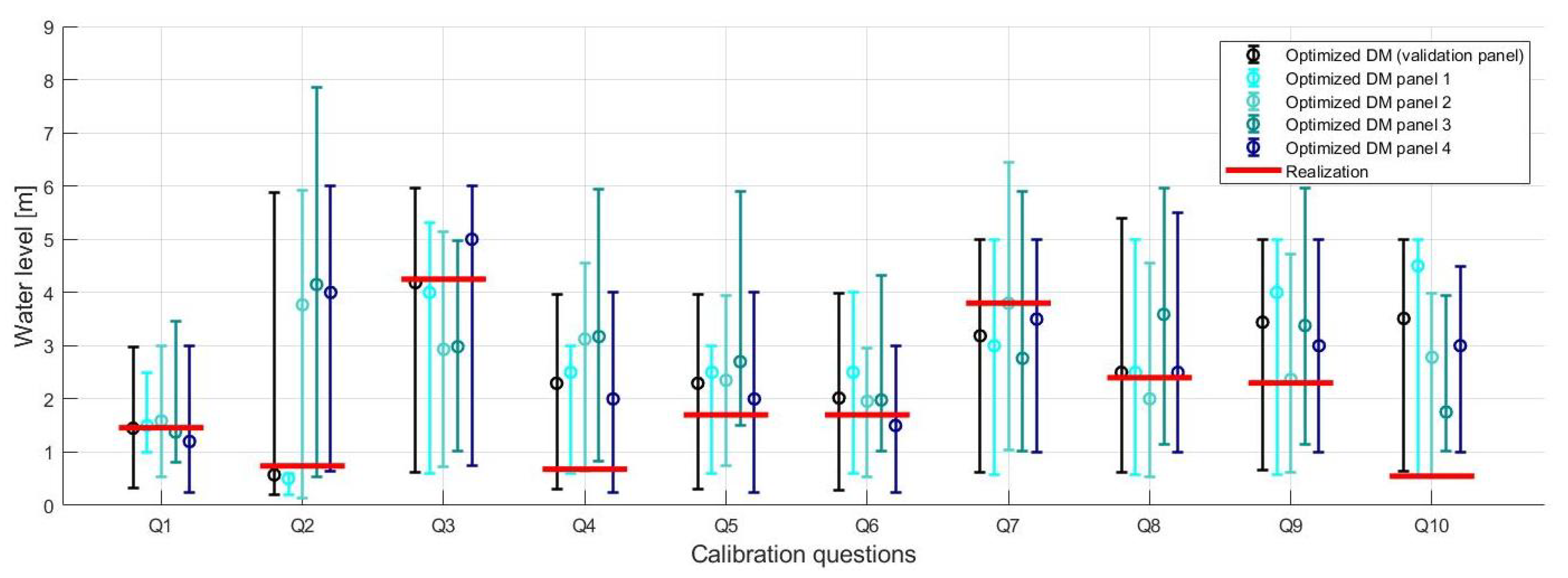
3.1. Structured Expert Judgment
3.1.1. Panel 1
3.1.2. Panel 2
3.1.3. Panel 3
3.1.4. Panel 4
3.1.5. Validation Panel
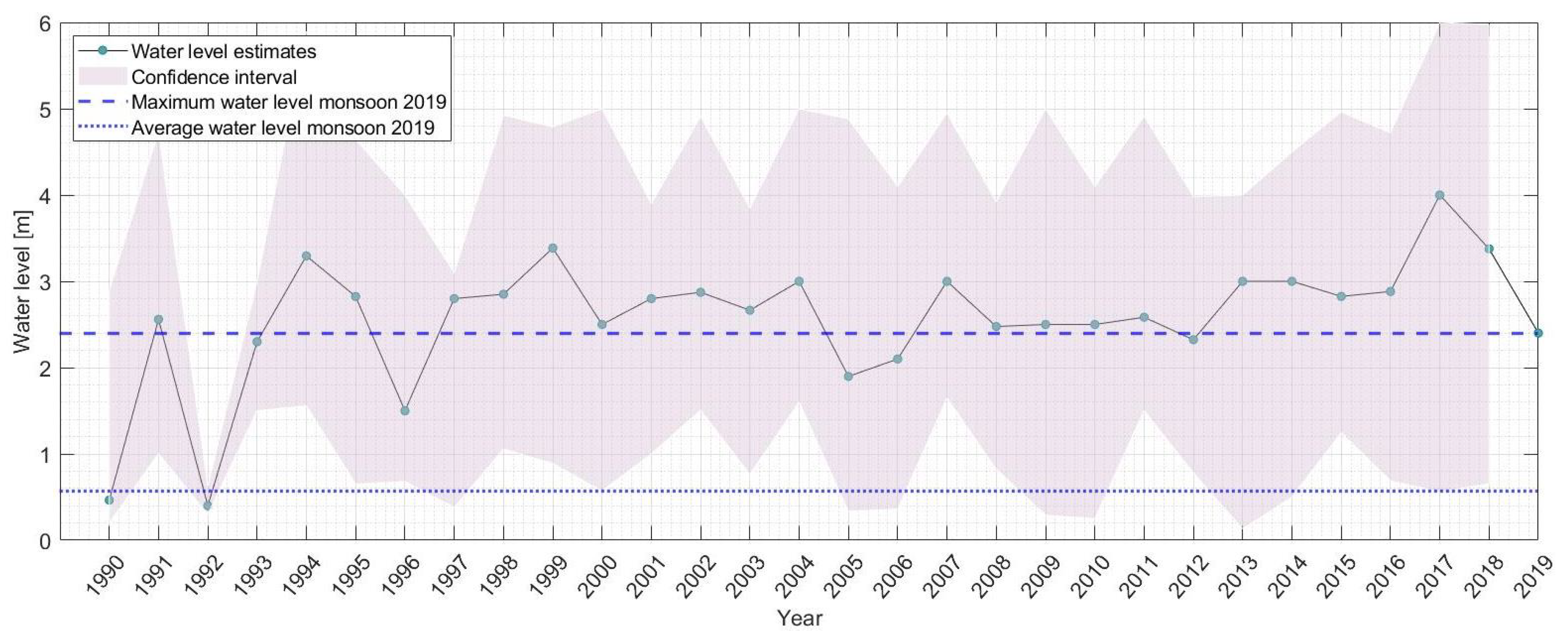
3.2. Maximum Water Levels
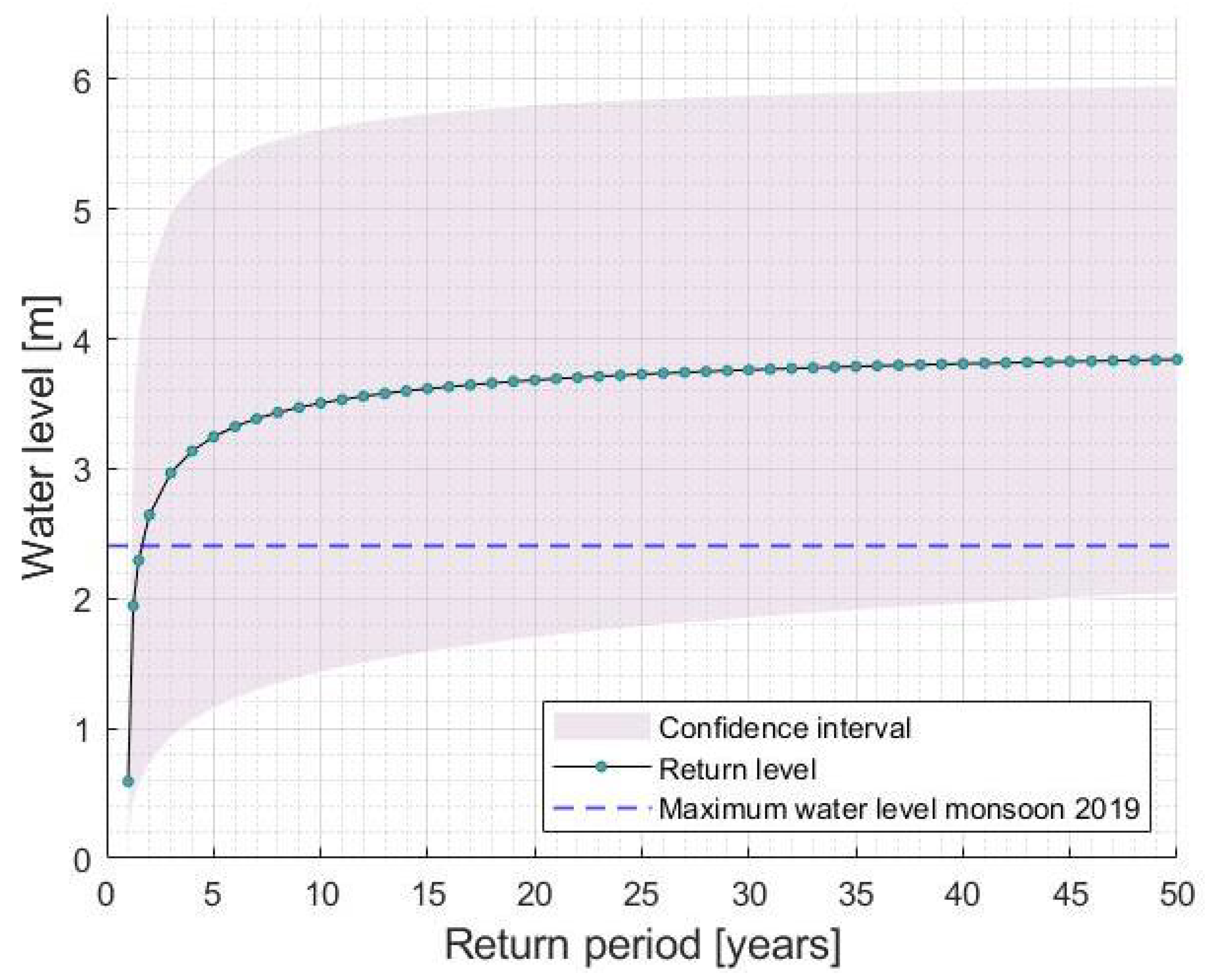
3.3. Return Level Analysis
4. Discussion
- The experts should be better prepared for the questionnaires. An elaborate (oral) explanation of the method is extremely important. Especially the importance of the confidence intervals should be well explained. Moreover, it is advisable to provide the experts with even more background information. It would be useful to give the value of one recent monthly maximum water level. The experts could use this value to refer months of the past to a month that they remember and to understand how much the maximum can deviate from the median.
- It could be useful to ask the experts to start by estimating the water levels of months in which they remember that a flood or very high water level occurred. In this way, it is avoided that experts oversee to assess those years with relatively high values while they are working themselves trough the long list of years. Of course, it cannot be avoided that experts might just forget flood events of the past.
- It is important to choose the calibration questions thoroughly. If possible, all calibration questions should be related to the location of interest. If this is not possible, the locations should be close to the location of interest and the experts should be familiar with them. Besides, it is important that the behaviour of the variable of interest is similar at the other locations. So, the mean and maximum water levels should be comparable at the different locations.
- It would be useful to find a way to validate the results of the SEJ with precipitation data. In order to do so, it is necessary to obtain more knowledge about the relation between precipitation, discharge and water level for the Hanumante River. Furthermore, validation by data time series only makes sense when the reconstructed water levels match to the correct years. We think that validation with precipitation data has potential when our recommendations for application of SEJ are followed.
- We would recommend to continue on evaluating the flood risk by the Hanumante River. Further research could be done on the expected damages due to floods or about the possibilities to reduce damages by floods. The damages can be reduced by a proper evacuation plan. The application of a Community-Based Early Warning System (CBEWS) can play a major role for this. [30].
- Probably our most important recommendation is to highlight the importance of continuing actual water level and discharge measurements in the Hanumante River, if possible on a daily basis. Over time, these efforts would provide the much needed data that would ultimately improve our understanding of the return levels.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CM | Classical Model |
| DHM | Department of Hydrology and Meteorology |
| DM | Decision Maker |
| DOAJ | Directory of open access journals |
| GEV | Generalized Extreme Value |
| ICIMOD | International Centre for Integrated Mountain Development |
| MDPI | Multidisciplinary Digital Publishing Institute |
| Probability Density Function | |
| SEJ | Structured Expert Judgment |
| S4W | Smartphones For Water Nepal |
Appendix A. Overview of the Questions Answered by Different Panels
| Specific Question Number Per Group | ||||||
|---|---|---|---|---|---|---|
| Question nr | Question | Validation Panel | Panel 1 | Panel 2 | Panel 3 | Panel 4 |
| CQ1 | What was the highest water level at the Bagmati River in July 2017? | 1 | 1 | 1 | 1 | 1 |
| CQ2 | What was the highest water level at the Godawari River in July 2017? | 2 | 2 | 2 | 2 | 2 |
| CQ3 | What was the highest water level at the HM06 in July 2018? | 3 | 3 | 3 | 3 | 3 |
| CQ4 | What was the highest water level at the HM06 in June 2019? | 4 | 4 | 4 | 4 | 4 |
| CQ5 | What was the highest water level at the HM06 in July 2019? | 5 | 5 | 5 | 5 | 5 |
| CQ6 | What was the highest water level at the HM06 in August 2018? | 6 | 6 | 6 | 6 | 6 |
| CQ7 | What was the highest water level at the HM04 in August 2015? | 7 | 7 | 7 | 7 | 7 |
| CQ8 | What was the highest water level at the HM04 in August 2019? | 8 | 8 | 8 | 8 | 8 |
| CQ9 | What was the highest water level at the HM04 in July 2019? | 9 | 9 | 9 | 9 | 9 |
| CQ10 | What was the highest water level at the HM04 in June 2019? | 10 | 10 | 10 | 10 | 10 |
| TQ1 | What was the highest water level in August 2018? | 11 | 11 | 11 | 11 | 11 |
| TQ2 | What was the highest water level in July 2018? | 12 | 12 | 12 | 12 | 12 |
| TQ3 | What was the highest water level in June 2018? | 13 | 13 | 13 | 13 | 13 |
| TQ4 | What was the highest water level in August 2017? | 14 | ||||
| TQ5 | What was the highest water level in July 2017? | 15 | ||||
| TQ6 | What was the highest water level in June 2017? | 16 | ||||
| TQ7 | What was the highest water level in August 2016? | 14 | ||||
| TQ8 | What was the highest water level in July 2016? | 15 | ||||
| TQ9 | What was the highest water level in June 2016? | 16 | ||||
| TQ10 | What was the highest water level in August 2015? | 14 | ||||
| TQ11 | What was the highest water level in July 2015? | 15 | ||||
| TQ12 | What was the highest water level in June 2015? | 16 | ||||
| TQ13 | What was the highest water level in August 2014? | 14 | ||||
| TQ14 | What was the highest water level in July 2014? | 15 | ||||
| TQ15 | What was the highest water level in June 2014? | 16 | ||||
| TQ16 | What was the highest water level in August 2013? | 17 | ||||
| TQ17 | What was the highest water level in July 2013? | 18 | ||||
| TQ18 | What was the highest water level in June 2013? | 19 | ||||
| TQ19 | What was the highest water level in August 2012? | 17 | ||||
| TQ20 | What was the highest water level in July 2012? | 18 | ||||
| TQ21 | What was the highest water level in June 2012? | 19 | ||||
| TQ22 | What was the highest water level in August 2011? | 17 | ||||
| TQ23 | What was the highest water level in July 2011? | 18 | ||||
| TQ24 | What was the highest water level in June 2011? | 19 | ||||
| TQ25 | What was the highest water level in August 2010? | 17 | ||||
| TQ26 | What was the highest water level in July 2010? | 18 | ||||
| TQ27 | What was the highest water level in June 2010? | 19 | ||||
| TQ28 | What was the highest water level in August 2009? | 20 | ||||
| TQ29 | What was the highest water level in July 2009? | 21 | ||||
| TQ30 | What was the highest water level in June 2009? | 22 | ||||
| TQ31 | What was the highest water level in August 2008? | 20 | ||||
| TQ32 | What was the highest water level in July 2008? | 21 | ||||
| TQ33 | What was the highest water level in June 2008? | 22 | ||||
| TQ34 | What was the highest water level in August 2007? | 20 | ||||
| TQ35 | What was the highest water level in July 2007? | 21 | ||||
| TQ36 | What was the highest water level in June 2007? | 22 | ||||
| TQ37 | What was the highest water level in August 2006? | 20 | ||||
| TQ38 | What was the highest water level in July 2006? | 21 | ||||
| TQ39 | What was the highest water level in June 2006? | 22 | ||||
| TQ40 | What was the highest water level in August 2005? | 14 | 23 | 23 | 23 | 23 |
| TQ41 | What was the highest water level in July 2005? | 15 | 24 | 24 | 24 | 24 |
| TQ42 | What was the highest water level in June 2005? | 16 | 25 | 25 | 25 | 25 |
| TQ43 | What was the highest water level in August 2004? | 26 | ||||
| TQ44 | What was the highest water level in July 2004? | 27 | ||||
| TQ45 | What was the highest water level in June 2004? | 28 | ||||
| TQ46 | What was the highest water level in August 2003? | 26 | ||||
| TQ47 | What was the highest water level in July 2003? | 27 | ||||
| TQ48 | What was the highest water level in June 2003? | 28 | ||||
| TQ49 | What was the highest water level in August 2002? | 26 | ||||
| TQ50 | What was the highest water level in July 2002? | 27 | ||||
| TQ51 | What was the highest water level in June 2002? | 28 | ||||
| TQ52 | What was the highest water level in August 2001? | 26 | ||||
| TQ53 | What was the highest water level in July 2001? | 27 | ||||
| TQ54 | What was the highest water level in June 2001? | 28 | ||||
| TQ55 | What was the highest water level in August 2000? | 29 | ||||
| TQ56 | What was the highest water level in July 2000? | 30 | ||||
| TQ57 | What was the highest water level in June 2000? | 31 | ||||
| TQ58 | What was the highest water level in August 1999? | 29 | ||||
| TQ59 | What was the highest water level in July 1999? | 30 | ||||
| TQ60 | What was the highest water level in June 1999? | 31 | ||||
| TQ61 | What was the highest water level in August 1998? | 29 | ||||
| TQ62 | What was the highest water level in July 1998? | 30 | ||||
| TQ63 | What was the highest water level in June 1998? | 31 | ||||
| TQ64 | What was the highest water level in August 1997? | 29 | ||||
| TQ65 | What was the highest water level in July 1997? | 30 | ||||
| TQ66 | What was the highest water level in June 1997? | 31 | ||||
| TQ67 | What was the highest water level in August 1996? | 32 | ||||
| TQ68 | What was the highest water level in July 1996? | 33 | ||||
| TQ69 | What was the highest water level in June 1996? | 34 | ||||
| TQ70 | What was the highest water level in August 1995? | 32 | ||||
| TQ71 | What was the highest water level in July 1995? | 33 | ||||
| TQ72 | What was the highest water level in June 1995? | 34 | ||||
| TQ73 | What was the highest water level in August 1994? | 32 | ||||
| TQ74 | What was the highest water level in July 1994? | 33 | ||||
| TQ75 | What was the highest water level in June 1994? | 34 | ||||
| TQ76 | What was the highest water level in August 1993? | 32 | ||||
| TQ77 | What was the highest water level in July 1993? | 33 | ||||
| TQ78 | What was the highest water level in June 1993? | 34 | ||||
| TQ79 | What was the highest water level in August 1992? | 35 | ||||
| TQ80 | What was the highest water level in July 1992? | 36 | ||||
| TQ81 | What was the highest water level in June 1992? | 37 | ||||
| TQ82 | What was the highest water level in August 1991? | 35 | ||||
| TQ83 | What was the highest water level in July 1991? | 36 | ||||
| TQ84 | What was the highest water level in June 1991? | 37 | ||||
| TQ85 | What was the highest water level in August 1990? | 17 | 38 | 38 | 35 | 35 |
| TQ86 | What was the highest water level in July 1990? | 18 | 39 | 39 | 36 | 36 |
| TQ87 | What was the highest water level in June 1990? | 19 | 40 | 40 | 37 | 37 |
| TQ88 | What do you expect to be the highest water level in the year 2025? | 20 | 41 | 41 | 38 | 38 |
Appendix B. Calibration and Information Scores per Expert
| Expert | Function | Calibration Score | Information Score (Seed) | Information Score (All) | Normalized Global Weights | Normalized Optimized Weights |
|---|---|---|---|---|---|---|
| Expert 1.1 | Citizen of Bhaktapur | 2.118 | 1.981 | 0.148 | 0 | |
| Expert 1.2 | Student | 2.300 | 1.893 | 0 | ||
| Expert 1.3 | Citizen of Bhaktapur | 0.113 | 0.664 | 0.680 | 0.087 | 0 |
| Expert 1.4 | Citizen of Bhaktapur | 0.314 | 0.789 | 0.460 | 0.284 | 0 |
| Expert 1.5 | Citizen of Bhaktapur | 1.633 | 1.503 | 0 | ||
| Expert 1.6 | Citizen of Bhaktapur | 1.517 | 1.172 | 0 | ||
| Expert 1.7 | Citizen of Bhaktapur | 1.398 | 1.010 | 0 | ||
| Expert 1.8 | Citizen of Bhaktapur | 1.154 | 1.255 | 0 | ||
| Expert 1.9 | Citizen of Bhaktapur | 0.774 | 0.843 | 0 | ||
| Expert 1.10 | Citizen of Bhaktapur | 1.277 | 1.298 | 0 | ||
| Expert 1.11 | Citizen of Bhaktapur | 0.395 | 0.829 | 0.795 | 0.376 | 1 |
| Expert 1.12 | Citizen of Bhaktapur | 0.694 | 0.625 | 0 | ||
| Expert 1.13 | Citizen of Bhaktapur | 0.438 | 0.510 | 0 | ||
| Expert 1.14 | Citizen of Bhaktapur | 2.032 | 1.847 | 0 | ||
| Expert 1.15 | Student | 0.228 | 0.356 | 0.395 | 0.093 | 0 |
| Expert 1.16 | Water specialist | 1.301 | 1.580 | 0 |
| Expert | Function | Calibration Score | Information Score (Seed) | Information Score (All) | Normalized Global Weights | Normalized Optimized Weights |
|---|---|---|---|---|---|---|
| Expert 2.1 | Citizen of Bhaktapur | 1.466 | 1.234 | |||
| Expert 2.2 | Citizen of Bhaktapur | 0.915 | 1.093 | 0.560 | 0.563 | |
| Expert 2.3 | Citizen of Bhaktapur | 0.925 | 1.287 | 0 | ||
| Expert 2.4 | Citizen of Bhaktapur | 0.799 | 0.939 | 0 | ||
| Expert 2.5 | Citizen of Bhaktapur | 0.708 | 0.602 | 0 | ||
| Expert 2.6 | Citizen of Bhaktapur | 1.190 | 1.225 | 0 | ||
| Expert 2.7 | Citizen of Bhaktapur | 0.602 | 0.529 | 0.284 | 0.286 | |
| Expert 2.8 | Citizen of Bhaktapur | 1.537 | 1.292 | 0 | ||
| Expert 2.9 | Citizen of Bhaktapur | 0.769 | 0.835 | 0 | ||
| Expert 2.10 | Water specialist | 1.294 | 0.653 | 0 | ||
| Expert 2.11 | Citizen of Bhaktapur | 1.894 | 1.664 | 0.114 | 0.115 | |
| Expert 2.12 | Citizen of Bhaktapur | 1.107 | 1.650 | 0 | ||
| Expert 2.13 | Citizen of Bhaktapur | 0.952 | 0.951 | 0 | ||
| Expert 2.14 | Citizen of Bhaktapur | 0.892 | 1.001 | 0 | ||
| Expert 2.15 | Student | 1.429 | 1.289 | 0 | ||
| Expert 2.16 | Water specialist | 1.855 | 1.656 |
| Expert | Function | Calibration Score | Information Score (Seed) | Information Score (All) | Normalized Global Weights | Normalized Optimized Weights |
|---|---|---|---|---|---|---|
| Expert 3.1 | Citizen of Bhaktapur | 1.109 | 1.059 | 0 | ||
| Expert 3.2 | Citizen of Bhaktapur | 1.859 | 1.575 | 0 | ||
| Expert 3.3 | Citizen of Bhaktapur | 1.195 | 1.253 | 0 | ||
| Expert 3.4 | Citizen of Bhaktapur | 1.336 | 1.118 | 0 | ||
| Expert 3.5 | Citizen of Bhaktapur | 0.650 | 0.588 | 0.555 | 0.573 | |
| Expert 3.6 | Citizen of Bhaktapur | 0.434 | 0.510 | 0 | ||
| Expert 3.7 | Citizen of Bhaktapur | 1.643 | 1.620 | 0 | ||
| Expert 3.8 | Citizen of Bhaktapur | 0.845 | 0.987 | 0.166 | 0.171 | |
| Expert 3.9 | Citizen of Bhaktapur | 0.995 | 0.906 | 0 | ||
| Expert 3.10 | Citizen of Bhaktapur | 0.904 | 0.831 | 0 | ||
| Expert 3.11 | Water specialist | 0.746 | 0.473 | 0 | ||
| Expert 3.12 | Citizen of Bhaktapur | 0.625 | 0.562 | 0 | ||
| Expert 3.13 | Water specialist | 2.423 | 2.407 | 0 | ||
| Expert 3.14 | Student | 2.038 | 1.647 | 0 | ||
| Expert 3.15 | Water specialist | 2.284 | 2.323 | 0 | ||
| Expert 3.16 | Water specialist | 1.645 | 1.120 | 0.247 | 0.255 |
| Expert | Function | Calibration Score | Information Score (Seed) | Information Score (All) | Normalized Global Weights | Normalized Optimized Weights |
|---|---|---|---|---|---|---|
| Expert 4.1 | Citizen of Bhaktapur | 0.722 | 1.110 | 0 | ||
| Expert 4.2 | Citizen of Bhaktapur | 1.192 | 1.832 | 0 | ||
| Expert 4.3 | Citizen of Bhaktapur | 0.493 | 0.485 | 0.547 | 0.877 | 1 |
| Expert 4.4 | Citizen of Bhaktapur | 0.228 | 0.252 | 0 | ||
| Expert 4.5 | Citizen of Bhaktapur | 1.172 | 1.361 | 0 | ||
| Expert 4.6 | Citizen of Bhaktapur | 1.684 | 1.757 | 0 | ||
| Expert 4.7 | Citizen of Bhaktapur | 0.811 | 0.912 | 0 | ||
| Expert 4.8 | Citizen of Bhaktapur | 0.483 | 0.424 | 0 | ||
| Expert 4.9 | Citizen of Bhaktapur | 2.119 | 2.269 | 0 | ||
| Expert 4.10 | Water specialist | 1.908 | 2.282 | 0 | ||
| Expert 4.11 | Student | 1.706 | 1.607 | 0 | ||
| Expert 4.12 | Citizen of Bhaktapur | 1.916 | 1.286 | 0 | ||
| Expert 4.13 | Water specialist | 2.733 | 2.717 | 0 | ||
| Expert 4.14 | Water specialist | 0.567 | 0.763 | 0 |
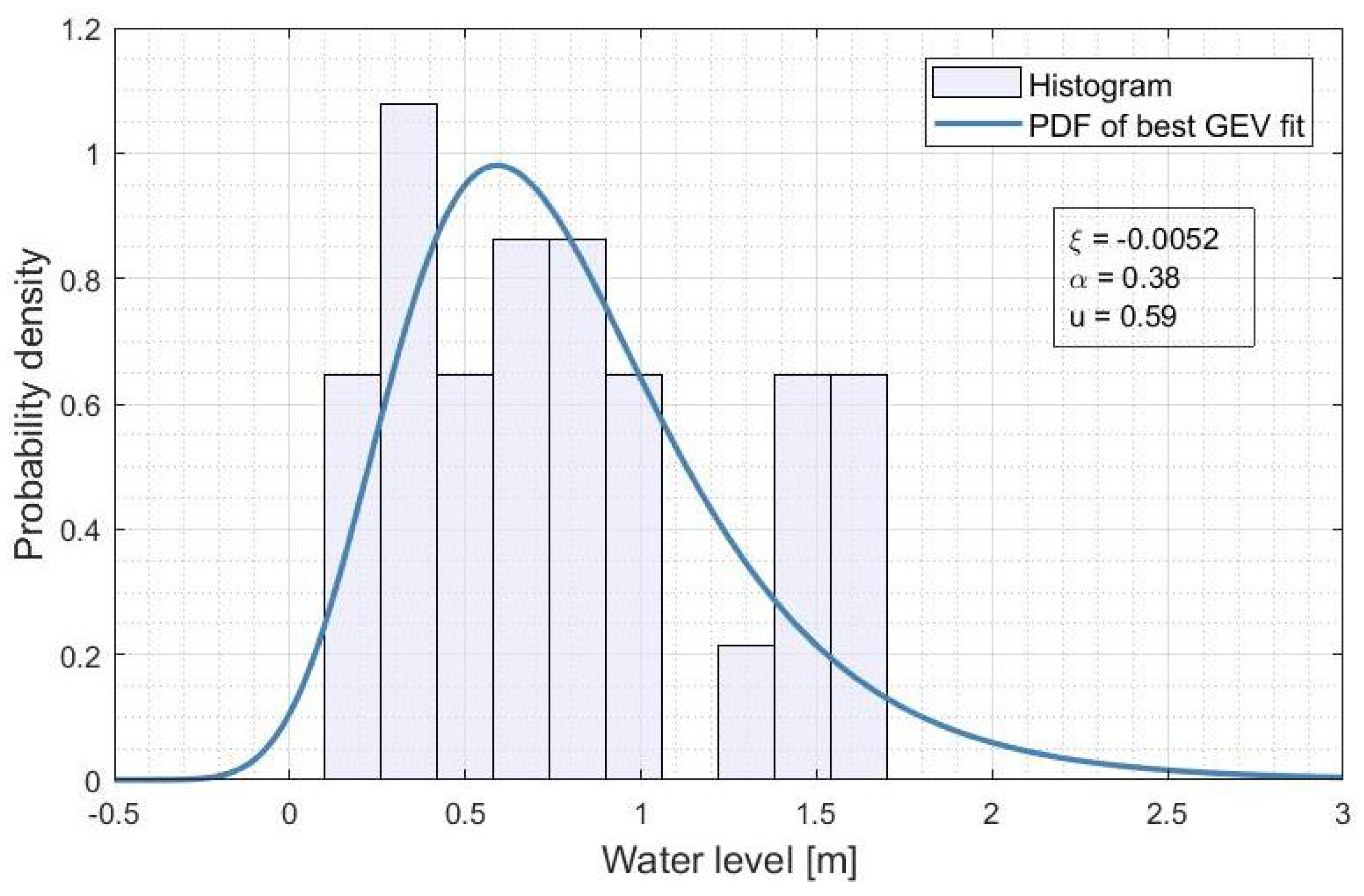
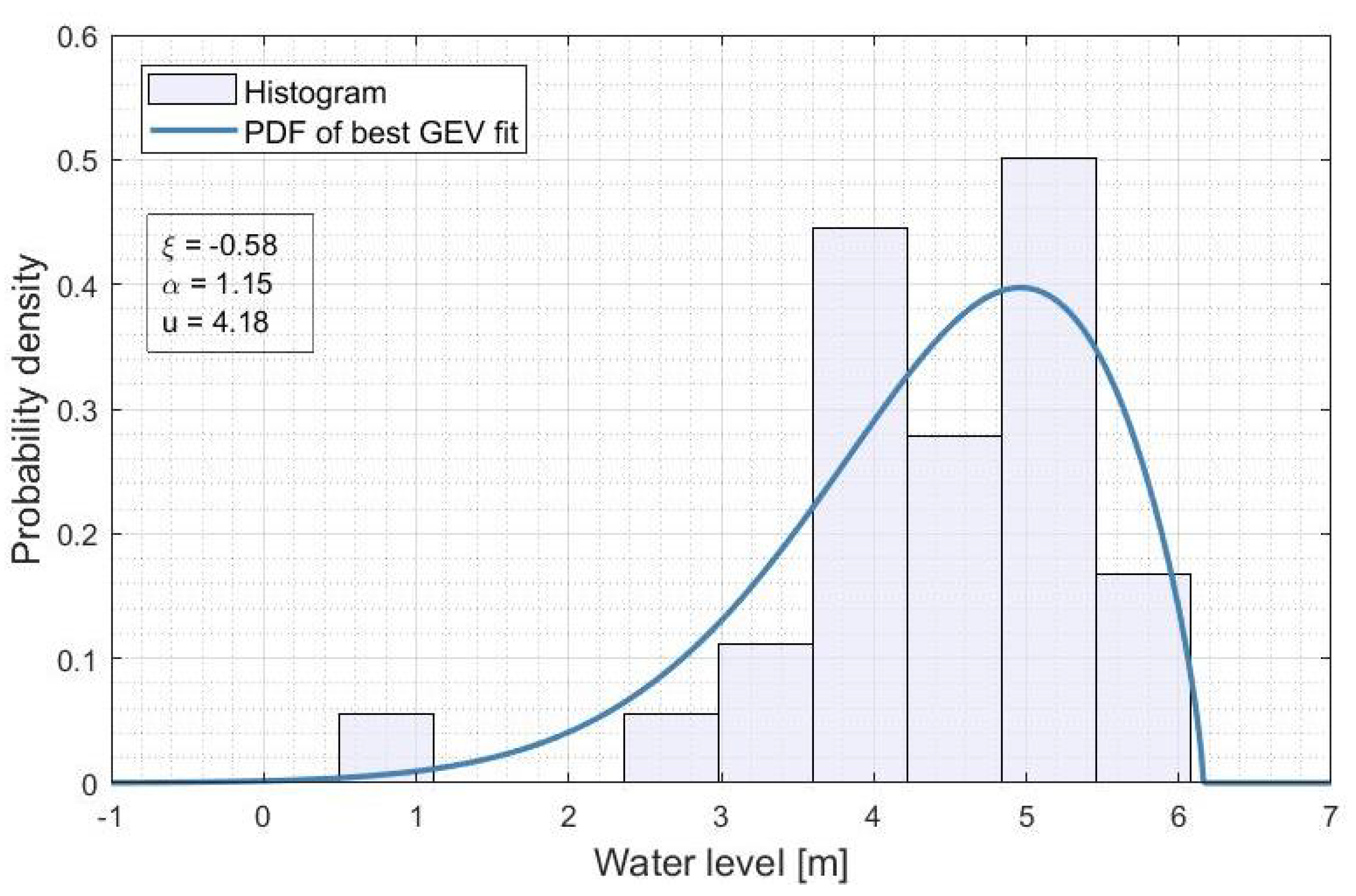
Appendix C. Best GEV for the 5% and 95% Quantiles of the Water Levels
References
- Prajapati, R.; Raj Thapa, B.; Talchabhadel, R. What flooded Bhaktapur? My Republica, 17 July 2018. [Google Scholar]
- Davids, J.C. Mobilizing Young Researchers, Citizen Scientists and Mobile Technology to Close Water Data Gaps. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Central Bureau of Statistics. National Population and Housing Census 2011; Technical Report 7; Government of Nepal, National Planning Commission Secretariat: Kathmandu, Nepal, 2012.
- ICIMOD. Land Cover Distribution for Bhaktapur; ICIMOD: Khumaltar Kathmandu Khumaltar, Nepal, 2010. [Google Scholar]
- Bhatta, B.P.; Pandey, R.K. Bhaktapur Urban Flood related Disaster Risk and Strategy after 2018. J. APF Command Staff Coll. 2020, 3, 72–89. [Google Scholar] [CrossRef]
- Pradhan-Salike, I.; Pokharel, J.R. Impact of Urbanization and Climate Change on Urban Flooding: A case of the Kathmandu Valley. J. Nat. Resour. Dev. 2017, 7, 56–66. [Google Scholar] [CrossRef]
- Department of Water Induced Disaster Prevention. Preparation of Flood Risk and Vulnerability Map Final Report; Technical Report; Government of Nepal, Ministry of Water Resources: Lalitpur, Nepal, 2009.
- Smartphones4Water. Projects S4W-Nepal. Available online: https://www.smartphones4water.org/projects/nepal/ (accessed on 16 October 2019).
- Cooke, R.M. Experts in Uncertainty, Opinion and Subjective Probability in Science; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Cooke, R.M.; Goossens, L.L. TU Delft expert judgment data base. Reliab. Eng. Syst. Saf. 2008, 93, 657–674. [Google Scholar] [CrossRef]
- Colson, A.R.; Cooke, R.M. Cross validation for the classical model of structured expert judgment. Reliab. Eng. Syst. Saf. 2017, 163, 109–120. [Google Scholar] [CrossRef]
- Cooke, R.M. Special issue on expert judgement. Reliab. Eng. Syst. Saf. 2008, 93, 655–656. [Google Scholar] [CrossRef]
- Hathout, M.; Vuillet, M.; Peyras, L.; Carvajal, C.; Diab, Y. Uncertainty and expert assessment for supporting evaluation of levees safety. In Proceedings of the 3rd European Conference on Flood Risk Management FLOODrisk Oct 2016, Lyon, France, 17–21 October 2016. [Google Scholar] [CrossRef]
- Cooke, R.M.; Slijkhuis, K.A. Expert judgment in the uncertainty analysis of dike ring failure frequency. Case Stud. Reliab. Maint. 2003, 480, 331. [Google Scholar]
- Sjöstrand, K.; Lindhe, A.; Söderqvist, T.; Rosén, L. Water Supply Delivery Failures—A Scenario-Based Approach to Assess Economic Losses and Risk Reduction Options. Water 2020, 12, 1746. [Google Scholar] [CrossRef]
- Burgman, M.A.; McBride, M.; Ashton, R.; Speirs-Bridge, A.; Flander, L.; Wintle, B.; Fidler, F.; Rumpff, L.; Twardy, C. Expert status and performance. PLoS ONE 2011, 6, e22998. [Google Scholar] [CrossRef] [PubMed]
- Page, S.E. The Difference: How the Power of Diversity Creates Better Groups, Firms, Schools, and Societies-New Edition; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Ungar, L.; Mellers, B.; Satopää, V.; Tetlock, P.; Baron, J. The good judgment project: A large scale test of different methods of combining expert predictions. In Proceedings of the 2012 AAAI Fall Symposium Series, Arlington, TX, USA, 2–4 November 2012. [Google Scholar]
- Tetlock, P.E.; Gardner, D. Superforecasting: The Art and Science of Prediction; Random House Books: Manhattan, NY, USA, 2016. [Google Scholar]
- Schumann, G.J.P.; Neal, J.C.; Mason, D.C.; Bates, P.D. The accuracy of sequential aerial photography and SAR data for observing urban flood dynamics, a case study of the UK summer 2007 floods. Remote Sens. Environ. 2011, 115, 2536–2546. [Google Scholar] [CrossRef]
- Carpenter, L.; Stone, J.; Griffin, C.R. Accuracy of aerial photography for locating seasonal (vernal) pools in Massachusetts. Wetlands 2011, 31, 573–581. [Google Scholar] [CrossRef]
- Sada, R. Hanumante River: Emerging uses, competition and implications. J. Sci. Eng. 2012, 1, 17–24. [Google Scholar] [CrossRef]
- Wittmann, M.E.; Cooke, R.M.; Rothlisberger, J.D.; Lodge, D.M. Using Structured Expert Judgment to Assess Invasive Species Prevention: Asian Carp and the Mississippi—Great Lakes Hydrologic Connection. Environ. Sci. Technol. 2014, 48, 2150–2156. [Google Scholar] [CrossRef] [PubMed]
- Leontaris, G.; Morales-Nápoles, O. ANDURIL—A MATLAB toolbox for ANalysis and Decisions with UnceRtaInty: Learning from expert judgments. SoftwareX 2018, 7, 313–317. [Google Scholar] [CrossRef]
- Bali, T.G. The generalized extreme value distribution. Econ. Lett. 2003, 79, 423–427. [Google Scholar] [CrossRef]
- De Haan, L.; Ferreira, A.F. Extreme Value Theory: An Introduction; Springer: New York, NY, USA, 2006; pp. 3–36. [Google Scholar]
- VNK. The National Flood Risk Analysis for the Netherlands; Technical Report; Rijkswaterstaat: Utrecht, The Netherlands, 2014. [Google Scholar]
- Soomere, T.; Eelsalu, M.; Pindsoo, K. Variations in parameters of extreme value distributions of water level along the eastern Baltic Sea coast. Estuar. Coast. Shelf Sci. 2018, 215, 59–68. [Google Scholar] [CrossRef]
- Ojha, A. Bhaktapur settlements submerged. Kathmandu Post, 28 August 2015. [Google Scholar]
- Smith, P.J.; Brown, S.; Dugar, S. Community-based early warning systems for flood risk mitigation in Nepal. Nat. Hazards Earth Syst. Sci. 2017, 17, 423–437. [Google Scholar] [CrossRef]



| Panels | |||||
|---|---|---|---|---|---|
| Function | Total | 1 | 2 | 3 | 4 |
| Number of experts | 62 | 16 | 16 | 16 | 14 |
| Number of specialists | 10 | 1 | 2 | 4 | 3 |
| Number of citizens | 47 | 13 | 13 | 11 | 10 |
| Number of students | 5 | 2 | 1 | 1 | 1 |
| Average age | 35.8 | 39.6 | 32.8 | 34.4 | 36.3 |
| Male/Female | 41/21 | 8/8 | 11/5 | 11/5 | 11/3 |
| Calibration Score | Information Score | Combined Score | |
|---|---|---|---|
| Optimized DM | 0.3946 | 0.8287 | 0.3270 |
| Global weight DM | 0.2894 | 0.2717 | 0.0786 |
| Item weight DM | 0.4735 | 0.4038 | 0.1912 |
| Equal weight DM | 0.0012 | 0.1405 | 0.0002 |
| Calibration Score | Information Score | Combined Score | |
|---|---|---|---|
| Optimized DM | 0.2894 | 0.3924 | 0.1136 |
| Global weight DM | 0.1242 | 0.4819 | 0.0599 |
| Item weight DM | 0.2441 | 0.4974 | 0.1214 |
| Equal weight DM | 0.0031 | 0.1475 | 0.0005 |
| Calibration Score | Information Score | Combined Score | |
|---|---|---|---|
| Optimized DM | 0.2441 | 0.3739 | 0.0913 |
| Global weight DM | 0.0357 | 0.6502 | 0.0232 |
| Item weight DM | 0.0357 | 0.6502 | 0.0232 |
| Equal weight DM | 0.0012 | 0.1542 | 0.0002 |
| Calibration Score | Information Score | Combined Score | |
|---|---|---|---|
| Optimized DM | 0.4926 | 0.4848 | 0.2388 |
| Global weight DM | 0.4926 | 0.3015 | 0.1485 |
| Item weight DM | 0.4926 | 0.3109 | 0.1531 |
| Equal weight DM | 0.0237 | 0.1489 | 0.0035 |
| Calibration Score | Information Score | Combined Score | |
|---|---|---|---|
| Optimized DM | 0.6828 | 0.5644 | 0.3854 |
| Global weight DM | 0.2894 | 0.3542 | 0.1025 |
| Item weight DM | 0.4735 | 0.4671 | 0.2212 |
| Equal weight DM | 0.0012 | 0.2487 | 0.0003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kindermann, P.E.; Brouwer, W.S.; van Hamel, A.; van Haren, M.; Verboeket, R.P.; Nane, G.F.; Lakhe, H.; Prajapati, R.; Davids, J.C. Return Level Analysis of the Hanumante River Using Structured Expert Judgment: A Reconstruction of Historical Water Levels. Water 2020, 12, 3229. https://doi.org/10.3390/w12113229
Kindermann PE, Brouwer WS, van Hamel A, van Haren M, Verboeket RP, Nane GF, Lakhe H, Prajapati R, Davids JC. Return Level Analysis of the Hanumante River Using Structured Expert Judgment: A Reconstruction of Historical Water Levels. Water. 2020; 12(11):3229. https://doi.org/10.3390/w12113229
Chicago/Turabian StyleKindermann, Paulina E., Wietske S. Brouwer, Amber van Hamel, Mick van Haren, Rik P. Verboeket, Gabriela F. Nane, Hanik Lakhe, Rajaram Prajapati, and Jeffrey C. Davids. 2020. "Return Level Analysis of the Hanumante River Using Structured Expert Judgment: A Reconstruction of Historical Water Levels" Water 12, no. 11: 3229. https://doi.org/10.3390/w12113229
APA StyleKindermann, P. E., Brouwer, W. S., van Hamel, A., van Haren, M., Verboeket, R. P., Nane, G. F., Lakhe, H., Prajapati, R., & Davids, J. C. (2020). Return Level Analysis of the Hanumante River Using Structured Expert Judgment: A Reconstruction of Historical Water Levels. Water, 12(11), 3229. https://doi.org/10.3390/w12113229








