Modeling the Matrix-Conduit Exchanges in Both the Epikarst and the Transmission Zone of Karst Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of the Usual Representation of Hydrodynamics in Karst Systems and Related Properties
2.1.1. Karst Subsystems
2.1.2. Matrix vs. Conduit Properties
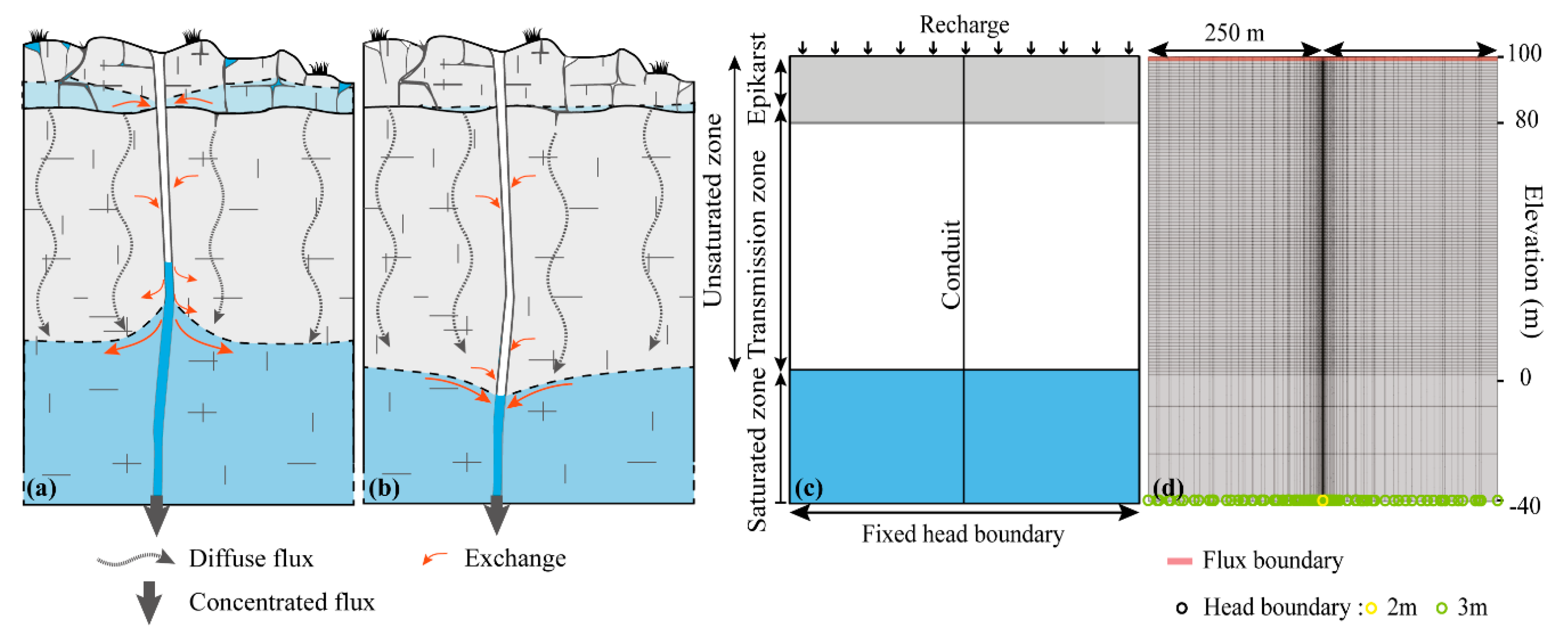
2.2. Modeling Approach
2.2.1. Model Description, Boundary Conditions, and Evaluation Criteria
2.2.2. Flow Equations and Model Parameters
3. Results
3.1. Spatio-Temporal Evolution of the Flows at the Conduit Scale
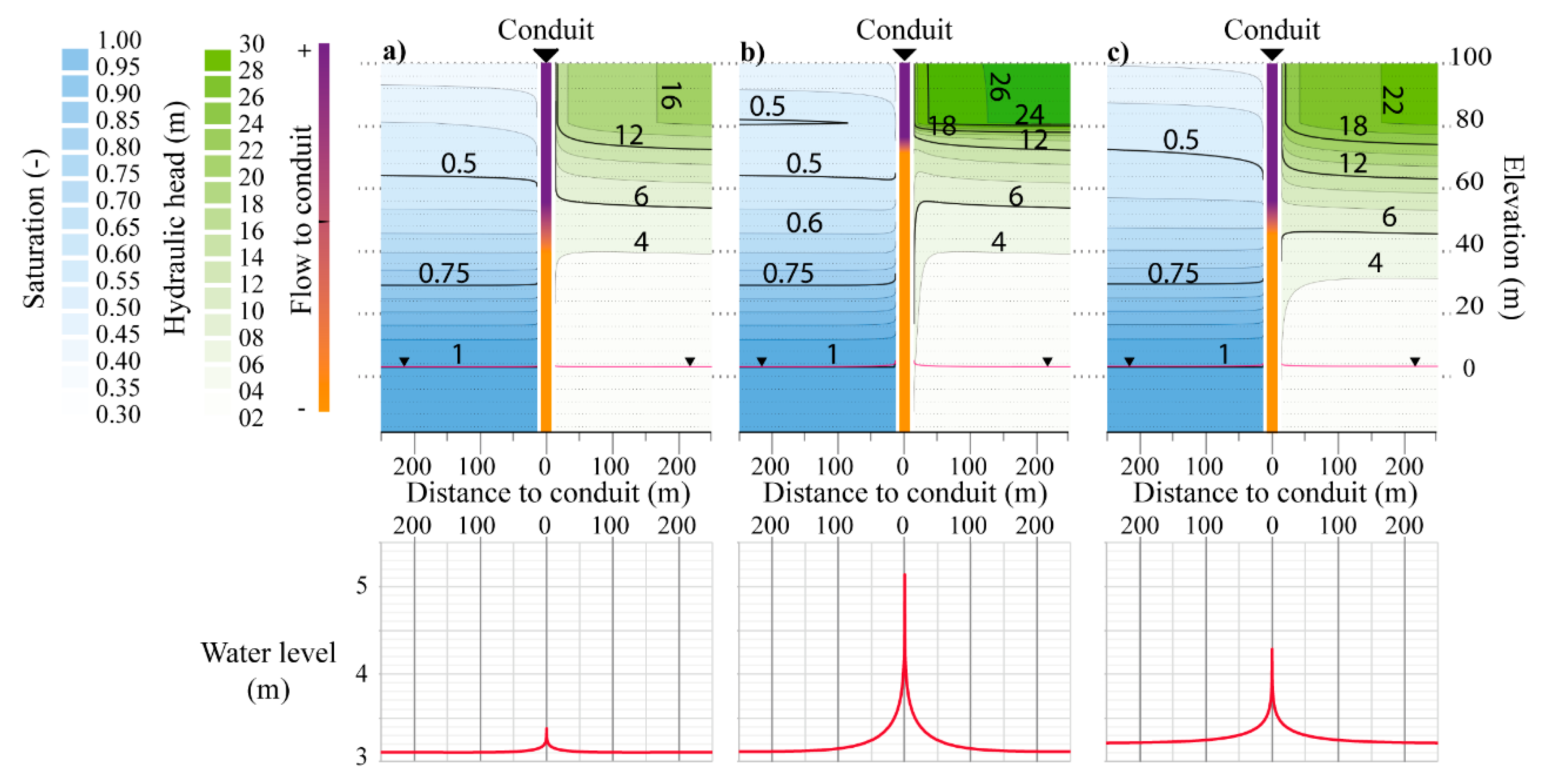
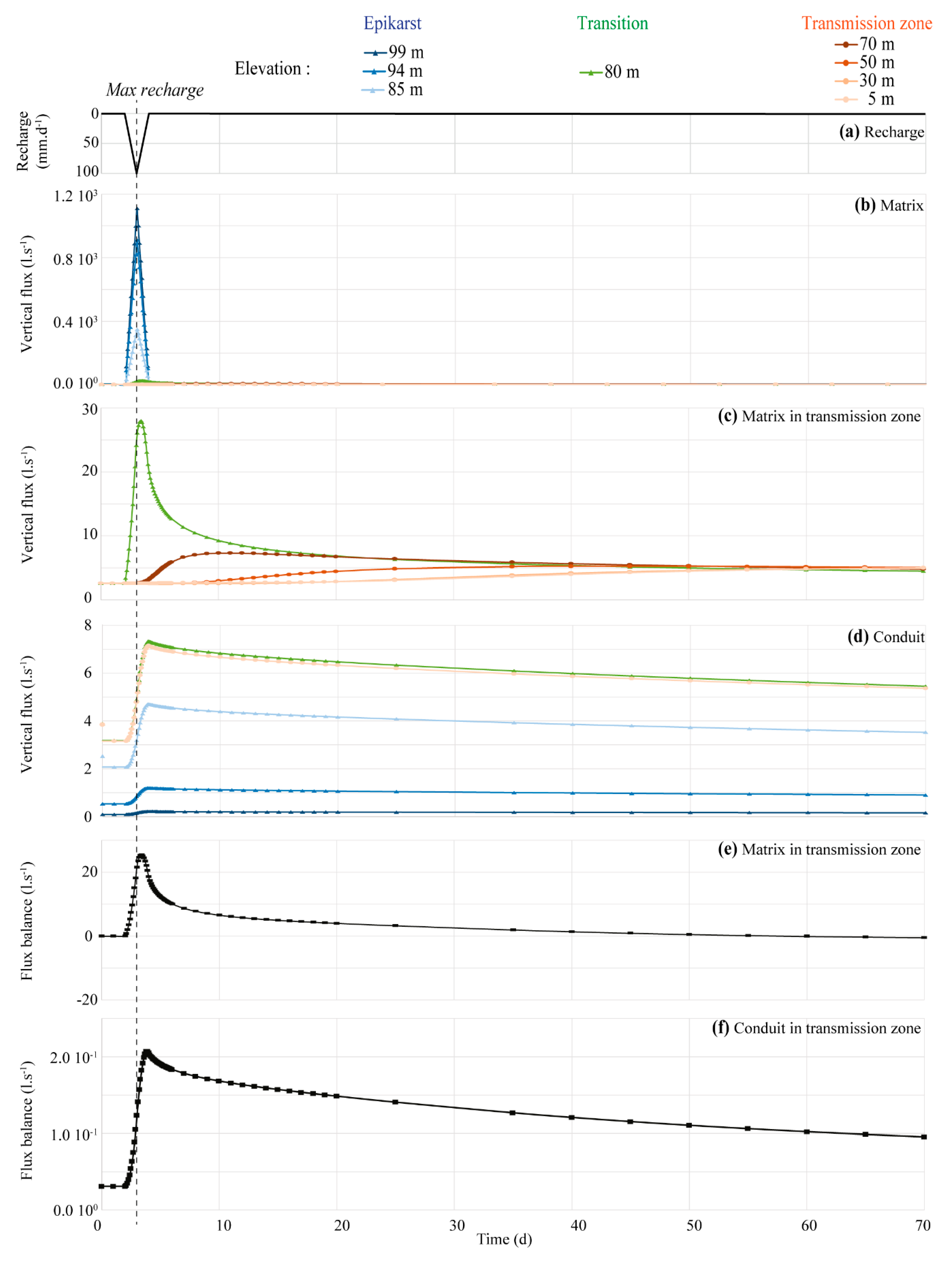
3.2. Impact of Parameter Variation at the Conduit Scale
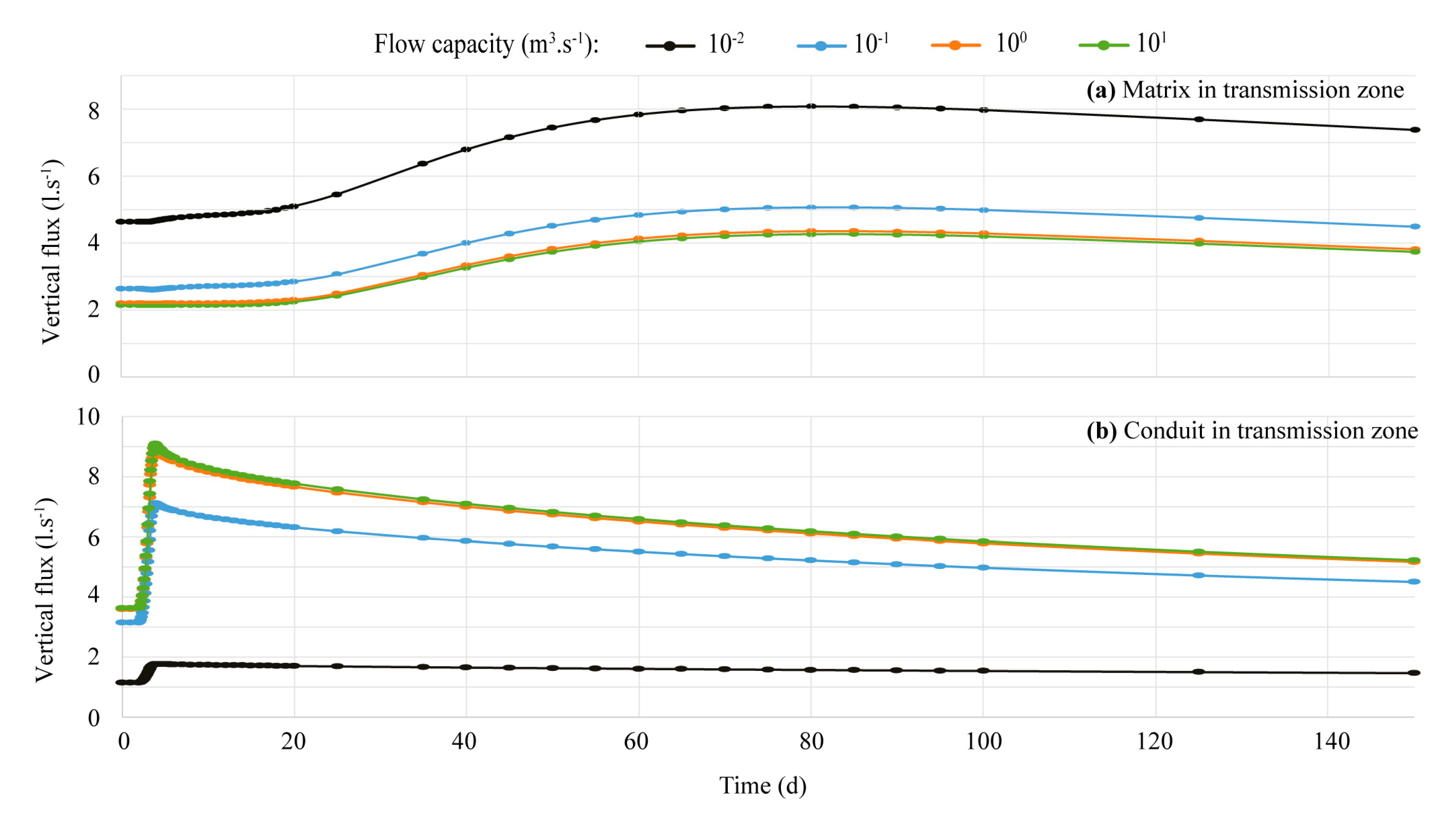
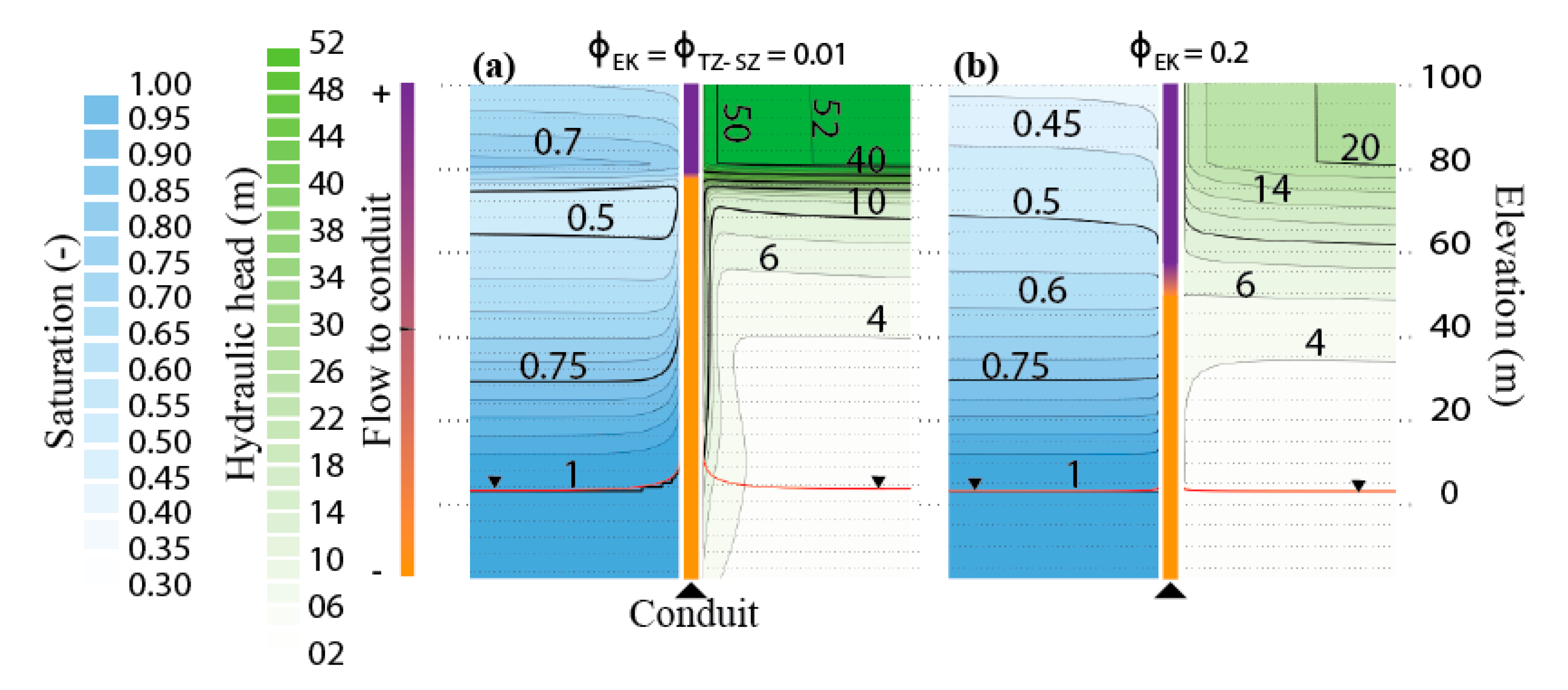
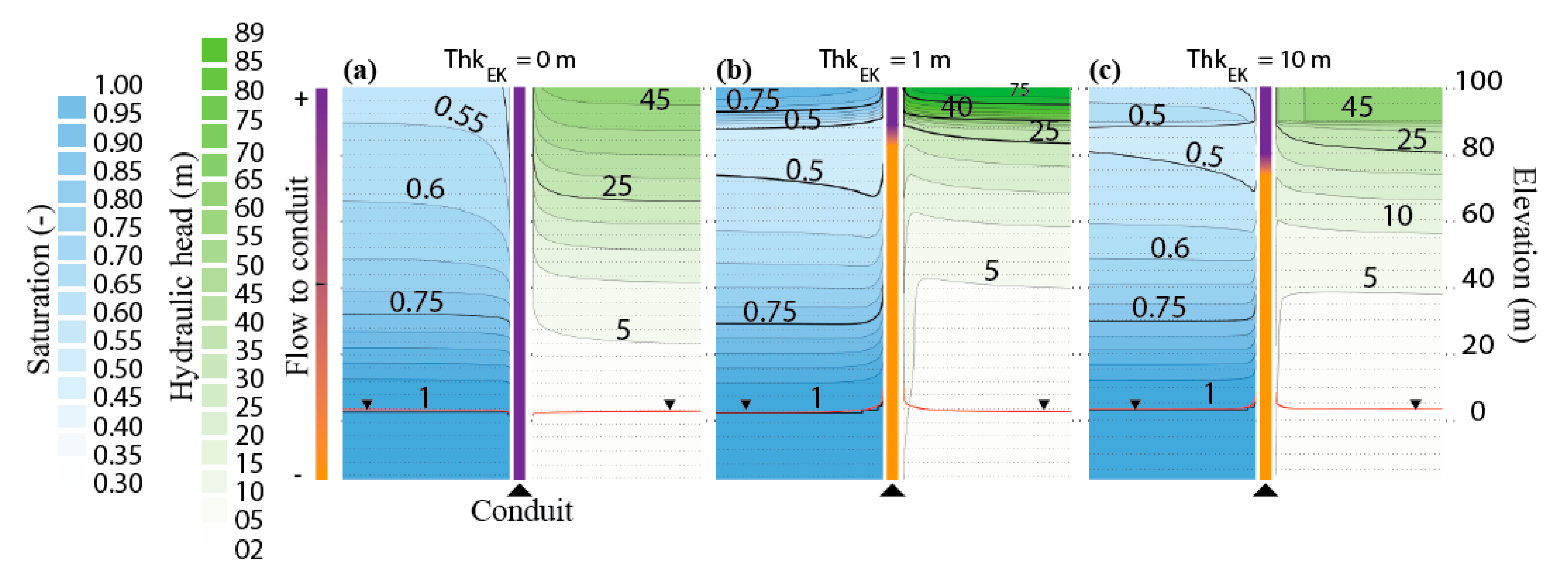
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Hartmann, A.J.; Goldscheider, N.; Wagener, T.; Lange, J.H.M.; Weiler, M. Karst water resources in a changing world: Review of hydrological modeling approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- White, W.B. Conceptual models for carbonate aquifers. Ground Water 2012, 50, 180–186. [Google Scholar] [CrossRef]
- White, W.B. Conceptual models for karstic aquifers. In Karst Modeling: Special Publication 5; Palmer, A.N., Palmer, M.V., Sasowsky, I.D., Eds.; The Karst Waters Institute: Charles Town, WV, USA, 1999; pp. 11–16. [Google Scholar]
- Shuster, E.T.; White, W.B. Seasonal fluctuations in the chemistry of lime-stone springs: A possible means for characterizing carbonate aquifers. J. Hydrol. 1971, 14, 93–128. [Google Scholar] [CrossRef]
- Shuster, E.T.; White, W.B. Source areas and climatic effects in carbonate groundwaters determined by saturation indices and carbon dioxide pressures. Water Resour. Res. 1972, 8, 1067–1073. [Google Scholar] [CrossRef]
- Worthington, S.R.H. Groundwater residence times in unconfined carbonate aquifers. J. Cave Karst Stud. 2007, 69, 94–102. [Google Scholar]
- Smart, P.L.; Hobbs, S.L. Characterisation of carbonate aquifers: A conceptual base. In Proceedings of the Environmental Problems in Karst Terranes and Their Solutions Conference, Dublin, OH, USA, 28–30 October 1986; pp. 1–14. [Google Scholar]
- Morales, T.; Uriarte, J.A.; Olazar, M.; Antigüedad, I.; Angulo, B. Solute transport modelling in karst conduits with slow zones during different hydrologic conditions. J. Hydrol. 2010, 390, 182–189. [Google Scholar] [CrossRef]
- Bailly-Comte, V.; Martin, J.B.; Jourde, H.; Screaton, E.J.; Pistre, S.; Langston, A. Water exchange and pressure transfer between conduits and matrix and their influence on hydrodynamics of two karst aquifers with sinking streams. J. Hydrol. 2010, 386, 55–66. [Google Scholar] [CrossRef]
- Mangin, A. Contribution à l’Étude Hydrodynamique des Aquifères Karstiques. Ph.D. Thesis, Université de Dijon, Dijon, France, 1975. [Google Scholar]
- Mudarra, M.; Andreo, B. Relative importance of the saturated and the unsaturated zones in the hydrogeological functioning of karst aquifers: The case of Alta Cadena (Southern Spain). J. Hydrol. 2011, 397, 263–280. [Google Scholar] [CrossRef]
- Perrin, J.; Jeannin, P.-Y.; Zwahlen, F. Epikarst storage in a karst aquifer: A conceptual model based on isotopic data, Milandre test site, Switzerland. J. Hydrol. 2003, 279, 106–124. [Google Scholar] [CrossRef]
- Pronk, M.; Goldscheider, N.; Zopfi, J.; Zwahlen, F. Percolation and particle transport in the unsaturated zone of a Karst aquifer. Ground Water 2009, 47, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Contractor, D.; Jenson, J. Simulated effect of vadose infiltration on water levels in the Northern Guam Lens Aquifer. J. Hydrol. 2000, 229, 232–254. [Google Scholar] [CrossRef]
- De Rooij, R.; Perrochet, P.; Graham, W. From rainfall to spring discharge: Coupling conduit flow, subsurface matrix flow and surface flow in karst systems using a discrete-continuum model. Adv. Water Resour. 2013, 61, 29–41. [Google Scholar] [CrossRef]
- Doummar, J.; Sauter, M.; Geyer, T. Simulation of flow processes in a large scale karst system with an integrated catchment model (Mike She)-Identification of relevant parameters influencing spring discharge. J. Hydrol. 2012, 426, 112–123. [Google Scholar] [CrossRef]
- Kaufmann, G. Modelling unsaturated flow in an evolving karst aquifer. J. Hydrol. 2003, 276, 53–70. [Google Scholar] [CrossRef]
- Kordilla, J.; Sauter, M.; Reimann, T.; Geyer, T. Simulation of saturated and unsaturated flow in karst systems at catchment scale using a double continuum approach. Hydrol. Earth Syst. Sci. 2012, 16, 3909–3923. [Google Scholar] [CrossRef] [Green Version]
- Pardo-Igúzquiza, E.; Dowd, P.; Bosch, A.P.; Luque-Espinar, J.A.; Heredia, J.; Durán-Valsero, J.J. A parsimonious distributed model for simulating transient water flow in a high-relief karst aquifer. Hydrogeol. J. 2018, 26, 2617–2627. [Google Scholar] [CrossRef]
- Roulier, S.; Baran, N.; Mouvet, C.; Stenemo, F.; Morvan, X.; Albrechtsen, H.-J.; Clausen, L.; Jarvis, N. Controls on atrazine leaching through a soil-unsaturated fractured limestone sequence at Brévilles, France. J. Contam. Hydrol. 2006, 84, 81–105. [Google Scholar] [CrossRef]
- Faulkner, J.; Hu, B.X.; Kish, S.; Hua, F. Laboratory analog and numerical study of groundwater flow and solute transport in a karst aquifer with conduit and matrix domains. J. Contam. Hydrol. 2009, 110, 34–44. [Google Scholar] [CrossRef]
- Malenica, L.; Gotovac, H.; Kamber, G.; Simunovic, S.; Allu, S.; Divić, V. Groundwater flow modeling in Karst aquifers: Coupling 3D matrix and 1D conduit flow via control volume isogeometric analysis-Experimental verification with a 3D physical model. Water 2018, 10, 1787. [Google Scholar] [CrossRef] [Green Version]
- Chen, N.; Gunzburger, M.; Hu, B.X.; Wang, X.; Woodruff, C. Calibrating the exchange coefficient in the modified coupled continuum pipe-flow model for flows in karst aquifers. J. Hydrol. 2012, 414, 294–301. [Google Scholar] [CrossRef]
- Ghasemizadeh, R.; Hellweger, F.; Butscher, C.; Padilla, I.; Vesper, D.; Field, M.; Alshawabkeh, A. Review: Groundwater flow and transport modeling of karst aquifers, with particular reference to the North Coast Limestone aquifer system of Puerto Rico. Hydrogeol. J. 2012, 20, 1441–1461. [Google Scholar] [CrossRef] [Green Version]
- Teutsch, G.; Sauter, M. Groundwater modeling in karst terranes: Scale effects, data acquisition and field validation. In Proceedings of the Third Conference on Hydrogeology, Ecology, Monitoring, and Management of Ground Water in Karst Terranes, Nashville, TN, USA, 4–6 December 1991; pp. 17–35. [Google Scholar]
- Wong, D.L.Y.; Doster, F.; Geiger-Boschung, S.; Kamp, A. Partitioning thresholds in hybrid implicit-Explicit representations of naturally fractured reservoirs. Water Resour. Res. 2020, 56, 16. [Google Scholar] [CrossRef]
- Binet, S.; Joigneaux, E.; Pauwels, H.; Albéric, P.; Fléhoc, C.; Bruand, A. Water exchange, mixing and transient storage between a saturated karstic conduit and the surrounding aquifer: Groundwater flow modeling and inputs from stable water isotopes. J. Hydrol. 2017, 544, 278–289. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.; Wu, J.; Jiang, G. Modeling the hydrological behavior of a karst spring using a nonlinear reservoir-pipe model. Hydrogeol. J. 2015, 23, 901–914. [Google Scholar] [CrossRef]
- Giese, M.; Reimann, T.; Bailly-Comte, V.; Maréchal, J.; Sauter, M.; Geyer, T. Turbulent and laminar flow in Karst conduits under unsteady flow conditions: Interpretation of pumping tests by discrete conduit-continuum modeling. Water Resour. Res. 2018, 54, 1918–1933. [Google Scholar] [CrossRef]
- Gallegos, J.J.; Hu, B.X.; Davis, H. Simulating flow in karst aquifers at laboratory and sub-regional scales using MODFLOW-CFP. Hydrogeol. J. 2013, 21, 1749–1760. [Google Scholar] [CrossRef]
- Saller, S.P.; Ronayne, M.J.; Long, A.J. Comparison of a karst groundwater model with and without discrete conduit flow. Hydrogeol. J. 2013, 21, 1555–1566. [Google Scholar] [CrossRef]
- Worthington, S.R.H. Diagnostic hydrogeologic characteristics of a karst aquifer (Kentucky, USA). Hydrogeol. J. 2009, 17, 1665–1678. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, B.X.; Davis, H.; Kish, S.A. Numerical study of groundwater flow cycling controlled by seawater/freshwater interaction in a coastal karst aquifer through conduit network using CFPv2. J. Contam. Hydrol. 2015, 182, 131–145. [Google Scholar] [CrossRef] [Green Version]
- Diersch, H.-J. FEFLOW. Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer: Berlin, Germany, 2014; p. 996. [Google Scholar] [CrossRef]
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a conduit flow process (CFP) for MODFLOW-2005. In Techniques and Methods; US Geological Survey: Reston, VA, USA, 2007; p. 6. [Google Scholar]
- Ford, D.; Williams, P. Karst Hydrogeology and Geomorphology; Wiley: Chichester, UK, 2007. [Google Scholar]
- Klimchouk, A.B. Towards defining, delimiting and classifying epikarst: Its origin, processes and variants of geomorphic evolution. In Special Publication 9: Epikarst; Jones, W.K., Culver, D.C., Herman, J.S., Eds.; Karst Waters Institute: Leesburg, VA, USA, 2004; pp. 23–35. [Google Scholar]
- Bakalowicz, M. The epikarst, the skin of karst. In Special Publication 9: Epikarst; Jones, W.K., Culver, D.C., Herman, J.S., Eds.; Karst Waters Institute: Leesburg, VA, USA, 2004; pp. 16–22. [Google Scholar]
- White, W.B. Karst hydrology: Recent developments and open questions. Eng. Geol. 2002, 65, 85–105. [Google Scholar] [CrossRef]
- White, W.B.; Harmon, R.S.; Wicks, C.M. Fifty years of karst hydrology and hydrogeology: 1953–2003. In Perspectives on Karst Geomorphology, Hydrology, and Geochemistry-A Tribute Volume to Derek C. Ford and William B. White; Geological Society of America: Boulder, CO, USA, 2006; pp. 139–152. [Google Scholar]
- Jukić, D.; Denić-Jukić, V. Groundwater balance estimation in karst by using a conceptual rainfall–runoff model. J. Hydrol. 2009, 373, 302–315. [Google Scholar] [CrossRef]
- Tritz, S.; Guinot, V.; Jourde, H. Modelling the behaviour of a karst system catchment using non-linear hysteretic conceptual model. J. Hydrol. 2011, 397, 250–262. [Google Scholar] [CrossRef]
- Al-Fares, W.; Bakalowicz, M.; Guérin, R.; Dukhan, M. Analysis of the karst aquifer structure of the Lamalou area (Hérault, France) with ground penetrating radar. J. Appl. Geophys. 2002, 51, 97–106. [Google Scholar] [CrossRef]
- Williams, P. The role of the epikarst in karst and cave hydrogeology: A review. Int. J. Speleol. 2008, 37, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Smart, C.C.; Ford, D.C. Structure and function of a conduit aquifer. Can. J. Earth Sci. 1986, 23, 919–929. [Google Scholar] [CrossRef]
- Williams, P.W. Subcutaneous hydrology and the development of doline and cockpit karst. Z. Geomorphol. Stuttg. 1985, 29, 463–482. [Google Scholar]
- Gilli, E.; Mangan, C.; Mudry, J.-N. Hydrogéologie: Objet, Méthodes, Applications, 2nd ed.; Dunod: Paris, France, 2008. [Google Scholar]
- Williams, P.W. The role of the subcutaneous zone in karst hydrology. J. Hydrol. 1983, 61, 45–67. [Google Scholar] [CrossRef]
- Carrière, S.D.; Chalikakis, K.; Danquigny, C.; Davi, H.; Mazzilli, N.; Ollivier, C.; Emblanch, C. The role of porous matrix in water flow regulation within a karst unsaturated zone: An integrated hydrogeophysical approach. Hydrogeol. J. 2016, 24, 1905–1918. [Google Scholar] [CrossRef] [Green Version]
- Mazzilli, N.; Boucher, M.; Chalikakis, K.; Legchenko, A.; Jourde, H.; Champollion, C. Contribution of magnetic resonance soundings for characterizing water storage in the unsaturated zone of karst aquifers. Geophysics 2016, 81, WB49–WB61. [Google Scholar] [CrossRef] [Green Version]
- Emblanch, C.; Zuppi, G.; Mudry, J.; Blavoux, B.; Batiot, C. Carbon 13 of TDIC to quantify the role of the unsaturated zone: The example of the Vaucluse karst systems (Southeastern France). J. Hydrol. 2003, 279, 262–274. [Google Scholar] [CrossRef]
- Palmer, A.N.; Harmon, R.S.; Wicks, C.M. Digital modeling of karst aquifers-Successes, failures, and promises. In Perspectives on Karst Geomorphology, Hydrology, and Geochemistry-A Tribute Volume to Derek C. Ford and William B. White; Geological Society of America: Boulder, CO, USA, 2006; Volume 404, pp. 243–250. [Google Scholar]
- De Marsily, G. Hydrogéologie Quantitative; Masson: Paris, France, 1981; p. 215. [Google Scholar]
- Bakalowicz, M. La zone d’infiltration des aquifères karstiques. Méthodes d’étude, structure et fonctionnement. Hydrogéologie 1995, 4, 3–21. [Google Scholar]
- Clemens, T.; Hückinghaus, D.; Liedl, R.; Sauter, M. Simulation of the development of karst aquifers: Role of the epikarst. Acta Diabetol. 1999, 88, 157–162. [Google Scholar] [CrossRef]
- Jeannin, P.-Y. Structure et Comportement Hydraulique des Aquifères Karstiques; University of Neuchâtel: Neuchâtel, Switzerland, 1996. [Google Scholar]
- Petrella, E.; Falasca, A.; Celico, F. Natural-gradient tracer experiments in epikarst: A test study in the Acqua dei Faggi experimental site, southern Italy. Geofluids 2008, 8, 159–166. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.-F.; Xue, X.; Zhang, Z.; Wei, L. Estimation of baseflow recession constants and effective hydraulic parameters in the karst basins of southwest China. Hydrol. Res. 2012, 43, 102–112. [Google Scholar] [CrossRef]
- Daher, W.; Pistre, S.; Kneppers, A.; Bakalowicz, M.; Najem, W. Karst and artificial recharge: Theoretical and practical problems. J. Hydrol. 2011, 408, 189–202. [Google Scholar] [CrossRef]
- Barbel-Périneau, A.; Barbiéro, L.; Danquigny, C.; Emblanch, C.; Mazzilli, N.; Babic, M.; Simler, R.; Valles, V. Karst flow processes explored through analysis of long-term unsaturated-zone discharge hydrochemistry: A 10-year study in Rustrel, France. Hydrogeol. J. 2019, 27, 1711–1723. [Google Scholar] [CrossRef]
- Chang, Y.; Wu, J.; Liu, L. Effects of the conduit network on the spring hydrograph of the karst aquifer. J. Hydrol. 2015, 527, 517–530. [Google Scholar] [CrossRef]
- Sauter, M. Quantification and Forecasting of Regional Groundwater Flow and Transport in a Karst Aquifer (Gallusquelle, Malm, SW Germany). Ph.D. Thesis, University of Tubingen, Tubingen, Germany, 1992. [Google Scholar]
- Worthington, S.R.H. A comprehensive strategy for understanding flow in carbonate aquifer. In Karst Modeling: Special Publication 5; Palmer, A.N., Palmer, M.V., Sasowsky, I.D., Eds.; The Karst Waters Institute: Charles Town, WV, USA, 1999; pp. 30–37. [Google Scholar]
- Király, L. Modelling karst aquifers by the combined discrete channel and continuum approach. Bull. Cent. Hydrogéol. 1998, 16, 77–98. [Google Scholar]
- Granger, D.E.; Fabel, D.; Palmer, A.N. Pliocene-Pleistocene incision of the Green River, Kentucky, determined from radioactive decay of cosmogenic 26Al and 10Be in Mammoth Cave sediments. GSA Bull. 2001, 113, 825–836. [Google Scholar] [CrossRef]
- Borgomano, J.; Masse, J.; Fenerci-Masse, M.; Fournier, F. Petrophysics of lower cretaceous platform carbonate outcrops in provence (SE France): Implications for carbonate reservoir characterisation. J. Pet. Geol. 2012, 36, 5–41. [Google Scholar] [CrossRef]
- Danquigny, C.; Massonnat, G.; Mermoud, C.; Rolando, J.-P. Intra- and Inter-Facies Variability of Multi-Physics Data in Carbonates. New Insights from Database of ALBION R&D Project. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Society of Petroleum Engineers (SPE), Abu Dhabi, UAE, 11–14 November 2019; p. 11. [Google Scholar]
- Jeannin, P.-Y. Modeling flow in phreatic and epiphreatic Karst conduits in the Hölloch Cave (Muotatal, Switzerland). Water Resour. Res. 2001, 37, 191–200. [Google Scholar] [CrossRef]
- Jeannin, P.Y.; Marechal, J.C. Lois de pertes de charge dans les conduits karstiques: Base théorique et observations; Laws of head loss in Karst conduits: Theoretical basis and observations. Bull. Hydrogéol. 1995, 14, 149–176. [Google Scholar]
- Chang, Y.; Wu, J.; Jiang, G.; Liu, L.; Reimann, T.; Sauter, M. Modelling spring discharge and solute transport in conduits by coupling CFPv2 to an epikarst reservoir for a karst aquifer. J. Hydrol. 2019, 569, 587–599. [Google Scholar] [CrossRef]
- Martin, J.B.; Screaton, E.J. Exchange of matrix and conduit water with examples from the Floridan aquifer. In U.S. Geological Survey Karst Interest Group Proceedings; Water-Resources Investigations Report 01-4011; Kuniansky, E.L., Ed.; US Geological Survey: Reston, VA, USA, 2001; pp. 38–44. [Google Scholar]
- Kaufmann, G. Modelling karst geomorphology on different time scales. Geomorphology 2009, 106, 62–77. [Google Scholar] [CrossRef]
- Kovács, A.; Perrochet, P.; Király, L.; Jeannin, P.-Y. A quantitative method for the characterisation of karst aquifers based on spring hydrograph analysis. J. Hydrol. 2005, 303, 152–164. [Google Scholar] [CrossRef] [Green Version]
- Liedl, R.; Sauter, M.; Hückinghaus, D.; Clemens, T.; Teutsch, G. Simulation of the development of Karst aquifers using a coupled continuum pipe flow model. Water Resour. Res. 2003, 39, 11. [Google Scholar] [CrossRef]
- Oehlmann, S.; Geyer, T.; Licha, T.; Birk, S. Influence of aquifer heterogeneity on Karst hydraulics and catchment delineation employing distributive modeling approaches. Hydrol. Earth Syst. Sci. 2013, 17, 4729–4742. [Google Scholar] [CrossRef] [Green Version]
- Trefry, M.G.; Muffels, C. FEFLOW: A finite-element ground water flow and transport modeling tool. Ground Water 2007, 45, 525–528. [Google Scholar] [CrossRef]
- Lastennet, R.; Mudry, J. Impact of an exceptional storm episode on the functioning of karst system-The case of the 22/9/92 storm at Vaison-La-Romaine (Vaucluse, France). C.-R. Acad. Sci. Serie II 1995, 320, 953–959. [Google Scholar]
- Maréchal, J.; Ladouche, B.; Dörfliger, N. Karst flash flooding in a Mediterranean karst, the example of Fontaine de Nîmes. Eng. Geol. 2008, 99, 138–146. [Google Scholar] [CrossRef]
- Reimann, T.; Geyer, T.; Shoemaker, W.B.; Liedl, R.; Sauter, M. Effects of dynamically variable saturation and matrix-conduit coupling of flow in karst aquifers. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A. Properties of porous media affecting fluid flow. Proc. Am. Soc. Civ. Eng. 1966, 92, 61–88. [Google Scholar]
- Corey, A.T. Mechanics of Immiscible Fluids in Porous Media; Water Resources Publication: Richmond, TX, USA, 1994. [Google Scholar]
- Kool, J.; Parker, J.; Van Genuchten, M. Parameter estimation for unsaturated flow and transport models-A review. J. Hydrol. 1987, 91, 255–293. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Van Genuchten, M. Convective-dispersive transport of solutes involved in sequential first-order decay reactions. Comput. Geosci. 1985, 11, 129–147. [Google Scholar] [CrossRef]
- Yeh, T.-C.J.; Harvey, D.J. Effective unsaturated hydraulic conductivity of layered sands. Water Resour. Res. 1990, 26, 1271–1279. [Google Scholar] [CrossRef]
- Leij, F.J.; Russell, W.B.; Lesch, S.M. Closed-form expressions for water retention and conductivity data. Ground Water 1997, 35, 848–858. [Google Scholar] [CrossRef]
- Huang, Z.-Q.; Yao, J.; Wang, Y.-Y. An Efficient numerical model for immiscible two-phase flow in fractured Karst reservoirs. Commun. Comput. Phys. 2013, 13, 540–558. [Google Scholar] [CrossRef]
- Dal Soglio, L.; Danquigny, C.; Mazzilli, N.; Emblanch, C.; Massonnat, G. Taking into account both explicit conduits and the unsaturated zone in karst reservoir hybrid models: Impact on the outlet hydrograph. Water 2020, 12, 3221. [Google Scholar] [CrossRef]
- Desai, C.; Li, G. A residual flow procedure and application for free surface flow in porous media. Adv. Water Resour. 1983, 6, 27–35. [Google Scholar] [CrossRef]
- Trček, B. How can the epikarst zone influence the karst aquifer hydraulic behaviour? Environ. Earth Sci. 2006, 51, 761–765. [Google Scholar] [CrossRef]
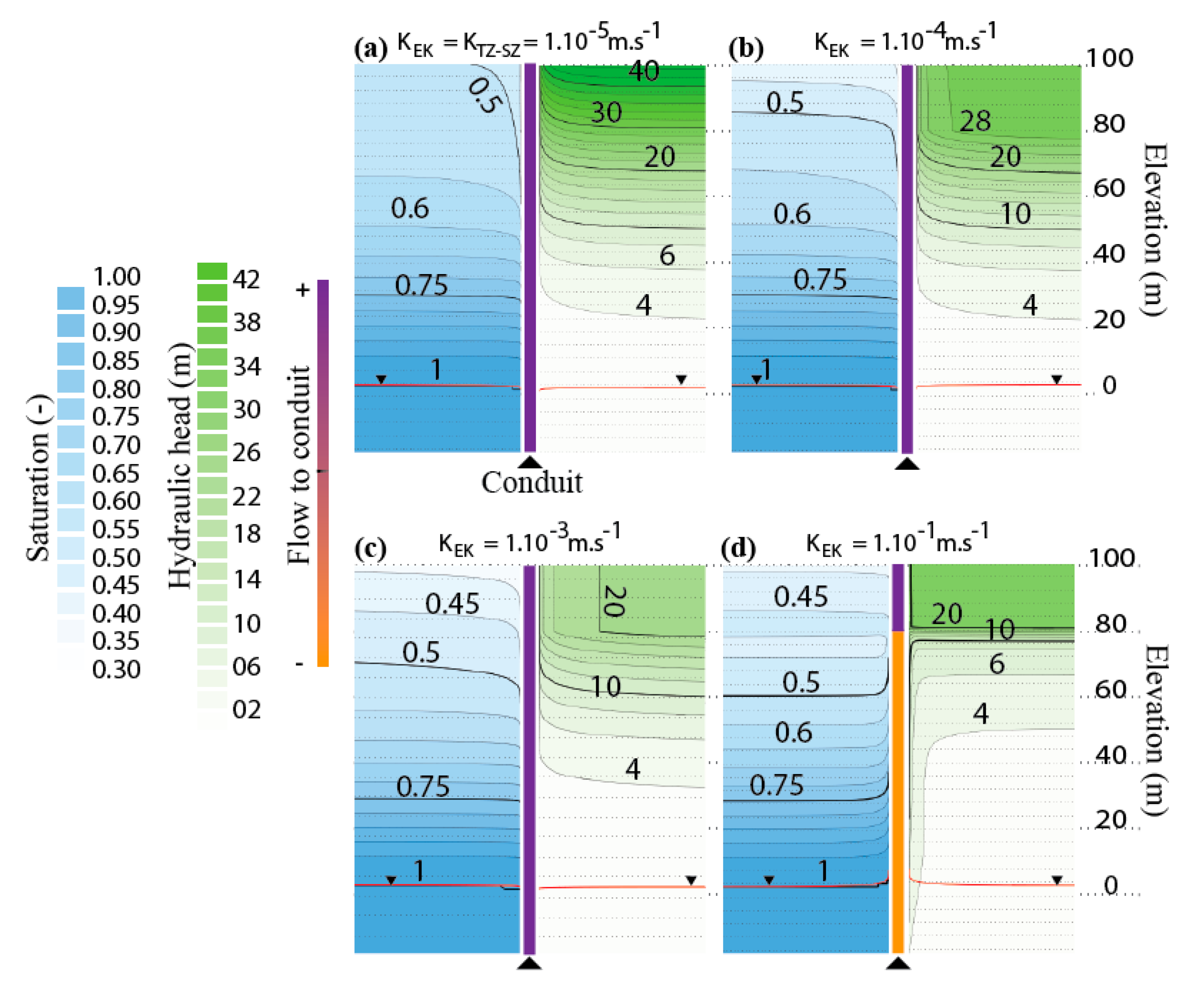
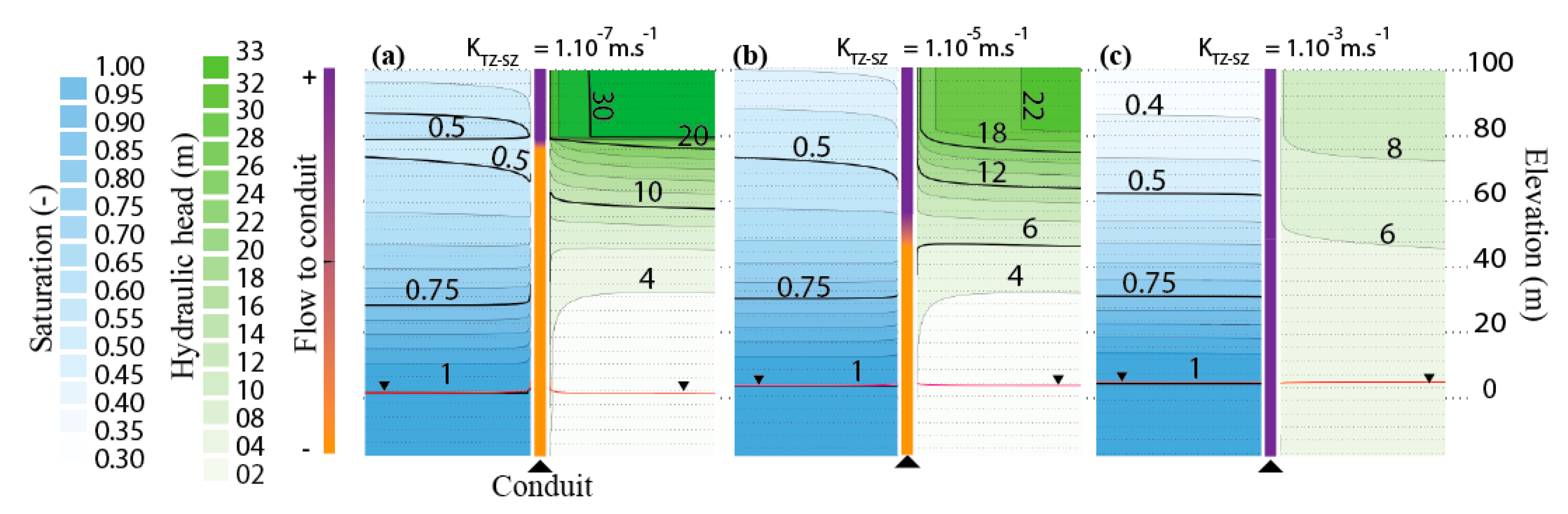
| Subsystem | Property (Units) | Values and Ranges of Values 1 from Literature [References] | Model’s Values and Range of ValuesMin–Ref–Max |
|---|---|---|---|
| Epikarst (EK) | Thickness ThkEK (m) | (0; >30) [45] (few meters; 10−15) [38] (3; 10) [37] (8; 12) [44] | 0–20–35 |
| Porosity ϕEK (-) | (0.05; 0.1) [45,55] (0.1; 0.3) [47] >0.2 [37] | 0.01–0.1–0.25 | |
| Horizontal 2 hydraulic conductivity KEK (m/s) | (10−7; 10−4) [13] 10−5 [56] (5 × 10−5; 10−3) [57] (2 × 10−4; 2 × 10−3) [58] 10−3 [59] >1000*KTZ-SZ [60] | 10−5–10−2–10−1 | |
| Transmission and saturated zones (TZ-SZ) | Thickness ThkTZ (m) | depending on the field site, usually tens of meters, <20; <50 [59] up to 700 [61] | 30–80–130 |
| Porosity ϕTZ-SZ (-) | (0.004; 0.01) [37] 0.005 [62] (0.01; 0.02) [63] (0.024; 0.3) [64] | 0.005–0.01–0.025 | |
| Horizontal 2 hydraulic conductivity KTZ-SZ (m/s) | (10−10; 7 × 10−5) [64] (10−7 [18]; 10−6 [19,37]) [57] (5 × 10−7; 5 × 10−6 [56]) [65] (10−6 [19,37]; 10−4 [62]) [63] (10−5; 10−3) [17] | 10−7–10−5–10−3 | |
| Conduit (C) | Diameter D (m) | (0.08; 15) [29] (2; 10) [33] | Flow Capacity AC * KC (m3/s−1) 10−2–10−1–101 |
| Section AC (m2) | (<1; >100) [66] | ||
| Hydraulic conductivity KC (m/s) | (6 × 10−5; 4 × 10−1) [64] (10−1; 10) [17,57] (3; 10) [63] 10 [19,65] | ||
| Van Genuchten Model | Coefficient α (m−1) | (3.28 × 10−3; 6.23 × 10−1) [15] 3.65 × 10−2 [19,21] 10−2 [17,18] | 3.65 × 10−2 |
| Empirical parameter n (-) | (0.01; 3) [15] 1.83 [19,21] 2 [17,18] | 1.83 | |
| Residual water content θr (-) or Residual water saturation Sr (-) | θr = Sr = 0 [18] θr ∈(0.01; 0.05) [15] Sr = 0.05 [19] θr = 0.171 [17] | Sr = 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dal Soglio, L.; Danquigny, C.; Mazzilli, N.; Emblanch, C.; Massonnat, G. Modeling the Matrix-Conduit Exchanges in Both the Epikarst and the Transmission Zone of Karst Systems. Water 2020, 12, 3219. https://doi.org/10.3390/w12113219
Dal Soglio L, Danquigny C, Mazzilli N, Emblanch C, Massonnat G. Modeling the Matrix-Conduit Exchanges in Both the Epikarst and the Transmission Zone of Karst Systems. Water. 2020; 12(11):3219. https://doi.org/10.3390/w12113219
Chicago/Turabian StyleDal Soglio, Lucie, Charles Danquigny, Naomi Mazzilli, Christophe Emblanch, and Gérard Massonnat. 2020. "Modeling the Matrix-Conduit Exchanges in Both the Epikarst and the Transmission Zone of Karst Systems" Water 12, no. 11: 3219. https://doi.org/10.3390/w12113219






