The Use of Water Vapor Isotopes to Determine Evapotranspiration Source Contributions in the Natural Environment
Abstract
1. Introduction
2. Methods
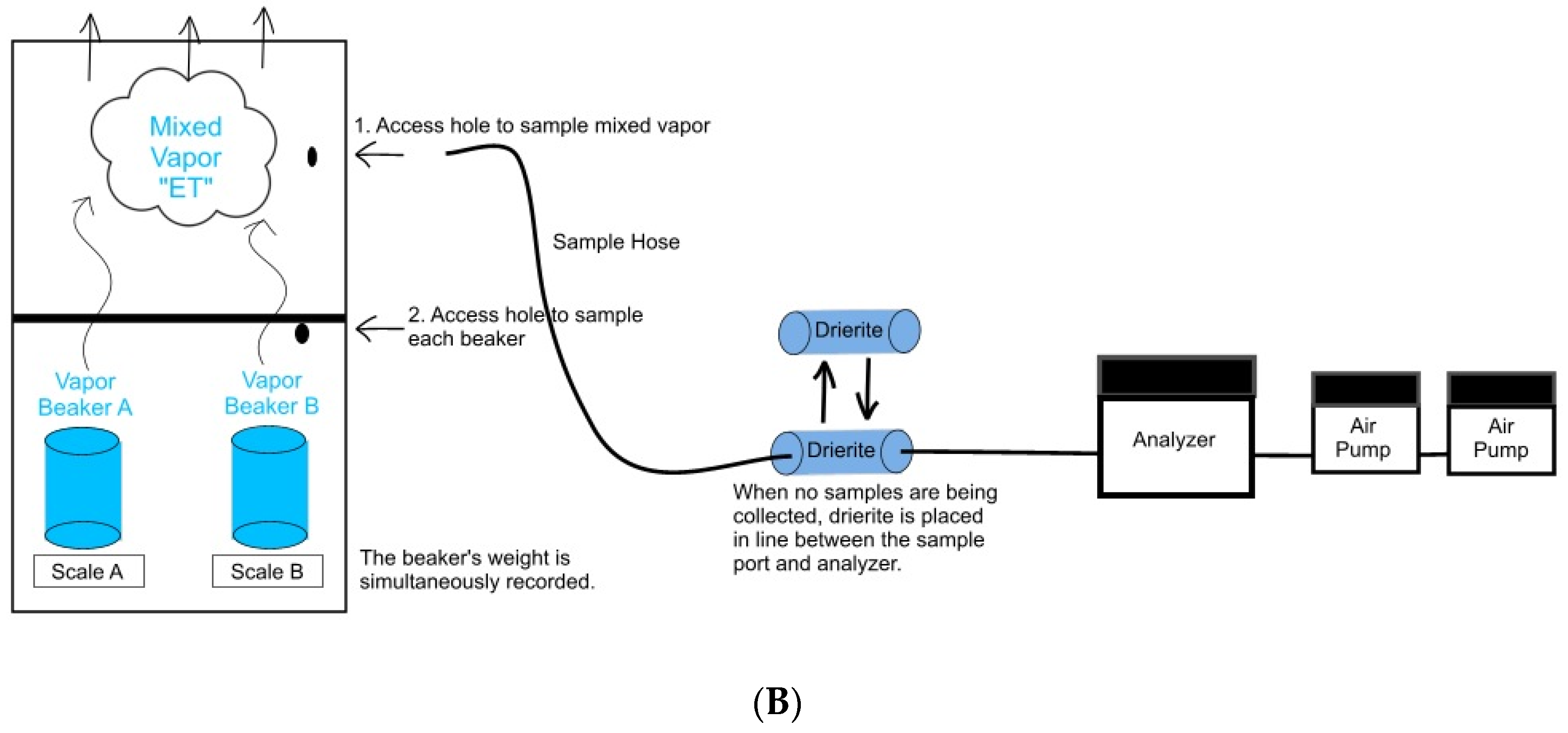
2.1. Laboratory Water-Vapor Isotopic Sampling
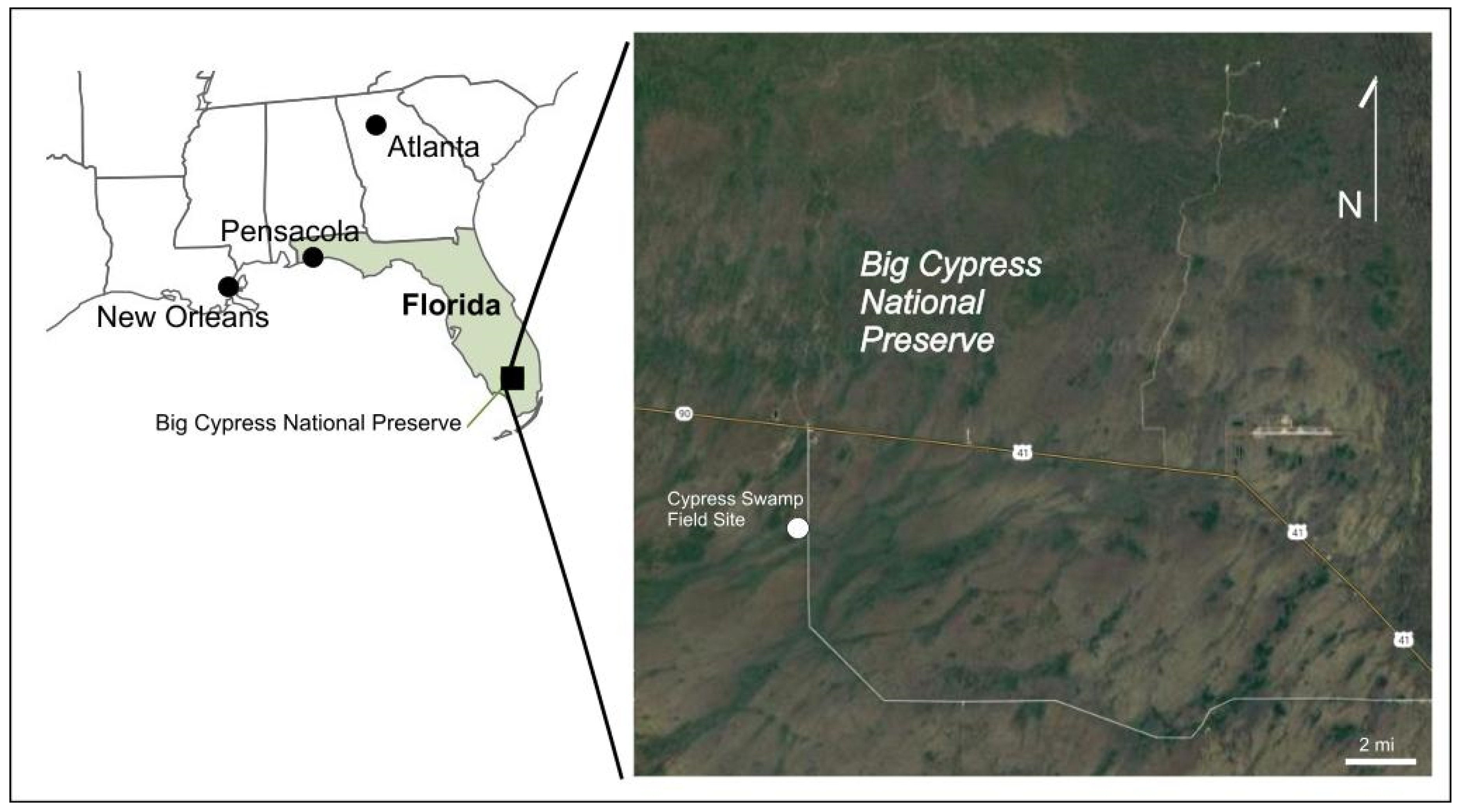
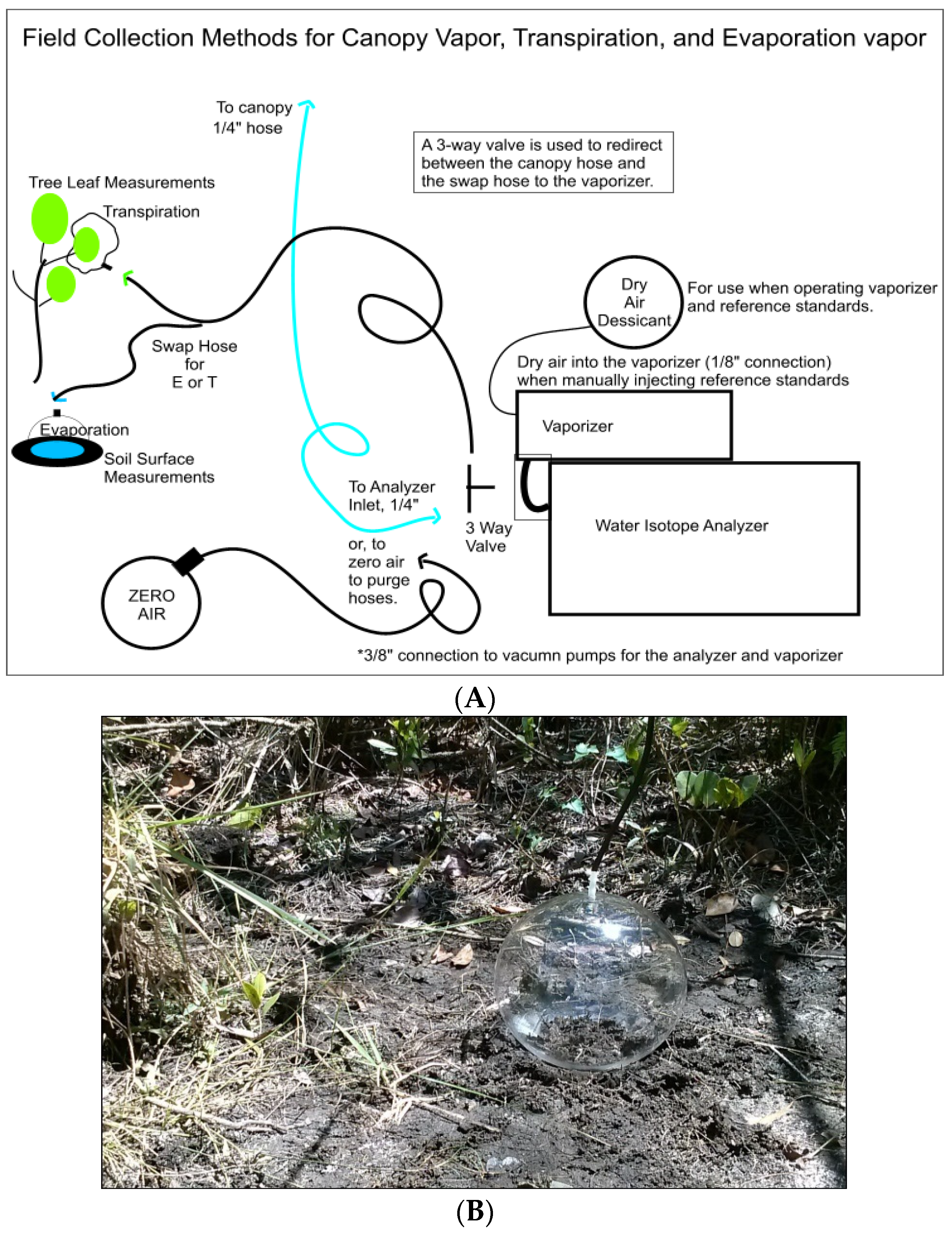
2.2. Field Water-Vapor Isotopic Sampling
2.3. EC Flux Data Sampling
3. Post-Sampling Data Processing
3.1. Data Screening, Instrument Drift Correction, and Data Calibration
3.2. Partitioning of Water-Vapor Sources Using the Isotope Mass Balance
3.3. Model Verification Using the Mass Balance Technique
4. Results
4.1. Mass Balance Partitioning in the Laboratory
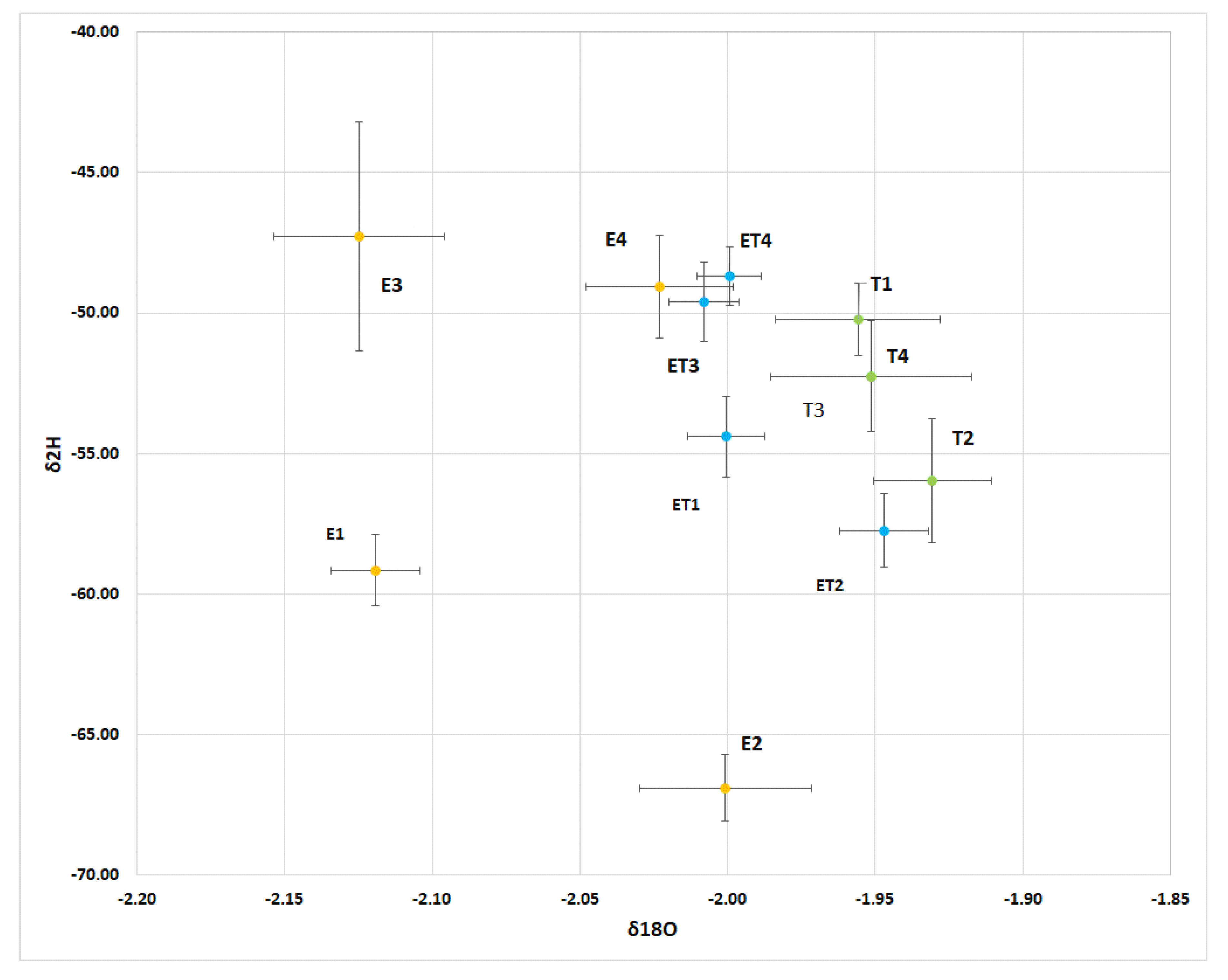
4.2. Mass Balance Partioning in Big Cypress, Florida
5. Discussion
5.1. Changing Isotopic Composition by Fractionation
5.2. The Significance of the Results
5.3. Uncertainty in the Measurements
- inconsistent distances from the evaporating surface,
- tubing effects,
- different temperatures,
- relative humidity,
- varying vapor pressures,
5.4. ET Ratios of This Study and Similar Studies
5.5. Comparison between Field Isotopic Mass Balance and the Flux Variance Similarity Partitioning Ratios
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Farquhar, G.D.; Cernusak, L.A.; Barnes, B. Heavy water fractionation during transpiration. Plant Physiol. 2007, 143, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Wenninger, J.; Beza, D.T.; Uhlenbrook, S. Experimental investigations of water fluxes within the soil–vegetation–atmosphere system: Stable isotope mass-balance approach to partition evaporation and transpiration. Phys. Chem. Earthparts A/B/C 2010, 35, 565–570. [Google Scholar] [CrossRef]
- Good, S.P.; Mallia, D.V.; Lin, J.C.; Bowen, G.J. Stable isotope analysis of precipitation samples obtained via crowdsourcing reveals the spatiotemporal evolution of superstorm sandy. PLoS ONE 2014, 9, e91117. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wen, X.; Wang, J.; Yu, G.; Sun, X. The use of stable isotopes to partition evapotranspiration fluxes into evaporation and transpiration. Acta Ecol. Sin. 2010, 30, 201–209. [Google Scholar] [CrossRef]
- Li, G.; Li, B. Isotope mass balance method to partition evaporation and transpiration in cropping field. IAEA Tecdoc. Ser. 2017, 75–82. Available online: https://www-pub.iaea.org/MTCD/Publications/PDF/TE-1813_web.pdf#page=84 (accessed on 9 November 2019).
- Talsma, C.; Good, S.; Miralles, D.; Fisher, J.; Martens, B.; Jimenez, C.; Purdy, A. Sensitivity of Evapotranspiration Components in Remote Sensing-Based Models. Remote Sens. 2018, 10, 1601. [Google Scholar] [CrossRef]
- Urbina, C.A.; van Dam, J.C.; Hendriks, R.F.A.; van den Berg, F.; Gooren, H.P.A.; Ritsema, C.J. Water flow in soils with heterogeneous macropore geometries. Vadose Zone J. 2019, 18, 1–17. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Hincks, B.B.; Meyers, T.P. Measuring biosphere-atmosphere exchanges of biologically related gases with micrometeorological methods. Ecology 1988, 69, 1331–1340. [Google Scholar] [CrossRef]
- Migliaccio, K.W.; Barclay Shoemaker, W. Estimation of urban subtropical bahiagrass (Paspalum notatum) evapotranspiration using crop coefficients and the eddy covariance method. Hydrol. Process. 2014, 28, 4487–4495. [Google Scholar] [CrossRef]
- Shoemaker, W.B.; Lopez, C.D.; Duever, M.J. Evapotranspiration over spatially extensive plant communities in the Big Cypress National Preserve, southern Florida, 2007–2010. U.S. Geol. Surv. Sci. Invest. Rep. 2011, 5212, 46. [Google Scholar]
- Gupta, P.; Noone, D.; Galewsky, J.; Sweeney, C.; Vaughn, B.H. Demonstration of high-precision continuous measurements of water vapor isotopologues in laboratory and remote field deployments using wavelength-scanned cavity ring-down spectroscopy (WS-CRDS) technology. Rapid Commun. Mass Spectrom. 2009, 23, 2534–2542. [Google Scholar] [CrossRef] [PubMed]
- Geldern, R.; Barth, J.A. Optimization of instrument setup and post-run corrections for oxygen and hydrogen stable isotope measurements of water by isotope ratio infrared spectroscopy (IRIS). Limnol. Oceanogr. Methods 2012, 10, 1024–1036. [Google Scholar] [CrossRef]
- Tremoy, G.; Vimeux, F.; Cattani, O.; Mayaki, S.; Souley, I.; Favreau, G. Measurements of water vapor isotope ratios with wavelength-scanned cavity ring-down spectroscopy technology: New insights and important caveats for deuterium excess measurements in tropical areas in comparison with isotope-ratio mass spectrometry. Rapid Commun. Mass Spectrom. 2011, 25, 3469–3480. [Google Scholar] [CrossRef] [PubMed]
- Yakir, D.; da SL Sternberg, L. The use of stable isotopes to study ecosystem gas exchange. Oecologia 2000, 123, 297–311. [Google Scholar] [CrossRef] [PubMed]
- Gaj, M.; Beyer, M.; Koeniger, P.; Wanke, H.; Hamutoko, J.; Himmelsbach, T. In situ unsaturated zone water stable isotope (2H and 18O) measurements in semi-arid environments: A soil water balance. Hydrol. Earth Syst. Sci. 2016, 20, 715–731. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Gat, J. Isotope Hydrology: A Study of the Water Cycle; Imperial College Press, World Scientific: Singapore, 2010; Volume 6. [Google Scholar]
- Clark, I.D.; Fritz, P. Environmental Isotopes in Hydrogeology; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Sutanto, S.J.; Van den Hurk, G.B.; Hoffmann, J.; Wenninger, P.A.; Dirmeyer, S.I.; Seneviratne, T.; Röckmann, K.E.; Trenberth, E.; Blyth, M. HESS Opinions “A perspective on isotope versus non-isotope approaches to determine the contribution of transpiration to total evaporation”. Hydrol. Earth Syst. Sci. 2014, 18, 2815–2827. [Google Scholar] [CrossRef]
- Craig, H.; Gordon, L.I. Deuterium and oxygen 18 variations in the ocean and the marine atmosphere. In Stable Isotopes in Oceanographic Studies and Paleotemperatures; Consiglio Nazionale Delle Ricerche Laboratorio Di Geologia Nucleare—Pisa: Spoleto, Italy, 1965; pp. 9–130. [Google Scholar]
- Majoube, M. Fractionnement en oxygene 18 et en deuterium entre l’eau et sa vapeur. J. De Chim. Phys. 1971, 68, 1423–1436. [Google Scholar] [CrossRef]
- Horita, J.; Wesolowski, D.J. Liquid-vapor fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature. Geochim. Et Cosmochim. Acta 1994, 58, 3425–3437. [Google Scholar] [CrossRef]
- Fang, G.; Ward, C.A. Temperature measured close to the interface of an evaporating liquid. Phys. Rev. E 1999, 59, 417–428. [Google Scholar] [CrossRef]
- Swain, E.; Decker, J. Measurement-derived Heat-budget Approaches for Simulating Coastal Wetland Temperature with a Hydrodynamic Model. Wetlands 2010, 30, 635–648. [Google Scholar] [CrossRef]
- Köstner, B. Evaporation and transpiration from forests in Central Europe–relevance of patch-level studies for spatial scaling. Meteorol. Atmos. Phys. 2001, 76, 69–82. [Google Scholar] [CrossRef]
- Raz-Yaseef, N.; Yakir, D.; Schiller, G.; Cohen, S. Dynamics of evapotranspiration partitioning in a semi-arid forest as affected by temporal rainfall patterns. Agric. For. Meteorol. 2012, 157, 77–85. [Google Scholar] [CrossRef]
- Scott, R.L.; Huxman, T.E.; Cable, W.L.; Emmerich, W.E. Partitioning of evapotranspiration and its relation to carbon dioxide exchange in a Chihuahuan Desert shrubland. Hydrol. Process. 2006, 20, 3227–3243. [Google Scholar] [CrossRef]
- Stannard, D.I.; Weltz, M.A. Partitioning evapotranspiration in sparsely vegetated rangeland using a portable chamber. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Skaggs, T.H.; Anderson, R.G.; Alfieri, J.G.; Scanlon, T.M.; Kustas, W.P. Fluxpart: Open source software for partitioning carbon dioxide and water vapor fluxes. Agric. For. Meteorol. 2018, 253–254, 218–224. [Google Scholar] [CrossRef]
- Eiko, N.; Mannarella, I.; Ibrom, A.; Aurela, M.; Burba, G.G.; Dengel, S.; Gielen, B. Standardisation of eddy-covariance flux measurements of methane and nitrous oxide. Int. Agrophys. 2018, 32, 517–549. [Google Scholar]
- Scheihing, K.W.; Moya, C.E.; Struck, U.; Lictevout, E.; Tröger, U. Reassessing Hydrological Processes That Control Stable Isotope Tracers in Groundwater of the Atacama Desert (Northern Chile). Hydrology 2017, 5, 3. [Google Scholar] [CrossRef]
- Markland, T.E.; Berne, B.J. Unraveling quantum mechanical effects in water using isotopic fractionation. Proc. Natl. Acad. Sci. USA 2012, 109, 7988–7991. [Google Scholar] [CrossRef]
- Jean-Louis, B.; Behrens, M.; Meyer, H.; Kipfstuhl, S.; Rabe, B.; Schönicke, L.; Steen-Larsen, H.C.; Werner, M. Resolving the controls of water vapour isotopes in the Atlantic sector. Nat. Commun. 2019, 10, 1–10. [Google Scholar]
- Galewsky, J.; Steen-Larsen, H.C.; Field, R.D.; Worden, J.; Risi, C.; Schneider, M. Stable isotopes in atmospheric water vapor and applications to the hydrologic cycle. Rev. Geophys. 2016, 54, 809–865. [Google Scholar] [CrossRef] [PubMed]
- Schneider, M.; Borger, C.; Wiegele, A.; Hase, F.; García, O.E.; Sepúlveda, E.; Werner, M. MUSICA MetOp/IASI {H2O,δD} pair retrieval simulations for validating tropospheric moisture pathways in atmospheric models. Atmos. Meas. Tech. 2017, 10, 507–525. [Google Scholar] [CrossRef]
- Kalua, M.; Rallings, A.M.; Booth, L.; Medellín-Azuara, J.; Carpin, S.; Viers, J.H. sUAS Remote Sensing of Vineyard Evapotranspiration Quantifies Spatiotemporal Uncertainty in Satellite-Borne ET Estimates. Remote Sens. 2020, 12, 3251. [Google Scholar] [CrossRef]


| δ18O | δ2H | Beaker A | Beaker B | δ18O Percent Difference | ||||
|---|---|---|---|---|---|---|---|---|
| Fa | Fb | Fa | Fb | Ba | Bb | Fa IMB (Ratio) | Fb IMB (Ratio) | |
| Date/ Time | IMB (Ratio) 1 | IMB (Ratio) 2 | IMB (Ratio) 3 | IMB (Ratio) 4 | Water Mass Bal 5 | Water Mass Bal 6 | and Ba Mass Bal (Ratio) 7 | and Bb Mass Bal (Ratio) 8 |
| 5/12 13:21 | 0.06 | 0.94 | 0.07 | 0.93 | 0.23 | 0.77 | 0.17 | 0.17 |
| 5/12 14:13 | 0.20 | 0.80 | 0.07 | 0.93 | 0.41 | 0.59 | 0.16 | 0.16 |
| Avg | 0.13 | 0.87 | 0.07 | 0.93 | 0.32 | 0.68 | 0.16 | 0.16 |
| 5/24 15:09 | 0.53 | 0.47 | 0.97 | 0.03 | 0.63 | 0.37 | 0.10 | 0.10 |
| 5/24 15:52 | 0.86 | 0.14 | 0.66 | 0.34 | 0.71 | 0.29 | 0.15 | 0.15 |
| 5/24 16:40 | 0.65 | 0.35 | 0.87 | 0.13 | 0.69 | 0.31 | 0.04 | 0.04 |
| Avg | 0.68 | 0.32 | 0.83 | 0.17 | 0.67 | 0.33 | 0.09 | 0.09 |
| 8/21 16:02 | 0.28 | 0.72 | 0.41 | 0.59 | 0.40 | 0.60 | 0.12 | 0.12 |
| 8/21 16:54 | 0.14 | 0.86 | 0.43 | 0.57 | 0.36 | 0.64 | 0.22 | 0.22 |
| 8/21 17:54 | 0.32 | 0.68 | 0.47 | 0.53 | 0.44 | 0.56 | 0.24 | 0.24 |
| Avg | 0.25 | 0.75 | 0.44 | 0.56 | 0.40 | 0.60 | 0.19 | 0.19 |
| Sample Time 1 | PAR 2 mmol/m2 | H2O PPMV 3 | δ18O ‰ 4 | Std. Dev. δ18O (‰) 5 | δ2H ‰ 6 | Std. Dev. δ2H (‰) 7 | Obs. Type 8 |
|---|---|---|---|---|---|---|---|
| 10:47:24 | 2542 | 21338 | −1.95 | 0.018 | −44.79 | 1.931 | ET |
| 11:53:13 | 2691 | 22394 | −1.96 | 0.028 | −50.23 | 1.295 | T |
| 12:00:59 | 2790 | 23401 | −2.00 | 0.013 | −54.40 | 1.442 | ET |
| 12:06:16 | 2837 | 29833 | −2.12 | 0.015 | −59.15 | 1.282 | E |
| 12:09:18 | 2835 | 29878 | −2.03 | 0.017 | −68.35 | 1.208 | T |
| 12:16:00 | 2781 | 22841 | −1.95 | 0.015 | −57.75 | 1.315 | ET |
| 12:43:10 | 2675 | 23069 | −1.93 | 0.020 | −55.96 | 2.199 | T |
| 12:56:34 | 2520 | 23600 | −2.00 | 0.010 | −66.90 | 1.182 | E |
| 13:15:01 | 2318 | 23850 | −2.01 | 0.012 | −49.60 | 1.416 | ET |
| 13:35:17 | 2542 | 34574 | −2.12 | 0.029 | −47.26 | 4.078 | E |
| 13:54:35 | 2691 | 27695 | −1.95 | 0.034 | −52.25 | 1.966 | T |
| 14:09:33 | 2790 | 22963 | −2.00 | 0.011 | −48.68 | 1.046 | ET |
| 14:31:22 | 2837 | 23386 | −2.02 | 0.025 | −49.06 | 1.813 | E |
| 14:58:25 | 2835 | 25880 | −2.01 | 0.013 | −41.55 | 4.373 | T |
| 15:08:03 | 2781 | 25111 | −2.00 | 0.037 | −47.22 | 1.124 | T |
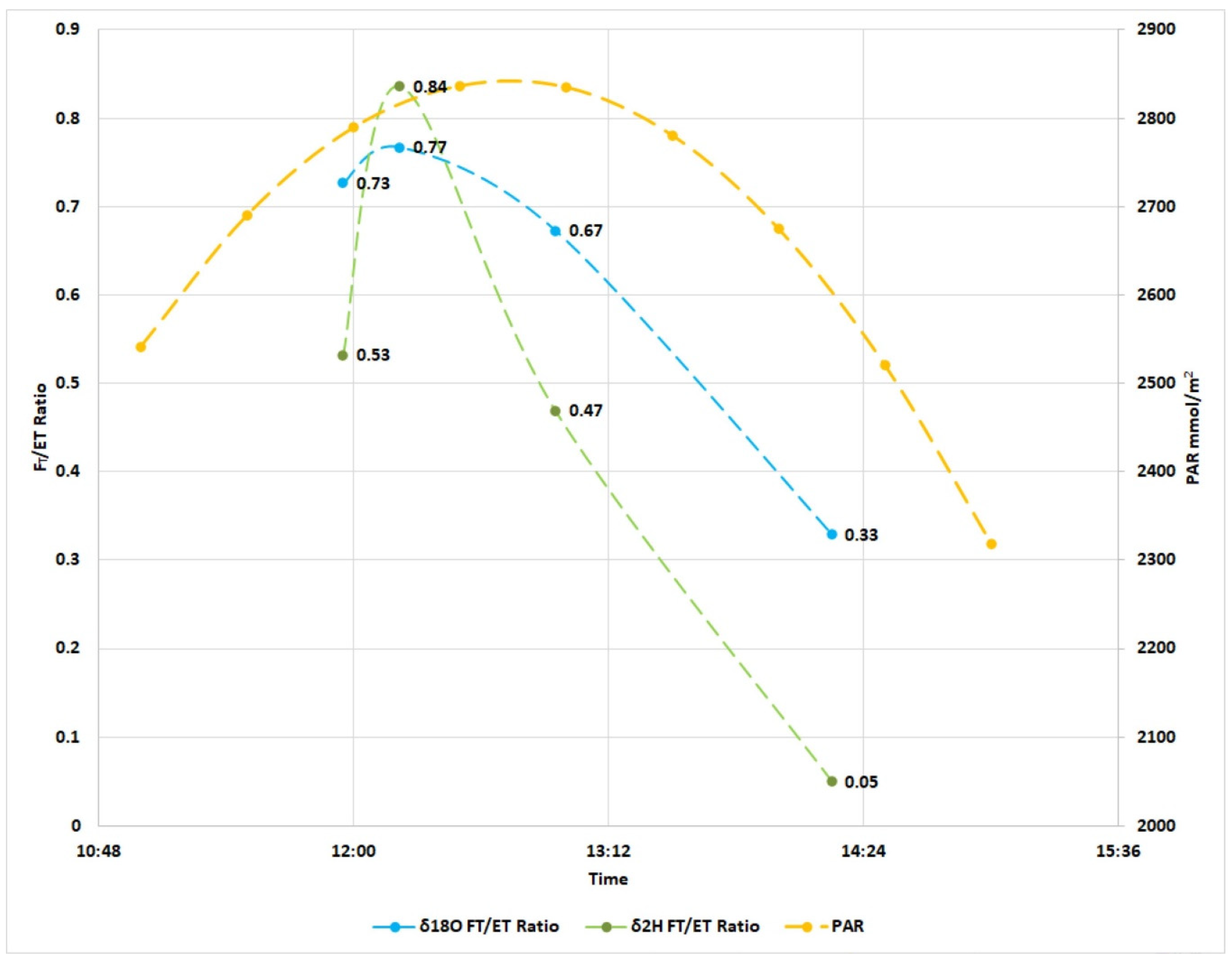
| IMB FT/ET 1 | IMB FE/ET 2 | IMB FT/ET 3 | IMB FE/ET 4 | |
|---|---|---|---|---|
| Time | δ18O ratio | δ18O ratio | δ2H ratio | δ2H ratio |
| 12:00 | 0.73 | 0.27 | 0.53 | 0.47 |
| 12:30 | 0.77 | 0.23 | 0.84 | 0.16 |
| 13:00 | 0.67 | 0.33 | 0.47 | 0.53 |
| 14:15 | 0.33 | 0.67 | 0.05 | 0.95 |
| Average | 0.62 | 0.38 | 0.47 | 0.53 |
| LandCover | Publication | E a | E/ET | T | T/ET | ET a | (E + T)/ET |
|---|---|---|---|---|---|---|---|
| Forest | Köstner (2001) b,c [25] | ML, Chamber | 0.07−0.15 | SF (HD) | 0.85−0.95 | EC, WB | NA |
| Forest | Raz-Yaseef et al. (2012) c [26] | Chamber | 0.44–0.53 | SF (HD, CHPV) | 0.44–0.57 | EC | 0.89–1.11 |
| Shrub | Scott et al. (2006) [27] | ET-T | NA | SF (SHB) | 0.58–0.70 | BREB | NA |
| Shrub | Stannard and Weltz (2006) [28] | Chamber | 0.16 | Chamber | 0.84 | EC | 1.26 |
| Forest | This study | Chamber | 0.23–0.67 | Bag | 0.33–0.77 | IMB | NA |
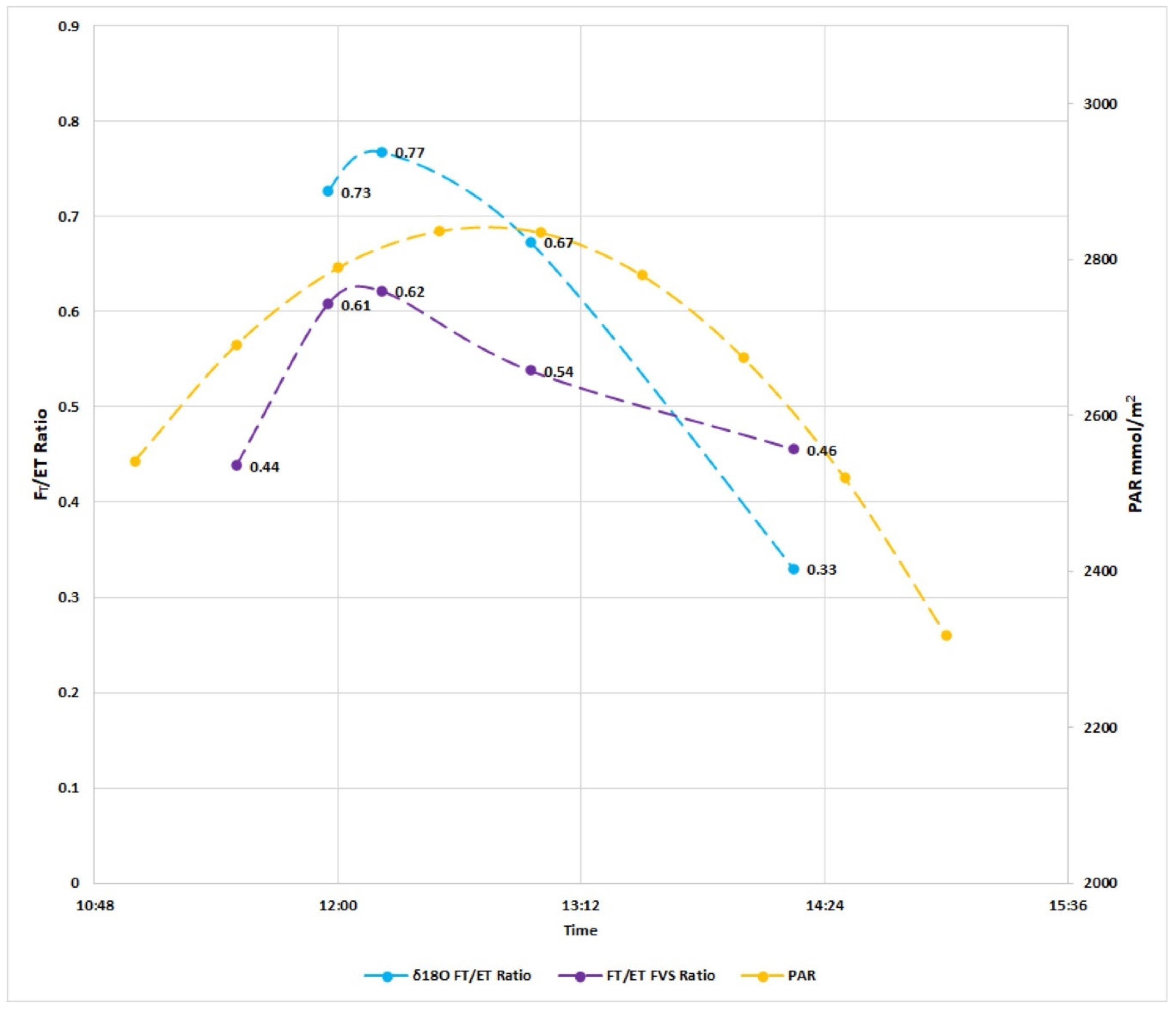
| Timestamp | FVS Ft/ET | FVS Fe/ET | δ18O Ft/ET | δ18O Fe/ET | δ2H Ft/ET | δ2H Fe/ET | % Diff δ18O-FVS | % Diff δ2H-FVS |
|---|---|---|---|---|---|---|---|---|
| 12:00:00 | 0.61 | 0.39 | 0.73 | 0.27 | 0.53 | 0.47 | 12% | 8% |
| 12:15:00 | 0.85 | 0.15 | - | - | - | - | - | - |
| 12:30:00 | 0.62 | 0.38 | 0.77 | 0.23 | 0.84 | 0.16 | 15% | 21% |
| 12:45:00 | 0.24 | 0.76 | - | - | - | - | - | - |
| 13:00:00 | 0.54 | 0.46 | 0.67 | 0.33 | 0.47 | 0.53 | 13% | 7% |
| 13:15:00 | 0.50 | 0.50 | - | - | - | - | - | - |
| 13:30:00 | 0.37 | 0.63 | - | - | - | - | - | - |
| 13:45:00 | 0.35 | 0.65 | - | - | - | - | - | - |
| 14:00:00 | 0.46 | 0.54 | - | - | - | - | - | - |
| 14:15:00 | 0.40 | 0.60 | 0.33 | 0.67 | 0.05 | 0.95 | 7% | 35% |
| Std Dev | 0.19 | 0.19 | 0.34 | 0.23 | 0.31 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernier, T.P. The Use of Water Vapor Isotopes to Determine Evapotranspiration Source Contributions in the Natural Environment. Water 2020, 12, 3203. https://doi.org/10.3390/w12113203
Bernier TP. The Use of Water Vapor Isotopes to Determine Evapotranspiration Source Contributions in the Natural Environment. Water. 2020; 12(11):3203. https://doi.org/10.3390/w12113203
Chicago/Turabian StyleBernier, Troy P. 2020. "The Use of Water Vapor Isotopes to Determine Evapotranspiration Source Contributions in the Natural Environment" Water 12, no. 11: 3203. https://doi.org/10.3390/w12113203
APA StyleBernier, T. P. (2020). The Use of Water Vapor Isotopes to Determine Evapotranspiration Source Contributions in the Natural Environment. Water, 12(11), 3203. https://doi.org/10.3390/w12113203





