1. Introduction
Flooding is the most common natural hazard and third most damaging globally after storms and earthquakes [
1]. Flood forecasting can provide key information for disaster warning and flood control, which plays an important role in reducing the damage caused by flooding [
2,
3]. The common flood forecasting methods generally use a deterministic hydrological model to predict the future flood process [
4,
5,
6,
7]. However, the traditional deterministic hydrological forecast cannot provide the hydrological forecast value in the forecast period to meet the needs of the corresponding river basin management department [
8].
Ensemble flow forecasting can provide more hydrological forecasting information for policymakers in order to better ensure the safety of life and property in downstream areas and improve the social and economic benefits [
9,
10]. Ensemble weather forecasting (EWF) plays an important role in ensemble flow forecasting [
11]. First, EWF contains more information, which can provide more comprehensive meteorological data for a hydrological forecast in a future period [
12]. Second, research shows that combining EWF with a hydrological forecast model can improve the reliability and accuracy of forecast results [
13]. However, due to the diversity of atmospheric conditions and topography, the simplification of physical and thermodynamic processes, the uncertainties of parameterization of models, and the limited spatial resolution, the standard EWF offers systematic deviations compared with the observations [
14]. Thus, EWF should be corrected first before being applied to the hydrological forecasting process. For example, Hamill et al. [
15] used a logistic regression method to process the set rainfall forecast and obtained the conditional distribution function of rainfall under given conditions. Sloughter et al. [
16] used a logistic regression function and the Gamma distribution to describe the distribution of rainfall events of zero value and non-zero value, respectively, then built a mixed distribution function to describe the distribution of rainfall events, and improved the Bayes Model Averaging (BMA) method to make it applicable to the post-processing of aggregate rainfall forecasts. Wilks [
17] improved the traditional logistic regression approach by introducing quartiles into the function as independent variables, thus, providing a continuous probability distribution function to describe the distribution of rainfall. However, the above methods need to make assumptions about the distribution of rainfall in EWF, and the calculation process is tedious. To overcome the above problems, the Autoregressive (AR) model, which is independent of the rainfall distribution, was used to post-process the precipitation value of EWF.
In recent years, great progress has been made in the research and theory of hydrological ensemble forecasting. Mylne [
18] conducted a multi-mode ensemble prediction test, proving that the information given by multi-mode ensemble prediction is more accurate than that provided by a single mode prediction in either the probabilistic sense (such as probability density distribution) or the deterministic sense (such as average ensemble prediction). Brown et al. [
19] used the National Center for Environmental Forecasting (NCEP) ensemble prediction model to drive the distributed hydrological model to obtain the hydrological ensemble prediction results, and the results showed that the ensemble prediction could improve the effective flood warning period. Choubin et al. [
20] proposed a new flood sensitivity set prediction method based on multiple discriminant analysis (MDA) and classification and regression trees (CART), combined with support vector machine (SVM). However, most of the above methods only consider the uncertainty of hydrological models or the uncertainty of rainfall input data, and fail to reflect the comprehensive impact of uncertainties from different sources in the prediction process and results. Therefore, this paper proposes a method that combines an AR model with a Bayesian forecast system (BFS). The proposed model, comprehensively considering the uncertainties of rainfall input, model structure, and parameters, is designed to yield good ensemble flow forecast results in this paper.
Krzysztofowicz constructed the theoretical system of BFS for the first time in 1999 [
21], and pointed out that the source of uncertainty in short-term runoff forecasting is mainly the future time series of rainfall as input to the hydrological model. BFS generates probabilistic forecasts of hydrological variables through deterministic hydrological models. As a result, the basic principle is to divide the sources of hydrological uncertainty into two categories: one is the input uncertainty with rainfall as the core and the other is the structural uncertainty of the hydrological model. Quantitative research, which is then combined into the final uncertainty probability forecast results, verifies that BFS can be combined with any deterministic hydrological model, and is independent of whether the hydrological model structure is linear or not [
22,
23].
Marshall [
24] realized the probabilistic forecast by combining the Markov Monte Carlo (MCMC) with Bayesian method, and compared it with conceptual rainfall-runoff model to illustrate the advantages of probabilistic prediction. Subsequently, Marshall [
25] used the Adaptive Metropolis Algorithm to calculate the posterior density of Bayesian probability prediction and verified the feasibility of Bayesian probability prediction as a hydrological prediction model. Henry [
26,
27] proposed a random ensemble Bayesian probabilistic forecast system (REBFS) based on the BFS. The REBFS model can output multiple set elements, effectively reducing the scale of the set weather prediction system, and making it more feasible to apply the BFS to large-scale regions. However, the process of parameter estimation of the above methods is complicated, which makes their application inconvenient. Feng et al. [
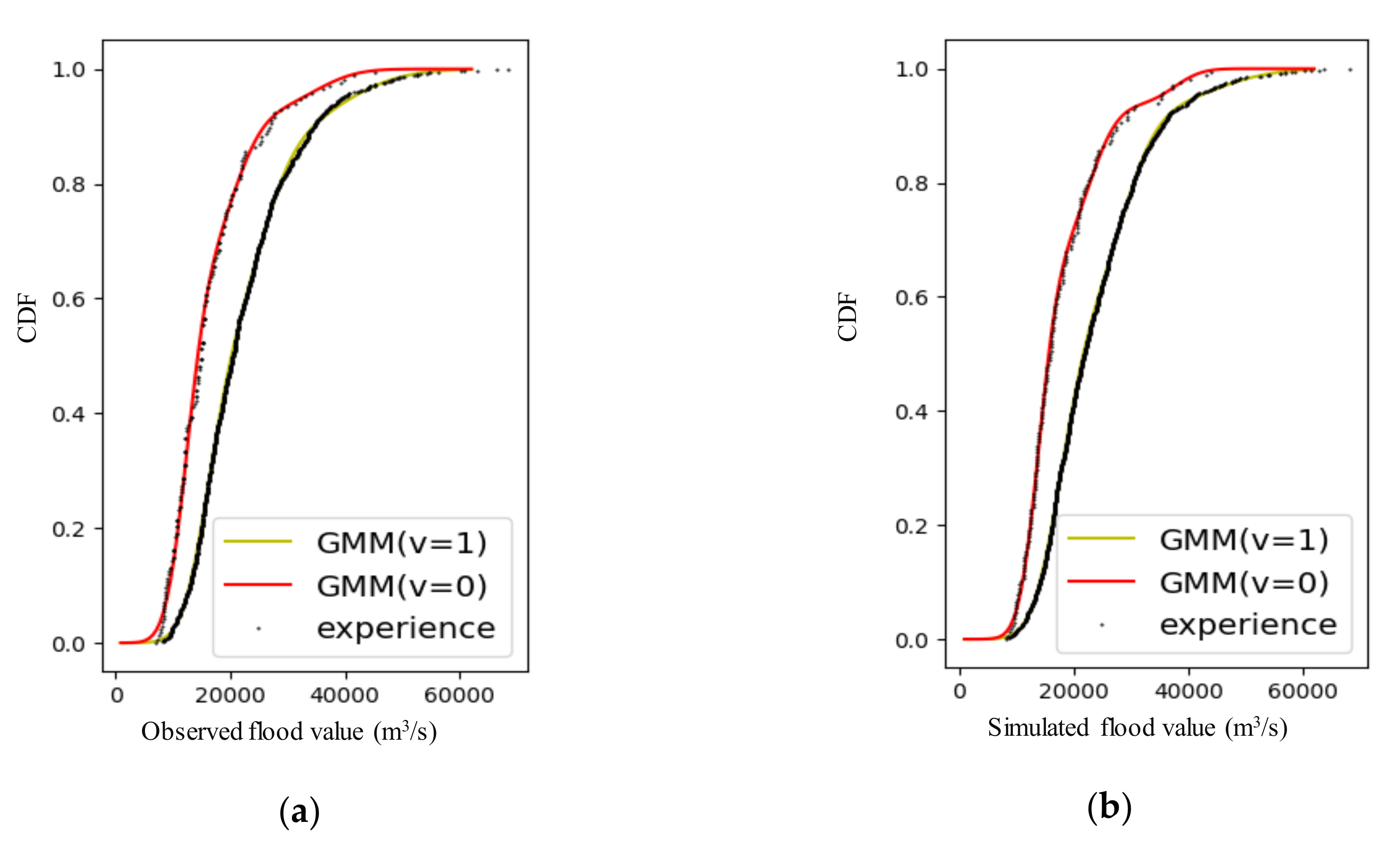
28] used the Gaussian mixture model (GMM) to fit the marginal distribution and applied it to the hydrological uncertainty processer (HUP), and concluded that GMM had good applicability in HUP. However, it did not consider the effect of precipitation uncertainty. In order to solve the above two problems, a method combining precipitation-dependent HUP (PD-HUP) and GMM is proposed in this paper. The GMM function is used as the marginal distribution function in BFS, and the uncertainty of precipitation input data is also considered.
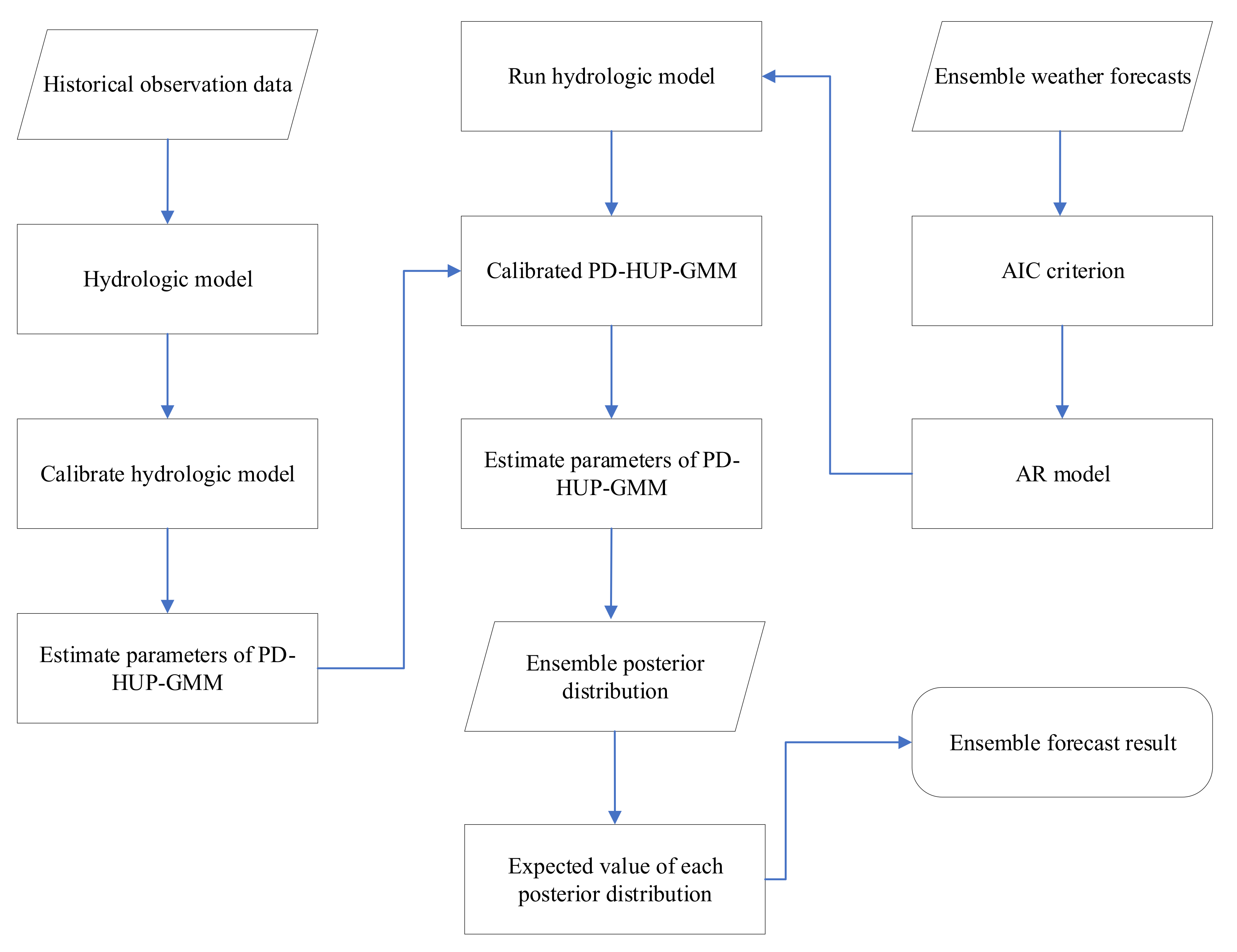
In summary, the main objective of this paper is to propose a Bayesian ensemble forecast method considering uncertainty of hydrological models and precipitation. First, the Autoregressive (AR) model is used to correct the rainfall data of Ensemble Weather Forecasts (EWF). Then, a precipitation-dependent HUP (PD-HUP) based on GMM is proposed to deal with the uncertainty of both the input data and the hydrological model. Finally, the ensemble flow forecast results are generated from the results determined by the PD-HUP method.
4. Conclusions
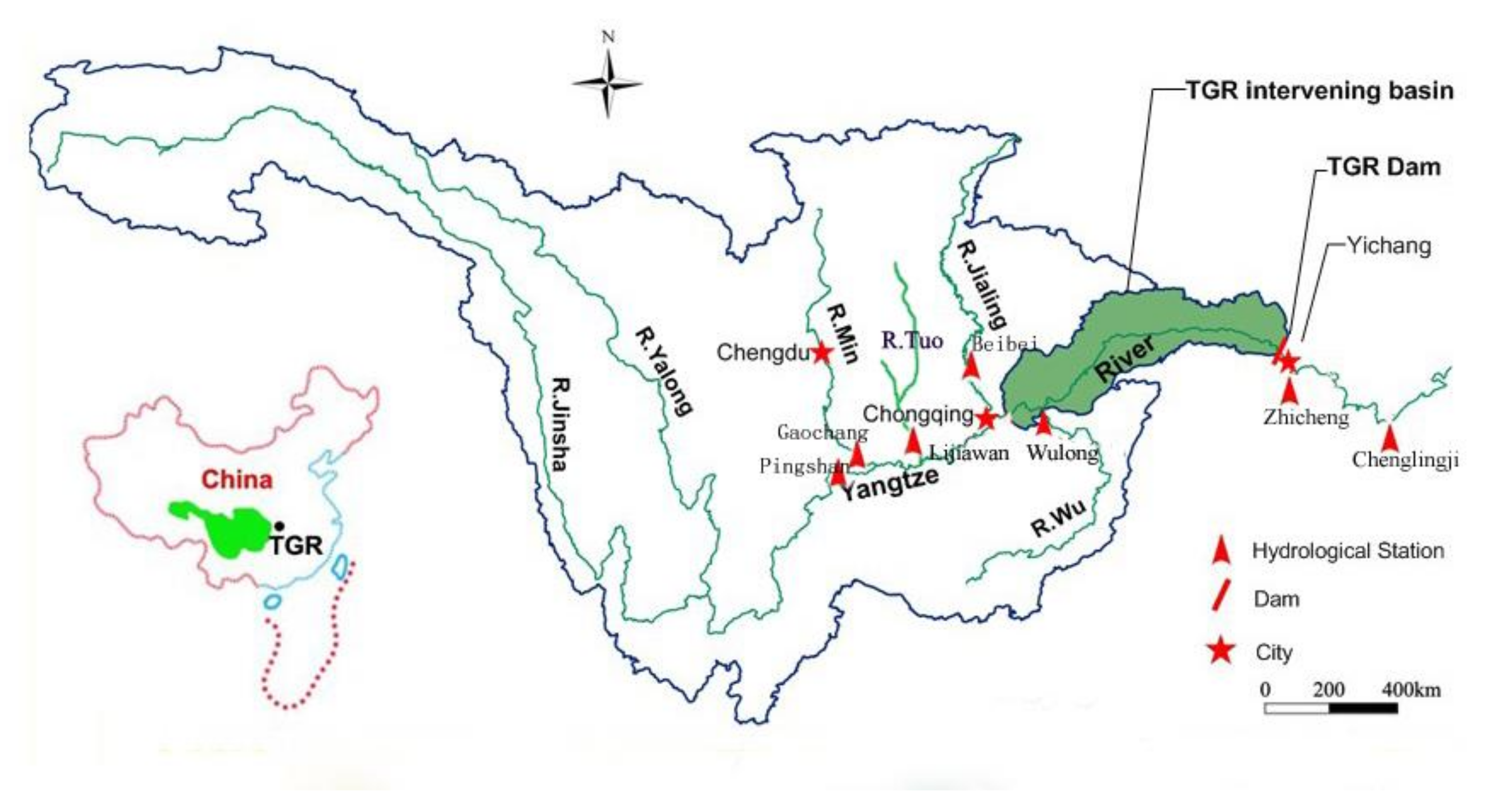
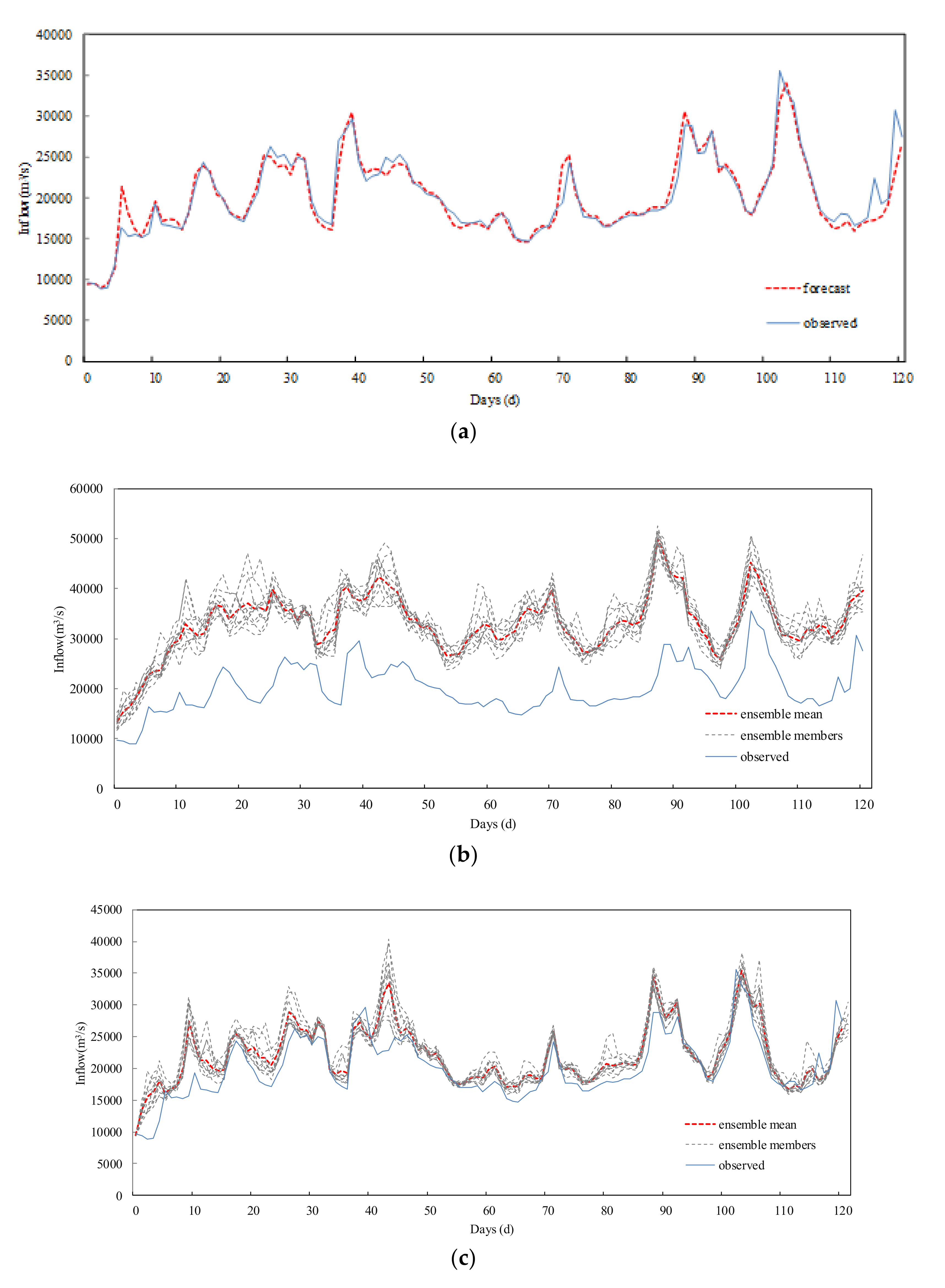
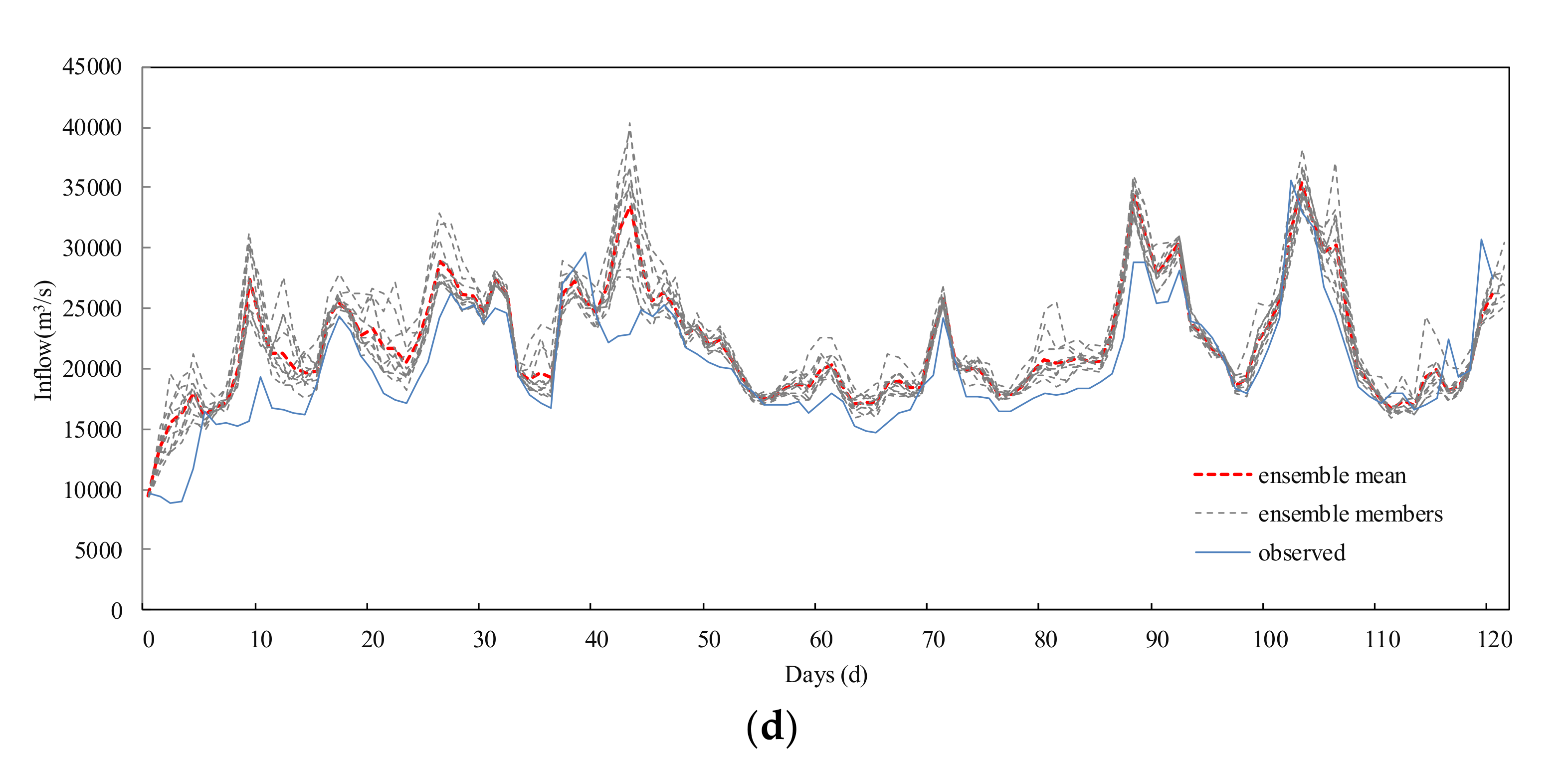
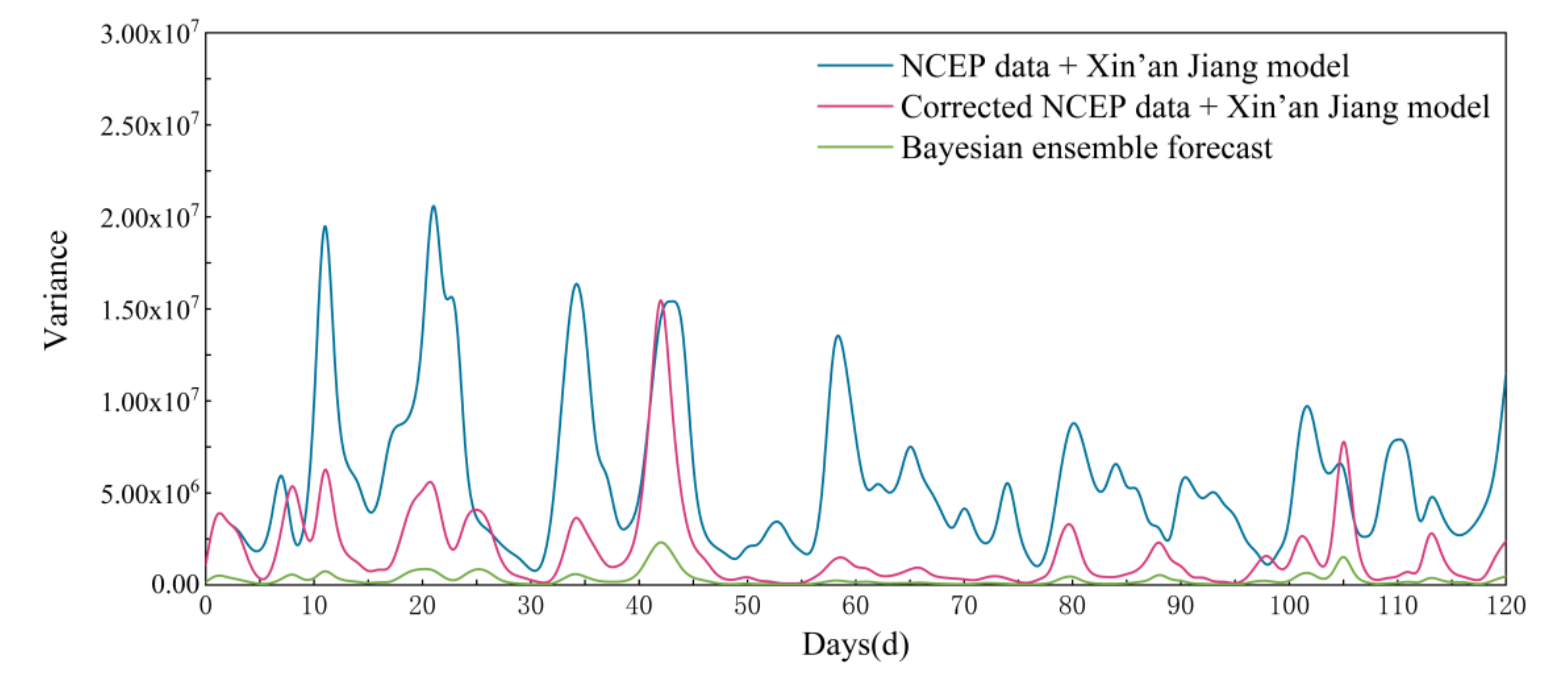
In this paper, the precipitation data of the Global Ensemble Forecast System (GEFS) was postprocessed by an Autoregressive (AR) model, and a precipitation-dependent hydrological uncertainty processor based on GMM (PD-HUP-GMM) was proposed to generate the ensemble flow forecast. Then, the Nash-Sutcliffe efficiency (NSE), root-mean square error (RMSE), and variances of ensemble members were used to evaluate the accuracy and uncertainty of the ensemble flow forecast. The TGR was selected as a case study. The main conclusions of this study are summarized as follows.
(1) The results of the AR model show that this model can effectively correct GEFS precipitation data, and it is simple and feasible. The use of AR models to correct the GEFS rainfall data also helps to improve the simulation accuracy of the deterministic hydrological model.
(2) The proposed method was compared with three different forecast methods. Results of the case study show that the PD-HUP-GMM method combined with the corrected GEFS data can significantly improve the NSE and RMSE of flow forecasting. From this point of view, the proposed method performs well.
(3) The proposed method can effectively deal with the uncertainty of precipitation input data and the hydrological model and, thus, improve the accuracy of the ensemble flow forecast average value to a useful level.
Future work will involve extending the forecast period to a longer horizon to further evaluate the potential of HUP in operational flow forecasting and improve its practical significance.