Modeling River Runoff Temporal Behavior through a Hybrid Causal–Hydrological (HCH) Method
Abstract
:1. Introduction
2. Materials and Methods
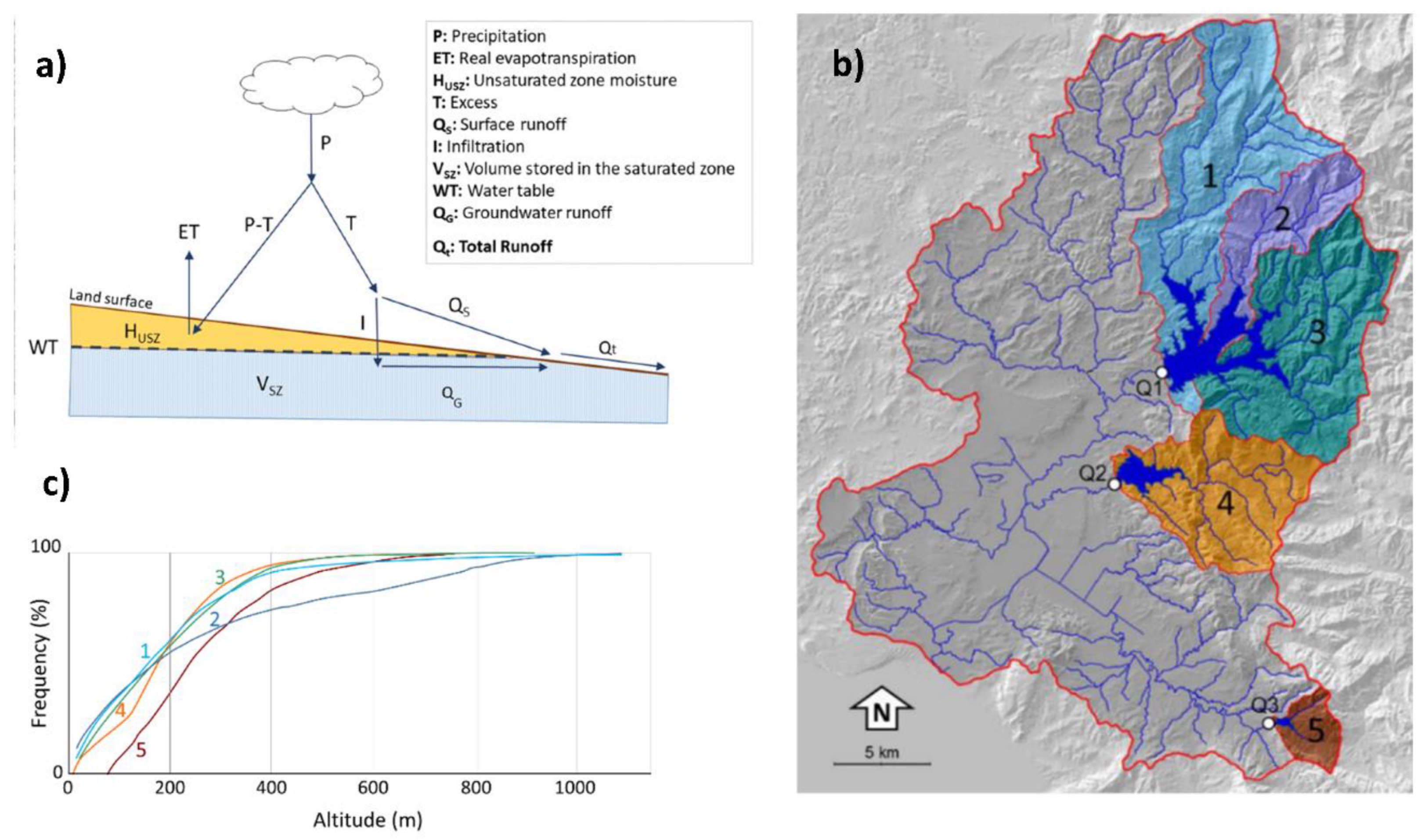
2.1. Case Study
2.2. Dataset Description
2.3. Justification of HCH Method Utility
2.4. General Methodology
2.4.1. Phase 1 Deterministic Module: Rainfall–Runoff Model Definition
2.4.2. Phase 2 Stochastic Module
Subphase 2a ARMA Model Definition
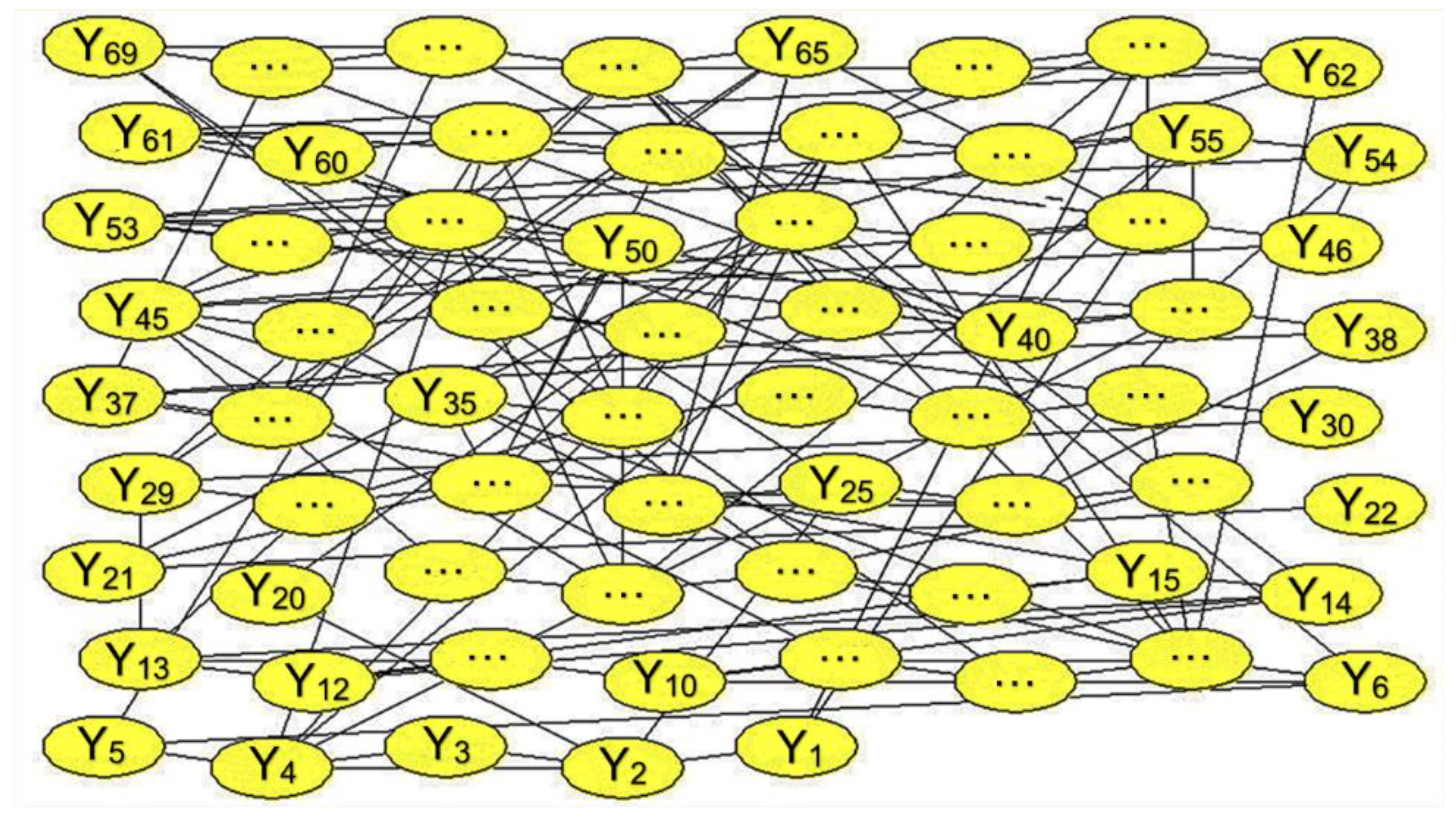
Subphase 2b Bayesian Causal Modeling (BCM) Design
2.4.3. Phase 3 Hybrid Causal–Hydrological (HCH) Modeling
2.4.4. Phase 4 Assessment of the Basin’s Hydrological Runoff Memory
3. Results
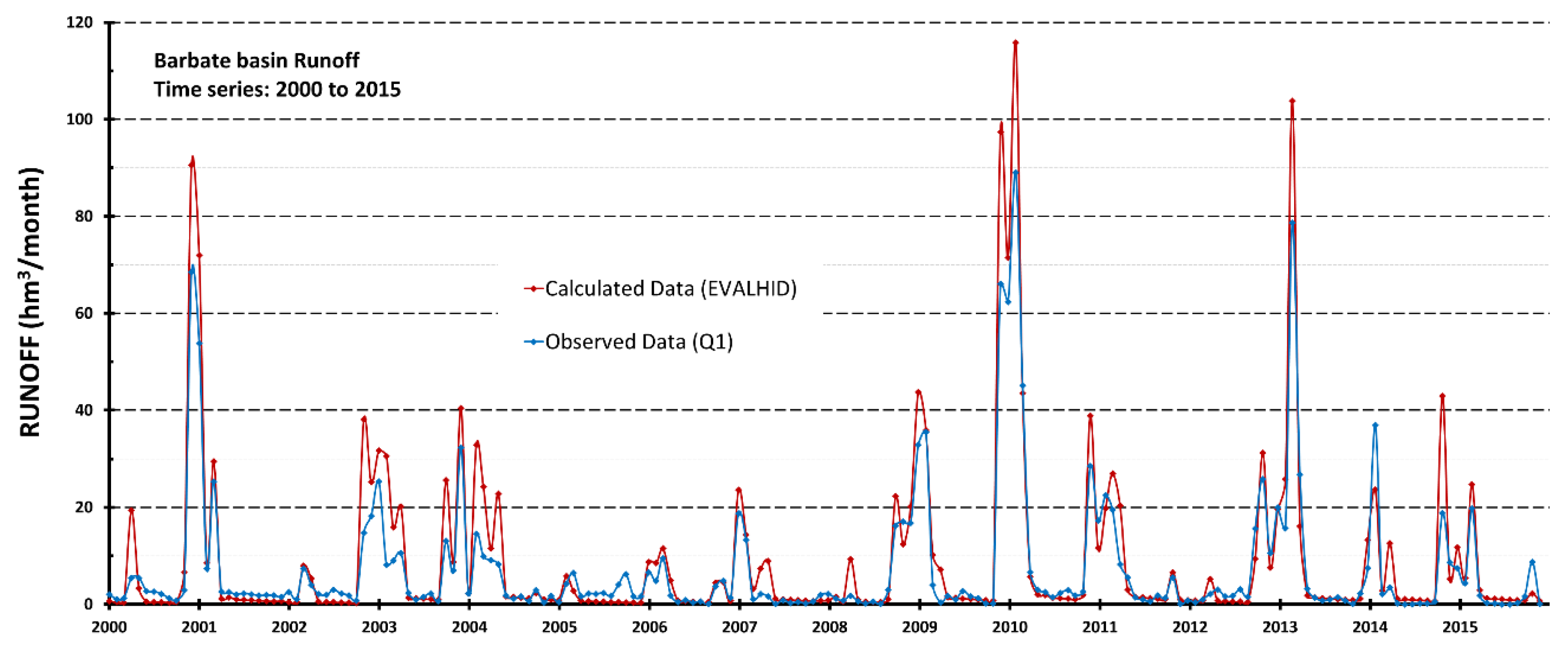
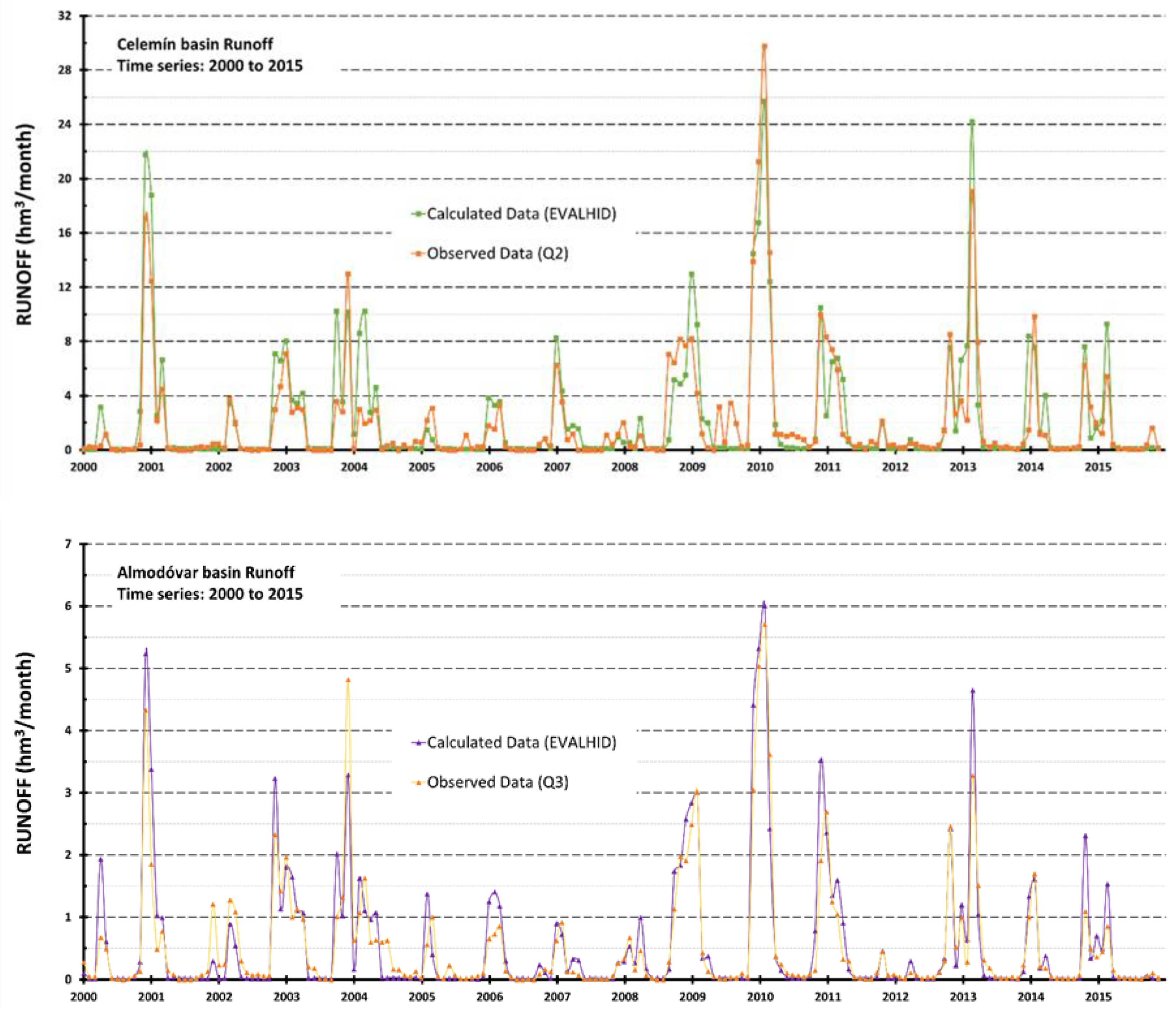
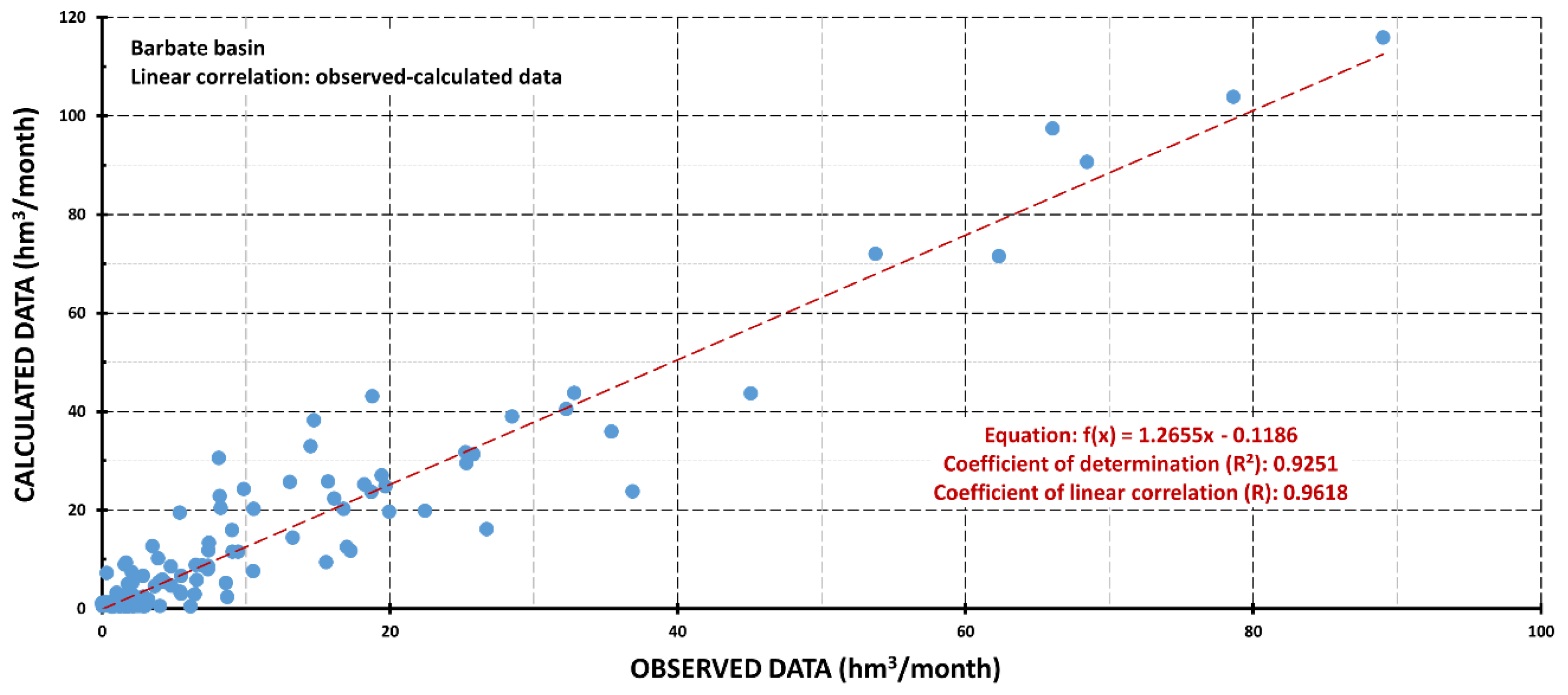
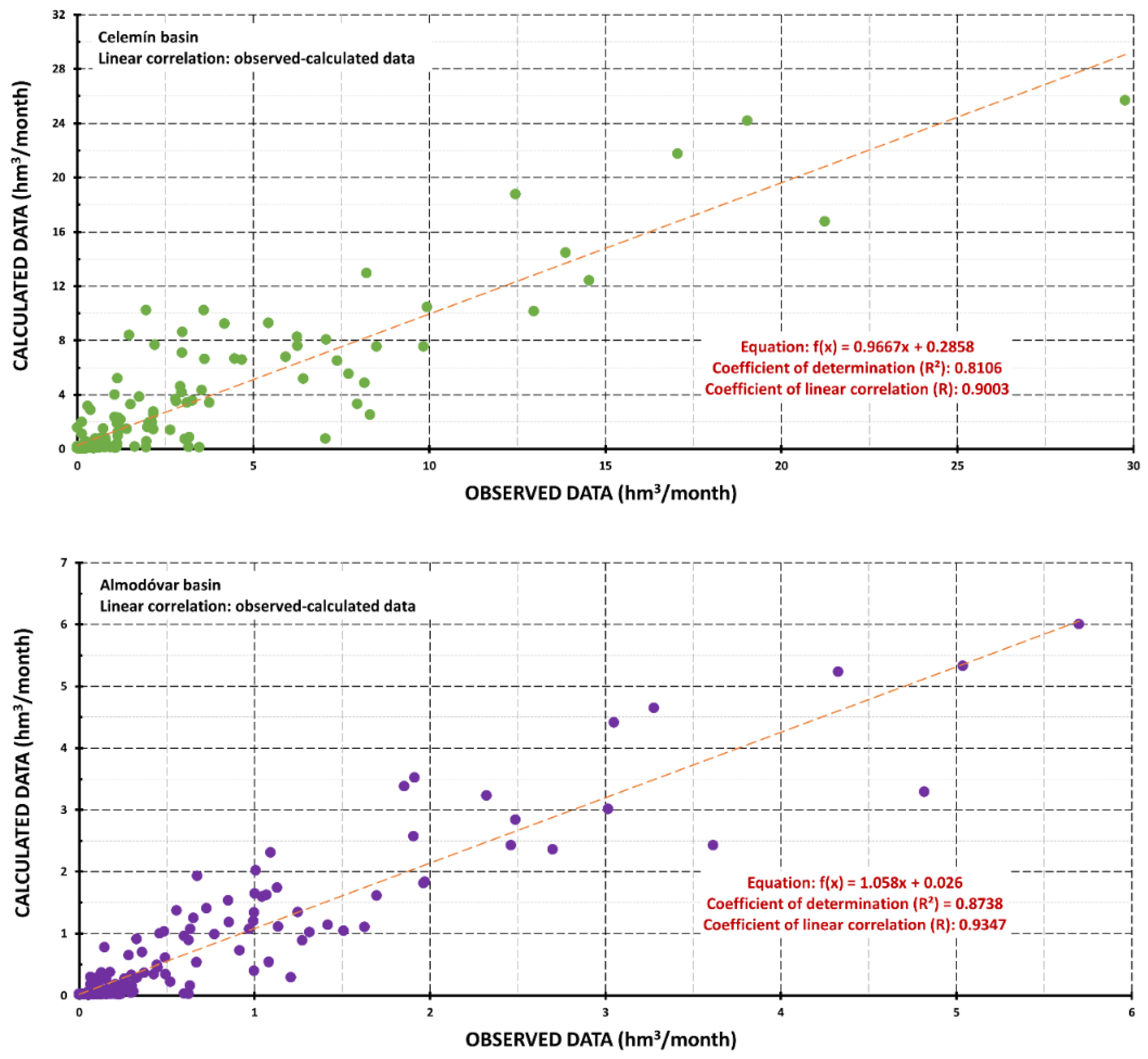
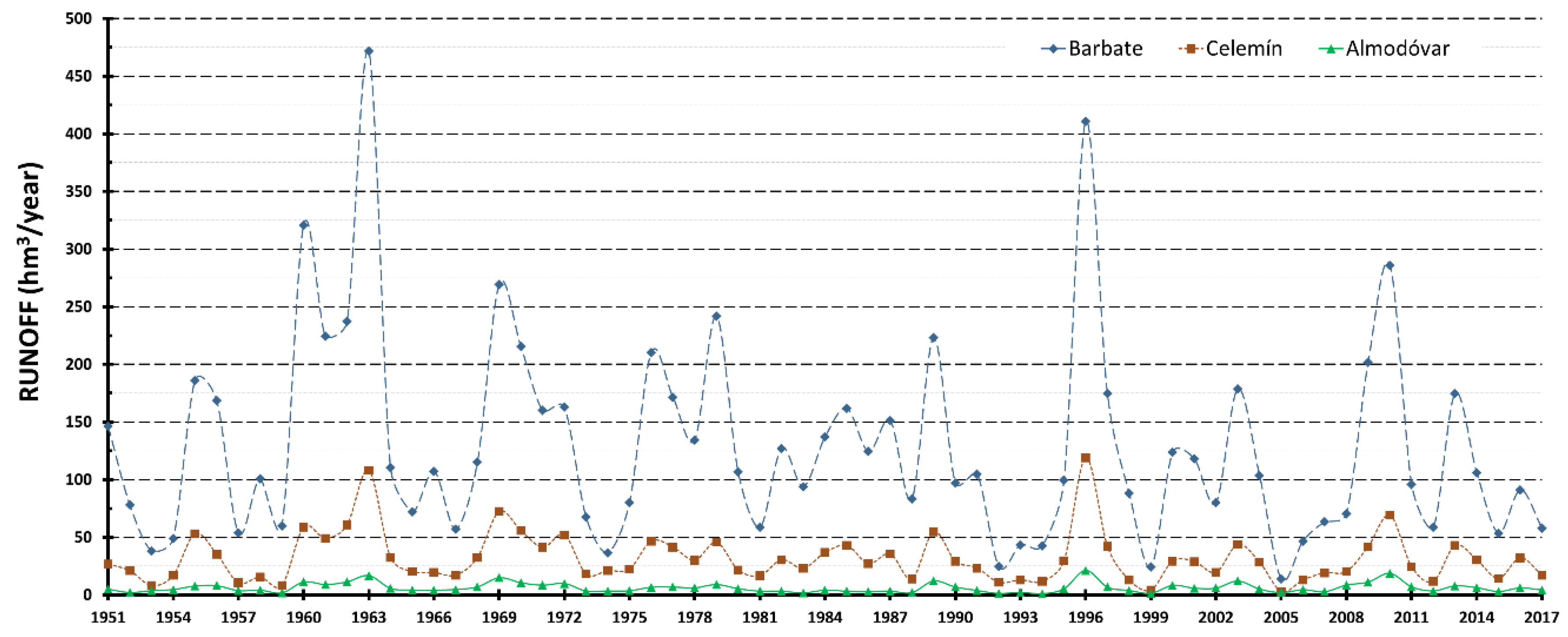
3.1. T-RRM Outputs
3.2. Stochastic Module: Statistical Parameters and Design of Bayesian Causal Modeling (BCM)
3.3. Runoff Basin Memory Assessment through Hybrid Causal–Hydrological (HCH) Modeling
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Botai, J.O.; Botai, C.M.; de Wit, J.P.; Muthoni, M.; Adeola, A.M. Analysis of Drought Progression Physiognomies in South Africa. Water 2019, 11, 299. [Google Scholar] [CrossRef] [Green Version]
- Jyrkama, M.I.; Sykes, J.F. The Impact of Climate Change on Spatially Varying Groundwater Recharge in the Grand River Watershed (Ontario). J. Hydrol. 2007, 338, 237–250. [Google Scholar] [CrossRef]
- Lepori, F.; Pozzoni, M.; Pera, S. What Drives Warming Trends in Streams? A Case Study from the Alpine Foothills. River Res. Appl. 2015, 31, 663–675. [Google Scholar] [CrossRef]
- Praskievicz, S. Impacts of Projected Climate Changes on Streamflow and Sediment Transport for Three Snowmelt-Dominated Rivers in the Interior Pacific Northwest. River Res. Appl. 2016, 32, 4–17. [Google Scholar] [CrossRef]
- Zazo, S.; Molina, J.L.; Rodriguez-Gonzalvez, P. Analysis of Flood Modeling through Innovative Geomatic Methods. J. Hydrol. 2015, 524, 522–537. [Google Scholar] [CrossRef]
- Berg, P.; Moseley, C.; Haerter, J.O. Strong Increase in Convective Precipitation in Response to Higher Temperatures. Nat. Geosci. 2013, 6, 181–185. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in Precipitation with Climate Change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef] [Green Version]
- O’Gorman, P.A. Precipitation Extremes under Climate Change. Curr. Clim. Chang. Rep. 2015, 1, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Pfahl, S.; O’Gorman, P.A.; Fischer, E.M. Understanding the Regional Pattern of Projected Future Changes in Extreme Precipitation. Nat. Clim. Chang. 2017, 7, 423–427. [Google Scholar] [CrossRef]
- Chávez Jiménez, A. Propuesta Metodológica Para la Identificación de Medidas de Adaptación al Cambio Climático en Sistemas de Recursos Hídricos. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2013; 232p. [Google Scholar]
- Merritt, W.S.; Alila, Y.; Barton, M.; Taylor, B.; Cohen, S.; Neilsen, D. Hydrologic Response to Scenarios of Climate Change in Sub Watersheds of the Okanagan Basin, British Columbia. J. Hydrol. 2006, 326, 79–108. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Luis Garcia-Arostegui, J.; Molina, J.; Pulido-Velazquez, M. Assessment of Future Groundwater Recharge in Semi-Arid Regions under Climate Change Scenarios (Serral-Salinas Aquifer, SE Spain). Could increased Rainfall Variability Increase the Recharge Rate? Hydrol. Process. 2015, 29, 828–844. [Google Scholar] [CrossRef]
- Molina, J.L.; Zazo, S. Assessment of Temporally Conditioned Runoff Fractions in Unregulated Rivers. J. Hydrol. Eng. 2018, 23, 04018015. [Google Scholar] [CrossRef]
- Voss, R.; May, W.; Roeckner, E. Enhanced Resolution Modelling Study on Anthropogenic Climate Change: Changes in Extremes of the Hydrological Cycle. Int. J. Clim. 2002, 22, 755–777. [Google Scholar] [CrossRef]
- Marcos, P.; Lopez-Nicolas, A.; Pulido-Velazquez, M. Analysis of Climate Change Impact on Meteorological and Hydrological Droughts through Relative Standardized Indices. In Proceedings of the 19th EGU General Assembly, Vienna, Austria, 23–28 April 2017; p. 1391. [Google Scholar]
- Molina, J.L.; Zazo, S.; Martín-Casado, A.; Patino-Alonso, M. Rivers’ Temporal Sustainability through the Evaluation of Predictive Runoff Methods. Sustainability 2020, 12, 1720. [Google Scholar] [CrossRef] [Green Version]
- Zazo, S.; Macian-Sorribes, H.; Sena-Fael, C.M.; Martín-Casado, A.M.; Molina, J.L.; Pulido-Velazquez, M. Qualitative Approach for Assessing Runoff Temporal Dependence through Geometrical Symmetry. In Proceedings of the ICEUBI 2019 International Congress on Engineering, Covilhã, Portugal, 27–29 November 2019. [Google Scholar]
- Molina, J.L.; Zazo, S.; Martín-Casado, A.M. Causal Reasoning: Towards Dynamic Predictive Models for Runoff Temporal Behavior of High Dependence Rivers. Water 2019, 11, 877. [Google Scholar] [CrossRef] [Green Version]
- Vogel, K.; Weise, L.; Schroeter, K.; Thieken, A.H. Identifying Driving Factors in Flood-Damaging Processes using Graphical Models. Water Resour. Res. 2018, 54, 8864–8889. [Google Scholar] [CrossRef]
- Molina, J.L.; Zazo, S.; Rodriguez-Gonzalvez, P.; Gonzalez-Aguilera, D. Innovative Analysis of Runoff Temporal Behavior through Bayesian Networks. Water 2016, 8, 484. [Google Scholar] [CrossRef] [Green Version]
- Molina, J.L.; Garcia-Arostegui, J.L.; Bromley, J.; Benavente, J. Integrated Assessment of the European WFD Implementation in Extremely Overexploited Aquifers through Participatory Modelling. Water Resour. Manag. 2011, 25, 3343–3370. [Google Scholar] [CrossRef]
- Zazo, S. Analysis of the Hydrodynamic Fluvial Behaviour through Causal Reasoning and Artificial Vision. Ph.D. Thesis, University of Salamanca, Ávila, Spain, 12 May 2017. [Google Scholar]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Salas, J.; Delleur, J.; Yevjevich, V.; Lane, W.L. Applied Modeling of Hydrologic Time Series, 1st ed.; Water Resources Publications: Littleton, CO, USA, 1980; p. 484. [Google Scholar]
- Díaz Caballero, F.F. Selección de Modelos Mediante Criterios de Información en Análisis Factorial: Aspectos Teóricos Y Computacionales; Editorial de la Universidad de Granada: Granada, Spain, 2011. [Google Scholar]
- Tyralis, H.; Koutsoyiannis, D. Simultaneous Estimation of the Parameters of the Hurst-Kolmogorov Stochastic Process. Stoch. Environ. Res. Risk Assess. 2011, 25, 21–33. [Google Scholar] [CrossRef]
- Farmer, W.H.; Vogel, R.M. On the Deterministic and Stochastic use of Hydrologic Models. Water Resour. Res. 2016, 52, 5619–5633. [Google Scholar] [CrossRef] [Green Version]
- Molina, J.L.; Zazo, S. Causal Reasoning for the Analysis of Rivers Runoff Temporal Behavior. Water Resour. Manag. 2017, 31, 4669–4681. [Google Scholar] [CrossRef]
- Koutroumanidis, T.; Sylaios, G.; Zafeiriou, E.; Tsihrintzis, V.A. Genetic Modeling for the Optimal Forecasting of Hydrologic Time-Series: Application in Nestos River. J. Hydrol. 2009, 368, 156–164. [Google Scholar] [CrossRef]
- Molina, J.L.; Bromley, J.; Garcia-Arostegui, J.L.; Sullivan, C.; Benavente, J. Integrated Water Resources Management of Overexploited Hydrogeological Systems using Object-Oriented Bayesian Networks. Environ. Model. Softw. 2010, 25, 383–397. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wang, B.; Liu, D.L.; Zhang, M.; Feng, P.; Cheng, L.; Yu, Q.; Eamus, D. Impacts of Future Climate Change on Water Resource Availability of Eastern Australia: A Case Study of the Manning River Basin. J. Hydrol. 2019, 573, 49–59. [Google Scholar] [CrossRef]
- Versini, P.-A.; Pouget, L.; McEnnis, S.; Custodio, E.; Escaler, I. Climate Change Impact on Water Resources Availability: Case Study of the Llobregat River Basin (Spain). Hydrol. Sci. J. 2016, 61, 2496–2508. [Google Scholar] [CrossRef]
- Giupponi, C.; Sgobbi, A. Decision Support Systems for Water Resources Management in Developing Countries: Learning from Experiences in Africa. Water 2013, 5, 798–818. [Google Scholar] [CrossRef] [Green Version]
- Sivapalan, M.; Savenije, H.H.G.; Bloeschl, G. Socio-Hydrology: A New Science of People and Water. Hydrol. Process. 2012, 26, 1270–1276. [Google Scholar] [CrossRef]
- Liu, D.; Tian, F.; Lin, M.; Sivapalan, M. A Conceptual Socio-Hydrological Model of the Co-Evolution of Humans and Water: Case Study of the Tarim River Basin, Western China. Hydrol. Earth Syst. Sci. 2015, 19, 1035–1054. [Google Scholar] [CrossRef] [Green Version]
- Aqil, M.; Kita, I.; Yano, A.; Nishiyama, S. A Comparative Study of Artificial Neural Networks and Neuro-Fuzzy in Continuous Modeling of the Daily and Hourly Behaviour of Runoff. J. Hydrol. 2007, 337, 22–34. [Google Scholar] [CrossRef]
- USACE. US Army Corps of Engineers. Hydrologic Engineering Center. Available online: https://www.hec.usace.army.mil/software/hec-hms/ (accessed on 10 August 2020).
- MITECO Ministerio para la Transición Ecológica. Modelo SIMPA 2019. Periodo de Simulación:1940/41 a 2017/18. Available online: https://www.miteco.gob.es/es/agua/temas/evaluacion-de-los-recursos-hidricos/evaluacion-recursos-hidricos-regimen-natural/ (accessed on 26 September 2019).
- Graf, R.; Zhu, S.; Sivakumar, B. Forecasting River Water Temperature Time Series using a Wavelet-Neural Network Hybrid Modelling Approach. J. Hydrol. 2019, 578, 124115. [Google Scholar] [CrossRef]
- Jayakrishnan, R.; Srinivasan, R.; Santhi, C.; Arnold, J.G. Advances in the Application of the SWAT Model for Water Resources Management. Hydrol. Process. 2005, 19, 749–762. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hydrology, Society, Change and Uncertainty. Geophys. Res. 2014, 16, 1–31. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Teshnehlab, M. Using Adaptive Neuro-Fuzzy Inference System for Hydrological Time Series Prediction. Appl. Soft Comput. 2008, 8, 928–936. [Google Scholar] [CrossRef]
- Nourani, V.; Kisi, O.; Komasi, M. Two Hybrid Artificial Intelligence Approaches for Modeling Rainfall-Runoff Process. J. Hydrol. 2011, 402, 41–59. [Google Scholar] [CrossRef]
- Molina, J.L.; Pulido-Velazquez, D.; Garcia-Arostegui, J.-L.; Pulido-Velazquez, M. Dynamic Bayesian Networks as a Decision Support Tool for Assessing Climate Change Impacts on Highly Stressed Groundwater Systems. J. Hydrol. 2013, 479, 113–129. [Google Scholar] [CrossRef] [Green Version]
- Spirtes, P. Introduction to Causal Inference. J. Mach. Learn. Res. 2010, 11, 1643–1662. [Google Scholar]
- Témez, J.R. Modelo Matemático de Trasformación “Precipitación-Escorrentía”. Comisión de “Explotación y Garantía”. Grupo de Trabajo de Predicción de Precipitaciones y Relación Entre Precipitaciones y Caudales; Asociación de Investigación Industrial Eléctrica (ASINTEL): Madrid, Spain, 1977. [Google Scholar]
- Témez, J.R. Cálculo Hidrometeorológico de Caudales Máximos en Pequeñas Cuencas Naturales; Ministerio de Obras Públicas y Urbanismo; Gobierno de España: Madrid, Spain, 1978. [Google Scholar]
- Témez, J. Extended and Improved Rational Method. Version of the Highways Administration of Spain. In Proceedings of the XXIV Congress IAHR, Madrid, Spain, 9–13 September 1991; pp. 33–40. [Google Scholar]
- Escriva-Bou, A.; Pulido-Velazquez, M.; Pulido-Velazquez, D. Economic Value of Climate Change Adaptation Strategies for Water Management in Spain’s Jucar Basin. J. Water Resour. Plann. Manag. 2017, 143, 04017005. [Google Scholar] [CrossRef]
- Estrela Monreal, T.; Cabezas Calvo-Rubio, F.; Estrada Lorenzo, F. La Evaluación De Los Recursos Hídricos En El Libro Blanco Del Agua En España. Ingeniería Agua 1999, 6, 125–138. [Google Scholar] [CrossRef] [Green Version]
- Perez-Sanchez, J.; Senent-Aparicio, J.; Segura-Mendez, F.; Pulido-Velazquez, D.; Srinivasan, R. Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain. Sustainability 2019, 11, 2872. [Google Scholar] [CrossRef] [Green Version]
- Rico, M.T.; Benito, G. Estimación de caudales de crecida en pequeñas cuencas de montaña: Revisión Metodológica y Aplicación a la cuenca de Montardit (Pirineos Centrales, España). Revista Cuaternario & Geomorfología 2002, 16, 127–138. [Google Scholar]
- Murillo, J.M.; Navarro, J.A. Aplicación Del Modelo De Témez a La Determinación De La Aportación Superficial Y Subterránea Del Sistema Hidrológico Cornisa-Vega De Granada Para Su Implementación En Un Modelo De Uso Conjunto. Boletín Geológico Minero 2011, 122, 363–388. [Google Scholar]
- Paredes-Arquiola, J.; Solera, A.; Álvarez, J.; Elvira, N. Manual Técnico Herramienta EvalHid Para la Evaluación de Recursos Hídricos Versión 1.1; 3 De Octubre 2017; Universidad Politécnica de Valencia: Valencia, Spain, 2017. [Google Scholar]
- UCA. Universidad de Cadiz. Departamento de Ciencias de la Tierra. Proyecto REMABAR: Análisis de Estrategias para reducir las pérdidas por evaporación y mejora del estado de los acuíferos bajo un contexto de Cambio Climático en la cuenca del río Barbate. In Informe de Modelización y Simulación de la Cuenca del río Barbate; Reina Sofía Cultural Center: Cádiz, Spain, 2019; pp. 2–3. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger Climate Classification Updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Lobo, F.J.; Hernandez-Molina, F.J.; Somoza, L.; Rodero, J.; Maldonado, A.; Barnolas, A. Patterns of Bottom Current Flow Deduced from Dune Asymmetries Over the Gulf of Cadiz Shelf (Southwest Spain). Mar. Geol. 2000, 164, 91–117. [Google Scholar] [CrossRef]
- Gomez-Pina, G.; Munoz-Perez, J.J.; Ramirez, J.L.; Ley, C. Sand Dune Management Problems and Techniques, Spain. J. Coast. Res. 2002, 36, 325–332. [Google Scholar] [CrossRef]
- Perez-Lopez, A.; Perez-Valera, F. Palaeogeography, Facies and Nomenclature of the Triassic Units in the Different Domains of the Betic Cordillera (S Spain). Palaeogeogr. Palaeoclimatol. Palaeoecol. 2007, 254, 606–626. [Google Scholar] [CrossRef]
- Luján, M.; Crespo-Blanc, A.; Balanyá, J.C. The Flysch Trough Thrust Imbricate (Betic Cordillera): A Key Element of the Gibraltar Arc Orogenic Wedge. Tectonics 2006, 25. [Google Scholar] [CrossRef]
- Vélez-Nicolás, M.; García-López, S.; Ruiz-Ortiz, V.; Sánchez-Bellón, Á. Towards a Sustainable and Adaptive Groundwater Management: Lessons from the Benalup Aquifer (Southern Spain). Sustainability 2020, 12, 5215. [Google Scholar] [CrossRef]
- Ruiz-Ortiz, V.; Garcia-Lopez, S.; Solera, A.; Paredes, J. Contribution of Decision Support Systems to Water Management Improvement in Basins with High Evaporation in Mediterranean Climates. Hydrol. Res. 2019, 50, 1020–1036. [Google Scholar] [CrossRef]
- Junta de Andalucia. Estaciones Agroclimáticas. Available online: https://www.juntadeandalucia.es/agriculturaypesca/ifapa/ria/servlet/FrontController (accessed on 10 January 2019).
- MITECO. Agencia Estatal de Meteorología. Estaciones Climáticas. Available online: https://www.miteco.gob.es/es/cartografia-y-sig/ide/descargas/otros/default.aspx (accessed on 10 January 2019).
- Karl, T.R.; Williams, C.N. An Approach to Adjusting Climatological Time-Series for Discontinuous Inhomogeneities. J. Clim. Appl. Meteorol. 1987, 26, 1744–1763. [Google Scholar] [CrossRef] [Green Version]
- Akbar, R.; Gianotti, D.S.; McColl, K.A.; Haghighi, E.; Salvucci, G.D.; Entekhabi, D. Hydrological Storage Length Scales Represented by Remote Sensing Estimates of Soil Moisture and Precipitation. Water Resour. Res. 2018, 54, 1476–1492. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, X.; Lei, W. Necessary Length of Daily Precipitation Time Series for Different Entropy Measures. Earth Sci. Inform. 2019, 12, 475–487. [Google Scholar] [CrossRef]
- Hidalgo, J.C.G.; de Luis Arrillaga, M.; Stepánek, P.; Bonvehi, J.R.; Prats, J.M.C. Reconstrucción, Estabilidad y Proceso de Homogeneizado de Series de Precipitación en ambientes de elevada Variabilidad Pluvial. In La Información Climática como herramienta de gestión ambiental Bases de Datos y Tratamiento de Series Climatólogicas: Reunión Nacional De Climatología (7th 2002 Albarracín, España); Universidad de Zaragoza: Zaragoza, Spain, 2002; pp. 47–58. ISBN 9788495480699. [Google Scholar]
- Squintu, A.A.; van der Schrier, G.; van den Besselaar, E.J.M.; Cornes, R.C.; Tank, A.M.G.K. Building Long Homogeneous Temperature Series Across Europe: A New Approach for the Blending of Neighboring Series. J. Appl. Meteorol. Climatol. 2020, 59, 175–189. [Google Scholar] [CrossRef]
- CEDEX. Centro de Estudios y Experimentación de Obras Públicas. Cálculo Hidrometeorológico De Aportaciones Y Crecidas (CHAC). Ministerio De Fomento Y Ministerio Para La Transición Ecológica. Gobierno De España. 2013. Available online: https://ceh.cedex.es/chac/ (accessed on 12 February 2019).
- Barrera Escoda, A. Técnicas de completado de series mensuales y aplicación al estudio de la influencia de la NAO en la distribución de la precipitación en España. In Trabajo para la obtención del Diploma de Estudios Avanzados (DEA). Programa de doctorado de Astronomía y Meteorología (Bienio 2002–2004); Universidad de Barcelona, Departamento de Astronomía y Meteorología: Barcelona, Spain, 2002; p. 96. [Google Scholar]
- HIDROSUR. Junta de Andalucía. Consejería de Agricultura, Ganadería, Pesca y Desarrollo Sostenible. Dirección General de Infraestructuras del Agua. Available online: http://www.redhidrosurmedioambiente.es/saih/ (accessed on 13 January 2019).
- Sang, Y.; Shang, L.; Wang, Z.; Liu, C.; Yang, M. Bayesian-Combined Wavelet Regressive Modeling for Hydrologic Time Series Forecasting. Chin. Sci. Bull. 2013, 58, 3796–3805. [Google Scholar] [CrossRef] [Green Version]
- See, L.; Openshaw, S. A Hybrid Multi-Model Approach to River Level Forecasting. Hydrol. Sci. J. 2000, 45, 523–536. [Google Scholar] [CrossRef]
- Jain, A.; Kumar, A.M. Hybrid Neural Network Models for Hydrologic Time Series Forecasting. Appl. Soft Comput. 2007, 7, 585–592. [Google Scholar] [CrossRef]
- Pearl, J. Graphical models for probabilistic and causal reasoning. In Computing Handbook, 3rd ed.; Tucker, A., Gonzalez, T., Topi, H., Diaz-Herrera, J., Eds.; Computer Science and Software Engineering: Boca Raton, FL, USA, 2014; Volume 1. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning, and Inference, 2nd ed.; Cambridge University Press: New York, NY, USA, 2009; p. 484. ISBN 978-0-521-89560-6. [Google Scholar]
- Garcia, A.; Sainz, A.; Revilla, J.A.; Alvarez, C.; Juanes, J.A.; Puente, A. Surface Water Resources Assessment in Scarcely Gauged Basins in the North of Spain. J. Hydrol. 2008, 356, 312–326. [Google Scholar] [CrossRef]
- Rao, K.H.V.D.; Rao, V.V.; Dadhwal, V.K. Improvement to the Thornthwaite Method to Study the Runoff at a Basin Scale using Temporal Remote Sensing Data. Water Resour. Manag. 2014, 28, 1567–1578. [Google Scholar]
- Paredes, J.; Andreu, J.; Solera, A. A Decision Support System for Water Quality Issues in the Manzanares River (Madrid, Spain). Sci. Total Environ. 2010, 408, 2576–2589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moghadam, E.; Boroumand, N.; Jalali, V.; Sanjari, S. Evaluation the Effect of Different Land use and Soil Characteristics on Saturated Hydraulic Conductivity. J. Water Soil 2017, 31, 1302–1312. [Google Scholar]
- Welde, K.; Gebremariam, B. Effect of Land use Land Cover Dynamics on Hydrological Response of Watershed: Case Study of Tekeze Dam Watershed, Northern Ethiopia. Int. Soil Water Conserv. Res. 2017, 5, 1–16. [Google Scholar] [CrossRef]
- Rea, W.; Oxley, L.; Reale, M.; Brown, J. Estimators for Long Range Dependence: An Empirical Study. arXiv 2009, arXiv:0901.0762. [Google Scholar]
- TRASERO. Tratamiento y Gestión de Series Temporales Hidrológicas; Diputación Provincial de Alicante-Departamento de Ciclo Hídrico: Alicante, Spain, 2015; pp. 28–30. ISBN 978-84-15327-28-8. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Francisco, CA, USA, 1988; p. 552. [Google Scholar]
- Hanea, A.M.; Gheorghe, M.; Hanea, R.; Ababei, D. Non-Parametric Bayesian Networks for Parameter Estimation in Reservoir Simulation: A Graphical Take on the Ensemble Kalman Filter (Part I). Comput. Geosci. 2013, 17, 929–949. [Google Scholar] [CrossRef]
- Castelletti, A.; Soncini-Sessa, R. Bayesian Networks and Participatory Modelling in Water Resource Management. Environ. Model. Softw. 2007, 22, 1075–1088. [Google Scholar] [CrossRef]
- Said, A. The Implementation of a Bayesian Network for Watershed Management Decisions. Water Resour. Manag. 2006, 20, 591–605. [Google Scholar] [CrossRef]
- Cabañas de Paz, R. New Methods and Data Structures for Evaluating Influence Diagrams. Ph.D. Thesis, University of Granada, Granada, Spain, 2017; 360p. [Google Scholar]
- Madsen, A.L.; Lang, M.; Kjærulff, U.B.; Jensen, F. The Hugin Tool for Learning Bayesian Networks. In European Conference on Symbolic and Quantitative Approaches to Reasoning and Uncertainty; Springer: Berlin/Heidelberg, Germany, 2003; pp. 594–605. [Google Scholar]
- Jensen, F.V. An Introduction to Bayesian Networks; UCL Press: London, UK, 1996. [Google Scholar]
- Cain, J. Planning Improvements in Natural Resources Management; Centre for Ecology and Hydrology: Wallingford, UK, 2001; Volume 124, pp. 1–123. [Google Scholar]
- Bayes, T. LII. An Essay towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, FRS Communicated by Mr. Price, in a Letter to John Canton, AMFR S. Philos. Trans. R. Soc. Lond. 1763, 53, 370–418. [Google Scholar]
- HUGIN. Hugin Expert A/S. 7.3. 2010. Available online: http://www.hugin.com (accessed on 23 April 2020).
- Verma, T.; Pearl, J. An Algorithm for Deciding if a Set of Observed Independencies has a Causal Explanation. In Proceedings of the 8th Conference on Uncertainty in Artificial Intelligence, Stanford, CA, USA, 17–19 July 1992; pp. 323–330. [Google Scholar]
- Bonissone, P.; Henrion, M.; Kanal, L.; Lemmer, J. Proceedings of the Sixth Conference on Uncertainty in Artificial Intelligence, 1990. arXiv 2013, arXiv:1304.3854. [Google Scholar]
- Le, T.; Hoang, T.; Li, J.; Liu, L.; Liu, H.; Hu, S. A Fast PC Algorithm for High Dimensional Causal Discovery with Multi-Core PCs. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 16, 1483–1495. [Google Scholar] [CrossRef] [Green Version]

| Sub-Basins/ | Qi 1 | Geological Materials | Extension (Km2) | Elevation (m) | ||||
|---|---|---|---|---|---|---|---|---|
| Code Number | Maximum | Minimum | Mean | Median | ||||
| /1 | Q1 | 2 Flysch. Trias, Jurassic | 149.7 | 1087.4 | 11.3 | 209.1 | 181.2 | |
| Barbate | /2 | Flysch | 59.7 | 1089.6 | 18.0 | 290.2 | 198.9 | |
| /3 | Flysch | 141.8 | 911.8 | 18.0 | 202.2 | 180.9 | ||
| Celemín | /4 | Q2 | Flysch | 94.1 | 630.3 | 19.4 | 196.7 | 185.1 |
| Almodóvar | /5 | Q3 | Flysch | 16.6 | 763.4 | 98.0 | 283.2 | 248.4 |
| Sub-Basin 1/Code Number | Hmax | C | Imax | α (Month−1) |
|---|---|---|---|---|
| /1 | 350 mm | 0.4 | 20 mm | 0.1 |
| Barbate/2 Q1 | 280 mm | 0.3 | 3 mm | 0.1 |
| /3 | 280 mm | 0.3 | 3 mm | 0.1 |
| Celemín/4 Q2 | 280 mm | 0.3 | 3 mm | 0.1 |
| Almodóvar/5 Q3 | 280 mm | 0.3 | 3 mm | 0.1 |
| Sub-Basins | Month | Average (Hm3) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | February | March | April | May | June | July | August | September | October | November | December | Monthly | Annual | |
| Barbate | 25.0 | 24.5 | 18.8 | 10.5 | 5.5 | 1.2 | 1.0 | 0.9 | 0.9 | 4.2 | 11.3 | 25.2 | 10.8 | 129.1 |
| Celemín | 6.7 | 6.3 | 5.0 | 2.3 | 1.1 | 0.2 | 0.1 | 0.1 | 0.1 | 0.8 | 2.8 | 6.3 | 2.7 | 31.8 |
| Almodóvar | 1.1 | 1.2 | 0.9 | 0.5 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.6 | 1.3 | 0.5 | 6.2 |
| Sub-Basins 1 | Parameters | T-RRM Results | Average SS 3 | |
|---|---|---|---|---|
| Long series: From 1951 to 2017 | Barbate/Q1 | Mean: | 129.10 Hm3 | 129.71 Hm3 |
| Standard deviation: | 87.78 Hm3 | 93.87 Hm3 | ||
| Skewness coefficient 2: | 1.64 | 1.83 | ||
| Variation coefficient: | 68% | 72% | ||
| Hurst coefficient: | 0.66 | ---------- | ||
| Celemín/Q2 | Mean: | 31.77 Hm3 | 31.89 Hm3 | |
| Standard deviation: | 21.47 Hm3 | 22.39 Hm3 | ||
| Skewness coefficient 2: | 1.84 | 1.73 | ||
| Variation coefficient: | 68% | 70% | ||
| Hurst coefficient: | 0.66 | ---------- | ||
| Almodóvar/Q3 | Mean: | 6.22 Hm3 | 6.16 Hm3 | |
| Standard deviation: | 4.14 Hm3 | 3.92 Hm3 | ||
| Skewness coefficient 2: | 1.54 | 1.42 | ||
| Variation coefficient: | 67% | 64% | ||
| Hurst coefficient: | 0.66 | ---------- | ||
| Sub-basins 1 | Parameters | T-RRM results | Average SS 3 | |
| Short series: From 2000 to 2015 | Barbate/Q1 | Mean: | 110.98 Hm3 | 111.71 Hm3 |
| Standard deviation: | 69.62 Hm3 | 62.46 Hm3 | ||
| Skewness coefficient 2: | 1.13 | 0.58 | ||
| Variation coefficient: | 63% | 56% | ||
| Hurst coefficient: | 0.66 | ---------- | ||
| Celemín/Q2 | Mean: | 27.50 Hm3 | 27.76 Hm3 | |
| Standard deviation: | 16.10 Hm3 | 15.62 Hm3 | ||
| Skewness coefficient 2: | 1.06 | 0.70 | ||
| Variation coefficient: | 59% | 56% | ||
| Hurst coefficient: | 0.61 | ---------- | ||
| Almodóvar/Q3 | Mean: | 7.05 Hm3 | 7.25 Hm3 | |
| Standard deviation: | 4.24 Hm3 | 4.23 Hm3 | ||
| Skewness coefficient 2: | 1.45 | 1.09 | ||
| Variation coefficient: | 60% | 58% | ||
| Hurst coefficient: | 0.69 | ---------- | ||
| Sub-basins 1 | Parameters | Gauging data | Average SS 3 | |
| Short series (Observed data): From 2000 to 2015 | Barbate/Q1 | Mean: | 88.82 Hm3 | 87.83 Hm3 |
| Standard deviation: | 56.08 Hm3 | 52.16 Hm3 | ||
| Skewness coefficient 2: | 1.69 | 1.28 | ||
| Variation coefficient: | 63% | 59% | ||
| 0.74 | ---------- | |||
| Celemín/Q2 | Mean: | 26.58 Hm3 | 28.08 Hm3 | |
| Standard deviation: | 18.54 Hm3 | 20.48 Hm3 | ||
| Skewness coefficient 2: | 1.89 | 1.54 | ||
| Variation coefficient: | 70% | 73% | ||
| 0.77 | ---------- | |||
| Almodóvar/Q3 | Mean: | 6.71 Hm3 | 6.53 Hm3 | |
| Standard deviation: | 4.30 Hm3 | 4.13 Hm3 | ||
| Skewness coefficient 2: | 1.14 | 1.11 | ||
| Variation coefficient: | 64% | 63% | ||
| Hurst coefficient: | 0.57 | ---------- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zazo, S.; Molina, J.-L.; Ruiz-Ortiz, V.; Vélez-Nicolás, M.; García-López, S. Modeling River Runoff Temporal Behavior through a Hybrid Causal–Hydrological (HCH) Method. Water 2020, 12, 3137. https://doi.org/10.3390/w12113137
Zazo S, Molina J-L, Ruiz-Ortiz V, Vélez-Nicolás M, García-López S. Modeling River Runoff Temporal Behavior through a Hybrid Causal–Hydrological (HCH) Method. Water. 2020; 12(11):3137. https://doi.org/10.3390/w12113137
Chicago/Turabian StyleZazo, Santiago, José-Luis Molina, Verónica Ruiz-Ortiz, Mercedes Vélez-Nicolás, and Santiago García-López. 2020. "Modeling River Runoff Temporal Behavior through a Hybrid Causal–Hydrological (HCH) Method" Water 12, no. 11: 3137. https://doi.org/10.3390/w12113137
APA StyleZazo, S., Molina, J.-L., Ruiz-Ortiz, V., Vélez-Nicolás, M., & García-López, S. (2020). Modeling River Runoff Temporal Behavior through a Hybrid Causal–Hydrological (HCH) Method. Water, 12(11), 3137. https://doi.org/10.3390/w12113137









