Implementation of the Kalman Filter for a Geostatistical Bivariate Spatiotemporal Estimation of Hydraulic Conductivity in Aquifers
Abstract
:1. Introduction
2. Materials and Methods
- Univariate estimation (based on the spatial correlation of hydraulic conductivity data only).
- Bivariate or cross estimation (hydraulic conductivity as the primary variable and hydraulic head for a single time as the secondary).
- Multivariate spatiotemporal estimation (based on the correlation between the hydraulic conductivity data and the hydraulic head spatiotemporal data).
2.1. Geostatistical Theory
2.1.1. The Spatial Variogram
2.1.2. The Cross Variogram
2.1.3. The Spatiotemporal Variogram
2.2. Multivariate Spatiotemporal Methodology
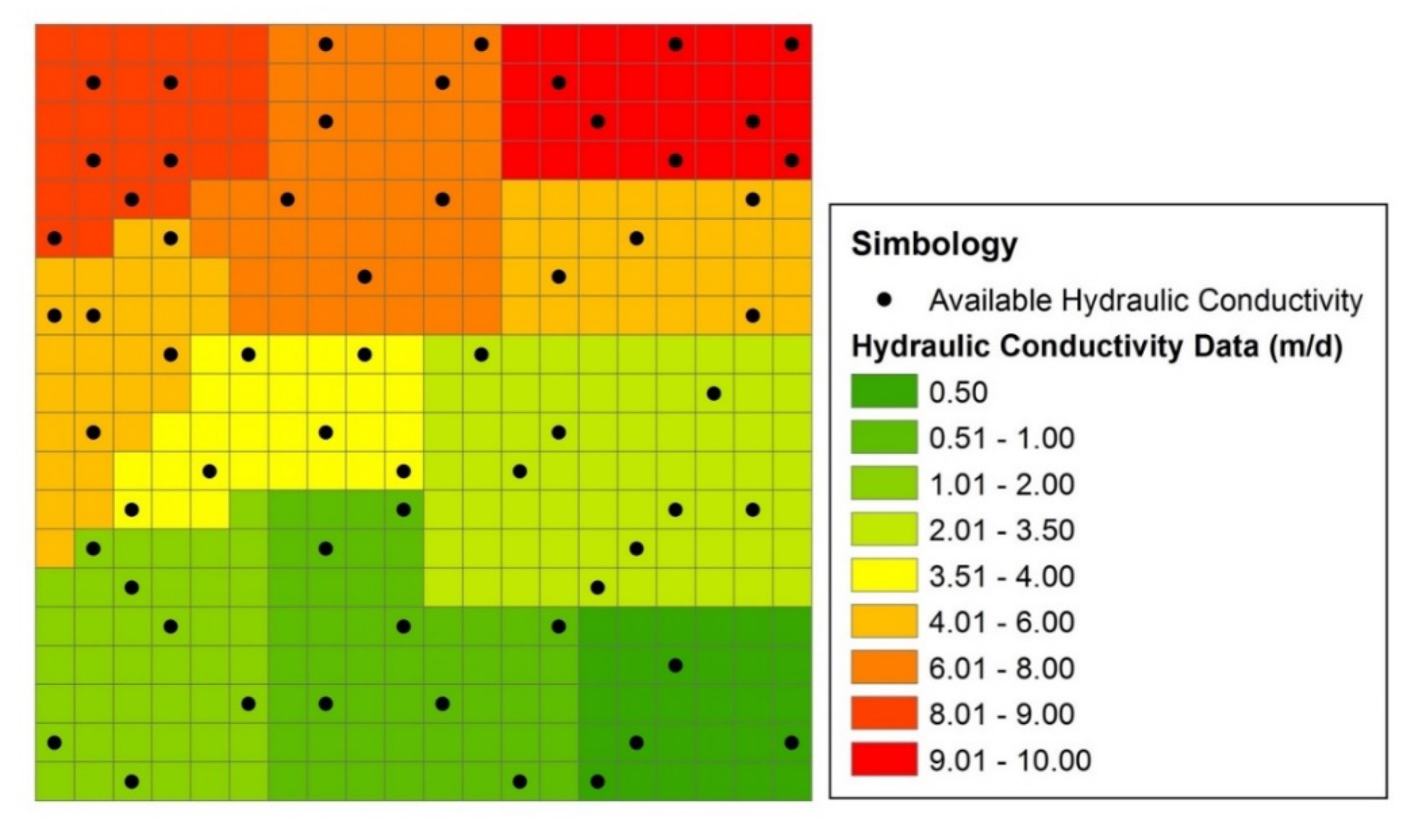
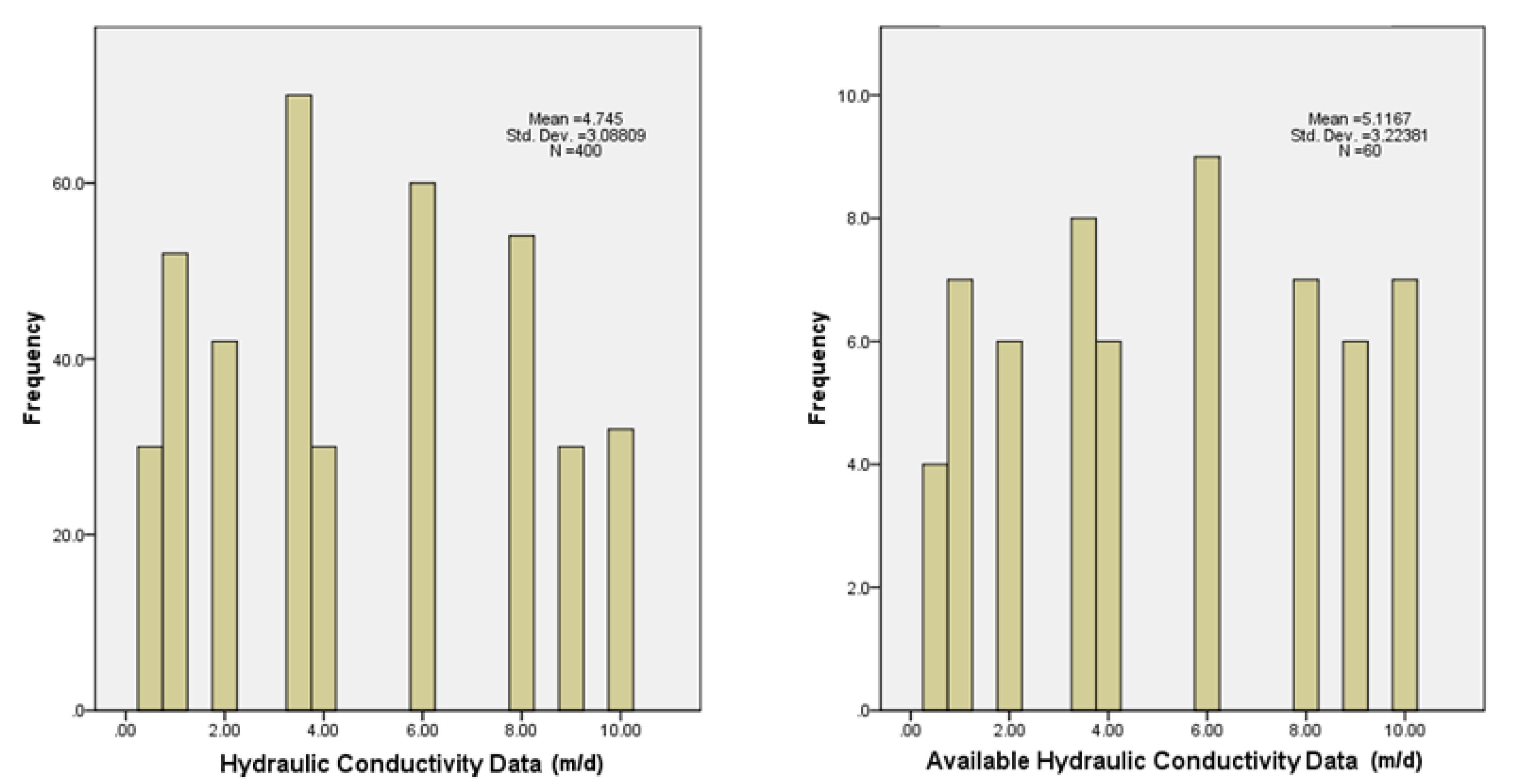
- From geostatistical analyses, obtain the spatial variogram model for the hydraulic conductivity with the available data (in the case study, it is assumed that only 60 of the total 400 hydraulic conductivity data of the model are known), the spatiotemporal variogram model for hydraulic head with the values simulated each 4 months for a 2-year period (2400 values in total), and the cross variograms for each simulation time of the model between the hydraulic conductivity (60 data) and the corresponding hydraulic head data (400 values).
- Derive separately the covariance matrices for the hydraulic conductivity, the spatiotemporal hydraulic head data and the cross covariances between the hydraulic conductivity and the hydraulic head for each time. The covariance values are obtained for all the estimation and sampling nodes.
- Integrate a multivariable covariance matrix that includes the spatial, spatiotemporal and cross covariances (Table 4).
- Estimate using the static Kalman filter, the hydraulic conductivity in all the nodes where these data were not available for the geostatistical analyses.
2.3. The Static Kalman Filter
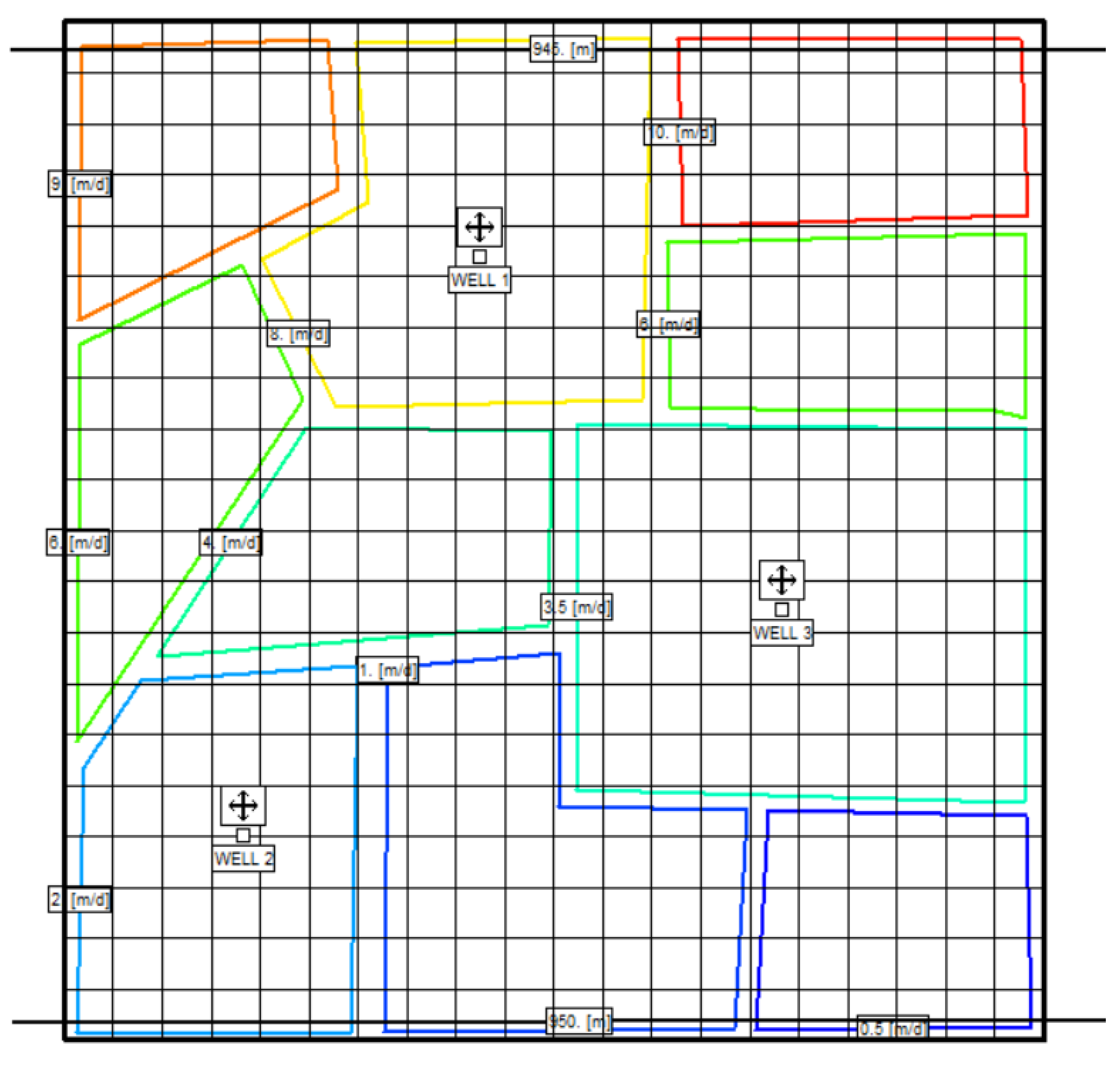
2.4. Case Study
3. Results and Discussion
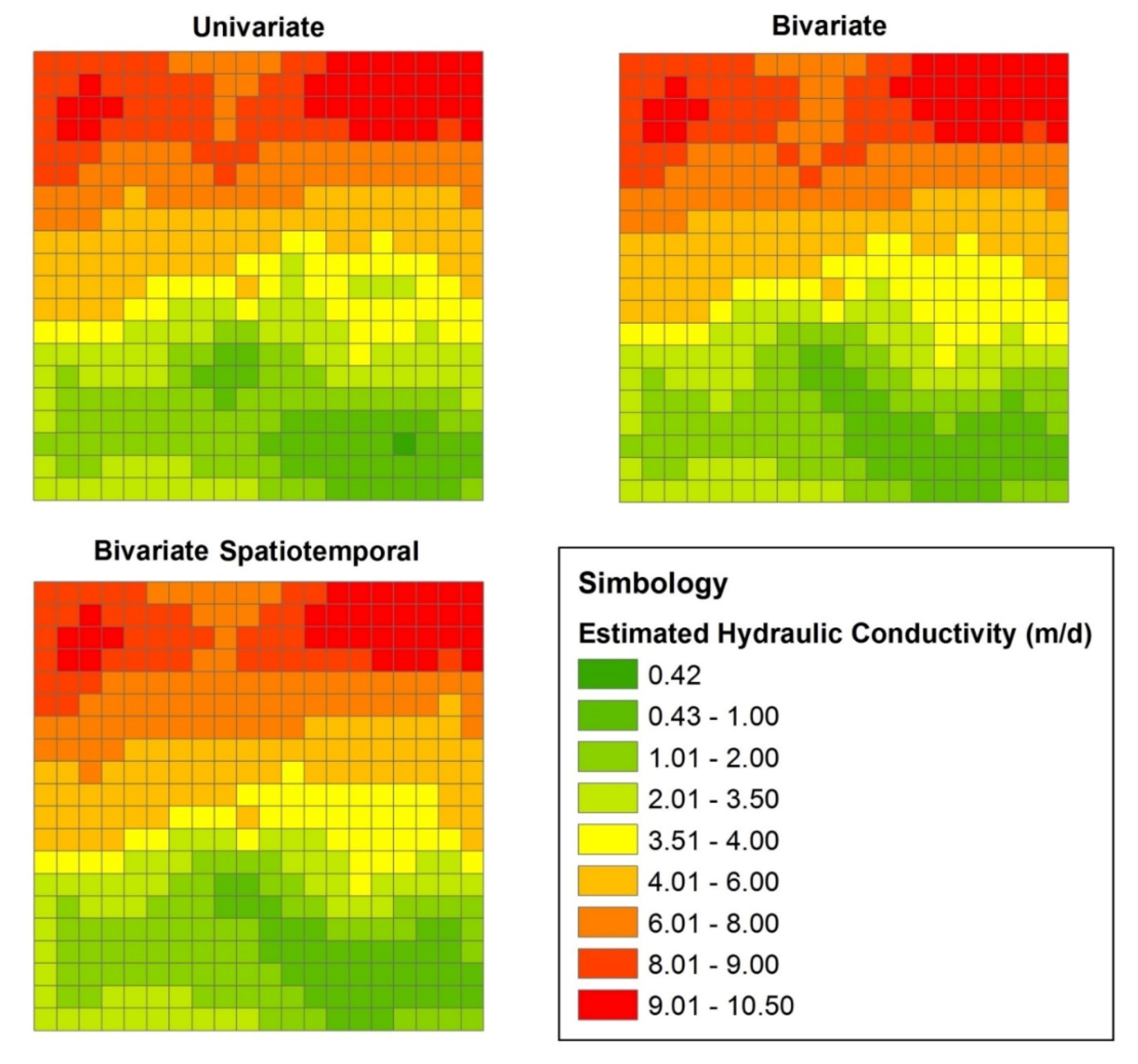
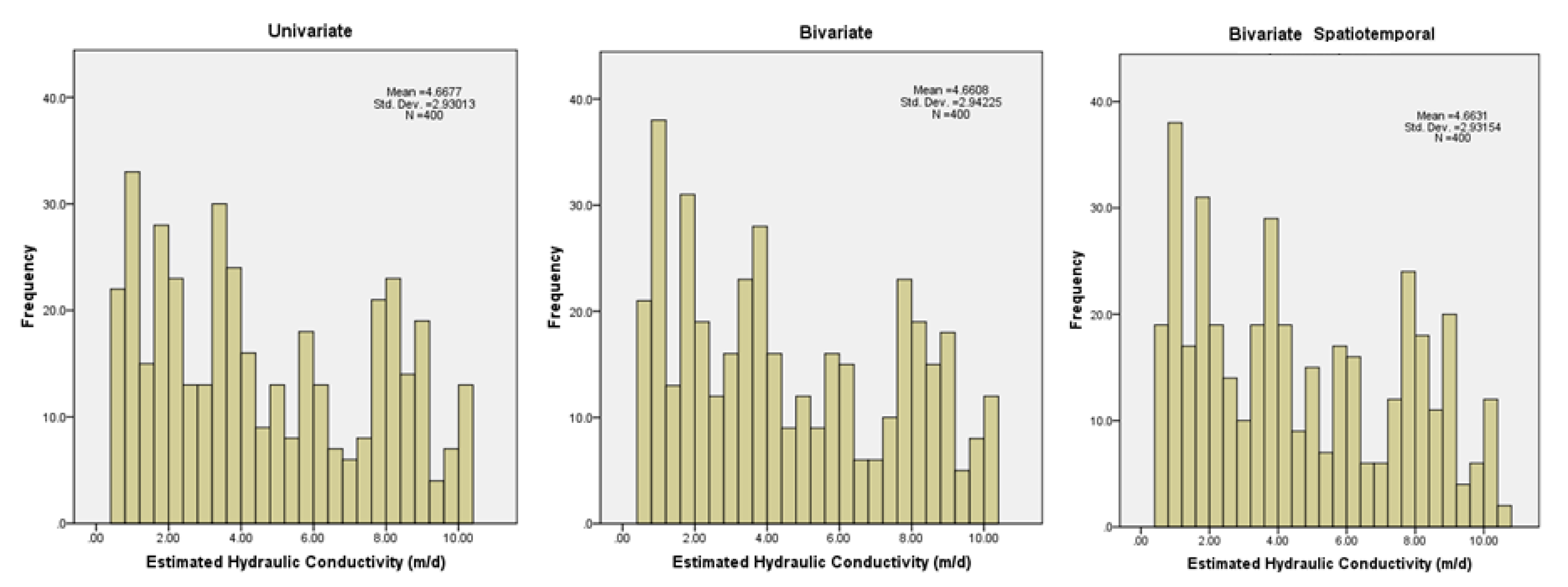
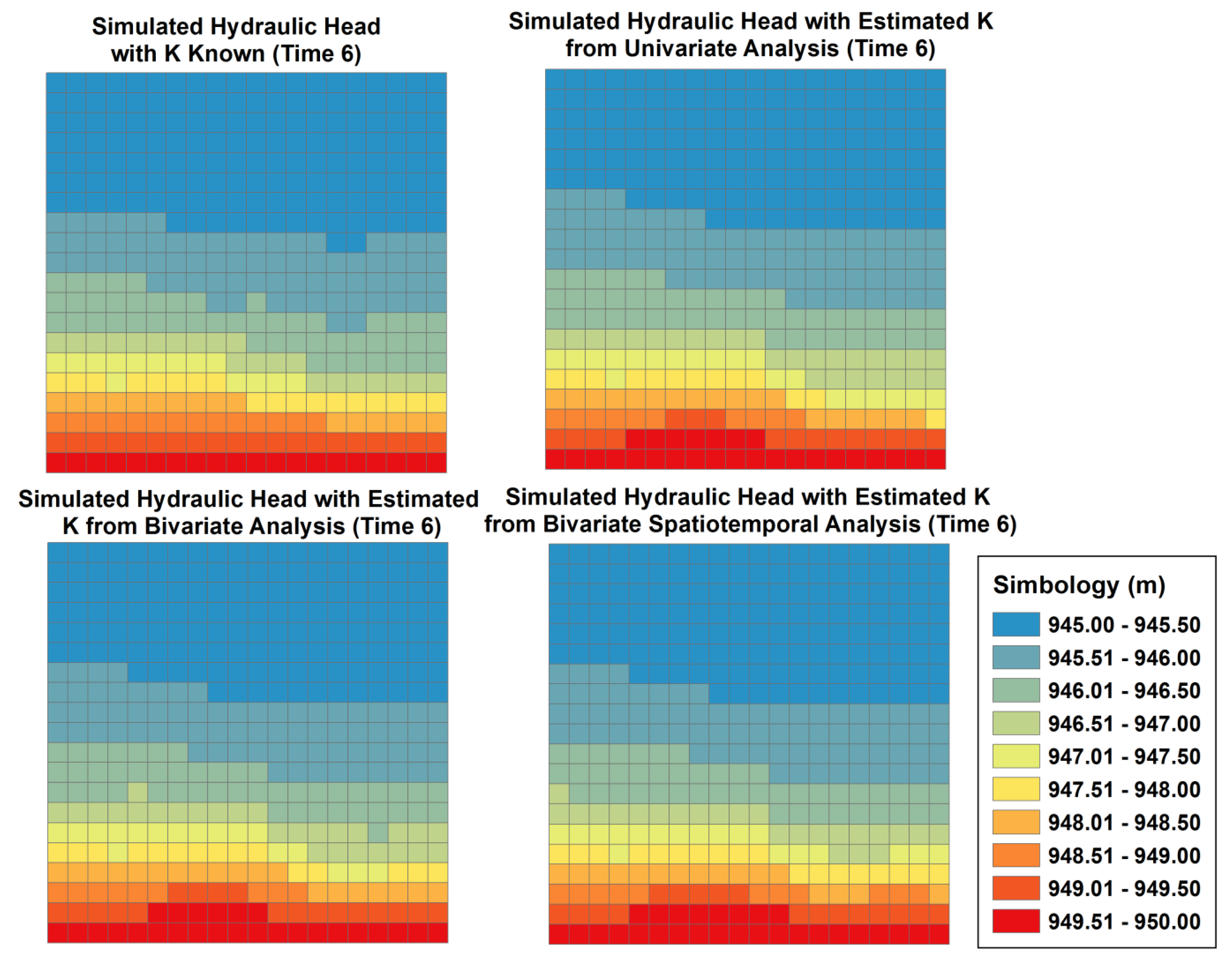
3.1. Univariate Estimation
3.2. Bivariate Estimation
3.3. Bivariate Spatiotemporal Estimation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cernicchiaro, G.; Barmak, R.; Teixeira, W.G. Digital interface device for field soil hydraulic conductivity measurement. J. Hydrol. 2019, 576, 58–64. [Google Scholar] [CrossRef]
- Lu, C.; Lu, J.; Zhang, Y.; Hastings-Puckett, M. A convenient method to estimate soil hydraulic conductivity using electrical conductivity and soil compaction degree. J. Hydrol. 2019, 575, 211–220. [Google Scholar] [CrossRef]
- Won, J.; Park, J.; Choo, H.; Burns, S. Estimation of saturated hydraulic conductivity of coarse-grained soils using particle shape and electrical resistivity. J. Appl. Geophys. 2019, 167, 19–25. [Google Scholar] [CrossRef]
- Divya, P.V.; Viswanadham, B.V.S.; Gourc, J.P. Hydraulic conductivity behaviour of soil blended with geofiber inclusions. Geotext. Geomembr. 2018, 46, 121–130. [Google Scholar] [CrossRef]
- Wu, J.; Deng, Y.; Zheng, X.; Cui, Y.; Zhao, Z.; Chen, Y.; Zha, F. Hydraulic conductivity and strength of foamed cement-stabilized marine clay. Constr. Build. Mater. 2019, 222, 688–698. [Google Scholar] [CrossRef]
- Ziccarelli, M.; Valore, C. Hydraulic conductivity and strength of pervious concrete for deep trench drains. Geomech. Energy Environ. 2019, 18, 41–55. [Google Scholar] [CrossRef]
- Zhong, R.; Xu, M.; Vieira, N.R.; Wille, K. Influence of pore tortuosity on hydraulic conductivity of pervious concrete: Characterization and modeling. Constr. Build. Mater. 2016, 125, 1158–1168. [Google Scholar] [CrossRef]
- Turco, M.; Brunetti, G.; Carbone, M.; Piro, P. Modelling the hydraulic behaviour of permeable pavements through a reservoir element model. Hydrology and Water Resources. Int. Multidiscip. Sci. Geoconf SGEM 2018, 18, 507–514. [Google Scholar] [CrossRef]
- Di Dato, M.; Bellin, A.; Fiori, A. Convergent radial transport in three-dimensional heterogeneous aquifers: The impact of the hydraulic conductivity structure. Adv. Water Resour. 2019, 131. [Google Scholar] [CrossRef]
- Jarzyna, J.A.; Puskarczyk, E.; Motyka, J. Estimating porosity and hydraulic conductivity for hydrogeology on the basis of reservoir and elastic petrophysical parameters. J. Appl. Geophys. 2019, 167, 11–18. [Google Scholar] [CrossRef]
- Tang, R.; Zhou, G.; Jiao, W.; Ji, Y. Theoretical model of hydraulic conductivity for frozen saline/non-saline soil based on freezing characteristic curve. Cold Reg. Sci. Technol. 2019, 165, 102794. [Google Scholar] [CrossRef]
- Luo, W.; Grudzinski, P.B.; Pederson, D. Estimating hydraulic conductivity from drainage patterns—A case study in the Oregon Cascades. Geology 2010, 38, 335–338. [Google Scholar] [CrossRef]
- Brunetti, G.; Šimůnek, J.; Bogena, H.; Baatz, R.; Huisman, J.A.; Dahlke, H.; Vereecken, H. On the information content of cosmic-ray neutron data in the inverse estimation of soil hydraulic properties. Vadose Zone J. 2019, 18, 180123. [Google Scholar] [CrossRef] [Green Version]
- Hörning, S.; Sreekanth, J.; Bárdossy, A. Computational efficient inverse groundwater modeling using Random Mixing and Whittaker–Shannon interpolation. Adv. Water Resour. 2019, 123, 109–119. [Google Scholar] [CrossRef]
- Batlle-Aguilar, J.; Cook, P.G.; Harrington, G.A. Comparison of hydraulic and chemical methods for determining hydraulic conductivity and leakage rates in argillaceous aquitards. J. Hydrol. 2016, 532, 102–121. [Google Scholar] [CrossRef]
- Kazakis, N.; Vargemezis, G.; Voudouris, K.S. Estimation of hydraulic parameters in a complex porous aquifer system using geoelectrical methods. Sci. Total Environ. 2016, 550, 742–750. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Estimation of saturated hydraulic conductivity with pedotransfer functions: A review. J. Hydrol. 2019, 575, 1011–1030. [Google Scholar] [CrossRef]
- Abdelbaki, A.M. Using automatic calibration method for optimizing the performance of Pedotransfer functions of saturated hydraulic conductivity. Ain Shams Eng. J. 2016, 7, 653–662. [Google Scholar] [CrossRef] [Green Version]
- Priyanka, B.N.; Mohan-Kumar, M.S.; Amai, M. Estimating anisotropic heterogeneous hydraulic conductivity and dispersivity in a layered coastal aquifer of Dakshina Kannada District, Karnataka. J. Hydrol. 2018, 565, 302–317. [Google Scholar] [CrossRef]
- Zhou, H.; Gómez-Hernández, J.J.; Hendricks-Franssen, H.J.; Li, L. An approach to handling non-Gaussianity of parameters and state variables in ensemble Kalman filtering. Adv. Water Resour. 2011, 34, 844–864. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Carle, S.F.; Fogg, G.E. Geologic heterogeneity and a comparison of two geostatistical models: Sequential Gaussian and transition probability-based geostatistical simulation. Adv. Water Resour. 2007, 30, 1914–1932. [Google Scholar] [CrossRef]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory, 1st ed.; Academic Press Elsevier: Amsterdam, The Netherlands, 1970; Volume 64, ISBN 9780080960906. [Google Scholar]
- Evensen, G. The Ensemble Kalman Filter: Theoreticalformulation and practicalimplementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- van Leeuwen, P.J.; Evensen, G. Data Assimilation and Inverse Methods in Terms of a Probabilistic Formulation. Mon. Weather Rev. 1996, 124, 2898–2913. [Google Scholar] [CrossRef]
- Herrera, G.S. Cost Effective Groundwater Quality Sampling Network Design. Ph.D. Thesis, University of Vermont, Vermont, VT, USA, 1998. [Google Scholar]
- Bailey, R.; Baù, D. Ensemble smoother assimilation of hydraulic head and return flow data to estimate hydraulic conductivity distribution. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Burgers, G.; Jan van Leeuwen, P.; Evensen, G. Analysis Scheme in the Ensemble Kalman Filter. Mon. Weather Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Evensen, G. Data Assimilation-The Ensemble Kalman Filter, 2nd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Franssen, H.J.H.; Kinzelbach, W. Real-time groundwater flow modeling with the Ensemble Kalman Filter: Joint estimation of states and parameters and the filter inbreeding problem. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Liu, G.; Chen, Y.; Zhang, D. Investigation of flow and transport processes at the MADE site using ensemble Kalman filter. Adv. Water Resour. 2008, 31, 12. [Google Scholar] [CrossRef]
- Briseño, J.V. Método Para la Calibración de Modelos Estocásticos de Flujo y Transporte en Aguas Subterráneas, Para el Diseño de Redes de Monitoreo de Calidad del Agua. Ph.D. Thesis, Universidad Nacional Autónoma de México, México, 2012. [Google Scholar]
- Li, L.; Zhou, H.; Gómez-Hernández, J.J.; Hendricks-Franssen, H.J. Jointly mapping hydraulic conductivity and porosity by assimilating concentration data via ensemble Kalman filter. J. Hydrol. 2012, 428–429, 152–169. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Gómez-Hernández, J.J. Probability fields revisited in the context of ensemble Kalman filtering. J. Hydrol. 2015, 531, 40–52. [Google Scholar] [CrossRef] [Green Version]
- Zovi, F.; Camporese, M.; Hendricks-Franssen, H.J.; Huisman, J.A.; Salandin, P. Identification of high-permeability subsurface structures with multiple point geostatistics and normal score ensemble Kalman filter. J. Hydrol. 2017, 548, 208–224. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Gómez-Hernández, J.J. Simultaneous identification of a contaminant source and hydraulic conductivity via the restart normal-score ensemble Kalman filter. Adv. Water Resour. 2018, 112, 106–123. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide, 2nd ed.; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Webster, R.; Oliver, M. Geostatistics for Environmental Scientists, Statistics in Practice, 2nd ed.; John Wiley & Sons: London, UK, 2007; p. 330. [Google Scholar]
- De Iaco, S.; Myers, D.E.; Posa, D. Space-time analysis using a general product-sum model. Stat. Probab. Lett. 2001, 52, 21–28. [Google Scholar] [CrossRef]
- De Cesare, L.; Myers, D.; Posa, D. Estimating and modeling space-time correlation structures. Stat. Probab. Lett. 2001, 51, 9–14. [Google Scholar] [CrossRef]
- Ahmadi, S.H.; Sedghamiz, A. Geostatistical analysis of spatial and temporal variations of groundwater level. Environ. Monit. Assess. 2007, 129, 277–294. [Google Scholar] [CrossRef]
- Júnez-Ferreira, H.E.; Herrera, G.S. A geostatistical methodology for the optimal design of space–time hydraulic head monitoring networks and its application to the Valle de Querétaro aquifer. Environ. Monit Assess 2013, 185, 3527–3549. [Google Scholar] [CrossRef] [PubMed]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, the U.S. geological surveymodular ground-water model—user guide to modularization concepts and the ground-water flow process. Open-File Rep. USA Geol. Surv. 2000, 92, 134. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Pub. Co.: New York, NY, USA, 1972. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Englewood Cliffs: Prentice-Hall, NJ, USA, 1979. [Google Scholar]

| ⋮ | ⋮ | ⋮ | ⋮ |
| ⋮ | ⋮ | ⋮ | ⋮ |
| … | … | … | … | |||||||||
| … | … | … | … | |||||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| … | … | … | … | |||||||||
| … | … | … | … | |||||||||
| … | … | … | … | |||||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| … | … | … | … | |||||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| … | … | … | … | |||||||||
| … | … | … | … | |||||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| … | … | … | … |
| Univariate spatial covariance matrix (hydraulic conductivity only) | Cross-covariance matrix (hydraulic conductivity–hydraulic head for time 1) | Cross-covariance matrix (hydraulic conductivity–hydraulic head for time 2) | … | Cross-covariance matrix (hydraulic conductivity–hydraulic head for time NT) |
| Cross-covariance matrix (hydraulic head for time 1–hydraulic conductivity) | Space–time covariance matrix (hydraulic head from time 1 to time NT) | |||
| Cross-covariance matrix (hydraulic head for time 2–hydraulic conductivity) | ||||
| … | ||||
| Cross-covariance matrix (hydraulic head for time NT–hydraulic conductivity) | ||||
| Case | Variable | Correlation | Nugget (m2) | Sill(m2) | Range (m) |
|---|---|---|---|---|---|
| Univariate | K | 0 * | 6.69 * | 2177.608 | |
| H1 | 0 | 0.075 | 1616.284 | ||
| H2 | 0 | 0.209 | 4327.53 | ||
| H3 | 0 | 0.413 | 4364.75 | ||
| H4 | 0 | 0.491 | 4364.75 | ||
| H5 | 0 | 0.541 | 4364.75 | ||
| H6 | 0 | 0.571 | 4364.75 | ||
| Bivariate | K-H1 | −0.282 | 0 µ | −0.200 µ | 1500 |
| K-H2 | −0.135 | 0 µ | −0.160 µ | 1500 | |
| K-H3 | −0.120 | 0 µ | −0.200 µ | 1800 | |
| K-H4 | −0.127 | 0 µ | −0.230 µ | 1800 | |
| K-H5 | −0.131 | 0 µ | −0.250 µ | 1800 | |
| K-H6 | −0.133 | 0 µ | −0.260 µ | 1800 | |
| H1-K | −0.173 | 0 µ | −0.200 µ | 1550 | |
| H2-K | −0.251 | 0 µ | −0.260 µ | 2000 | |
| H3-K | −0.294 | 0 µ | −0.340 µ | 1800 | |
| H4-K | −0.306 | 0 µ | −0.380 µ | 1800 | |
| H5-K | −0.309 | 0 ** | −0.400 µ | 1800 | |
| H6-K | −0.326 | 0 ** | −0.430 µ | 1800 | |
| Spatiotemporal | Space H | 0.09 | 0.41 | 3000 | |
| Time H | 0.14 Ω | 0.09 Ω | 1.20 β | ||
| Space-time H | 0.41 α |
| Case | Variable | Minimum Error (m) | Maximum Error (m) | Mean Error (m) | MSE (m2) | RMSE | SMSE |
|---|---|---|---|---|---|---|---|
| Univariate | K | −2.171 * | 3.063 * | 0.0031 * | 1.0343 ** | 1.017 * | 0.501 |
| H1 | −0.056 | 0.256 | −0.0002 | 0.0005 | 0.022 | 0.035 | |
| H2 | −0.098 | 0.254 | −0.0001 | 0.0006 | 0.024 | 0.028 | |
| H3 | −0.149 | 0.254 | −0.0001 | 0.0007 | 0.026 | 0.022 | |
| H4 | −0.183 | 0.264 | −0.0001 | 0.0007 | 0.027 | 0.020 | |
| H5 | -0.204 | 0.253 | −0.0001 | 0.0008 | 0.028 | 0.019 | |
| H6 | −0.217 | 0.263 | −0.0001 | 0.0008 | 0.028 | 0.019 | |
| Bivariate | K-H1 | −2.146 * | 2.608 * | 0.0346 * | 0.9754 ** | 0.988 * | 0.283 |
| K-H2 | −2.140 * | 2.612 * | 0.0361 * | 0.9738 ** | 0.987 * | 0.282 | |
| K-H3 | −2.138 * | 2.613 * | 0.0366 * | 0.9732 ** | 0.986 * | 0.282 | |
| K-H4 | −2.138 * | 2.615 * | 0.0368 * | 0.9729 ** | 0.986 * | 0.282 | |
| K-H5 | −2.137 * | 2.615 * | 0.0370 * | 0.9728 ** | 0.986 * | 0.282 | |
| K-H6 | −2.137 * | 2.616 * | 0.0370 * | 0.9729 ** | 0.986 * | 0.282 | |
| H1-K | −0.056 | 0.260 | −0.0002 | 0.0005 | 0.023 | 0.167 | |
| H2-K | −0.093 | 0.255 | −0.0003 | 0.0006 | 0.025 | 0.080 | |
| H3-K | −0.142 | 0.256 | −0.0004 | 0.0007 | 0.027 | 0.063 | |
| H4-K | −0.175 | 0.265 | −0.0005 | 0.0008 | 0.029 | 0.058 | |
| H5-K | −0.195 | 0.255 | −0.0005 | 0.0009 | 0.029 | 0.054 | |
| H6-K | −0.208 | 0.265 | −0.0006 | 0.0009 | 0.030 | 0.054 | |
| Spatiotemporal | Space-time H | −0.366 | 0.351 | −0.0018 | 0.0047 | 0.069 | 0.023 |
| Case | Data within the Confidence Interval | Data above the Confidence Interval | Data below the Confidence Interval | Data out of the Confidence Interval |
|---|---|---|---|---|
| Univariate | 59.25% | 23.25% | 17.50% | 40.75% |
| Bivariate K–H1 | 58.25% | 23.25% | 18.50% | 41.75% |
| Bivariate K–H2 | 57.50% | 23.25% | 19.25% | 42.50% |
| Bivariate K–H3 | 58.50% | 23.25% | 18.25% | 41.50% |
| Bivariate K–H4 | 58.50% | 23.25% | 18.25% | 41.50% |
| Bivariate K–H5 | 58.50% | 23.25% | 18.25% | 41.50% |
| Bivariate K–H6 | 58.50% | 23.50% | 18.00% | 41.50% |
| Bivariate spatiotemporal | 58.50% | 22.25% | 19.25% | 41.50% |
| Case | Variables | Mean Error (m/day) | MSE (m2/day2) | RMSE (m/day) | SMSE |
|---|---|---|---|---|---|
| Univariate | K | 0.091 | 0.691 | 0.831 | 0.403 |
| Bivariate | K and H1 | 0.096 | 0.909 | 0.953 | 0.574 |
| Bivariate | K and H2 | 0.099 | 0.722 | 0.850 | 0.449 |
| Bivariate | K and H3 | 0.098 | 0.720 | 0.848 | 0.438 |
| Bivariate | K and H4 | 0.099 | 0.722 | 0.850 | 0.441 |
| Bivariate | K and H5 | 0.100 | 0.724 | 0.851 | 0.444 |
| Bivariate | K and H6 | 0.099 | 0.724 | 0.851 | 0.445 |
| Bivariate spatiotemporal | K, H1, H2, H3, H4, H5 and H6 | 0.095 | 0.757 | 0.870 | 0.469 |
| Time | Univariate | Bivariate | Bivariate Spatiotemporal | |||
|---|---|---|---|---|---|---|
| Mean Error (m) | MSE (m2) | Mean Error (m) | MSE (m2) | Mean Error (m) | MSE (m2) | |
| 1 | −0.0133 | 0.0044 | −0.0146 | 0.0031 | −0.0192 | 0.0033 |
| 2 | −0.0220 | 0.0072 | −0.0248 | 0.0050 | −0.0340 | 0.0056 |
| 3 | −0.0290 | 0.0088 | −0.0329 | 0.0064 | −0.0460 | 0.0077 |
| 4 | −0.0339 | 0.0097 | −0.0389 | 0.0073 | −0.0554 | 0.0094 |
| 5 | −0.0375 | 0.0103 | −0.0434 | 0.0081 | −0.0623 | 0.0109 |
| 6 | −0.0398 | 0.0107 | −0.0461 | 0.0085 | −0.0670 | 0.0120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Júnez-Ferreira, H.E.; González-Trinidad, J.; Júnez-Ferreira, C.A.; Robles Rovelo, C.O.; Herrera, G.S.; Olmos-Trujillo, E.; Bautista-Capetillo, C.; Contreras Rodríguez, A.R.; Pacheco-Guerrero, A.I. Implementation of the Kalman Filter for a Geostatistical Bivariate Spatiotemporal Estimation of Hydraulic Conductivity in Aquifers. Water 2020, 12, 3136. https://doi.org/10.3390/w12113136
Júnez-Ferreira HE, González-Trinidad J, Júnez-Ferreira CA, Robles Rovelo CO, Herrera GS, Olmos-Trujillo E, Bautista-Capetillo C, Contreras Rodríguez AR, Pacheco-Guerrero AI. Implementation of the Kalman Filter for a Geostatistical Bivariate Spatiotemporal Estimation of Hydraulic Conductivity in Aquifers. Water. 2020; 12(11):3136. https://doi.org/10.3390/w12113136
Chicago/Turabian StyleJúnez-Ferreira, Hugo Enrique, Julián González-Trinidad, Carlos Alberto Júnez-Ferreira, Cruz Octavio Robles Rovelo, G.S. Herrera, Edith Olmos-Trujillo, Carlos Bautista-Capetillo, Ada Rebeca Contreras Rodríguez, and Anuard Isaac Pacheco-Guerrero. 2020. "Implementation of the Kalman Filter for a Geostatistical Bivariate Spatiotemporal Estimation of Hydraulic Conductivity in Aquifers" Water 12, no. 11: 3136. https://doi.org/10.3390/w12113136
APA StyleJúnez-Ferreira, H. E., González-Trinidad, J., Júnez-Ferreira, C. A., Robles Rovelo, C. O., Herrera, G. S., Olmos-Trujillo, E., Bautista-Capetillo, C., Contreras Rodríguez, A. R., & Pacheco-Guerrero, A. I. (2020). Implementation of the Kalman Filter for a Geostatistical Bivariate Spatiotemporal Estimation of Hydraulic Conductivity in Aquifers. Water, 12(11), 3136. https://doi.org/10.3390/w12113136







