Lumped Approach for Reactive Transport of Organic Compound Mixtures through Simulated Aquifer Sands in Lab-Scale Column Tests
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulated Aquifer Sands
2.2. Mixtures of Organic Compounds
2.3. Analytical Method
2.4. Column Tests
2.5. Numerical Modeling
2.6. Lumped Approach
3. Results and Discussion
3.1. Comparison of Breakthrough Curves and Concentration Profiles of 12 Organic Compounds in Mixture
3.2. Comparison of Freundlich Sorption Parameters
3.3. Hierarchical Cluster Analysis
3.4. Development of A Priori Grouping Criteria from Column Tests
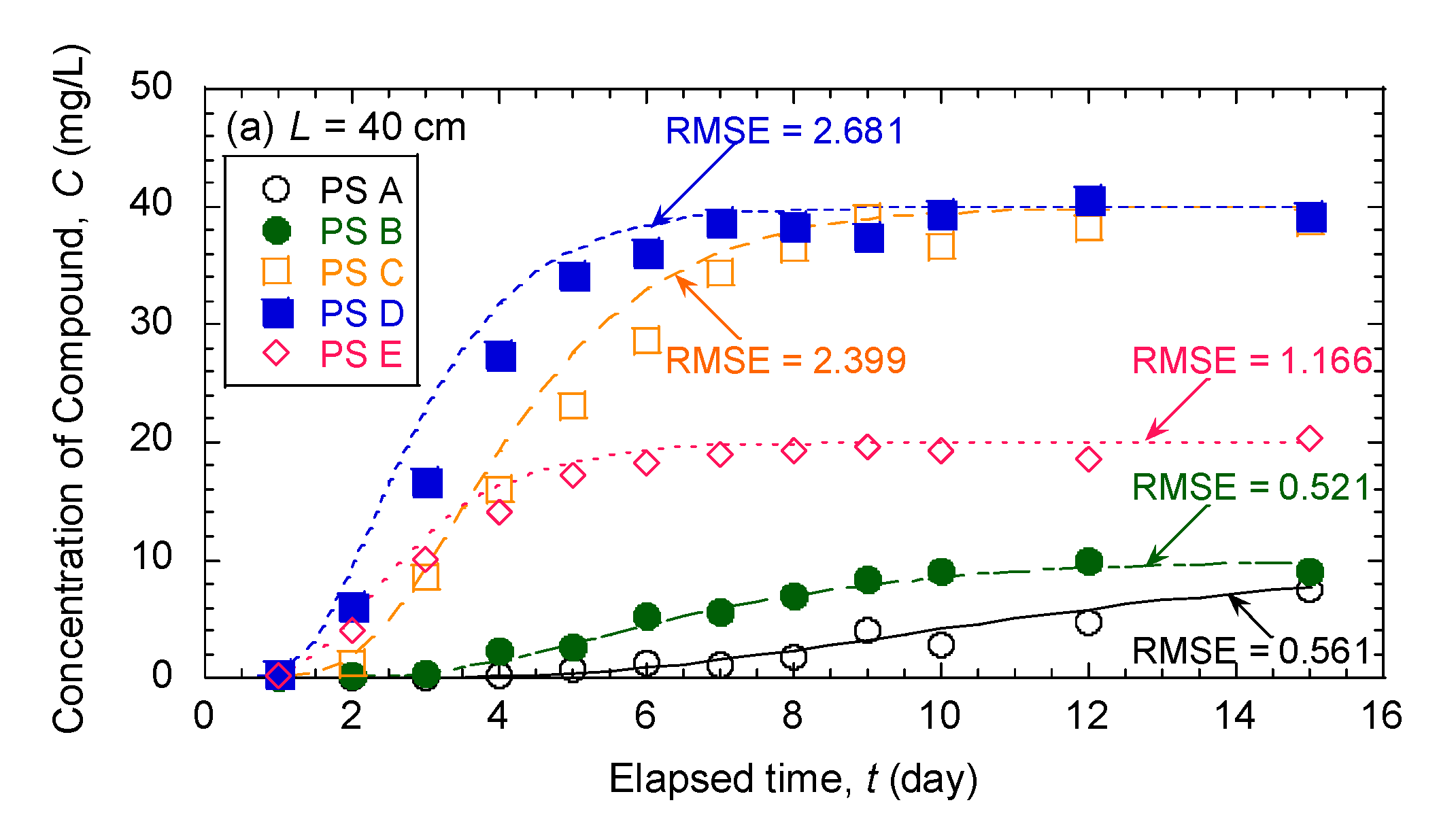
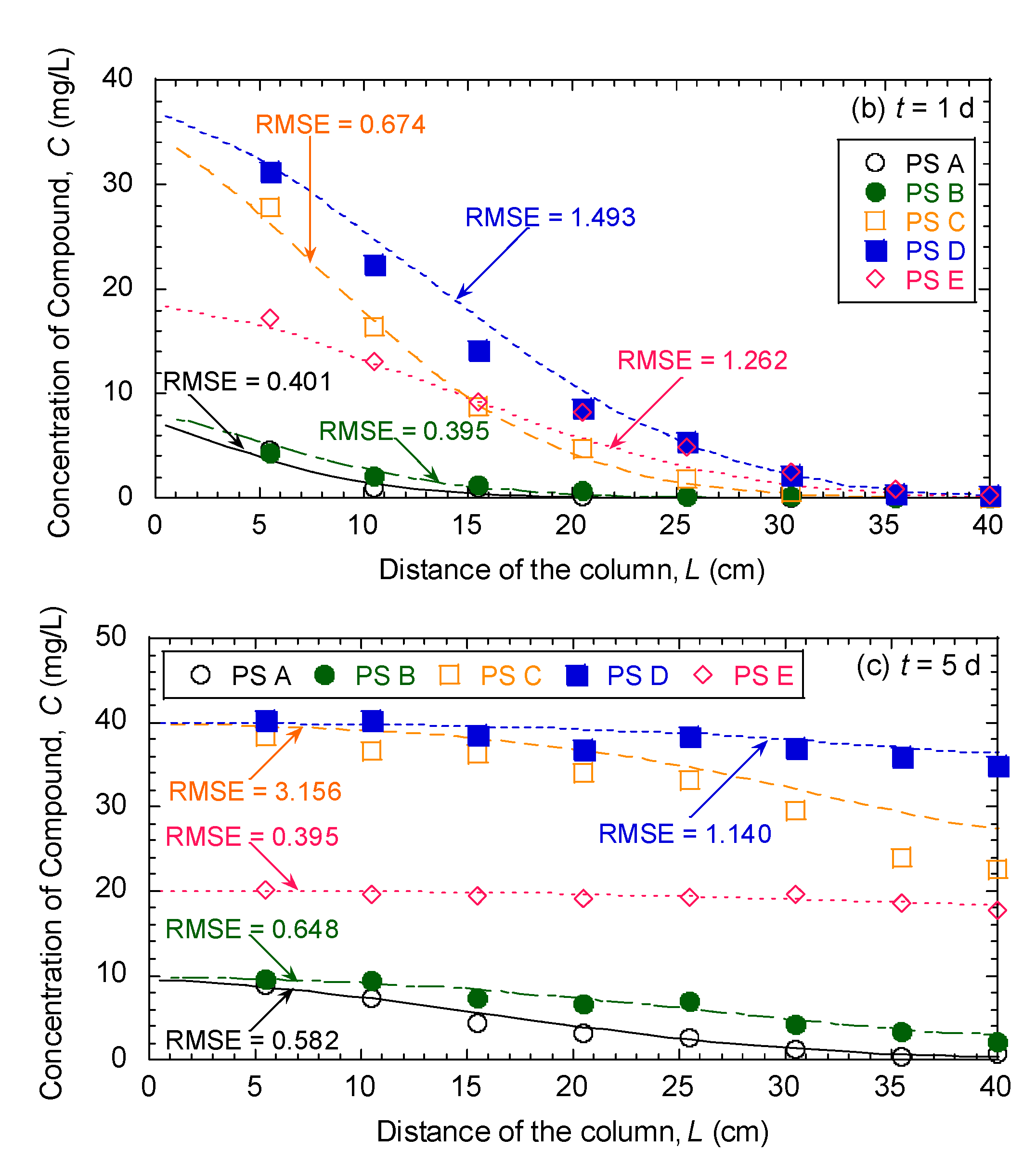
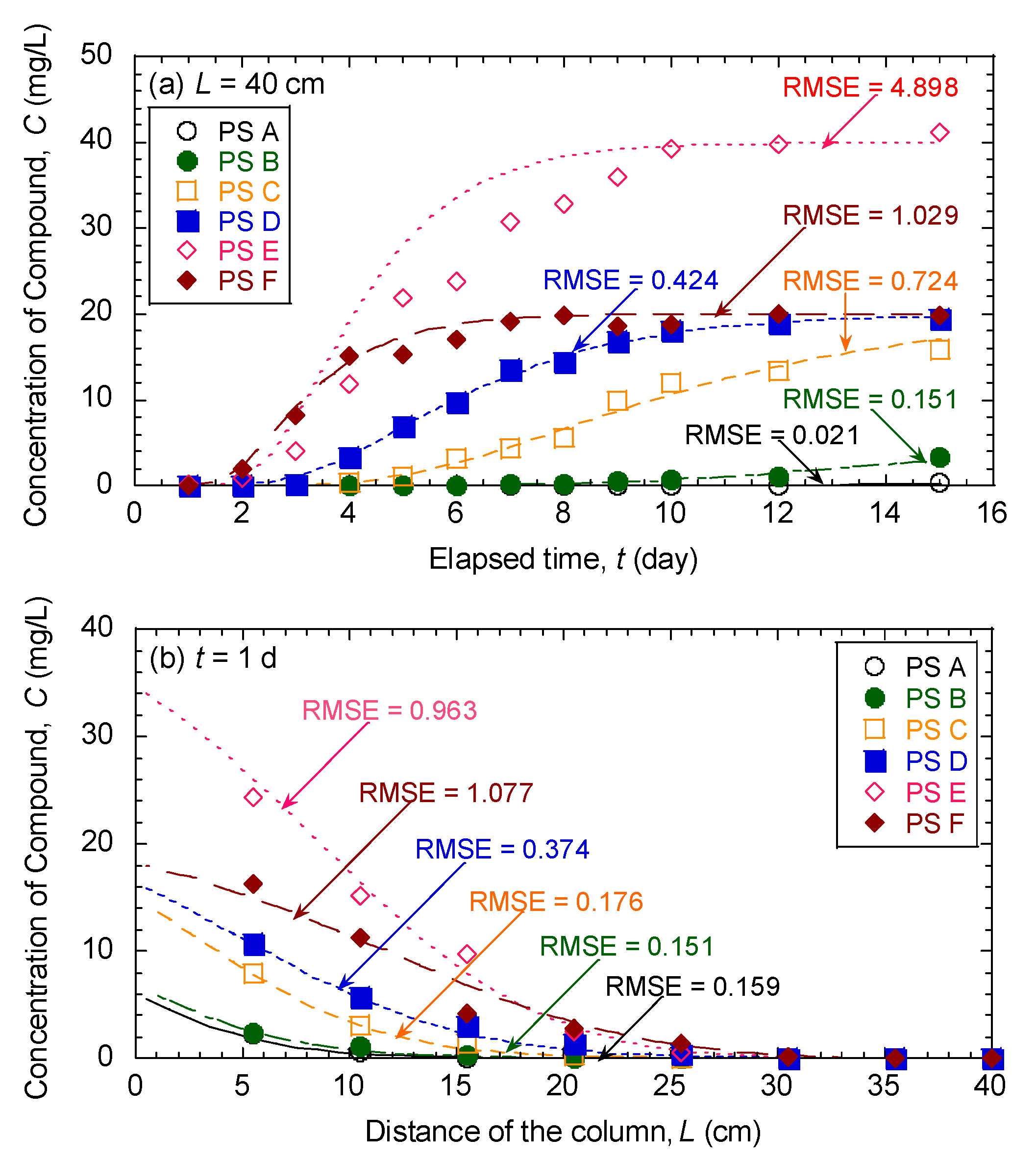
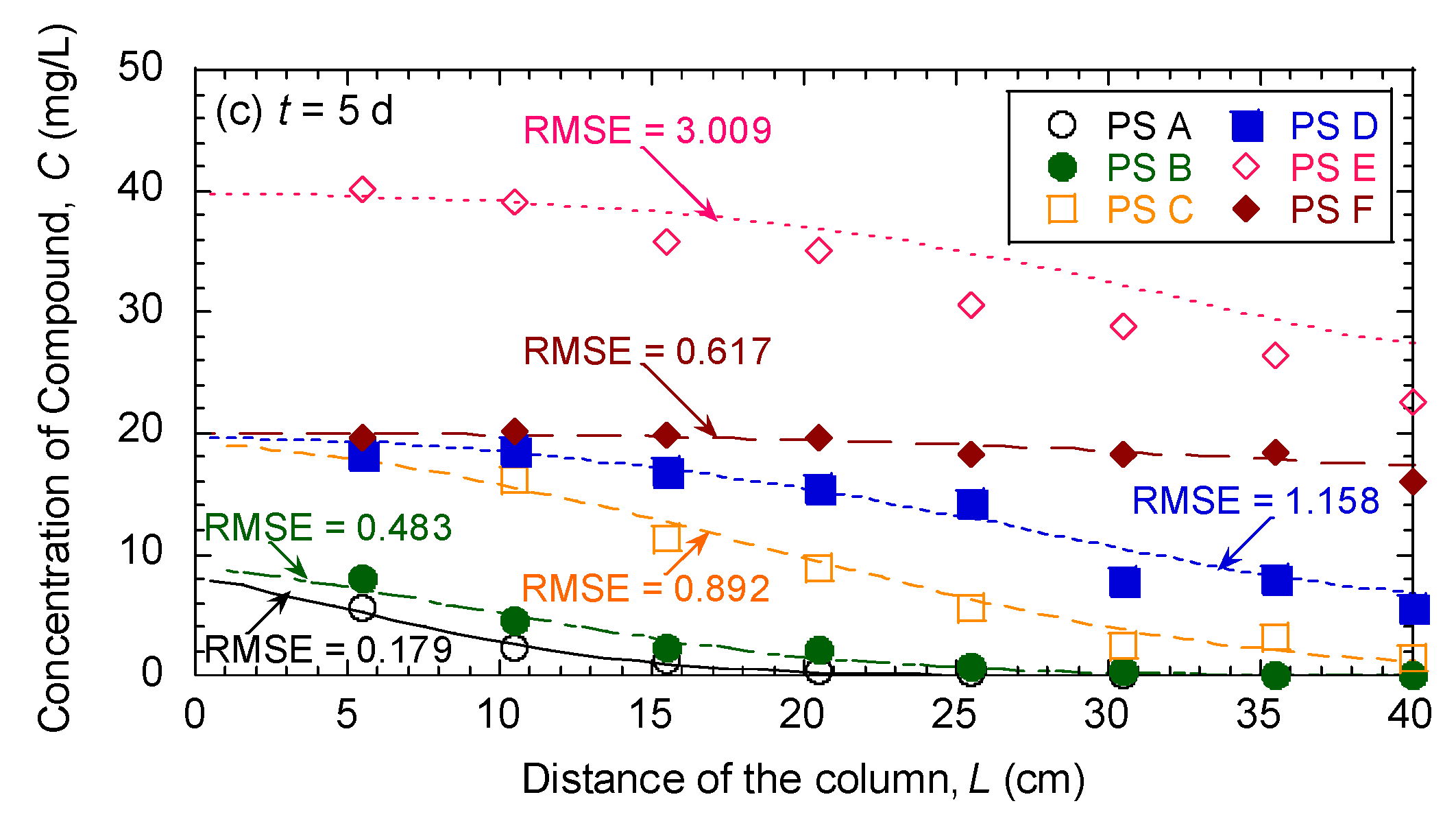
3.5. Evaluation of Effectiveness of Pseudocompounds to Simulated Aquifer Sands
3.6. Estimation of Sorption Parameters for Pseudocompounds from Average Sorption Parameters for Components
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Joo, J.C.; Shackelford, C.D.; Reardon, K.F. Lumping analysis for sorption of neutral organic compounds in mixtures to simulated aquifer sorbents. J. Environ. Engrg. 2011, 138, 552–561. [Google Scholar] [CrossRef]
- Joo, J.C.; Shackelford, C.D.; Reardon, K.F. Sorption of neutral organic compounds in mixtures to mineral surfaces and humic acid-mineral complexes. J. Hazard. Toxic Radioact. Waste 2012, 15, 188–198. [Google Scholar] [CrossRef]
- Joo, J.C.; Shackelford, C.D.; Reardon, K.F. Modeling sorption of neutral organic compound mixtures to simulated aquifer sorbents with pseudocompounds. J. Environ. Qual. 2013, 42, 852–860. [Google Scholar] [CrossRef] [PubMed]
- Essaid, H.; Bekins, B.A.; Cozzarelli, I.A. Organic contaminant transport and fate in the subsurface: Evolution of knowledge and understanding. Water Resour. Res. 2015, 51, 4861–4902. [Google Scholar] [CrossRef]
- Barbagli, A.; Jensen, B.N.; Raza, M.; Schueth, C.; Rossetto, R. Assessment of soil buffer capacity on nutrients and pharmaceuticals in nature-based solution applications. Environ. Sci. Pollut. Res. 2019, 26, 759–774. [Google Scholar] [CrossRef] [PubMed]
- Leharne, S. Transfer phenomena and interactions of non-aqueous phase liquids in soil and groundwater. ChemTexts 2019, 5, 5–25. [Google Scholar] [CrossRef]
- Ossai, I.C.; Ahmed, A.; Hassan, A.; Hamid, F.S. Remediation of soil and water contaminated with petroleum hydrocarbon: A review. Environ. Technol. Innov. 2020, 17, 100526. [Google Scholar] [CrossRef]
- De Oliveira, L.P.; Hudebine, D.; Guillaume, D.; Verstraete, J.J. A review of kinetic modeling methodologies for complex processes. Oil Gas Sci. Technol. 2016, 71, 45–93. [Google Scholar] [CrossRef]
- Nguyen TT, H.; Teratani, S.; Tanaka, R.; Endo, A.; Hirao, M. Development of a structure-based lumping kinetic model for light gas oil hydrodesulfurization. Energy Fuels 2017, 31, 5673–5681. [Google Scholar] [CrossRef]
- Jaffe, S.B.; Freund, H.; Olmstead, W.N. Extension of structure-oriented lumping to vaccum residua. Ind. Eng. Chem. Res. 2005, 44, 9840–9852. [Google Scholar] [CrossRef]
- Yu, Y.S.; Bailey, G.W.; Xianchan, J. Heavy metals in the environment. J. Environ. Qual. 1996, 25, 552–561. [Google Scholar] [CrossRef]
- Li, L.; Crain, N.; Gloyna, E.F. Kinetic lumping applied to wastewater treatment. Water Environ. Res. 1996, 68, 841–854. [Google Scholar] [CrossRef]
- Martins, R.C.; Lopes RJ, G.; Quinta-Ferreira, R.M. Lumped kinetic models for single ozonation of phenolic effluents. Chem. Eng. J. 2010, 165, 678–685. [Google Scholar] [CrossRef]
- Bian, F.; Bowman, F.M. A lumped model for composition- and temperature-dependent partitioning of secondary organic aerosols. Atmos. Environ. 2005, 39, 1263–1274. [Google Scholar] [CrossRef]
- Dennison, J.E.; Andersen, M.E.; Clewell, H.J.; Yang RS, H. Development of a physiologically based pharmacokinetic model for volatile fractions of gasoline using chemical lumping analysis. Environ. Sci. Technol. 2004, 38, 5674–5681. [Google Scholar] [CrossRef] [PubMed]
- Desalegn, A.; Bopp, S.; Asturiol, D.; Lamon, L.; Worth, A.; Paini, A. Role of physiologically based kinetic modelling in addressing environmental chemical mixtures—A review. Comput. Toxicol. 2019, 10, 158–168. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Yeh, G.-T.; Parker, J.C.; Brooks, S.C.; Pace, M.N.; Kim, Y.-J.; Jardine, P.M.; Wastson, D.B. A reaction-based paradigm to model reactive chemical transport in groundwater with general kinetic and equilibrium reactions. J. Contam. Hydrol. 2007, 92, 10–32. [Google Scholar] [CrossRef] [PubMed]
- McDonald, M.G.; Harbaugh, A.W. A.W. A Modular Three-Dimensional Finite-Difference Ground-Water Flow Model. In Techniques of Water-Resources Investigations; U.S. Geological Survey Publications: Denver, CO, USA, 1988; Chapter A1; p. 586. [Google Scholar]
- Clement, T.P. RT3D-A Modular Computer Code for Simulating Reactive Multi-Species Transport in 3-Dimensional Groundwater Aquifers. Draft Report. PNNL-SA-28967; Pacific Northwest National Laboratory: Richland, WA, USA, 1997. [Google Scholar]
- Clement, T.P.; Sun, Y.; Hooker, B.S.; Petersen, J.N. Modeling multi-species reactive transport in groundwater aquifers. Groundw. Monit. Remediat. 2007, 18, 79–92. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?-Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Coxson, P.G.; Bischoff, K.B. Lumping strategy. 1. Introductory techniques and applications of cluster analysis. Ind. Eng. Chem. Res. 1987, 26, 1239–1248. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Demissie, M. Hydrologic Modeling of the Iroquois River Watershed Using HSPF and SWAT; ISWS CR 2004-08; Illinois State Water Survey: Champaign, IL, USA, 2004. [Google Scholar]
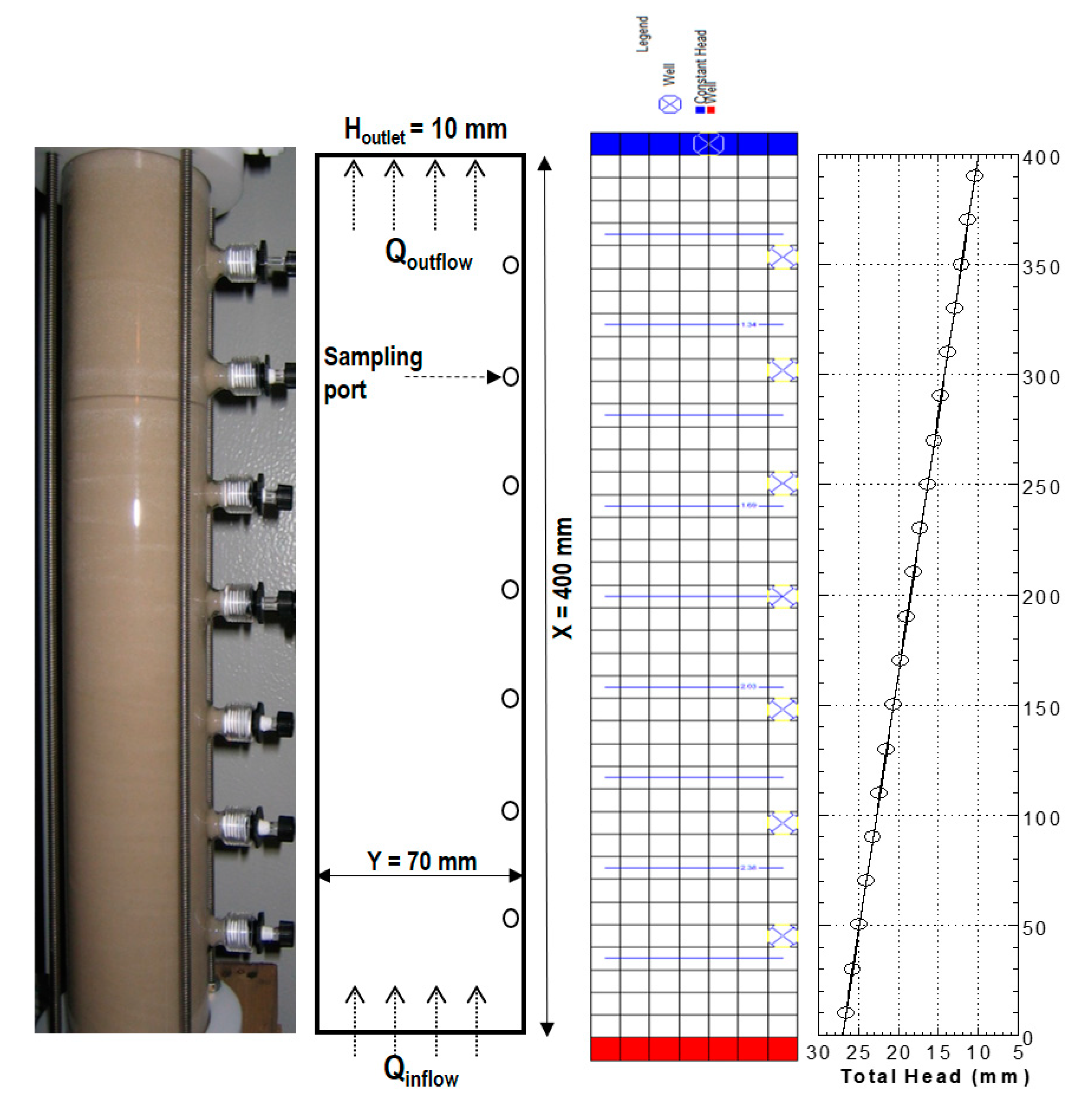
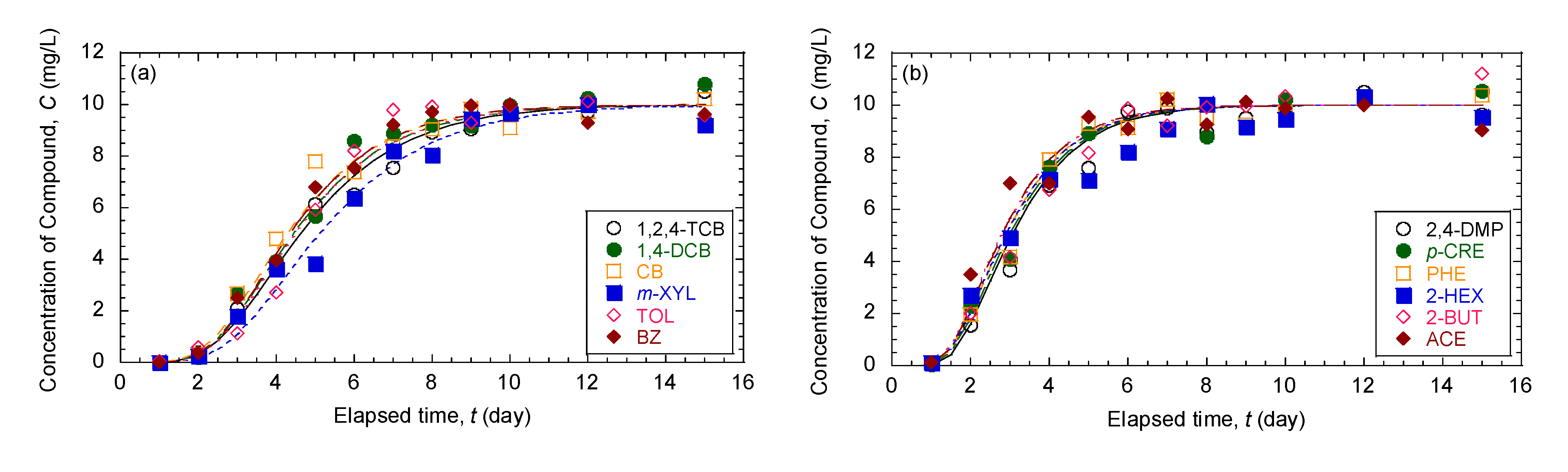
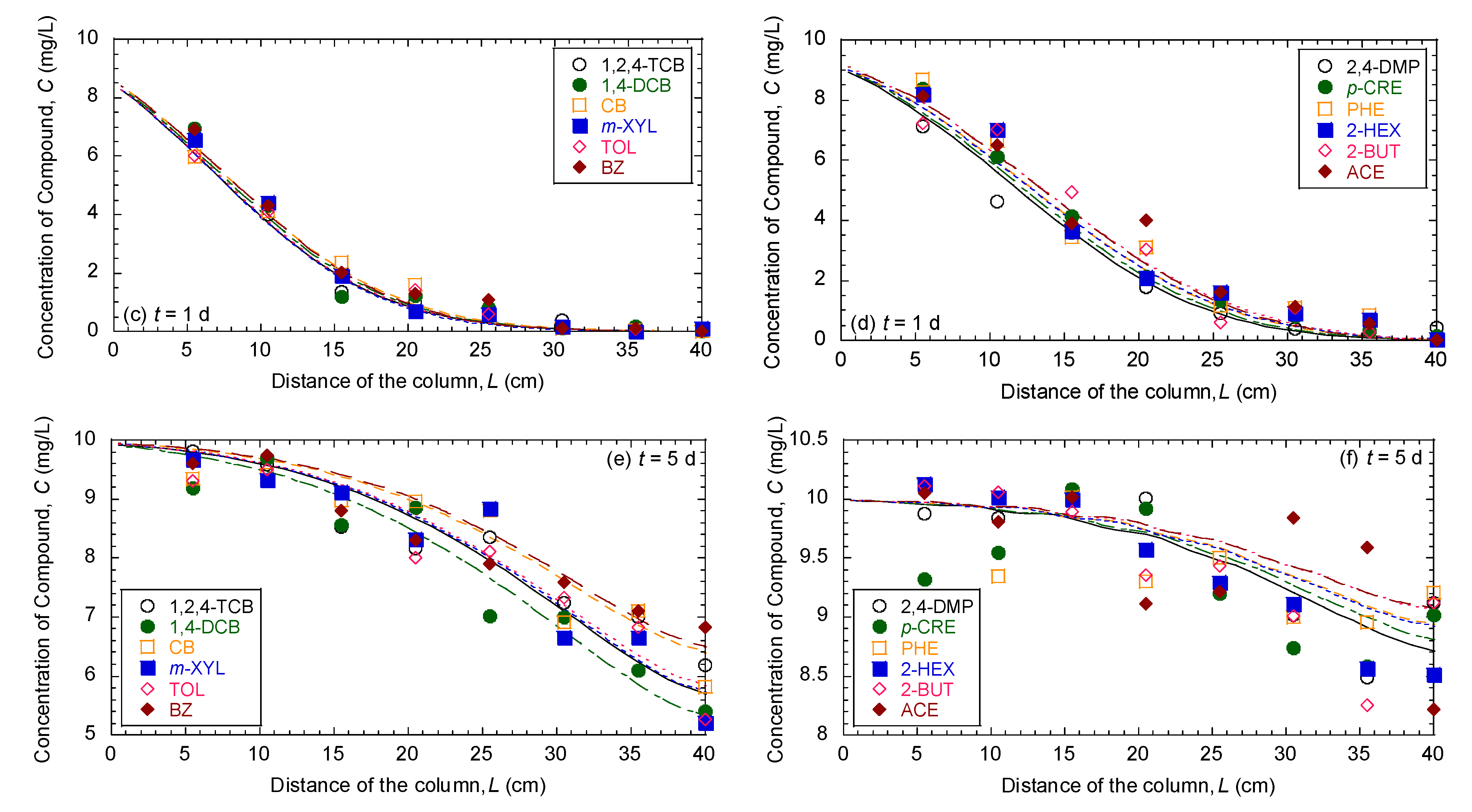
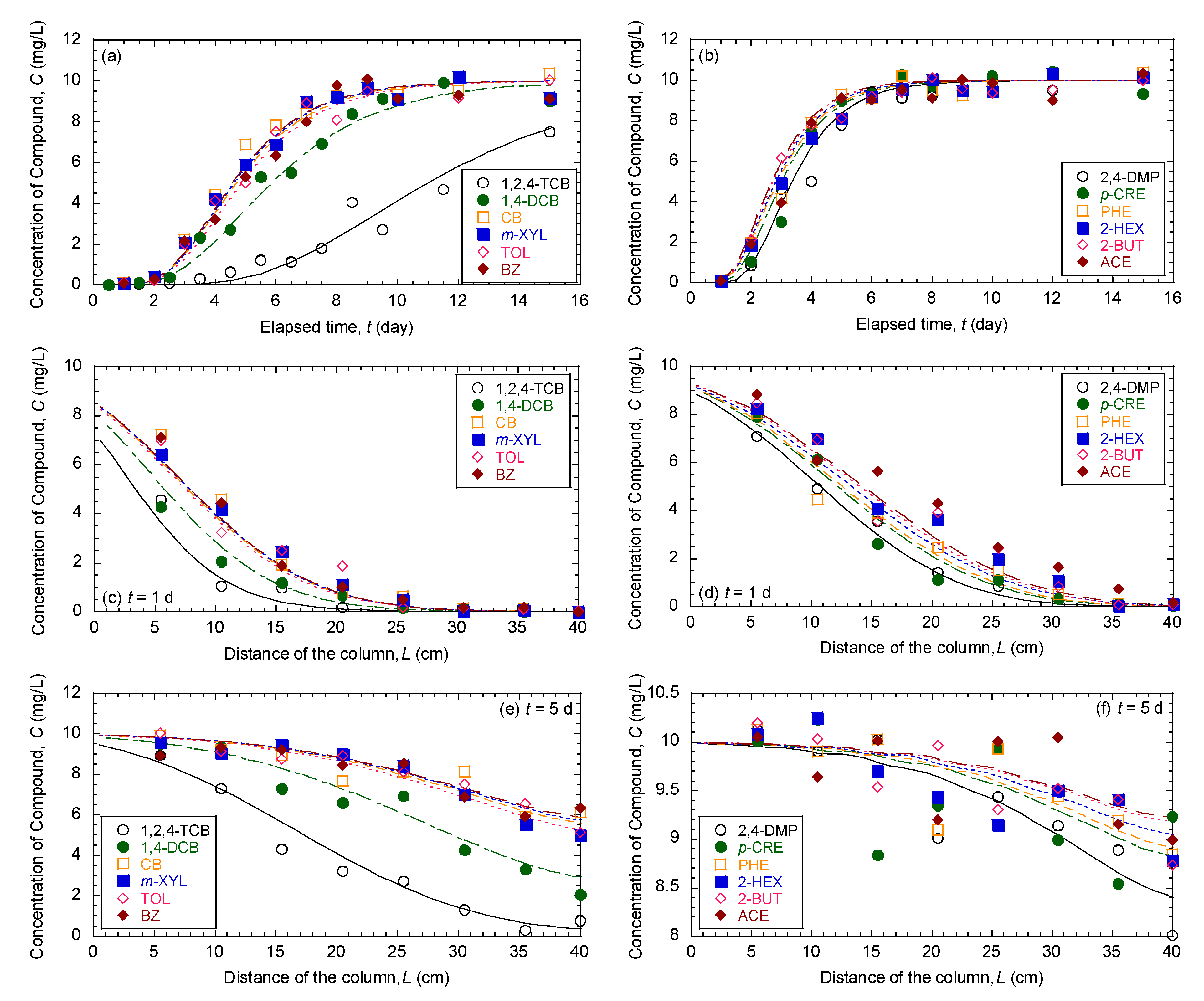
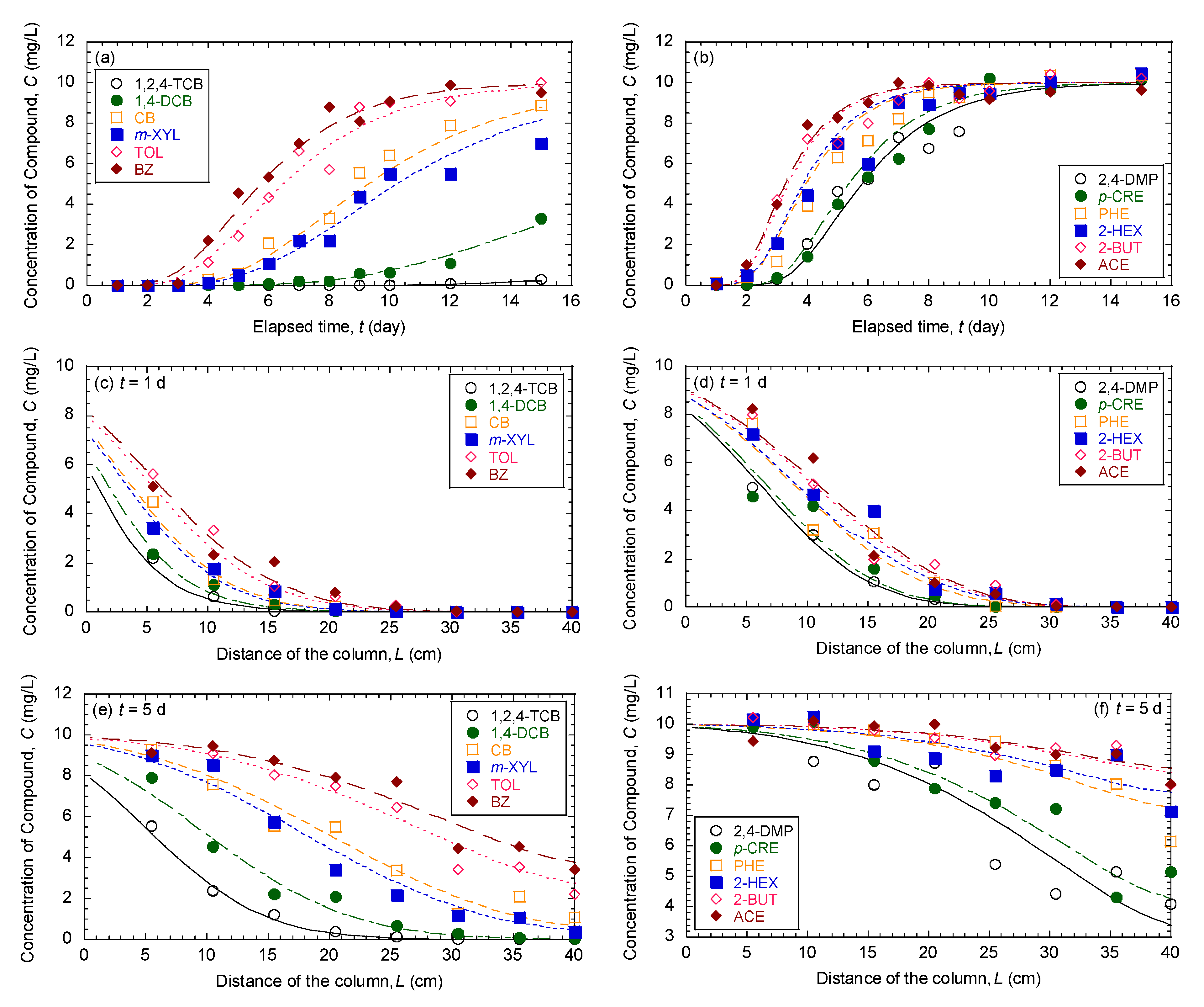
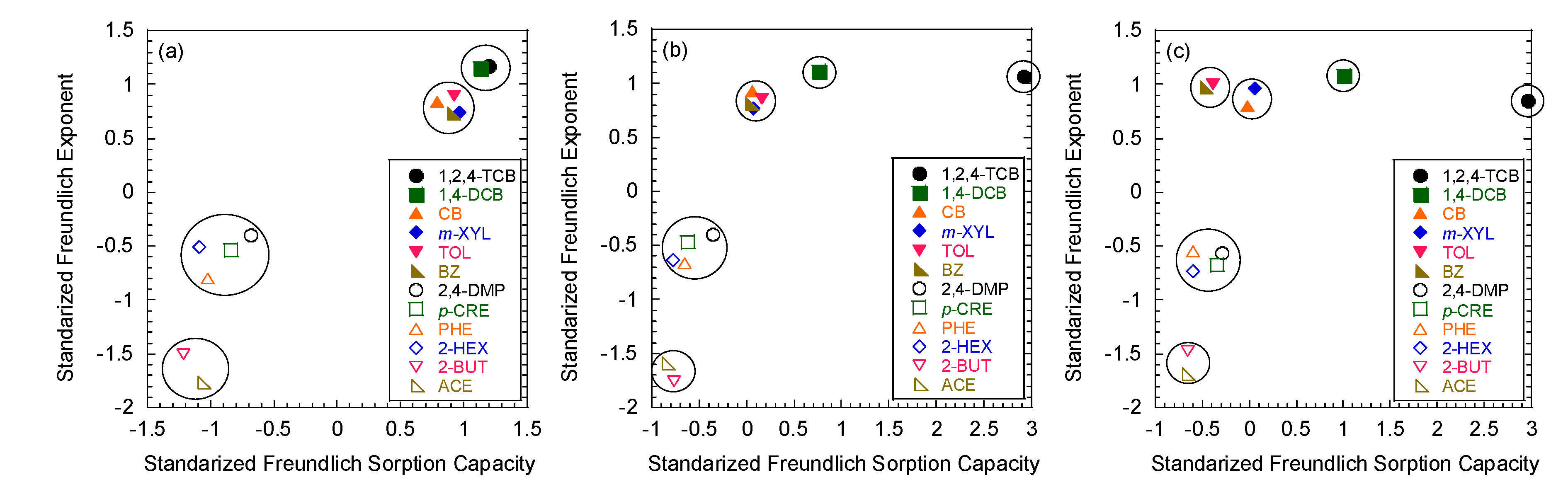
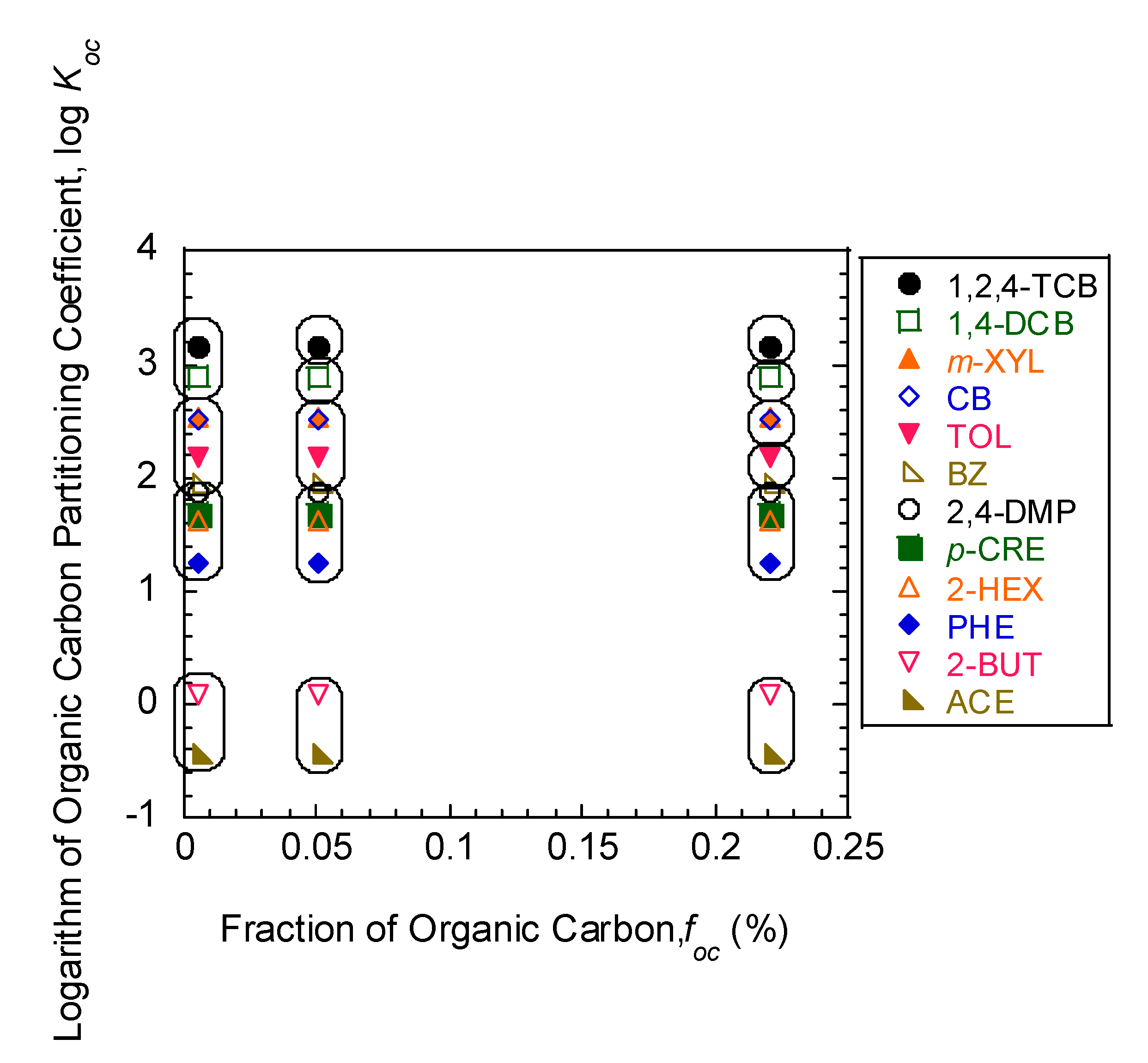
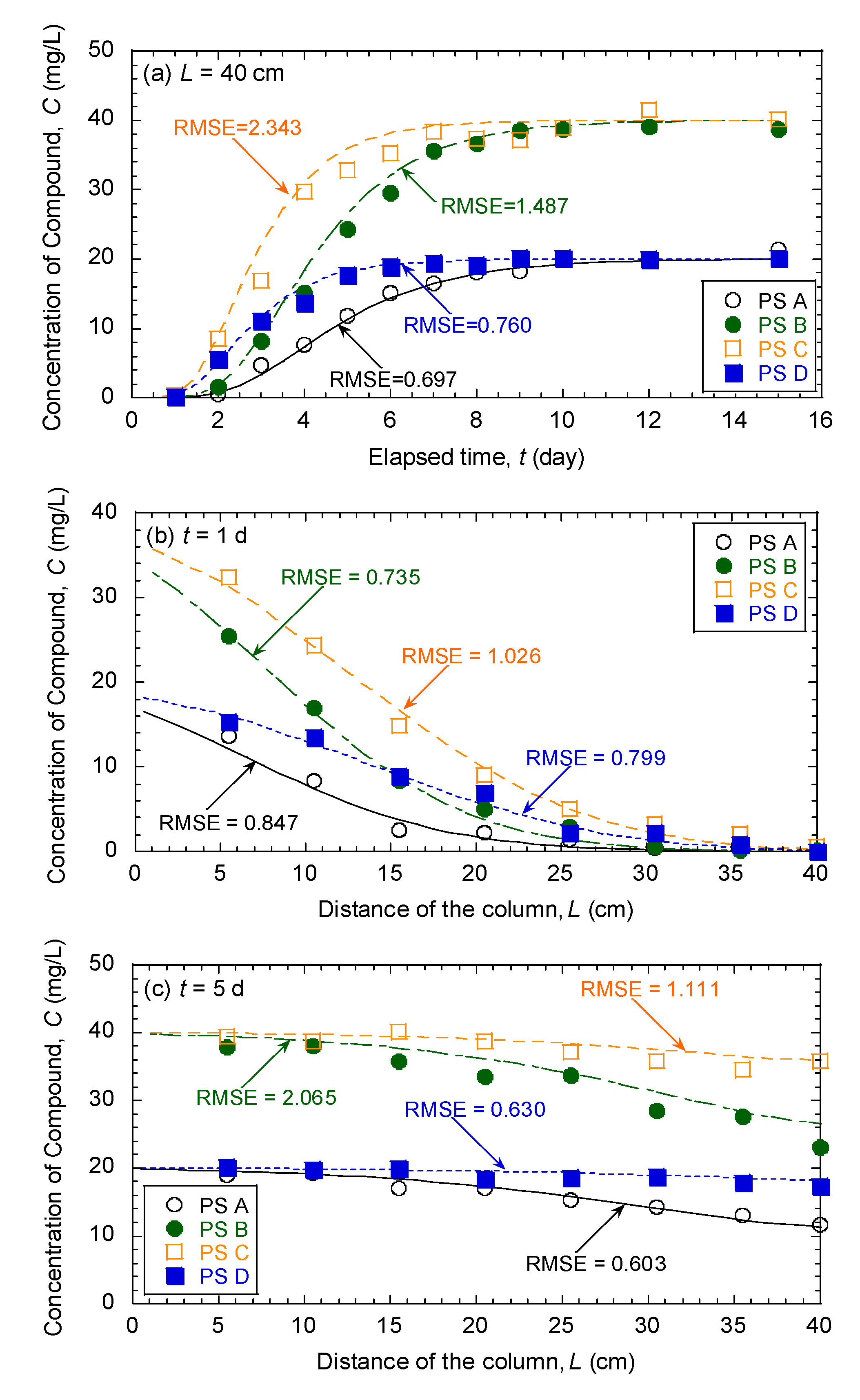
| Model Parameters | Test No. | ||
|---|---|---|---|
| Column 1 | Column 2 | Column 3 | |
| Organic carbon content, foc (%) | 0.006 | 0.051 | 0.221 |
| Hydraulic conductivity, Kh (m/day) | 1.489 | 1.523 | 1.471 |
| Volumetric flow rate, Q (mL/day) | 246.6 | 252.0 | 243.4 |
| Liquid flux, q (m/day) | 0.0641 | 0.0655 | 0.0632 |
| Seepage velocity, vs (m/day) | 0.186 | 0.200 | 0.181 |
| Porosity, n | 0.34 | 0.33 | 0.35 |
| Pore volume, PV (mL) | 562.5 | 532.8 | 570.2 |
| Bulk (dry) density, ρb (mg/m3) | 1.74 | 1.78 | 1.72 |
| Residence time, RT (days) | 2.28 | 2.11 | 2.34 |
| Hydrodynamic dispersion coefficient, Dh (× 10−3 m2/day), from KCl tracer tests | 7.06 | 7.21 | 6.59 |
| Pseudocompound | Components | Mixture | Pseudocompound | Comparison of Parameters | |||||
|---|---|---|---|---|---|---|---|---|---|
| Kf_mix | Nmix | RMSE | Kf,PS | NPS | RMSE | Kf,mix/Kf,PS | Nmix/NPS | ||
| A | 1,2,4-TCB | 0.263 | 0.989 | 0.411 | 0.255 | 0.992 | 0.697 | 1.02 | 0.996 |
| 1,4-DCB | 0.258 | 0.987 | 0.506 | ||||||
| Average | 0.261 | 0.988 | 0.459 | ||||||
| B | CB | 0.232 | 0.951 | 0.546 | 0.249 | 0.938 | 1.48 | 0.963 | 1.01 |
| m-XYL | 0.245 | 0.940 | 0.521 | ||||||
| TOL | 0.242 | 0.958 | 0.639 | ||||||
| BZ | 0.241 | 0.939 | 0.399 | ||||||
| Average | 0.240 | 0.947 | 0.526 | ||||||
| C | 2,4-DMP | 0.121 | 0.808 | 0.623 | 0.111 | 0.779 | 2.34 | 0.937 | 1.02 |
| p-CRE | 0.109 | 0.792 | 0.686 | ||||||
| PHE | 0.095 | 0.762 | 0.502 | ||||||
| 2-HEX | 0.090 | 0.796 | 0.784 | ||||||
| Average | 0.104 | 0.789 | 0.649 | ||||||
| D | 2-BUT | 0.081 | 0.681 | 0.743 | 0.079 | 0.662 | 0.760 | 1.10 | 1.01 |
| ACE | 0.092 | 0.650 | 0.718 | ||||||
| Average | 0.087 | 0.665 | 0.731 | ||||||
| Pseudocompound | Components | Mixture | Pseudocompound | Comparison of Parameters | |||||
|---|---|---|---|---|---|---|---|---|---|
| Kf_mix | Nmix | RMSE | Kf,PS | NPS | RMSE | Kf,mix/Kf,PS | Nmix/NPS | ||
| A | 1,2,4-TCB | 0.933 | 0.985 | 0.561 | 0.933 | 0.985 | 0.561 | 1.00 | 1.00 |
| B | 1,4-DCB | 0.438 | 0.991 | 0.521 | 0.438 | 0.991 | 0.521 | 1.00 | 1.00 |
| C | CB | 0.277 | 0.969 | 0.583 | 0.278 | 0.952 | 2.39 | 1.02 | 1.01 |
| m-XYL | 0.281 | 0.950 | 0.451 | ||||||
| TOL | 0.301 | 0.961 | 0.553 | ||||||
| BZ | 0.272 | 0.955 | 0.619 | ||||||
| Average | 0.283 | 0.959 | 0.552 | ||||||
| C | 2,4-DMP | 0.185 | 0.811 | 0.679 | 0.112 | 0.781 | 2.68 | 1.14 | 1.02 |
| p-CRE | 0.124 | 0.802 | 0.669 | ||||||
| PHE | 0.115 | 0.779 | 0.503 | ||||||
| 2-HEX | 0.088 | 0.783 | 0.663 | ||||||
| Average | 0.128 | 0.794 | 0.629 | ||||||
| D | 2-BUT | 0.089 | 0.649 | 0.703 | 0.091 | 0.648 | 1.17 | 0.89 | 1.02 |
| ACE | 0.073 | 0.668 | 0.758 | ||||||
| Average | 0.081 | 0.659 | 0.731 | ||||||
| Pseudocompound | Components | Mixture | Pseudocompound | Comparison of Parameters | |||||
|---|---|---|---|---|---|---|---|---|---|
| Kf_mix | Nmix | RMSE | Kf, PS | NPS | RMSE | Kf,mix/Kf,PS | Nmix/NPS | ||
| A | 1,2,4-TCB | 3.57 | 0.959 | 0.021 | 3.57 | 0.959 | 0.021 | 1.00 | 1.00 |
| B | 1,4-DCB | 1.75 | 0.983 | 0.151 | 1.75 | 0.983 | 0.151 | 1.00 | 1.00 |
| C | CB | 0.799 | 0.954 | 0.416 | 0.827 | 0.969 | 0.723 | 1.01 | 0.992 |
| m-XYL | 0.874 | 0.971 | 0.552 | ||||||
| Average | 0.836 | 0.962 | 0.484 | ||||||
| D | TOL | 0.458 | 0.975 | 0.563 | 0.428 | 0.971 | 0.424 | 0.978 | 1.01 |
| BZ | 0.379 | 0.972 | 0.452 | ||||||
| Average | 0.419 | 0.974 | 0.508 | ||||||
| E | 2,4-DMP | 0.552 | 0.814 | 0.678 | 0.380 | 0.811 | 1.89 | 1.03 | 0.995 |
| p-CRE | 0.496 | 0.803 | 0.626 | ||||||
| PHE | 0.265 | 0.816 | 0.502 | ||||||
| 2-HEX | 0.259 | 0.797 | 0.476 | ||||||
| Average | 0.393 | 0.807 | 0.571 | ||||||
| F | 2-BUT | 0.211 | 0.721 | 0.669 | 0.210 | 0.705 | 0.994 | 0.976 | 1.01 |
| ACE | 0.199 | 0.699 | 0.785 | ||||||
| Average | 0.205 | 0.710 | 0.727 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joo, J.C.; Moon, H.S.; Chang, S.W. Lumped Approach for Reactive Transport of Organic Compound Mixtures through Simulated Aquifer Sands in Lab-Scale Column Tests. Water 2020, 12, 3103. https://doi.org/10.3390/w12113103
Joo JC, Moon HS, Chang SW. Lumped Approach for Reactive Transport of Organic Compound Mixtures through Simulated Aquifer Sands in Lab-Scale Column Tests. Water. 2020; 12(11):3103. https://doi.org/10.3390/w12113103
Chicago/Turabian StyleJoo, Jin Chul, Hee Sun Moon, and Sun Woo Chang. 2020. "Lumped Approach for Reactive Transport of Organic Compound Mixtures through Simulated Aquifer Sands in Lab-Scale Column Tests" Water 12, no. 11: 3103. https://doi.org/10.3390/w12113103
APA StyleJoo, J. C., Moon, H. S., & Chang, S. W. (2020). Lumped Approach for Reactive Transport of Organic Compound Mixtures through Simulated Aquifer Sands in Lab-Scale Column Tests. Water, 12(11), 3103. https://doi.org/10.3390/w12113103






