Short-Term River Flow Forecasting Framework and Its Application in Cold Climatic Regions
Abstract
:1. Introduction
2. Materials and Methods
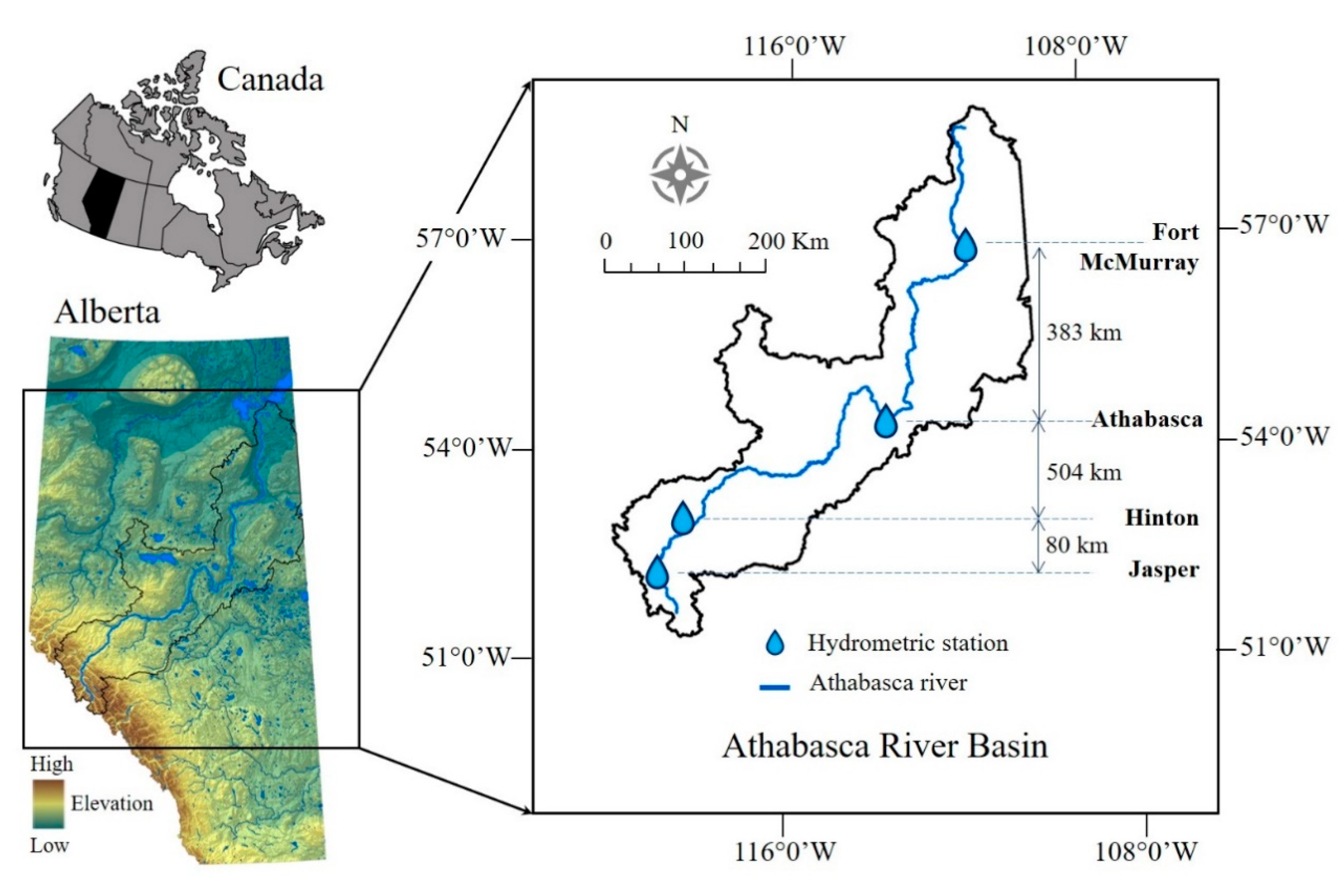
2.1. Study Area
2.2. Methods
2.2.1. Data Selection Approaches
2.2.2. Estimation of Optimal Lead Time
2.2.3. Model Development and Validation
3. Results and Discussion
3.1. Optimal Lead Time
3.2. Calibration and Validation Datasets
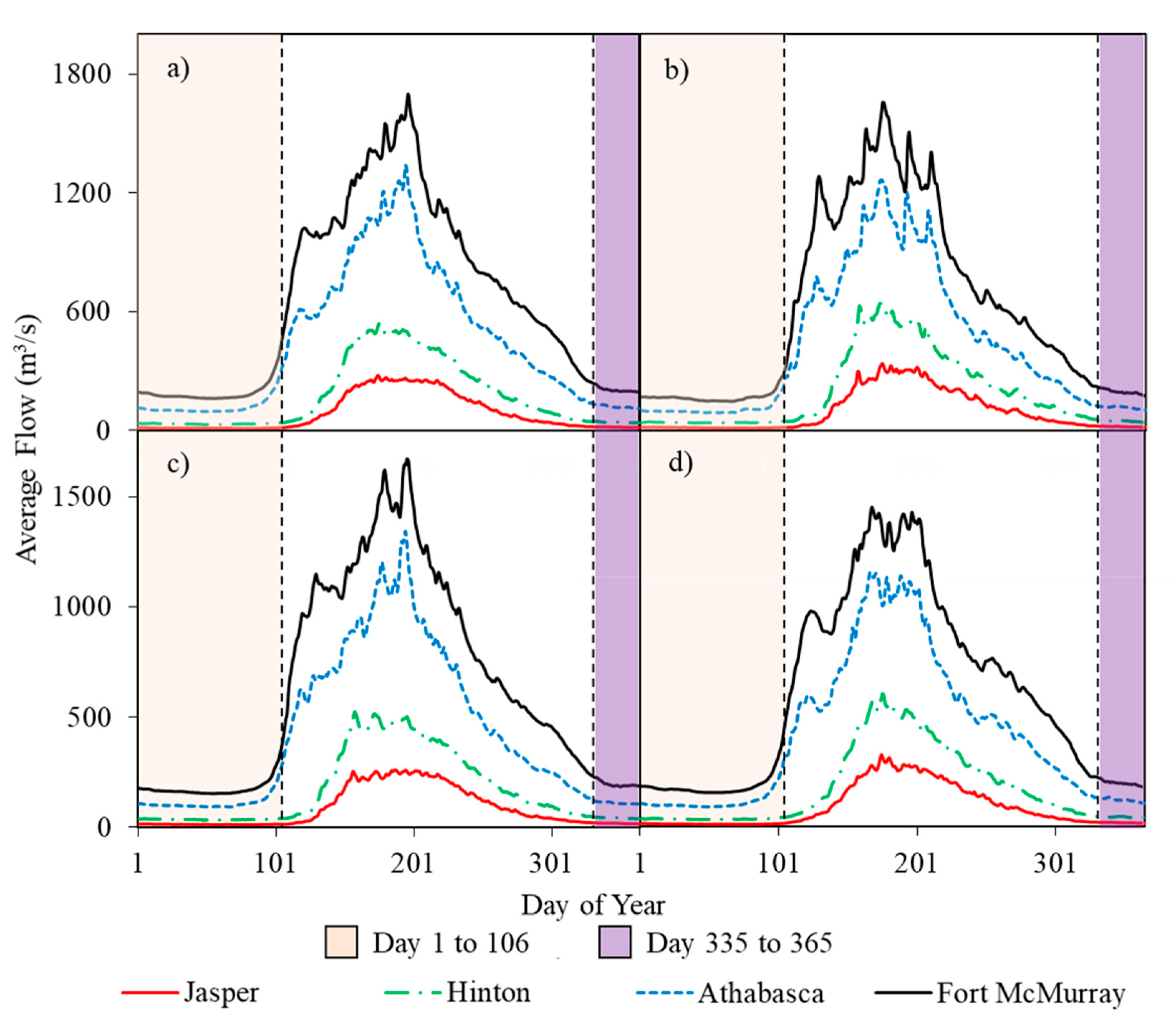
3.3. Base Difference
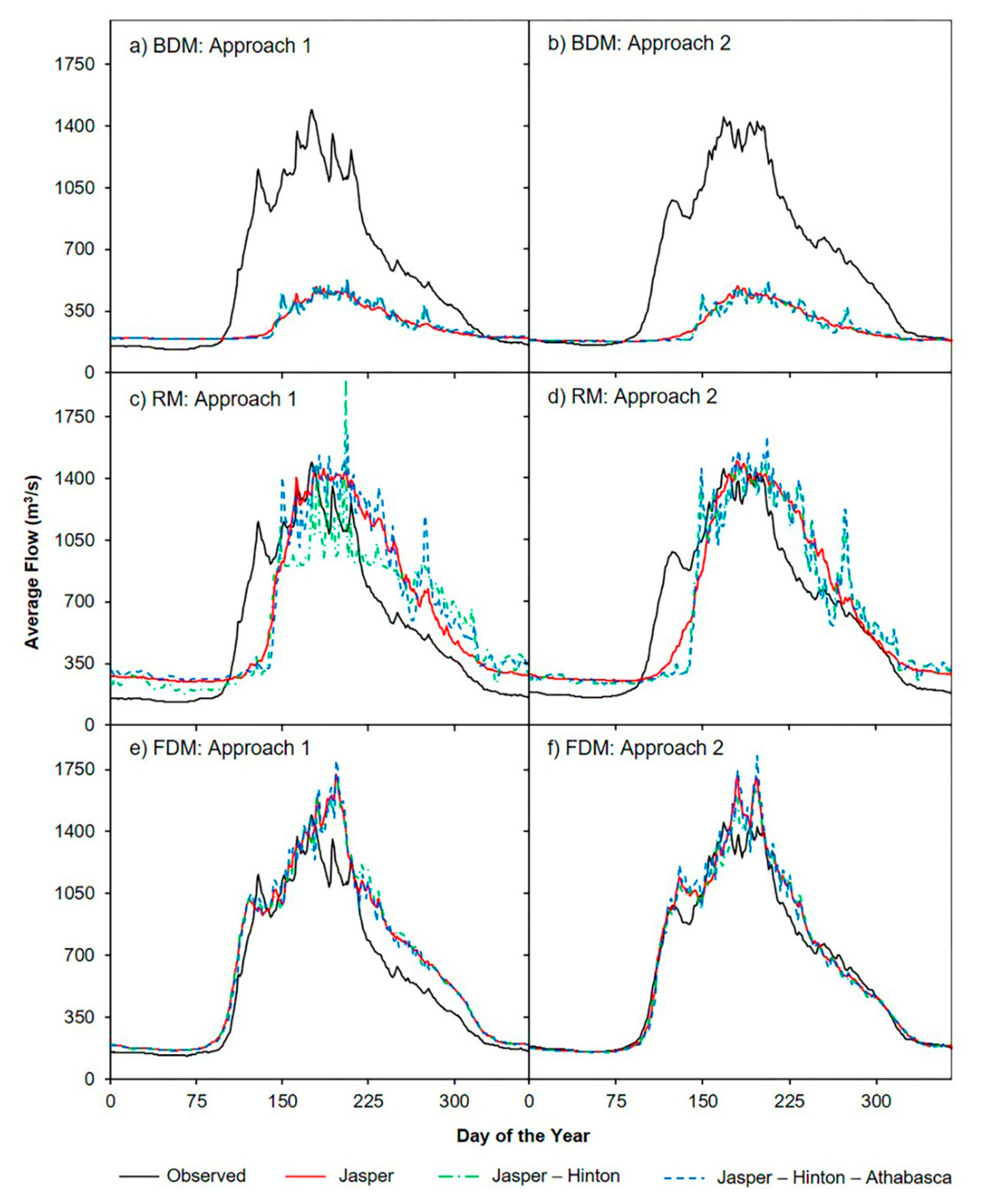
3.4. Performance of Models
3.4.1. BDM
3.4.2. RM
3.4.3. FDM
3.4.4. Graphical Presentation of the Modelled Outputs Using Daily Average Flow
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Renji, R.; Jimson, M. Hydrological Data–Driven Modeling; A Case Study Approach. In Earth Systems Data and Models 1; Springer: Heidelberg, Germany, 2015; ISBN 978-3-319-09235-5. [Google Scholar]
- Belvederesi, C.; Dominic, J.A.; Hassan, Q.K.; Gupta, A.; Achari, G. Predicting River Flow Using an AI-Based Sequential Adaptive Neuro-Fuzzy Inference System. Water 2020, 12, 1622. [Google Scholar] [CrossRef]
- Hayat, H.; Akbar, T.A.; Tahir, A.A.; Hassan, Q.K.; Dewan, A.; Irshad, M. Simulating Current and Future River-Flows in the Karakoram and Himalayan Regions of Pakistan Using Snowmelt-Runoff Model and RCP Scenarios. Water 2019, 11, 761. [Google Scholar] [CrossRef] [Green Version]
- Government of Canada. Historical Climate Data. Available online: https://climate.weather.gc.ca/ (accessed on 23 October 2020).
- Shah, M.I.; Khan, A.; Akbar, T.A.; Hassan, Q.K.; Khan, A.J.; Dewan, A. Predicting Hydrologic Responses to Climate Changes in Highly Glacierized and Mountainous Region Upper Indus Basin. R. Soc. Open Sci. 2020, 7, 191957. [Google Scholar] [CrossRef] [PubMed]
- Bhuiyan, H.A.K.M.; McNairn, H.; Powers, J.; Merzouki, A. Application of HEC-HMS in a Cold Region Watershed and Use of RADARSAT-2 Soil Moisture in Initializing the Model. Hydrology 2017, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Cordeiro, M.R.C.; Wilson, H.F.; Vanrobaeys, J.; Pomeroy, J.W.; Fang, X. Simulating Cold-Region Hydrology in an Intensively Drained Agricultural Watershed in Manitoba, Canada, Using the Cold Regions Hydrological Model. Hydrol. Earth Syst. Sci. 2017, 21, 3483–3506. [Google Scholar] [CrossRef] [Green Version]
- Aygün, O.; Kinnard, C.; Campeau, S. Impacts of Climate Change on the Hydrology of Northern Midlatitude Cold Regions. Prog. Phys. Geogr. Earth Environ. 2020, 44, 338–375. [Google Scholar] [CrossRef]
- Singh, V.P.; Woolhiser, D.A. Mathematical Modeling of Watershed Hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef] [Green Version]
- Hill, D.F.; Bruhis, N.; Calos, S.E.; Arendt, A.; Beamer, J. Spatial and Temporal Variability of Freshwater Discharge into the Gulf of Alaska. J. Geophys. Res. Ocean. 2015, 120, 2. [Google Scholar] [CrossRef]
- Tsakiri, K.G.; Marsellos, A.E.; Zurbenko, I.G. An Efficient Prediction Model for Water Discharge in Schoharie Creek, NY. Int. J. Climatol 2014, 2014, 284137. [Google Scholar] [CrossRef]
- Darwen, P.J. Bayesian Model Averaging for River Flow Prediction. Appl. Intell. 2018, 49, 103–111. [Google Scholar] [CrossRef]
- Delgado-Ramos, F.; Hervas–Gamez, C. Simple and Low–Cost Procedure for Monthly and Yearly Streamflow Forecasts during the Current Hydrological Year. Water 2018, 10, 1038. [Google Scholar] [CrossRef] [Green Version]
- Tourian, M.J.; Schwatke, C.; Sneeuw, N. River Discharge Estimation at Daily Resolution from Satellite Altimetry over an Entire River Basin. J. Hydrol. 2017, 546, 230–247. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H. Ensemble Combination of Seasonal Streamflow Forecasts. J. Hydrol. Eng. 2016, 21, 04015043. [Google Scholar] [CrossRef]
- Spence, C.; Whitfield, P.H.; Pomeroy, J.W.; Pietroniro, A.; Burn, D.H.; Peters, D.L.; St-Hilaire, A. A Review of the Prediction in Ungauged Basins (PUB) Decade in Canada. Can. Water Resour. J. 2013, 38, 253–262. [Google Scholar] [CrossRef]
- Spence, C.; Burn, D.H.; Davison, B.; Hutchinson, D.; Ouarda, T.B.M.J.; St-Hilaire, A.; Weber, F.; Whitfield, P.H. A Canadian Viewpoint on Data, Information and Uncertainty in the Context of Prediction in Ungauged Basins. Hydrol. Res. 2013, 44, 419–429. [Google Scholar] [CrossRef]
- Veiga, V.B.; Hassan, Q.K.; He, J. Development of Flow Forecasting Models in the Bow River at Calgary, Alberta, Canada. Water 2014, 7, 99–115. [Google Scholar] [CrossRef] [Green Version]
- Leong, D.N.S.; Donner, S.D. Climate Change Impacts on Streamflow Availability for the Athabasca Oil Sands. Clim. Chang. 2015, 133, 651–663. [Google Scholar] [CrossRef]
- Hwang, H.T.; Park, Y.J.; Sudicky, E.A.; Berg, S.J.; McLaughlin, R.; Jones, J.P. Understanding the Water Balance Paradox in the Athabasca River Basin, Canada. Hydrol. Process. 2018, 32, 729–746. [Google Scholar] [CrossRef]
- Sauchyn, D.J.; St-Jacques, J.M.; Luckman, B.H. Long-Term Reliability of the Athabasca River (Alberta, Canada) as the Water Source for Oil Sands Mining. Proc. Natl. Acad. Sci. USA 2015, 112, 12621–12626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Athabasca River Basin Research Institute, Athabasca University: About the Athabasca River Basin. Available online: http://arbri.athabascau.ca/About-the-Athabasca-River-basin/Index.php (accessed on 23 October 2020).
- Regional Aquatics Monitoring Program (RAMP). Overview of Athabasca River Basin Landscape. Available online: http://www.ramp-alberta.org/river/geography/basin+landscape.aspx (accessed on 23 October 2020).
- Government of Canada. Water Survey of Canada. Available online: https://www.canada.ca/en/environment-climate-change/services/water-overview/quantity/monitoring/survey.html (accessed on 23 October 2020).
- Rood, S.B.; Stupple, G.W.; Gill, K.M. Century-Long Records Reveal Slight, Ecoregion-Localized Changes in Athabasca River Flows. Hydrol. Process. 2014, 29, 805–816. [Google Scholar] [CrossRef]
- Khazaee Poul, A.; Shourian, M.; Ebrahimi, H. A Comparative Study of MLR, KNN, ANN and ANFIS Models with Wavelet Transform in Monthly Stream Flow Prediction. Water Resour. Manag. 2019, 33, 2907–2923. [Google Scholar] [CrossRef]
- Moradi, A.M.; Dariane, A.B.; Yang, G.; Block, P. Long-Range Reservoir Inflow Forecasts Using Large-Scale Climate Predictors. Int. J. Climatol. 2020, 2020, 1–22. [Google Scholar] [CrossRef]
- Zheng, F.; Maier, H.R.; Wu, W.; Dandy, G.C.; Gupta, H.V.; Zhang, T. On Lack of Robustness in Hydrological Model Development Due to Absence of Guidelines for Selecting Calibration and Evaluation Data: Demonstration for Data–Driven Models. Water Resour. Manag. 2018, 54, 1013–1030. [Google Scholar] [CrossRef]
- Toth, B.; Pietroniro, A.; Conly, F.M.; Kouwen, N. Modelling Climate Change Impacts in the Peace and Athabasca Catchment and Delta: Hydrological Model Application. Hydrol. Process. 2006, 20, 4197–4214. [Google Scholar] [CrossRef]
- Muhammad, A.; Stadnyk, T.A.; Unduche, F.; Coulibaly, P. Multi-Model Approaches for Improving Seasonal Ensemble Streamflow Prediction Scheme with Various Statistical Post-Processing Techniques in the Canadian Prairie Region. Water 2018, 10, 1604. [Google Scholar] [CrossRef] [Green Version]
- Unduche, F.; Tolossa, H.; Senbeta, D.; Zhu, E. Evaluation of Four Hydrological Models for Operational Flood Forecasting in a Canadian Prairie Watershed. Hydrol. Sci. J. 2018, 63, 1133–1149. [Google Scholar] [CrossRef] [Green Version]
- Awol, F.S.; Coulibaly, P.; Tsanis, I.; Unduche, F. Identification of Hydrological Models for Enhanced Ensemble Reservoir Inflow Forecasting in a Large Complex Prairie Watershed. Water 2019, 11, 2201. [Google Scholar] [CrossRef] [Green Version]
- Bomhof, J.; Tolson, B.A.; Kouwen, N. Comparing Single and Multi–Objective Hydrologic Model Calibration Considering Reservoir Inflow and Streamflow Observations. Can. Water Resour. J. 2019, 44, 319–336. [Google Scholar] [CrossRef]
- Stadnyk, T.A.; Holmes, T.L. On the Value of Isotope–Enabled Hydrological Model Calibration. Hydrol. Sci. J. 2020, 65, 1525–1538. [Google Scholar] [CrossRef]
- Eum, H.-I.; Yonas, D.; Prowse, T. Uncertainty in Modelling the Hydrologic Responses of a Large Watershed: A Case Study of the Athabasca River Basin, Canada. Hydrol. Process. 2014, 28, 4272–4293. [Google Scholar] [CrossRef]
- Eum, H.-I.; Dibike, Y.; Prowse, T. Climate-Induced Alteration of Hydrologic Indicators in the Athabasca River Basin, Alberta, Canada. J. Hydrol. 2017, 544, 327–342. [Google Scholar] [CrossRef]
- Droppo, I.; Prowse, T.; Bonsal, B.; Dibike, Y.; Beltaos, S.; Krishnappan, B.; Eum, H.; Kashyap, S.; Shakibaeinia, A.; Gupta, A. Regional Hydroclimatic and Sediment Modeling: Oil Sands Monitoring Program; Technical Report Series; Government of Alberta: Edmonton, AB, Canada, 2018; ISBN 978-1-4601-4030-7. [Google Scholar]
- Golmohammadi, G.; Rudra, R.; Dickinson, T.; Goel, P.; Veliz, M. Predicting the Temporal Variation of Flow Contributing Areas using SWAT. J. Hydrol. 2017, 547, 375–386. [Google Scholar] [CrossRef]
- Chilkoti, V.; Bolisetti, T.; Balachandar, R. Multi–Objective Autocalibration of SWAT Model for Improved Low Flow Performance for a Small Snowfed Catchment. Hydrol. Sci. J. 2018, 63, 1482–1501. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; Lee, S.; Moglen, G.E.; Sadeghi, A.M.; McCarty, G.W. A Coupled Surface Water Storage and Subsurface Water Dynamics Model in SWAT for Characterizing Hydroperiod of Geographically Isolated Wetlands. Adv. Water Resour. 2019, 131, 131. [Google Scholar] [CrossRef]
- Muhammad, A.; Evenson, G.R.; Stadnyk, T.A.; Boluwade, A.; Jha, S.K.; Coulibaly, P. Impact of Model Structure on the Accuracy of Hydrological Modeling of a Canadian Prairie Watershed. J. Hydrol. Reg. Stud. 2019, 21, 40–56. [Google Scholar] [CrossRef]
- Shrestha, N.; Du, X.; Wang, J. Assessing Climate Change Impacts on Freshwater Resources of the Athabasca River Basin, Canada. Sci. Total Environ. 2017, 601, 425–440. [Google Scholar] [CrossRef]
| Approach 1: Calibration 1971–2000 | |||||||||
| Validation Year | Jasper | Jasper–Hinton | Jasper–Hinton–Athabasca | ||||||
| r2 | ENS | RMSE (m3/s) | r2 | ENS | RMSE (m3/s) | r2 | ENS | RMSE (m3/s) | |
| 2001 | 0.65 | 0.13 | 447.75 | 0.63 | 0.12 | 448.86 | 0.64 | 0.17 | 448.29 |
| 2002 | 0.70 | 0.45 | 198.64 | 0.69 | 0.43 | 199.94 | 0.71 | 0.62 | 198.27 |
| 2003 | 0.55 | 0.03 | 389.67 | 0.53 | 0.01 | 390.60 | 0.50 | 0.04 | 392.50 |
| 2004 | 0.61 | −0.12 | 473.99 | 0.61 | −0.16 | 475.21 | 0.62 | −0.19 | 481.81 |
| 2005 | 0.63 | −0.45 | 609.03 | 0.61 | −0.49 | 610.26 | 0.61 | −0.37 | 610.39 |
| 2006 | 0.62 | −0.02 | 293.85 | 0.61 | −0.04 | 295.13 | 0.63 | 0.06 | 294.09 |
| 2007 | 0.18 | −0.25 | 635.44 | 0.20 | −0.21 | 632.02 | 0.19 | −0.19 | 632.64 |
| 2008 | 0.50 | −0.08 | 437.71 | 0.47 | −0.09 | 439.73 | 0.46 | −0.09 | 440.28 |
| 2009 | 0.56 | 0.01 | 360.44 | 0.54 | −0.01 | 362.63 | 0.54 | 0.05 | 362.99 |
| 2010 | 0.67 | −0.01 | 303.83 | 0.66 | −0.02 | 304.79 | 0.67 | 0.08 | 304.12 |
| 2011 | 0.67 | −0.07 | 815.15 | 0.67 | −0.09 | 816.07 | 0.65 | −0.06 | 817.40 |
| 2012 | 0.77 | 0.03 | 614.94 | 0.76 | 0.01 | 616.78 | 0.76 | 0.04 | 616.85 |
| 2013 | 0.56 | −0.15 | 797.72 | 0.55 | −0.17 | 799.32 | 0.52 | −0.12 | 801.22 |
| 2014 | 0.41 | −0.17 | 536.61 | 0.40 | −0.18 | 537.44 | 0.40 | −0.18 | 538.03 |
| Average | 0.73 | −0.12 | 438.93 | 0.67 | −0.11 | 438.60 | 0.72 | −0.12 | 439.66 |
| Approach 2: Calibration 1971–2014 Odd Years | |||||||||
| 1972 | 0.55 | −0.25 | 733.39 | 0.52 | −0.29 | 733.39 | 0.51 | −0.25 | 733.79 |
| 1974 | 0.33 | −0.50 | 874.04 | 0.29 | −0.53 | 879.02 | 0.28 | −0.34 | 880.00 |
| 1976 | 0.69 | −0.41 | 571.68 | 0.65 | −0.46 | 578.18 | 0.66 | −0.42 | 577.66 |
| 1978 | 0.57 | −0.55 | 681.00 | 0.57 | −0.59 | 686.66 | 0.58 | −0.45 | 686.37 |
| 1980 | 0.56 | −0.50 | 690.25 | 0.52 | −0.52 | 694.33 | 0.51 | −0.46 | 694.52 |
| 1982 | 0.59 | −0.15 | 641.82 | 0.57 | −0.17 | 646.87 | 0.58 | −0.17 | 546.21 |
| 1984 | 0.50 | −0.36 | 495.29 | 0.47 | −0.40 | 498.19 | 0.47 | −0.40 | 498.73 |
| 1986 | 0.48 | −0.26 | 717.74 | 0.65 | −0.29 | 478.10 | 0.47 | −0.25 | 714.37 |
| 1988 | 0.64 | −0.05 | 439.78 | 0.39 | −0.39 | 743.35 | 0.68 | 0.08 | 429.28 |
| 1990 | 0.54 | −0.25 | 717.41 | 0.75 | 0.16 | 390.92 | 0.45 | −0.24 | 722.17 |
| 1992 | 0.59 | −0.10 | 330.87 | 0.64 | −0.32 | 733.92 | 0.57 | 0.02 | 332.00 |
| 1994 | 0.65 | −0.16 | 531.54 | 0.57 | −0.15 | 331.73 | 0.65 | −0.17 | 532.33 |
| 1996 | 0.66 | −0.50 | 834.21 | 0.64 | −0.15 | 527.70 | 0.65 | −0.37 | 830.58 |
| 1998 | 0.64 | −0.24 | 377.45 | 0.68 | −0.55 | 839.42 | 0.64 | −0.14 | 378.95 |
| 2000 | 0.84 | 0.11 | 377.91 | 0.83 | 0.09 | 380.63 | 0.84 | 0.21 | 380.20 |
| 2002 | 0.70 | 0.39 | 205.06 | 0.69 | 0.38 | 207.96 | 0.71 | 0.67 | 206.35 |
| 2004 | 0.61 | −0.23 | 487.55 | 0.61 | −0.21 | 485.62 | 0.62 | −0.24 | 492.15 |
| 2006 | 0.63 | −0.10 | 300.93 | 0.55 | −0.12 | 305.78 | 0.63 | 0.13 | 304.77 |
| 2008 | 0.50 | −0.15 | 450.40 | 0.47 | −0.14 | 449.03 | 0.46 | −0.08 | 449.57 |
| 2010 | 0.65 | −0.10 | 315.97 | 0.66 | −0.09 | 315.03 | 0.67 | 0.15 | 314.38 |
| 2012 | 0.77 | −0.01 | 624.71 | 0.76 | −0.02 | 626.37 | 0.76 | −0.01 | 626.43 |
| 2014 | 0.43 | −0.25 | 541.72 | 0.40 | −0.22 | 546.85 | 0.40 | −0.22 | 547.44 |
| Average | 0.78 | –0.34 | 491.71 | 0.71 | –0.36 | 495.35 | 0.77 | –0.34 | 492.27 |
| Approach 1: Calibration 1971–2000 | |||||||||
| Validation Year | Jasper | Jasper–Hinton | Jasper–Hinton–Athabasca | ||||||
| r2 | ENS | RMSE (m3/s) | r2 | ENS | RMSE (m3/s) | r2 | ENS | RMSE (m3/s) | |
| 2001 | 0.58 | 0.54 | 282.58 | 0.63 | 0.52 | 332.95 | 0.61 | 0.50 | 337.74 |
| 2002 | 0.73 | −0.48 | 321.38 | 0.72 | 0.56 | 330.16 | 0.76 | −0.75 | 349.23 |
| 2003 | 0.52 | 0.25 | 340.25 | 0.57 | 0.46 | 289.38 | 0.51 | 0.22 | 346.98 |
| 2004 | 0.63 | 0.56 | 291.86 | 0.64 | 0.63 | 269.05 | 0.63 | 0.57 | 290.63 |
| 2005 | 0.65 | 0.64 | 299.20 | 0.66 | 0.65 | 295.45 | 0.65 | 0.64 | 300.77 |
| 2006 | 0.61 | −0.12 | 305.64 | 0.58 | 0.31 | 239.43 | 0.62 | −0.06 | 297.88 |
| 2007 | 0.19 | 0.09 | 549.71 | 0.20 | 0.11 | 542.72 | 0.20 | 0.09 | 548.31 |
| 2008 | 0.51 | 0.38 | 331.34 | 0.52 | 0.38 | 330.42 | 0.49 | 0.36 | 337.84 |
| 2009 | 0.54 | 0.29 | 303.89 | 0.50 | 0.43 | 271.95 | 0.53 | 0.27 | 308.34 |
| 2010 | 0.71 | 0.24 | 263.40 | 0.76 | 0.59 | 193.33 | 0.73 | 0.27 | 257.11 |
| 2011 | 0.67 | 0.60 | 496.65 | 0.66 | 0.59 | 500.53 | 0.66 | 0.58 | 533.80 |
| 2012 | 0.76 | 0.75 | 310.37 | 0.62 | 0.60 | 390.17 | 0.78 | 0.77 | 298.78 |
| 2013 | 0.55 | 0.54 | 499.00 | 0.57 | 0.55 | 495.93 | 0.54 | 0.53 | 508.34 |
| 2014 | 0.41 | 0.33 | 404.73 | 0.46 | 0.37 | 392.85 | 0.39 | 0.32 | 407.20 |
| Average | 0.73 | 0.66 | 241.46 | 0.61 | 0.60 | 264.09 | 0.72 | 0.65 | 246.11 |
| Approach 2: Calibration 1971–2014 Odd Years | |||||||||
| 1972 | 0.52 | 0.48 | 466.37 | 0.50 | 0.47 | 467.30 | 0.50 | 0.49 | 463.04 |
| 1974 | 0.32 | 0.22 | 628.63 | 0.34 | 0.23 | 624.31 | 0.32 | 0.22 | 627.27 |
| 1976 | 0.69 | 0.68 | 271.33 | 0.68 | 0.67 | 276.16 | 0.69 | 0.67 | 273.60 |
| 1978 | 0.64 | 0.59 | 347.51 | 0.63 | 0.59 | 349.21 | 0.63 | 0.59 | 349.06 |
| 1980 | 0.55 | 0.53 | 387.80 | 0.55 | 0.53 | 387.29 | 0.54 | 0.53 | 387.85 |
| 1982 | 0.59 | 0.59 | 382.23 | 0.59 | 0.58 | 385.22 | 0.60 | 0.59 | 380.85 |
| 1984 | 0.52 | 0.43 | 317.47 | 0.54 | 0.46 | 310.19 | 0.52 | 0.39 | 330.25 |
| 1986 | 0.52 | 0.50 | 447.43 | 0.46 | 0.43 | 475.66 | 0.54 | 0.49 | 451.54 |
| 1988 | 0.68 | 0.57 | 279.71 | 0.74 | 0.50 | 301.00 | 0.69 | 0.59 | 273.01 |
| 1990 | 0.53 | 0.52 | 443.84 | 0.54 | 0.53 | 439.59 | 0.52 | 0.51 | 447.28 |
| 1992 | 0.60 | 0.02 | 306.60 | 0.61 | 0.04 | 303.08 | 0.60 | −0.05 | 317.33 |
| 1994 | 0.67 | 0.66 | 287.22 | 0.67 | 0.66 | 287.25 | 0.67 | 0.65 | 289.70 |
| 1996 | 0.72 | 0.57 | 443.82 | 0.72 | 0.56 | 445.74 | 0.66 | 0.62 | 416.11 |
| 1998 | 0.65 | 0.39 | 267.38 | 0.66 | 0.40 | 265.24 | 0.64 | 0.34 | 276.99 |
| 2000 | 0.85 | 0.75 | 201.06 | 0.84 | 0.74 | 203.14 | 0.86 | 0.74 | 203.92 |
| 2002 | 0.73 | −0.48 | 321.38 | 0.72 | −0.47 | 320.66 | 0.75 | −0.86 | 359.98 |
| 2004 | 0.63 | 0.56 | 291.86 | 0.63 | 0.57 | 288.02 | 0.62 | 0.54 | 299.02 |
| 2006 | 0.56 | 0.45 | 310.85 | 0.59 | −0.13 | 307.54 | 0.62 | −0.13 | 307.17 |
| 2008 | 0.51 | 0.38 | 331.34 | 0.52 | 0.40 | 326.50 | 0.49 | 0.34 | 342.97 |
| 2010 | 0.71 | 0.24 | 263.40 | 0.70 | 0.23 | 264.10 | 0.71 | 0.23 | 264.36 |
| 2012 | 0.76 | 0.75 | 310.37 | 0.77 | 0.76 | 306.77 | 0.78 | 0.78 | 293.81 |
| 2014 | 0.41 | 0.33 | 404.73 | 0.42 | 0.35 | 400.31 | 0.40 | 0.31 | 411.77 |
| Average | 0.80 | 0.78 | 198.99 | 0.74 | 0.70 | 231.82 | 0.79 | 0.76 | 208.17 |
| Approach 1: Calibration 1971–2000 | |||||||||
| Validation Year | Jasper | Jasper–Hinton | Jasper–Hinton–Athabasca | ||||||
| r2 | ENS | RMSE (m3/s) | r2 | ENS | RMSE (m3/s) | r2 | ENS | RMSE (m3/s) | |
| 2001 | 0.92 | 0.83 | 180.79 | 0.92 | 0.85 | 159.70 | 0.96 | 0.89 | 155.94 |
| 2002 | 0.90 | 0.86 | 173.75 | 0.89 | 0.82 | 174.21 | 0.90 | 0.45 | 195.59 |
| 2003 | 0.93 | 0.89 | 156.34 | 0.92 | 0.87 | 147.38 | 0.94 | 0.89 | 131.68 |
| 2004 | 0.90 | 0.84 | 160.88 | 0.93 | 0.75 | 190.20 | 0.93 | 0.90 | 139.71 |
| 2005 | 0.91 | 0.83 | 172.80 | 0.94 | 0.83 | 180.50 | 0.94 | 0.94 | 117.99 |
| 2006 | 0.91 | 0.80 | 179.77 | 0.91 | 0.89 | 149.73 | 0.88 | 0.79 | 133.23 |
| 2007 | 0.92 | 0.89 | 157.88 | 0.85 | 0.81 | 193.30 | 0.92 | 0.91 | 171.36 |
| 2008 | 0.92 | 0.81 | 173.20 | 0.89 | 0.91 | 166.09 | 0.93 | 0.90 | 130.85 |
| 2009 | 0.95 | 0.85 | 161.45 | 0.91 | 0.93 | 156.77 | 0.95 | 0.92 | 104.36 |
| 2010 | 0.94 | 0.86 | 167.83 | 0.93 | 0.85 | 184.61 | 0.94 | 0.93 | 80.92 |
| 2011 | 0.92 | 0.84 | 165.26 | 0.91 | 0.85 | 186.42 | 0.98 | 0.97 | 138.95 |
| 2012 | 0.90 | 0.93 | 138.31 | 0.83 | 0.73 | 232.24 | 0.96 | 0.95 | 139.01 |
| 2013 | 0.92 | 0.90 | 141.47 | 0.89 | 0.80 | 183.30 | 0.89 | 0.81 | 323.77 |
| 2014 | 0.93 | 0.89 | 155.02 | 0.92 | 0.89 | 161.15 | 0.92 | 0.91 | 146.59 |
| Average | 0.94 | 0.86 | 156.51 | 0.95 | 0.86 | 153.44 | 0.94 | 0.86 | 157.58 |
| Approach 2: Calibration 1971–2014 Odd Years | |||||||||
| 1972 | 0.88 | 0.89 | 117.78 | 0.92 | 0.91 | 124.05 | 0.94 | 0.94 | 153.37 |
| 1974 | 0.90 | 0.93 | 112.71 | 0.86 | 0.87 | 144.98 | 0.97 | 0.95 | 151.59 |
| 1976 | 0.95 | 0.96 | 90.58 | 0.92 | 0.91 | 125.10 | 0.85 | 0.83 | 194.39 |
| 1978 | 0.92 | 0.94 | 107.69 | 0.95 | 0.95 | 105.04 | 0.91 | 0.90 | 168.71 |
| 1980 | 0.91 | 0.84 | 118.41 | 0.96 | 0.96 | 95.07 | 0.92 | 0.91 | 173.15 |
| 1982 | 0.96 | 0.90 | 104.19 | 0.88 | 0.88 | 142.40 | 0.96 | 0.95 | 128.82 |
| 1984 | 0.95 | 0.92 | 103.75 | 0.92 | 0.90 | 122.82 | 0.88 | 0.88 | 147.67 |
| 1986 | 0.85 | 0.78 | 124.36 | 0.91 | 0.89 | 118.76 | 0.97 | 0.97 | 111.39 |
| 1988 | 0.92 | 0.85 | 114.04 | 0.95 | 0.97 | 97.63 | 0.95 | 0.94 | 105.82 |
| 1990 | 0.97 | 0.97 | 88.16 | 0.90 | 0.90 | 130.73 | 0.93 | 0.92 | 181.80 |
| 1992 | 0.87 | 0.92 | 113.43 | 0.94 | 0.94 | 108.53 | 0.92 | 0.89 | 102.80 |
| 1994 | 0.95 | 0.94 | 98.90 | 0.92 | 0.91 | 125.27 | 0.97 | 0.95 | 105.94 |
| 1996 | 0.95 | 0.91 | 102.93 | 0.95 | 0.95 | 105.96 | 0.93 | 0.91 | 203.46 |
| 1998 | 0.94 | 0.93 | 105.23 | 0.93 | 0.90 | 122.55 | 0.87 | 0.81 | 150.29 |
| 2000 | 0.91 | 0.89 | 110.78 | 0.90 | 0.92 | 113.48 | 0.94 | 0.86 | 150.25 |
| 2002 | 0.93 | 0.85 | 115.25 | 0.88 | 0.88 | 137.21 | 0.91 | 0.45 | 195.34 |
| 2004 | 0.90 | 0.92 | 103.50 | 0.86 | 0.85 | 145.10 | 0.93 | 0.90 | 138.85 |
| 2006 | 0.88 | 0.88 | 113.54 | 0.95 | 0.97 | 98.70 | 0.88 | 0.79 | 133.61 |
| 2008 | 0.92 | 0.91 | 106.37 | 0.93 | 0.94 | 109.94 | 0.93 | 0.91 | 128.56 |
| 2010 | 0.86 | 0.89 | 114.30 | 0.92 | 0.92 | 127.24 | 0.93 | 0.91 | 88.44 |
| 2012 | 0.95 | 0.94 | 97.18 | 0.91 | 0.90 | 119.52 | 0.96 | 0.95 | 135.95 |
| 2014 | 0.93 | 0.92 | 102.10 | 0.90 | 0.89 | 118.98 | 0.93 | 0.93 | 133.48 |
| Average | 0.97 | 0.95 | 90.98 | 0.97 | 0.97 | 83.40 | 0.97 | 0.95 | 99.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belvederesi, C.; Dominic, J.A.; Hassan, Q.K.; Gupta, A.; Achari, G. Short-Term River Flow Forecasting Framework and Its Application in Cold Climatic Regions. Water 2020, 12, 3049. https://doi.org/10.3390/w12113049
Belvederesi C, Dominic JA, Hassan QK, Gupta A, Achari G. Short-Term River Flow Forecasting Framework and Its Application in Cold Climatic Regions. Water. 2020; 12(11):3049. https://doi.org/10.3390/w12113049
Chicago/Turabian StyleBelvederesi, Chiara, John Albino Dominic, Quazi K. Hassan, Anil Gupta, and Gopal Achari. 2020. "Short-Term River Flow Forecasting Framework and Its Application in Cold Climatic Regions" Water 12, no. 11: 3049. https://doi.org/10.3390/w12113049
APA StyleBelvederesi, C., Dominic, J. A., Hassan, Q. K., Gupta, A., & Achari, G. (2020). Short-Term River Flow Forecasting Framework and Its Application in Cold Climatic Regions. Water, 12(11), 3049. https://doi.org/10.3390/w12113049






