The Influence of Regional Freeze–Thaw Cycles on Loess Landslides: Analysis of Strength Deterioration of Loess with Changes in Pore Structure
Abstract
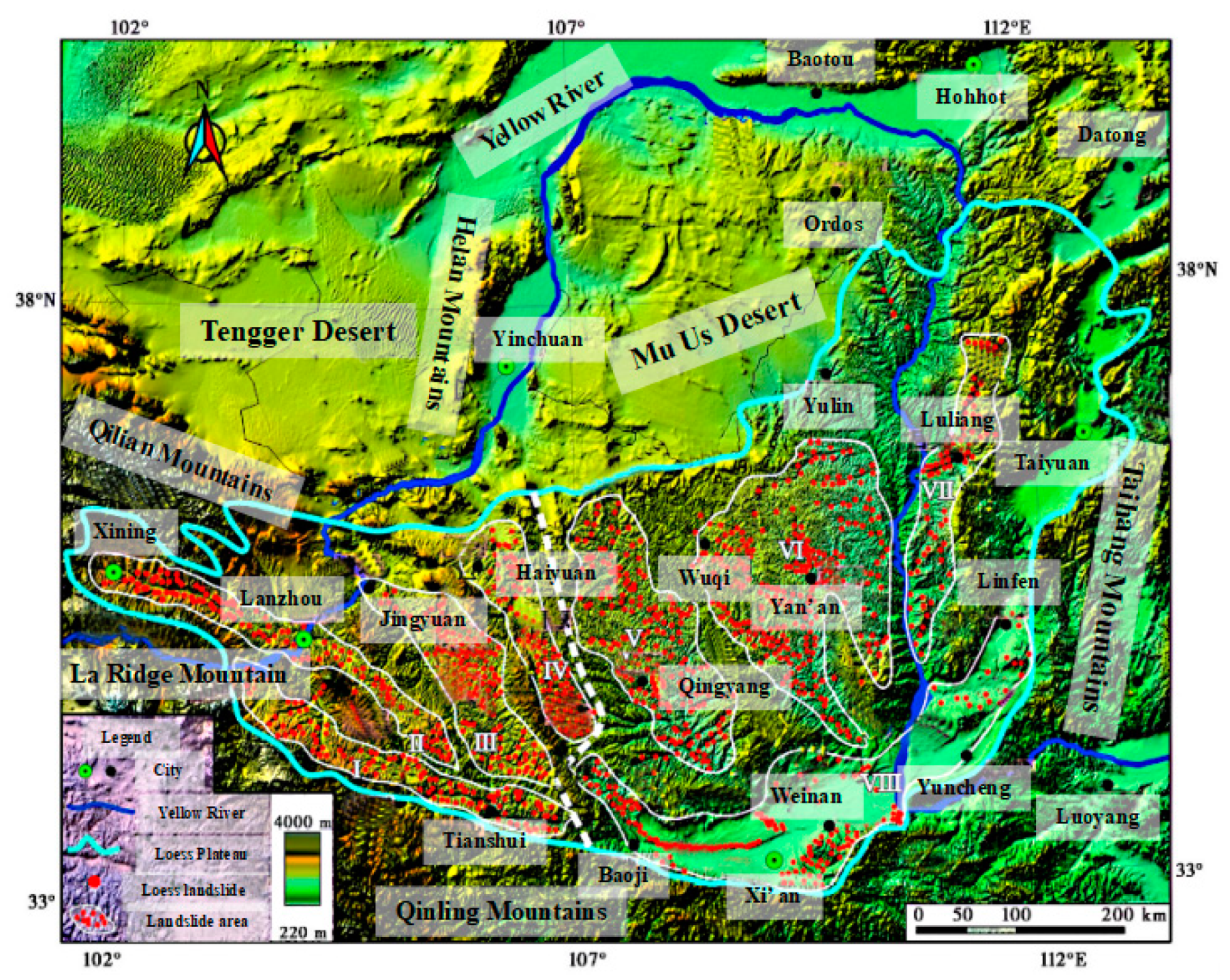
1. Introduction
2. Test Scheme
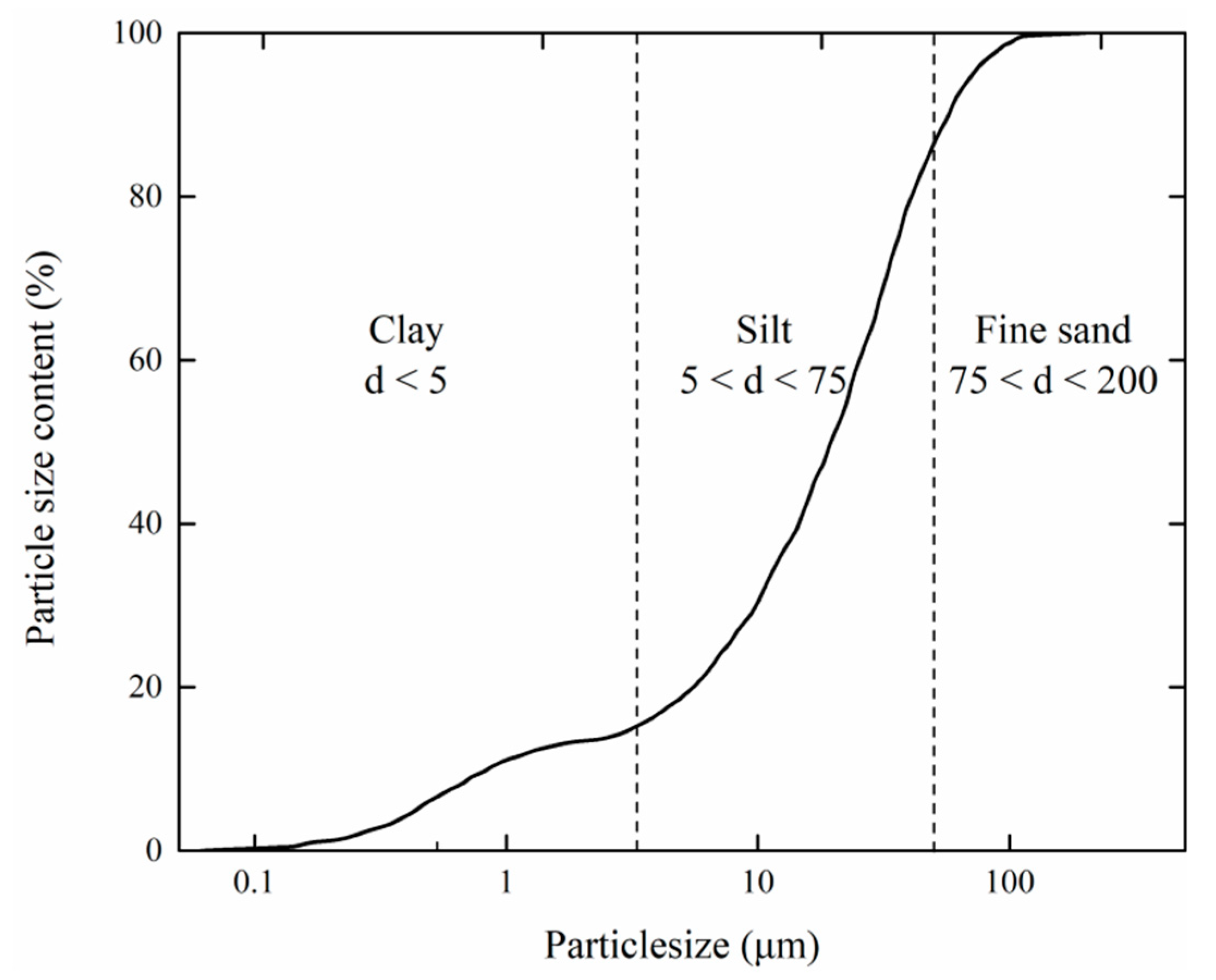
2.1. Materials and Methods
2.2. Freeze–Thaw Cycle Tests
2.3. SEM
2.4. Nuclear Magnetic Resonance Tests
2.5. Triaxial Compression Tests
3. Test Results
3.1. SEM Results
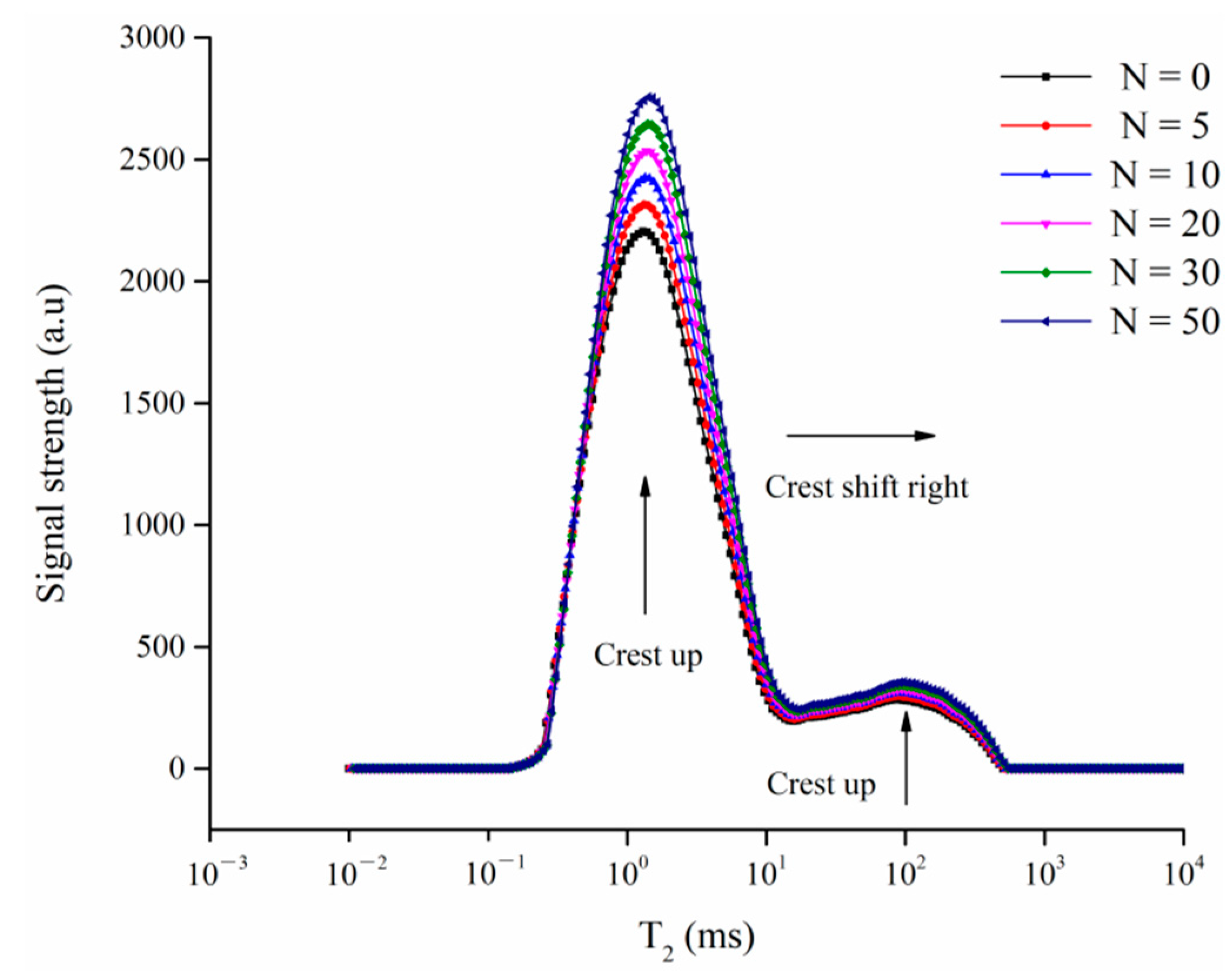
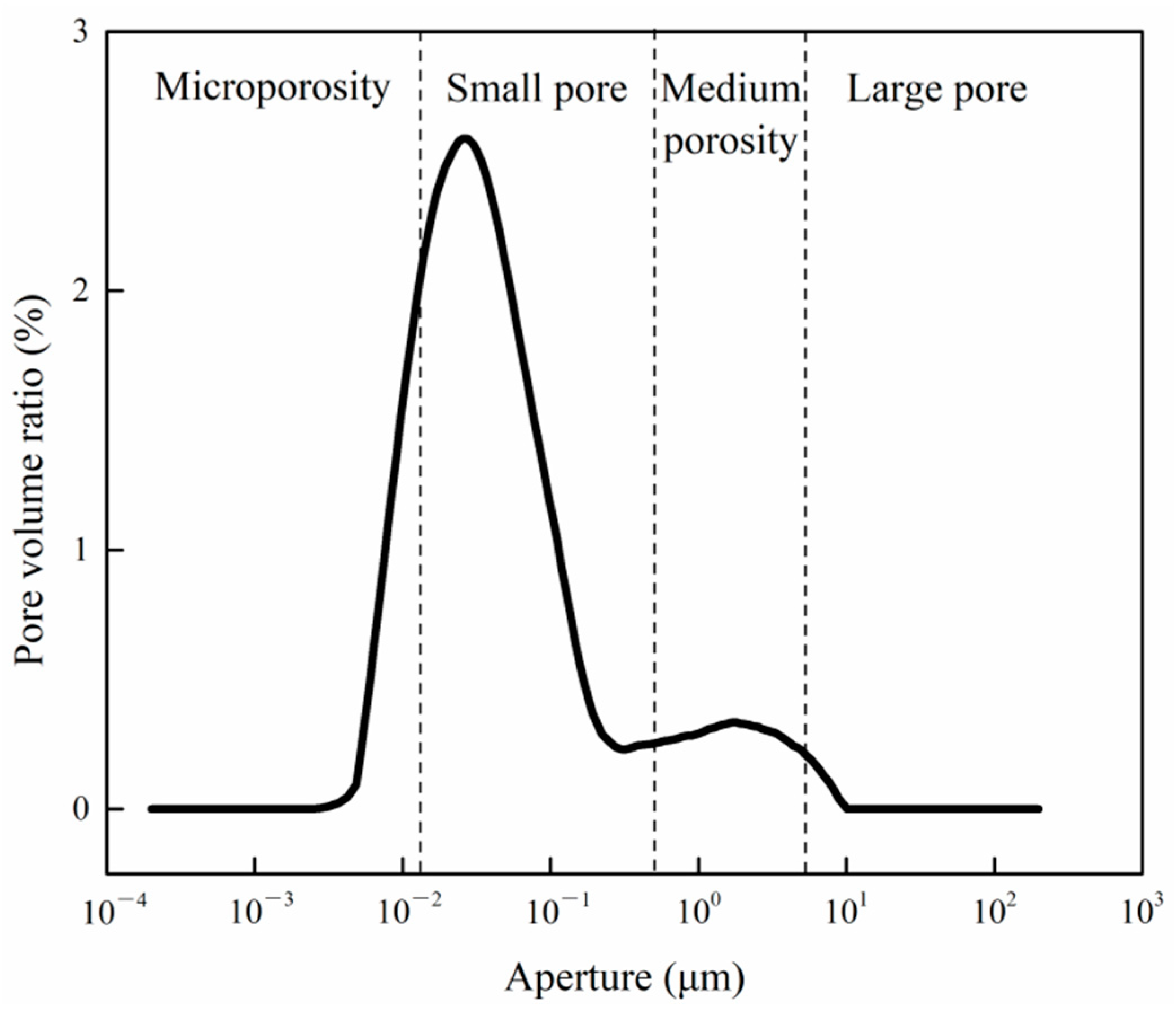
3.2. NMR Test Results
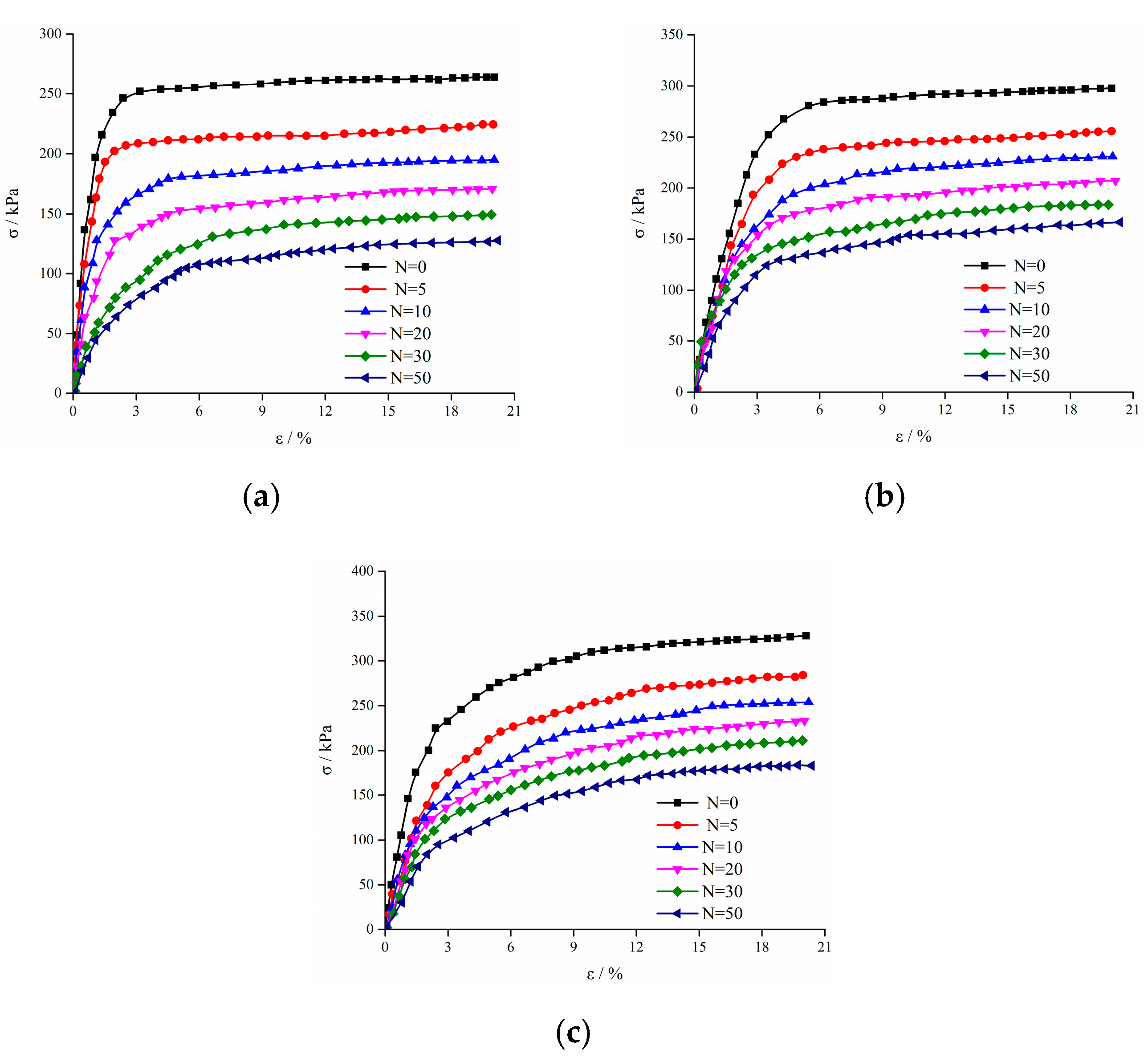
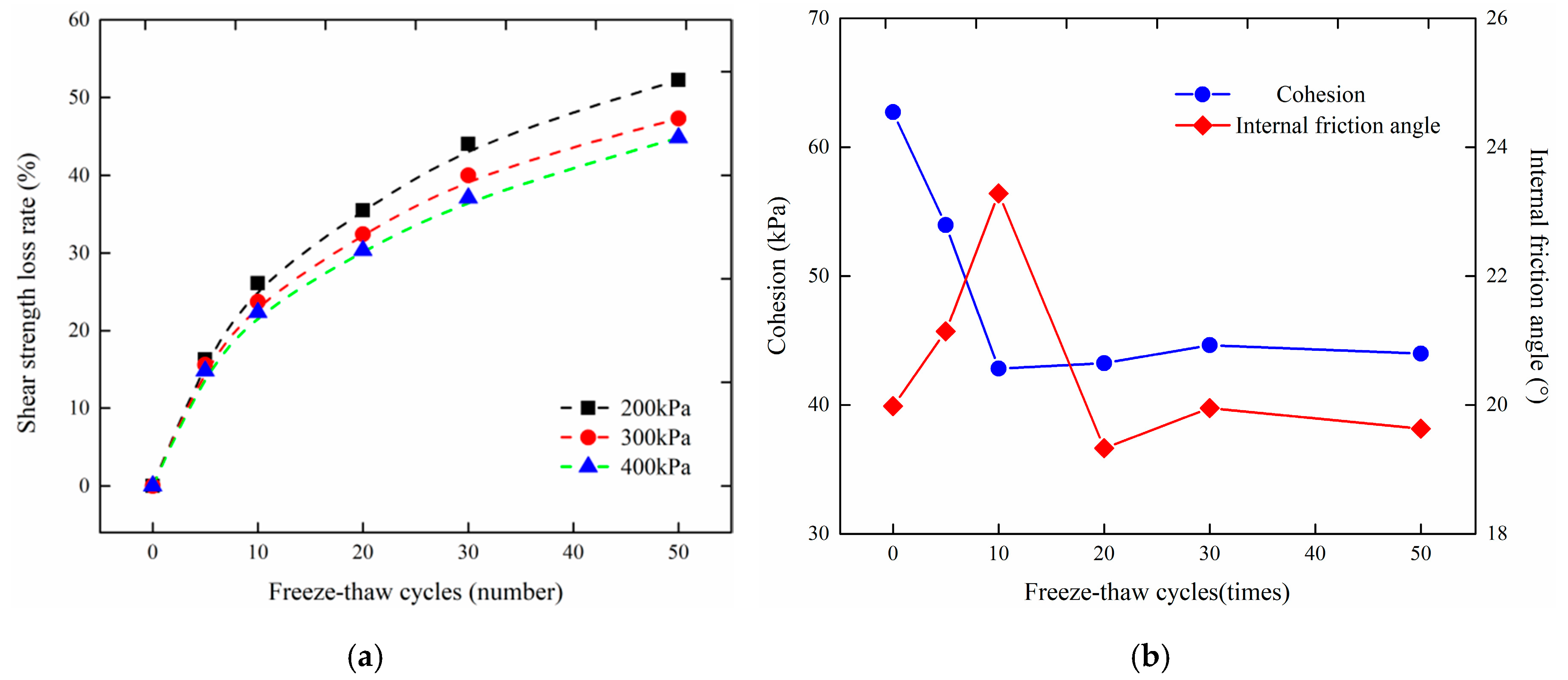
3.3. Triaxial Compression Test Results
- (1)
- The freezing and thawing times of loess are divided into 6 gradients. The peak intensity decreases with increasing freeze–thaw times, under different confining pressure conditions.
- (2)
- The greater the number of freeze–thaw cycles, the less the peak intensity degradation of the gradient compared to the previous one.
- (3)
- As the confining pressure increases, the phenomenon of peak intensity degradation becomes less obvious.
4. Discussion
4.1. Strength Damage
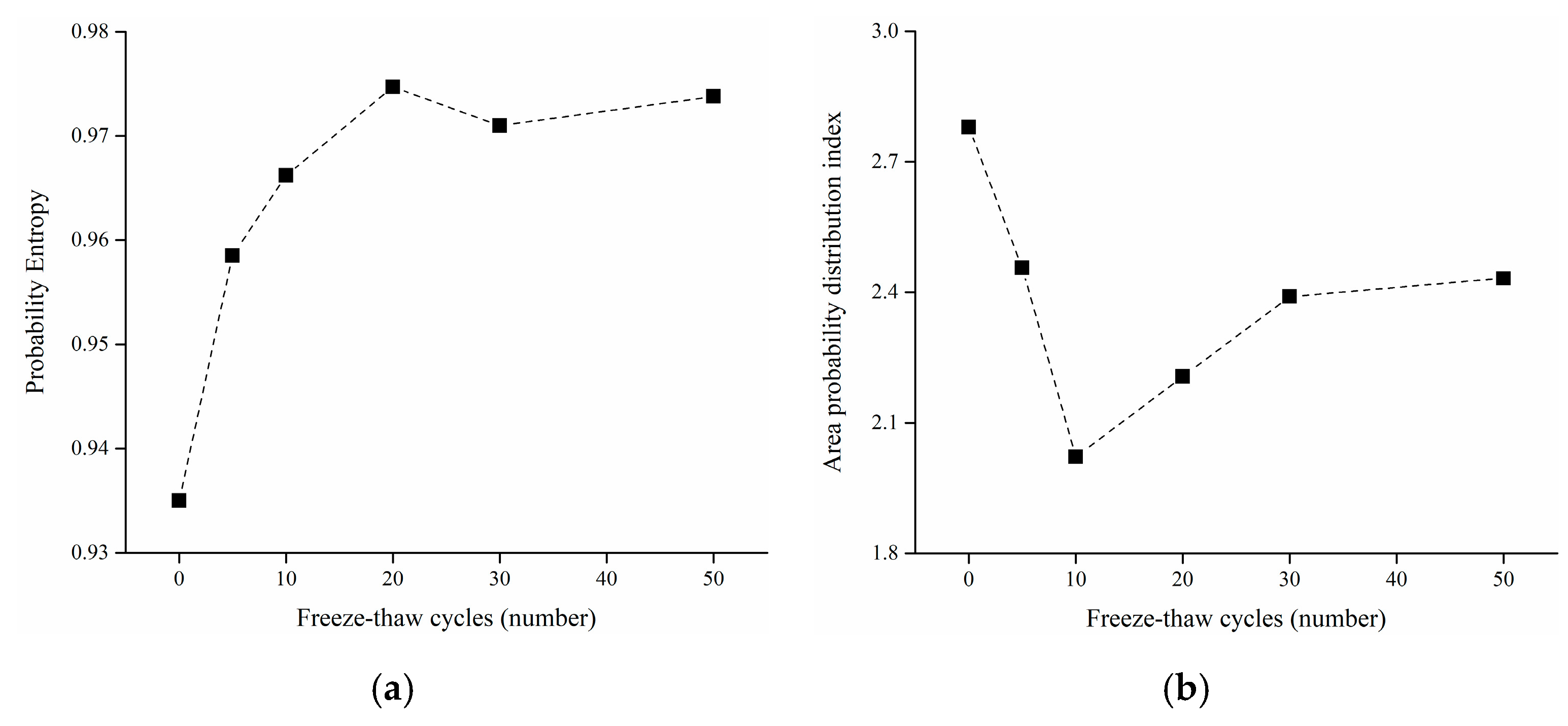
4.2. SEM Test Result Analysis
- (1)
- Probability entropy
- (2)
- Area probability distribution index
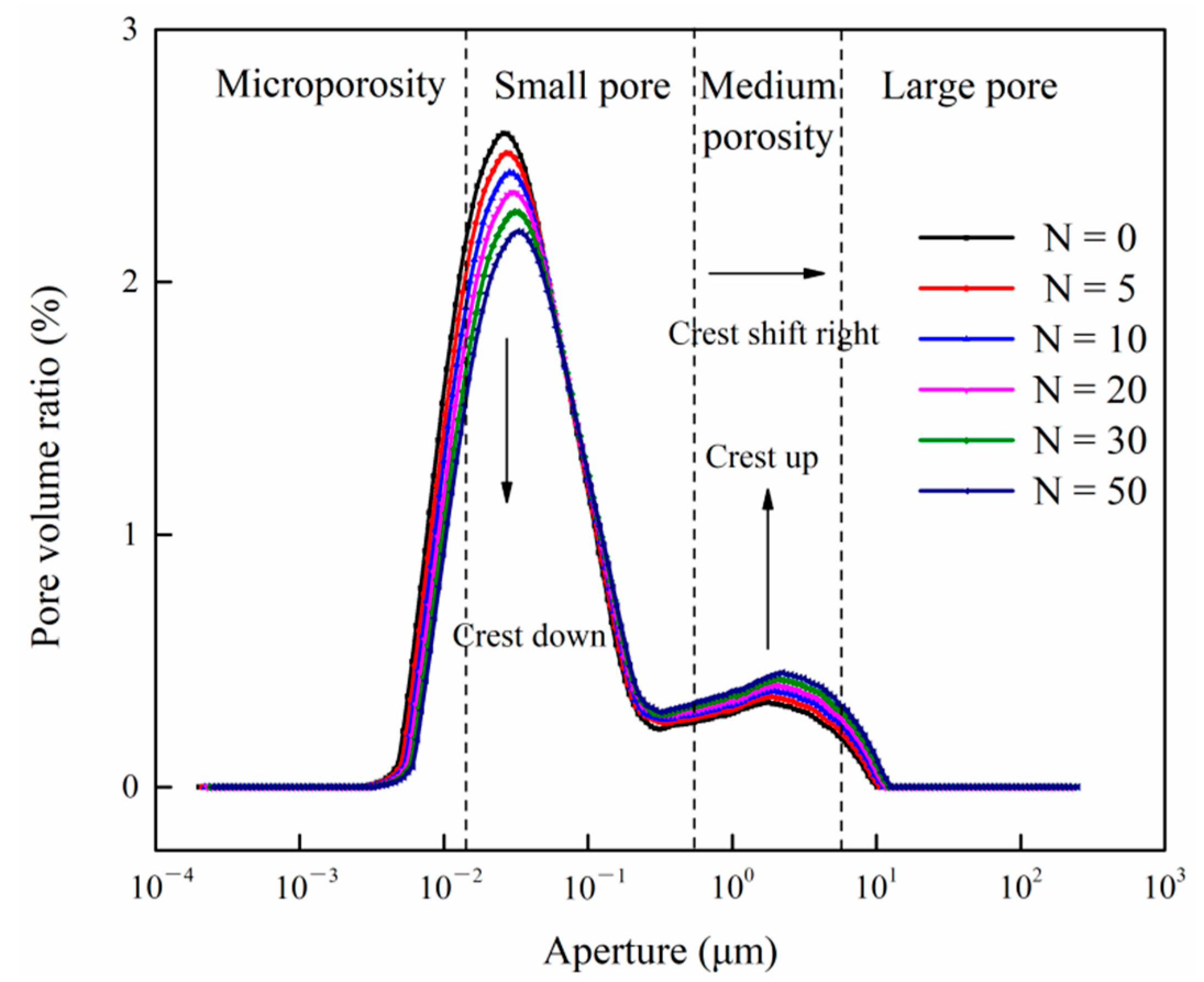
4.3. NMR Test Result Analysis
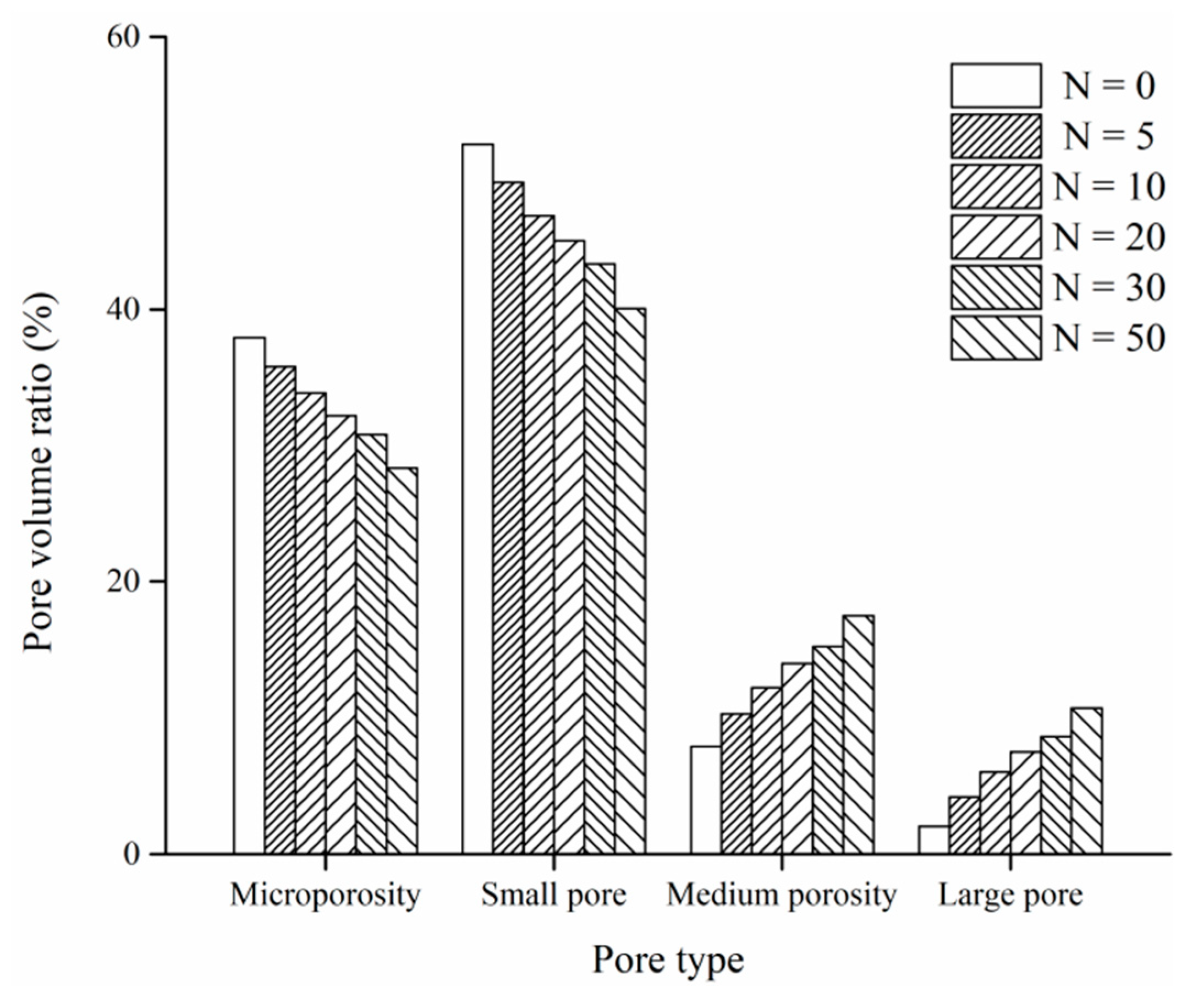
- (1)
- The freeze–thaw cycle is 0 to 10 times, and the pore volume of each type varies greatly, which indicates that the soil mesostructure has a higher degree of freeze–thaw damage and a faster damage rate.
- (2)
- When the number of freeze–thaw cycles is 10~30, the change of pore volume of each type is small, which shows that the degree of freeze–thaw damage of the mesostructure of the soil body is reduced and the damage rate is reduced. This is because the soil forms new pore structure characteristics, which changes the degree of influence of the freeze–thaw cycle on the microstructure of the soil. After the number of freeze–thaw cycles reached 50 times, there was almost no change in the pore volume of each type. This was because the soil was basically destroyed and the pore structure was stabilized to a certain extent.
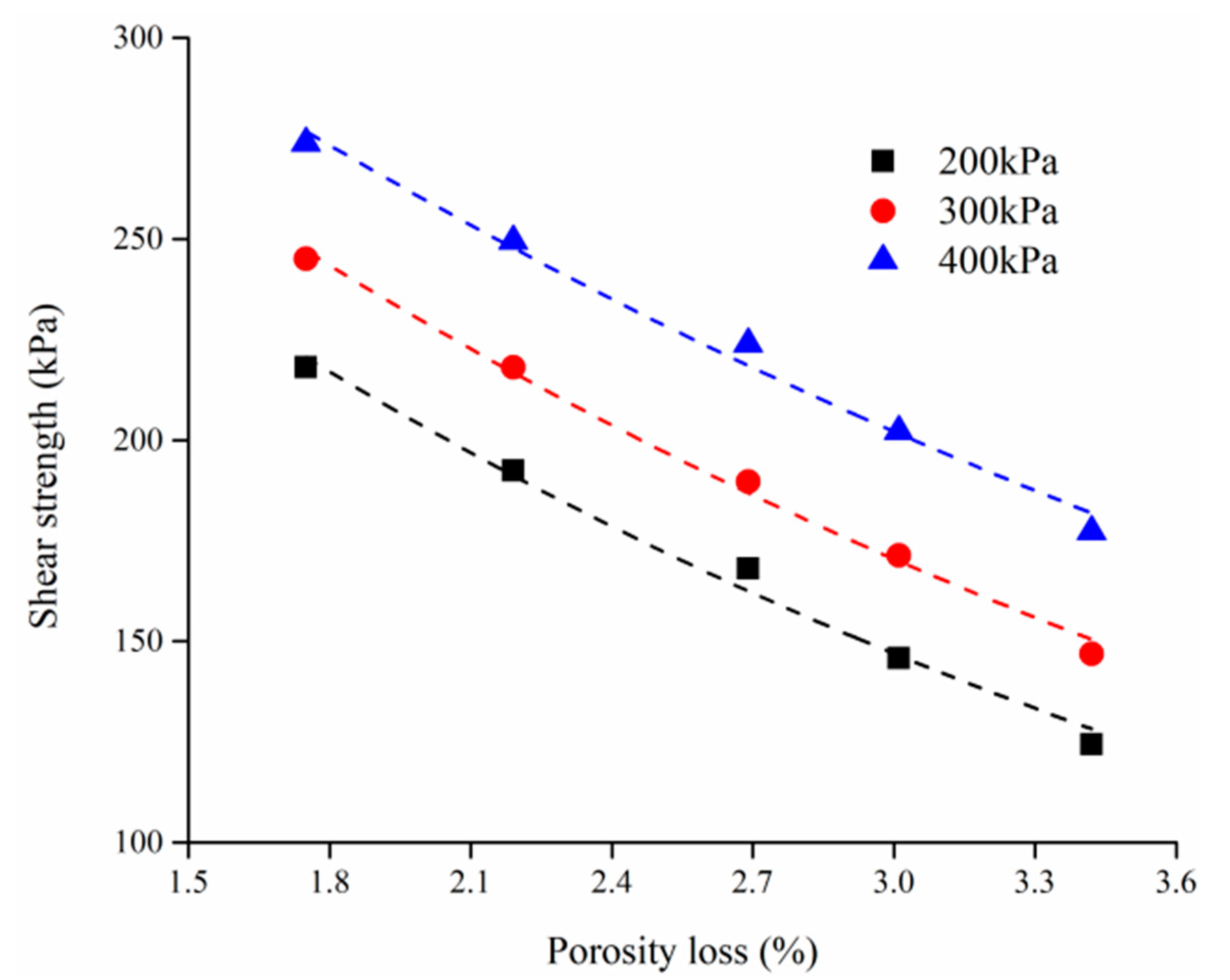
4.4. Correlation Between Strength and Pore Structure
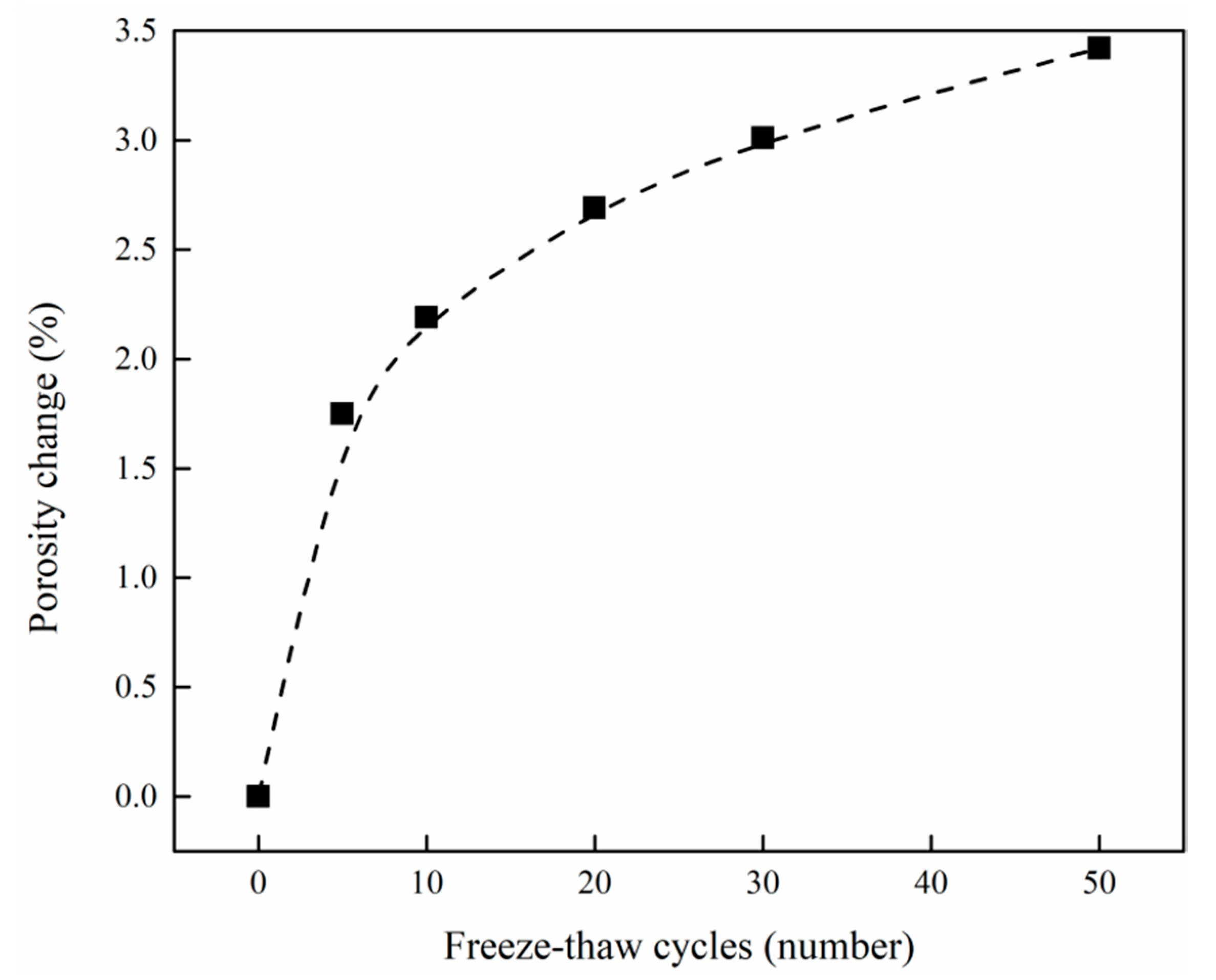
4.4.1. Changes in Porosity
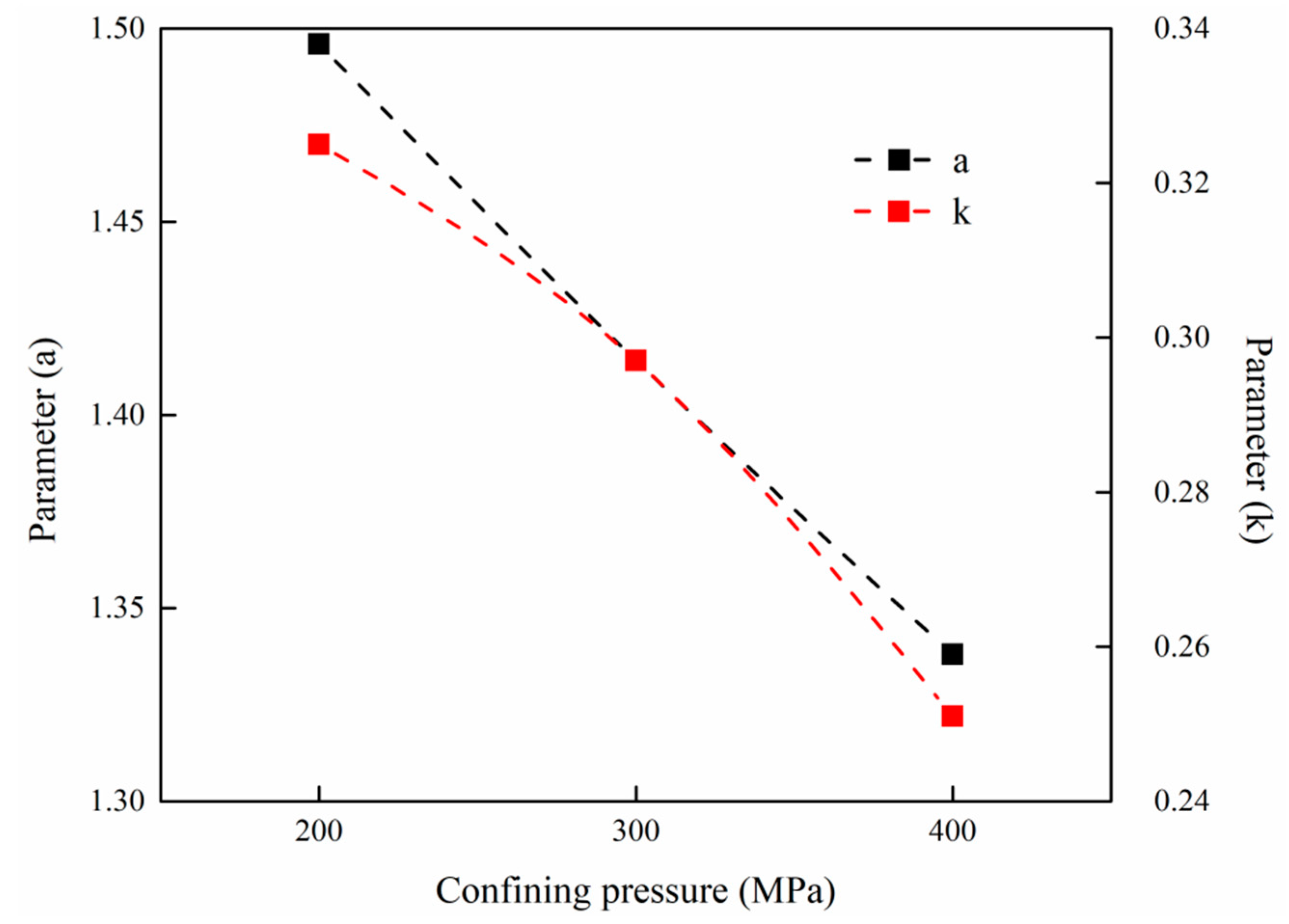
4.4.2. Verification of Test Results
5. Conclusions
- (1)
- The freeze–thaw damage evolution of saturated undisturbed loess under freeze–thaw cycles was observed by scanning electron microscopy. It is found that the micro and small pores in the soil increase first and then decrease, and the medium and large pores reduce first and then increase. This is closely related to changes in the internal microstructure of the soil. The T2 spectrum distribution curve of saturated undisturbed loess under freeze–thaw cycles was obtained by using nuclear magnetic resonance technology. The pore distribution curve of loess under freeze–thaw cycles is obtained by equation inversion, which shows that the micro and small pores in the loess are gradually transitioning to the larger medium and large pores with the increase of the number of freeze–thaw cycles. It is reported that the freeze–thaw cycle is a dynamic process for the internal pore expansion of loess. The results obtained by NMR and SEM experiments confirm each other, and the pore distribution has similar changes.
- (2)
- For saturated undisturbed loess, the freeze–thaw cycle breaks the original balance of the sample itself. During the freezing process, the soil particles are squeezed by the growth of ice crystals, the volume expands, and pores and fissures develop, forming a new soil skeleton structure. During the melting process, the melting of solid ice inside the rock sample cannot cause the complete restoration of the deformation of the soil skeleton particles. Therefore, during the freeze–thaw cycle, due to the effect of the frost-heaving force, the loess sample shows a decrease in strength and an increase in porosity.
- (3)
- The strength of saturated undisturbed loess under freeze–thaw cycles is related to the change of porosity. The measurement of porosity is relatively simple. Therefore, consider establishing a functional relationship with the shear strength based on the change in porosity. According to the concept of freeze–thaw damage, an exponential function distribution between the two is derived. Fitting the variation of the porosity and the shear strength under different cycle times, the correlation between the two is good. Therefore, this research provides a new method for the non-destructive analysis of the strength of saturated loess by freezing and thawing, and a new idea for analyzing the loess landslide caused by the freezing and thawing cycle.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peng, J.; Wang, G.; Wang, Q.; Zhang, F. Shear wave velocity imaging of landslide debris deposited on an erodible bed and possible movement mechanism for a loess landslide in Jingyang, Xi’an, China. Landslides 2017, 14, 1503–1512. [Google Scholar] [CrossRef]
- Xu, X.; Guo, W.-Z.; Liu, Y.; Ma, J.; Wang, W.; Zhang, H.; Gao, H. Landslides on the Loess Plateau of China: A latest statistics together with a close look. Nat. Hazards 2017, 86, 1393–1403. [Google Scholar] [CrossRef]
- Zhang, F.; Kang, C.; Chan, D.; Zhang, X.; Pei, X.; Peng, J. A study of a flowslide with significant entrainment in loess areas in China. Earth Surf. Process. Landf. 2017, 42, 2295–2305. [Google Scholar] [CrossRef]
- Peng, J.; Sun, X.; Wang, W.; Sun, G. Characteristics of land subsidence, earth fissures and related disaster chain effects with respect to urban hazards in Xi’an, China. Environ. Earth Sci. 2016, 75, 1190. [Google Scholar] [CrossRef]
- Qi, J.; Vermeer, P.A.; Cheng, G. A review of the influence of freeze-thaw cycles on soil geotechnical properties. Permafr. Periglac. Process 2010, 17, 245–252. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Ren, J.; Wang, S.; Jin, L. Mechanism of slope failure in loess terrains during spring thawing. J. Mt. Sci. 2018, 15, 845–858. [Google Scholar] [CrossRef]
- Li, G.; Ma, W.; Mu, Y.; Wang, F.; Fan, S.; Wu, Y. Effects of freeze-thaw cycle on engineering properties of loess used as road fills in seasonally frozen ground regions, North China. J. Mt. Sci. 2017, 14, 356–368. [Google Scholar] [CrossRef]
- Peng, J.; Lan, H.-X.; Qian, H.; Li, R.; Li, Z.; Zhuang, J.; Li, X.; Liu, S. Scientific research framework of livable yellow river. J. Eng. Geol. 2020, 28, 189–201. [Google Scholar] [CrossRef]
- Xu, J.; Ren, J.; Wang, Z.; Wang, S.; Yuan, J. Strength behaviors and meso-structural characters of loess after freeze-thaw. Cold Reg. Sci. Technol. 2018, 148, 104–120. [Google Scholar] [CrossRef]
- Wang, S.; Lv, Q.; Baaj, H.; Li, X.; Zhao, Y. Volume change behaviour and microstructure of stabilized loess under cyclic freeze-thaw conditions. Can. J. Civ. Eng. 2016, 43, 865–874. [Google Scholar] [CrossRef]
- Li, G.; Wang, F.; Ma, W.; Fortier, R.; Mu, Y.; Mao, Y.; Hou, X. Variations in strength and deformation of compacted loess exposed to wetting-drying and freeze-thaw cycles. Cold Reg. Sci. Technol. 2018, 151, 159–167. [Google Scholar] [CrossRef]
- Li, J.; Zhou, K.; Liu, W.; Deng, H. NMR research on deterioration characteristics of microscopic structure of sandstones in freeze-thaw cycles. Trans. Non-Ferrous Metals Soc. Ch. 2016, 26, 2997–3003. [Google Scholar] [CrossRef]
- Tian, H.; Wei, C.; Wei, H.; Zhou, J. Freezing and thawing characteristics of frozen soils: Bound water content and hysteresis phenomenon. Cold Reg. Sci. Technol. 2014, 103, 74–81. [Google Scholar] [CrossRef]
- Lu, Z.; Xian, S.; Yao, H.; Fang, R.; She, J. Influence of freeze-thaw cycles in the presence of a supplementary water supply on mechanical properties of compacted soil. Cold Reg. Sci. Technol. 2019, 157, 42–52. [Google Scholar] [CrossRef]
- Yan, C.-G.; Zhang, Z.-Q.; Jing, Y.-L. Characteristics of strength and pore distribution of lime-flyash loess under freeze-thaw cycles and dry-wet cycles. Arab. J. Geosci. 2017, 10, 544. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Ren, J.; Yuan, J. Mechanism of shear strength deterioration of loess during freeze-thaw cycling. Geomech. Eng. 2018, 14, 307–314. [Google Scholar] [CrossRef]
- Guo, L.; Shi, M.; Song, N.; Wan, Z.; Liu, H.; Liu, L. Anchorage of curcumin onto PVP enhances anti-tumor effect of curcumin. Med. Chem. Res. 2019, 28, 646–656. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Ren, Y.; Cai, X. Preparation and thermal performance of novel form-stable phase change materials based on polyethylene glycol (PEG)/hollow glass microsphere composites for thermal energy storage. Polym. Bull. 2019, 76, 2711–2724. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, S.; Wang, J.; Hsu, S.; Ma, C.C.M. Preparation and properties of graphene/carbon nanotube hybrid reinforced mortar composites. Mag. Concr. Res. 2019, 71, 395–407. [Google Scholar] [CrossRef]
- Bakhshipour, Z.; Asadi, A.; Huat, B.; Sridharan, A.; Kawasaki, S. Effect of acid rain on geotechnical properties of residual soils. Soils Found 2016, 56, 1008–1020. [Google Scholar] [CrossRef]
- Khodayar, A.; Nejati, H.-R. Effect of thermal-induced microcracks on the failure mechanism of rock specimens. Comput. Concr. 2018, 22, 93–100. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, A.; Li, M. Experimental investigation of the time-dependent behavior of quartz sandstone and quartzite under the combined effects of chemical erosion and freeze-thaw cycles. Cold Reg. Sci. Technol. 2019, 161, 51–62. [Google Scholar] [CrossRef]
- Cardoso, R.; Ribeiro, D.; Neri, R. Bonding effect on the evolution with curing time of compressive and tensile strength of sand-cement mixtures. Soils Found 2018, 57, 655–668. [Google Scholar] [CrossRef]
- Mousavi, S. Stabilization of compacted clay with cement and/or lime containing peat ash. Road Mater. Pavement Des. 2016, 18, 1304–1321. [Google Scholar] [CrossRef]
- Lin, T.; Zhang, Y.; Yi, X.; Fan, T.; Wan, L. Time-frequency peak filtering for random noise attenuation of magnetic resonance sounding signal. Geophys. J. Int. 2018, 213, 727–738. [Google Scholar] [CrossRef]
- Lin, T.; Yang, Y.; Teng, F.; Muller-Petke, M. Enabling surface nuclear magnetic resonance at high-noise environments using a pre-polarization pulse. Geophys. J. Int. 2018, 212, 1463–1467. [Google Scholar] [CrossRef]
- Shushakov, O.; Maryasov, A. Bloch-Siegert Effect in Magnetic-Resonance Sounding. Appl. Magn. Reason. 2016, 47, 1021–1032. [Google Scholar] [CrossRef]
- Coates, G.; Marschall, D.; Mardon, D.; Galford, J. A new characterization of bulk-volume irreducible using magnetic resonance. Log. Anal. 1997, 39, 51–63. [Google Scholar]
- Lu, Y.; Liu, S.; Alonso, E.; Wang, L.; Xu, L.; Li, Z. Volume changes and mechanical degradation of a compacted expansive soil under freeze-thaw cycles. Cold Reg. Sci. Technol. 2019, 157, 206–214. [Google Scholar] [CrossRef]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Design 1987, 80, 233–245. [Google Scholar] [CrossRef]
- Jia, H.; Xiang, W.; Shen, Y.; Yang., G. Discussion of the key issues within calculation of the fatigue damage of rockssubjected to freeze-thaw cycles. Ch. J. Rock Mech. Eng. 2017, 36, 335–346. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yang, G.; Liu, H. The Influence of Regional Freeze–Thaw Cycles on Loess Landslides: Analysis of Strength Deterioration of Loess with Changes in Pore Structure. Water 2020, 12, 3047. https://doi.org/10.3390/w12113047
Li Z, Yang G, Liu H. The Influence of Regional Freeze–Thaw Cycles on Loess Landslides: Analysis of Strength Deterioration of Loess with Changes in Pore Structure. Water. 2020; 12(11):3047. https://doi.org/10.3390/w12113047
Chicago/Turabian StyleLi, Zuyong, Gengshe Yang, and Hui Liu. 2020. "The Influence of Regional Freeze–Thaw Cycles on Loess Landslides: Analysis of Strength Deterioration of Loess with Changes in Pore Structure" Water 12, no. 11: 3047. https://doi.org/10.3390/w12113047
APA StyleLi, Z., Yang, G., & Liu, H. (2020). The Influence of Regional Freeze–Thaw Cycles on Loess Landslides: Analysis of Strength Deterioration of Loess with Changes in Pore Structure. Water, 12(11), 3047. https://doi.org/10.3390/w12113047




