Comparison of Ensembles Projections of Rainfall from Four Bias Correction Methods over Nigeria
Abstract
1. Introduction
2. Study Area and Data
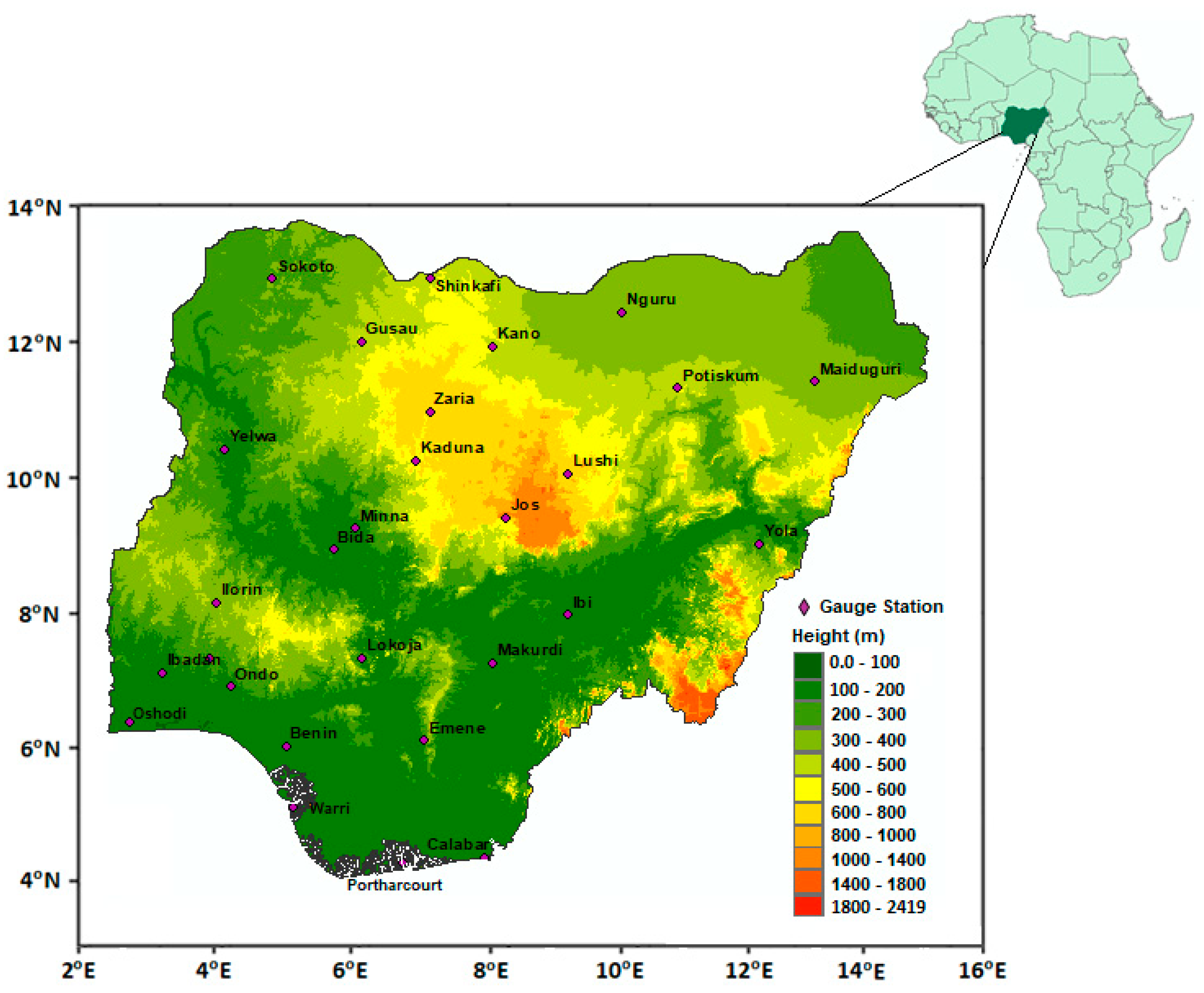
2.1. Study Area
2.2. Data
2.2.1. Historical Rainfall Data
2.2.2. CMIP5 Datasets
3. Methods
3.1. Bias Correction of GCMs
3.1.1. Gamma Quantile Mapping (GAQM)
3.1.2. General Quantile Mapping (GEQM)
3.1.3. Power Transformation (PT)
3.1.4. Linear Scaling (LS)
3.2. Performance Assessment of Bias Correction (BC) Methods
3.3. Ensemble Projections
4. Results
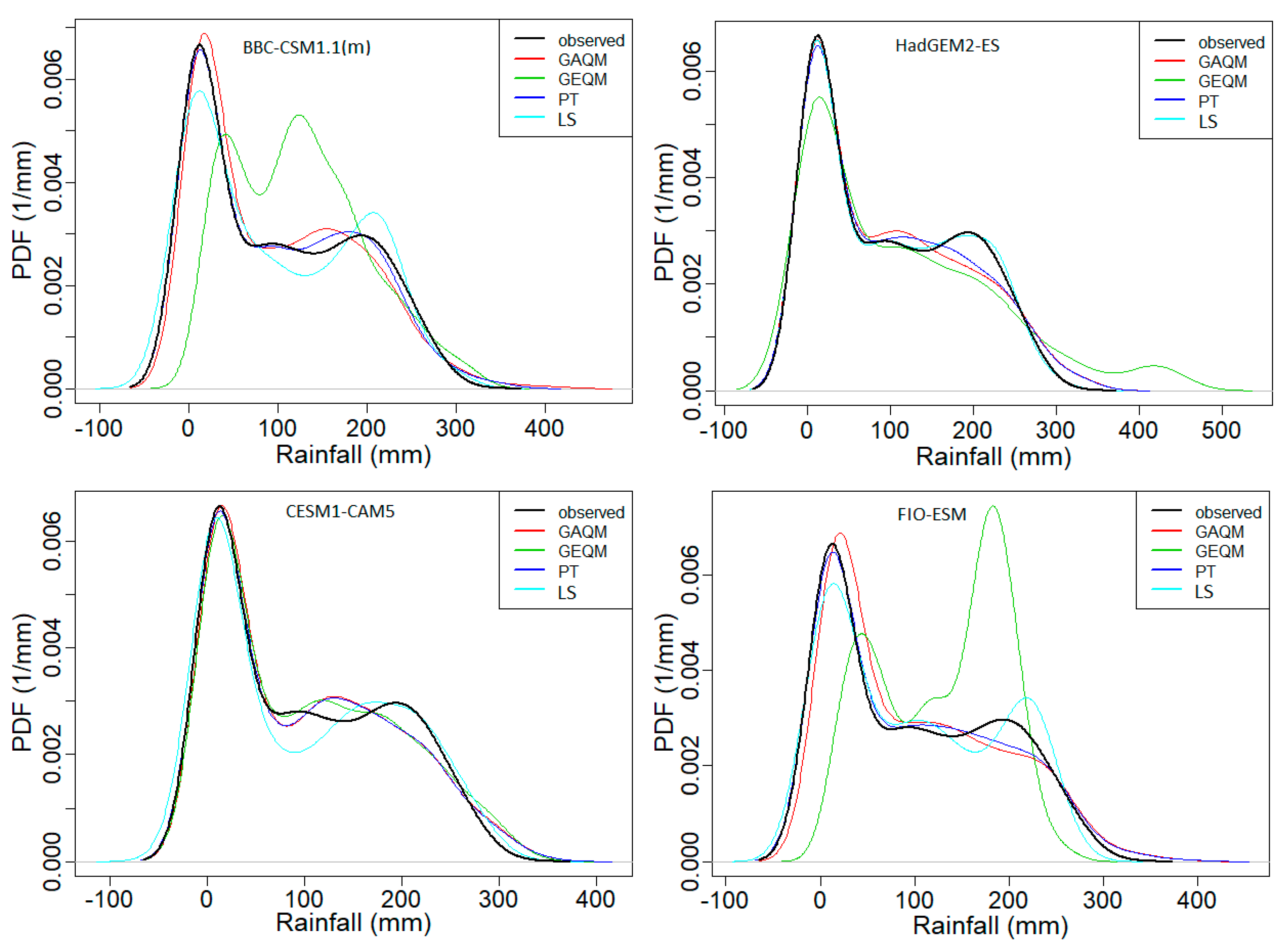
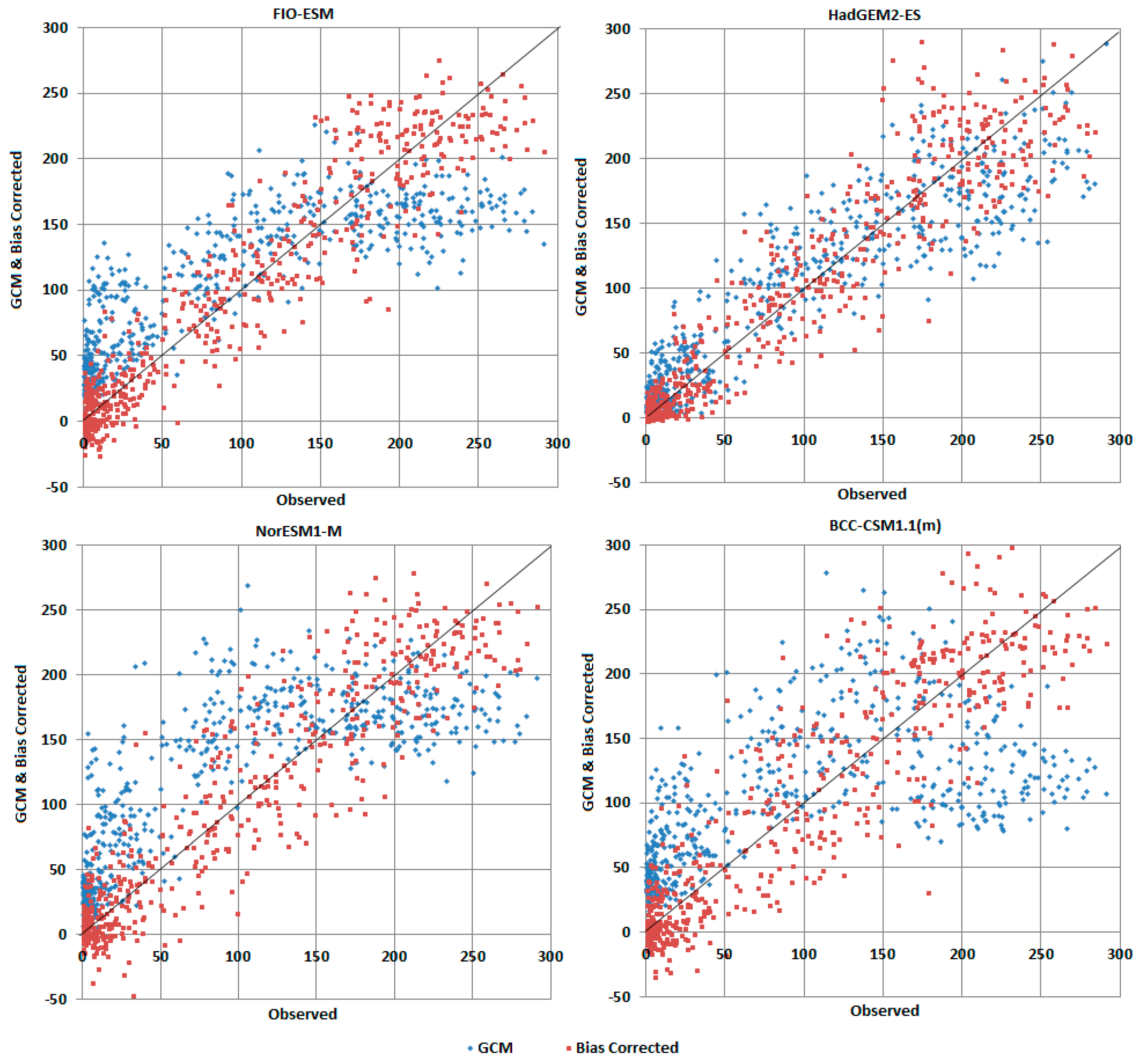
4.1. Performance Evaluation of Bias Corrected Models
4.2. Performance Assessment of Bias Correction Methods
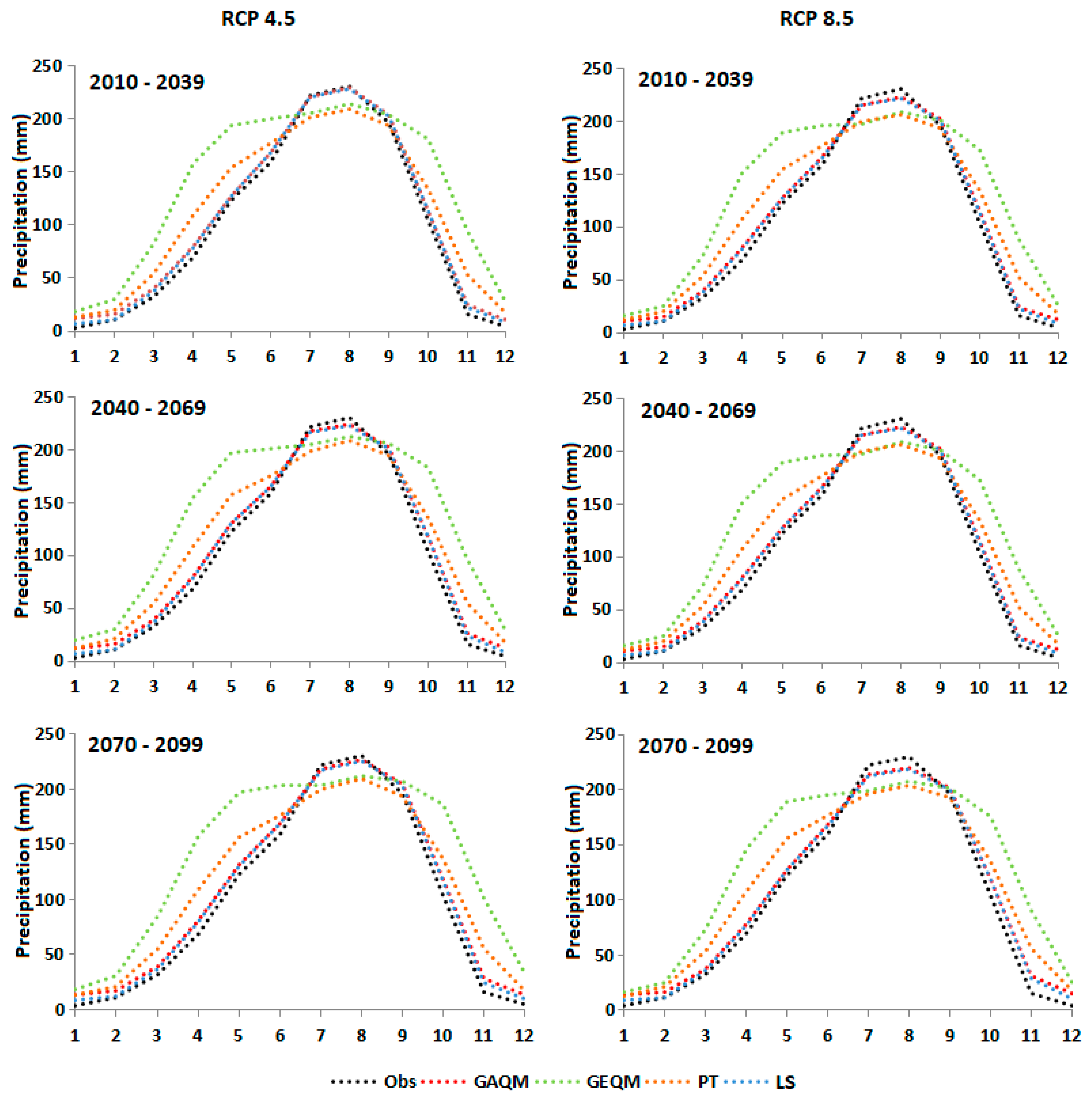
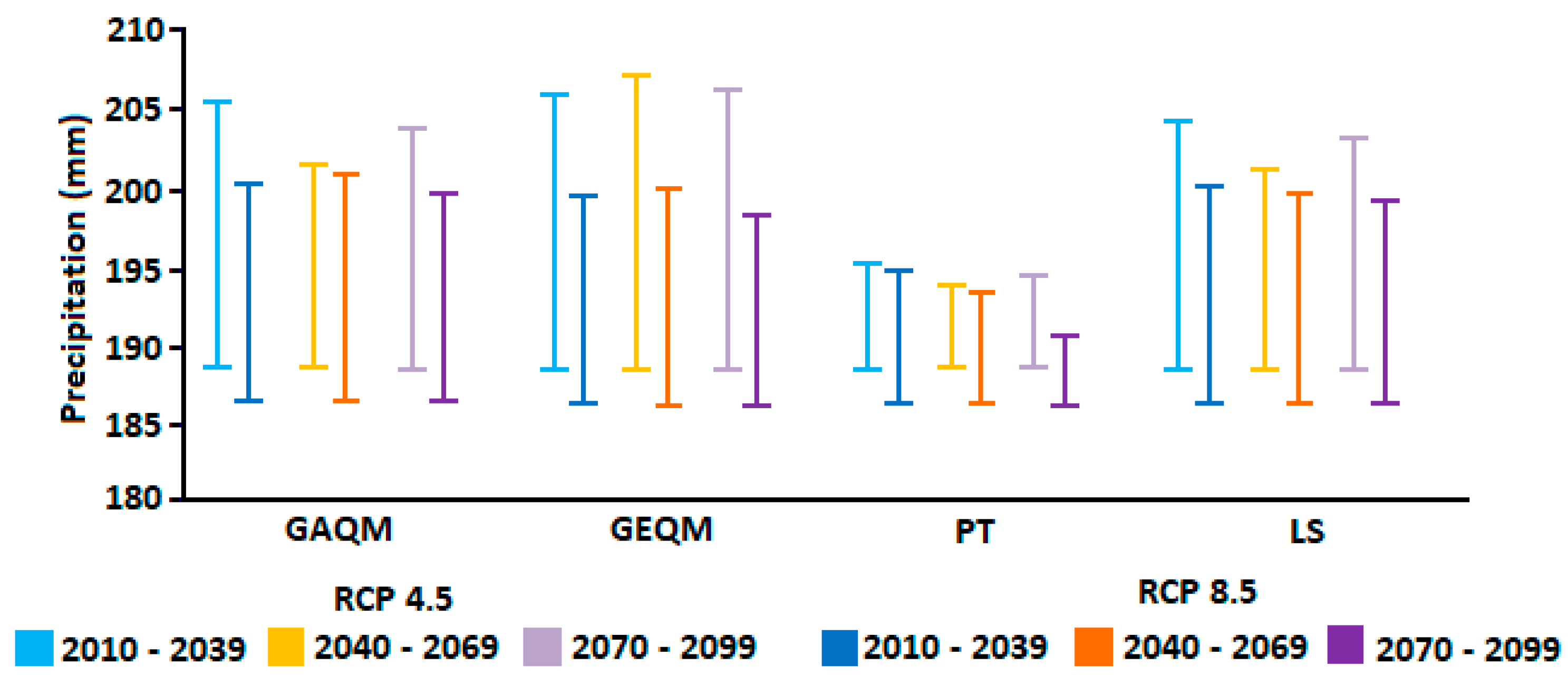
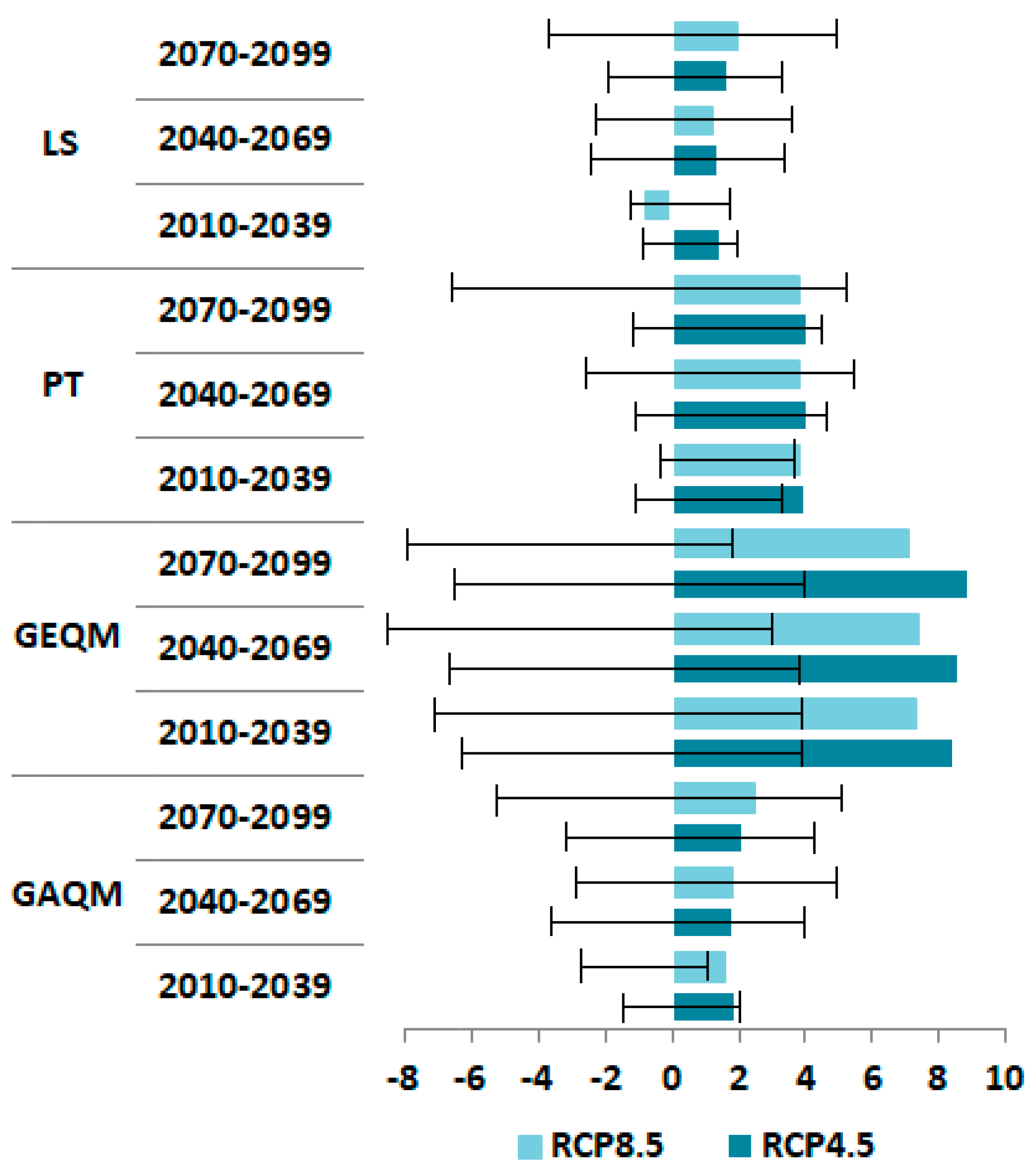
4.3. Rainfall Projection
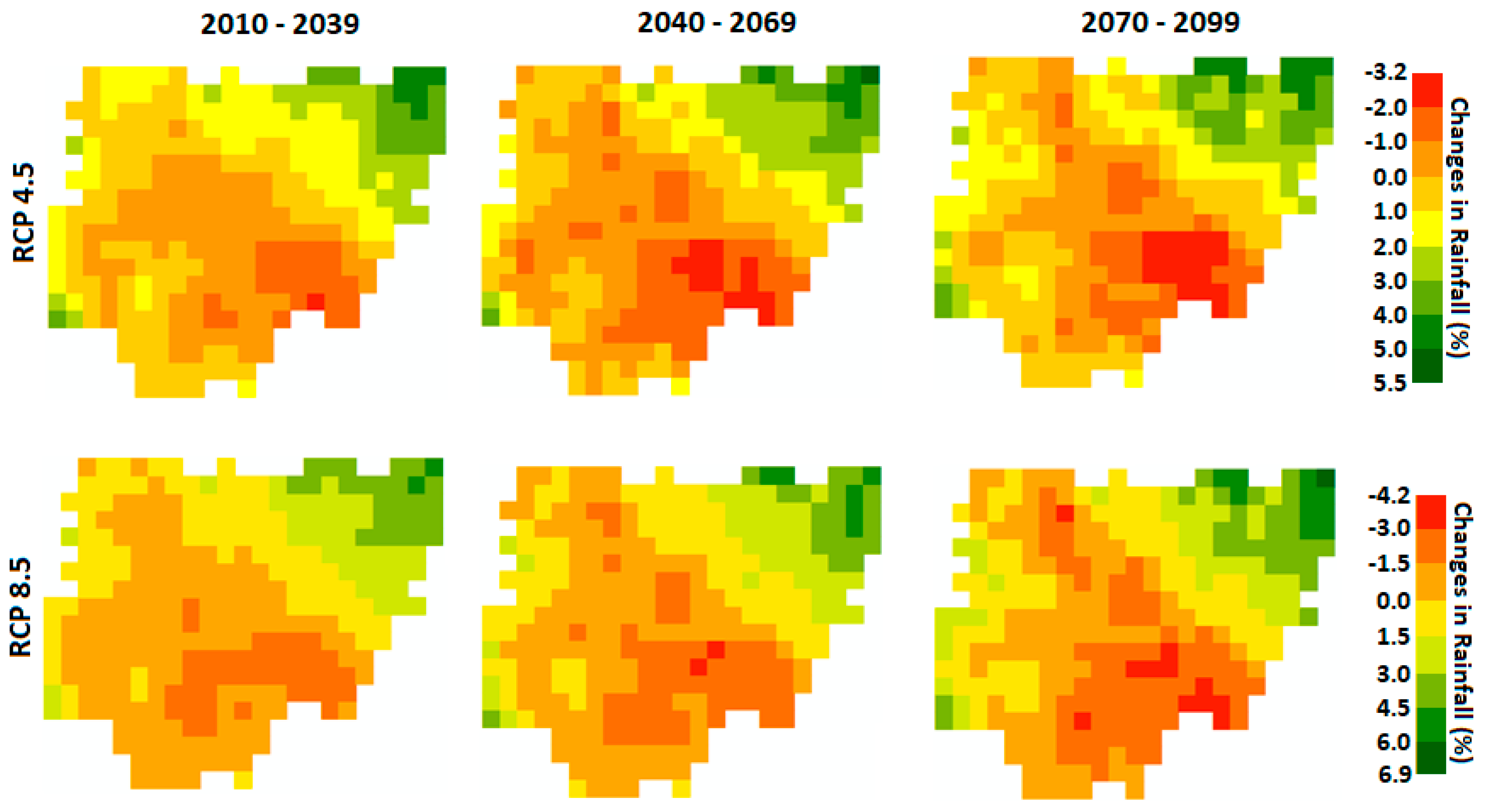
4.3.1. Spatial Changes in Wet Season Rainfall for LS
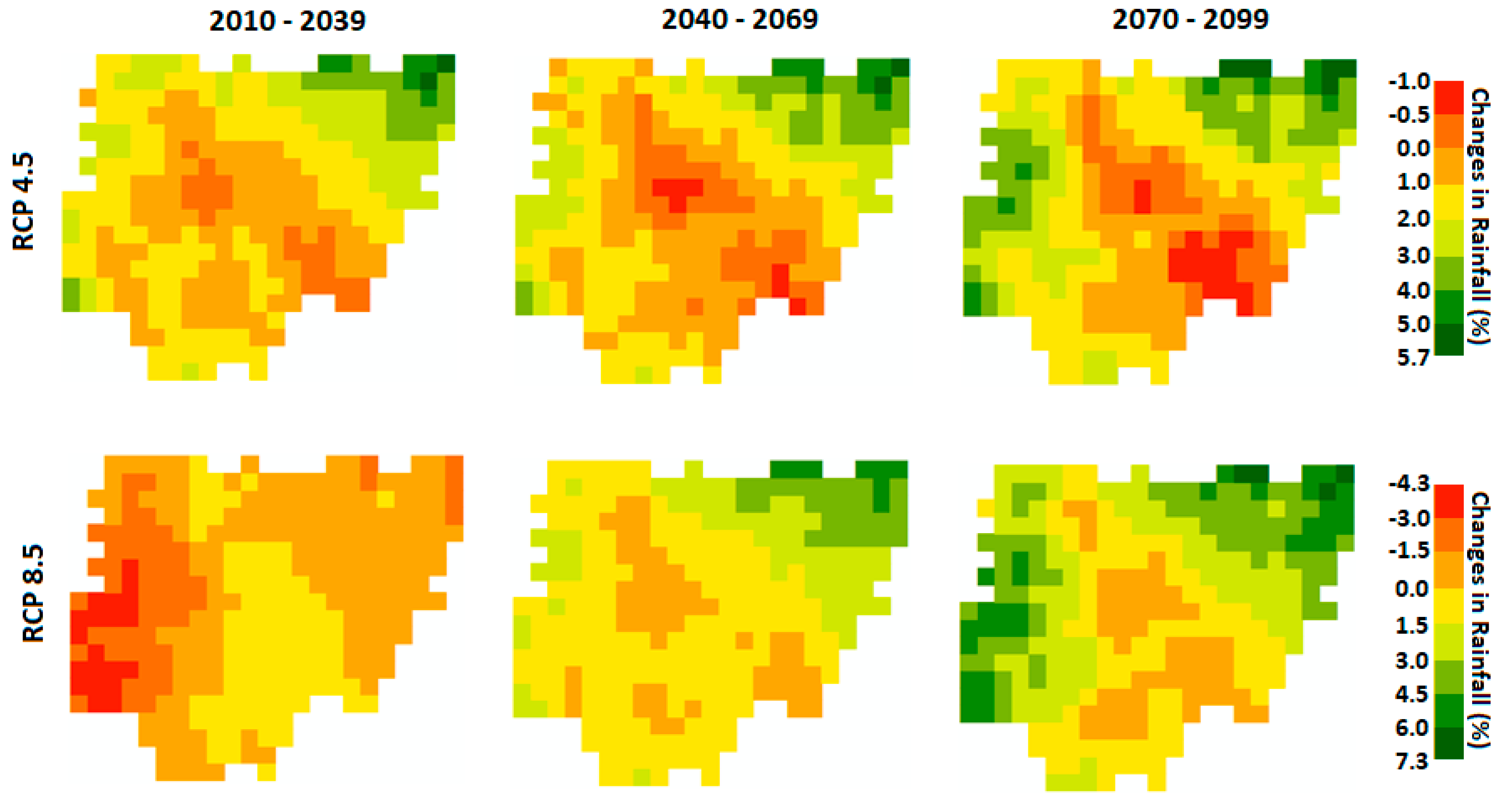
4.3.2. Spatial Changes in Annual Rainfall
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alamgir, M.; Mohsenipour, M.; Homsi, R.; Wang, X.; Shahid, S.; Shiru, M.S.; Alias, N.E.; Yuzir, A. Parametric Assessment of Seasonal Drought Risk to Crop Production in Bangladesh. Sustainability 2019, 11, 1442. [Google Scholar] [CrossRef]
- Hay, L.E.; Clark, M. Use of statistically and dynamically downscaled atmospheric model output for hydrologic simulations in three mountainous basins in the western United States. J. Hydrol. 2003, 282, 56–75. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Afan, H.A.; Shiru, M.S.; Al-Ansari, N.; Yaseen, Z.M. Changes in Climatic Water Availability and Crop Water Demand for Iraq Region. Sustainability 2020, 12, 3437. [Google Scholar] [CrossRef]
- Sylla, M.B.; Elguindi, N.; Giorgi, F.; Wisser, D. Projected robust shift of climate zones over West Africa in response to anthropogenic climate change for the late 21st century. Clim. Chang. 2016, 134, 241–253. [Google Scholar] [CrossRef]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global increasing trends in annual maximum daily precipitation. J. Clim. 2012, 26, 3904–3918. [Google Scholar] [CrossRef]
- Rudd, A.C.; Kay, A.L.; Wells, S.C.; Aldridge, T.; Cole, S.J.; Kendon, E.J.; Stewart, E.J. Investigating potential future changes in surface water flooding hazard and impact. Hydrol. Process. 2020, 34, 139–149. [Google Scholar]
- Sa’adi, Z.; Shiru, M.S.; Shahid, S.; Ismail, T. Selection of general circulation models for the projections of spatio-temporal changes in temperature of Borneo Island based on CMIP5. Theor. Appl. Clim. 2019, 139, 351–371. [Google Scholar] [CrossRef]
- Ahmed, K.; Iqbal, Z.; Khan, N.; Rasheed, B.; Nawaz, N.; Malik, I.; Noor, M. Quantitative assessment of precipitation changes under CMIP5 RCP scenarios over the northern sub-Himalayan region of Pakistan. Environ. Dev. Sustain. 2019, 1–15. [Google Scholar] [CrossRef]
- Khan, N.; Shahid, S.; Ahmed, K.; Wang, X.; Ali, R.; Ismail, T.; Nawaz, N. Selection of GCMs for the projection of spatial distribution of heat waves in Pakistan. Atmos. Res. 2020, 233, 104688. [Google Scholar] [CrossRef]
- Van Huijgevoort, M.; Van Lanen, H.; Teuling, A.; Uijlenhoet, R. Identification of changes in hydrological drought characteristics from a multi-GCM driven ensemble constrained by observed discharge. J. Hydrol. 2014, 512, 421–434. [Google Scholar] [CrossRef]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.; Carrao, H.; Spinoni, J.; Feyen, L. Global changes in drought conditions under different levels of warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Pathways and challenges of the application of artificial intelligence to geohazards modelling. Gondwana Res. 2020, in press. [Google Scholar] [CrossRef]
- Khan, N.; Sachindra, D.; Shahid, S.; Ahmed, K.; Shiru, M.S.; Nawaz, N. Prediction of droughts over Pakistan using machine learning algorithms. Adv. Water Resour. 2020, 139, 103562. [Google Scholar] [CrossRef]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Rashid, M.M.; Beecham, S.; Chowdhury, R.K. Statistical downscaling of CMIP5 outputs for projecting future changes in rainfall in the Onkaparinga catchment. Sci. Total Environ. 2015, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Hundecha, Y.; Sunyer, M.A.; Lawrence, D.; Madsen, H.; Willems, P.; Bürger, G.; Kriaucˇiuniene, J.; Loukas, A.; Martinkove, M.; Osuch, M.; et al. Inter-comparison of statistical downscaling methods for projection of extreme flow indices across Europe. J. Hydrol. 2016, 541, 1273–1286. [Google Scholar] [CrossRef]
- Wang, B.; Zheng, L.; Liu, D.L.; Ji, F.; Clark, A.; Yu, Q. Using multi-model ensembles of CMIP5 global climate models to reproduce observed monthly rainfall and temperature with machine learning methods in Australia. Int. J. Climatol. 2018, 38, 4891–4902. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Wang, X.-J. Selection of climate models for projection of spatiotemporal changes in temperature of Iraq with uncertainties. Atmos. Res. 2018, 213, 509–522. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Lucas-Picher, P.; Caya, D. Impacts of weighting climate models for hydro-meteorological climate change studies. J. Hydrol. 2017, 549, 534–546. [Google Scholar] [CrossRef]
- Brown, J.D.; Seo, D.J. Evaluation of a nonparametric post-processor for bias correction and uncertainty estimation of hydrologic predictions. Hydrol. Process. 2013, 27, 83–105. [Google Scholar] [CrossRef]
- Gaborit, É.; Anctil, F.; Fortin, V.; Pelletier, G. On the reliability of spatially disaggregated global ensemble rainfall forecasts. Hydrol. Process. 2013, 27, 45–56. [Google Scholar] [CrossRef]
- Sa’adi, Z.; Shahid, S.; Chung, E.S.; Ismail, T. Projection of spatial and temporal changes of rainfall in Sarawak of Borneo Island using statistical downscaling of CMIP5 models. Atmos. Res. 2017, 197, 446–460. [Google Scholar] [CrossRef]
- Khan, N.; Shahid, S.; Ahmed, K.; Ismail, T.; Nawaz, N.; Son, M. Performance assessment of general circulation model in simulating daily precipitation and temperature using multiple gridded datasets. Water 2018, 10, 1793. [Google Scholar] [CrossRef]
- Shiru, M.S.; Chung, E.-S.; Shahid, S.; Alias, N. GCM selection and temperature projection of Nigeria under different RCPs of the CMIP5 GCMS. Theor. Appl. Climatol. 2020, 141, 1611–1627. [Google Scholar] [CrossRef]
- Akstinas, V.; Jakimavicius, D.; Meilutyte-Lukauskiene, D.; Kriauciuniene, J.; Sarauskiene, D. Uncertainty of annual runoff projections in Lithuanian rivers under a future climate. Hydrol. Res. 2020, 51, 257–271. [Google Scholar] [CrossRef]
- Wooten, A.; Terando, A.; Reich, B.J.; Boyles, R.P.; Semazzi, F. Characterizing Sources of Uncertainty from Global Climate Models and Downscaling Techniques. J. Appl. Meteorol. Climatol. 2017, 56, 3245–3262. [Google Scholar] [CrossRef]
- Sharma, T.; Vittal, H.; Chhabra, S.; Salvi, K.; Ghosh, S.; Karmakar, S. Understanding the cascade of GCM and downscaling uncertainties in hydro-climatic projections over India. Int. J. Climatol. 2018, 38, 178–190. [Google Scholar] [CrossRef]
- Medugu, N.I.; Majid, M.R.; Johar, F. Drought and desertification management in arid and semi-arid zones of Northern Nigeria. Manag. Environ. Qual. Int. J. 2011, 22, 595–611. [Google Scholar] [CrossRef]
- Usman, M.T.; Abdulkadir, A. Review: An experiment in intra-seasonal agricultural drought monitoring and early warning in the Sudano-Sahelian Belt of Nigeria. Int. J. Climatol. 2014, 34, 2129–2135. [Google Scholar] [CrossRef]
- Oloruntade, A.J.; Mohammad, T.A.; Ghazali, A.H.; Wayayok, A. Analysis of meteorological and hydrological droughts in the Niger-South Basin, Nigeria. Glob. Planet. Chang. 2017, 155, 225–233. [Google Scholar] [CrossRef]
- Shiru, M.S.; Shahid, S.; Alias, N.; Chung, E.-S. Trend Analysis of Droughts during Crop Growing Seasons of Nigeria. Sustainability 2018, 10, 871. [Google Scholar] [CrossRef]
- Douglas, I.; Alam, K.; Maghenda, M.; McDonnel, Y.; McLean, L.; Campbell, J. Unjust waters: Climate change, flooding and the urban poor in Africa. Environ. Urban. 2008, 20, 187–205. [Google Scholar] [CrossRef]
- National Emergency Management Agency (NEMA). Worst Flooding in Decades. Available online: http://reliefweb.int/report/nigeria/worst-flooding-decades (accessed on 6 April 2020).
- Macdonald, A.M.; Cobbing, J.; Davies, J. Developing Groundwater for Rural Water Supply in Nigeria: A Report of the May 2005 Training Course and Summary of the Groundwater Issues in the Eight Focus States; British Geological Survey Commissioned Report, CR/05/219N; ITDG: Bradford, UK, 2005; p. 32. [Google Scholar]
- Adelana, S.M.A.; Olasehinde, P.I.; Vrbka, P. A quantitative estimation of groundwater recharge in part of the sokoto basin, Nigeria. J. Environ. Hydrol. 2006, 14, 1–14. [Google Scholar]
- Shiru, M.S.; Shahid, S.; Chung, E.-S.; Alias, N. Changing characteristics of meteorological droughts in Nigeria during 1901–2010. Atmos. Res. 2019, 223, 60–73. [Google Scholar] [CrossRef]
- World Bank Group. Agriculture, Value Added (% of GDP). Available online: http://data.worldbank.org/indicator/NV.AGR.TOTL.ZS (accessed on 18 April 2020).
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the global precipitation climatology Centre with sample applications including centennial (trend) analysis from 1901-present. Earth Syst. Sci. 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Clim. 2014, 34, 2792–2804. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Chung, E.-S.; Ismail, T.; Wang, X.-J. Spatial distribution of secular trends in annual and seasonal precipitation over Pakistan. Clim. Res. 2017, 74, 95–107. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Knutti, R.; Sedlácek, J. Robustness and uncertainties in the new CMIP5 climate model projections. Nat. Clim. Change 2013, 3, 369–373. [Google Scholar] [CrossRef]
- Akhter, J.; Das, L.; Deb, A. CMIP5 ensemble-based spatial rainfall projection over homogeneous zones of India. Clim. Dyn. 2017, 49, 1885–1916. [Google Scholar] [CrossRef]
- Moron, V.; Robertson, A.W.; Ward, M.N.; Ndiaye, O. Weather types and rainfall over Senegal, Part II: Downscaling of GCM simulations. J. Clim. 2008, 21, 288–307. [Google Scholar] [CrossRef]
- Hay, L.E.; Wilby, R.J.L.; Leavesley, G.H. A comparison of delta change and downscaled GCM scenarios for three mountainous basins in the United States. J. Am. Water Resour. Assoc. 2000, 36, 387–397. [Google Scholar] [CrossRef]
- Fowler, H.; Kilsby, C. Using regional climate model data to simulate historical and future river flows in northwest England. Clim. Chang. 2007, 80, 337–367. [Google Scholar] [CrossRef]
- Sharma, D.; Das Gupta, A.; Babel, M.S. Spatial disaggregation of bias-corrected GCM precipitation for improved hydrologic simulation: Ping River Basin, Thailand. Hydrol. Earth Syst. Sci. 2007, 11, 1373–1390. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Piani, C.; Weedon, G.P.; Best, M.; Gomes, S.M.; Viterbo, P.; Hagemann, S.; Haerter, J.O. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Mahmood, R.; JIA, S. An extended linear scaling method for downscaling temperature and its implication in the Jhelum River basin, Pakistan, and India, using CMIP5 GCMs. Theor. Appl. Climatol. 2017, 130, 725–734. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modelling of Extreme Values; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Leander, R.; Buishand, T.A. Resampling of regional climate model output for the simulation of extreme river flows. J. Hydrol. 2007, 332, 487–496. [Google Scholar] [CrossRef]
- Terink, W.; Hurkmans, R.T.W.L.; Torfs, P.J.J.F.; Uijlenhoet, R. Bias correction of temperature and precipitation data for regional climate model application to the Rhine basin. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 5377–5413. [Google Scholar] [CrossRef]
- Lenderink, G.; van Ulden, A.; van den Hurk, B.; Keller, F. A study on combining global and regional climate model results for generating climate scenarios of temperature and precipitation for the Netherlands. Clim. Dyn. 2007, 29, 157–176. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Manawi, S.M.A.; Nasir, K.A.M.; Shiru, M.S.; Hotaki, S.F.; Sediqi, M.N. Urban Flooding in the Northern Part of Kabul City: Causes and Mitigation. Earth Sys. Environ. 2020, 4, 569–610. [Google Scholar] [CrossRef]
- Adegoke, J.; Sylla, M.B.; Taylor, C.; Klein, C.; Bossa, A.; Kehinde Ogunjobi, K.; Adounkpe, J. On the 2017 Rainy Season Intensity and Subsequent Flood Events over West Africa. In Regional Climate Change Series: Floods; WASCAL: Accra, Ghana, 2019; pp. 10–15. [Google Scholar]
- Homsi, R.; Shiru, M.S.; Shahid, S.; Ismail, T.; Harun, S.; Al-Ansari, N.; Chau, K.-W.; Yaseen, Z.M. Precipitation projection using a CMIP5 GCM ensemble model: A regional investigation of Syria. Eng. Appl. Comput. Fluid Mech. 2020, 14, 90–106. [Google Scholar] [CrossRef]
- Jiang, M.; Felzer, B.S.; Sahagian, D. Predictability of precipitation over the conterminous US based on the CMIP5 multi-model ensemble. Sci. Rep. 2016, 6, 1–9. [Google Scholar]
- Palomino-Lemus, R.; Córdoba-Machado, S.; Gámiz-Fortis, S.R.; Castro-Díez, Y.; Esteban-Parra, M.J. Climate change projections of boreal summer precipitation over tropical America by using statistical downscaling from CMIP5 models. Environ. Res. Lett. 2017, 12, 124011. [Google Scholar] [CrossRef]
- Ruosteenoja, K.; Markkanen, T.; Venäläinen, A.; Räisänen, P.; Peltola, H. Seasonal soil moisture and drought occurrence in Europe in CMIP5 projections for the 21st century. Clim. Dyn. 2018, 50, 1177–1192. [Google Scholar] [CrossRef]
- Shiru, M.S.; Shahid, S.; Dewan, A.; Chung, E.-S.; Alias, N.; Ahmed, K.; Hassan, Q.K. Projection of meteorological droughts in Nigeria during growing seasons under climate change scenarios. Sci. Rep. 2020, 10, 1–18. [Google Scholar] [CrossRef]
- Obuobie, E.; Amisigo, B.; Logah, F.; Kankam-Yeboah, K. Analysis of changes in downscaled rainfall and temperature projections in the Volta River Basin. In Dams, Development and Downstream Communities: Implications for Re-Optimising the Operations of the Akosombo and Kpong Dams in Ghana; Ntiamoa-Baidu, Y., Ampomah, B.Y., Ofosu, E.A., Eds.; Digibooks Gh. Ltd.: Tema, Ghana, 2017. [Google Scholar]
- Abiodun, B.J.; Lawal, K.A.; Salami, A.T.; Abatan, A.A. Potential influences of global warming on future climate and extreme events in Nigeria. Reg. Environ. Chang. 2013, 13, 477–491. [Google Scholar] [CrossRef]
- Brekke, L.; Barsugli, J. Uncertainties in projections of future changes in extremes. In Extremes in a Changing Climate: Detection, Analysis and Uncertainty; AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 309–346. [Google Scholar]
- Strobach, E.; Bel, G. The contribution of internal and model variabilities to the uncertainty in CMIP5 decadal climate predictions. Clim. Dyn. 2017, 49, 3221–3235. [Google Scholar] [CrossRef]
- Woldemeskel, F.; Sharma, A.; Sivakumar, B.; Mehrotra, R. Quantification of precipitation and temperature uncertainties simulated by CMIP3 and CMIP5 models. J. Geophys. Res. Atmos. 2016, 121, 3–17. [Google Scholar] [CrossRef]
| No | Model Name | Resolution (Lon × Lat) | Institution |
|---|---|---|---|
| 1 | CESM1-CAM5 | 1.25 × 0.95 | National Center for Atmospheric Research, USA |
| 2 | CCSM4 | 1.25 × 0.95 | |
| 3 | BCC-CSM1.1(m) | 1.125 × 1.125 | Beijing Climate Center, China Meteorological Administration |
| 4 | BCC-CSM1-1 | 2.8 × 2.8 | |
| 5 | FIO-ESM | 2.8 × 2.8 | The First Institute of Oceanography, SOA, China |
| 6 | CSIRO-Mk3-6-0 | 1.875 × 1.875 | Commonwealth Scientific and Industrial Research Organization, Australia |
| 7 | MIROC5 | 1.4 × 1.4 | The University of Tokyo, National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology |
| 8 | MIROC-ESM-CHEM | 2.8 × 2.8 | |
| 9 | MIROC-ESM | 2.8 × 2.8 | |
| 10 | GISS-E2-R | 2.5 × 2.0 | NASA Goddard Institute for Space Studies |
| 11 | GISS-E2-H | 2.5 × 2.0 | |
| 12 | IPSL-CM5A-MR | 2.5 × 1.25 | Institut Pierre-Simon Laplace, France |
| 13 | IPSL-CM5A-LR | 3.75 × 1.875 | |
| 14 | HadGEM2-ES | 1.875 × 1.25 | Met Office Hadley Centre, UK |
| 15 | HadGEM2-AO | 1.875 × 1.25 | |
| 16 | GFDL-CM3 | 2.5 × 2.0 | Geophysical Fluid Dynamics Laboratory, USA |
| 17 | GFDL-ESM2M | 2.5 × 2.0 | |
| 18 | GFDL-ESM2G | 2.5 × 2.0 | |
| 19 | NorESM1-M | 2.5 × 1.875 | Norwegian Meteorological Institute, Norway |
| 20 | MRI-CGCM3 | 1.25 × 1.25 | Meteorological Research Institute |
| NRMSE | RSD | NSE | MD | VE | Pbias | |
|---|---|---|---|---|---|---|
| GAQM | 47.19 | 0.97 | 0.70 | 0.81 | 0.69 | 12.44 |
| GEQM | 91.45 | 0.47 | 0.12 | 0.63 | 0.3 | −40.11 |
| PT | 53.93 | 0.97 | 0.72 | 0.75 | 0.69 | 10.36 |
| LS | 24.87 | 0.98 | 0.90 | 0.89 | 0.83 | −0.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiru, M.S.; Park, I. Comparison of Ensembles Projections of Rainfall from Four Bias Correction Methods over Nigeria. Water 2020, 12, 3044. https://doi.org/10.3390/w12113044
Shiru MS, Park I. Comparison of Ensembles Projections of Rainfall from Four Bias Correction Methods over Nigeria. Water. 2020; 12(11):3044. https://doi.org/10.3390/w12113044
Chicago/Turabian StyleShiru, Mohammed Sanusi, and Inhwan Park. 2020. "Comparison of Ensembles Projections of Rainfall from Four Bias Correction Methods over Nigeria" Water 12, no. 11: 3044. https://doi.org/10.3390/w12113044
APA StyleShiru, M. S., & Park, I. (2020). Comparison of Ensembles Projections of Rainfall from Four Bias Correction Methods over Nigeria. Water, 12(11), 3044. https://doi.org/10.3390/w12113044






