Abstract
The aim of the present study is to apply the three-dimensional Princeton Ocean Model to study the wind effects on Kuroshio-induced island wake in the lee of Green Island, Taiwan. Numerical results indicate that the effect of NE winds squeezes the Kuroshio-induced island vortex street close to the coast and the SW winds tend to push the island vortex street farther away from the coast. The simulated vortex streets are analyzed by the dimensionless spatial lengths to quantify the prescribed feature. By comparing the three-dimensional results with different wind conditions, the Ekman transports are observed and the influence depths of wind effects are studied. Additionally, some cold eddies are found in temperature fields resulting from numerical simulations. These results are in qualitative agreement with field measurements and satellite images.
1. Introduction
The Kuroshio current originates from the North Equatorial Current and flows northward from Luzon Island to the eastern coast of Taiwan; the southward branch is the Mindanao Current [1,2,3]. In general, the Kuroshio current has a dimension of 100~150 km wide, 800 m deep, with a characteristic speed of 1.0–1.5 ms−1. The high-velocity core at 23.75° N ranges from 30–120 km wide near the coast of Taiwan [4]. If the Kuroshio’s core is divided into three parts in the vertical direction, its speeds are about 1.0 ms−1 in the top layer (0–200 m), 0.5 ms−1 in the middle layer (200–400 m), and 0.3 ms−1 in the bottom layer (400–800 m) [5,6].
As the Kuroshio transports water mass, heat, and salt from tropics, it affects the climate globally and also plays a crucial role in ocean-atmosphere interactions along this mainstream [7]. Therefore, the Kuroshio current is of not only regional but also basin-wide importance in the climate and ocean balance [8,9]. Several investigations have been conducted for the mass transport of the Kuroshio current. For example, Jan et al. [10] reported that the Kuroshio core transport varied between 10.5 and 22.9 Sv from ship-based surveys in September 2012 and September 2014, respectively. Additionally, the observations from the World Ocean Circulation Experiment [11] and Kuroshio Transport and Variability project [12] indicated that the Kuroshio transport are 21.5 ± 4.1 Sv (September 1994 to May 1996) and 17.2 ± 5% Sv (November 2012 to October 2014), respectively.
Since the Kuroshio current is known for its strong and fast flows all year around, it could be a potential source of marine energy [10]. Chen [13] predicted that the Kuroshio energy in the eastern coastal waters of Taiwan is about 30 GW and proposed several conceptual designs for the Kuroshio power plants. According to a report by Hsu et al. [14], Taiwan can significantly reduce its dependence on imported energy if the current energy of Kuroshio can be explored and used effectively. Furthermore, the Green Island is located at (121°29’ E, 22°39’ N) and 40 km off the southeastern coast of Taiwan with the passage of energetic Kuroshio and is usually considered as a site for the extraction of Kuroshio current energy. Usually, the plant site is selected to be located in the lee side of the Green Island to take off the Kuroshio current energy [14,15]. Therefore, Kuroshio-induced wake in the lee of Green Island is one of the main concerns for locating the current power site. By using the ensemble prediction system [16,17,18] with the present numerical model, the location of the current power site can be determined in the power plant design process.
It is well known that the so-called “von Kármán vortex sheet” is generated in the downstream when fluids flow passing a cylindrical body [19]. Based on the previous studies [20,21], the type of the wake and vortex shedding is classified by the Reynolds number , where , , and are the representative velocity, diameter of cylinder, and kinematic eddy viscosity, respectively. Following the description in Chapter 3 of Tritton’s book [22], the flow field is symmetric and laminar when . When , the flow field is no longer symmetric, and a laminar separation occurs with two attached eddies formed behind the cylindrical body. Sequentially, the periodic von Kármán vortex street can be observed as and the separated flow becomes turbulent as .
Based on the field data observed on the lee of the Green Island [23], the evaluated Reynolds number is about 91. Therefore, it is supposed that a periodic von Kármán vortex street is generated in the lee of the Green Island by the passing of the Kuroshio current. Several field observations were reported for the occurrence of the Kuroshio-induced wake in the lee of the Green Island [9,12,23,24,25,26]. For example, the Kuroshio-induced wake in the lee of the Green Island was observed by using the shipboard ADCP (Acoustic Doppler Current Profiler), CTD (Conductivity-temperature-depth) profiler [9,12,23], and the MODIS (Moderate Resolution Imaging Spectroradiometer) satellite image datasets [24,25,26]. These data can also be used to analyse the physical phenomena of the vortex shedding or to validate numerical models.
When wind blows over sea, its shear stresses induce ocean currents [27]. Ekman [28] indicated that the consequence of the Coriolis effect on the induced ocean currents is the Ekman transport, which is to the right of the wind direction in the northern hemisphere, as depicted in Figure 1. The previous studies [29,30] remarked that the path of the Kuroshio current changes seasonally. In Taiwan, northeasterly (NE) winds prevail from November to February and southwesterly (SW) winds appear from July to September [31]. Therefore, the Ekman transport is to push the main axis of the Kuroshio current farther from the eastern coast of Taiwan in the summer when compared with that in the winter [21].
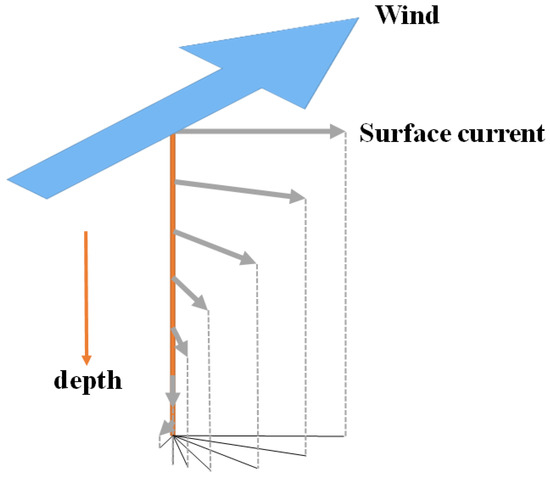
Figure 1.
Schamatic diagram of the Ekman sprial.
Although the monsoon effects on the Kuroshio current in the east of Taiwan were studied previously [4,32,33], their effects on the Kuroshio-induced wake in the lee of the Green Island are rarely studied, except for a two-dimensional numerical model [21] and surface satellite imagery [24]. These studies indicated that in the situation of SW winds, the monsoon effects tend to elongate the resulted vortex street. On the other hand, the resulted vortex street moves westerly by the Ekman transport in the NE winds during winter monsoon. Additionally, Hsu et al. [34] studied the typhoon effect on the Kuroshio-induced wake in the lee of the Green Island.
It was addressed in the literature [23,24,35,36] that current-induced island wakes result in colder, saltier water, with higher chlorophyll concentrations in the lee of the island. The prescribed phenomena often enhance biological productivity through the upwelling of colder water and turbulent mixing. By using the shipboard CTD profiler, Chang et al. [23] observed a cold eddy originating from the leeward side of the Green Island showed up 14 km downstream of the island. By analyzing the sea surface temperature (SST) from the satellite MODIS, it was convinced that the Kuroshio-induced wake also generates a lower SST feature in the lee of the Green Island.
Numerical models can be used to obtain the flow, temperature, and salinity fields of the Kuroshio-induced wake in the lee of the Green Island. Some of the previous researches were scenario studies driven by some artificial forcing conditions in two [21,26] and three dimensions [36]. Some other studies have focused on realistic simulations by real forcing conditions [14,34].
In the late 1970s, Blumberg and Mellor [37,38,39] developed the three-dimensional Princeton Ocean Model (3D POM), formulated in primitive equations with a second-moment turbulence closure sub-model [40,41] for the vertical mixing. Additionally, the vertical and horizontal spaces are discretized by a curvilinear sigma coordinate and orthogonal “Arakawa C” grids, respectively. In order to stabilize the time marching, the 3D POM uses the mode-splitting scheme, which integrates the barotropic (external) and baroclinic (internal) modes. A comprehensive review of the 3D POM can be found in the literature [42].
In this study, the 3D POM is utilized to simulate the flow field of Kuroshio-induced wake in the lee of the Green Island by the SW or NE wind conditions. In addition, temperature and salinity transports are also incorporated into the model. The accompanying three-dimensional cold eddies are also simulated and studied.
2. Materials and Methods
2.1. Numerical Model
In this study, the 3D POM is used to model the ocean current. The 3D POM is governed by the continuity equation, the hydrostatic equation, the conservations of horizontal momentums, temperature, and salinity, as well as, the turbulence closure condition as:
and
where , , , and are respectively the velocity, temperature, salinity, and pressure, which are functions of the Cartesian coordinates and time . , , and are the total density of the seawater, the reference density of the seawater, and the perturbation density, respectively. In addition, and are the vertical eddy viscosity diffusivities of turbulence of momentum mixing and heat, respectively. In the 3D POM, and are evaluated from the Level 2.5 turbulence closure model introduced by Mellor [43] and Mellor and Yamada [41]. Details can be found in [42]. Furthermore, and represent the gravity acceleration and the Coriolis force, respectively. Lastly, , , , and are diffusion coefficients, which are usually required to damp small scale numerical modes.
In the 3D POM, the vertical space is transformed to the curvilinear sigma coordinate by:
where and are the bottom topography and surface elevation, respectively. From Equation (7), it is clear to have and for and , respectively.
In the horizontal direction, the computation is performed in two nested domains as addressed in Table 1. In the TW model, the domain covers the region between 117° E–124.5° E and 18° N–26.5° N with horizontal resolution 1/50° × 1/50° (approximately 2 km), as depicted in Figure 2a. In the GI model, the local domain ranges in 120.88° E–122.5° E and 22.06° N–24.25° N with horizontal resolution 1/200° × 1/200° (approximately 0.5 km), as shown in Figure 2b. Here, the grid resolution of the GI model is set by following previous studies [14,36]. In addition, the computational domain of the GI model is embedded in the one-way nesting domain of the TW model and it provides the high-resolution results in the present study. In addition, there are 33 and 31 sigma levels in the TW and GI models, respectively.

Table 1.
The detailed configurations of the nested models.
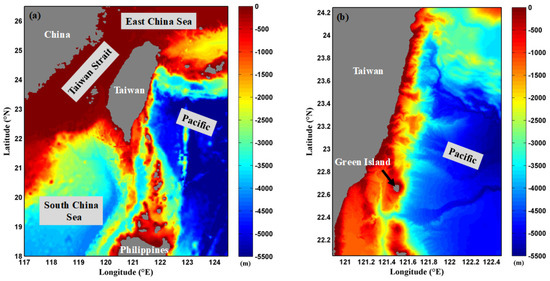
Figure 2.
Bathymetry of (a) the TW and (b) GI models.
It is well-known that the 3D POM uses the mode-splitting scheme to save the computing time [44,45]. Basically, the external mode is barotropic, two-dimensional, and with a shorter time step, DTE. In addition, the internal mode is baroclinic, three-dimensional, and with a longer time step, DTI, as addressed in Table 1.
Boundary conditions are required to close the problem. In both the TW and GI models, the boundary conditions of the external mode are the given elevation:
and the velocity radiation condition as
and
where and with being the depth-averaged velocity of the external mode, being the unit outward normal vector of the boundary, and being its corresponding unit tangential vector. In Equation (8), is the known surface elevation from the lower-resolution models, as addressed in Table 1.
Then, we consider the boundary conditions for the internal mode. For the temperature transport Equation (5), the upstream advection condition is imposed as:
where is the normal component of the horizontal velocity of internal mode. According to the 3D POM user guide [46], is evaluated by the upwind finite difference. If the water flows into the domain (), the finite difference is performed by the temperature of the previous time step on a boundary point and on a ghost point away from the boundary point. Here, is the known temperature from the lower-resolution models, as addressed in Table 1. The boundary condition for the salinity transport Equation (6) is the same and thus neglected here.
For the velocity boundary conditions of the internal mode, the radiation condition is imposed for the TW model as:
and
where is the tangential component of the horizontal velocity of internal mode and is the baroclinic phase speed defined in the 3D POM user guide [46]. For the GI model, the inflow condition is imposed as:
and
where and are the known velocity components from the lower-resolution TW model.
In summary, the boundary driving forces of the TW model are the surface elevation, temperature, and salinity from the HYCOM [47]. The boundary driving forces of the GI model are the temperature, salinity, and velocity from the TW model in addition to the composed surface elevation of the TOPEX tidal model [48,49] and the TW model. To make the nested model more stable, the nudging scheme [50,51] is applied to smooth the input data in the spatial coordinates. In addition, the wind forcing conditions are imposed in the domain from the depth-integrated governing equation of the external mode. The detailed formulation can be found in the 3D POM user guide [46].
2.2. Data
The ocean datasets are required to drive the prescribed model, as depicted in Figure 3. This will be introduced in the following section.
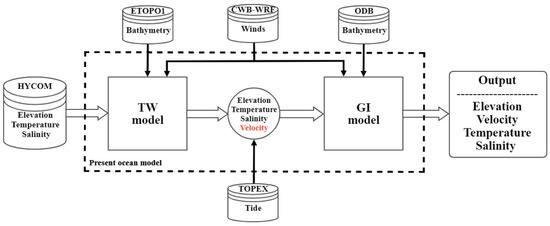
Figure 3.
The driving forces of the present model.
2.2.1. Bathymetry Data
Bathymetry data is combined by the ETOPO1 [52] and ODB [53] data. Here, the ETOPO1 is a bathymetry dataset which is available in resolutions up to 1.8 km. The ODB bathymetry dataset is provided in resolutions up to 200 m. The ETOPO1 and ODB bathymetry datasets are used in the TW and GI models, respectively.
2.2.2. Winds Data
In Taiwan, the Weather Research and Forecasting (WRF) model has been operationally used since 1997 by the Central Weather Bureau (CWB) of Taiwan to forecast regional wind and weather [54]. The WRF is used as the numerical weather prediction at the National Center for Atmospheric Research (NCAR) of National Center for Environmental Predictions (NCEP). In this study, the CWB-WRF wind dataset is adopted as the wind forcing condition. The CWB-WRF wind dataset covers a domain at 10° E to 35° E and 110° N to 137° N and it has spatial and temporal resolutions of 0.25 degree and 3 h, respectively. Wind data are used in the external mode of both the TW and GI models
2.2.3. HYCOM Data
In the TW model, the boundary driving forces of surface elevation, temperature, and salinity are obtained from the Global Hybrid Coordinate Ocean Model (HYCOM) [47], whose spatial and time resolution are about 1/12 degree and 1 day, respectively. In addition, these data are also used as the initial conditions to warm up the present model.
2.2.4. Tidal-Force Data
Since the HYCOM data do not include the tidal effect, the results of the TW model contain no tidal effect as well. Therefore, the boundary driving forces of the surface elevation for the high-resolution GI model has to be set by the superposition of the TOPEX global tidal model [48,49] data and the resulting surface elevation of the TW model. Here, the TOPEX tidal data has a resolution of 1/30 degree on the computational boundary of the GI model. In the TOPEX tidal data, 11 major constituents (M2, S2, N2, K2, K1, O1, P1, Q1, M4, Mm, and Mf) are included.
3. Results
3.1. Model Validation
In order to validate the proposed model, we first performed a simulation from 3 September to 18 September 2010, UTC. The numerical results are compared with the data from the tidal station, the MODIS satellite image dataset, and the results of the Argo Program for surface elevation, surface vortex shedding characteristics, as well as the vertical profiles of temperature and salinity, respectively.
The surface elevation obtained by the present model is compared with the measurements from the Green Island tidal station, which is located at latitude 22.65° N and longitude 121.45° E near the Nanliao Fishery Harbor of the Green Island, as shown in Figure 4. The time histograms of surface elevations from the measurements and numerical model are presented in Figure 5. From the figure, the root mean square errors (RMSE) between the numerical result and the in-situ data can be evaluated to be 0.067 m with Nash–Sutcliffe efficiency [55] equal to 0.97, which shows an excellent agreement. This result indicates that the present model is able to simulate the tidal effect well.
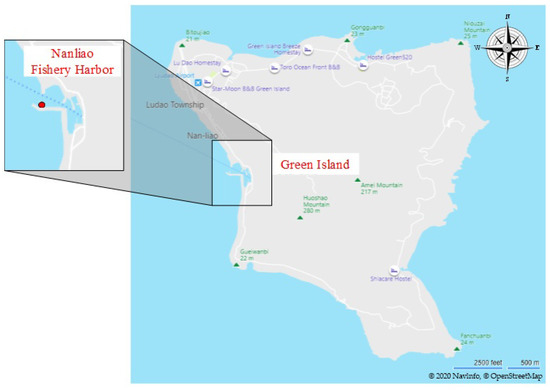
Figure 4.
The geographic location of the NanLiao fishery harbor in Green Island; the red dots show the Green Island tidal station.
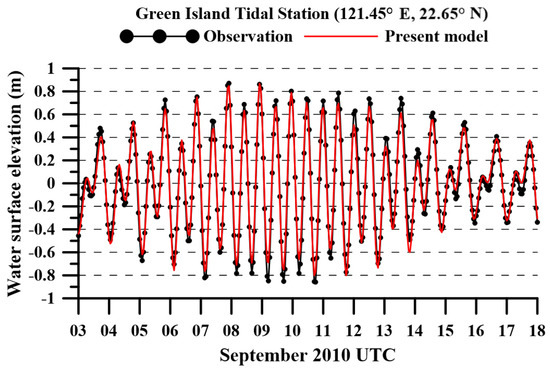
Figure 5.
Historical water surface elevation at the Green Island tidal station.
Then, the surface streamline obtained by the present model is compared with the datasets from the MODIS satellite images [23]. In Figure 6, the MODIS satellite image and the computed surface streamlines are shown to have similar vortex shedding characteristics. Here, the satellite data is adopted at A.M. 4:55 15 September 2010, UTC. These results show that the proposed model is capable of simulating well the surface velocity field of the Kuroshio-induce vortex shedding in the leeward side of the Green Island.
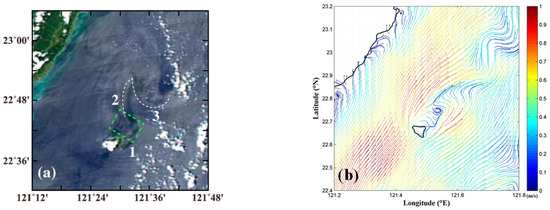
Figure 6.
Vortex shedding characteristics from the (a) MODIS satellite image and (b) the present model.
Finally, the vertical profiles of the temperature and salinity by the present model is compared with the measurements from the Argo Program [56]. The Argo Program has created the first global array for observing the subsurface ocean and provides a large amount of data with high temporal and spatial resolutions. In this study, the data are adopted from the US Argo, supported by the National Oceanic and Atmospheric Administration and the US Navy. Figure 7 depicts the vertical profiles of the temperature and salinity from the Argo measurement and numerical model, which are in good agreement. These results demonstrate that the proposed model can simulate the vertical profiles of the temperature and salinity as well.
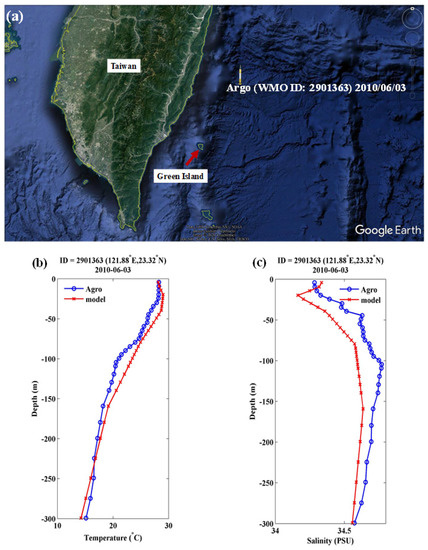
Figure 7.
(a) Location of the Argo station as well as the measured; (b) temperature and (c) salinity profiles of the Argo data and the present model.
3.2. Input Wind Data
Before preforming deeper studies on the numerical vortex shedding, the input wind field from the CWB-WRF dataset will be studied. As the simulation is focused on the period of September 2010, a wind rose chart for the period is provided in Figure 8 based on the automatic weather station, called C0S730, located on 121.48 E and 22.67 N [57]. From the figure, it is obvious that SW winds dominate in September 2010 and the average wind speed is about 3~7 m/s. This is consistent with the previous study [31] that showed SW winds dominating from July to September in Taiwan.
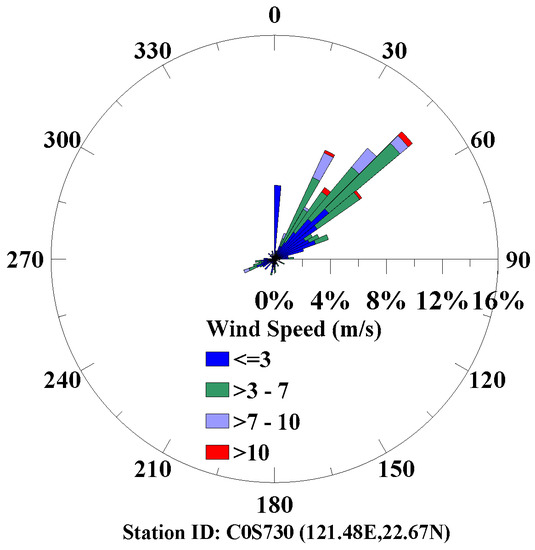
Figure 8.
Wind rose chart for September 2010.
In addition to wind data on a specific location, the wind field in the computational domain at 01:00 UTC on 9 September 2010 is obtained from the observation of the satellite scatterometer ASCAT [58]. The ASCAT provides wind field datasets by daily gridded files with spatial resolution of 0.5° [59]. In Figure 9a, the wind fields of the CWB-WRF and satellite ASCAT datasets are compared and a good agreement can be observed. In addition, the average wind speeds are 3.82 and 3.63 m/s for the CWB-WRF and satellite ASCAT datasets, respectively. As the CWB-WRF datasets have higher spatial and temporal resolutions (0.25 degree and 3 h), they are adopted as the input wind data in the present model. Additionally, Figure 9b depicts the corresponding SST and the surface velocity fields obtained by the present model under the CWB-WRF wind datasets. In the figure, it is also clear that the main axis of the Kuroshio-induced wake is closer to the coast as the wind is mainly in the NE direction at 01:00 UTC on 9 September 2010. More details of the wind effects on the vortex shedding will be given in the following section.
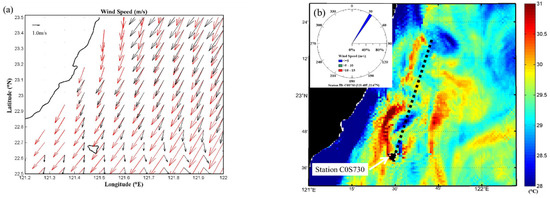
Figure 9.
(a) Wind fields of the CWB-WRF (red arrows) and satellite ASCAT (black arrows) datasets as well as (b) numerical SST and velocity fields at 01:00 UTC on 9 September 2010.
3.3. Cold Eddy and Wind Effect
In the literature [23,24,35,36], it is indicated that the Kuroshio-induce wakes result in the upwelling of colder and saltier water in the leeward side of the Green Island. By analyzing the SST from the satellite image, Chang et al. [23] found a lower SST in the lee of the Green Island.
Additionally, Hsu et al. [21] studied the wind effects on the Kuroshio-induced wake in the lee of the Green Island by a two-dimensional numerical model. The results demonstrated that the main axis of the Kuroshio-induced wake is pushed farther away from the eastern coast of Taiwan in SW winds when compared with that in NE winds.
By analyzing the SST from the VIIRS-NPP satellite image, we found several cold eddies in both the SW and NE wind conditions, as shown in Figure 10. In the figure, it is obvious that the Ekman transport pushes the main axis of the Kuroshio-induced wake farther from the coast in the SW wind when compared with that in the NE wind. Here, the VIIRS-NPP satellite dataset has a resolution of 1.6 km [60]. It is organized by the National Oceanic and Atmospheric Administration (NOAA) and is a significant advancement from its heritage of MODIS satellite image datasets [61].
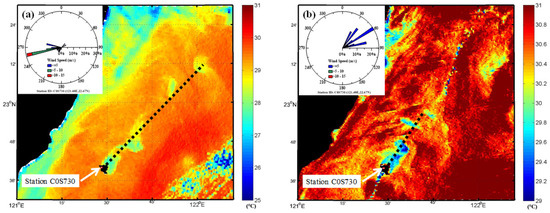
Figure 10.
VIIRS-NPP SST images under (a) the SW wind condition at 18:00 UTC on 8 August 2017 and (b) the NE wind condition at 05:00 UTC on 11 September 2017.
The wind effects on the Kuroshio-induced wake are also studied by the present numerical model. Figure 11 depicts the SST and surface velocity fields obtained by the present model under the simulated SW and NE wind conditions. As depicted in Figure 12, the real SW and NE wind conditions are set by the CWB-WRF wind datasets at 4:00 UTC on 11 September 2010 and at 20:00 UTC on 20 September 2010, respectively. At these two specific time instances, the wind fields are shown to be more steady, both in spatial and temporal domains. In the figure, it is also clear that the main axis of the Kuroshio-induced wake is closer to the coast during the NE wind than it is during the SW wind.
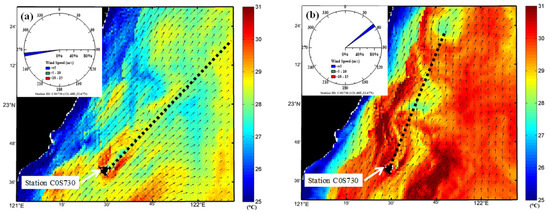
Figure 11.
Numerical SST and velocity fields under (a) the SW wind condition and (b) the NE wind condition.
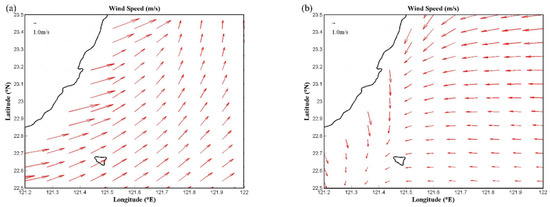
Figure 12.
Velocity fields of (a) the SW wind condition and (b) the NE wind condition.
4. Discussion
In order to further discuss the wind effects on the Kuroshio-induced wake in the leeward side of the Green Island, two scenario studies based on different wind conditions are performed and the three-dimensional results are discussed.
4.1. Real and No Wind Conditions
In the previous subsection, the proposed model is applied to study the Kuroshio-induced wakes under the real SW and NE wind conditions, which are based on the CWB-WRF wind datasets at the two specific time instances. Here, we perform a scenario study where the wind inputs of the TW and GI models are removed. In other words, the results of real and no wind conditions, as in Table 2, are compared. It needs to be mentioned that the boundary conditions of the TW model are imposed from the HYCOM, which is still affected by winds. However, the wind effect should be limited as it only affects the numerical results near the boundary of the low-resolution TW model.

Table 2.
The wind conditions in this study.
Figure 13 depicts the surface velocity fields and SST obtained by the present model with real SW and no wind conditions at 4:00 UTC on 11 September 2010. The Ekman transport indicates that the consequence of the Coriolis effect is to the right of the wind direction in the northern hemisphere. Therefore, in the situation of SW wind, the wind effects tend to elongate the resulted vortex street or push the main axis of the Kuroshio-induced wake farther from the coast. From our results, it is obvious that the Ekman transport pushes the main axis of the Kuroshio-induced wake farther from the coast in the SW wind condition, as in Figure 13a,c, when compared with the results in Figure 13b,d by the no wind condition. In additions, cold eddies are significant in the leeward side of Green Island, as shown in Figure 13c,d.
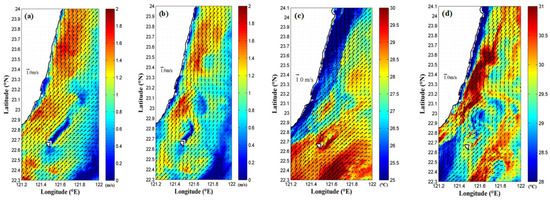
Figure 13.
The surface velocity fields of the results obtained by (a) real SW and (b) no wind conditions as well as the SST of the results obtained by (c) real SW and (d) no wind conditions.
In addition, Figure 14 shows the surface velocity fields and SST obtained by the present model with real NE and no wind conditions at 20:00 UTC on 20 September 2010. As the main axis of the Kuroshio-induced wake obtained by the present model with no wind condition is already close to the coast, the effect of Ekman transport is limited when the results from the NE wind condition is considered. In addition, cold eddies are also significant in the leeward side of Green Island, as shown in Figure 14c,d.
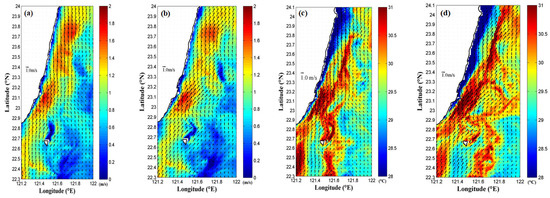
Figure 14.
The surface velocity fields of the results obtained by (a) real NE and (b) no wind conditions as well as the SST of the results obtained by (c) real NE and (d) no wind conditions.
As the Ekman transport has a more significant effect on the Kuroshio-induced wakes under the SW wind condition than that under the NE wind condition, three-dimensional results are studied for the scenario of the SW wind condition. Figure 15 depicts velocity fields at water depths of 20, 50, 100, and 150 m for the numerical results obtained by the present model with the real SW and no wind conditions at 4:00 UTC on 11 September 2010. In the figure, the Ekman transport is significant at water depths of 20 and 50 m. This indicates that the Ekman transport can affect the Kuroshio-induced wakes to approximately 50 m depth, whereas the vortex shedding occurs deeper than 150 m. A more detailed study on the combined effects of the Ekman transport and the three-dimensional vortex tube needs extra-higher-resolution simulations, which still require further investigations.
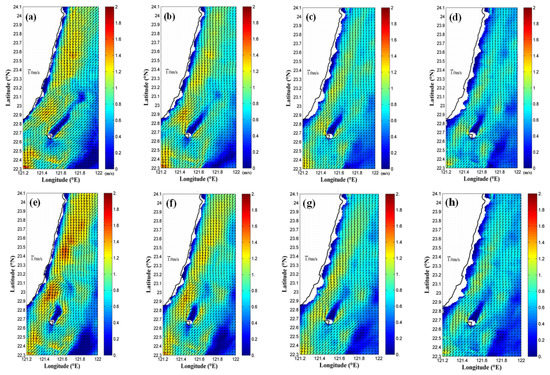
Figure 15.
The velocity fields at water depths of (a,e) 20, (b,f) 50, (c,g) 100, and (d,h) 150 m of the numerical results obtained by (a–d) real SW and (e–h) no wind conditions.
4.2. Constant Wind Fields
The second scenario study is considered: when the real wind condition is replaced by 10 m/s constant wind fields in SW and NE directions, as in Table 2. Figure 16 depicts the surface velocity fields and SST obtained by the present model with constant SW and NE wind conditions at 19:00 UTC on 9 September 2010. In the figure, it is obvious that the SW wind effect tends to push the main axis of the Kuroshio-induced wake farther from the coast when compared with the results in the constant NE wind condition. In addition, cold eddies are also significant in the leeward side of Green Island as shown in Figure 16c,d.
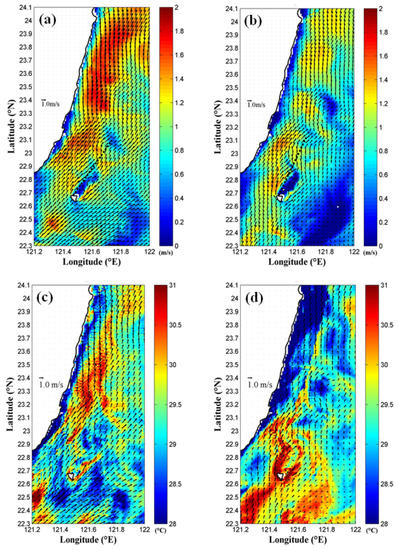
Figure 16.
The surface velocity fields of the results obtained by (a) constant SW and (b) NE wind conditions as well as the SST of the results obtained by (c) the constant SW and (d) NE wind conditions.
The three-dimensional results are also studied. Figure 17 depicts the velocity fields at water depths of 20, 50, 100, and 150 m for the numerical results obtained by the present model with constant SW and NE wind conditions at 19:00 UTC on 9 September 2010. In the figure, the Ekman transport is also significant at water depths of 20 and 50 m. When compared to the results of the real wind condition in Figure 15c,g, the present results at the same water depth of 100 m in Figure 17c,g depicts that the Ekman transport can also be observed at this depth. As the wind duration is long for the present scenario study, the results indicate that the constant wind fields can affect the Kuroshio-induced wakes to approximately 100 m depth and the vortex shedding occurs deeper than 150 m.
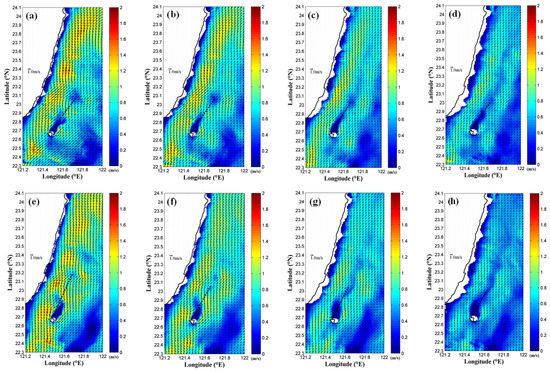
Figure 17.
The velocity fields at water depths of (a,e) 20, (b,f) 50, (c,g) 100, and (d,h) 150 m of the numerical results obtained by (a–d) constant SW and (e–h) NE wind conditions.
4.3. Characteristics of Vortex Streets
The characteristics of vortex shedding can be described by dimensionless spatial lengths. First, the streamwise length (a), transverse length (b), and diameter (L) are defined as depicted in Figure 18. In this study, the diameter of Green island is set to L = 7 km, as per a previous study [24]. Following Hsu et al. [14], the aspect ratio and dimensionless width are defined as Ar = a/b and Br = b/L, respectively. Table 3 addresses the dimensionless spatial lengths of the simulated vortex streets and results in the literature. In the table, it can be observed that larger aspect ratios and smaller dimensionless widths are resulted when the wind conditions tend to elongate the vortex street. On the other hand, smaller aspect ratios are found when the results of the wind conditions squeeze the simulated vortex streets to the coast. In the table, it is found that these trends of wind effects on Kuroshio-induced vortex streets are similar to those in the literature [24].
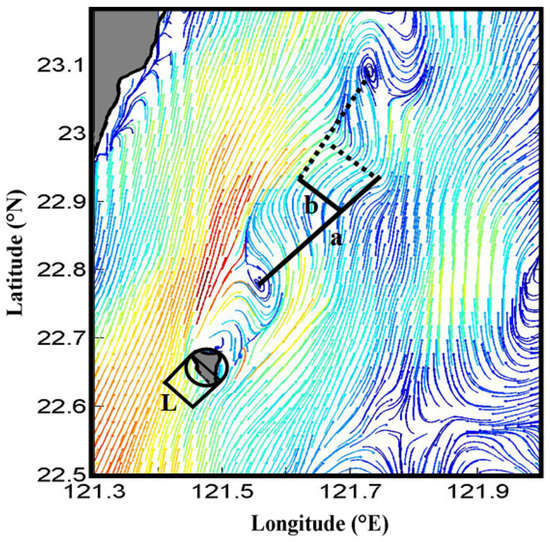
Figure 18.
Schematic diagram for several definitions of vortex streets.

Table 3.
Characteristics of Green Island vortex streets.
5. Conclusions
The 3D POM is used to simulate three-dimensional Kuroshio-induced vertex streets downstream of Green Island. The model is implemented in two nested domains and driven by the surface elevation, temperature, and salinity on the boundary as well as the input wind fields in the computational domain. Tidal effects were also included into the boundary driving force of the surface elevation. Some significant vortex streets at different water depths were found in the numerical results. In order to validate the proposed model, the numerical results were compared with the data from the tidal station, the MODIS satellite image dataset, and the results of the Argo Program for surface elevation, surface vortex shedding characteristics, as well as the vertical profiles of temperature and salinity, respectively. Good agreements were found.
Two scenario studies based on different wind conditions were also performed to study wind effects on the Kuroshio-induced wakes in the leeward side of the Green Island. As the Ekman transport is to the right of the wind direction in the northern hemisphere, our numerical results demonstrated that in the situation of SW winds, the wind effects tend to push the main axis of the Kuroshio-induced wake farther from the coast and elongate the resulted vortex street when compared with the results in the NE wind conditions. Numerical results indicated that the aspect ratio, defined by streamwise length over transverse length, is 3.54 under the constant SW wind condition, which is much larger than 1.86 under the constant NE wind condition. The numerical results also depicted that the Ekman transport is significant at water depths of 20 and 50 m. By comparing the three-dimensional results with different wind conditions, it was found that the influence depth of wind effect is about 50 to 100 m deep whereas the vortex shedding occurs deeper than 150 m. In addition, some cold eddies are found in temperature fields resulting from our numerical data.
Recently, climate changes have intensified typhoons around Taiwan [62]. If the low pressure condition can be imposed into the present model, it can be used to study the combined effects of typhoon wind field and storm surge [63] on the Kuroshio-induced vertex streets downstream of Green Island. This is currently under investigation.
Author Contributions
Conceptualization, T.-H.H., J.-Y.C., C.-C.T., and T.-W.H.; formal analysis, T.-H.H.; funding acquisition, J.-Y.C., C.-C.T., and T.-W.H.; methodology, J.-Y.C. and C.-C.T.; software, T.-H.H. and J.-Y.C.; supervision, C.-C.T. and T.-W.H.; visualization, T.-H.H.; writing—original draft, T.-H.H. and C.-C.T.; writing—review & editing, T.-H.H., J.-Y.C., C.-C.T., and T.-W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by the Ministry of Science and Technology, Taiwan, under grant no. MOST 109-2221-E-992-046-MY3 and MOST 109-2811-E-992-501-MY3.
Acknowledgments
The authors greatly appreciate the support provided by the Ministry of Science and Technology, Taiwan.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yaremchuk, M.; Qu, T. Seasonal variability of the large-scale currents near the coast of the Philippines. J. Phys. Oceanogr. 2004, 34, 844–855. [Google Scholar] [CrossRef]
- Centurioni, L.R.; Niiler, P.P.; Lee, D.-K. Observations of inflow of Philippine Sea surface water into the South China Sea through the Luzon Strait. J. Phys. Oceanogr. 2004, 34, 113–121. [Google Scholar] [CrossRef]
- Nitani, H. Beginning of the Kuroshio, in Kuroshio. Phys. Asp. Jpn. Curr. 1972, 129–163. [Google Scholar]
- Hsin, Y.C.; Wu, C.R.; Shaw, P.T. Spatial and temporal variations of the Kuroshio east of Taiwan, 1982–2005: A numerical study. J. Geophys. Res. Ocean. 2008, 113, C04002. [Google Scholar] [CrossRef]
- Shen, H.-C.; Wang, Y.-H. Topography induced flow variations between Taitung-Lutao off Southeast Taiwan. Master‘s Thesis, National Sun Yat-sen University, Gaoxiong, Taiwan, 2012. [Google Scholar]
- Jan, S.; Wang, S.-H.; Yang, K.-C.; Yang, Y.J.; Chang, M.-H. Glider observations of interleaving layers beneath the Kuroshio primary velocity core east of Taiwan and analyses of underlying dynamics. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kwon, Y.-O.; Alexander, M.A.; Bond, N.A.; Frankignoul, C.; Nakamura, H.; Qiu, B.; Thompson, L.A. Role of the Gulf Stream and Kuroshio–Oyashio systems in large-scale atmosphere–ocean interaction: A review. J. Clim. 2010, 23, 3249–3281. [Google Scholar] [CrossRef]
- Andres, M.; Park, J.-H.; Wimbush, M.; Zhu, X.-H.; Chang, K.-I.; Ichikawa, H. Study of the Kuroshio/Ryukyu Current system based on satellite-altimeter and in situ measurements. J. Oceanogr. 2008, 64, 937–950. [Google Scholar] [CrossRef]
- Chang, M.-H.; Jan, S.; Mensah, V.; Andres, M.; Rainville, L.; Yang, Y.J.; Cheng, Y.-H. Zonal migration and transport variations of the Kuroshio east of Taiwan induced by eddy impingements. Deep Sea Res. Part I Oceanogr. Res. Pap. 2018, 131, 1–15. [Google Scholar] [CrossRef]
- Jan, S.; Yang, Y.J.; Wang, J.; Mensah, V.; Kuo, T.H.; Chiou, M.D.; Chern, C.S.; Chang, M.H.; Chien, H. Large variability of the Kuroshio at 23.75 N east of Taiwan. J. Geophys. Res. Ocean. 2015, 120, 1825–1840. [Google Scholar] [CrossRef]
- Johns, W.E.; Lee, T.N.; Zhang, D.; Zantopp, R.; Liu, C.-T.; Yang, Y. The Kuroshio east of Taiwan: Moored transport observations from the WOCE PCM-1 array. J. Phys. Oceanogr. 2001, 31, 1031–1053. [Google Scholar] [CrossRef]
- Chang, M.-H.; Jan, S.; Liu, C.-L.; Cheng, Y.-H.; Mensah, V. Observations of island wakes at high Rossby numbers: Evolution of submesoscale vortices and free shear layers. J. Phys. Oceanogr. 2019, 49, 2997–3016. [Google Scholar] [CrossRef]
- Chen, F. The Kuroshio Power Plant; Springer: London, UK, 2013. [Google Scholar]
- Hsu, T.-W.; Liau, J.-M.; Liang, S.-J.; Tzang, S.-Y.; Doong, D.-J. Assessment of Kuroshio current power test site of Green Island, Taiwan. Renew. Energy 2015, 81, 853–863. [Google Scholar] [CrossRef]
- Tang, T.; He, C.; Wang, Y.; Jan, S.; Hsu, S.; Wen, L.; Yang, T.; Song, S.; Chen, H.; Song, G. Comprehensive Research on the Natural Resources of the East Waters of Taiwan: A Precisely Topographic, Geological, Hydrological, and Ecological Surveys of the Waters around Green Island; National Science Council: Taipei, Taiwan, 2008.
- Mel, R.; Sterl, A.; Lionello, P. High resolution climate projection of storm surge at the Venetian coast. Nat. Hazards Earth Syst. Sci. 2013, 13, 1135–1142. [Google Scholar] [CrossRef]
- Mel, R.; Lionello, P. Probabilistic Dressing of a Storm Surge Prediction in the Adriatic Sea. Adv. Meteorol. 2016, 2016, 3764519. [Google Scholar] [CrossRef]
- Flowerdew, J.; Horsburgh, K.; Wilson, C.; Mylne, K. Development and evaluation of an ensemble forecasting system for coastal storm surges. Q. J. R. Meteorol. Soc. 2010, 136, 1444–1456. [Google Scholar] [CrossRef]
- Von Kármán, T. Aerodynamics; McGraw-Hill: New York, NY, USA, 1954; p. 203. [Google Scholar]
- Jiménez, B.; Sangra, P.; Mason, E. A numerical study of the relative importance of wind and topographic forcing on oceanic eddy shedding by tall, deep water islands. Ocean Model. 2008, 22, 146–157. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Doong, D.-J.; Hsieh, K.-J.; Liang, S.-J. Numerical Study of Monsoon Effect on Green Island Wake. J. Coast. Res. 2015, 31, 1141–1150. [Google Scholar] [CrossRef]
- Tritton, D.J. Physical Fluid Dynamics; Van Nostrand Reinhold Company: New York, NY, USA, 1977. [Google Scholar]
- Chang, M.H.; Tang, T.Y.; Ho, C.R.; Chao, S.Y. Kuroshio-induced wake in the lee of Green Island off Taiwan. J. Geophys. Res. Ocean 2013, 118, 1508–1519. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Chang, M.-H.; Lin, C.-C.; Huang, S.-J.; Ho, C.-R. Investigation of the island-induced ocean vortex train of the Kuroshio Current using satellite imagery. Remote Sens. Environ. 2017, 193, 54–64. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Cheng, K.-H.; Jan, S.; Lee, H.-J.; Ho, C.-R. Vertical structure and surface patterns of Green Island wakes induced by the Kuroshio. Deep Sea Res. Part I Oceanogr. Res. Pap. 2019, 143, 1–16. [Google Scholar] [CrossRef]
- Huang, S.-J.; Ho, C.-R.; Lin, S.-L.; Liang, S.-J. Spatial-temporal scales of Green Island wake due to passing of the Kuroshio current. Int. J. Remote Sens. 2014, 35, 4484–4495. [Google Scholar] [CrossRef]
- Mel, R.; Carniello, L.; D’Alpaos, L. Addressing the effect of the Mo.S.E. barriers closure on wind setup within the Venice lagoon. Estuar. Coast. Shelf Sci. 2019, 225, 106249. [Google Scholar] [CrossRef]
- Ekman, V.W. On the Influence of the Earth’s Rotation on Ocean-Currents; ProQuest: Ann Arbor, MI, USA, 1905. [Google Scholar]
- Chao, S.-Y. Circulation of the East China Sea, a numerical study. J. Oceanogr. 1990, 46, 273–295. [Google Scholar] [CrossRef]
- Su, J.; Guan, B.; Jiang, J. The kuroshio. Part i. Physical. Oceanogr. Mar. Biol. 1990, 28, 11–71. [Google Scholar]
- Tung, Y.-S.; Wang, S.-Y.S.; Chu, J.-L.; Wu, C.-H.; Chen, Y.-M.; Cheng, C.-T.; Lin, L.-Y. Projected increase of the East Asian summer monsoon (Meiyu) in Taiwan by climate models with variable performance. Meteorol. Appl. 2020, 27, e1886. [Google Scholar] [CrossRef]
- Sheu, W.-J.; Wu, C.-R.; Oey, L.-Y. Blocking and westward passage of eddies in the Luzon Strait. Deep Sea Res. Part II Top. Stud. Oceanogr. 2010, 57, 1783–1791. [Google Scholar] [CrossRef]
- Hsin, Y.-C.; Qiu, B.; Chiang, T.-L.; Wu, C.-R. Seasonal to interannual variations in the intensity and central position of the surface Kuroshio east of Taiwan. J. Geophys. Res. Oceans 2013, 118, 4305–4316. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Chou, M.-H.; Hou, T.-H.; Liang, S.-J. Typhoon effect on Kuroshio and Green Island wake: A modelling study. Ocean Sci. Discuss. 2015, 12, 3199–3233. [Google Scholar] [CrossRef]
- Zheng, Z.-W.; Zheng, Q. Variability of island-induced ocean vortex trains, in the Kuroshio region southeast of Taiwan Island. Cont. Shelf Res. 2014, 81, 1–6. [Google Scholar] [CrossRef]
- Liu, C.L.; Chang, M.H. Numerical Studies of Submesoscale Island Wakes in the Kuroshio. J. Geophys. Res. Ocean 2018, 123, 5669–5687. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Mellor, G.L. Whole Basin Model of the Gulf of Mexico; Dynalysis of Princeton: Princeton, NJ, USA, 1979. [Google Scholar]
- Blumberg, A.F.; Mellor, G.L. A coastal ocean numerical model. In Mathematical Modelling of Estuarine Physics; Springer: Berlin, Germany, 1980; pp. 203–219. [Google Scholar]
- Blumberg, A.F.; Mellor, G.L. A Numerical Calculation of the Circulation in the Gulf of Mexico; Dynalysis of Princeton: Princeton, NJ, USA, 1981. [Google Scholar]
- Mellor, G.L.; Yamada, T. A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci. 1974, 31, 1791–1806. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Mellor, G.L. A description of a three-dimensional coastal ocean circulation model. Three-Dimens. Coast. Ocean Models 1987, 4, 1–16. [Google Scholar]
- Mellor, G.L. Analytic Prediction of the Properties of Stratified Planetary Surface Layers. J. Atmos. Sci. 1973, 30, 1061–1069. [Google Scholar] [CrossRef]
- Madala, R.V.; Piacseki, S.A. A semi-implicit numerical model for baroclinic oceans. J. Comput. Phys. 1977, 23, 167–178. [Google Scholar] [CrossRef]
- Simons, T.J. Verification of numerical models of Lake Ontario: Part I. Circulation in spring and early summer. J. Phys. Oceanogr. 1974, 4, 507–523. [Google Scholar] [CrossRef]
- Mellor, G.L. Users Guide for a Three Dimensional, Primitive Equation, Numerical Ocean Model; Princeton University: Princeton, NJ, USA, 1998. [Google Scholar]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. Ocean 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Anthes, R.A. Data assimilation and initialization of hurricane prediction models. J. Atmos. Sci. 1974, 31, 702–719. [Google Scholar] [CrossRef]
- Hoke, J.E.; Anthes, R.A. The initialization of numerical models by a dynamic-initialization technique. Mon. Weather Rev. 1976, 104, 1551–1556. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; US Department of Commerce, National Oceanic and Atmospheric Administration, National Environmental Satellite, Data, and Information Service, National Geophysical Data Center, Marine Geology and Geophysics Division Colorado: Washington, DC, USA, 2009.
- MOST. Ocean Data Bank of the Ministry of Science and Technology. Available online: http://www.odb.ntu.edu.tw (accessed on 10 August 2019).
- Liou, C.-S.; Chen, J.-H.; Terng, C.-T.; Wang, F.-J.; Fong, C.-T.; Rosmond, T.E.; Kuo, H.-C.; Shiao, C.-H.; Cheng, M.-D. The second-generation global forecast system at the Central Weather Bureau in Taiwan. Weather Forecast. 1997, 12, 653–663. [Google Scholar] [CrossRef][Green Version]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Roemmich, D.; Johnson, G.C.; Riser, S.; Davis, R.; Gilson, J.; Owens, W.B.; Garzoli, S.L.; Schmid, C.; Ignaszewski, M.J.O. The Argo Program: Observing the global ocean with profiling floats. Oceanography 2009, 22, 34–43. [Google Scholar] [CrossRef]
- Li, C.C.; Chang, M.H.; Chen, Y.C. Oceanic typhoon rainfall estimation using Advanced Microwave Sounding Unit-A data. Int. J. Remote Sens. 2006, 27, 1477–1490. [Google Scholar] [CrossRef]
- Bentamy, A.; Croize-Fillon, D.J.I.T.R. Daily ASCAT Surface Wind Fields; IFREMER Technology Report; Laboratoire d‘Oceanographie Spatiale: Paris, France, 2015. [Google Scholar]
- Saldías, G.S.; Largier, J.L.; Mendes, R.; Pérez-Santos, I.; Vargas, C.A.; Sobarzo, M. Satellite-measured interannual variability of turbid river plumes off central-southern Chile: Spatial patterns and the influence of climate variability. Prog. Oceanogr. 2016, 146, 212–222. [Google Scholar] [CrossRef]
- Miller, S.D.; Hawkins, J.D.; Kent, J.; Turk, F.J.; Lee, T.F.; Kuciauskas, A.P.; Richardson, K.; Wade, R.; Hoffman, C. NexSat: Previewing NPOESS/VIIRS imagery capabilities. Bull. Am. Meteorol. Soc. 2006, 87, 433–446. [Google Scholar] [CrossRef]
- Hillger, D.; Kopp, T.; Lee, T.; Lindsey, D.; Seaman, C.; Miller, S.; Solbrig, J.; Kidder, S.; Bachmeier, S.; Jasmin, T.J. First-light imagery from Suomi NPP VIIRS. Bull. Am. Meteorol. Soc. 2013, 94, 1019–1029. [Google Scholar] [CrossRef]
- Liu, C.-M.; Lin, S.-H.; Schneider, S.H.; Root, T.L.; Lee, K.-T.; Lu, H.-J.; Lee, P.-F.; Ko, C.-Y.; Chiou, C.-R.; Lin, H.-J. Climate Change Impact Assessment in Taiwan; National Taiwan University: Taipei, Taiwan, 2010. [Google Scholar]
- Mel, R.; Lionello, P. Storm Surge Ensemble Prediction for the City of Venice. Weather Forecast. 2014, 29, 1044–1057. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).