1. Introduction
Hydropower constitutes the historically most widely used renewable energy source. All Alpine countries in Europe started the production of electrical energy with run-of-river hydropower plants (RoR HPPs) in the same period around 1880 [
1]. After the first world war (WW I), the importance of hydropower increased. With the end of the second world war (WW II), HPP construction boomed, lasting till the 1980s. During the 1970s, a broad public discussion about negative ecological effects caused by hydropower began, initiating a turning point. This led to a decreasing number of new HPPs [
1]. With the implementation of the Water Framework Directive (WFD) [
2] in 2000 and the aim to establish the good ecological status in European freshwater systems, hydropower faced new challenges. This affected new projects as well as operating HPPs [
1]. Still, hydropower is capable of playing an important role in the energy transition [
3]. The Revised Renewable Energy Directive RRED [
4] of the EU clarifies its importance.
The Alps are often described as Europe’s water reservoir and constitute an important sediment source for big streams like Rhone, Rhine, Po, and Danube [
5]. In the Alpine region, defined by the Alpine Space programme [
6], 1019 HPPs with a capacity >5 MW (RoR-HPP > 5 MW) are situated. These subdivide into 59% RoR HPPs, 33% storage plants, and 8% pumped storage plants. Together they contribute about 40% to the total hydropower capacity of the European Union [
7]. In Austria 115 RoR-HPP > 5 MW are in operation. Their share is about 4% of all 2770 RoR HPPs located in Austria and only 3% exceed a capacity of 10 MW [
8]. Despite the capacity or size, every single RoR HPP is capable of disrupting the natural river continuum and therefore matters in terms of sediment connectivity, which is one key aspect to reach a “good ecological status” as described in the WFD [
2].
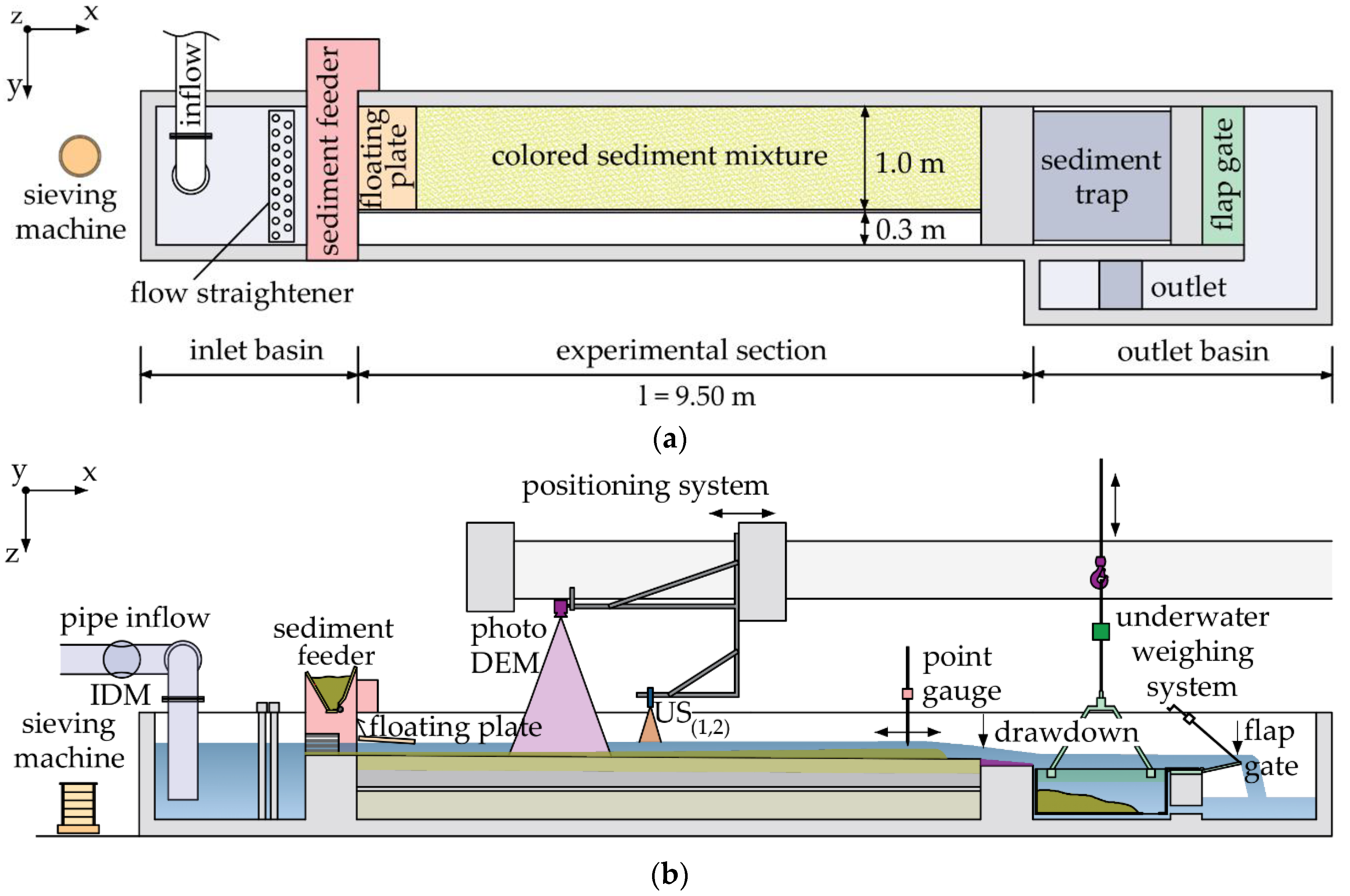
The focus of this paper was to investigate sediment transport processes at low head RoR HPPs located in medium-sized gravel bed rivers, since most of the existing literature is about large dams, with large storage volumes, dominated by different sedimentation characteristics [
9]. During projected operations at RoR HPP facilities, usually the incoming bed load material is held back in the impoundment, while most parts of the suspended load is expected to pass the dam [
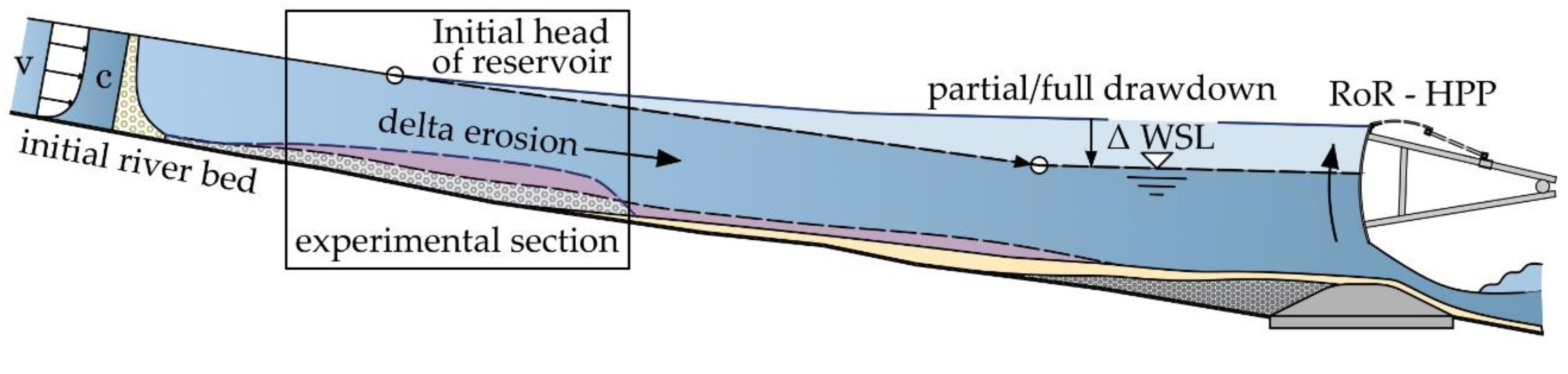
10]. Starting at the headwater section of an impoundment, the flow parameters rapidly change due to the reduction in energy slope. The flow depth increases continuously while the flow velocity and the sediment transport capacity decrease. This causes deposition and sorting of the incoming material. Due to the aggregation of coarse particles at the head of the reservoir, typical delta formations occur. Finer bed load fractions are carried further downstream, causing reservoir sedimentation [
11]. Therefore, sustainable sediment management strategies are necessary to extend the life expectancy of the RoR impoundment. A disrupted sediment balance further impacts the downstream river reach, leading to uncontrolled bed erosion and land loss [
12]. There is a rising awareness of the importance of sediment management strategies among HPP operators initiated by changing legal, political, social, and scientific conditions [
9]. Still, there is a deficit in systematical approaches how sediment management strategies at RoR HPPs must be established. According to Kondolf et al. [
13] reservoir sediment management strategies split up into three main categories: (i) reduction of the sediment yield from the catchment area, (ii) reduction of the sediment deposition, and (iii) volume increase and recovery. Least anthropogenically disturbed sediment connectivity constitutes the best ecological state and should therefore be reflected in the choice of management strategies. Per definition sluicing and flushing differ by two main aspects. First, sluicing aims at the passing of sediments through the reservoir without deposition, while flushing refers to the removal of preliminary deposited sediments. Secondly, flushing is not necessarily connected to the occurrence of high flow rates. However, non-flood flushing is assumed to only be suitable for reservoirs with large storage volumes and low-level outlets [
13,
14]. Hence, for small and medium sized RoR HPPs sluicing, as well as flushing operations, depend on high flow rates. According to [
14] reservoir flushing is often dominated by backward evolving erosion. This process, termed as “retrogressive erosion”, is often caused by discontinuous longitudinal profiles which lead to a change in hydraulic energy. Retrogressive erosion is indicated by high erosion rates and an upward moving degradation process [
14].
The present paper constitutes Part II of a two-part study concerning sediment management of RoR HPPs in medium sized gravel bed rivers. Part I deals with delta formation processes at operation water levels and forms a prerequisite of this paper [
9]. The aim of this present Part II is (i) to investigate the reservoir sedimentation of a low-head RoR HPP, (ii) to characterize the erosion process of existing headwater delta aggregations during low flood drawdown flushing, and (iii) to discuss the results in terms of future HPP operation. The discharge during the experiments was set to 70% of the 1-year flood (0.7 × HQ
1), since this constitutes a good standard for initiating drawdown operations [
9,
15].
4. Discussion
The knowledge of the mean flood reoccurrence and the corresponding sediment transport rates is a prerequisite for the implementation of sustainable and successful sediment management strategies for hydropower. Therefore, it is useful to distinguish between flood events where gate operations are necessary from a flood risk perspective and events where gate operations are not required for flood prevention but where open gates could avoid reservoir sedimentation [
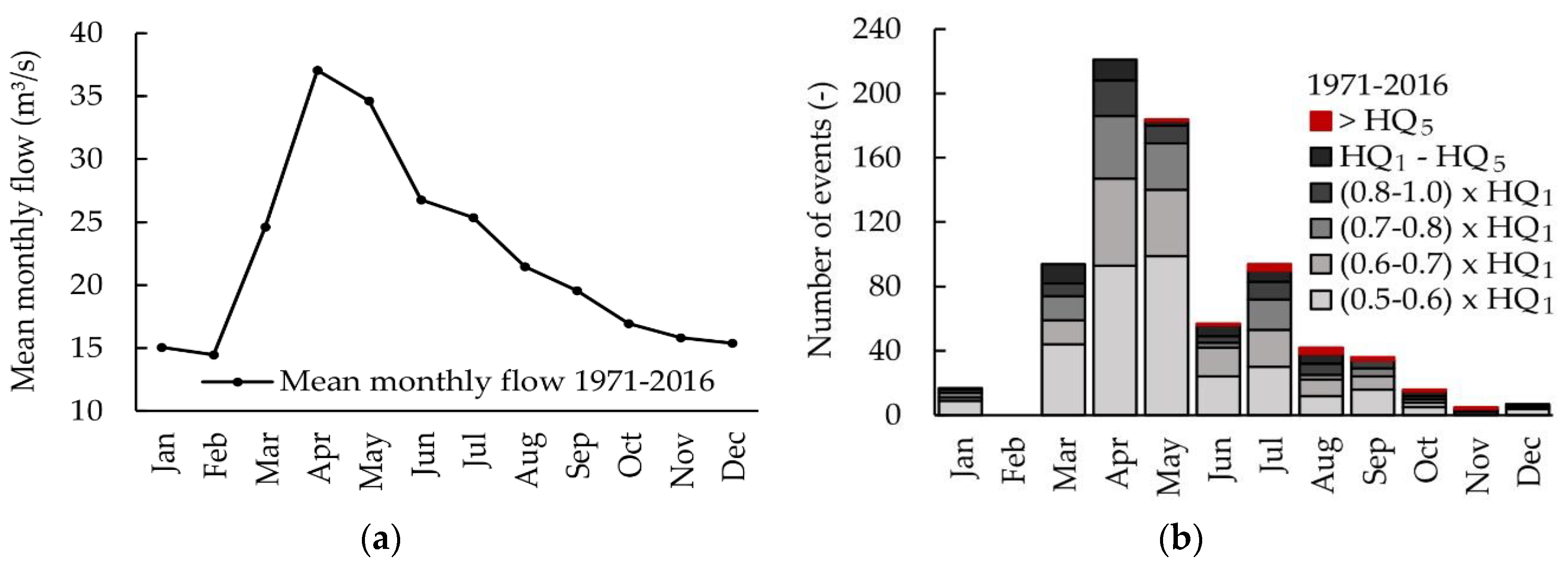
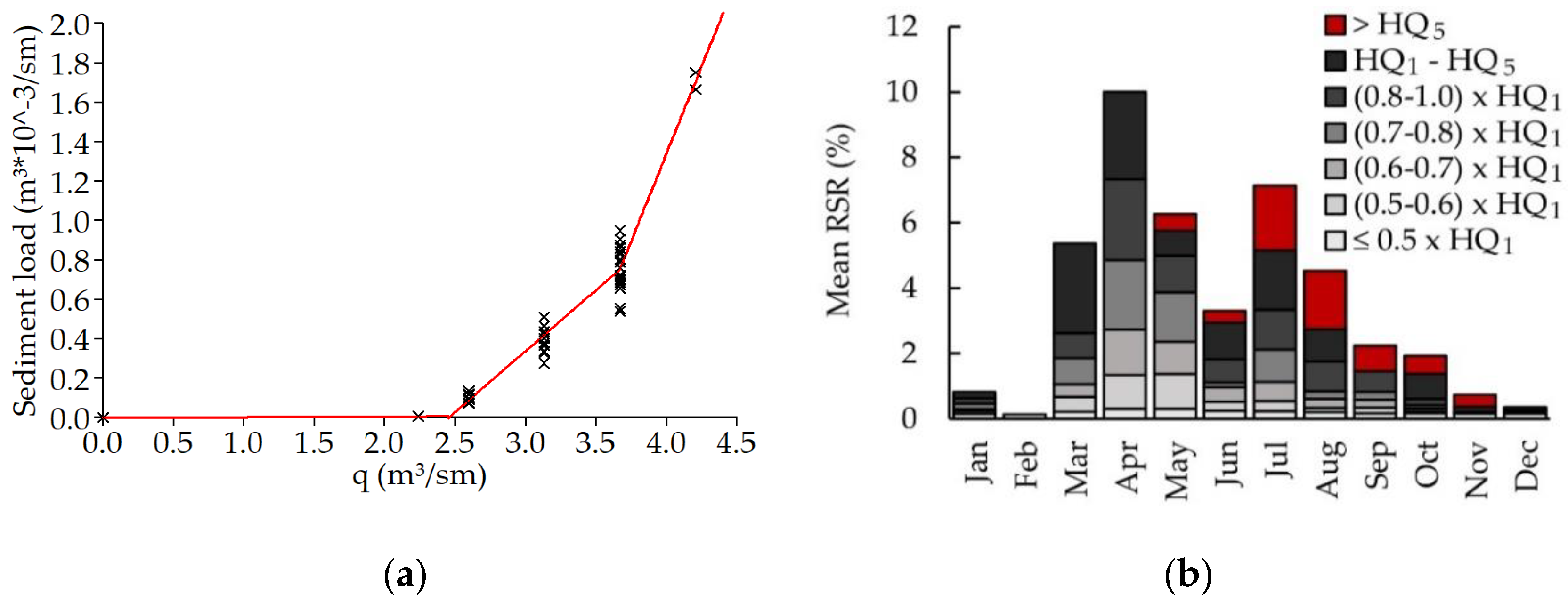
9]. The findings show the importance of gate operations for discharges in the range of 0.7 × HQ
1—HQ
1 because of their significant contribution to the mean annual RSR. Statistically, for the Mürz river gauging station Kapfenberg-Diemlach this would lead to about four drawdowns per year due to flow rates between 0.7 × HQ
1—HQ
1 and additional two for events exceeding HQ
1. For events >0.6 × HQ
1, the mean reoccurrence is 10 drawdowns per year, considering the period 1971–2016.
From field studies done by Harb et al. [
19] and Badura [
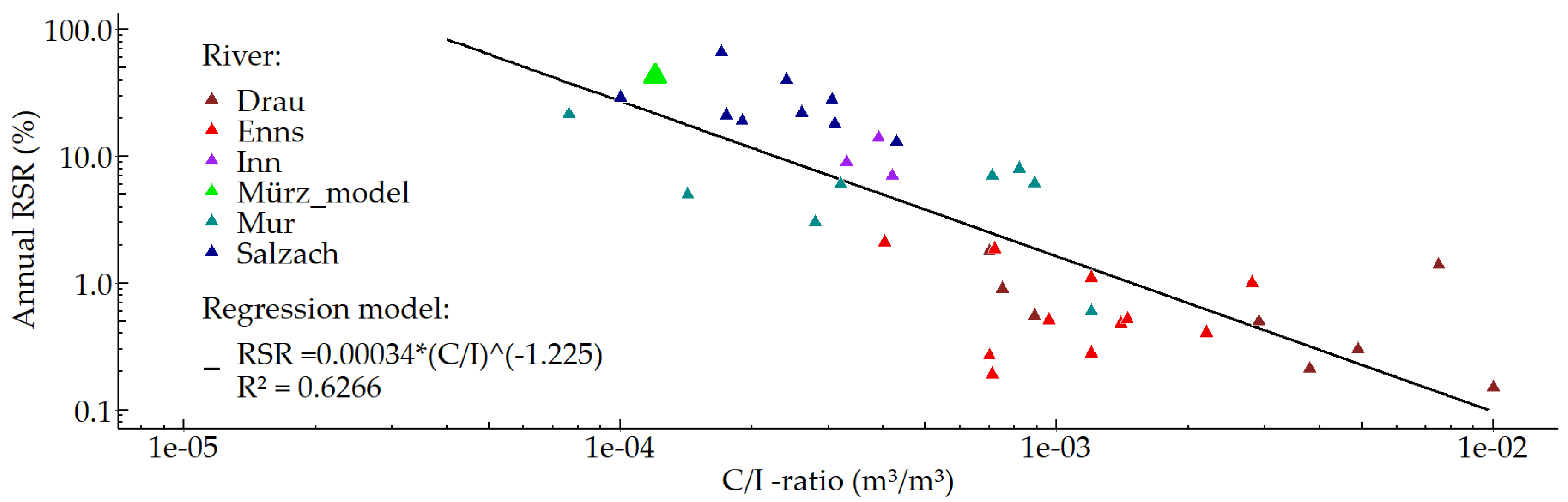
10] a data set comparing annual RSR to the corresponding C/I-ratios for many HPP all over Austria was provided (
Figure 10). The field data show the strong correlation of rising annual RSR with decreasing C/I-ratios, best described by an exponential regression model (black line in
Figure 10). In addition, the estimated annual RSR of the Mürz_model is displayed (green triangle).
The estimated annual 43% RSR of the Mürz_model fits into the data structure. For example, the Salzach HPPs show RSR values in the range from 13% up to 66% with a mean of 28% and a standard deviation of 16%. Based on the model simplifications and the assumption of full sediment availability, the Mürz_model represents a realistic scenario regarding the RSR of a medium sized gravel bed river.
To discuss the applicability of the model results regarding the implementation of sediment management strategies, a comparison to existing RoR HPPs was made, since some cases are already known for an improved flushing concept. Exemplarily, a newly constructed RoR HPP considering sluicing as well as flushing operations in terms of a sustainable reservoir management is the joint venture RoR HPP Gries, located at the Salzach river in Austria. With a design flow of 115 m
3/s, a hydraulic head of 8.9 m, and an installed capacity of about 8.85 MW, it is on the transition between a small or medium sized HPP. Sediment connectivity aspects were considered in the structural planning as well as in the operation concept. Unlike most other RoR HPPs, the HPP Gries consists of two powerhouses, one each on the left and on the right riverbank, with two radial gates in between. The gates form a spillway aligned with the river axis [
20]. Another feature of the Gries HPP is the low concrete weir height, since this is crucial to reduce the dead storage volume as described in [
9,
16]. Drawdowns are planned to be initiated for discharges in the range from (0.63–0.86) × HQ
1 based on a newly erected gauging station combined with flood forecasting. The operators expect 10–20 drawdown events per year [
21].
Compared to the Mürz model in Kapfenberg/Diemlach, the mean flow at the Gries HPP is 2.6 times higher, the HQ
1 is 2.4 times higher, the HQ
5 is 2.3 times higher, and the HQ
10 is 2.25 times higher. Nevertheless, the starting interval for a drawdown is in a similar range. Another example is the small or medium sized RoR HPP Bodendorf located in the Mur river in Austria. It has an installed capacity of 7 MW and a mean flow rate of 33 m
3/s [
10]. For Bodendorf, Schneider et al. [
22] found values above >0.62 × HQ
1 to be suitable for the initiation of drawdown operations. In terms of the annual RSR these RoR HPPs differ as this is strongly influenced by many local factors, such as (i) sediment availability, (ii) reservoir geometry and size, and (iii) the interaction with other HPPs (chain of HPPs) [
9]. Still, the value of 0.7 × HQ
1 is stated to be a good reference point for the initiating of flushing events, as it seems to be applicable for a wide scope of RoR HPPs regarding the installed capacity.
With a gross head of 4.6 m, a resulting reservoir length of 1500 m and a design flow of 35 m³/s, a maximum capacity of 1.4 MW can be calculated for the RoR HPP represented by the Mürz_Model. Compared to the installed capacity of the HPP Bodendorf and the HPP Gries, this value is about 5–6 times smaller. Considering all HPP located in Austria, approximately 87% do not exceed this capacity. Therefore, the Mürz_Model represents a wide range of RoR HPPs.
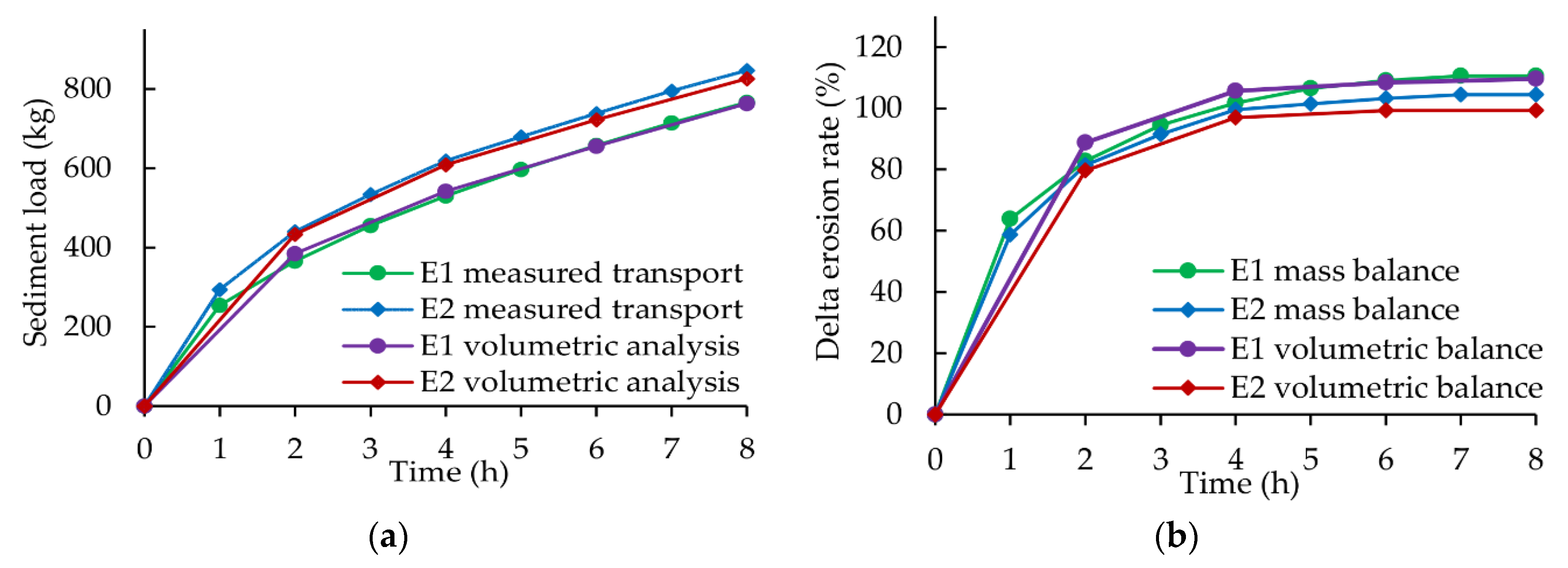
In this study drawdown operations at a RoR HPP headwater section were investigated at a flow rate of 0.7 × HQ1. The findings show the suitability of low flood events for reservoir flushing if a drawdown is performed. The flood rate was capable of remobilizing an existing delta formation, built under the same flow rate without a drawdown. In addition, the entering sediment load from the free-flowing section upstream was also sluiced downstream. Thereby, the flow rate of 0.7 × HQ1 was able to mobilize all grain size classes used in this study (14–120 mm in 1:1 scale).
In Sindelar et al. [
9] the reservoir sedimentation process at the headwater section of the same RoR HPP was simulated with the water levels kept at operation level and a discharge of 0.7 × HQ
1. The findings revealed that under these conditions the bed load transport stops for grain sizes >14 mm at a 1:1 scale. Almost all sediments settle in the reservoir head section resulting in a rise of bed and water levels. This rise will not increase flood risk for the simulated event. However, these events show a high reoccurrence probability and will therefore lead to a further rise of the delta and the water levels if the reservoir is not drawn down. For a subsequent high flood events this could lead to a significant increased flood risk [
9].
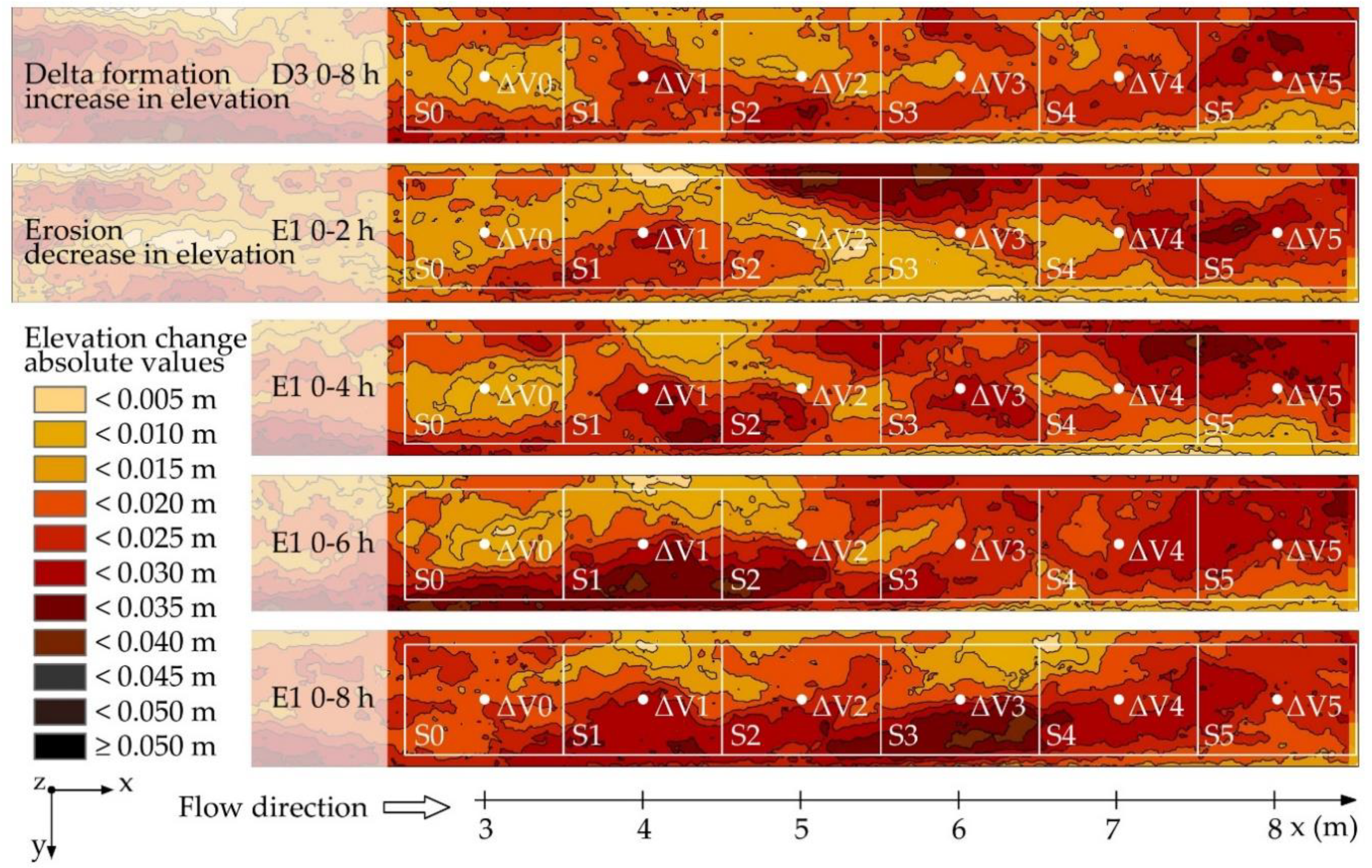
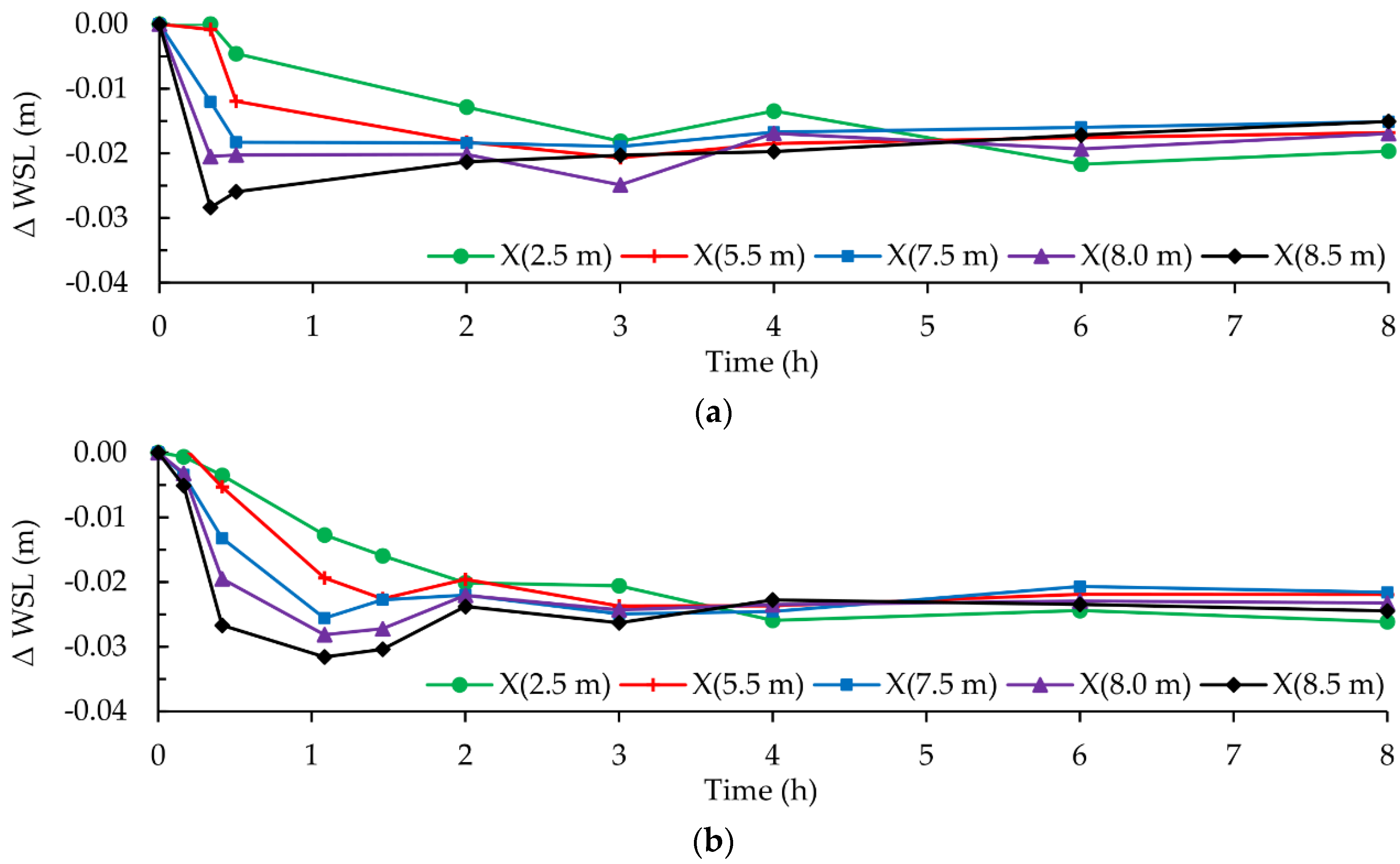
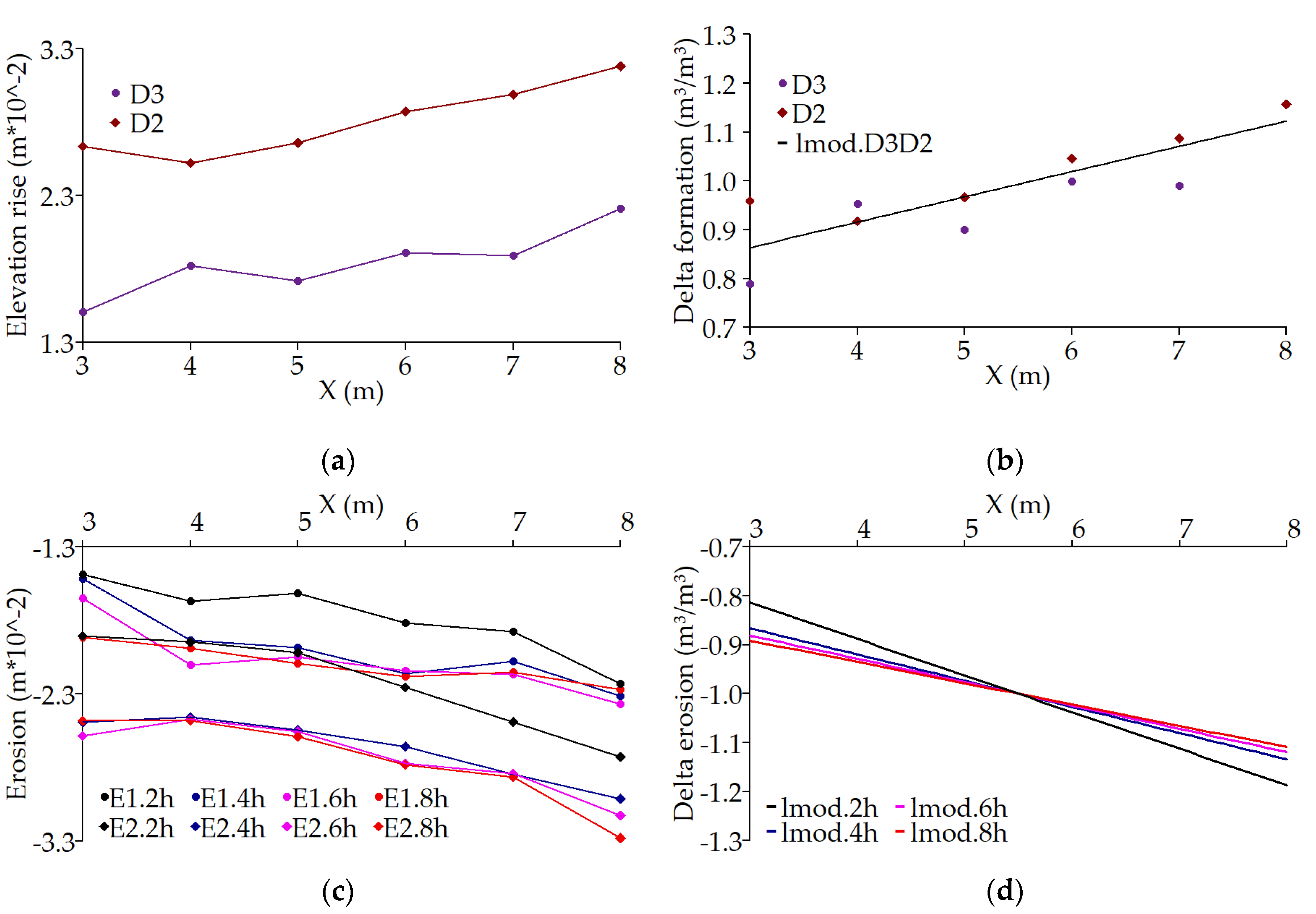
With the beginning of the drawdown, the sediment transport capacity increased rapidly due to the high energy slope and therefore high shear stresses. The maximal erosion occurred at the downstream end of the deposition. The erosion continuously evolved upstream, causing the steep slope at the former delta front to decrease. The slope at the delta top and tail increased until both slopes equalized. This indicated the end of the retrogressive erosion as described by [
14]. For the water surface evolution, the same trend was observed. This also matches the findings of [
14]. Hence, the increased flood risk caused by deltaic depositions was diminished.
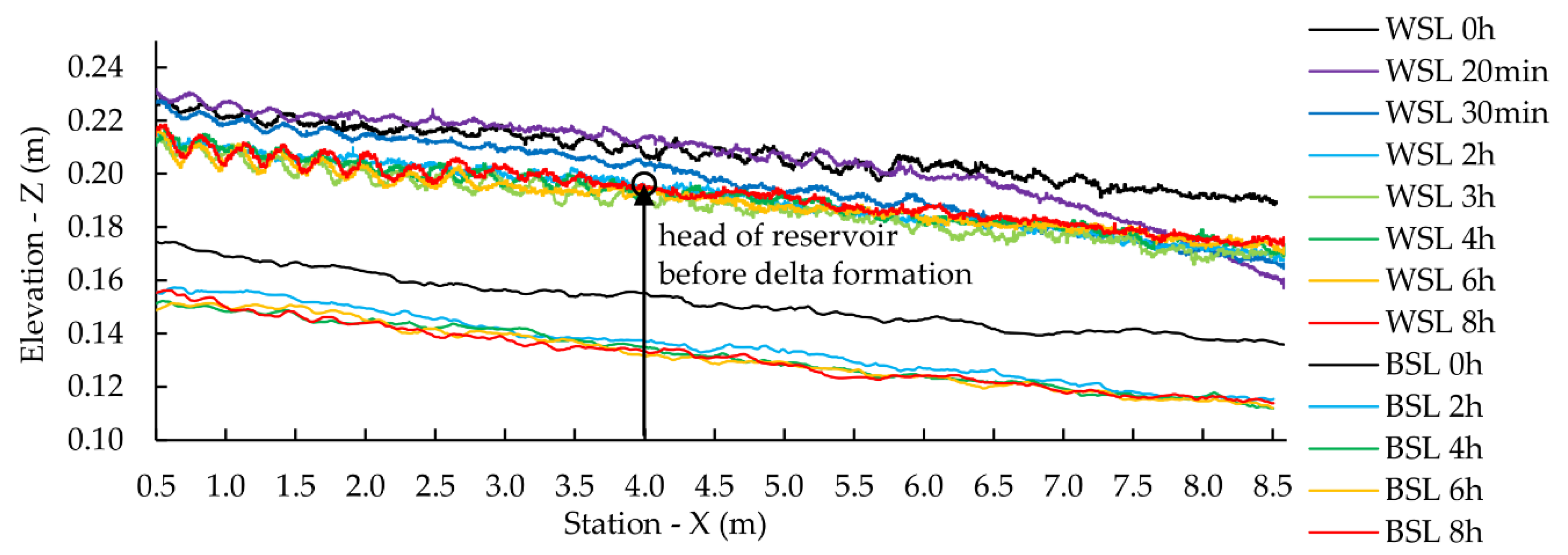
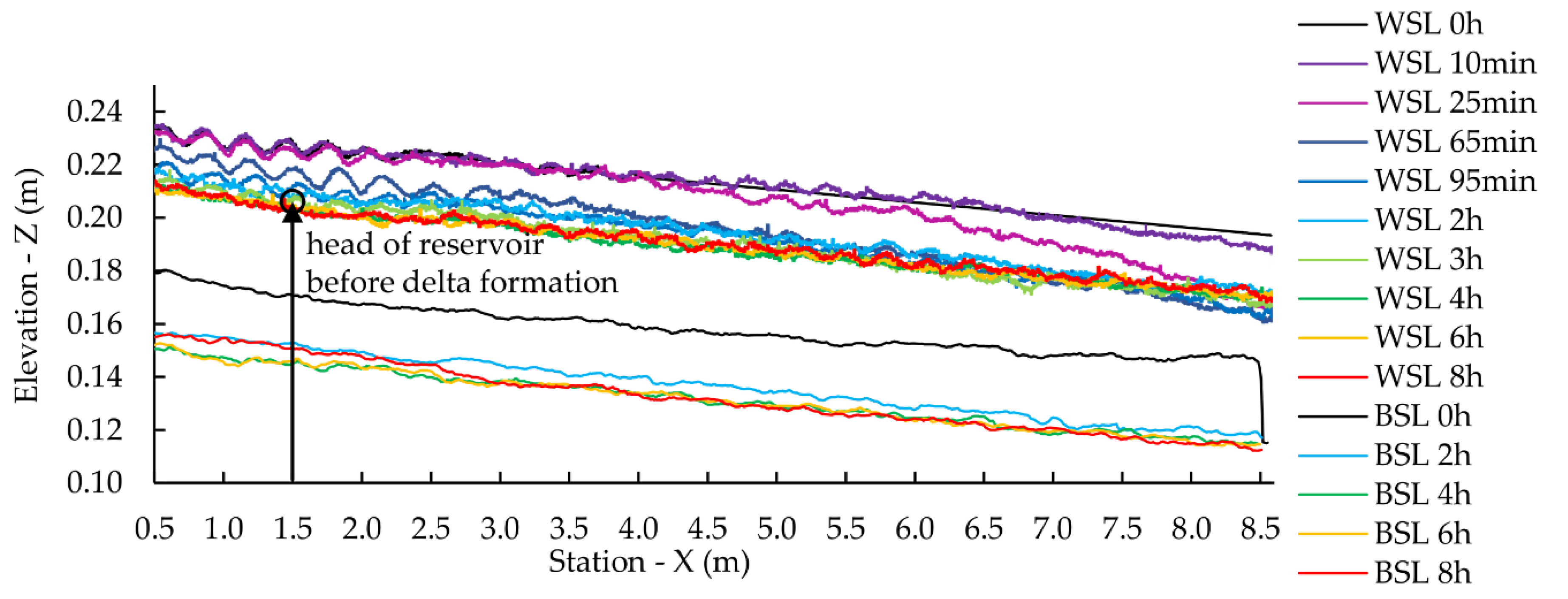
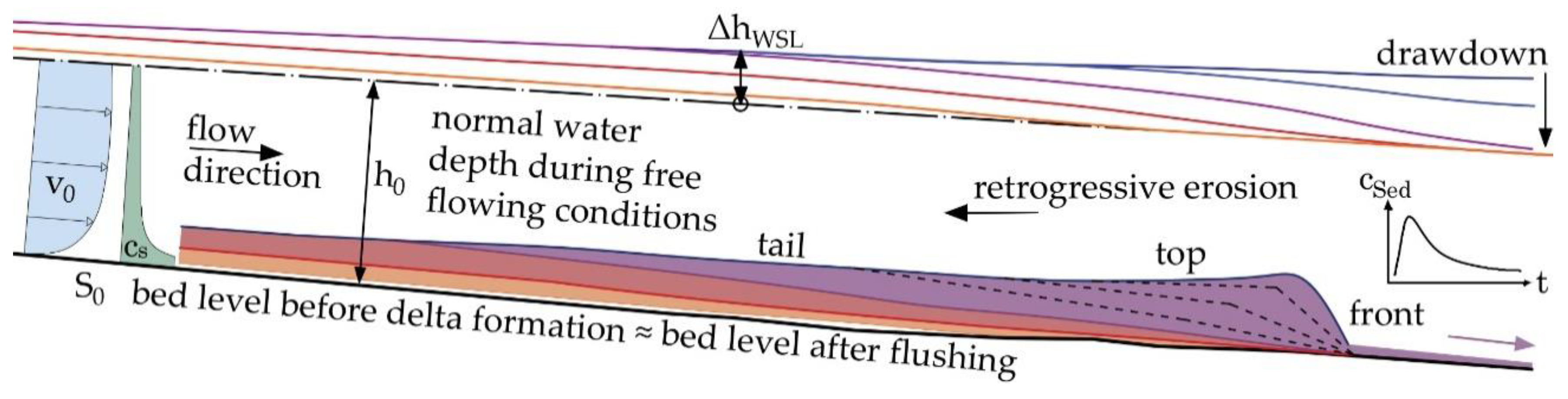
Figure 11 shows a scheme of the retrogressive delta erosion process for equal time steps, each illustrated by a different color. After reaching free-flowing conditions the erosion process was initiated at the downstream end of the delta deposition caused by the high energy slope at the delta front. Starting with high transport rates, the sediment concentration decreased for each timestep, which is also illustrated by the graph of the sediment concentration at the downstream end of the scheme. The erosion scheme also illustrates the water level decrease based on the experimental observations.
According to [
14] there is no dependency on any specific grain sizes for the appearance of a retrogressive erosion, still the characteristics and possible erosion patterns are influenced by the grain size distribution of the deposits. For the Hengshan storage reservoir in China the retrogressive erosion of unconsolidated silt material took less than 24 h for a 2000 m long section [
14].
Additionally, retrogressive erosion was observed and investigated for a coarse river delta by Randle and Lyon [
23], at the Elwha river in Washington [
14]. This is in line with the findings of the present paper, as presented in the retrogressive erosion scheme of
Figure 11. For the Sanmenxia reservoir at the Yellow River rapid full drawdown operations led to retrogressive erosion accompanied by high amounts of mobilized sediments. This caused serious depositions and increased flood risk in the downstream river section [
24].
When the delta front started to degrade, the bed load transport rate was nearly four times higher than the corresponding value during free-flowing equilibrium conditions. In total, the delta was remobilized twice as fast, as it aggregated in the first place. Over time the sediment transport decelerated as the delta formation was mostly eroded and the sediment availability converged towards the initial equilibrium conditions. This points out the suitability of drawdowns, even for short periods under the present conditions. Together with the results of Sindelar et al. [
9,
25] and the present findings, a resettling of the eroded material is expected for partial drawdowns as the backwater effects reoccur downstream. Still, partial drawdowns can be suitable at the headwater section during flood events of low intensity to (i) remobilize deposited sediments and (ii) sluice the incoming bedload further downstream within the reservoir. Combining more frequent partial drawdowns with ensuing full drawdown flushing may result in a good outcome. This strategy may be described as a combination of reservoir head sluicing and near weir flushing. This means that flood events with low intensities are used to sluice the incoming sediments downstream into the impoundment. For events with high intensity a full drawdown is initiated to remobilize the deposited material. As the subsequent filling of the reservoir is less time consuming, partial drawdowns reduce the energy revenue losses. This fact could be relevant for RoR HPPs with high C/I ratios. The energy costs may further decrease, as the turbine may be kept in operation [
19]. To provide evidence, further investigations of sections in the vicinity of the weir are necessary.
Discussing the consequences of these findings for future hydropower operations, the following key aspects are worth considering: (i) ecology, (ii) flood risk, (iii) technical issues and energy revenue. In terms of ecology and river morphology the conservation of sediment connectivity should be pursued. This is mostly achievable if reservoirs are drawn down in periods of high sediment transport, enabling the sediments to pass the impoundment. Further, the design of the HPP shows significant influence on the success of flushing operations. Especially, the effects of fixed weir heights and reservoir widenings must be considered [
16].
From a flood risk perspective, aggregations in the headwater section have the potential to increase flood risk as they raise the bed levels and therefore reduce the effective cross section. Considering the impoundment as a component of the HPP-facility, reservoir sedimentation can cause operational problems due to blocking of the turbine inlet or outlet [
19]. Resulting maintenance work is cost intensive while simultaneously restraining the energy production. Further, possible loss in gross head can reduce the energy revenue. In contrast, drawdown operations also potentially harm the environment, if there is no adequate concept. High additional suspended sediment load, increased bed load transport, and the release of organic material provoke high environmental stress, such as critical oxygen consumption [
15]. Further, drawdown operations lead to additional costs and energy revenue losses. The attempt to bring all these issues in line, highlights the challenges future hydropower development must face to keep its key role in the energy transition.