Assessment of Wave Storm-Induced Flood Vulnerability in Rhodes Island, Greece
Abstract
1. Introduction
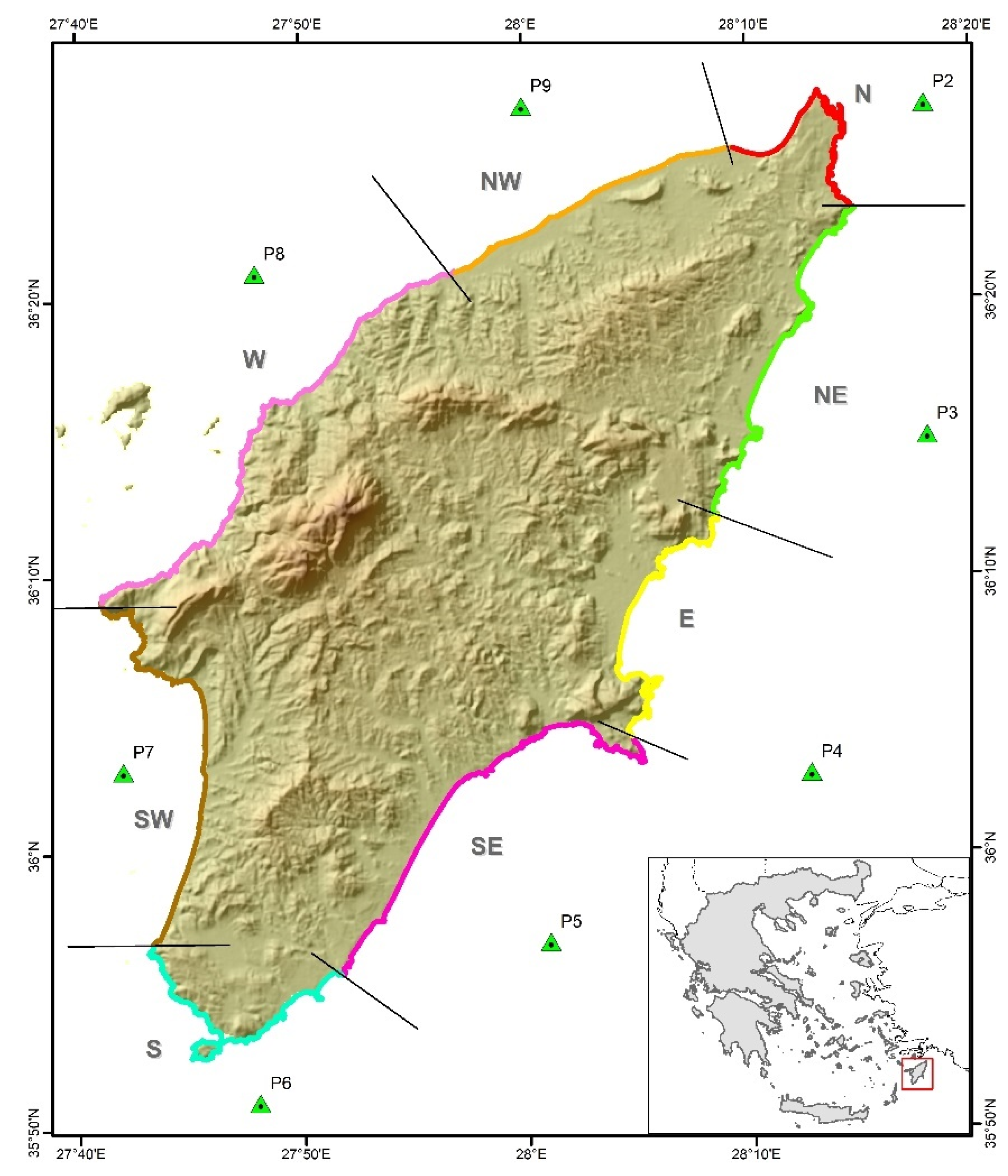
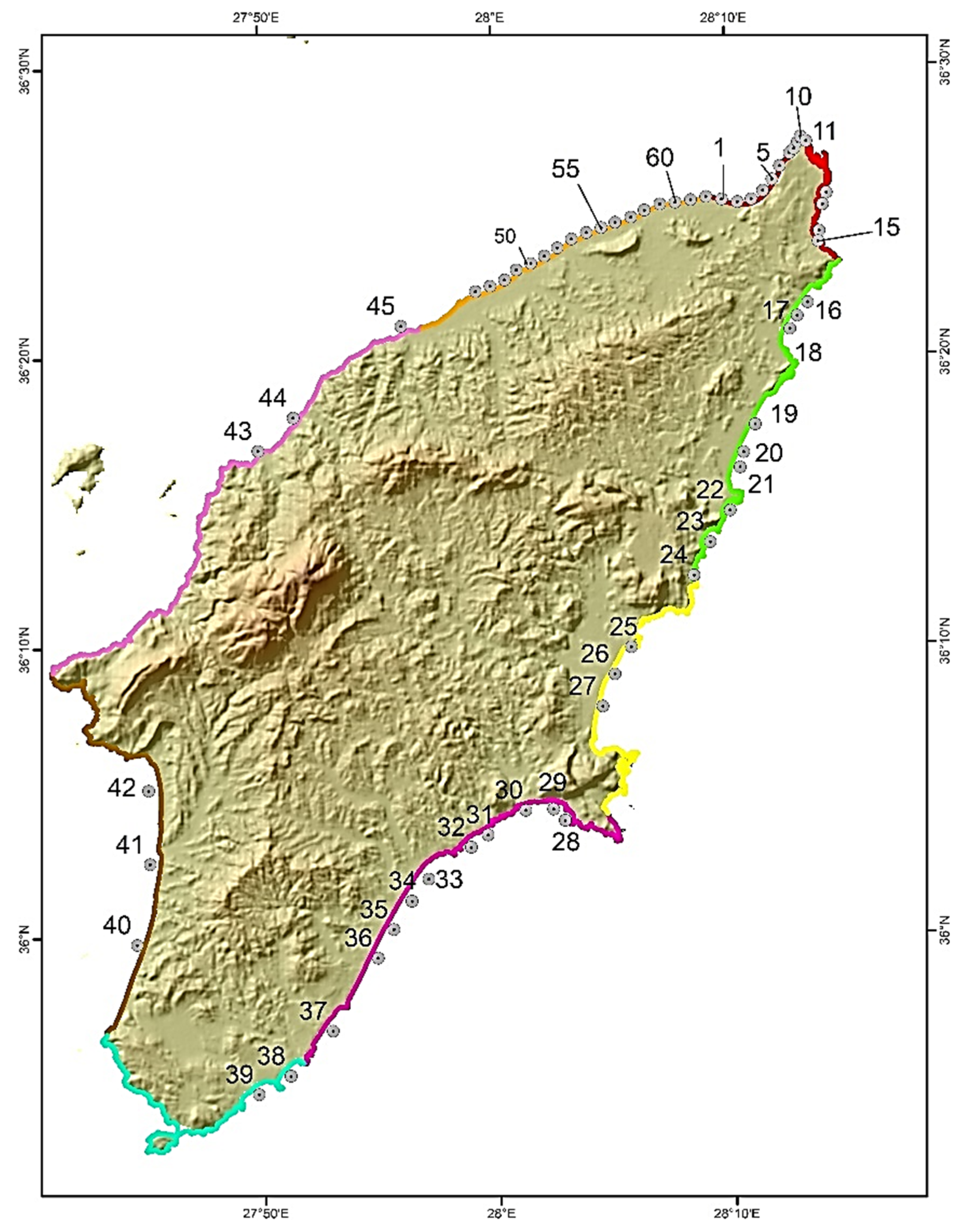
2. The Study Area
3. Materials and Methods
3.1. Data
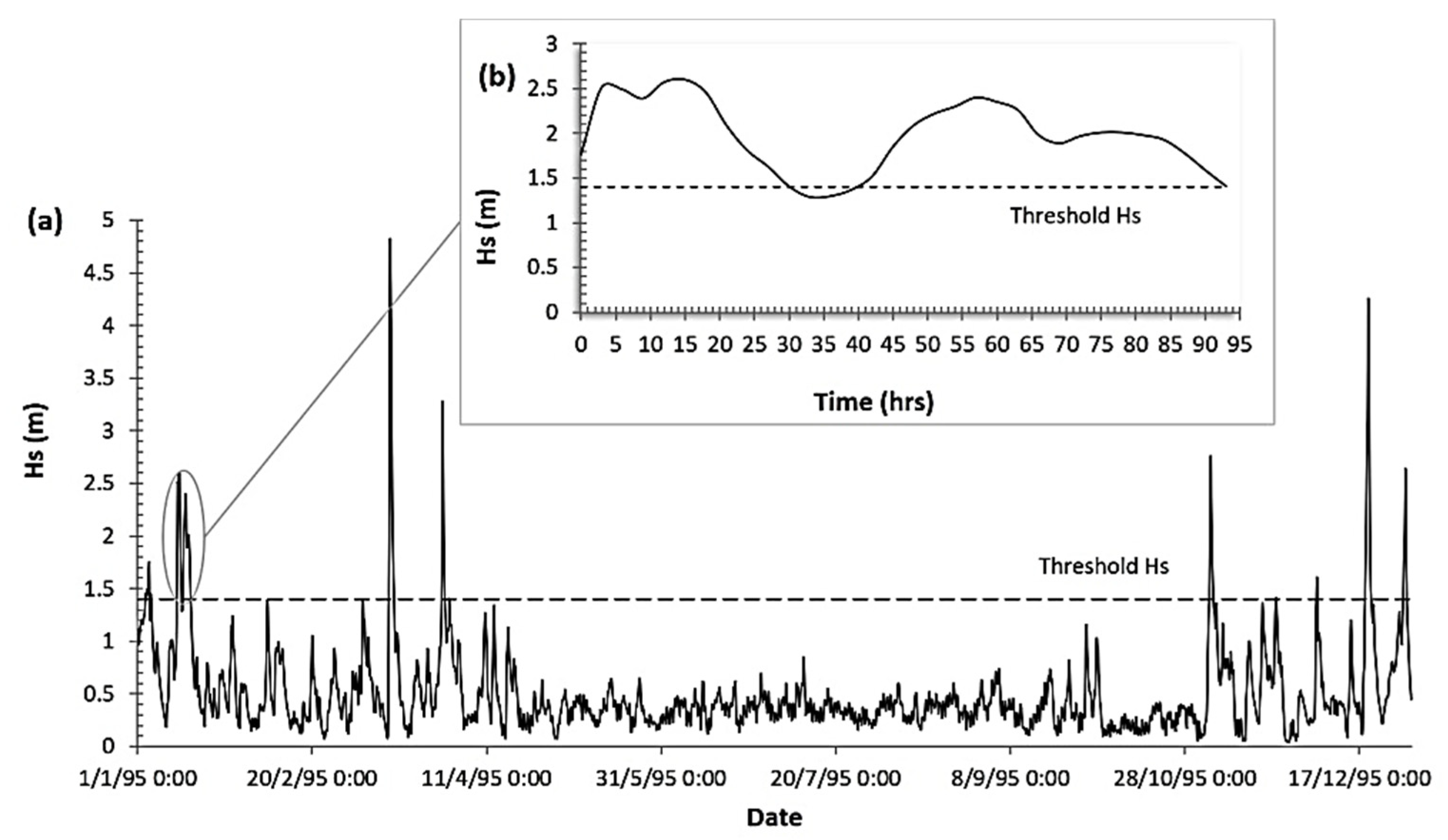
3.2. Analysis of Wave Storms
3.3. Flood Hazard Assessment
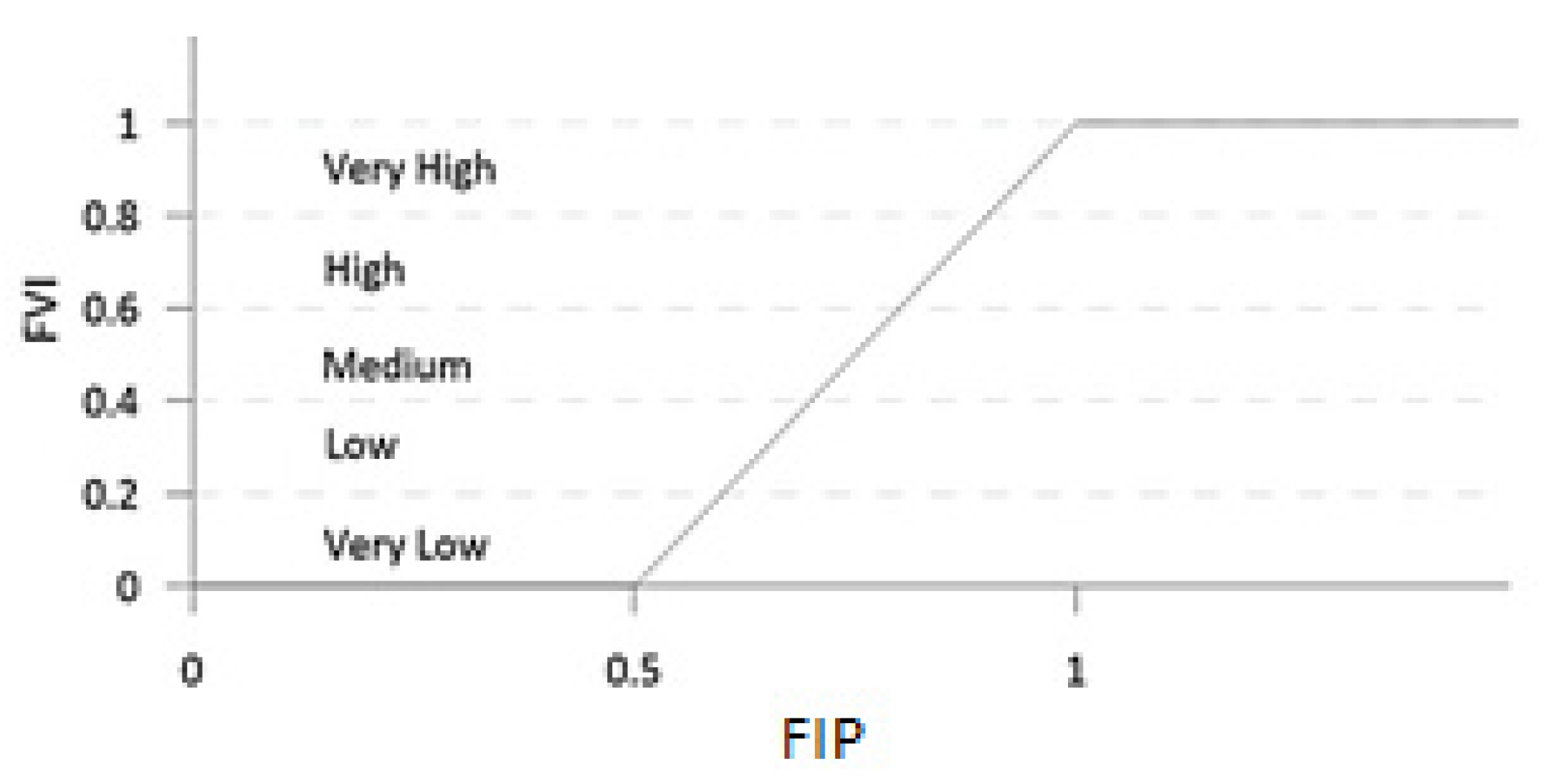
3.4. Flood Vulnerability Index
4. Results
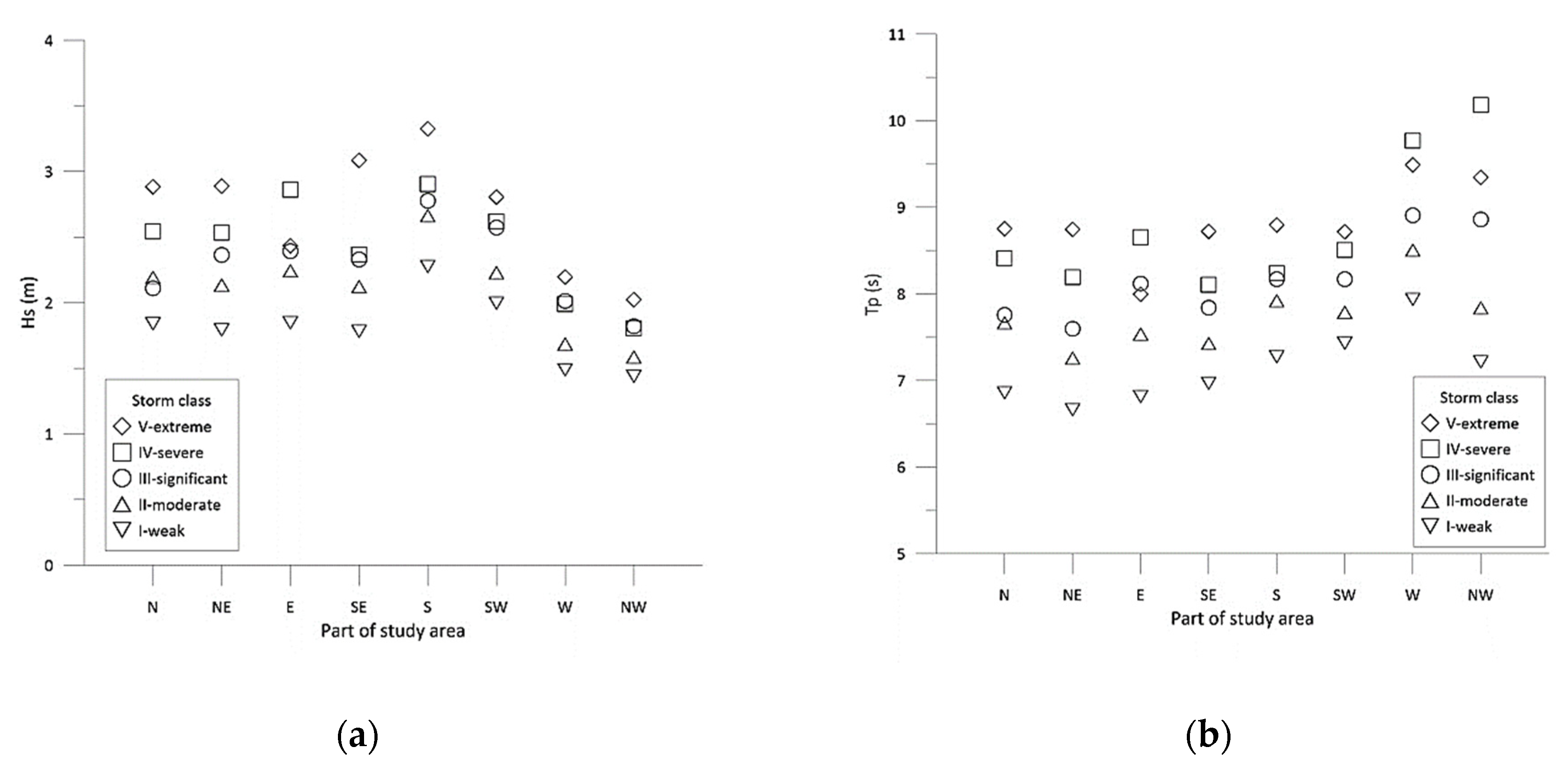
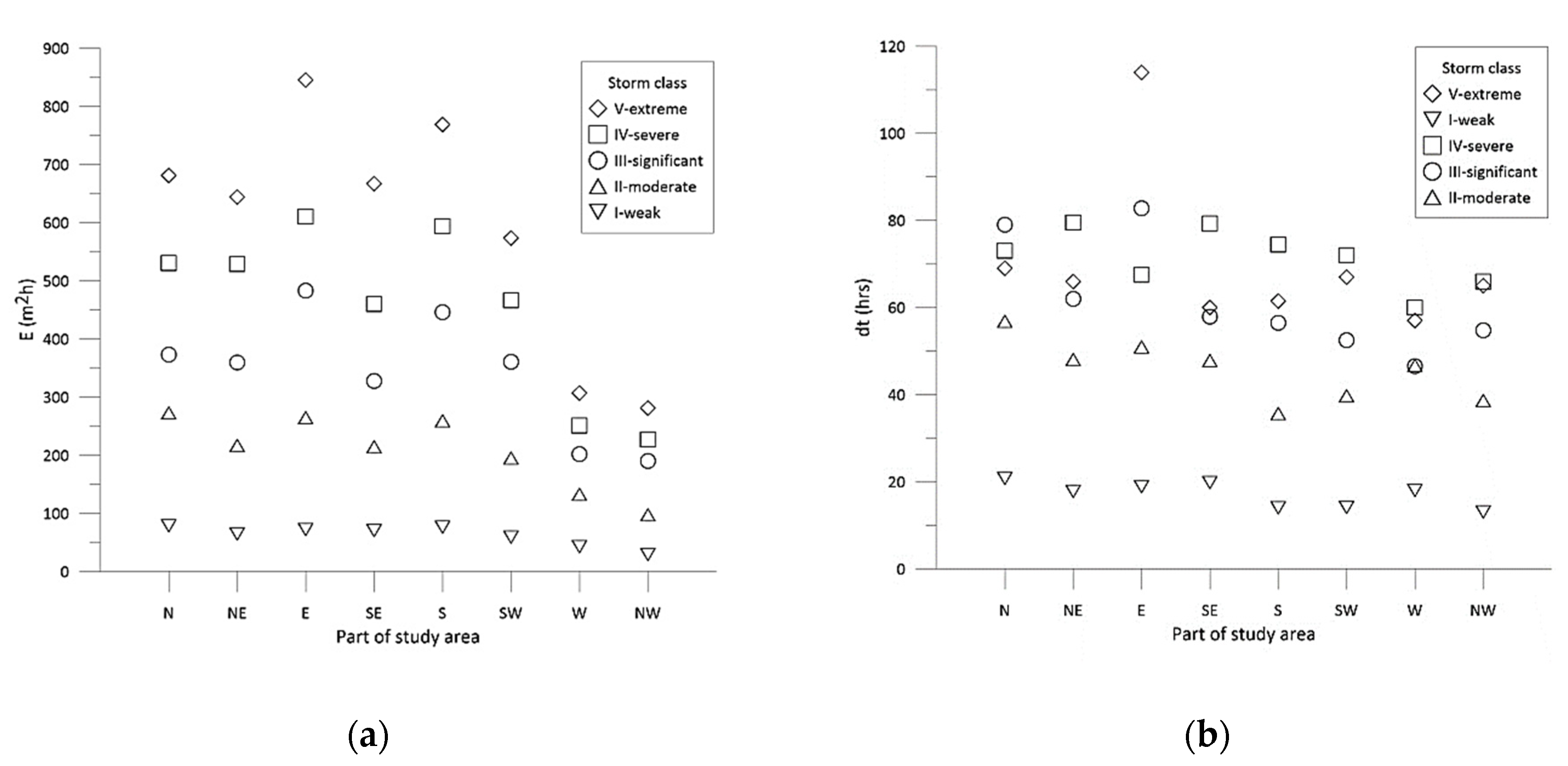
4.1. Analysis of Wave Storm Events
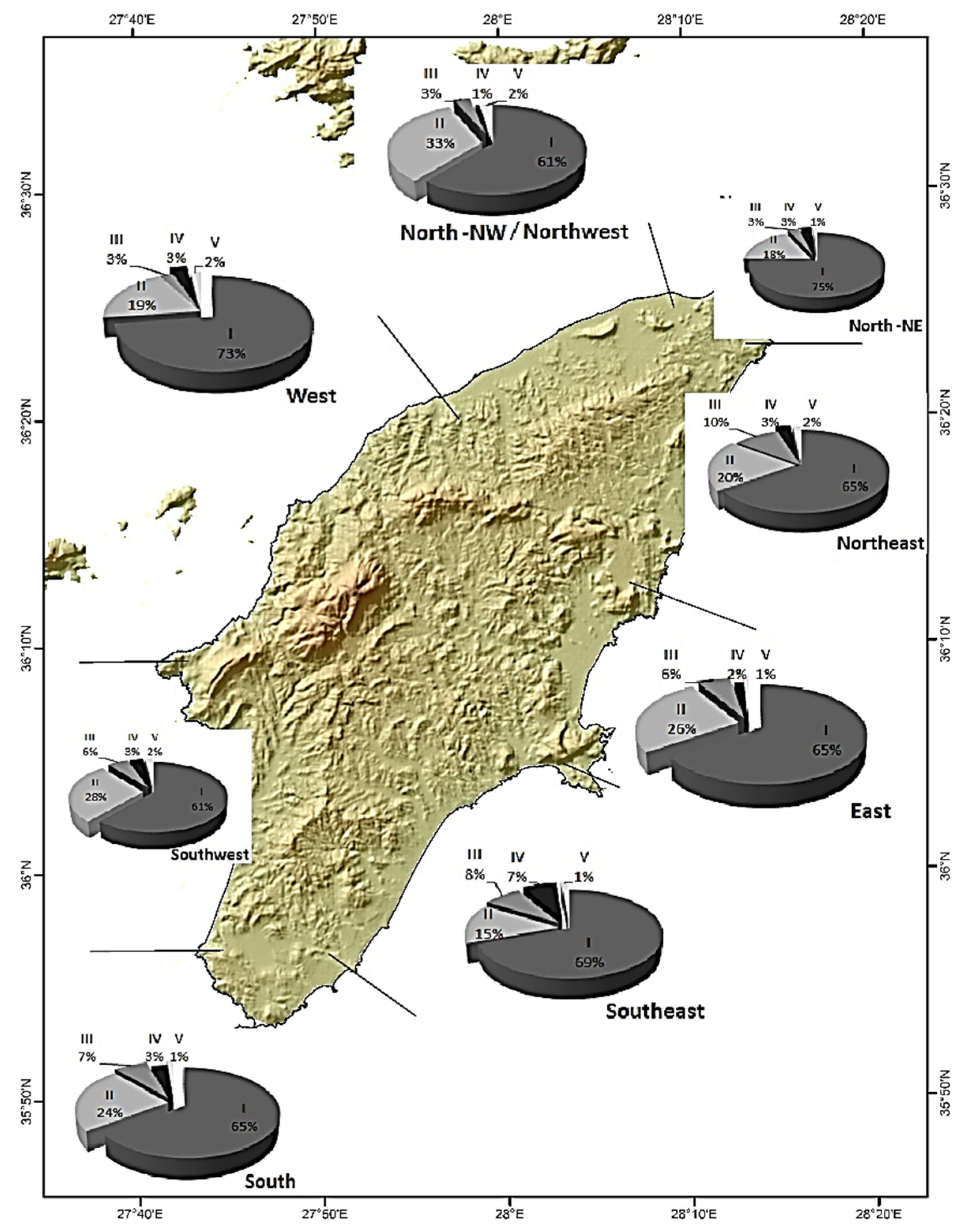
4.2. Assessment of Flood Vulnerability
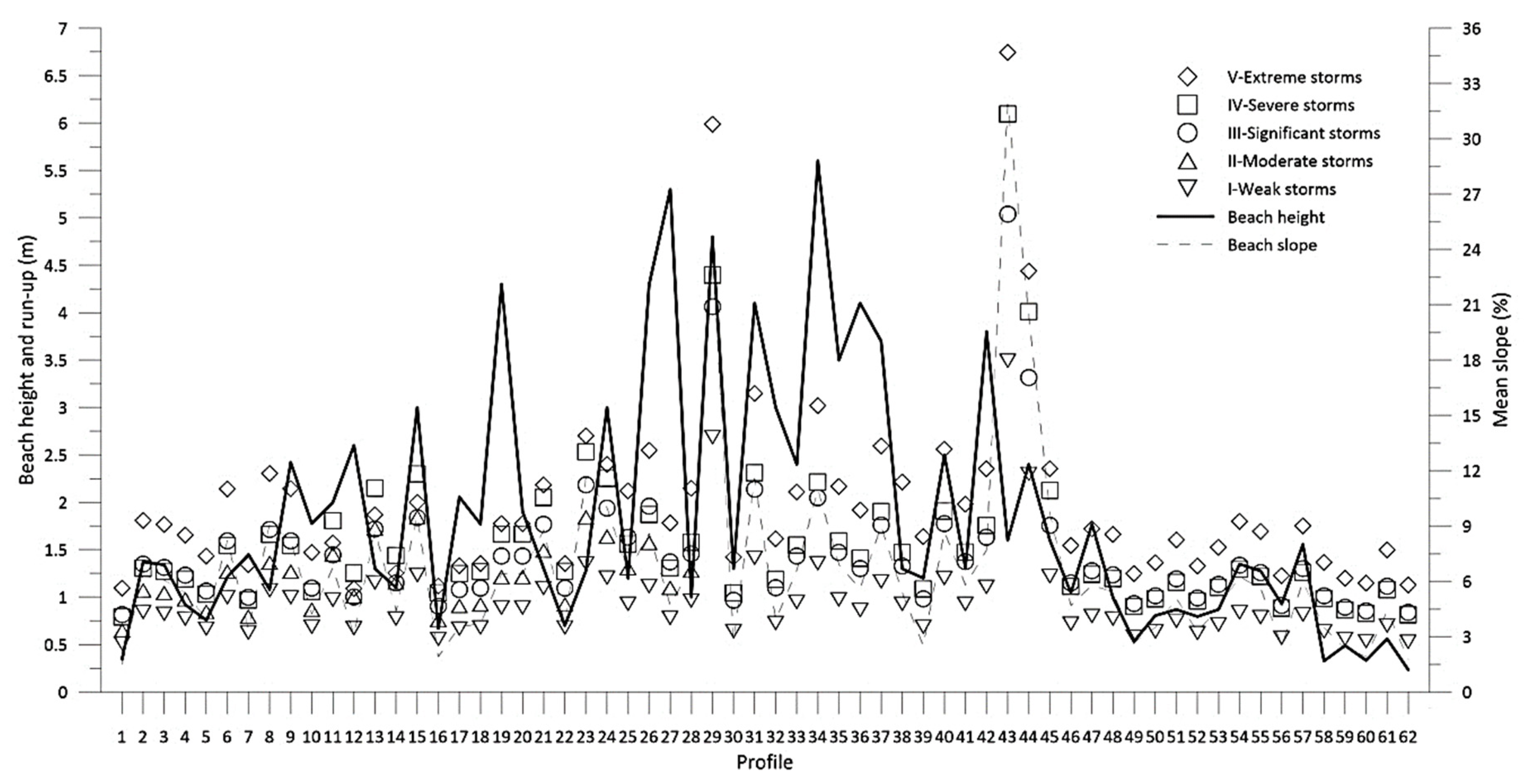
4.2.1. Results of Wave Run-up
4.2.2. Storm Surge during Storm Events
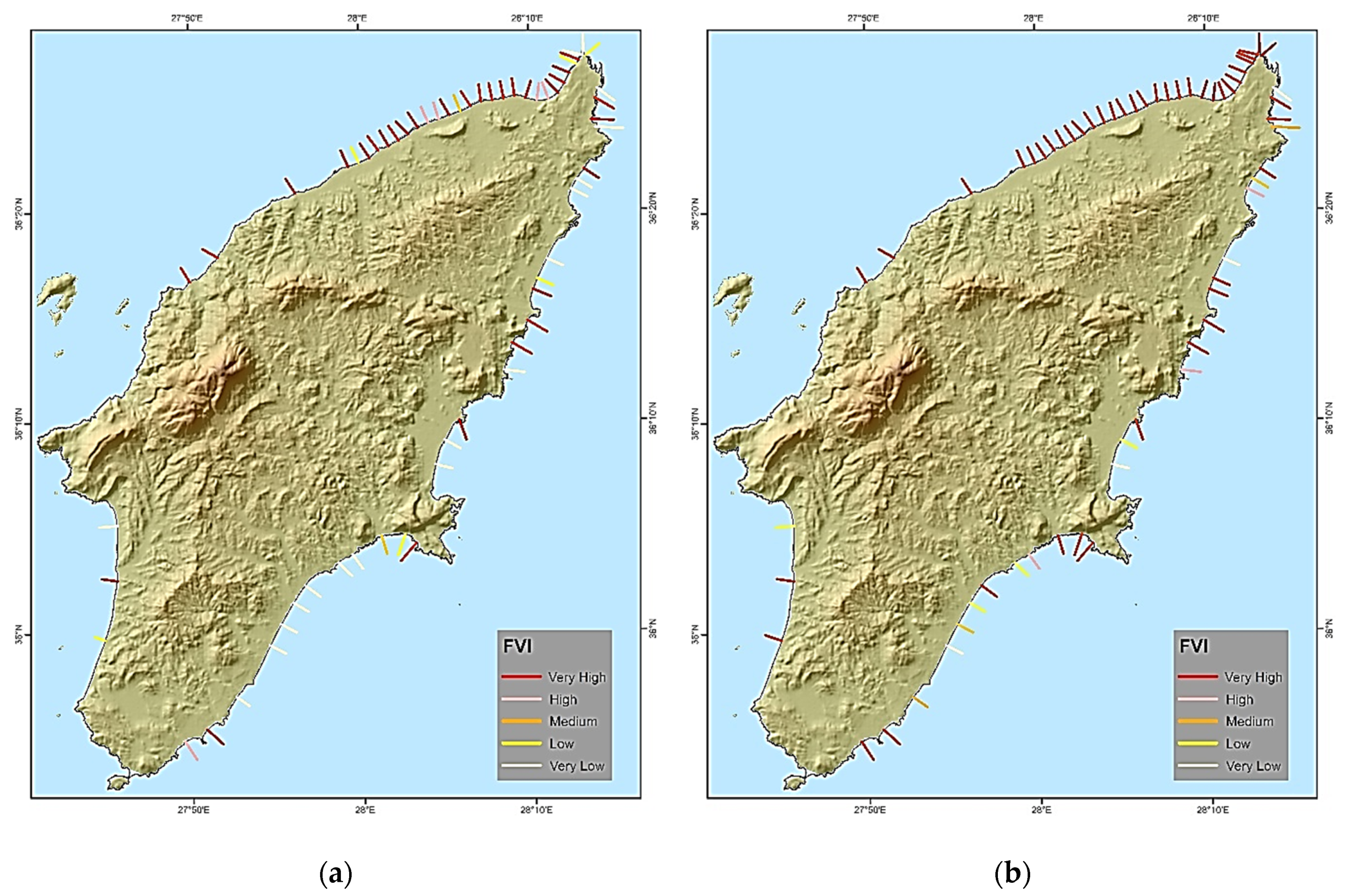
4.2.3. Results of Flood Vulnerability Index (FVI)
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karim, M.F.; Mimura, N. Impacts of Climate Change and Sea-Level Rise on Cyclonic Storm Surge Floods in Bangladesh. Glob. Environ. Chang. 2008, 18, 490–500. [Google Scholar] [CrossRef]
- Ciavola, P.; Ferreira, O.; Haerens, P.; Van Koningsveld, M.; Armaroli, C.; Lequeux, Q. Storm Impacts along European Coastlines. Part 1: The Joint Effort of the MICORE and ConHaz Projects. Environ. Sci. Policy 2011, 14, 912–923. [Google Scholar] [CrossRef]
- Bertin, X.; Bruneau, N.; Breilh, J.-F.; Fortunato, A.B.; Karpytchev, M. Importance of Wave Age and Resonance in Storm Surges: The Case Xynthia, Bay of Biscay. Ocean Model. 2012, 42, 16–30. [Google Scholar] [CrossRef]
- Jiménez, J.A.; Sancho-García, A.; Bosom, E.; Valdemoro, H.I.; Guillén, J. Storm-Induced Damages along the Catalan Coast (NW Mediterranean) during the Period 1958–2008. Geomorphology 2012. [Google Scholar] [CrossRef]
- Tsoukala, V.K.; Chondros, M.; Kapelonis, Z.G.; Martzikos, N.; Lykou, A.; Belibassakis, K.; Makropoulos, C. An Integrated Wave Modelling Framework for Extreme and Rare Events for Climate Change in Coastal Areas—The Case of Rethymno, Crete. Oceanologia 2016, 58, 71–89. [Google Scholar] [CrossRef]
- Perini, L.; Calabrese, L.; Salerno, G.; Ciavola, P.; Armaroli, C. Evaluation of Coastal Vulnerability to Flooding: Comparison of Two Different Methodologies Adopted by the Emilia-Romagna Region (Italy). Nat. Hazards Earth Syst. Sci. 2016, 16, 181–194. [Google Scholar] [CrossRef]
- Garnier, E.; Ciavola, P.; Spencer, T.; Ferreira, O.; Armaroli, C.; McIvor, A. Historical Analysis of Storm Events: Case Studies in France, England, Portugal and Italy. Coast. Eng. 2018, 134, 10–23. [Google Scholar] [CrossRef]
- UNEP/MAP/PAP. Protocol on Integrated Coastal Zone Management in the Mediterranean. Priority Actions Programme; UNEP/MAP/PAP: Split, Croatia, 2008. [Google Scholar]
- Dolan, R.; Davis, R.E. An Intensity Scale for Atlantic Coast Northeast Storms. J. Coast. Res. 1992, 8, 840–853. [Google Scholar]
- Dolan, R.; Davis, R.E. Coastal Storm Hazards. J. Coast. Res. 1994, 12, 103–114. [Google Scholar]
- Bosom García, E.; Jiménez Quintana, J.A. Probabilistic Coastal Vulnerability Assessment to Storms at Regional Scale: Application to Catalan Beaches (NW Mediterranean). Nat. Hazards Earth Syst. Sci. 2011, 11, 475–484. [Google Scholar] [CrossRef]
- Di Risio, M.; Bruschi, A.; Lisi, I.; Pesarino, V.; Pasquali, D. Comparative Analysis of Coastal Flooding Vulnerability and Hazard Assessment at National Scale. J. Mar. Sci. Eng. 2017, 5, 51. [Google Scholar] [CrossRef]
- Holman, R.A. Extreme Value Statistics for Wave Run-up on a Natural Beach. Coast. Eng. 1986, 9, 527–544. [Google Scholar] [CrossRef]
- Nielsen, P.; Hanslow, D.J. Wave Runup Distributions on Natural Beaches. J. Coast. Res. 1991, 7, 1139–1152. [Google Scholar]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H., Jr. Empirical Parameterization of Setup, Swash, and Runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Hubbard, M.E.; Dodd, N. A 2D Numerical Model of Wave Run-up and Overtopping. Coast. Eng. 2002, 47, 1–26. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Kowalik, Z.; Cheung, K.F. Depth-integrated, Non-hydrostatic Model for Wave Breaking and Run-up. Int. J. Numer. Methods Fluids 2009, 61, 473–497. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; Van Dongeren, A.P.; de van Thiel Vries, J.; McCall, R.; Lescinski, J. Modelling Storm Impacts on Beaches, Dunes and Barrier Islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Westerink, J.J.; Luettich, R.A.; Baptists, A.M.; Scheffner, N.W.; Farrar, P. Tide and Storm Surge Predictions Using Finite Element Model. J. Hydraul. Eng. 1992, 118, 1373–1390. [Google Scholar] [CrossRef]
- Hubbert, G.D.; Mclnnes, K.L. A Storm Surge Inundation Model for Coastal Planning and Impact Studies. J. Coast. Res. 1999, 15, 168–185. [Google Scholar]
- Mendoza, E.T.; Jiménez, J.A. Regional Vulnerability Analysis of Catalan Beaches to Storms. In Proceedings of the Institution of Civil Engineers-Maritime Engineering; Thomas Telford Ltd: London, UK, 2009; Volume 162, pp. 127–135. [Google Scholar]
- Rangel-Buitrago, N.; Anfuso, G. An Application of Dolan and Davis (1992) Classification to Coastal Storms in SW Spanish Littoral. J. Coast. Res. 2011, 64, 1891–1895. [Google Scholar]
- Mendoza, E.T.; Trejo-Rangel, M.A.; Salles, P.; Appendini, C.M.; Lopez-Gonzalez, J.; Torres-Freyermuth, A. Storm Characterization and Coastal Hazards in the Yucatan Peninsula. J. Coast. Res. 2013, 65, 790–795. [Google Scholar] [CrossRef]
- Mendoza, E.T.; Jimenez, J.A.; Mateo, J. A Coastal Storms Intensity Scale for the Catalan Sea (NW Mediterranean). Nat. Hazards Earth Syst. Sci. 2011, 11, 2453–2462. [Google Scholar] [CrossRef]
- Kokkinos, D.; Prinos, P.; Galiatsatou, P. Assessment of Coastal Vulnerability for Present and Future Climate Conditions in Coastal Areas of the Aegean Sea. In Proceedings of the 11th International Conference on Hydroscience & Engineering, Hamburg, Germany, 28 September–2 October 2014; pp. 1043–1052. [Google Scholar]
- Martzikos, N.; Lykou, A.; Makropoulos, C.; Tsoukala, V. Cluster Analysis and Classification of Storm Events at Rethymno. Eur. Water 2017, 57, 57–62. [Google Scholar]
- Gad, F.K.; Hatiris, G.A.; Loukaidi, V.; Dimitriadou, S.; Drakopoulou, P.; Sioulas, A.; Kapsimalis, V. Long-Term Shoreline Displacements and Coastal Morphodynamic Pattern of North Rhodes Island, Greece. Water 2018, 10, 849. [Google Scholar] [CrossRef]
- Soukissian, T.; Hatzinaki, M.; Korres, G.; Papadopoulos, A.; Kallos, G.; Anadranistakis, E. Wind and Wave Atlas of the Hellenic Seas; Hellenic Centre for Marine Research: Anavyssos, Greece, 2007. [Google Scholar]
- Copernicus Climate Change Service. Water Level Change Indicators for the European Coast From 1977 to 2100 Derived from Climate Projections. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/sis-water-level-change-indicators?tab=overview (accessed on 4 October 2020).
- EMODnet Bathymetry Consortium. EMODnet Digital Bathymetry (DTM). EMODnet Bathymetry 2018. [Google Scholar] [CrossRef]
- Soukissian, T.; Antoniou, P.; Kapsimalis, V.; Drakopoulou, P.; Kyriakidou, H.; Panagiotopoulos, I.; Anagnostou, C. A Scientific Approach to the Constitutional Law for Seashore Delimitation in Greece. In Proceedings of the 5th National Conference of Management and Improvement on Coastal Zone, Athens, Greece, 21–24 November 2011; pp. 165–174. [Google Scholar]
- Martzikos, N.; Afentoulis, V.; Tsoukala, V. Storm Clustering and Classification for the Port of Rethymno in Greece. Water Util. J. 2018, 20, 67–79. [Google Scholar]
- De Michele, C.; Salvadori, G.; Passoni, G.; Vezzoli, R. A Multivariate Model of Sea Storms Using Copulas. Coast. Eng. 2007, 54, 734–751. [Google Scholar] [CrossRef]
- Soukissian, T.H. Probabilistic Modeling of Directional and Linear Characteristics of Wind and Sea States. Ocean Eng. 2014, 91, 91–110. [Google Scholar] [CrossRef]
- Härdle, W.; Simar, L. Applied Multivariate Statistical Analysis; Springer: Berlin/Heidelberg, Germany, 2007; Volume 22007. [Google Scholar]
- Vandarakis, D.; Kyriakou, K.; Gad, F.-K.; Kapsimalis, V.; Panagiotopoulos, I.; Loukaidi, V.; Hatiris, G.A.; Sioulas, A. The carrying capacity and environmental friendly plans for future tourism development in Rhodes Island, Greece. Eur. J. Geogr. 2019, 10, 149–159. [Google Scholar]
- Mendoza, E.T.; Jiménez, J.A. Storm-Induced Beach Erosion Potential on the Catalonian Coast. J. Coast. Res. 2006, 48, 81–88. [Google Scholar]
- Jimenez, J.A.; Ciavola, P.; Balouin, Y.; Armaroli, C.; Bosom, E.; Gervais, M. Geomorphic Coastal Vulnerability to Storms in Microtidal Fetch-Limited Environments: Application to NW Mediterranean & N Adriatic Seas. J. Coast. Res. 2009, 56, 1641–1645. [Google Scholar]
- Krestenitis, Y.N.; Androulidakis, Y.S.; Kontos, Y.N.; Georgakopoulos, G. Coastal Inundation in the North-Eastern Mediterranean Coastal Zone Due to Storm Surge Events. J. Coast. Conserv. 2011, 15, 353–368. [Google Scholar] [CrossRef]
- Idier, D.; Bertin, X.; Thompson, P.; Pickering, M.D. Interactions between mean sea level, tide, surge, waves and flooding: Mechanisms and contributions to sea level variations at the coast. Surv. Geophys. 2019, 40, 1603–1630. [Google Scholar] [CrossRef]
- Petroliagkis, T.I.; Voukouvalas, E.; Disperati, J.; Bidlot, J. Joint Probabilities of Storm Surge, Significant Wave Height and River Discharge Components of Coastal Flooding Events. Eur. Comm. Tech. Rep. 2016. Available online: eu/en/joint-probabilities-of-storm-surge-significant-wave-height-and-river-discharge-components-of-coastal-flooding-eventspbLBNA2782420160KABstXJMAAAEjt5AY4e5L (accessed on 4 October 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gad, F.-K.; Chatzinaki, M.; Vandarakis, D.; Kyriakidou, C.; Kapsimalis, V. Assessment of Wave Storm-Induced Flood Vulnerability in Rhodes Island, Greece. Water 2020, 12, 2978. https://doi.org/10.3390/w12112978
Gad F-K, Chatzinaki M, Vandarakis D, Kyriakidou C, Kapsimalis V. Assessment of Wave Storm-Induced Flood Vulnerability in Rhodes Island, Greece. Water. 2020; 12(11):2978. https://doi.org/10.3390/w12112978
Chicago/Turabian StyleGad, Fragkiska-Karmela, Maria Chatzinaki, Dimitris Vandarakis, Chara Kyriakidou, and Vasilios Kapsimalis. 2020. "Assessment of Wave Storm-Induced Flood Vulnerability in Rhodes Island, Greece" Water 12, no. 11: 2978. https://doi.org/10.3390/w12112978
APA StyleGad, F.-K., Chatzinaki, M., Vandarakis, D., Kyriakidou, C., & Kapsimalis, V. (2020). Assessment of Wave Storm-Induced Flood Vulnerability in Rhodes Island, Greece. Water, 12(11), 2978. https://doi.org/10.3390/w12112978





