Using High-Frequency Water Vapor Isotopic Measurements as a Novel Method to Partition Daily Evapotranspiration in an Oak Woodland
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Micrometeorology
2.3. Sap Flow Sensors
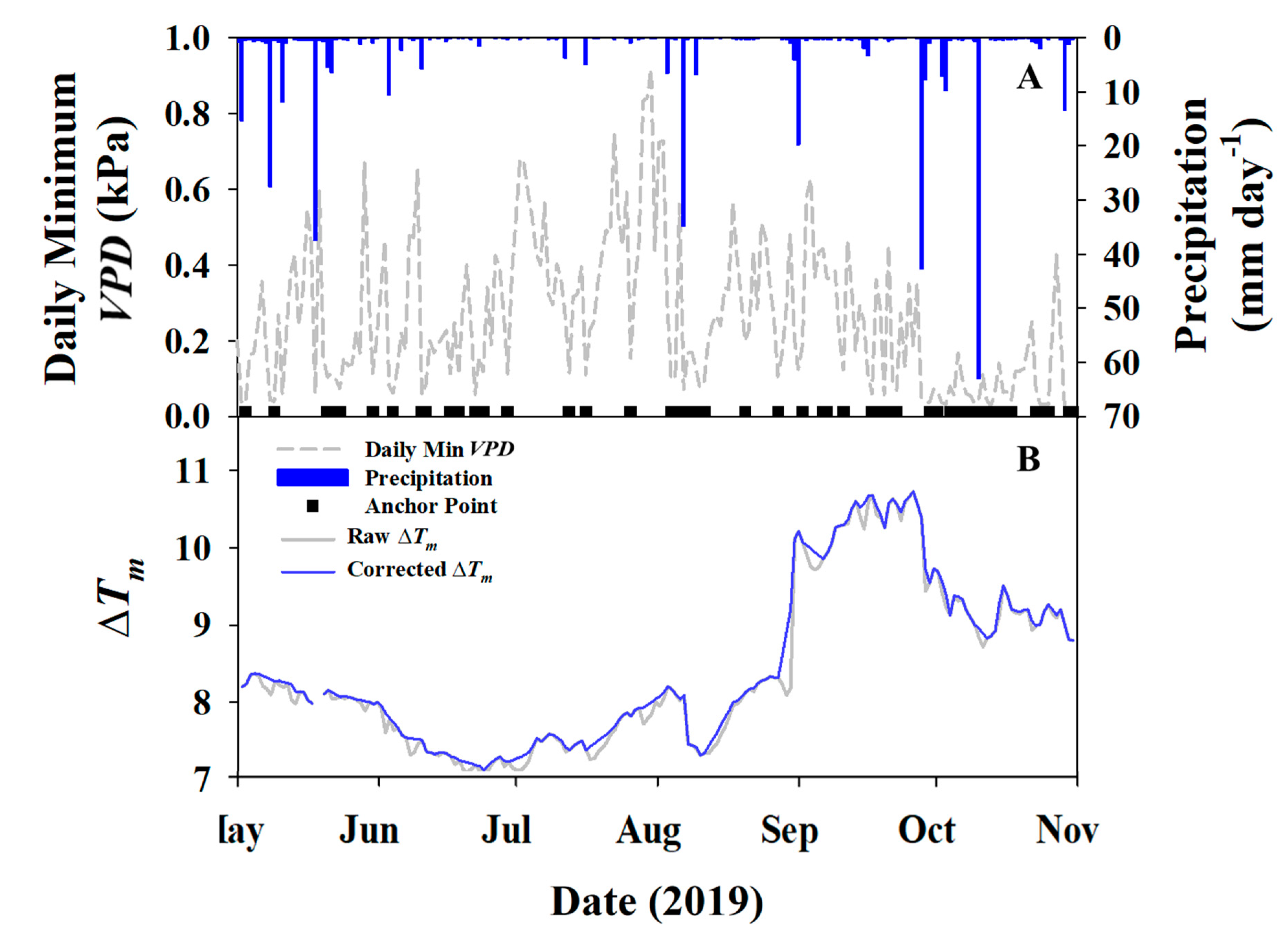
2.3.1. Baseline Corrections
2.3.2. Transpiration Scaling
2.4. Stable Isotopes
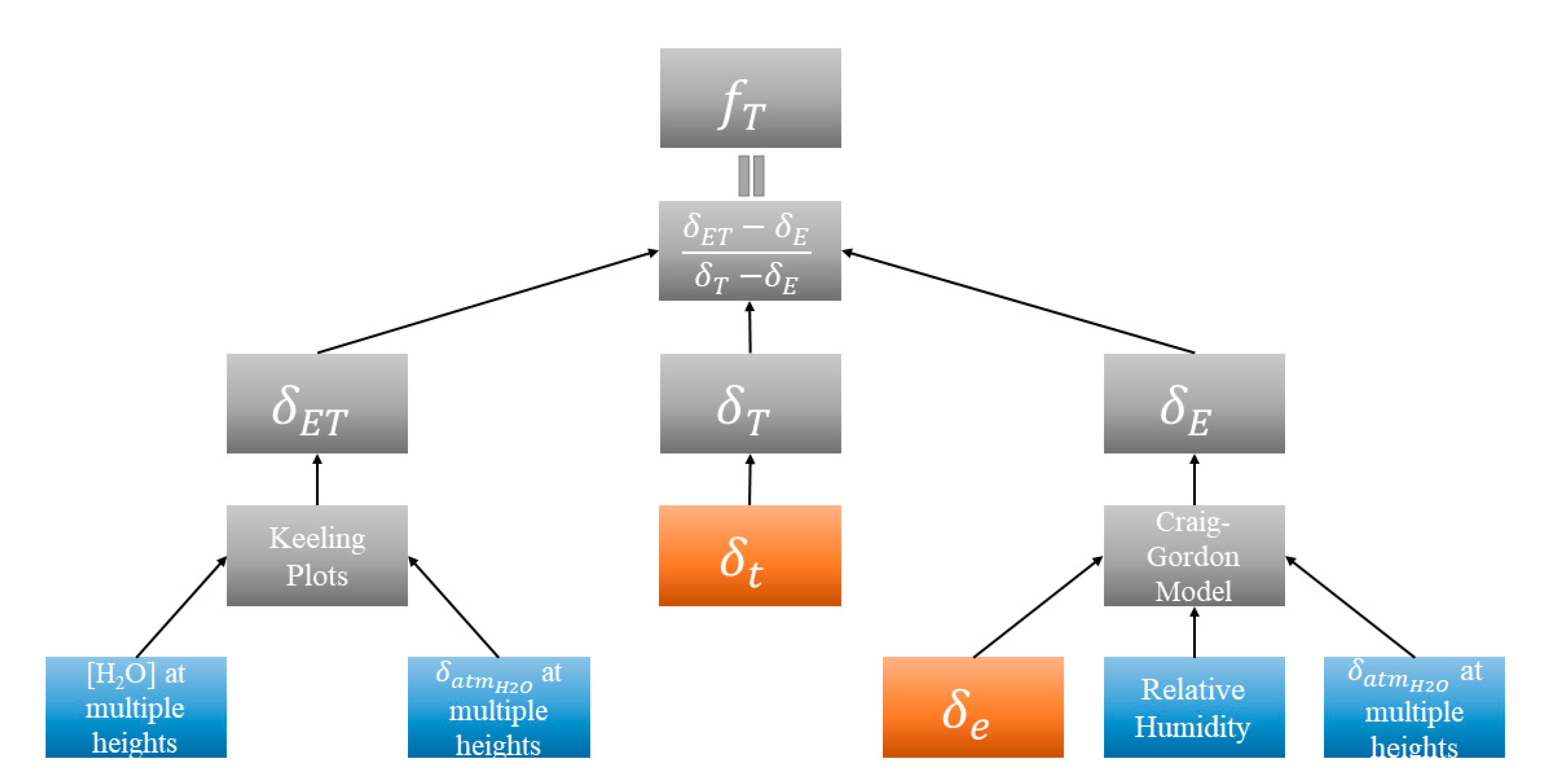
2.4.1. Method Framework
2.4.2. δET, δE, and δT
2.5. Field Sampling and Sample Analysis
2.5.1. Soil and Twig Sampling
2.5.2. Cryogenic Water Extractions and Analysis
2.6. fT Analysis for Sampling Days
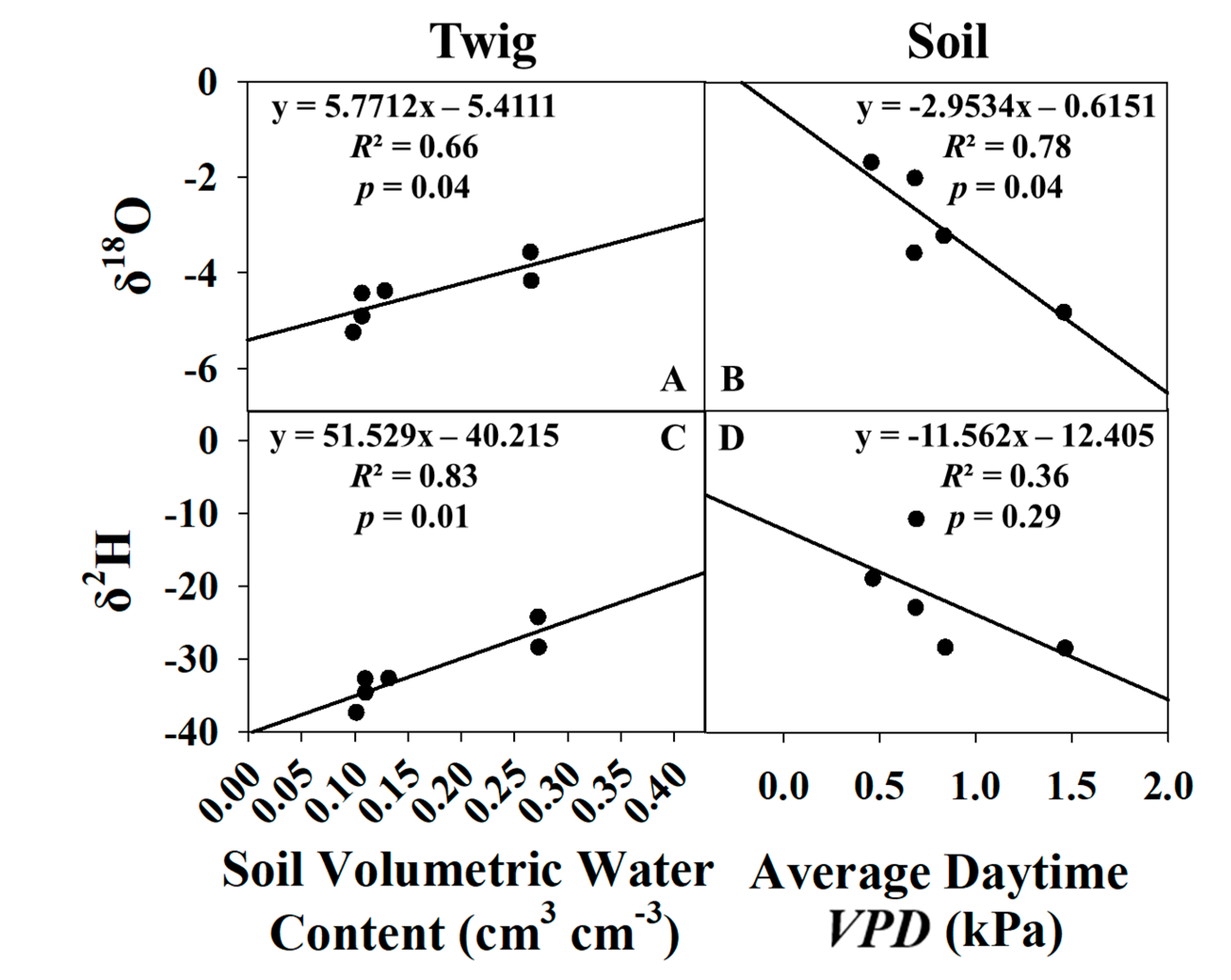
2.7. Predictive Model Development
3. Results
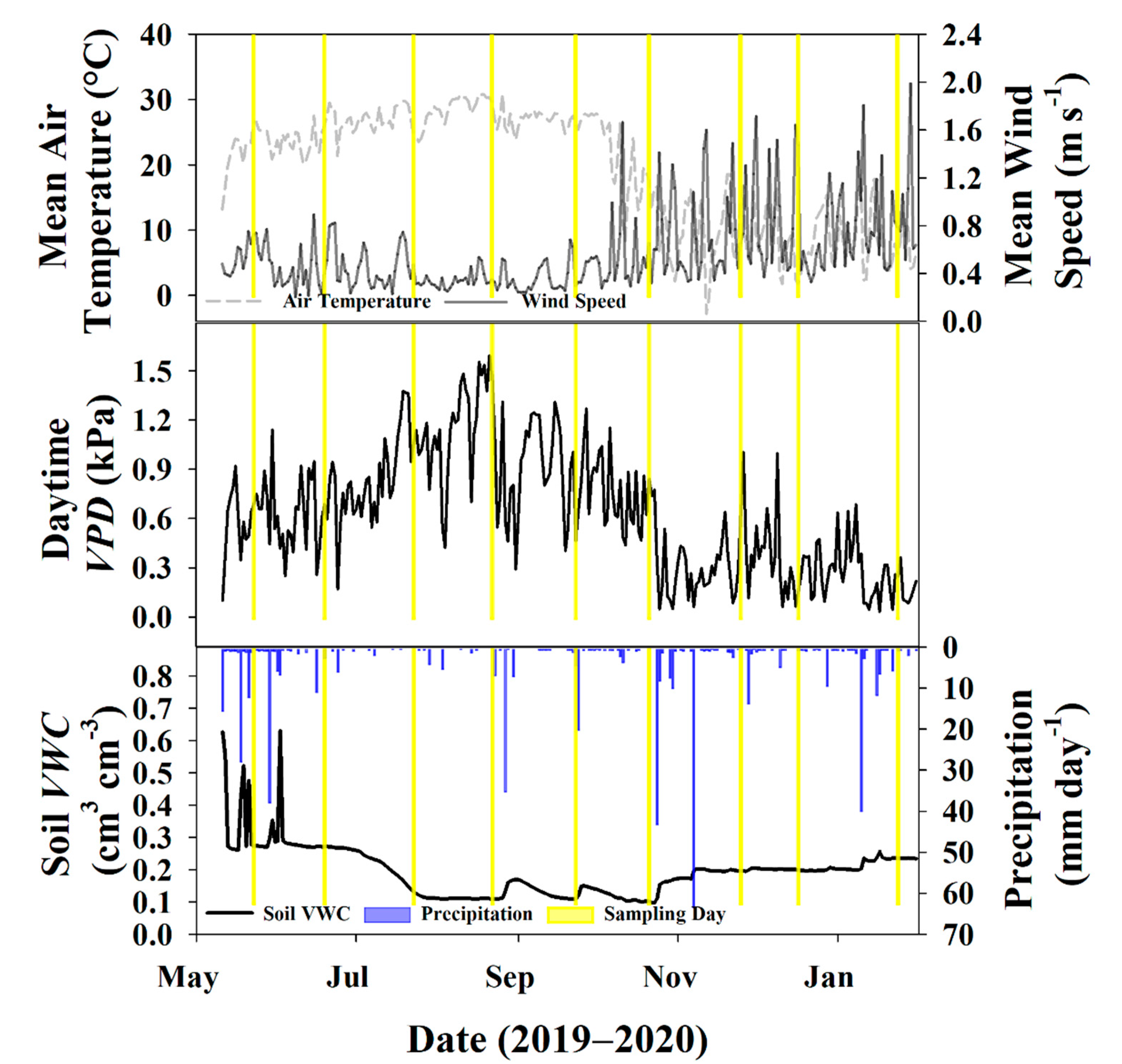
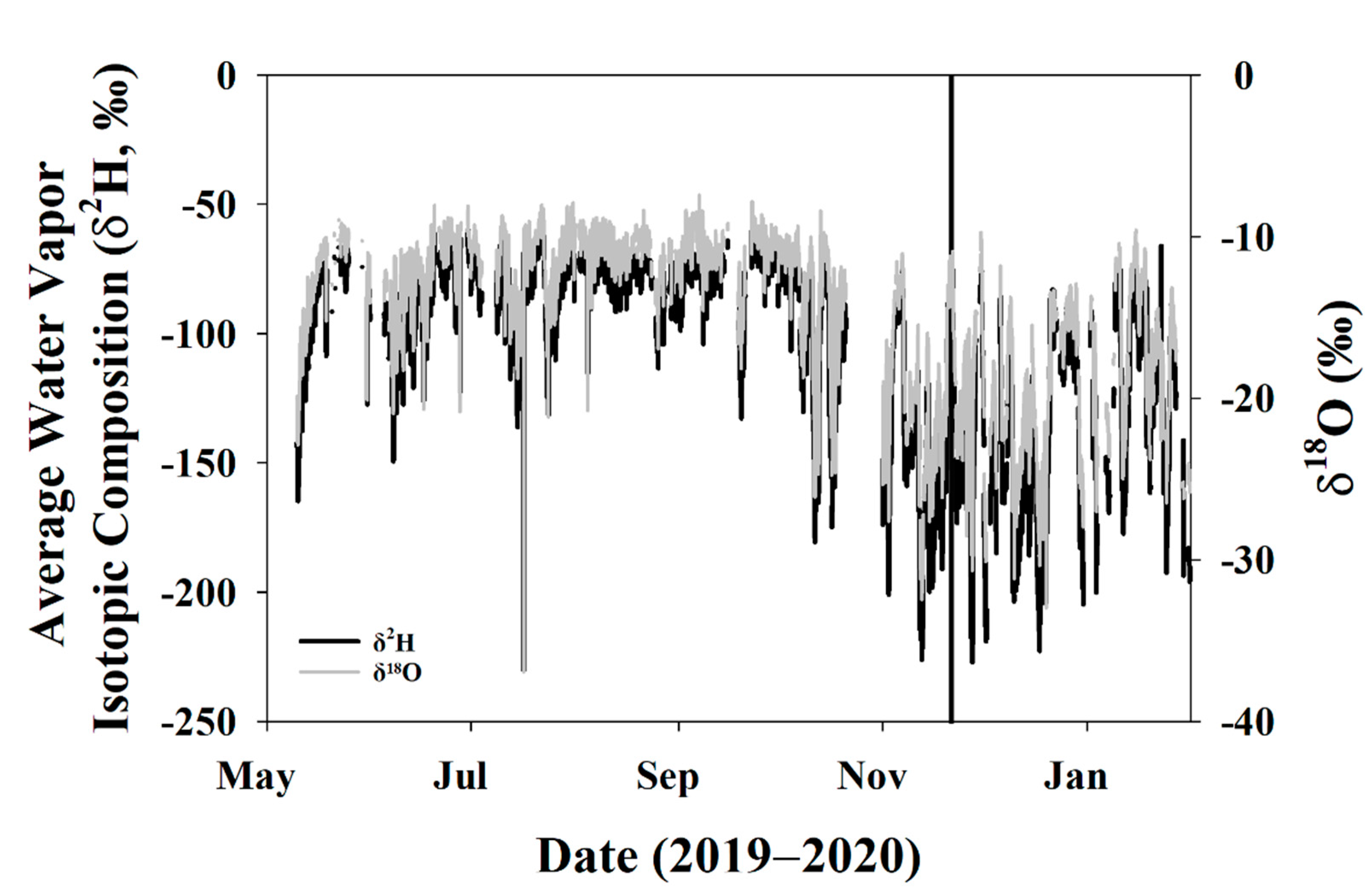
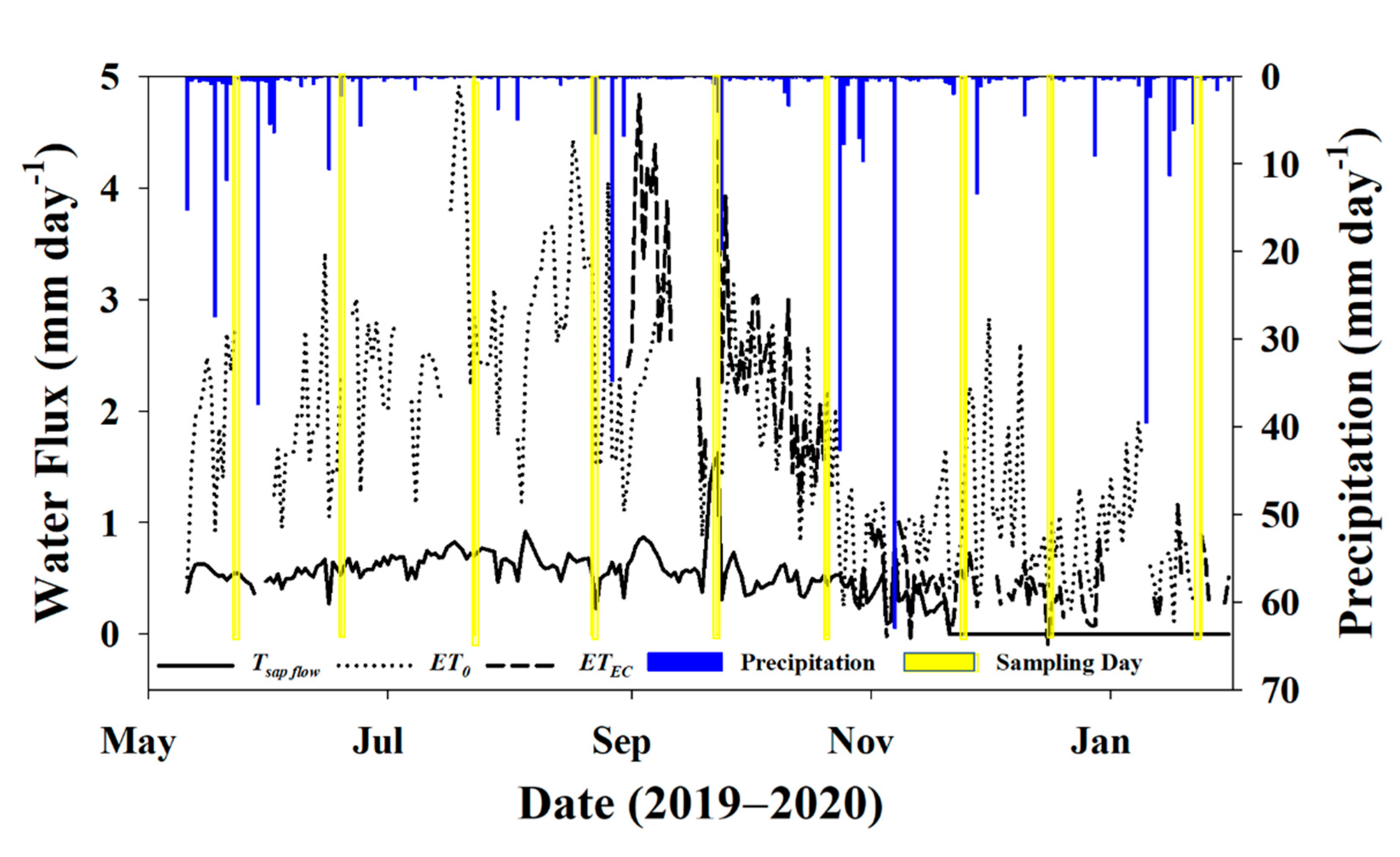
3.1. Environmental Data
3.2. Water Fluxes
3.3. Sampling Days
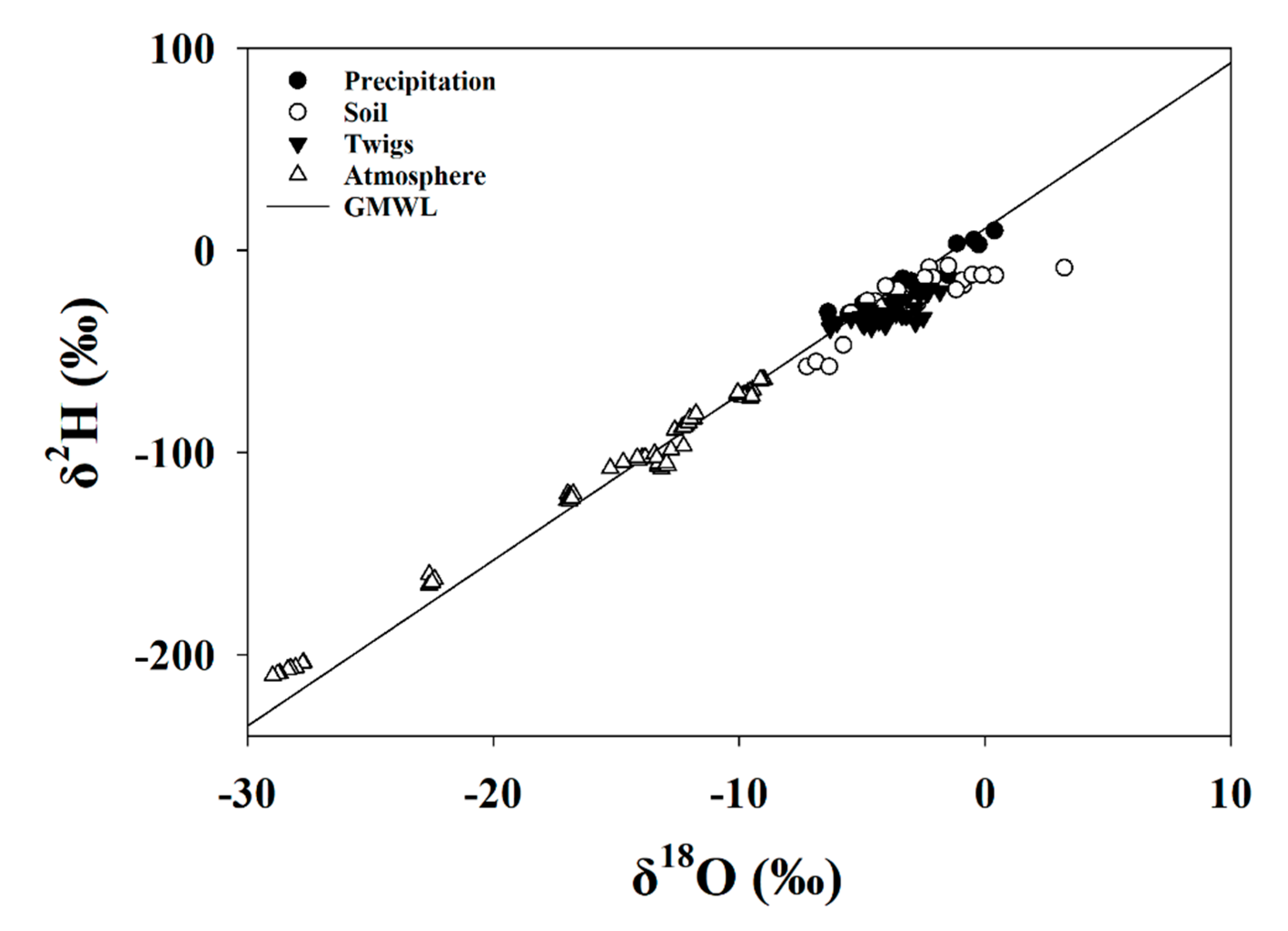
3.3.1. Global Meteoric Water Line and Keeling Plot
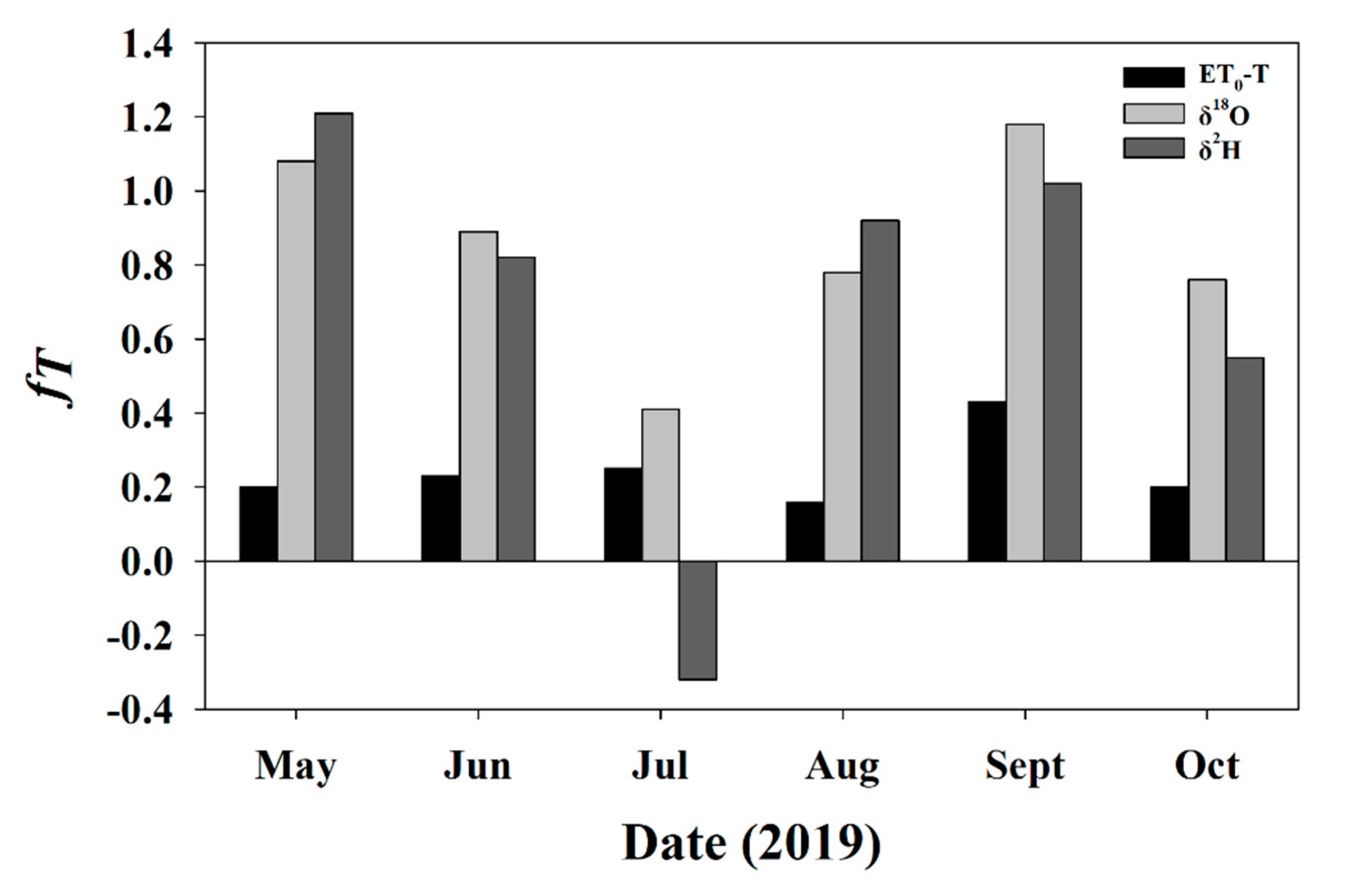
3.3.2. fT for Soil and Twig Sampling Days
3.4. Predictive Models for Growing Season and Dormant Season Sampling Days
3.5. Entire Growing Season
3.5.1. Keeling Plot
3.5.2. Craig-Gordon Model
3.5.3. Daily fT for Entire Study Period
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trenberth Kevin, E.; Smith, L.; Qian, T.; Dai, A.; Fasullo, J. Estimates of the Global Water Budget and Its Annual Cycle Using Observational and Model Data. J. Hydrometeorol. 2007, 8, 758. [Google Scholar] [CrossRef]
- Wilcox, B.; Breshears, D.; Seyfried, M. Water Balance on Rangelands. Encycl. Water Sci. 2003, 791–794. [Google Scholar] [CrossRef]
- Good, S.P.; Moore, G.W.; Miralles, D.G. A mesic maximum in biological water use demarcates biome sensitivity to aridity shifts. Nat. Ecol. Evol. 2017, 1, 1883–1888. [Google Scholar] [CrossRef]
- Helman, D.; Lensky, I.M.; Osem, Y.; Rohatyn, S.; Rotenberg, E.; Yakir, D. A biophysical approach using water deficit factor for daily estimations of evapotranspiration and CO2 uptake in Mediterranean environments. Biogeosciences 2017, 14, 3909–3926. [Google Scholar] [CrossRef]
- Ford, C.R.; Hubbard, R.M.; Kloeppel, B.D.; Vose, J.M. A comparison of sap flux-based evapotranspiration estimates with catchment-scale water balance. Agric. For. Meteorol. 2007, 145, 176–185. [Google Scholar] [CrossRef]
- Shi, T.T.; Guan, D.X.; Wu, J.B.; Wang, A.Z.; Jin, C.J.; Han, S.J. Comparison of methods for estimating evapotranspiration rate of dry forest canopy: Eddy covariance, Bowen ratio energy balance, and Penman-Monteith equation. J. Geophys. Res. Atmos. 2008, 113, 15. [Google Scholar] [CrossRef]
- Tie, Q.; Hu, H.; Tian, F.; Holbrook, N.M. Comparing different methods for determining forest evapotranspiration and its components at multiple temporal scales. Sci. Total Environ. 2018, 633, 12–29. [Google Scholar] [CrossRef] [PubMed]
- Williams, D.G.; Cable, W.; Hultine, K.; Hoedjes, J.C.B.; Yepez, E.A.; Simonneaux, V.; Er-Raki, S.; Boulet, G.; de Bruin, H.A.R.; Chehbouni, A.; et al. Evapotranspiration components determined by stable isotope, sap flow and eddy covariance techniques. Agric. For. Meteorol. 2004, 125, 241–258. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Aouade, G.; Ezzahar, J.; Amenzou, N.; Er-Raki, S.; Benkaddour, A.; Khabba, S.; Jarlan, L. Combining stable isotopes, Eddy Covariance system and meteorological measurements for partitioning evapotranspiration, of winter wheat, into soil evaporation and plant transpiration in a semi-arid region. Agric. Water Manag. 2016, 177, 181–192. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, H.; Liu, F.; An, S.; Cui, J.; Wang, Z.; Liu, S. Partitioning evapotranspiration flux components in a subalpine shrubland based on stable isotopic measurements. Bot. Stud. 2008, 49, 351–361. [Google Scholar]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]
- Moore, G.W.; Cleverly, J.R.; Owens, M.K. Nocturnal transpiration in riparian Tamarix thickets authenticated by sap flux, eddy covariance and leaf gas exchange measurements. Tree Physiol. 2008, 28, 521–528. [Google Scholar] [CrossRef]
- Granier, A. Evaluation of transpiration in a Douglas-fir stand by means of sap flow measurements. Tree Physiol. 1987, 3, 309–320. [Google Scholar] [CrossRef] [PubMed]
- Granier, A. Une nouvelle méthode pour la mesure du flux de sève brute dans le tronc des arbres. Ann. Sci. 1985, 42, 193–200. [Google Scholar] [CrossRef]
- Nier, A. The development of A high-resolution mass-spectrometer—A reminiscence. J. Am. Soc. Mass Spectrom. 1991, 2, 447–452. [Google Scholar] [CrossRef][Green Version]
- Walker, C.D.; Brunel, J.P. Examining evapotranspiration in a semi-arid region using stable isotopes of hydrogen and oxygen. J. Hydrol. 1990, 118, 55–75. [Google Scholar] [CrossRef]
- Brunel, J.-P.; Walker, G.R.; Kennett-Smith, A.K. Field validation of isotopic procedures for determining sources of water used by plants in a semi-arid environment. J. Hydrol. 1995, 167, 351–368. [Google Scholar] [CrossRef]
- Brunel, J.P.; Walker, G.R.; Dighton, J.C.; Monteny, B. Use of stable isotopes of water to determine the origin of water used by the vegetation and to partition evapotranspiration. A case study from HAPEX-Sahel. J. Hydrol. 1997, 188, 466–481. [Google Scholar] [CrossRef]
- Munksgaard, N.C.; Wurster, C.M.; Bird, M.I. Continuous analysis of δ18O and δD values of water by diffusion sampling cavity ring-down spectrometry: A novel sampling device for unattended field monitoring of precipitation, ground and surface waters. Rapid Commun. Mass Spectrom. 2011, 25, 3706–3712. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Yoshimura, K.; Okazaki, A.; Kim, W.; Liu, Z.; Yokoi, M. Partitioning of evapotranspiration using high-frequency water vapor isotopic measurement over a rice paddy field. Water Resour. Res. 2015, 51, 3716–3729. [Google Scholar] [CrossRef]
- Soil Survey Staff, NRCS. Web Soil Survey; United States Department of Agriculture: Washington, DC, USA, 2019.
- NEON. National Ecological Observatory Network; Battelle: Boulder, CO, USA, 2020. [Google Scholar]
- Michael, W.; Jan, H. Biohydrologic effects of eastern redcedar encroachment into grassland, Oklahoma, USA. Biologia 2013, 68, 1132–1135. [Google Scholar] [CrossRef]
- Jones, H.G. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology; Cambridge University Press: Cambridge, UK, 1992; p. 428. [Google Scholar]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Venkatram, A. Estimating the Monin-Obukhov length in the stable boundary layer for dispersion calculations. Bound. Layer Meteorol. 1980, 19, 481–485. [Google Scholar] [CrossRef]
- Zotarelli, L.; Dukes, M.D.; Romero, C.C.; Migliaccio, K.W.; Morgan, K.T. Step by Step Calculation of the Penman-Monteith Evapotranspiration (FAO-56 Method); Institute of Food and Agricultural Sciences. University of Florida: Gainesville, FL, USA, 2018. [Google Scholar]
- Moore, G.W.; Bond, B.J.; Jones, J.A.; Phillips, N.; Meinzer, F.C. Structural and compositional controls on transpiration in 40-and 450-year-old riparian forests in western Oregon, USA. Tree Physiol. 2004, 24, 481–491. [Google Scholar] [CrossRef] [PubMed]
- Vertessy, R.A.; Watson, F.G.R.; O′Sullivan, S.K. Factors determining relations between stand age and catchment water balance in mountain ash forests. For. Ecol. Manag. 2001, 143, 13–26. [Google Scholar] [CrossRef]
- McDowell, N.; Barnard, H.; Bond, B.J.; Hinckley, T.; Hubbard, R.M.; Ishii, H.; Köstner, B.; Magnani, F.; Marshall, J.D.; Meinzer, F.C.; et al. Relatsh between Tree Height Leaf Area: Sapwood Area Ratio. Oecologia 2002, 132, 12. [Google Scholar] [CrossRef]
- Gebauer, T.; Horna, V.; Leuschner, C. Variability in radial sap flux density patterns and sapwood area among seven co-occurring temperate broad-leaved tree species. Tree Physiol. 2008, 28, 1821–1830. [Google Scholar] [CrossRef]
- Clearwater, M.J.; Goldstein, G.; Holbrook, N.M.; Meinzer, F.C.; Andrade, J.L. Potential errors in measurement of nonuniform sap flow using heat dissipation probes. Tree Physiol. 1999, 19, 681–687. [Google Scholar] [CrossRef]
- Mackay, D.S.; Ewers, B.E.; Loranty, M.M.; Kruger, E.L. On the representativeness of plot size and location for scaling transpiration from trees to a stand. J. Geophys. Res. Biogeosci. 2010, 115, 14. [Google Scholar] [CrossRef]
- Xiao, W.; Wei, Z.; Wen, X. Evapotranspiration partitioning at the ecosystem scale using the stable isotope method—A review. Agric. For. Meteorol. 2018, 263, 346–361. [Google Scholar] [CrossRef]
- Zhang, S.; Wen, X.; Wang, J.; Yu, G.; Sun, X. The use of stable isotopes to partition evapotranspiration fluxes into evaporation and transpiration. Acta Ecol. Sin. 2010, 30, 201–209. [Google Scholar] [CrossRef]
- Barnes, C.J.; Allison, G.B. Tracing of water movement in the unsaturated zone using stable isotopes of hydrogen and oxygen. J. Hydrol. 1988, 100, 143–176. [Google Scholar] [CrossRef]
- Sprenger, M.; Leistert, H.; Gimbel, K.; Weiler, M. Illuminating hydrological processes at the soil-vegetation-atmosphere interface with water stable isotopes. Rev. Geophys. 2016, 54, 674–704. [Google Scholar] [CrossRef]
- Zimmermann, U.; Ehhalt, D.; Muennich, K.O. Soil-Water Movement and Evapotranspiration: Changes in the Isotopic Composition of the Water; International Atomic Energy Agency: Vienna, Austria, 1967. [Google Scholar]
- Ehleringer, J.R.; Dawson, T.E. Water uptake by plants: Perspectives from stable isotope composition. Plant Cell Environ. 1992, 15, 1073–1082. [Google Scholar] [CrossRef]
- Yepez, E.A.; Williams, D.G.; Scott, R.L.; Lin, G. Partitioning overstory and understory evapotranspiration in a semiarid savanna woodland from the isotopic composition of water vapor. Agric. For. Meteorol. 2003, 119, 53–68. [Google Scholar] [CrossRef]
- Flanagan, L.B.; Comstock, J.P.; Ehleringer, J.R. Comparison of Modeled and Observed Environmental Influences on the Stable Oxygen and Hydrogen Isotope Composition of Leaf Water in Phaseolus vulgaris L. Plant Physiol. 1991, 96, 588. [Google Scholar] [CrossRef]
- Keeling, C.D. The concentration and isotopic abundances of atmospheric carbon dioxide in rural areas. Geochim. Cosmochim. Acta 1958, 13, 322–334. [Google Scholar] [CrossRef]
- Keeling, C.D. The concentration and isotopic abundances of carbon dioxide in rural and marine air. Geochim. Cosmochim. Acta 1961, 24, 277–298. [Google Scholar] [CrossRef]
- Yakir, D.; Sternberg, L.d.S.L. The use of stable isotopes to study ecosystem gas exchange. Oecologia 2000, 123, 297–311. [Google Scholar] [CrossRef] [PubMed]
- Craig, H.; Gordon, L.I. Deuterium and oxygen 18 variations in the ocean and the marine atmosphere. In Proceedings of the Conference on Stable Isotopes in Oceanographic Studies and Paleotemperatures, Spoleto, Italy, 26–30 July 1965; pp. 9–130. [Google Scholar]
- Majoube, M. Fractionnement en oxygène 18 et en deutérium entre l’eau et sa vapeur. J. De Chim. Phys. 1971, 68, 1423–1436. [Google Scholar] [CrossRef]
- Cappa, C.D.; Hendricks, M.B.; DePaolo, D.J.; Cohen, R.C. Isotopic fractionation of water during evaporation. J. Geophys. Res. Atmos. 2003, 108, 10. [Google Scholar] [CrossRef]
- Merlivat, L. Molecular diffusivities of H216O, HD16O, and H218O in gases. J. Chem. Phys. 1978, 69, 2864–2871. [Google Scholar] [CrossRef]
- Service, N.W. Weather for Decatur; National Oceanic and Atmospheric Administration: College Station, TX, USA, 2020. [Google Scholar]
- Nehemy, M.F.; Benettin, P.; Asadollahi, M.; Pratt, D.; Rinaldo, A.; McDonnell, J.J. How plant water status drives tree source water partitioning. Hydrol. Earth Syst. Sci. Discuss. 2019, 2019, 1–26. [Google Scholar] [CrossRef]
- Wilson, K.B.; Hanson, P.J.; Baldocchi, D.D. Factors controlling evaporation and energy partitioning beneath a deciduous forest over an annual cycle. Agric. For. Meteorol. 2000, 102, 83–103. [Google Scholar] [CrossRef]
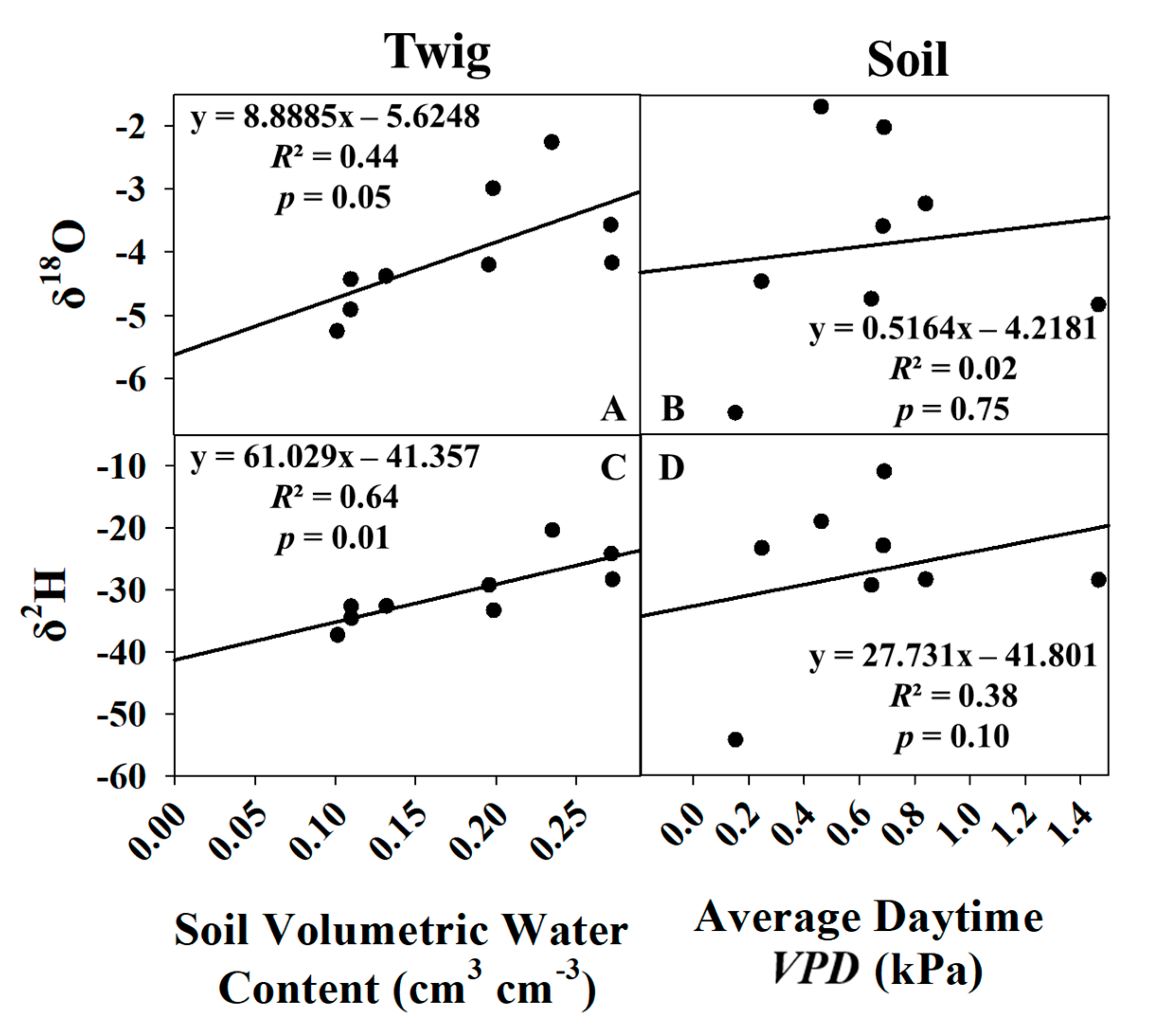
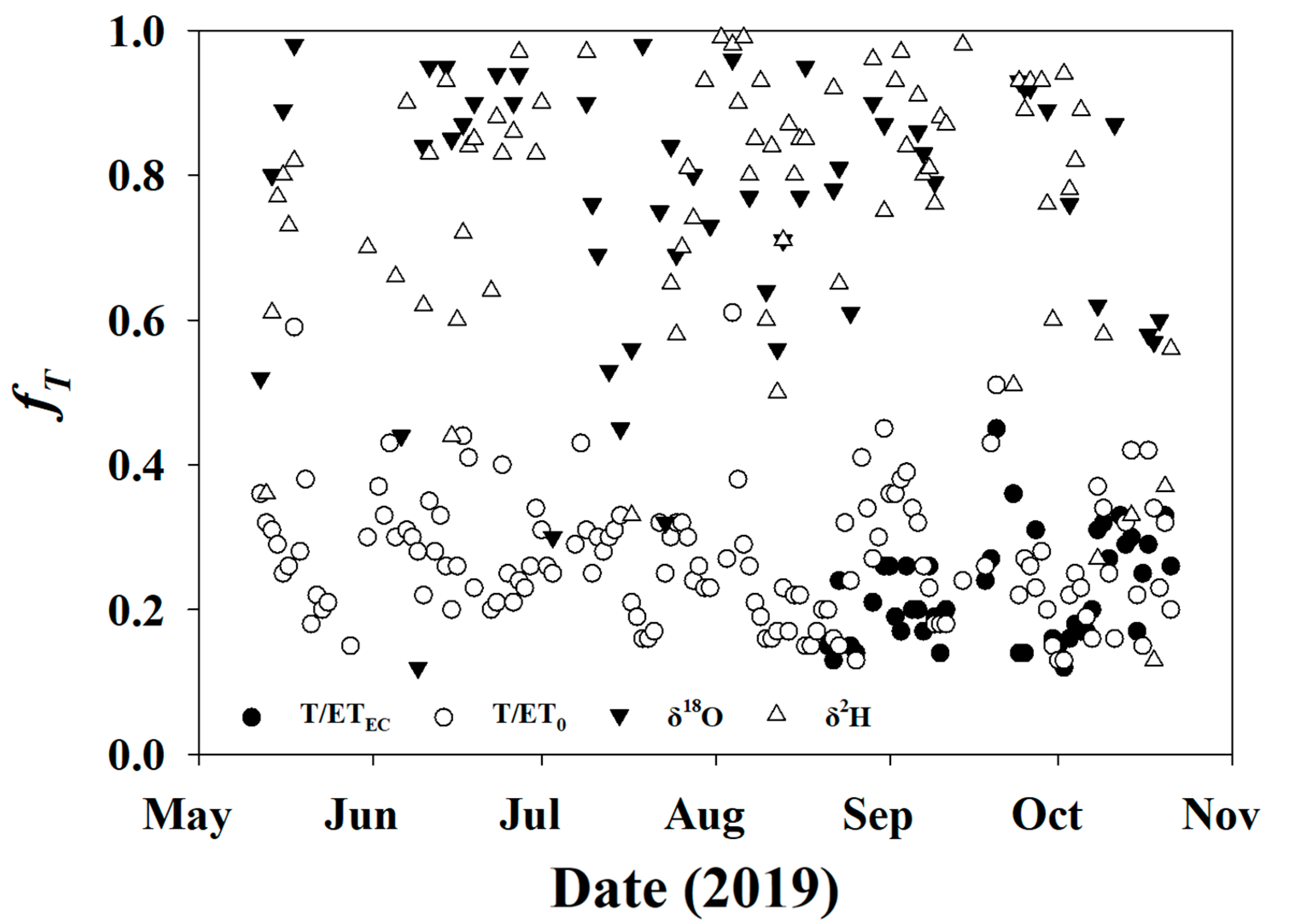
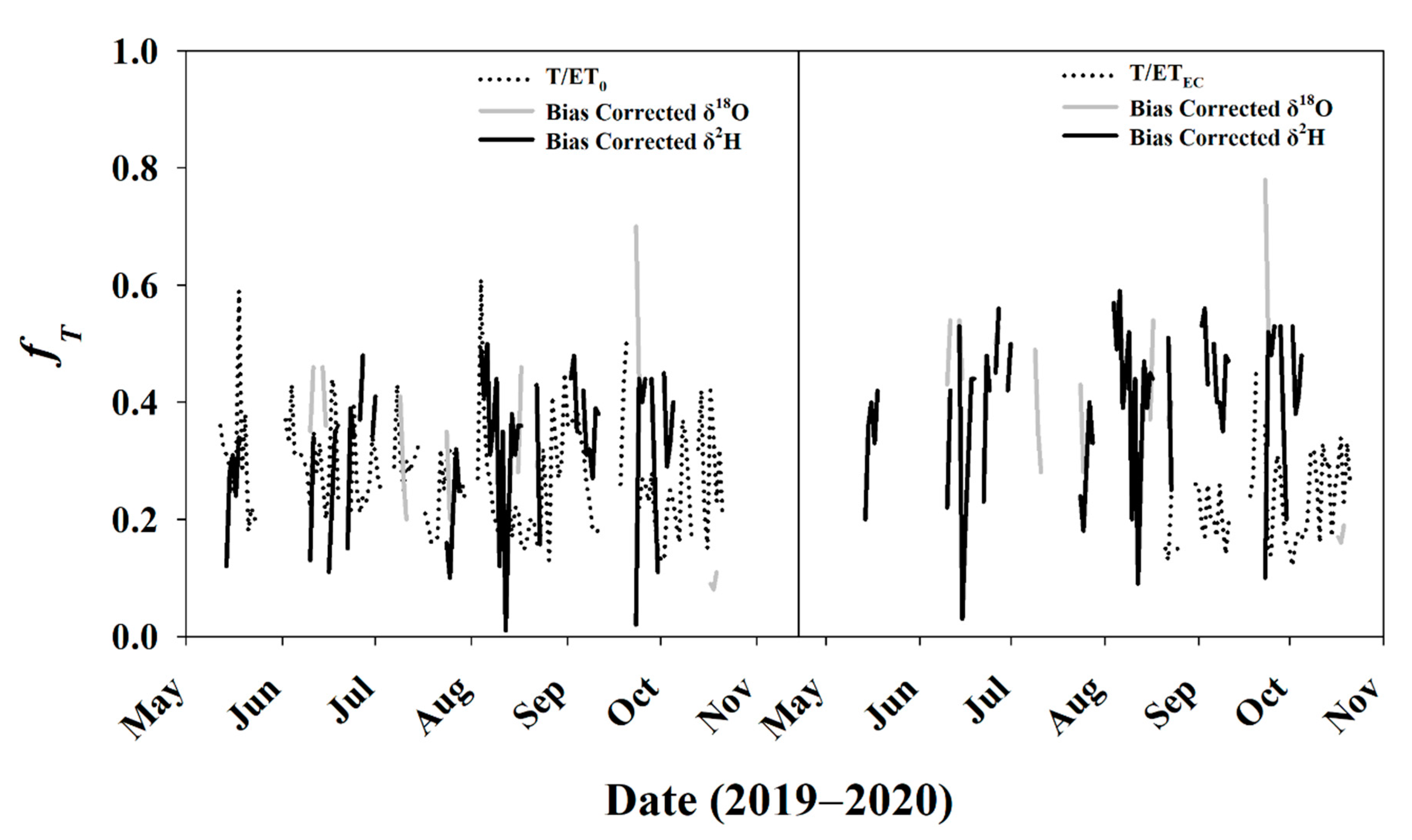
| Sampling DOY 2019 | Stable Isotope | Keeling Plot | ||||
|---|---|---|---|---|---|---|
| N | Slope | δET | R2 | p-Value | ||
| 143 | δ18O | 21 | −236.37 | −1.07 | 0.71 | <0.001 |
| δ2H | 21 | −1853.90 | −3.37 | 0.77 | <0.001 | |
| 170 | δ18O | 29 | −97.11 | −7.86 | 0.61 | <0.001 |
| δ2H | 29 | −864.74 | −47.32 | 0.86 | <0.001 | |
| 204 | δ18O | 29 | 109.86 | −19.60 | 0.09 | 0.11 |
| δ2H | 29 | 184.18 | −112.54 | 0.02 | 0.52 | |
| 234 | δ18O | 29 | 103.95 | −13.95 | 0.13 | 0.05 |
| δ2H | 29 | −682.05 | −44.91 | 0.57 | <0.001 | |
| 266 | δ18O | 16 | −368.38 | 3.03 | 0.44 | 0.005 |
| δ2H | 16 | −1084.78 | −28.37 | 0.29 | 0.03 | |
| 294 | δ18O | 28 | 7.11 | −13.57 | 0.03 | 0.4 |
| δ2H | 28 | −331.99 | −76.86 | 0.72 | <0.001 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adkison, C.; Cooper-Norris, C.; Patankar, R.; Moore, G.W. Using High-Frequency Water Vapor Isotopic Measurements as a Novel Method to Partition Daily Evapotranspiration in an Oak Woodland. Water 2020, 12, 2967. https://doi.org/10.3390/w12112967
Adkison C, Cooper-Norris C, Patankar R, Moore GW. Using High-Frequency Water Vapor Isotopic Measurements as a Novel Method to Partition Daily Evapotranspiration in an Oak Woodland. Water. 2020; 12(11):2967. https://doi.org/10.3390/w12112967
Chicago/Turabian StyleAdkison, Christopher, Caitlyn Cooper-Norris, Rajit Patankar, and Georgianne W. Moore. 2020. "Using High-Frequency Water Vapor Isotopic Measurements as a Novel Method to Partition Daily Evapotranspiration in an Oak Woodland" Water 12, no. 11: 2967. https://doi.org/10.3390/w12112967
APA StyleAdkison, C., Cooper-Norris, C., Patankar, R., & Moore, G. W. (2020). Using High-Frequency Water Vapor Isotopic Measurements as a Novel Method to Partition Daily Evapotranspiration in an Oak Woodland. Water, 12(11), 2967. https://doi.org/10.3390/w12112967





