Abstract
Electrical conductivity (EC), one of the most widely used indices for water quality assessment, has been applied to predict the salinity of the Babol-Rood River, the greatest source of irrigation water in northern Iran. This study uses two individual—M5 Prime (M5P) and random forest (RF)—and eight novel hybrid algorithms—bagging-M5P, bagging-RF, random subspace (RS)-M5P, RS-RF, random committee (RC)-M5P, RC-RF, additive regression (AR)-M5P, and AR-RF—to predict EC. Thirty-six years of observations collected by the Mazandaran Regional Water Authority were randomly divided into two sets: 70% from the period 1980 to 2008 was used as model-training data and 30% from 2009 to 2016 was used as testing data to validate the models. Several water quality variables—pH, HCO3−, Cl−, SO42−, Na+, Mg2+, Ca2+, river discharge (Q), and total dissolved solids (TDS)—were modeling inputs. Using EC and the correlation coefficients (CC) of the water quality variables, a set of nine input combinations were established. TDS, the most effective input variable, had the highest EC-CC (r = 0.91), and it was also determined to be the most important input variable among the input combinations. All models were trained and each model’s prediction power was evaluated with the testing data. Several quantitative criteria and visual comparisons were used to evaluate modeling capabilities. Results indicate that, in most cases, hybrid algorithms enhance individual algorithms’ predictive powers. The AR algorithm enhanced both M5P and RF predictions better than bagging, RS, and RC. M5P performed better than RF. Further, AR-M5P outperformed all other algorithms (R2 = 0.995, RMSE = 8.90 μs/cm, MAE = 6.20 μs/cm, NSE = 0.994 and PBIAS = −0.042). The hybridization of machine learning methods has significantly improved model performance to capture maximum salinity values, which is essential in water resource management.
1. Introduction
Rivers are the principal sources of water for human consumption, irrigation, municipal, and industrial demands, and provide habitat for aquatic species in many regions of the world [1]. The deterioration of water quality of rivers causes irreparable damage to the environments and human health [2,3]. Monitoring and assessments of water quality parameters (e.g., salinity, dissolved oxygen (DO), algae, nitrogen (N), among others) are necessary to develop water management plans [4], as more than one billion people lack access to safe drinking water. Thus, robust and flexible models are urgently needed to accurately predict water quality and to estimate future supplies.
Numerous physical or mathematical models have been developed to predict and plan for the management of water quality (i.e., QUAL2K, MOUSE), but the models are complex, time-consuming (especially during the calibration phase), and data-intensive. These models are challenging for users in developing countries where data are insufficient or where background information is scant. Statistical models of water quality have been developed based on both linear and non-linear relationships between input and output variables. These models, however, often fail to adequately represent the complexity of these phenomena in environments with multivariate non-linear relationships [5,6]. There are non-linear, stochastic, and lagging relationships among several water quality parameters, and it is challenging to create a mathematical model to predict events in these circumstances with traditional approaches [7].
Artificial intelligence (AI) algorithms for water quality modeling have been explored in recent years. These algorithms explore hidden and complex relationships among input and output variables to craft models that best represent these relationships. Several advantages of AI models over traditional physical and statistical models include: the data that are needed for the AI models can be collected relatively easily, sometimes from remote sensing platforms; AI models are less sensitive than traditional approaches to missing data; the structures of AI models are flexible, non-linear, and robust; and AI models can handle huge amounts of data and data at different scales [8,9,10]. Research over the last couple of decades has explored water quality modeling using numerous machine learning (ML) algorithms [11,12,13,14,15,16,17,18,19,20,21,22,23,24].
Among the ML algorithms, artificial neural networks (ANN)—backpropagation neural networks (BPNN), multilayer perceptron (MLP), and feed-forward neural networks (FFNN)—have been used to predict, forecast, model, and estimate salinity in soils [25,26,27,28], groundwater [29,30,31,32], and oceans [33,34]. Also, only a few studies have attempted to estimate salinity in rivers [35,36,37]. Huang and Foo [36] applied an ANN model to estimate salinity in the Apalachicola River, Florida. Najah et al. [4,20] also used ANN to predict EC in Malaysia’s Johor River.
ANN, the most widely used ML algorithm, has poor prediction power, especially when validation data are not in the range of the training data, and when using small datasets [38,39,40,41,42]. Thus, a hybrid of ANN and fuzzy logic (FL) was proposed in an adaptive neuro-fuzzy inference system (ANFIS) to overcome this weakness. Although ANFIS was successful and had higher prediction accuracy than both ANN and FL, it was still unable to properly determine the weight of the membership function. To resolve this, bioinspired (or metaheuristic) algorithms have been used to automatically determine these weights. Some, using metaheuristic algorithms with ANFIS, have found that hybrid algorithms have higher powers of prediction than any standalone ANFIS [43,44].
Decision-tree algorithms are more powerful predictors than those algorithms with hidden layers in their structure (i.e., ANN, ANFIS, and support vector machine (SVM)) [8]. Barzegar et al. [45] used extreme learning machine (ELM) and wavelet-extreme learning machine hybrid (WA-ELM) to predict EC in the Aji-Chay River watershed and compared the prediction powers of those models to ANFIS. They found that WA-ELM outperformed the other models. ELM is popular and well-known for fast training, but has the disadvantage of being unable to encode more than one layer of abstraction.
Currently, data-mining algorithms like RF, logistic model tree (LMT), and naïve Bayes trees (NBT) are widely used in flood-susceptibility mapping [46,47], groundwater vulnerability assessments using the bootstrap aggregating (BA) algorithm [48], and landslide-susceptibility mapping with Bayesian algorithms [49,50]. It is clear from that these algorithms have been widely used for spatial modeling, and their accuracies have been vetted with field data, but they are seldom used for prediction with time-series data. They have been used to predict suspended sediment load with a reduced error pruning tree (REPT), M5P, and instance-based learning (IBK), and random committee-REPT (RC-REPT) [9], to predict apparent shear stress with RF, M5 Prime (M5P), and random tree (RT) algorithms [51] to predict concentrations of dissolved oxygen in rivers with M5P and SVM [52] and to estimate solar radiation with RF, RT, M5P, and REPT [53].
This paper develops, explores, and compares the effectiveness of two standalone (M5P and RF) and eight novel hybrid algorithms (bagging-M5P, bagging-RF, random subspace (RS)-M5P, RS-RF, random committee (RC)-M5P, RC-RF, additive regression (AR)-M5P, and AR-RF) to predict salinity in the Babol-Rood River in northern Iran. The models’ performances are evaluated using model efficiency indices and graphical comparison. These hybrid algorithms have not previously been used to predict surface water quality (salinity). In fact, there have been no prior attempts to apply them for any geoscientific purpose. Thus, the main contribution of this study is that it develops and evaluates these hybrid algorithms for the first time and offers new insights into the applicability of hybrid ML algorithms. Not only will their use enhance the capacity to predict salinity in rivers, but also in other studies of hydrology and hydraulics.
2. Materials and Methods
2.1. Study Area
The Babol-Rood River is in the Savadkouh district of Mazandaran Province, Iran (Figure 1) in the Alborz Mountains near the Caspian Sea. The elevation in the catchment ranges from 55.36 to 3317.38 m. The average elevation is 923.55 m. Rangelands are located between 1800 and 3100 m. Ninety percent of the area is between 2200 and 2900 m. Forestlands are found between 150 and 2500 m. The slopes of the watershed have been categorized into five classes. The largest proportion of the slopes are from 30 to 60%, whereas slopes less than 5% are least common.
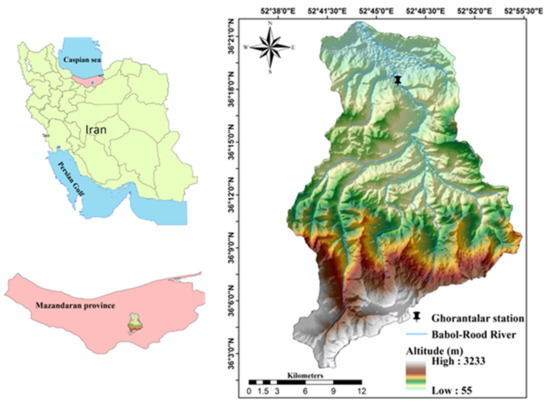
Figure 1.
Babol-Rood River catchment and location of Ghorantalar hydrometric station.
A large part of the region’s geology, mostly in the central part of the watershed near the North Alborz fault, is Mesozoic bedrock and sediments are from the Cenozoic. The soils are dictated by geomorphology, climate, and vegetation. The soils of steep slopes with sparse vegetation cover, particularly in the watershed’s upperparts, are semi-deep with light to medium texture. In contrast, soils of the middle and lower parts, where slopes are gentler and where vegetation is moderately dense to dense, are moderately deep to deep and have medium to heavy textures. The soils of the area are classified as B and C in terms of permeability. The catchment is characterized by high precipitation of up to 2000 mm annually with fall and winter maxima. Summers are hot, and winters are mild. In the coastal plains and in the highest mountain areas, the climate is Mediterranean with dry summers. The Ghorantalar hydrometric station at the catchment outlet provides observation records. Most river salinity in northern Iran, and especially in the study area, is due to the seawater intrusion, saline water discharge of agricultural regions, and the carbonate formations [54].
2.2. Methodology
2.2.1. Data Collection and Preparation
The Babol-Rood River’s water salinity was calculated as EC (μs/cm) and was modeled using ten water quality variables: water discharge (Q), total dissolved solids (TDS), pH, HCO3−, Cl−, SO42−, Ca2+, Mg2+, and Na+. A 36-year (1980 to 2016) monthly record of water quality was obtained from the Mazandaran Regional Water Authority (MRWA). The data were randomly divided into two sets—70% and 30%, a ratio widely used for both spatial [46,47], temporal, and time-series modeling [9,49]. The first 28 years of data (1980–2008) were used for training to build the models, and the remaining eight years (2009–2016) were used for testing that validated the models (Table 1). EC values ranged from 0.03 to 900 μs/cm. To remove the impacts of the different scales of the variables and to guarantee prediction flexibility [38], the data values were normalized () to a range from 0 to 1 [55,56,57,58,59]:
where, , , and are measured data, the minimum value of variable xi, and the maximum value of the of variable , respectively.

Table 1.
Statistics of the training and testing datasets.
The chemistry of rivers in the study region is mainly affected by effluents and nutrient loads from agricultural runoff and seawater intrusion. Water temperature affects solution concentrations in shallow non-flowing waters where evaporation can enhance salinity and push it to high levels. Therefore, modeling of water bodies, like lakes, reservoirs, or marshes, ought to factor temperature. Flowing rivers, by contrast, are more affected by agricultural contaminants, sea level rise, and saltwater intrusion in coastal areas than by temperature, and thus it is not an important factor.
2.2.2. Selection of Input Combinations
There are two main steps to devise appropriate input combinations: determination of the most effective input variables and identification of the optimum values for each model’s operator. First, the proposed algorithms were tested using several input combinations to determine the most effective input variable or combination of variables. In total, nine input combinations were devised according to the correlation coefficient (CC) of EC with each water quality variable (Table 2). The most effective variable (i.e., variable with the highest CC), in this case TDS, was introduced into each model. The working hypothesis is that the variable with the highest CC suffices to accurately predict EC. The variable with the next highest CC was added to the first and each subsequent variable was added in a stepwise fashion to the growing string until the variable with lowest CC was added (i.e., a combination of all 9) (Table 3). To identify the best input combination, the individual and hybrid models were performed using a fixed set of parameters (operator) [8]. All models were evaluated using the 10 input combinations, and the root mean square error (RMSE) determined the most effective combination in the test set. Several other model forms are possible, considering all possible input combinations (29 − 1 = 511). Hence, we limited our candidate set of models to the input combination in accordance with previous studies [53,60].

Table 2.
Pearson correlation coefficient between EC and input water quality variables.

Table 3.
Various input combinations used in the modeling.
2.2.3. Identification of Optimum Values of Operators
After determining the best input variable combination, optimum values for each model’s operators were determined by trial and error [8]. There are no optimum global values for each operator [61,62,63,64]. Therefore, different values were tested and the optimum value was selected according to the RMSE of the testing phase as in the previous stage. In the first iteration, the models were run using the default values. Then according to the result of each iteration, values above and below the default values were examined randomly. This continued until the optimum values for each model’s operator were obtained.
2.2.4. Models Development
Two standalone algorithms—M5P and RF—and 8 novel hybrid algorithms—BA, RS, RC, and AR combined with the standalone algorithms: BA-M5P, BA-RF, RS-M5P, RS-RF, RC-M5P, RC-RF, AR-M5P, and AR-RF—were developed to predict Babol-Rood River salinity.
M5P Algorithm
Quinlan [65] introduced the M5 algorithm as a type of decision-tree. Mosavi et al., [66] expanded the original M5 algorithm to create the M5P. A remarkable capability of the M5P algorithm is that it can handle large datasets efficiently, as well as many variables and many dimensions. M5P is also able to handle missing data [67]. An example depicts the M5P model predicting electrical conductivity (Figure 2).
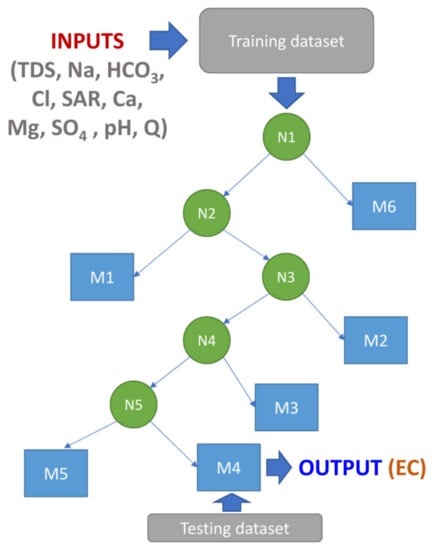
Figure 2.
An example M5P tree model for predicting electrical conductivity.
To process data and build a decision tree, the M5P algorithm performs 4 steps:
Step 1: Divide the initial input space into multiple subspaces. Separation criteria are used to minimize the intra-subspace overlap (from root to the node). Standard deviation (sd) is used to measure the variability of the intra-subspace. The standard deviation reduction (SDR) criterion is used to construct the tree:
where D is the dataset that reached the node and Di denotes the sub-space (splitting node).
Step 2: Develop a linear regression model for each sub-space using the sub-dataset.
Step 3: Prune the nodes of the developed tree. If SDR is lower than the expected error while developing the linear model (for sub-tree), over-fitting can occur. Pruning is undertaken to overcome this.
Step 4: Smooth the discontinuities caused by the pruning process. A final tree is created by combining the leaf and root to filter the predicted value. Combining the linear model and the node from leaf to root uses:
where P’ indicates the predicted value passed to higher nodes; ppassed denotes the predicted values passed to the current node from the previous nodes; pmodel is the predicted values of the model at the current nodes; ntrain is the number of observations in the training dataset that reach the previous nodes; σ is a constant. The M5P model has a simple structure and also a few operators to set, thus hybridization can improve the prediction power of the RF standalone model.
Random Forest (RF)
RF is a decision-tree algorithm introduced by Breiman [68] enhanced and used in numerous studies [69,70,71,72,73,74,75]. RF is flexible, able to deal with classification and continuity issues (i.e., regression problems). It was extended based on bagging [76] and competed with the boosting approach [71]. To make predictions, RF employs bootstrapping to split data into multiple sub-datasets. Subsequently, decision trees are developed for each sub-dataset. Finally, predictions from the sub-decision trees are ensembled, and the final prediction reflects the entire RF model [77,78]. RF has become a favorite ML algorithm for practical engineers because it is able to handle both regression and classification data and learns and predicts very quickly. The performance of the RF model depends on only one or two hyper-parameter(s); it is premised upon generalized error estimation and is able to process data with a large number of dimensions. A pseudo-code of the RF algorithm was developed (Figure 3, adapted from [79]) to use RF for prediction of the water salinity levels of the Babol-Rood River. RF does not give precise continuous predictions in the form of regressions but achieves high performance in classification. Hence, hybridization can also improve the prediction power of the standalone RF model.

Figure 3.
The pseudo-code of the RF model
Bagging
Small changes in the dataset will lead to instability in ML algorithms. Breiman [76] proposed a technique called “bagging” to overcome model instability and to improve performance. Many studies have successfully employed bagging to increase the effectiveness of predictions [80]. The general concept of the bagging algorithm is:
Consider a dataset , in which is the output (i.e., EC) and denotes the input variables (i.e., TDS, Na+, Hco3−, Cl−, SAR, Ca2+, Mg2+, So42− PH, Q). For any given ML algorithm or artificial intelligence model, a model (classifier or regressor) is generated. Five forms of ML models are created: M5P, RF, random subspace (RS), random committee (RC), and additive regression (AR). Bagging tries to combine them to improve the accuracies of single models from , where is the number of learning sets generated from D. For each , a small change is made in D.
Bagging can be applied to improve many base learners, like decision trees. For example, bagging was used to train the M5P and RF base learners to predict river salinity.
Random Subspace (RS)
Like bagging, RS uses the powers of bootstrapping and aggregation to build a forecasting model. RS, however, uses the bootstraps in the feature space instead of training samples, as bagging does [81]. Like RF and bagging, RS can handle both regression and classification data. It consists of 4 main components: the training dataset , the number of subspaces , the classifier or regressor , and the number of features [82]. In RS, the number of subsets is generated randomly in features. Subsequently, they are saved in the subspace . In the second step, each base regressor/classifier is trained/learned on each of the subsets to create a different regressor/classifier. Then, these are combined to build an ensemble regressor/classifier . More details of RS can be found in Kuncheva and Plumpton [83] and Kuncheva et al. [84]. Herein, RS is used to construct hybrid models with the M5P and RF for EC prediction.
Random Committee (RC)
A meta-algorithm, RC is an ensemble of random tree classifiers that can improve the learning performance of classification. RC uses a number of random seeds on the same dataset to build a group of random classifications, upon which predictions are made. Finally, averages are computed as outcome predictions based on the predictions generated by each of those classifiers [85]. RC has been employed in many fields. It has been combined with ANN for electrical disturbance classification [86], with the random tree by voting for classifying anomalies [87], and with bagging and J48 algorithms for efficient intrusions classification [88]. In this study, RC was used to predict EC.
Additive Regression (AR)
AR is a nonparametric algorithm proposed by Breiman and Friedman [89]. It is an essential part of the alternating conditional-expectations algorithm. To build a restricted class of nonparametric regression models, AR uses a one-dimensional smoother. It is more flexible than linear models. It is also more easily interpreted than is a general regression model. However, overfitting, model selection, and multicollinearity are the disadvantages of AR. A brief description of AR algorithm is:
Consider a dataset , in which is the output (i.e., EC) and denotes the input variables (i.e., TDS, Na+, HCO3−, Cl−, SAR, Ca2+, Mg2+, So42− PH, Q). The AR model will take a form:
In other words, the AR model can take a form:
where functions are unknown smooth functions, which are used to fit the dataset.
The back-fitting algorithm can be used to fit the AR model in this case [90].
2.2.5. Model Evaluation Criteria
To evaluate the models’ performances, five statistical criteria—root mean square error (RMSE), r squared (R2), mean absolute error (MAE), Nash–Sutcliffe efficiency (NSE), and percent bias (PBIAS)—were calculated in their testing phases. These criteria were calculated as follows [91,92,93,94,95,96]:
where , , , and denote the measured, mean of measured, predicted, and mean of predicted values of EC, respectively, and n is the number of observations.
In addition, the Taylor diagram [97] and box plot [98] were used to provide for visual assessment of the models. The Taylor diagram provides an overview of correlations and standard deviations of each model. The closer the predicted value of CC and SD are to the observed value, the higher is the prediction capacity. The box plot provided an overview of the models’ capabilities using extreme values, medians, and the first- and third-quartile predictions.
3. Results
3.1. Best Determinant Combination of EC
Ten water quality variables were selected to be tested as potential predictors of EC (Table 2). The analyses of correlations between EC and the water quality variables show a strong linear relationship (R = 0.91) between EC and TDS. Therefore, because TDS was the most effective input variable, it was included in all ten input combinations. In this step, the analysis was limited and compared only with the RMSE statistic calculated in the testing phase (Table 4). The results reveal that the best input combination was constructed with TDS alone (i.e., combination 1), which is consistent with the high CC of TDS to EC. In other words, including other variables in the model only distorts the models’ abilities. This result, however, is case specific and studies of other variables may find that other combinations are more predictive. For instance, Khosravi et al. [9] predicted suspended sediment load with data mining algorithms using best-input combinations with eight, nine, and ten variables. Barzegar et al. [32,41] used Ca2+, Mg2+, Na+, So42−, and Cl− as best-input variables to predict water salinity in the Aji-Chay River, Iran. Combining other explanatory variables with TDS consistently decreased the models’ accuracies, reflected in increasing RMSE values.

Table 4.
Training and testing-phase RMSE (μs/cm) values. The testing values were used to identify the most effective input variables.
Alongside the model’s structure, data accuracy, data type, and data structure have strong effects on the result. The best input combination, therefore, should be examined for each new dataset and should not rely solely on the variables with the highest correlation coefficients. To sum up, the best input combination is input No 1, in which TDS is the only input to the models.
3.2. Models’ Performances and Validation
After determining the most effective input variable and the optimum value of each model’s operator, every model was trained with the training dataset and was evaluated with the testing dataset [99]. The standalone- and the hybrid-models’ results were compared and validated using time-series of EC predictions and observations, scatter plots, box plots, and Taylor diagrams (Figure 4, Figure 5 and Figure 6). A deeper look into these comparisons was also provided and validated with several quantitative statistical indices (Table 5). Using time-series and scatter plots (Figure 4), the first observation is that there is high agreement between the values predicted by the algorithms and the values measured by the M5P, bagging-M5P, RS-M5P, and AR-M5P algorithms. There was no apparent bias between the measured and calculated values, and the models captured the extreme EC values well. This performance is partially explained by the high correlation coefficient between EC and TDS (R = 0.99, Table 2) and the data-mining techniques’ high prediction ability.
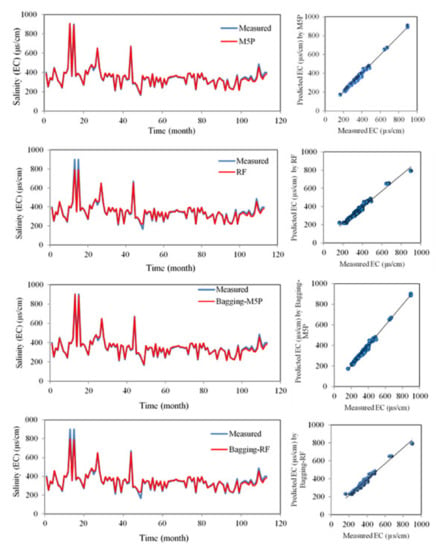
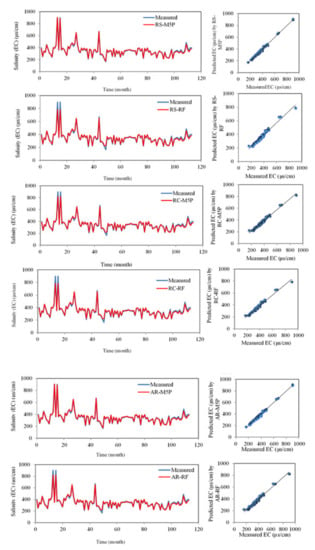
Figure 4.
Time-variation and scatter plots of observed and predicted EC in the testing phase.
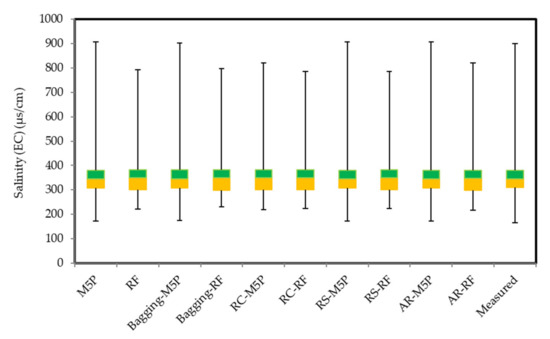
Figure 5.
Box plot of predictions used for model evaluation in the testing phase.
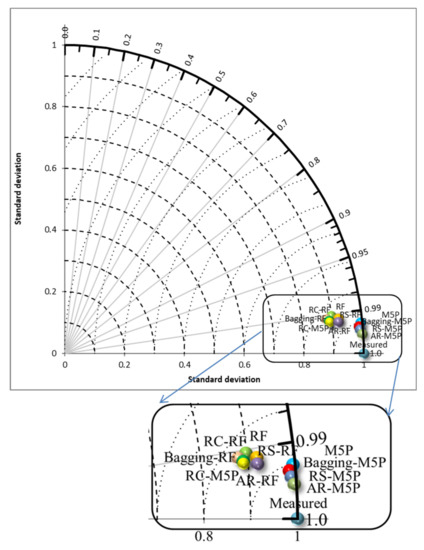
Figure 6.
Taylor diagram for measured and predicted EC.

Table 5.
Quantitatively statistical criteria for model validation in testing phase.
There is no visible difference between the predicted EC values of the four best models (M5P, bagging-M5P, RS-M5P, AR-M5P) and the measured values (Figure 5). Nor can one see differences between the predicted median values, the predicted 25th and 75th percentiles, and even the extreme values. The more flexible algorithms—M5P, bagging-M5P, RS-M5P, AR-M5P—marginally overestimate maximums above the measured 900 μs/cm at 906, 901, 906, and 906 μs/cm, respectively. Furthermore, they slightly underestimate the minimums above the measured 165 μs/cm to 173, 172, 172 and 172 μs/cm, respectively. Our results reveal that the models with highest predictive powers based on RMSE can generally predict extreme values properly, but the results are inconsistent. As Khosravi et al. [100] showed, although hybrids of ANFIS-bioinspired models generally fit the data well, they were less robust in their estimates of the extreme values of reference evaporation. By contrast, random-tree algorithms which have generally poorer overall performance, predict extreme values accurately. Khozani et al. [51] found results similar to Khosravi et al. [100] when predicting apparent shear stress.
It is also clear from the Taylor diagram (Figure 6) that the models are systematically comparable to the measured values. This is good proof of the models’ performance and point to their usefulness for water quality modeling if implemented properly using suitable input variables. Although all of the models have good performance metrics (i.e., CC > 0.99), EC predicted by M5P, bagging-M5P, RS-M5P, and AR-M5P have similar standard deviations, and higher CC with EC, while the rest of the models have smaller standard deviations. To sum up, AR-M5P is the best predictor among the algorithms.
Although all models performed well (NSE > 0.75 and PBIAS < ±10%), the best accuracy was achieved by the hybrid AR-M5P algorithm, which had excellent accuracy (NSE = 0.994, RMSE = 8.9, MAE = 6.20), approximately equal to the success of RS-M5P. These were followed by the bagging-M5P (NSE = 0.992, RMSE = 8.96, MAE = 6.24) and the M5P (NSE = 0.991, RMSE = 9.04, MAE = 6.29). These had significantly better results than the other models. RC-M5P, and AR-RF had comparable results (NSE > 0.97, MAE < 10 μs/cm, RMSE < 10 μs/cm). RF, bagging-RF, RS-RF, and the RC-RF had lower accuracy (RMSE and MAE > 18 μs/cm) and thus are less suitable for modeling EC. The RMSE was the greatest for the RS-RF and RC-RF hybrid models (19.30 μs/cm). The model with the next largest was bagging-RF (19.01 μs/cm) and then the individual RF model (18.50 μs/cm). It might be argued that such large RMSE values calculated using the individual and hybrid RF models leads to clearer conclusions. But comparing the individual models, M5P is a better prediction model than RF; the M5P had at least 51.13% lower RMSE and 38.21% lower MAE than the RF model. The M5P algorithm is a better predictor than hybrid-RF algorithms, as well. M5P has advantages over RF: it can manage large datasets with large numbers of attributes and with numerous dimensions, and it can deal with missing data without any ambiguity [9].
4. Discussion
Now adays application of machine learning algorithms as a practical tool in a different field of geoscience increased rapidly such as flood forecasting [101,102,103,104,105], relationship between fish community and environmental factor [106], groundwater modeling [48], and many other field of study which declared in introduction section.
Hybrid algorithms might increase the prediction power of individual algorithms (e.g., compare the M5P results with the results of M5P hybrids as well as RF with its hybrids). There is an exception to this: RC reduces prediction quality below the individual M5P and RF models. Therefore, though some hybrid algorithms enhance performance of individual algorithms, this isn’t always true. Based on PBIAS, M5P and its hybrids tend to overestimate (except in the case of RC-M5P) and RF and its hybrids (and also RC-M5P) underestimate their predictions.
As the M5P model has a higher prediction power than RF (Table 5), hybrid M5P algorithms are more suitable for predicting EC than either the individual or hybrid RF models. In another words, hybrid algorithms generate results that are dependent upon the results of the individual models themselves. Generally, additive regression (AR) algorithms may increase the prediction power of the individual M5P and RF algorithms more than other hybridizing algorithms. This is a result of their flexibility and structural consistency with the other models. RC causes a lowering of the performance of the individual algorithms.
Since the dataset used to predict EC was the same for all models, the difference in performance is the result of each model’s structure (i.e., its flexibility, prediction capacity, and tendency to over-fit). The computational capabilities and the complexity of each ML model dictate its results [107]. Generally, decision tree-based algorithms (M5P and RF) require no assumptions about the data distribution, adapt to outliers by isolating them in small regions of the feature space [108], have no hidden layers in their structure, and use tree algorithms to estimation by pattern recognition, and therefore perform better; particularly in comparison to the data-intelligence algorithms which have hidden layers in their structures [8]. This finding conforms to previous studies that indicated the superiority of tree-based models in terms of estimation capacity [109]. Due to the non-linear nature of many environmental phenomena (e.g., EC), more flexible models with non-linear structures will yield better results [110]. According to the literature, hybrid algorithms in most of the cases are more flexible and can enhance the prediction power of standalone models [9,49,51,111].
Previous studies [112,113,114,115,116], have applied several kind of ML models to estimate river EC. Compared to these studies, our results seem to be more accurate. Rohmer and Brisset [112] linked EC to seawater levels and Q using a kernel-based support vector machine (SVM) technique and reported a CC around 0.90; this is significantly less accurate than the results of our study. Ravansalar and Rajaee [113] applied the multilayer perception neural network (MLPNN) and the MLPNN combined with wavelet decomposition (WMLPNN) to predict EC in the Asi River at the Demirköprü gauging station, Turkey, using Q and the EC measured in the previous period. They demonstrated that wavelet decomposition significantly improves the model’s accuracy and the WMLPNN (R2 = 0.94) significantly outperformed the standard MLPNN (R2 = 0.38). However, the WMLPNN was less accurate than the AR-M5P (R2 = 0.99) in our study. Azad et al. [114] compared adaptive neuro-fuzzy inference system (ANFIS), ANFIS optimized with particle swarm optimization (PSO) called ANFIS-PSO, and ANFIS with ant-colony optimization for continuous domains (ACOR) called ANFIS-ACOR while predicting EC using TH, Cl−, and Na+. The results revealed high performances of all three models: R2 = 0.99 for ANFIS-PSO, R2 = 0.98 for ANFIS-ACOR, and R2 = 0.94 for ANFIS. The hybrid algorithms in this study performed just a bit better, but the individual M5P and RF algorithms compared to ANFIS had higher prediction powers and it is in accord with Choubin et al. [109] which reported that decision-tree algorithms of classification and regression trees (CART) outperformed ANFIS, SVM, and ANN in their prediction of suspended sediment load. Tutmez et al. [115] used ANFIS model to predict EC using the TDS and achieved R2 = 0.937. Al-Mukhtar and Al-Yaseen [116] compared the ANFIS, MLPNN, and the MLR models while predicting EC using several water quality variables and achieved NSE = 0.98. Barzegar et al. [41] used several water quality parameters to forecast EC with ELM, WA-ELM, and ANFIS, and reported NSE ranging from 0.6 to 0.95. And Ghorbani et al. [81] predicted EC with MLPNN and MLR models. The MLPNN was more accurate (R2 = 0.965, RMSE = 50.810 μs/cm, and MAE = 37.495 μs/cm). In sum, the algorithms used in this study outperformed all of the algorithms used in previous efforts to predict EC.
The results show that these models can be used for river salinity prediction and even forecasting with high accuracy. The outcome is undoubtedly useful for water quality protection and management. It is better to use these types of models for real-time river salinity forecasting which is beneficial and practical.
5. Conclusions
The Babol-Rood River is the main source of irrigation and drinking water in its watershed. Deterioration of its water supply can cause irreparable damage to the environment and the resident population. Monitoring to predict its future conditions need accurate models. These tasks are the foundations of planning to conserve and manage crucial resources. This study is a pioneering evaluation of the use of two standalone and eight novel hybrid-algorithms to predict river salinity. The algorithms used include M5P, RF, bagging-M5P, bagging-RF, RS-M5P, RS-RF, RC-M5P, RC-RF, AR-M5P, and AR-RF. Monthly data collected over a 36-year period were used to construct several sets of variable combinations as inputs for model building and evaluation. Qualitative (visual) and quantitative criteria were applied to validate and compare models. The results reveal that TDS is the most important variable for predicting EC (r = 0.99). Among 10 input combinations, the first, a standalone TDS, was significantly important to the results. The combinations demonstrate that not only does a model’s structure have significant effects on prediction accuracy, but so too do the input variables. According to the validation criteria, M5P has greater prediction power than RF and those hybrid algorithms with M5P performed better than those hybridized with RF. The M5P algorithm and its hybrids (except RC-M5P) can accurately predict EC, even in extreme conditions. The results also reveal that hybrid algorithms enhanced the performances of standalone algorithms, except in the case of the RC model, which reduced prediction power when hybridized with M5P and RF. Although all algorithms showed very good prediction capacities, AR-M5P outperformed all of the others. The rest, in order of accuracy, were RS-M5P, bagging-M5P, M5P, RC-M5P, AR-RF, bagging-RF, RF, RS-RF, and RC-RF. These results cannot be generalized to other study areas or with other hydrological data, but AR-M5P would undoubtedly be one of the more accurate algorithms, if not the most accurate. Hybridized models outperformed the standalone models in this study. Overall, the river water quality can be accurately predicted through such enhanced machine learning algorithms and several readily available input variables.
Author Contributions
Conceptualization, K.K., and A.M.; methodology, K.K. and A.M.; software, K.K. and A.M.; formal analysis, K.K.; data curation, K.K.; writing—original draft preparation, A.M.; K.K., S.H., S.K., A.M., and B.T.P.; writing—review and editing, A.M. and J.P.T.; supervision A.M.M., J.P.T. and S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research in part is supported by the Hungarian State and the European Union under the EFOP-3.6.2-16-2017-00016 project. Support of European Union, the new Szechenyi plan, European Social Fund and the Alexander von Humboldt Foundation are acknowledged.
Acknowledgments
Authors would like to thank Nhu Viet Ha for the support during preparation of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adamowski, J.J.; Sun, K. Development of a coupled wavelet transform and neural network method for flow forecasting of non-perennial rivers in semi-arid watersheds. J. Hydrol. 2014, 390, 85–91. [Google Scholar] [CrossRef]
- Liou, S.M.M.; Lo, S.L.L.; Wang, S.H. A generalized water quality index for Taiwan. Environ. Monit. Assess. 2004, 96, 32–35. [Google Scholar] [CrossRef] [PubMed]
- Khalil, B.B.; Ouarda, T.B.M.J.J.; St-Hilaire, A. Estimation of water quality characteristics at ungauged sites using artificial neural networks and canonical correlation analysis. J. Hydrol. 2011, 405, 277–287. [Google Scholar] [CrossRef]
- Najah, A.A.; Elshafie, A.A.; Karim, O.A.A.; Jaffar, O. Prediction of Johor River water quality parameters using artificial neural networks. Eur. J. Sci. Res. 2009, 28, 422–435. [Google Scholar]
- Tiwari, M.K.K.; Adamowski, J.F. Medium-term urban water demand forecasting with limited data using an ensemble wavelet–bootstrap machine-learning approach. J. Water Resour. Plan. Manag. 2015, 141, 04014053. [Google Scholar] [CrossRef]
- Tiwari, M.K.K.; Adamowski, J.F. An ensemble wavelet bootstrap machine learning approach to water demand forecasting: A case study in the city of Calgary, Canada. Urban Water J. 2015, 14, 185–201. [Google Scholar] [CrossRef]
- Liu, S.; Tai, H.; Ding, Q.; Li, D.; Xu, L.; Wei, Y. A hybrid approach of support vector regression with genetic algorithm optimization for aquaculture water quality prediction. Math. Comput. Model. 2013, 58, 458–465. [Google Scholar] [CrossRef]
- Kisi, O.O.; Dailr, A.H.H.; Cimen, M.M.; Shiri, J. Suspended sediment modeling using genetic programming and soft computing techniques. J. Hydrol. 2012, 450, 48–58. [Google Scholar] [CrossRef]
- Khosravi, K.; Mao, L.; Kisi, O.; Yaseen, Z.; Shahid, S. Quantifying hourly suspended sediment load using data mining models: Case study of a glacierized Andean catchment in Chile. J. Hydrol. 2018, 567, 165–179. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.; Kisi, O.; Adamowski, J.; Quilty, J. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Aguilera, P.A.; Frenich, A.G.; Torres, J.A.; Castro, H.; Vidal, J.M.; Canton, M. Application of the Kohonen neural network in coastal water management: Methodological development for the assessment and prediction of water quality. Water Res. 2001, 35, 4053–4062. [Google Scholar] [CrossRef]
- Zhang, Y.; Pulliainen, J.; Koponen, S.; Hallikainen, M. Application of an empirical neural network to surface water quality estimation in the Gulf of Finland using combined optical data and microwave data. Remote Sens. Environ. 2002, 812, 327–336. [Google Scholar] [CrossRef]
- Zou, R.; Lung, W.S.; Guo, H. Neural network embedded Monte Carlo approach for water quality modeling under input information uncertainty. J. Comput. Civ. Eng. 2002, 162, 135–142. [Google Scholar] [CrossRef]
- Ha, H.; Stenstrom, M.K. Identification of land use with water quality data in stormwater using a neural network. Water Res. 2003, 37, 4222–4230. [Google Scholar] [CrossRef]
- Diamantopoulou, M.J.; Antonopoulos, V.Z.; Papamichail, D.M. Cascade correlation artificial neural networks for estimating missing monthly values of water quality parameters in rivers. Water Resour. Manag. 2007, 21, 649–662. [Google Scholar] [CrossRef]
- Diamantopoulou, M.J.; Papamichail, D.M.; Antonopoulos, V.Z. The use of a neural network technique for the prediction of water quality parameters. Oper. Res. 2005, 5, 115–125. [Google Scholar] [CrossRef]
- Schmid, B.H.; Koskiaho, J. Artificial neural network modeling of dissolved oxygen in a wetland pond: The case of Hovi, Finland. J. Hydrol. Eng. 2006, 11, 188–192. [Google Scholar] [CrossRef]
- Zhao, Y.; Nan, J.; Cui, F.Y.; Guo, L. Water quality forecast through application of BP neural network at Yuqiao reservoir. J. Zhejiang Univ. Sci. A 2007, 8, 1482–1487. [Google Scholar] [CrossRef]
- Dogan, E.; Sengorur, B.; Koklu, R. Modeling biological oxygen demand of the Melen River in Turkey using an artificial neural network technique. J. Environ. Manag. 2009, 90, 1229–1235. [Google Scholar] [CrossRef]
- Najah, A.; El-Shafie, A.; Karim, O.A.; El-Shafie, A.H. Performance of ANFIS versus MLP-NN dissolved oxygen prediction models in water quality monitoring. Environ. Sci. Pollut. Res. 2014, 21, 1658–1670. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, N.; Gupta, S. Support vector machines in water quality management. Anal. Chim. Acta 2011, 703, 152–162. [Google Scholar] [CrossRef]
- Ay, M.; Kisi, O. Modeling of dissolved oxygen concentration using different neural network techniques in Foundation Creek, El Paso County, Colorado. J. Environ. Eng. 2011, 138, 654–662. [Google Scholar] [CrossRef]
- Ay, M.; Kisi, O. Modelling of chemical oxygen demand by using ANNs, ANFIS and k-means clustering techniques. J. Hydrol. 2014, 511, 279–289. [Google Scholar] [CrossRef]
- Chen, D.; Lu, J.; Shen, Y. Artificial neural network modelling of concentrations of nitrogen, phosphorus and dissolved oxygen in a non-point source polluted river in Zhejiang Province, southeast China. Hydrol. Process. 2010, 24, 290–299. [Google Scholar] [CrossRef]
- Patel, R.M.; Prasher, S.O.; God, P.K.; Bassi, R. Soil salinity prediction using artificial neural networks. JAWRA J. Am. Water Resour. Assoc. 2002, 38, 91–100. [Google Scholar] [CrossRef]
- Zou, P.; Yang, J.; Fu, J.; Liu, G.; Li, D. Artificial neural network and time series models for predicting soil salt and water content. Agric. Water Manag. 2010, 97, 2009–2019. [Google Scholar] [CrossRef]
- Dai, X.; Huo, Z.; Wang, H. Simulation for response of crop yield to soil moisture and salinity with artificial neural network. Field Crop. Res. 2011, 121, 441–449. [Google Scholar] [CrossRef]
- Akramkhanov, A.; Vlek, P.L. The assessment of spatial distribution of soil salinity risk using neural network. Environ. Monit. Assess. 2012, 184, 2475–2485. [Google Scholar] [CrossRef]
- Banerjee, P.; Singh, V.S.; Chatttopadhyay, K.; Chandra, P.C.; Singh, B. Artificial neural network model as a potential alternative for groundwater salinity forecasting. J. Hydrol. 2011, 398, 212–220. [Google Scholar] [CrossRef]
- Seyam, M.; Mogheir, Y. Application of artificial neural networks model as analytical tool for groundwater salinity. J. Environ. Prot. 2011, 2, 56. [Google Scholar] [CrossRef]
- Nasr, M.; Zahran, H.F. Using of pH as a tool to predict salinity of groundwater for irrigation purpose using artificial neural network. Egypt. J. Aquat. Res. 2014, 40, 111–115. [Google Scholar] [CrossRef]
- Barzegar, R.; Asghari Moghaddam, A.; Adamowski, J.F. Multi-step water quality forecasting using a boosting ensemble multi-wavelet extreme learning machine model. Stoch. Environ. Res. Risk Assess. 2016, 22, 799–813. [Google Scholar] [CrossRef]
- DeSilet, L.; Golden, B.; Wang, Q.; Kumar, R. Predicting salinity in the Chesapeake Bay using backpropagation. Comput. Oper. Res. 1992, 19, 277–285. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Multi-objective management of saltwater intrusion in coastal aquifers using genetic programming and modular neural network based surrogate models. J. Hydrol. 2010, 393, 245–256. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Empirical comparison of various methods for training feed-Forward neural networks for salinity forecasting. Water Resour. Res. 1999, 35, 2591–2596. [Google Scholar] [CrossRef]
- Huang, W.; Foo, S. Neural network modeling of salinity variation in Apalachicola River. Water Res. 2002, 36, 356–362. [Google Scholar] [CrossRef]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Input determination for neural network models in water resources applications. Part 2. Case study: Forecasting salinity in a river. J. Hydrol. 2005, 301, 93–107. [Google Scholar] [CrossRef]
- Melesse, A.M.; Ahmad, S.; McClain, M.E.; Wang, X.; Lim, Y. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Chen, M.; Wu, P.; Kim, M.J. Integration of BIM and GIS: IFC geometry transformation to shapefile using enhanced open-source approach. Autom. Constr. 2019, 106, 102859. [Google Scholar] [CrossRef]
- Sun, G.; Yang, B.; Yang, Z.; Xu, G. An adaptive differential evolution with combined strategy for global numerical optimization. Soft Comput. 2020, 24, 6277–6296. [Google Scholar] [CrossRef]
- Xie, J.; Wen, D.; Liang, L.; Jia, Y.; Gao, L.; Lei, J. Evaluating the Validity of Current Mainstream Wearable Devices in Fitness Tracking Under Various Physical Activities: Comparative Study. JMIR mHealth uHealth 2018, 6, e94. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Zhang, X.; Liu, X.; Lei, J. Evaluating the Consistency of Current Mainstream Wearable Devices in Health Monitoring: A Comparison under Free-Living Conditions. J. Med. Internet Res. 2017, 19, e68. [Google Scholar] [CrossRef] [PubMed]
- Khosravi, K.; Panahi, M.; Bui, D. Spatial prediction of groundwater spring potential mapping based on an adaptive neuro-fuzzy inference system and metaheuristic optimization. Hydrol. Earth Syst. Sci. 2018, 22, 4771–4792. [Google Scholar] [CrossRef]
- Termeh, S.V.; Khosravi, K.; Sartaj, M.; Keesstra, S.D.; Tsai, F.; Dijksma, R.; Pham, B. Optimization of an adaptive neuro-fuzzy inference system for groundwater potential mapping. Hydrogeol. J. 2019, 27, 2511–2534. [Google Scholar] [CrossRef]
- Barzegar, R.; Adamowski, J.; Asghari Moghaddam, A. Application of wavelet-artificial intelligence hybrid models for water quality prediction: A case study in Aji-Chay River, Iran. Stoch Environ. Res. Risk Assess. 2016, 30, 1797–1819. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Bui, D. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Khosravi, K.; Shahabi, H.; Pham, B.T.; Adamowski, J.; Shirzadi, A.; Pradhan, B.; Dou, J.; Ly, H.-B.; Gróf, G.; Ho, H.L.; et al. A comparative assessment of flood susceptibility modeling using Multi-Criteria Decision-Making Analysis and Machine Learning Methods. J. Hydrol. 2019, 573, 311–323. [Google Scholar] [CrossRef]
- Khosravi, K.; Sartaj, M.; Tsai, F.T.C.; Singh, V.; Kazakis, N.; Melesse, A.; Pham, B. A comparison study of DRASTIC methods with various objective methods for groundwater vulnerability assessment. Sci. Total Environ. 2018, 642, 1032–1049. [Google Scholar] [CrossRef]
- Pham, B.; Prakhsh, I.; Khosravi, K.; Chapi, K.; Trinh, P.; Ngo, T.; Hesseini, S.V. A comparison of Support Vector Machines and Bayesian algorithms for landslide susceptibility modelling. Geocarto Int. 2018, 34, 1385–1407. [Google Scholar] [CrossRef]
- Chen, W.; Pradhan, B.; Li, S.; Shahabi, H.; Rizeei, H.M.; Hou, E.; Wang, S. Novel Hybrid Integration Approach of Bagging-Based Fisher’s Linear Discriminant Function for Groundwater Potential Analysis. Nat. Resour. Res. 2019, 28, 1239–1258. [Google Scholar] [CrossRef]
- Khozani, Z.; Khosravi, K.; Pham, B.; Kløve, B.; Mohtar, W.; Yaseen, Z. Determination of compound channel apparent shear stress: Application of novel data mining models. J. Hydroinform. 2019, 21, 798–811. [Google Scholar] [CrossRef]
- Heddam, S.; Kisi, O. Modelling daily dissolved oxygen concentration using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J. Hydrol. 2018, 559, 499–509. [Google Scholar] [CrossRef]
- Sharafati, A.; Khosravi, K.; Khosravinia, P.; Ahmed, K.; Salman, S.A.; Yaseen, Z.M. The potential of novel data mining models for global solar radiation prediction. Int. J. Environ. Sci. Technol. 2019, 16, 7147–7164. [Google Scholar] [CrossRef]
- Eilbeigy, M.; Jamour, R. Investigating the Factors Affecting the Salinity of the Ghezelozan River Water. J. Environ. Water Eng. 2019, 5, 120–136. [Google Scholar]
- Liu, J.; Wu, C.; Wu, G.; Wang, X. A novel differential search algorithm and applications for structure design. Appl. Math. Comput. 2015, 268, 246–269. [Google Scholar] [CrossRef]
- Singh, V.; Gu, N.; Wang, X. A theoretical framework of a BIM-based multi-disciplinary collaboration platform. Autom. Constr. 2011, 20, 134–144. [Google Scholar] [CrossRef]
- Zhu, J.; Shi, Q.; Wu, P.; Sheng, Z.; Wang, X. Complexity Analysis of Prefabrication Contractors’ Dynamic Price Competition in Mega Projects with Different Competition Strategies. Complexity 2018, 2018, 5928235. [Google Scholar] [CrossRef]
- Long, Q.; Wu, C.; Wang, X. A system of nonsmooth equations solver based upon subgradient method. Appl. Math. Comput. 2015, 251, 284–299. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Wang, P.; Wu, Z.; Kim, M.J. Integration of BIM and GIS: Geometry from IFC to shapefile using open-source technology. Autom. Constr. 2019, 102, 105–119. [Google Scholar] [CrossRef]
- Mosavi, A.; Shirzadi, A.; Choubin, B.; Taromideh, F.; Hosseini, F.S.; Borji, M.; Shahabi, H.; Salvati, A.; Dineva, A.A. Towards an Ensemble Machine Learning Model of Random Subspace Based Functional Tree Classifier for Snow Avalanche Susceptibility Mapping. IEEE Access 2020, 8, 145968–145983. [Google Scholar] [CrossRef]
- Shi, K.; Wang, J.; Tang, Y.; Zhong, S. Reliable asynchronous sampled-data filtering of T–S fuzzy uncertain delayed neural networks with stochastic switched topologies. Fuzzy Sets Syst. 2020, 381, 1–25. [Google Scholar] [CrossRef]
- Shi, K.; Wang, J.; Zhong, S.; Tang, Y.; Cheng, J. Hybrid-driven finite-time H∞ sampling synchronization control for coupling memory complex networks with stochastic cyber-attacks. Neurocomputing 2020, 387, 241–254. [Google Scholar] [CrossRef]
- Shi, K.; Wang, J.; Zhong, S.; Tang, Y.; Cheng, J. Non-fragile memory filtering of T-S fuzzy delayed neural networks based on switched fuzzy sampled-data control. Fuzzy Sets Syst. 2019, 394, 40–64. [Google Scholar] [CrossRef]
- Shi, K.; Tang, Y.; Zhong, S.; Yin, C.; Huang, X.; Wang, W. Nonfragile asynchronous control for uncertain chaotic Lurie network systems with Bernoulli stochastic process. Int. J. Robust Nonlinear Control 2018, 28, 1693–1714. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In 5th Australian Joint Conference on Artificial Intelligence; World Scientific: Singapore, 1992; Volume 92, pp. 343–348. [Google Scholar]
- Mosavi, A.; Hosseini, F.S.; Choubin, B.; Goodarzi, M.; Dineva, A.A. Groundwater Salinity Susceptibility Mapping Using Classifier Ensemble and Bayesian Machine Learning Models. IEEE Access 2020, 8, 145564–145576. [Google Scholar] [CrossRef]
- Behnood, A.; Behnood, V.; Gharehveran, M.M.; Alyamac, K.E. Prediction of the compressive strength of normal and high-performance concretes using M5P model tree algorithm. Constr. Build. Mater. 2017, 142, 199–207. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Random forests. In The Elements of Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2009; pp. 587–604. [Google Scholar]
- Bernard, S.; Adam, S.; Heutte, L. Dynamic random forests. Pattern Recognit. Lett. 2012, 33, 1580–1586. [Google Scholar] [CrossRef]
- Nosratabadi, S.; Mosavi, A.; Duan, P.; Ghamisi, P.; Filip, F.; Band, S.S.; Reuter, U.; Gama, J.; Gandomi, A.H. Data Science in Economics: Comprehensive Review of Advanced Machine Learning and Deep Learning Methods. Mathematics 2020, 8, 1799. [Google Scholar] [CrossRef]
- Shi, K.; Tang, Y.; Liu, X.; Zhong, S. Non-fragile sampled-data robust synchronization of uncertain delayed chaotic Lurie systems with randomly occurring controller gain fluctuation. ISA Trans. 2017, 66, 185–199. [Google Scholar] [CrossRef]
- Shi, K.; Tang, Y.; Liu, X.; Zhong, S. Secondary delay-partition approach on robust performance analysis for uncertain time-varying Lurie nonlinear control system. Optim. Control Appl. Methods 2017, 38, 1208–1226. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Tian, L.; Waller, L.; Asundi, A. Transport of intensity phase retrieval and computational imaging for partially coherent fields: The phase space perspective. Opt. Lasers Eng. 2015, 71, 20–32. [Google Scholar] [CrossRef]
- Zuo, C.; Sun, J.; Li, J.; Zhang, J.; Asundi, A.; Chen, Q. High-resolution transport-of-intensity quantitative phase microscopy with annular illumination. Sci. Rep. 2017, 7, 7622–7654. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, R.; Xiong, Y. Mapping Mineral Prospectivity via Semi-supervised Random Forest. Nat. Resour. Res. 2020. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, K.; Carranza, E.J.M.; Yang, F. Maximum Entropy and Random Forest Modeling of Mineral Potential: Analysis of Gold Prospectivity in the Hezuo–Meiwu District, West Qinling Orogen, China. Nat. Resour. Res. 2019, 28, 645–664. [Google Scholar] [CrossRef]
- Anderson, G.; Pfahringer, B. Random Relational Rules. Ph.D. Thesis, University of Waikato, Hamilton, New Zealand, 2009. [Google Scholar]
- Nguyen, H.; Bui, X.-N. Predicting Blast-Induced Air Overpressure: A Robust Artificial Intelligence System Based on Artificial Neural Networks and Random Forest. Nat. Resour. Res. 2019, 28, 893–907. [Google Scholar] [CrossRef]
- Tao, D.; Tang, X.; Li, X.; Wu, X. Asymmetric bagging and random subspace for support vector machines-based relevance feedback in image retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1088–1099. [Google Scholar]
- Skurichina, M.; Duin, R.P. Bagging, boosting and the random subspace method for linear classifiers. Pattern Anal. Appl. 2002, 5, 121–135. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Plumpton, C.O. Choosing parameters for random subspace ensembles for fMRI classification. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 54–63. [Google Scholar]
- Kuncheva, L.I.; Rodríguez, J.J.; Plumpton, C.O.; Linden, D.E.; Johnston, S.J. Random subspace ensembles for fMRI classification. IEEE Trans. Med. Imaging 2010, 29, 531–542. [Google Scholar] [CrossRef]
- Qassim, Q.; Zin, A.M.; Ab Aziz, M.J. Anomalies Classification Approach for Network-based Intrusion Detection System. Int. J. Netw. Secur. 2016, 18, 1159–1172. [Google Scholar]
- Lira, M.M.; de Aquino, R.R.; Ferreira, A.A.; Carvalho, M.A.; Neto, O.N.; Santos, G.S. Combining multiple artificial neural networks using random committee to decide upon electrical disturbance classification. In 2007 International Joint Conference on Neural Networks; IEEE: Piscataway, NJ, USA, 2007; pp. 2863–2868. [Google Scholar]
- Niranjan, A.; Nutan, D.; Nitish, A.; Shenoy, P.D.; Venugopal, K. ERCR TV: Ensemble of Random Committee and Random Tree for Efficient Anomaly Classification Using Voting. In Proceedings of the 2018 3rd International Conference for Convergence in Technology (I2CT), Pune, India, 6–8 April 2018; pp. 1–5. [Google Scholar]
- Niranjan, A.; Prakash, A.; Veenam, N.; Geetha, M.; Shenoy, P.D.; Venugopal, K. EBJRV: An Ensemble of Bagging, J48 and Random Committee by Voting for Efficient Classification of Intrusions. In Proceedings of the 2017 IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Dehradun, India, 18–19 December 2017; pp. 51–54. [Google Scholar]
- Breiman, L.; Friedman, J.H. Estimating optimal transformations for multiple regression and correlation. J. Am. Stat. Assoc. 1985, 80, 580–598. [Google Scholar] [CrossRef]
- Buja, A.; Hastie, T.; Tibshirani, R. Linear smoothers and additive models. Ann. Stat. 1989, 17, 453–510. [Google Scholar] [CrossRef]
- Quan, Q.; Zou, H.; Huang, X.; Lei, J. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2020, 1–10. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Li, Z.; Zhu, Y.; Wang, J.; Yu, Z. Geographically weighted regression based methods for merging satellite and gauge precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Zhang, K.; Ruben, G.B.; Li, X.; Li, Z.; Yu, Z.; Xia, J.; Dong, Z. A comprehensive assessment framework for quantifying climatic and anthropogenic contributions to streamflow changes: A case study in a typical semi-arid North China basin. Environ. Model. Softw. 2020, 128, 104704. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, K.; van Beek, L.P.H.; Tian, X.; Bogaard, T.A. Physically-based landslide prediction over a large region: Scaling low-resolution hydrological model results for high-resolution slope stability assessment. Environ. Model. Softw. 2020, 124, 104607. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Q.; Chao, L.; Ye, J.; Li, Z.; Yu, Z.; Ju, Q. Ground observation-based analysis of soil moisture spatiotemporal variability across a humid to semi-humid transitional zone in China. J. Hydrol. 2019, 574, 903–914. [Google Scholar] [CrossRef]
- Jiang, Q.; Shao, F.; Gao, W.; Chen, Z.; Jiang, G.; Ho, Y. Unified No-Reference Quality Assessment of Singly and Multiply Distorted Stereoscopic Images. IEEE Trans. Image Process. 2019, 28, 1866–1881. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Space Phys. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Williamson, D.F.; Parker, R.A.; Kendrick, J.S. The box plot: A simple visual method to interpret data. Ann. Intern. Med. 1989, 110, 916–921. [Google Scholar] [CrossRef]
- Khosravi, K.; Nohani, E.; Maroufinia, E.; Pourghasemi, H.R. A GIS-based flood susceptibility assessment and its mapping in Iran: A comparison between frequency ratio and weights-of-evidence bivariate statistical models with multi-criteria decision making techniques. Nat. Hazards 2016, 83, 947–987. [Google Scholar] [CrossRef]
- Khosravi, K.; Daggupati, P.; Alami, M.; Awadh, S.; Ghareb, M.; Panahi, M.; Pham, B.; Rezaei, F.; Chongchong, Q.; Yaseen, Z. Meteorological data mining and hybrid data-intelligence models for reference evaporation simulation: A case study in Iraq. Comput. Electron. Agric. 2019, 167, 105041. [Google Scholar] [CrossRef]
- Chang, F.J.; Hsu, K.; Chang, L.C. (Eds.) Flood Forecasting Using Machine Learning Methods; MDPI: Basel, Switzerland, 2019. [Google Scholar] [CrossRef]
- Chang, F.J.; Guo, S. Advances in hydrologic forecasts and water resources management. Water 2020, 12, 1819. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J.; Yang, S.N.; Tsai, F.H.; Chang, T.H.; Herricks, E.E. Self-organizing maps of typhoon tracks allow for flood forecasts up to two days in advance. Nat. Commun. 2020, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Guo, S.; Chang, F.J. Explore an evolutionary recurrent ANFIS for modelling multi-step-ahead flood forecasts. J. Hydrol. 2019, 570, 343–355. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Hu, J.H.; Tsai, W.P.; Cheng, S.T.; Chang, F.J. Explore the relationship between fish community and environmental factors by machine learning techniques. Environ. Res. 2020, 184, 109262. [Google Scholar] [CrossRef]
- Kisi, O.; Heddam, S.; Yaseen, Z.M. The implementation of univariable scheme-based air temperature for solar radiation prediction: New development of dynamic evolving neural-fuzzy inference system model. Appl. Energy 2019, 241, 184–195. [Google Scholar] [CrossRef]
- Loh, W.-Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Choubin, B.; Darabi, H.; Rahmati, O.; Sajedi-Hosseini, F.; Kløve, B. River suspended sediment modelling using the CART model: A comparative study of machine learning techniques. Sci. Total Environ. 2018, 615, 272–281. [Google Scholar] [CrossRef] [PubMed]
- De’ath, G.; Fabricius, K.E. Classification and regression trees: A powerful yet simple technique for ecological data analysis. Ecology 2000, 81, 3178–3192. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Aalami, M.T.; Naghipour, L. Use of artificial neural networks for electrical conductivity modeling in Asi River. Appl. Water Sci. 2017, 7, 1761–1772. [Google Scholar] [CrossRef]
- Rohmer, J.; Brisset, N. Short-term forecasting of saltwater occurrence at La Comté River (French Guiana) using a kernel-based support vector machine. Environ. Earth Sci. 2017, 76, 246. [Google Scholar] [CrossRef]
- Ravansalar, M.; Rajaee, T. Evaluation of wavelet performance via an ANN-based electrical conductivity prediction model. Environ. Monit. Assess. 2015, 187, 366. [Google Scholar] [CrossRef]
- Azad, A.; Karami, H.; Farzin, S.; Mousavi, S.F.; Kisi, O. Modeling river water quality parameters using modified adaptive neuro fuzzy inference system. Water Sci. Eng. 2019, 12, 45–54. [Google Scholar] [CrossRef]
- Tutmez, B.; Hatipoglu, Z.; Kaymak, U. Modelling electrical conductivity of groundwater using an adaptive neuro-fuzzy inference system. Comput. Geosci. 2006, 32, 421–433. [Google Scholar] [CrossRef]
- Al-Mukhtar, M.; Al-Yaseen, F. Modeling water quality parameters using data-driven models, a case study Abu-Ziriq marsh in south of Iraq. Hydrology 2019, 6, 24. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).