Investigating Sediment Dynamics in a Landslide-Dominated Catchment by Modeling Landslide Area and Fluvial Sediment Export
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Development
2.1.1. Landslide Model
2.1.2. Sediment Transport Model
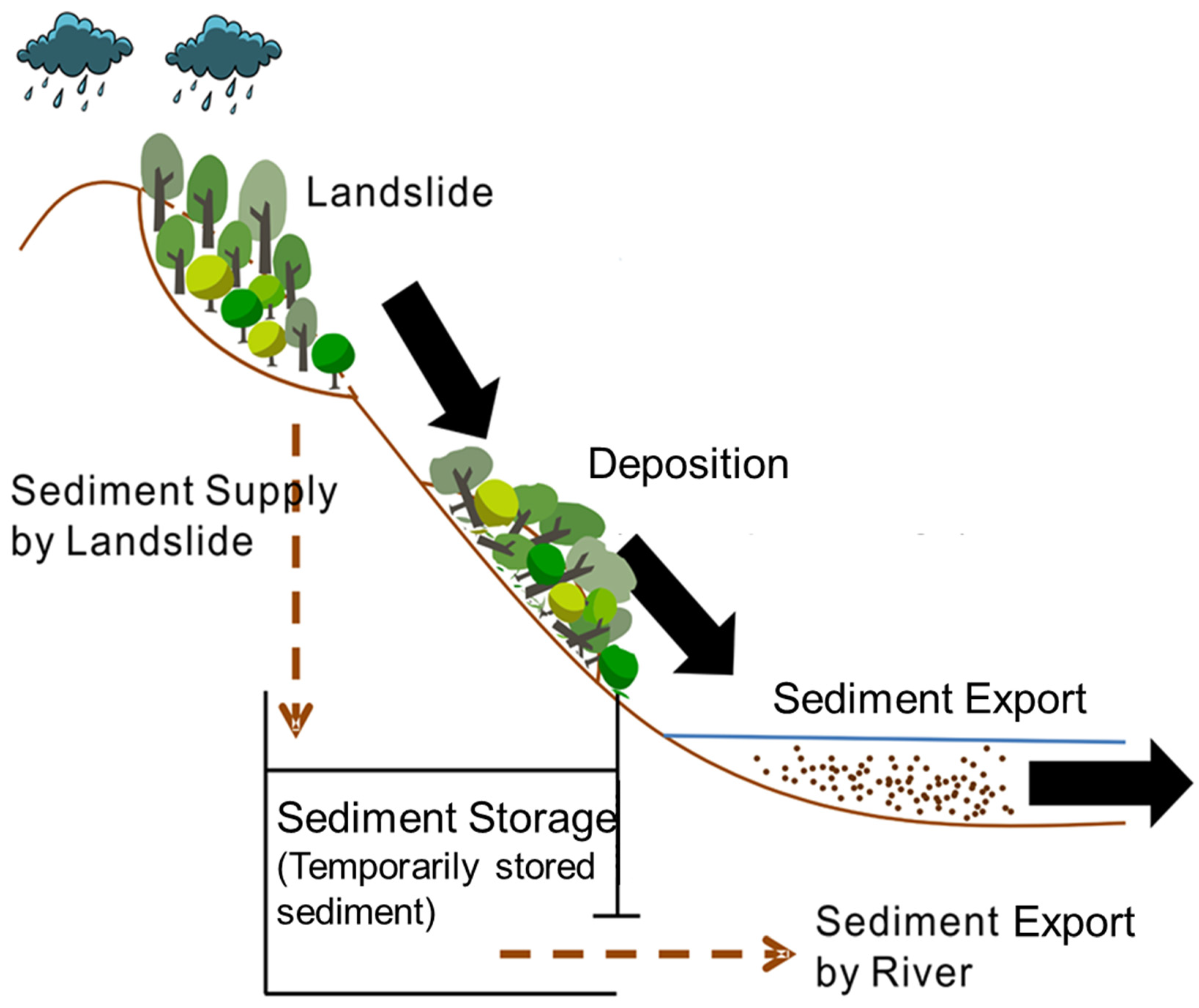
2.1.3. Sediment Storage
2.1.4. Calibration of Landslide and Sediment Transport Model
2.2. Study Area
2.3. Landslide Data
2.4. Hydrometric Data and Calculation of Sediment Transport
3. Results
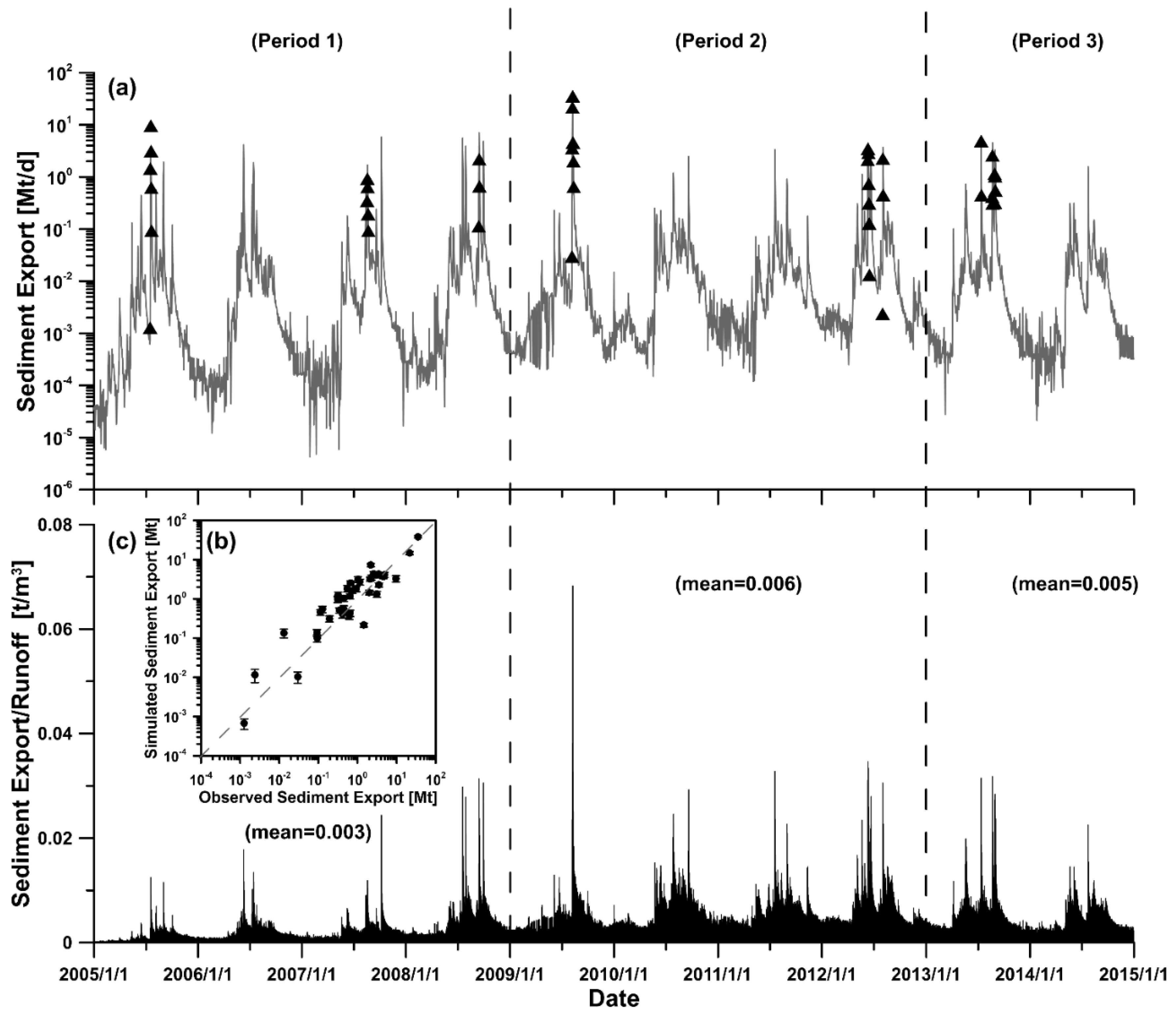
3.1. Observed Total Landslide Area and Sediment Export in Tsengwen Reservoir Watershed
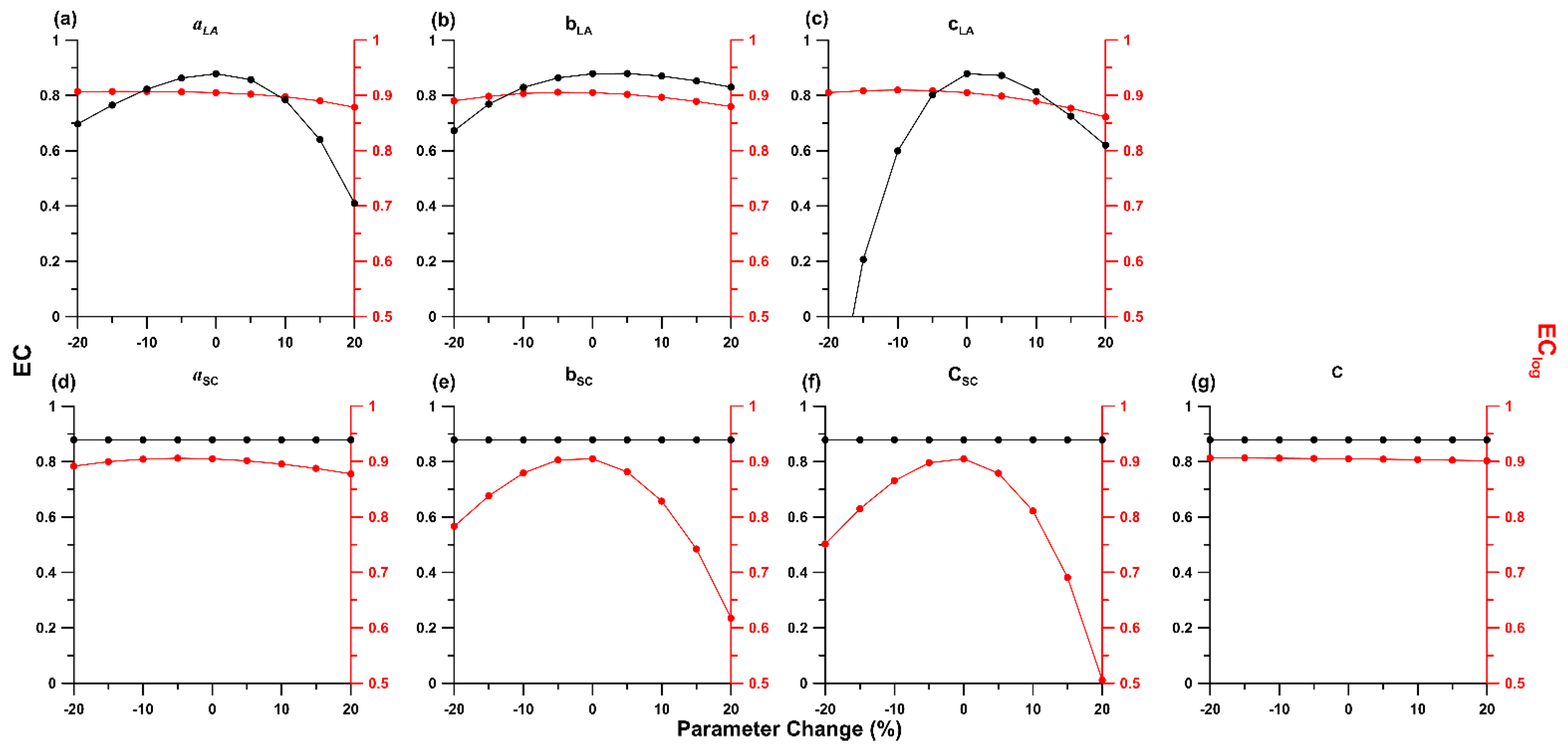
3.2. Calibration of Model Parameters
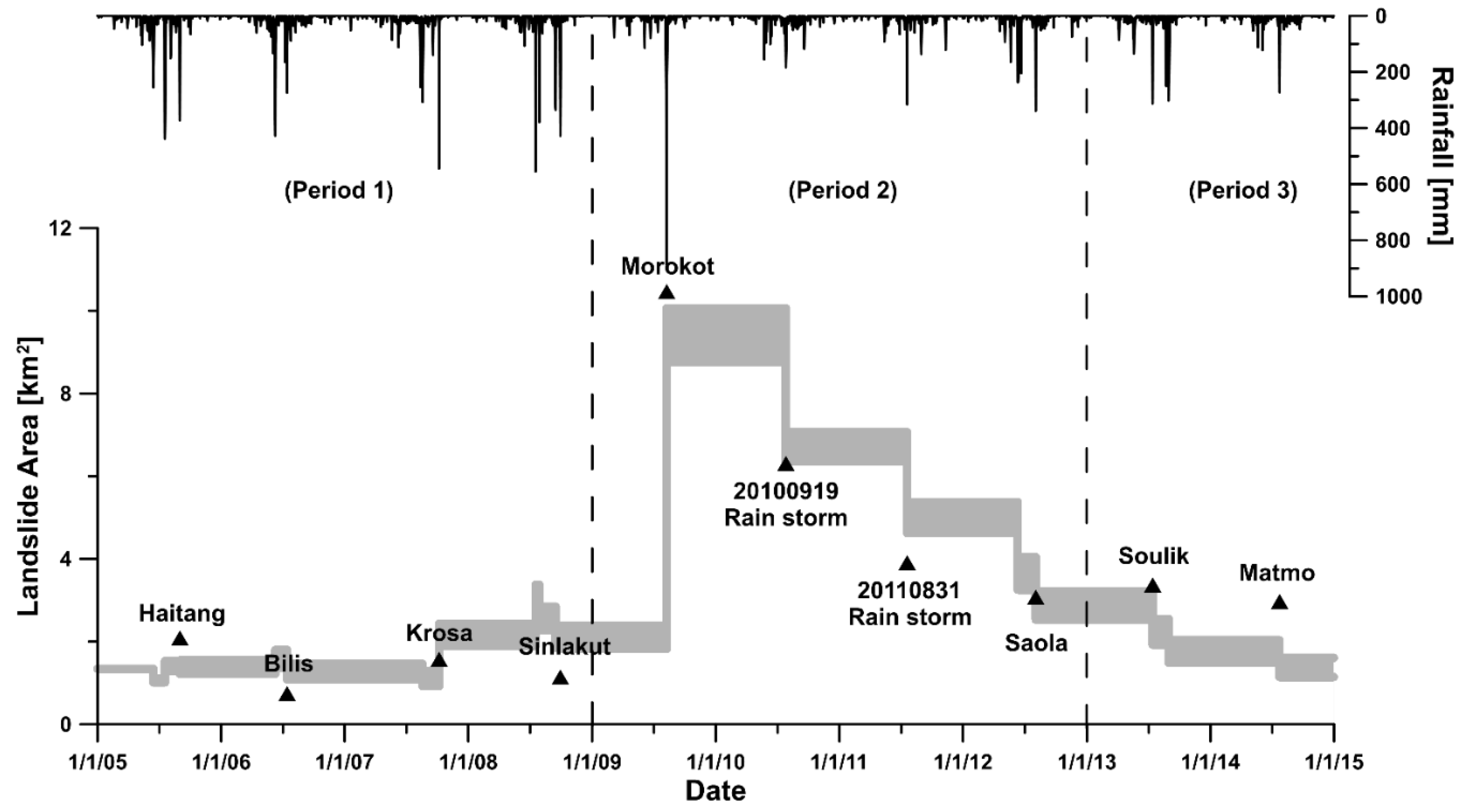
3.3. Simulated Time-Series Total Landslide Area
3.4. Simulated Sediment Export
4. Discussion
4.1. Best-Fit Parameter Sets
4.2. Sensitivity Analysis
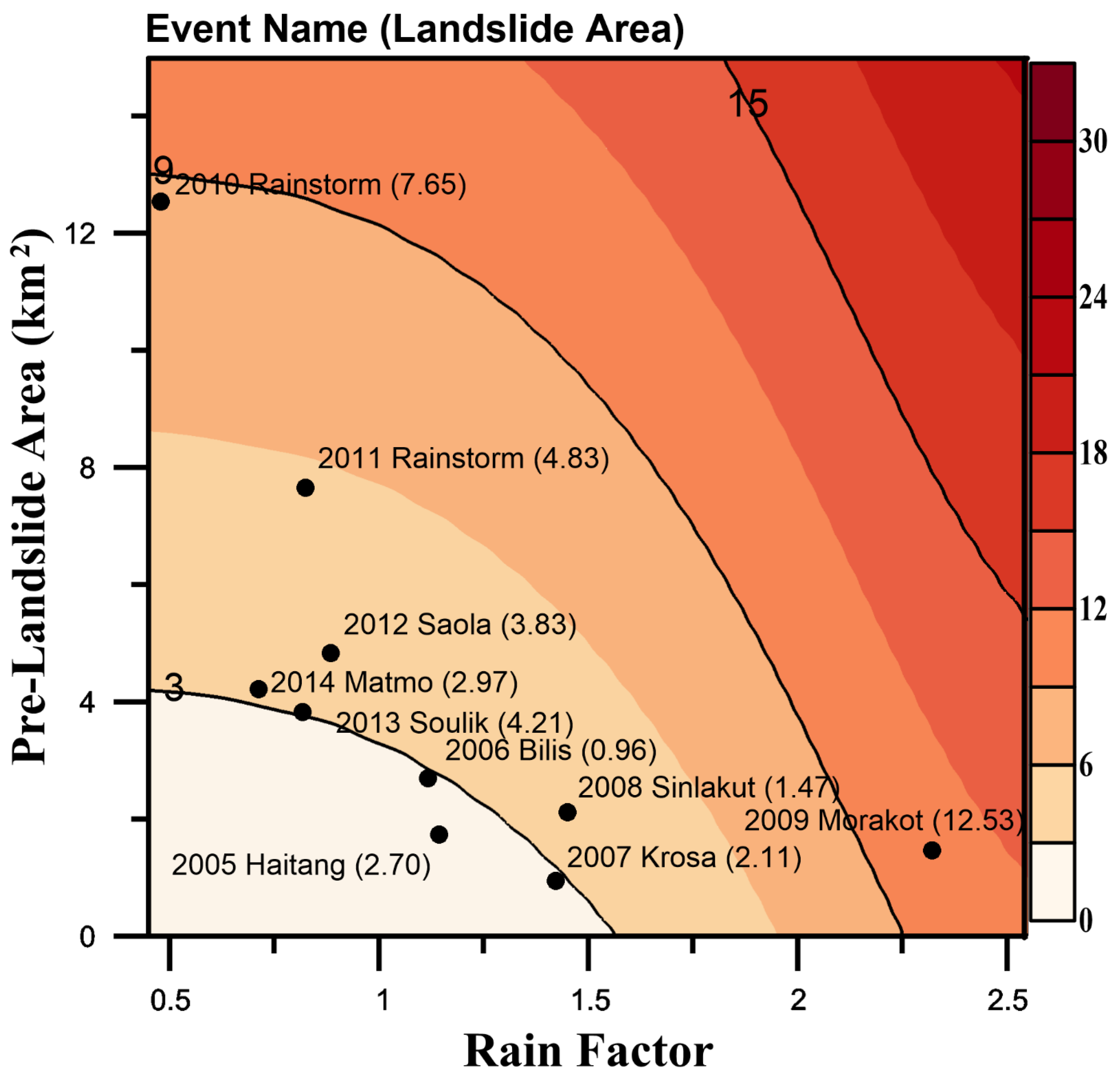
4.3. The Controlling Factors of Total Landslide Area
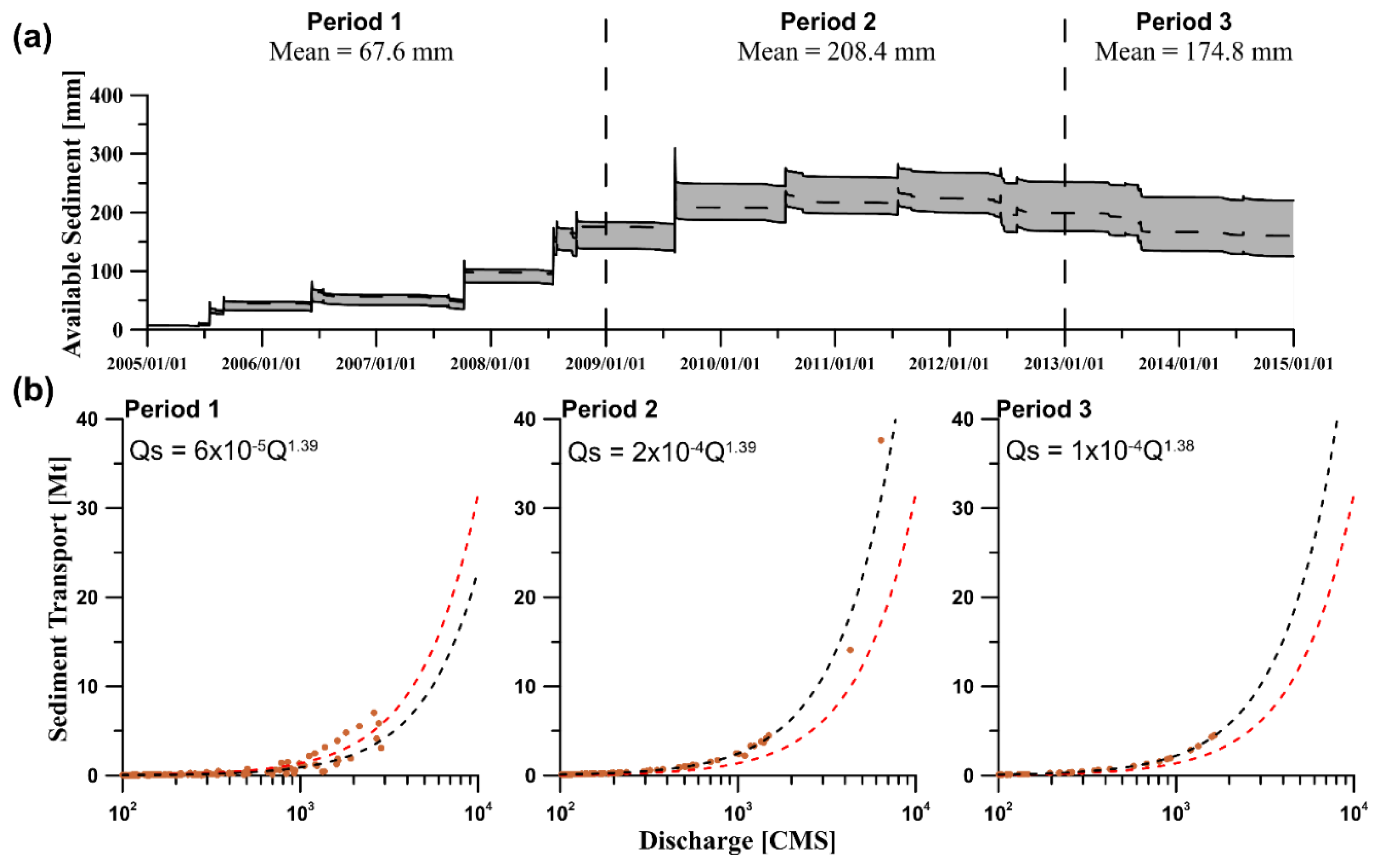
4.4. The Sediment Storage and Controlling Factors of Sediment Export
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dadson, S.; Hovius, N.; Chen, H.; Dade, W.B.; Hsieh, M.-L.; Willett, S.D.; Hu, J.-C.; Horng, M.-J.; Chen, M.-C.; Stark, C.P.; et al. Links between erosion, runoff variability and seismicity in the Taiwan orogen. Nat. Cell Biol. 2003, 426, 648–651. [Google Scholar] [CrossRef]
- Schmidt, J.C.; Parnell, R.A.; Grams, P.E.; Hazel, J.E.; Kaplinski, M.A.; Stevens, L.E.; Hoffnagle, T.L. The 1996 controlled flood in Grand Canyon: Flow, sediment transport, and geomorphic change. Ecol. Appl. 2001, 11, 657–671. [Google Scholar] [CrossRef]
- West, A.J.; Galy, A.; Bickle, M. Tectonic and climatic controls on silicate weathering. Earth Planet. Sci. Lett. 2005, 235, 211–228. [Google Scholar] [CrossRef]
- Neil, D.T.; Orpin, A.R.; Ridd, P.V.; Yu, B. Sediment yield and impacts from river catchments to the Great Barrier Reef lagoon: A review. Mar. Freshw. Res. 2002, 53, 733–752. [Google Scholar] [CrossRef]
- Rabalais, N.N.; Turner, R.E.; Gupta, B.K.S.; Platon, E.; Parsons, M.L. Sediments Tell the History of Eutrophication and Hypoxia in the Northern Gulf of Mexico. Ecol. Appl. 2007, 17, S129–S143. [Google Scholar] [CrossRef]
- Hilton, R.G.; Galy, A.; Hovius, N.; Horng, M.-J.; Chen, H. The isotopic composition of particulate organic carbon in mountain rivers of Taiwan. Geochim. Cosmochim. Acta 2010, 74, 3164–3181. [Google Scholar] [CrossRef]
- Kao, S.-J.; Shiah, F.-K.; Wang, C.-H.; Liu, K.-K. Efficient trapping of organic carbon in sediments on the continental margin with high fluvial sediment input off southwestern Taiwan. Cont. Shelf Res. 2006, 26, 2520–2537. [Google Scholar] [CrossRef]
- Galy, V.; France-Lanord, C.; Lartiges, B. Loading and fate of particulate organic carbon from the Himalaya to the Ganga–Brahmaputra delta. Geochim. Cosmochim. Acta 2008, 72, 1767–1787. [Google Scholar] [CrossRef]
- Hilton, R.G.; Galy, A.; Hovius, N.; Chen, M.-C.; Horng, M.-J.; Chen, H. Tropical-cyclone-driven erosion of the terrestrial biosphere from mountains. Nat. Geosci. 2008, 1, 759–762. [Google Scholar] [CrossRef]
- Hilton, R.G.; Galy, A.; Hovius, N.; Horng, M.-J.; Chen, H. Efficient transport of fossil organic carbon to the ocean by steep mountain rivers: An orogenic carbon sequestration mechanism. Geology 2011, 39, 71–74. [Google Scholar] [CrossRef]
- Kao, S.-J.; Liu, K.-K. Particulate organic carbon export from a subtropical mountainous river (Lanyang Hsi) in Taiwan. Limnol. Oceanogr. 1996, 41, 1749–1757. [Google Scholar] [CrossRef]
- Huang, J.-C.; Kao, S.-J.; Hsu, M.-L.; Lin, J.-C. Stochastic procedure to extract and to integrate landslide susceptibility maps: An example of mountainous watershed in Taiwan. Nat. Hazards Earth Syst. Sci. 2006, 6, 803–815. [Google Scholar] [CrossRef]
- Lee, T.-Y.; Huang, J.-C.; Lee, J.-Y.; Jien, S.-H.; Zehetner, F.; Kao, S.-J. Magnified Sediment Export of Small Mountainous Rivers in Taiwan: Chain Reactions from Increased Rainfall Intensity under Global Warming. PLoS ONE 2015, 10, e0138283. [Google Scholar] [CrossRef] [PubMed]
- Kao, S.J.; Huang, J.C.; Lee, T.Y.; Liu, C.C.; Walling, D.E. The changing rainfall–runoff dynamics and sediment response of small mountainous rivers in Taiwan under a warming climate. In Sediment Problems and Sediment Management in Asian River Basins; (IAHS Publ 349); IAHS Press: Wallingford, UK, 2011. [Google Scholar]
- Milliman, J.D.; Syvitski, J.P. Geomorphic/Tectonic Control of Sediment Discharge to the Ocean: The Importance of Small Mountainous Rivers. J. Geol. 1992, 100, 525–544. [Google Scholar] [CrossRef]
- Milliman, J.D.; Farnsworth, K.L. River Discharge to the Coastal Ocean: A Global Synthesis; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Kao, S.-J.; Lee, T.-Y.; Milliman, J.D. Calculating Highly Fluctuated Suspended Sediment Fluxes from Mountainous Rivers in Taiwan. Terr. Atmos. Ocean. Sci. 2005, 16, 653. [Google Scholar] [CrossRef]
- Lee, T.-Y.; Huang, J.-C.; Kao, S.-J.; Tung, C.-P. Temporal variation of nitrate and phosphate transport in headwater catchments: The hydrological controls and land use alteration. Biogeosciences 2013, 10, 2617–2632. [Google Scholar] [CrossRef]
- Fuller, C.W.; Willett, S.D.; Hovius, N.; Slingerland, R. Erosion Rates for Taiwan Mountain Basins: New Determinations from Suspended Sediment Records and a Stochastic Model of Their Temporal Variation. J. Geol. 2003, 111, 71–87. [Google Scholar] [CrossRef]
- Milliman, J.D.; Lee, T.Y.; Huang, J.-C.; Kao, S.J. Temporal and spatial responses of river discharge to tectonic and climatic perturbations: Choshui River, Taiwan, and Typhoon Mindulle (2004). Proc. Int. Assoc. Hydrol. Sci. 2015, 367, 29–39. [Google Scholar] [CrossRef][Green Version]
- Van Sickle, J.; Beschta, R.L. Supply-based models of suspended sediment transport in streams. Water Resour. Res. 1983, 19, 768–778. [Google Scholar] [CrossRef]
- Hovius, N.; Stark, C.P.; Allen, P.A. Sediment flux from a mountain belt derived by landslide mapping. Geology 1997, 25, 231–234. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide inventories and their statistical properties. Earth Surf. Process. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
- Amos, K.J.; Alexander, J.; Horn, A.; Pocock, G.D.; Fielding, C.R. Supply limited sediment transport in a high-discharge event of the tropical Burdekin River, North Queensland, Australia. Sedimentology 2004, 51, 145–162. [Google Scholar] [CrossRef]
- Lin, G.-W.; Chen, H.; Chen, Y.-H.; Horng, M.-J. Influence of typhoons and earthquakes on rainfall-induced landslides and suspended sediments discharge. Eng. Geol. 2008, 97, 32–41. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Chang, K.-T.; Chiu, Y.-J.; Lau, S.-M.; Lee, H.-Y. Quantifying rainfall controls on catchment-scale landslide erosion in Taiwan. Earth Surf. Process. Landf. 2013, 38, 372–382. [Google Scholar] [CrossRef]
- Aerial Survey Office, Taiwan Forestry Bureau. Report of Aerial Survey of Landslide in Tsengwen Reservoir Watershed; Management Bureau of Tsengwen Reservoir, Taiwan Press: Taipei, Taiwan, 1980. [Google Scholar]
- Turowski, J.M.; Rickenmann, D.; Dadson, S.J. The partitioning of the total sediment load of a river into suspended load and bedload: A review of empirical data. Sedimentology 2010, 57, 1126–1146. [Google Scholar] [CrossRef]
- Madsen, H. Automatic calibration of a conceptual rainfall–runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Li, Y.-H. Denudation of Taiwan Island since the Pliocene Epoch. Geology 1976, 4, 105–108. [Google Scholar] [CrossRef]
- Milliman, J.D.; Meade, R.H. World-Wide Delivery of River Sediment to the Oceans. J. Geol. 1983, 91, 1–21. [Google Scholar] [CrossRef]
- Liu, C.-C. Processing of FORMOSAT-2 Daily Revisit Imagery for Site Surveillance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3206–3214. [Google Scholar] [CrossRef]
- Liu, C.-C.; Shieh, C.-L.; Lin, J.-C.; Wu, A.-M. Classification of non-vegetated areas using Formosat-2 high spatiotemporal imagery: The case of Tseng-Wen Reservoir catchment area (Taiwan). Int. J. Remote Sens. 2011, 32, 8519–8540. [Google Scholar] [CrossRef]
- Milliman, J.D.; Lin, S.-W.; Kao, S.-J.; Liu, J.-P.; Liu, C.-S.; Chiu, J.-K.; Lin, Y.-C. Short-term changes in seafloor character due to flood-derived hyperpycnal discharge: Typhoon Mindulle, Taiwan, July 2004. Geology 2007, 35, 779. [Google Scholar] [CrossRef]
- Chen, H.; Lin, G.-W.; Lu, M.-H.; Shih, T.-Y.; Horng, M.-J.; Wu, S.-J.; Chuang, B. Effects of topography, lithology, rainfall and earthquake on landslide and sediment discharge in mountain catchments of southeastern Taiwan. Geomorphology 2011, 133, 132–142. [Google Scholar] [CrossRef]
- Asselman, N. Fitting and interpretation of sediment rating curves. J. Hydrol. 2000, 234, 228–248. [Google Scholar] [CrossRef]
- Tsai, Z.-X.; You, G.J.-Y.; Lee, H.-Y.; Chiu, Y.-J. Use of a total station to monitor post-failure sediment yields in landslide sites of the Shihmen reservoir watershed, Taiwan. Geomorphology 2012, 139, 438–451. [Google Scholar] [CrossRef]
- Clapuyt, F.; Vanacker, V.; Christl, M.; Van Oost, K.; Schlunegger, F. Spatio-temporal dynamics of sediment transfer systems in landslide-prone Alpine catchments. Solid Earth 2019, 10, 1489–1503. [Google Scholar] [CrossRef]
- Koi, T.; Hotta, N.; Ishigaki, I.; Matuzaki, N.; Uchiyama, Y.; Suzuki, M. Prolonged impact of earthquake-induced landslides on sediment yield in a mountain watershed: The Tanzawa region, Japan. Geomorphology 2008, 101, 692–702. [Google Scholar] [CrossRef]
- Hovius, N.; Meunier, P.; Lin, C.-W.; Chen, H.; Chen, Y.-G.; Dadson, S.; Horng, M.-J.; Lines, M. Prolonged seismically induced erosion and the mass balance of a large earthquake. Earth Planet. Sci. Lett. 2011, 304, 347–355. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Wu, Y.-H.; Shen, C.-W.; Chiu, Y.-J. Dynamic Modeling of Sediment Budget in Shihmen Reservoir Watershed in Taiwan. Water 2018, 10, 1808. [Google Scholar] [CrossRef]
- Zhang, F.; Jin, Z.; West, A.J.; An, Z.; Hilton, R.G.; Wang, J.; Li, G.; Densmore, A.L.; Yu, J.; Qiang, X.; et al. Monsoonal control on a delayed response of sedimentation to the 2008 Wenchuan earthquake. Sci. Adv. 2019, 5, eaav7110. [Google Scholar] [CrossRef]
- Lisle, T.E.; Church, M. Sediment transport-storage relations for degrading, gravel bed channels. Water Resour. Res. 2002, 38, 1-1-1-14. [Google Scholar] [CrossRef]
- Chang, C.-T.; Wang, L.-J.; Huang, J.-C.; Liu, C.-P.; Wang, C.-P.; Lin, N.-H.; Wang, L.; Lin, T.-C. Precipitation controls on nutrient budgets in subtropical and tropical forests and the implications under changing climate. Adv. Water Resour. 2017, 103, 44–50. [Google Scholar] [CrossRef]
- Syvitski, J.P.; Burrell, D.C.; Skei, J.M. Fjords: Processes and Products; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Claude, N.; Rodrigues, S.; Bustillo, V.; Breheret, J.-G.; Macaire, J.-J.; Jugé, P. Estimating bedload transport in a large sand–gravel bed river from direct sampling, dune tracking and empirical formulas. Geomorphology 2012, 179, 40–57. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, M.E.; Syvitski, J.P. Sediment transport and terrigenous fluxes. Sea 1998, 10, 253–292. [Google Scholar]

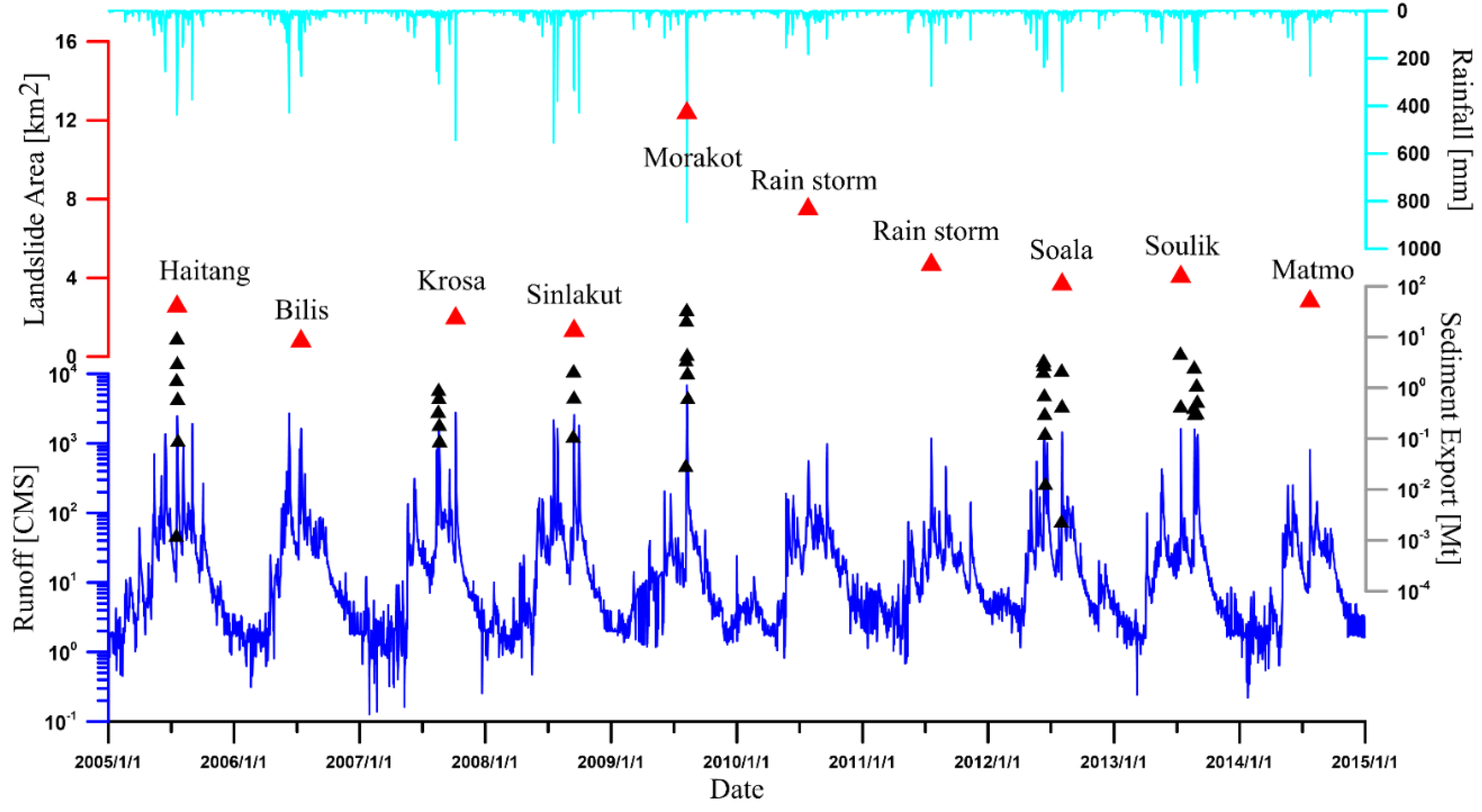
| Rainstorm | Date | Max Daily Rainfall (mm) | Max Daily Discharge (m3 s−1) | Date of Landslide Map | Total Landslide Area (km2) |
|---|---|---|---|---|---|
| Haitang | 20/7/2005 | 437.4 | 2475.2 | 27/6/2006 | 2.70 |
| Bilis | 15/7/2006 | 427.1 | 2698.1 | 3/7/2007 | 0.94 |
| Krosa | 7/10/2007 | 544.1 | 2770.1 | 19/1/2008 | 2.11 |
| Sinlakut | 15/9/2008 | 554.6 | 2572.5 | 10/122008 | 1.47 |
| Morakot | 9/8/2009 | 887.9 | 6814.9 | 1/4/2010 | 12.53 |
| Rainstorm | 19/9/2010 | 183.0 | 979.1 | 16/4/2011 | 7.65 |
| Rainstorm | 31/8/2011 | 315.5 | 1175.3 | 28/6/2012 | 4.83 |
| Saola | 3/8/2012 | 338.4 | 1491.1 | 3/6/2013 | 3.83 |
| Soulik | 14/7/2013 | 312.4 | 1615.7 | 10/4/2014 | 4.21 |
| Matmo | 25/7/2014 | 272.3 | 808.3 | 9/6/2015 | 2.97 |
| ID | Typhoon Name | Sampling Period | Numbers of Sample | Maximum Sampled Sediment Concentration (g L−1) | Maximum Sampled Discharge (m3 s−1) | Rating Curve F(g s−1) = aQb | R2 | Bias Correction Factor | Sediment Export (Mt) | |
|---|---|---|---|---|---|---|---|---|---|---|
| From | To | |||||||||
| 2005 | Haitang | N.A. | N.A. | 61 | 16.32 | 1208 | 24.61Q1.89 | 0.83 | 0.21 | 14.97 |
| 2007 | Sepat | N.A. | N.A. | 42 | 9.01 | 1307 | 766.32Q1.27 | 0.76 | 0.10 | 2.21 |
| 2008 | Sinlakut | 14/9/2008 01:00 | 15/9/2008 18:00 | 43 | 14.91 | 4251 | 78.19Q1.61 | 0.93 | 0.02 | 2.97 |
| 2009 | Morakot | N.A. | N.A. | 49 | 68.20 | 5797 | 5011.1Q1.28 | 0.95 | 0.01 | 67.57 |
| 2012 | Rainstorm | 11/6/2012 17:00 | 14/6/2012 14:00 | 31 | 38.72 | 2314 | 1.92Q2.28 | 0.91 | 0.08 | 9.67 |
| 2012 | Saola | 1/8/2012 14:00 | 3/8/2012 12:00 | 19 | 25.54 | 2634 | 142.57Q1.63 | 0.99 | 0.11 | 2.72 |
| 2013 | Sulik | 13/7/2013 06:00 | 14/7/2013 09:00 | 15 | 56.71 | 2712 | 520.28Q1.55 | 0.94 | 0.03 | 5.34 |
| 2013 | Trami | 22/8/2013 00:00 | 23/8/2013 10:00 | 17 | 33.60 | 2303 | 4.00Q2.13 | 0.96 | 0.01 | 3.33 |
| 2013 | Kong-rey | 29/8/2013 10:00 | 31/8/2013 12:00 | 24 | 18.33 | 2743 | 24.91Q1.81 | 0.94 | 0.01 | 2.03 |
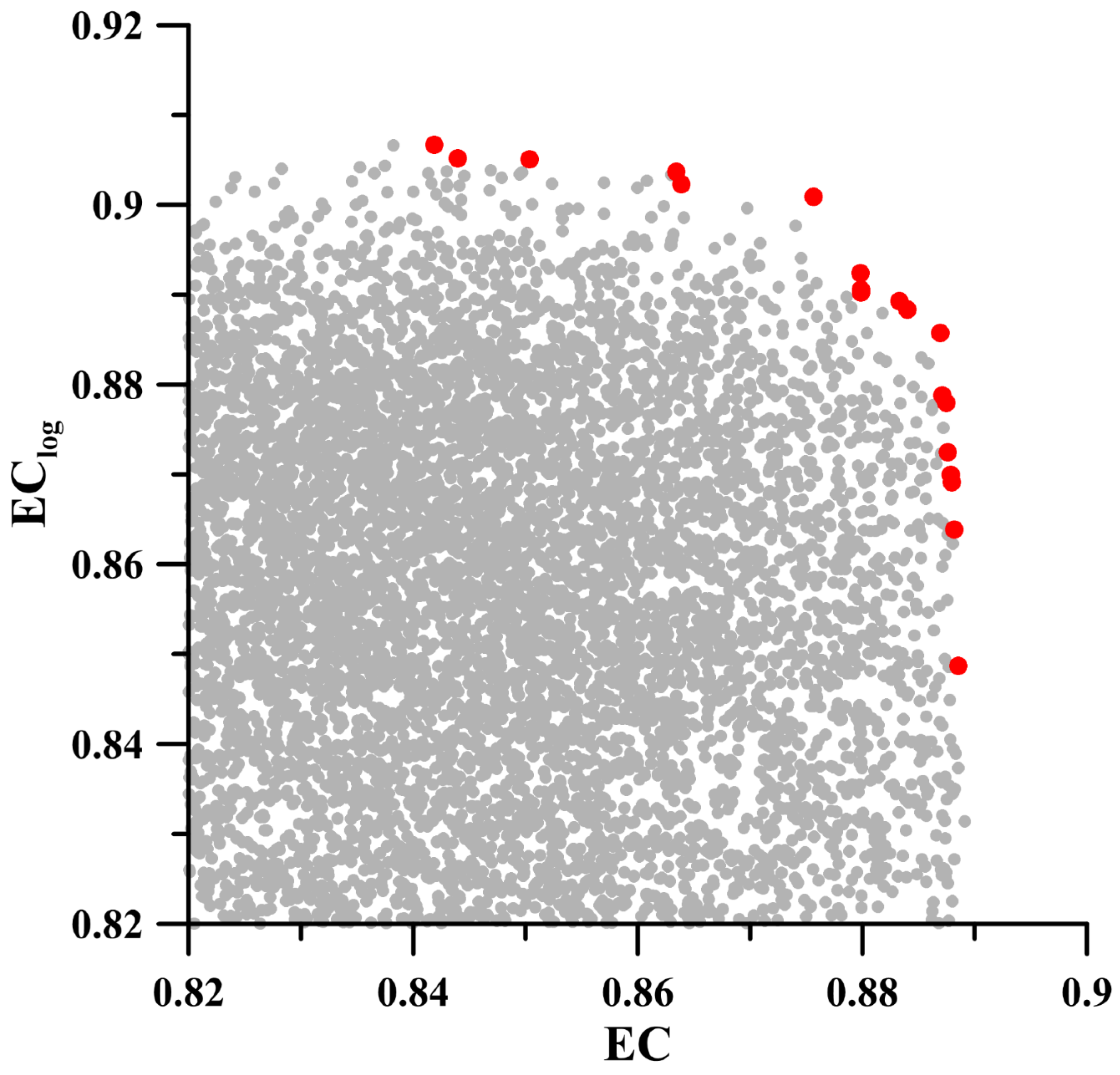
| aLA | bLA | cLA | aSC | bSC | cSC | C | EC | EClog | |
|---|---|---|---|---|---|---|---|---|---|
| Range | 0.6–0.8 | 0.3–0.5 | 3–5 | 0.1–0.3 | 0.7–0.9 | 0.3–0.5 | 0.8–1 | - | - |
| 1 | 0.70 | 0.50 | 3.26 | 0.20 | 0.71 | 0.33 | 0.88 | 0.88 | 0.91 |
| 2 | 0.72 | 0.39 | 3.57 | 0.11 | 0.72 | 0.40 | 0.91 | 0.89 | 0.90 |
| 3 | 0.68 | 0.46 | 3.46 | 0.13 | 0.71 | 0.38 | 0.94 | 0.88 | 0.91 |
| 4* | 0.72 | 0.39 | 3.62 | 0.15 | 0.71 | 0.36 | 0.86 | 0.89 | 0.90 |
| 5 | 0.73 | 0.32 | 3.86 | 0.19 | 0.75 | 0.33 | 0.96 | 0.89 | 0.88 |
| 6 | 0.69 | 0.48 | 3.42 | 0.20 | 0.70 | 0.33 | 0.82 | 0.88 | 0.91 |
| 7 | 0.72 | 0.35 | 3.73 | 0.12 | 0.73 | 0.37 | 0.87 | 0.89 | 0.89 |
| 8 | 0.72 | 0.36 | 3.70 | 0.10 | 0.76 | 0.39 | 0.93 | 0.89 | 0.89 |
| 9 | 0.69 | 0.42 | 3.58 | 0.11 | 0.72 | 0.40 | 0.99 | 0.89 | 0.90 |
| 10 | 0.74 | 0.31 | 3.89 | 0.17 | 0.78 | 0.33 | 0.99 | 0.89 | 0.87 |
| 11 | 0.73 | 0.30 | 3.92 | 0.16 | 0.80 | 0.30 | 0.98 | 0.89 | 0.86 |
| 12 | 0.70 | 0.43 | 3.56 | 0.11 | 0.73 | 0.39 | 1.00 | 0.89 | 0.90 |
| 13 | 0.72 | 0.48 | 3.19 | 0.15 | 0.70 | 0.37 | 0.84 | 0.87 | 0.91 |
| 14 | 0.68 | 0.44 | 3.53 | 0.13 | 0.71 | 0.38 | 0.81 | 0.88 | 0.91 |
| 15 | 0.68 | 0.50 | 3.27 | 0.24 | 0.71 | 0.31 | 0.81 | 0.88 | 0.91 |
| 16 | 0.73 | 0.37 | 3.65 | 0.17 | 0.70 | 0.35 | 0.84 | 0.89 | 0.89 |
| 17 | 0.72 | 0.38 | 3.64 | 0.14 | 0.70 | 0.37 | 0.89 | 0.89 | 0.90 |
| 18 | 0.74 | 0.35 | 3.70 | 0.14 | 0.70 | 0.38 | 0.93 | 0.89 | 0.90 |
| 19 | 0.71 | 0.45 | 3.44 | 0.13 | 0.71 | 0.38 | 0.88 | 0.89 | 0.90 |
| 20 | 0.70 | 0.46 | 3.38 | 0.18 | 0.71 | 0.34 | 0.91 | 0.88 | 0.91 |
| 21 | 0.74 | 0.30 | 3.88 | 0.10 | 0.70 | 0.42 | 1.00 | 0.89 | 0.89 |
| 22 | 0.70 | 0.42 | 3.55 | 0.17 | 0.71 | 0.35 | 0.91 | 0.89 | 0.90 |
| 23 | 0.72 | 0.38 | 3.64 | 0.14 | 0.75 | 0.35 | 0.87 | 0.89 | 0.89 |
| Avg. | 0.71 | 0.40 | 3.58 | 0.15 | 0.72 | 0.36 | 0.91 | 0.88 | 0.90 |
| Std. | 0.02 | 0.06 | 0.20 | 0.03 | 0.03 | 0.03 | 0.06 | 0.01 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, T.-Y.; Huang, J.-C.; Lee, T.-Y.; Chen, Y.-C.; Jan, M.-Y.; Liu, C.-C. Investigating Sediment Dynamics in a Landslide-Dominated Catchment by Modeling Landslide Area and Fluvial Sediment Export. Water 2020, 12, 2907. https://doi.org/10.3390/w12102907
Teng T-Y, Huang J-C, Lee T-Y, Chen Y-C, Jan M-Y, Liu C-C. Investigating Sediment Dynamics in a Landslide-Dominated Catchment by Modeling Landslide Area and Fluvial Sediment Export. Water. 2020; 12(10):2907. https://doi.org/10.3390/w12102907
Chicago/Turabian StyleTeng, Tse-Yang, Jr-Chuan Huang, Tsung-Yu Lee, Yi-Chin Chen, Ming-Young Jan, and Cheng-Chien Liu. 2020. "Investigating Sediment Dynamics in a Landslide-Dominated Catchment by Modeling Landslide Area and Fluvial Sediment Export" Water 12, no. 10: 2907. https://doi.org/10.3390/w12102907
APA StyleTeng, T.-Y., Huang, J.-C., Lee, T.-Y., Chen, Y.-C., Jan, M.-Y., & Liu, C.-C. (2020). Investigating Sediment Dynamics in a Landslide-Dominated Catchment by Modeling Landslide Area and Fluvial Sediment Export. Water, 12(10), 2907. https://doi.org/10.3390/w12102907









